Evidence for wide range of time scales in oculomotor plant dynamics: Implications for models of eye-movement control

Abstract

Oculomotor-plant dynamics are not well characterised, despite their importance for modelling eye-movement control. We analysed the time course of the globe’s return after horizontal displacements in three rhesus monkeys lightly anaesthetised with ketamine. The eye-position traces were well fitted by a sum of four exponentials (time constants 0.012, 0.099, 0.46, 7.8 s). The two long time-constant terms accounted for 25% of plant compliance, and led to a model that accounted for hitherto unexplained features of ocular motoneuron firing such as (i) hysteresis, and (ii) the inability of a 2 time-constant model to fit data for both fast and slow eye-movements.

1. Introduction

Eye movements are produced by neural commands acting on the tissues of the extraocular muscles (EOMs) and the globe. For convenience, these tissues are together referred to as the oculomotor ‘plant’, a term from control theory to denote that which is controlled. Characterising the dynamics of the oculomotor plant is a necessary first step for deciphering the neural commands that control eye movements. For example, the movement- related firing patterns of ocular motoneurons (OMNs) can only be understood by reference to plant dynamics (Cullen, Galiana, & Sylvestre, 2000; Delgado-Garcia, Del Pozo, & Baker, 1986; Fuchs, Scudder, & Kaneko, 1988; Keller, 1981; Ling, Fuchs, & Phillips, 1999; Ramachandran & Lisberger, 2003; Stahl & Simpson, 1995; Sylvestre & Cullen, 1999, 2002). Moreover, a description of the plant is required for any quantitative model of eye-movement control (e.g. Blazquez, Hirata, Heiney, Green, & Highstein, 2003; Enderle, Blanchard, & Bronzino, 1999; Galiana, 1990; Hirata & Highstein, 2001; Leung, Suh, & Kettner, 2000; Scudder, Kaneko, & Fuchs, 2002; Van Gisbergen & Van Opstal, 1989), and is central to those models that specifically address how eye-velocity commands are translated into motor commands by taking into account the mechanics of the plant (Dean, Porrill, & Stone, 2002; Goldstein & Robinson, 1984; Gomi et al., 1998; Optican & Miles, 1985; Skavenski & Robinson, 1973; Takemura, Inoue, Gomi, Kawato, &Kawano, 2001; Yamamoto, Kobayashi, Takemura, Kawano, & Kawato, 2002). Finally, although most of the above studies concern horizontal eye movements, recent investigations of orbital tissue anatomy have drawn particular attention to the importance of plant dynamics for understanding the neural control of eye movements in three dimensions (e.g. Angelaki & Hess, 2004; Demer, 2002; Porrill, Warren, & Dean, 2003).

Surprisingly, this widespread use of plant descriptions appears to be based on remarkably few actual measurements. The qualitative mechanics of the oculomotor plant were first described by Robinson (1964), who found that its inertia was of minor importance compared with its viscosity and elasticity, and that its passive viscoelastic characteristics could be approximated by Voigt elements in series (Fig. 1A). A Voigt element consists of a viscosity (c) and elasticity (k) in parallel, and its return motion after release from displacement is an exponential curve with a time constant (TC) of c/k (see Appendix A). Conveniently, Voigt elements in series generate a release motion that is a linear combination of exponential curves, the TC of each curve being the TC of the individual element (Fig. 1B). Thus, important characteristics of the oculomotor plant can be estimated from measurements of its behaviour when released from displacement. Nonetheless, despite the availability of this method, it has been used very sparingly to make direct measurements of oculomotor plant mechanics. In Robinson’s original study release trajectories were recorded, but appeared to be “made up of a distribution of time constants which cannot be resolved at this degree of recording accuracy” (Robinson, 1964, p. 251). The characteristics of the passive plant (two Voigt elements with TCs of 0.012 and 0.285 s) were instead derived from a complex model (Robinson, 1964, Fig. 5) that included the active elements of the extraocular muscles, and was subsequently assessed by its author as “very elementary” and designed to emphasise qualitative features of plant mechanics (Robinson, 1981, p. 35). Implementation of this model in fact gives release TCs for the system as a whole of 0.060 and 0.299 s (and a pair of complex poles with an associated TC of 0.005 s: unpublished results).

Fig. 1.

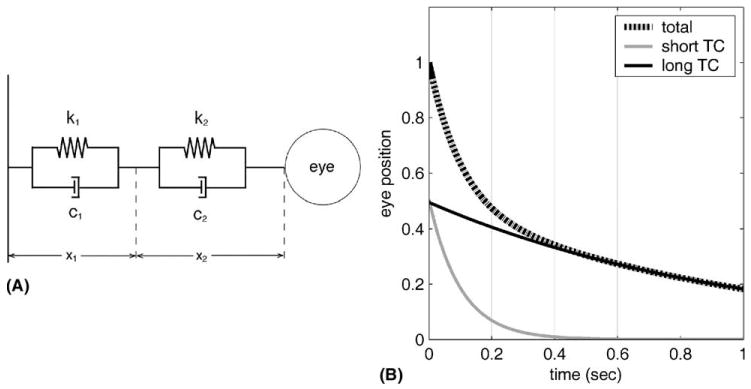
(A) Schematic of eyeball (right) attached to orbital wall (left) by two Voigt elements. Each Voigt element has an elastic element (k₁, k₂) and a viscous element (c₁, c₂). The lengths (x₁, x₂) of the Voigt elements are defined relative to length = 0 at the resting position. A change in eye position (i.e., eye rotation) from rest is associated with a change in length x = x₁ + x₂. (B) Behaviour of model in A with k₁ = k₂ = 0.5 gf/deg, the first TC = 0.1 s (c₁ = 0.05 gf/deg s⁻¹) and the second TC = 1 s (c₂ = 0.5 gf/deg s⁻¹). The eye has been held at an arbitrary position until the Voigt elements reached equilibrium, then released. Shown are the instantaneous lengths of two component Voigt elements (gray and black lines), which sum (hatched line) to determine eye position (‘total’), here measured as the fraction of original displacement. The short-TC element (0.1 s) accounts for almost all the movement for the first 0.3 s: subsequently, the contribution of the long-TC element (1 s) dominates.

Fig. 5.

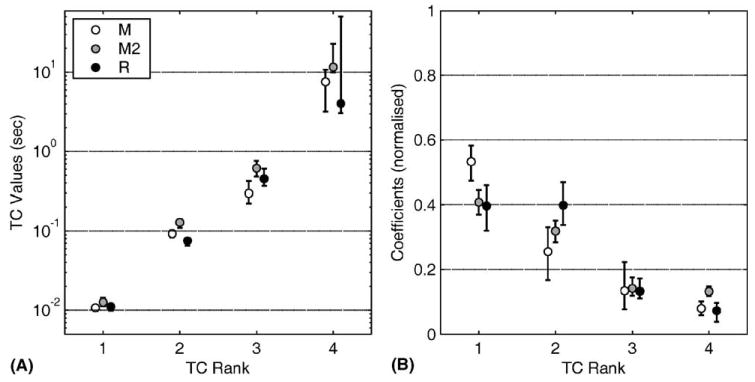
(A) The values for the best-fit four TCs for each of the three animals, plotted on a log scale. The error bars show 95% confidence limits derived by the bootstrap method. The upper confidence limit for the longest TC (rank 4) of animal R was plotted at 50 s for convenience, because its actual value was >10¹² s. (B) The values for the coefficients of the best-fit TCs shown in panel A. The error bars show 95% confidence limits derived by the bootstrap method (Section 2).

There have been four studies that report actual measurements of release TCs. A single eye-position trace was shown by Collins (1971, Fig. 28) to illustrate the release time course of the human globe (with horizontal recti detached). According to the figure legend this trace could be fitted by two exponential curves with TCs of 0.02 and 1 s. In a study of rhesus monkeys, Keller and Robinson (1971) attached a contact lens to one eye, and used it to rotate that eye while the animal was fixating on a target with the other, un-occluded, eye. The return movements could be approximated by a single exponential with a TC of 0.095 s (Keller & Robinson, 1971, p. 912). Pola and Robinson (1978) mention the effects of stimulating the medial longitudinal fasciculus with brief suprathreshold pulse trains. The eye “returned to near its original position with an exponential- like movement with an average time constant of about 68 ms” (p. 251). Finally, Seidman, Leigh, Tomsak, Grant, and Dell’Osso (1995) estimated release TCs in human subjects after abduction or torsional displacement. Although “a more complex model containing two time constants might more accurately describe the response” (p. 681), a first order model was sufficient for the main purpose of the experiment (the dynamics of the vestibulo-ocular reflex). For abduction, the single TC ranged in three subjects from 0.18 to 0.35 s.

It can be seen that, although there are only a few measurement-based estimates of plant TCs, they all manage to disagree with one other. The informal nature of the fitting techniques is probably responsible for some of the disagreement: because TC estimation tended to be subsidiary to the main point of the study, none of these reports provide figures that show both fitted curves and original data points, or describe the effects on fitting errors of varying the number of fitted TCs. This lack of systematic measurement and data-fitting means that we are not sure of the number or the values of the release TCs for the oculomotor plant. The main consequence of this uncertainty is that there are almost as many different plant descriptions as there are studies that use them, whether implicitly or explicitly (see references above).

The resulting confusion particularly affects studies of ocular motoneuron (OMN) firing rates. Early reports (Keller, 1981) approximated them by

$$\text{FR}=K\phi +R\frac{\text{d}\phi }{\text{d}t}-K{\phi }_0$$ (1)

where FR is firing rate, φ is eye-position, dφ/dt is eye velocity, φ₀ is the eye-position threshold at which the unit begins firing, and K and R are constants. Although both K and R were found to vary by more than ten-fold between OMNs, the ratio R/K varied much less, consistent with a first order plant (single Voigt element) with time constant R/K. However, subsequent measurements of smooth pursuit movements over the frequency range 0.3–2.0 Hz by Fuchs et al. (1988) showed that the values of the parameters R and K in Eq. (1) are constant only for eye movements of a particular frequency. Different frequencies required different parameters R and K in Eq. (1). The required parameter changes were not minor: the value of R/K ranged from approximately 220 ms (0.3 Hz) to 75 ms (2.0 Hz). This behaviour is incompatible with a single Voigt element, whose TC is independent of frequency, but could be produced by two Voigt elements in series (Fig. 1). Since the behaviour of a two element model becomes more dominated by the short TC element as frequency increases, it is qualitatively consistent with the results for OMN firing rates. In fact, Stahl and Simpson (1995) have simulated quantitatively the above variation of R/K with frequency using a two Voigt element model with TCs of 57 and 369 ms. However, these are higher than the TC values of 14–20 and 240–300 ms that have been used in two element models for saccades (Goldstein & Reinecke, 1994; Goldstein & Robinson, 1984; Optican & Miles, 1985), suggesting that models with two Voigt elements will also require different parameters when the frequency range of the eye-movements under consideration is extended sufficiently. This suggestion is consistent with the results of a recent major study that in effect identified the relevant best-fit parameters for a two-element model from OMN firing rates during both slow and rapid eye movements (Sylvestre & Cullen, 1999). No single set of parameters could be found that described the firing rates during the two types of movement.

An important first step in bringing order to this confusion would be more systematic measurements of plant behaviour covering the range of time scales appropriate for both fast and slow eye movements. The present study analysed data for the eye’s return after release from an eccentric horizontal position, originally gathered in a study of the horizontal neural integrator (Kaneko, 1997) in rhesus monkeys. The animals were anaesthetised with ketamine, which had two advantages: (i) it was possible to secure longer release traces than those obtained from alert subjects (usually interrupted by a saccade within 0.5 s), thus allowing better estimates of plant behaviour at long (1–10 s) time scales, and (ii) insofar as ketamine has relatively modest effects on the extraocular muscle (EOM) tone, the dynamics of the plant (orbital tissue plus EOMs) may resemble those of the alert animal (see Section 4). A novel fitting procedure was used to allow for the variability in the way the globe was initially perturbed, and the number of fitted TCs was varied systematically and related to fitting error.

The results indicated that four TCs, ranging from approximately 0.01 to 10 s, were required to fit the release trajectories, with the two longest TCs accounting for a substantial proportion, i.e. at least 25%, of total plant compliance (compliance is the reciprocal of stiffness—see Appendix A). The plausibility of these values was then assessed by constructing the corresponding four Voigt element plant model and showing that the neural control signals it required were qualitatively similar to those previously observed in a study of hysteresis in OMN firing rates (Goldstein & Robinson, 1986).

2. Materials and methods

2.1. Experimental procedure

Measurements were obtained from three juvenile rhesus monkeys M, R and M2 (Macaca mulatta). Two were the animals referred to as M and R in Kaneko (1997); all three had been implanted with a scleral search coil, a recording chamber and stabilising lugs. The location of the nucleus prepositus hypoglossi had been mapped with standard extracellular electrophysiological recording techniques in both M and R, but the nucleus itself had not been injected with ibotenic acid when these measurements were taken. The third animal M2 had been implanted only and trained to track the target spot.

Following calibration of eye movements by requiring the animals to fixate targets at known eccentricities, each animal was lightly anaesthetised with ketamine (~10 mg/kg). Ketamine was chosen so that the animal would tolerate mechanical manipulation of the globe and because it is a dissociative anaesthetic and should thus minimise the affects on normal activity level in brainstem structures. Topical anaesthetic could not be used because completely alert animals do not tolerate manipulation of the globe even when it is anaesthetised. The exact dosage was titrated to the minimum level necessary to allow the animal to tolerate manipulation of the globe. It was low enough to avoid precipitating the vertical nystagmus that often accompanies higher doses (e.g. 25 mg/kg). If the threshold for vertical nystagmus was exceeded measurements were postponed until a future session. Horizontal nystagmus was never observed.

After a sufficient anaesthesia level was attained, the coiled eye was deviated manually with small forceps to between 15° and 45° either medial or lateral in the horizontal plane and abruptly released. Care was taken to avoid vertical deviation by monitoring eye position via the coil output. Trials were excluded if the return to resting position could be seen not to follow a smooth velocity trajectory due to the occurrence of a blink, saccade or slow eye movement. The procedure was repeated until at least 12 suitable traces were collected for each animal. Eye position was sampled at 1 kHz.

2.2. Curve fitting

2.2.1. Preprocessing of traces

For each animal, the resting position of the eye (in each case lateral to the primary position) was estimated from inspection of all the eye-position traces. Traces that were interrupted within ~400 ms of release by discontinuities of slope (possibly corresponding to active components such as small saccades that are often associated with ketamine anaesthesia) were excluded from further analysis. Each remaining trace was fitted from the time of its maximum velocity, rather than from the time of release. In theory these two times should coincide for a pure viscoelastic system released instantaneously, i.e. the acceleration time should be zero. However, in the actual traces the time from release to peak velocity ranged from 8 to 20 ms, reflecting an unknown combination of (small) globe inertia and the release time of the forceps opening. Fitting from the time of peak velocity was an attempt to avoid these complexities: its effects on the estimated TCs are described in Section 3.

2.2.2. Group fitting of TCs

The behaviour of the eye after release was represented by

$$\phi (t)=A_1{\text{e}}^{-\frac{t}{T_1}}+A_2{\text{e}}^{-\frac{t}{T_2}}+\cdots +A_n{\text{e}}^{-\frac{t}{T_n}}$$ (2)

where φ(t) = position of the eye (relative to the resting position) at time t, T₁ … T_n are TCs, and A₁ … A_n are coefficients. Because the TCs T_i reflect intrinsic mechanical properties of the system, they should remain constant across releases, whereas the coefficients A_i depend on both the intrinsic mechanics of the system and the manner in which it is disturbed (e.g., a rapid pull and immediate release would produce a relatively greater contribution from mechanical elements with short TCs), and hence could vary from release to release (Appendix A). This reasoning leads to a procedure for fitting in which (a) all the suitable traces for an individual animal were fitted simultaneously with the same TCs T_i, and (b) each trace was allowed its own values of the coefficients A_i, calculated to minimise the least-squares fitting error for that individual trace (see Appendix A).

2.2.3. Optimisation of TCs

The above procedure determines the coefficients A_i required for a given set of TCs T_i. With both A_i and T_i known, the summed fitting error for all an animal’s traces can be calculated. The above steps thus constitute a procedure for calculating overall fitting error as a function of the TCs T_i. Consequently, the function can be minimised by numerical methods, in our case by using the MATLAB^™ function fminunc, which uses the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, a variable-metric minimisation method (Press, Teukolsky, Vetterling, & Flannery, 1992). The function is initialised with a plausible starting set of TCs (routinely varied to check for local minima), and returns the TC values that minimise the summed fitting error for the designated set of traces. This nonlinear fitting method is preferable to using linear methods based on the equation-error formulation, because the latter are well-known to lead to unacceptable estimation bias in the presence of noise (Ljung, 1999).

2.3. Statistical analysis

2.3.1. Principal component analysis (PCA)

An important question is whether the release data indicate an underlying system that is well described by a linear model. The solution of a generic stable nth-order linear system for zero input can be expressed as a linear combination of n exponentially decaying responses with coefficients determined by the initial values of the state variables. Hence for such a system the maximum possible dimensionality of a set of release curves is n. If in addition the release position is held stable for long enough to ensure that the state variables associated with small TCs come to their equilibrium values, then the observed dimensionality will be lower than n. This means that the release curves of a low order linear system necessarily form a set of low dimensionality. In contrast a set of release curves for a non-linear system will generally have full dimensionality (i.e the number of release curves) if the system is allowed to come fully to equilibrium, because the shape of the curve changes with amplitude and in general an infinite number of components are required to describe this change in shape.

This distinction suggests that principal component analysis, which allows measurement of the proportion of variance in the data accounted for by each principle component, could be a useful technique for distinguishing release curves generated by linear as opposed to non-linear systems. In practice the complications introduced by noisy data, limited variation in initial conditions, and small non-linearities, mean that unambiguously identifying non-linearity from limited data sets is still a research issue (cf. Schreiber & Schmitz, 1997). However, very low dimensionality for the present data would indicate that a low-order linear model for the underlying system was viable, and that any non-linearities were likely to be small.

A principal component analysis (PCA) was therefore performed to assess the linearity of our data, and the proportion of variance accounted for by the first few principal components was measured. Since PCA requires traces of equal length, and the traces for each animal were in fact of differing durations, either trace length has to be set to the minimum duration trace for each animal, or a small number of short traces must be discarded. The compromise procedure adopted here was to select a duration of 2.1 s for animal M (seven traces), 1.1 s for animal M2 (seven traces) and 1.4 s for animal R (six traces). Initial investigation suggested that the dependent variable of the analysis, i.e., the proportion of variance accounted for, was relatively insensitive to the precise duration selected.

2.3.2. Significance of additional TCs

The sum square (SS) fitting errors for the best TC estimates were calculated for each animal, for each number of TCs included in the fitting model. The most straightforward method of assessing the statistical significance of the reduction in SS error by the addition of a TC, which uses the F-statistic, has problems in this particular case. The p-values associated with the F-statistic distribution are based on the assumption that the residual noise is independent and normally distributed. If this is not the case, then the p-values are artefactually low so that the test gives false positives. To check for independence in the present data the mean autocorrelations of the residuals were plotted, and these were found to indicate the presence of structure on a 0.1–0.3 s time scale. In an attempt to counteract this effect, the data were resampled by taking every nth point until, after fitting, the residual structure was no longer apparent. The standard F-statistic was then used for the resampled data. It is worth noting that the presence of structure in these residuals makes it difficult to estimate model order using other procedures from system identification such as Akaike’s information theoretic criterion (Ljung, 1999).

2.3.3. Confidence intervals of measurements

Since standard methods for estimating confidence intervals also assume that there is no patterning of the residuals, their use is likely to lead to gross under-estimation of the confidence interval magnitudes in the present case. Accordingly, the bootstrap method (Press et al., 1992) was used to provide confidence limits for the TC estimates. In this procedure, the n traces for a given animal were sampled with replacement to provide 500 new sets of n traces (because the sampling was with replacement, some of the traces in any particular set could be duplicates). The best-fit TCs were estimated for each of the 500 new sets and the confidence limits taken as the 5th and 95th percentiles of the 500 estimates. This procedure was also applied to the coefficients of the best-fit TCs. In this case, each new set of n traces provides n coefficients per TC: it was the mean of these n coefficients that was taken as the value for that set. Thus, for the coefficients, confidence limits were taken as the 5th and 95th percentiles of these 500 means.

2.4. Terminology

Because the globe was displaced (approximately) horizontally, the resultant measurements relate to the stiffness and viscosity of the oculomotor plant close to the horizontal plane alone. Unless the plant dynamics are strictly isotropic, additional measurements for vertical and torsional displacements would also be required for a complete description (see Section 4). However, for brevity in what follows, and following conventions in other published material, this qualification is not further mentioned. Thus, terms such as “eye displacement”, or “time constant” should be taken as referring to “horizontal eye displacement” etc.

3. Results

The characteristics of the traces accepted for fitting are summarised in Table 1. It can be seen that overall ~38% of traces were discarded because of discontinuities occurring shortly after release of the globe (see Section 2), and that for each animal the amplitudes of the eye displacements in the accepted traces had a 1.5–1.9 fold range.

Table 1.

Summary of data that were analysed

		Time range (s)			Amplitude (deg)
Monkey	# traces	Min	Mean	Max	Min	Mean	Max
M	11/19 (6L)	0.51	1.32	2.43	30.6	41.6	47.5
M2	12/21 (3L)	0.74	2.44	6.57	28.5	33.7	43.1
R	9/12 (4L)	0.67	1.58	3.27	20.1	31.5	37.6

The second column shows the number of traces selected for analysis, compared with the total number of traces. The figure in brackets indicates how many traces were lateral pulls (that is, a medial return movement). The figures for the time range and amplitude refer to the selected traces.

3.1. Varying the number of time constants

The effects of varying the number of TCs used for fitting are illustrated in Fig. 2 by an example from animal R. Fig. 2A shows one of the nine traces for this animal, after all nine traces had been fitted simultaneously with the same two TCs. The RMS fitting error for the example shown is 0.27°. In Fig. 2B the same trace is shown fitted with four TCs (which again were identical for all the nine traces). The fit is visibly better with four TCs, an impression confirmed by the reduction in RMS fitting error to 0.087°.

Fig. 2.

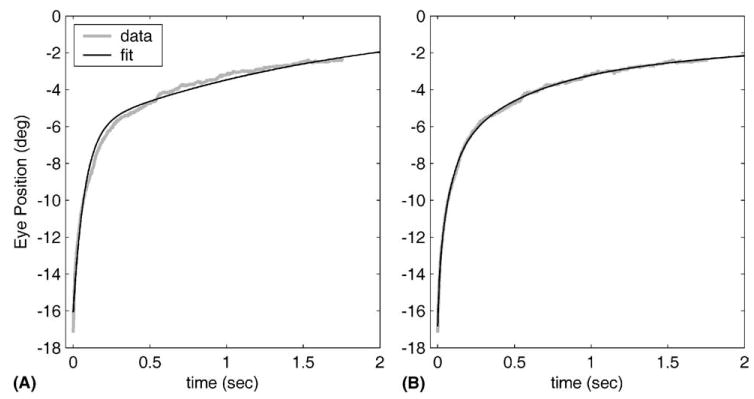
Results of fitting either two or four TCs to all nine traces from animal R, illustrated here by a single representative trace. Sign convention: medial displacements from the resting position are positive, lateral negative. (A) Best fit for two TCs (0.075 s and 1.46 s), which gave an RMS fitting error of 0.27°. (B) Best fit for four TCs (0.0111, 0.0752, 0.452, 4.05 s), which gave an RMS fitting error of 0.087°.

The effects on fitting errors of varying the number of TCs are shown for all animals in Fig. 3. The left panel (Fig. 3A) plots the sum squared fitting errors against number of TCs, starting with the original data (i.e., no TCs fitted). It can be seen that the slope of the plot appears fairly constant over the range 1–4 TCs and then decreases noticeably. Because the ordinate of the graph has a logarithmic scale, the roughly constant slope suggests that each successive time constant reduces the fitting error by a constant factor. This can be seen more clearly in the right panel (Fig. 3B), which shows the percent reduction in fitting error with each additional time constant. The reduction is 80–90% for 1–4 TCs, then at five TCs, drops to ~30%.

Fig. 3.

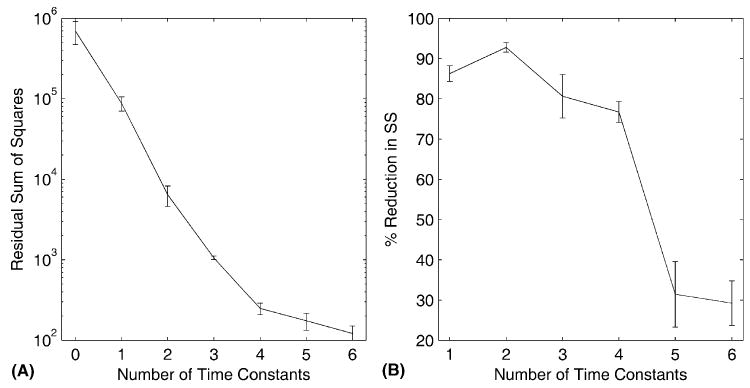
(A) Fitting errors plotted as a function of the number of TCs used for fitting. Fitting errors were calculated as the sum of squared errors for each animal’s data set. The value shown for zero fitted TC’s corresponds to the sum square amplitude of the original data sets before fitting. The plot shows group mean and the standard error of the mean. The y-axis uses a logarithmic scale. (B) The successive reduction in fitting error, expressed as a percentage, produced by fitting with each additional TC. The plot shows group mean and the standard error of the mean. The x-axis starts at one, corresponding to the reduction in variance of the original data sets produced by fitting a single TC.

The graphs shown in Fig. 3 suggest that four might be a suitable number of TCs to fit the present data. However, as explained in Section 2, it is not straightforward to demonstrate that this is the case with standard statistical methods. Use of the F-statistic in analysis of variance assumes that the residual fitting errors are independent, whereas for the present data the error at time step t tended to be correlated with that at time step t + 1. This lack of independence spuriously inflates the value of the F-statistic, leading to false positives in significance levels.

Two techniques were used to try and address this issue. First, the time interval over which the errors were correlated was assessed by plotting the mean autocorrelation of the residual fitting error for each animal. The data were then resampled at this time interval (range 120–300 ms), and the new fitting errors tested for significance. For all three animals the effects of fitting four TCs were significantly better than fitting with three TCs (F-ratios 11.5–23.8, p < 10⁻⁸), even though the number of data points were reduced by a factor of 120–300. The effects of subsequently fitting with five TCs were, however, significant only for one animal (M2, F-ratio 7.1, p < 10⁻⁸). Secondly, the data were subjected to the bootstrapping procedure (see Section 2), in order to assess the confidence limits of each TC estimate. This procedure indicated substantial overlap between estimates if five TCs were fitted, but not when four TCs were fitted (next section). We therefore selected four TCs to fit the present data sets (see Section 4).

3.2. Values for four time constants

Examples of the fits obtained with four TCs are given in Fig. 4, which shows the longest traces obtained for each animal. The fits appear quite close, with the main discrepancies tending to appear at the beginning and end of the trace. The TCs that produced the fits, together with their 95% confidence limits as assessed by the bootstrap method, are shown in Fig. 5A. It can be seen that the three animals behaved fairly similarly, with each having one TC around 10 ms (mean 12 ms), a second around 100 ms (mean 99 ms), a third around 500 ms (mean 460 ms) and a fourth much longer TC (mean 7.8 s). The confidence limits suggest that the precision of the TC estimates decreased as the magnitude of the TC increased: thus, the two shortest TCs appeared precisely estimated from these data, whereas the estimate of the longest TC was more uncertain. This is consistent with the fact that the duration of the longest TC (~8 s) was substantially longer than the mean duration of the traces used to estimate it (1.4–2.3 s, Table 1). It is important to emphasise, however, that despite this problem there was (as Fig. 5A shows) no overlap between the confidence limits of adjacent TC estimates for any of the three animals (see above).

Fig. 4.

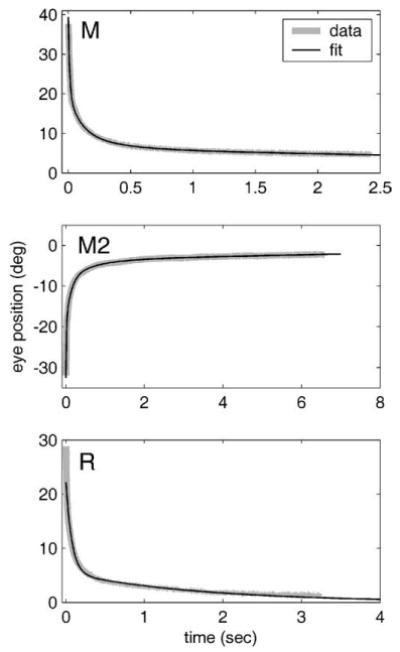
Illustrates the fit obtained with four TCs for the longest trace for each animal (M, M2, R). Sign convention: medial displacements from the resting position are positive, lateral negative.

3.3. Values for coefficients

For all three animals, the values of the coefficients for the fitted exponentials were linearly related to the initial position of the eye. The r² values were generally high (mean values for the three animals for each exponential, in order of increasing TC, were 0.91, 0.95, 0.87, and 0.83), with the coefficients for the longer TCs being less well determined as might be expected from both the duration of the traces, and the unstandardised displacement procedure.

The mean values and 95% confidence limits of the coefficients as derived by the bootstrap procedure are illustrated for each animal in Fig. 5B. This figure shows values for the coefficients that have been adjusted in two ways from those obtained by the original fitting method. First, the change in eye position between release and the time of peak velocity was added to the coefficient of the shortest TC for each trace. Because the coefficients correspond to the initial lengths of the corresponding Voigt elements, the initial length of the element with the shortest TC (~10 ms) would otherwise be underestimated because the early part of the trace (also ~10 ms) is not fitted (see Section 2). Secondly, for ease of comparison across animals, the values of the coefficients for a given trace were divided by their sum. This sum corresponds to the amplitude of the initial displacement, so that the adjusted coefficients were normalised (i.e., their sum equalled one) and thus independent of displacement amplitude. Fig. 5B indicates that for all three animals there is a tendency for the coefficients to decrease as the length of the corresponding TCs increase (mean coefficient values 0.45, 0.32, 0.14, 0.095 for TC estimates in order of increasing duration). Nonetheless, the coefficients for the two longest TCs sum to ~0.25. If the globe had been held long enough for the plant to reach equilibrium, then this value would correspond to 25% of the plant’s total (Appendix A). If not, then the value of 0.25 would be an underestimate of the compliance of the long TC elements. Thus, the present data indicate that at least 25% of the plant’s total compliance resides in elements with long TCs.

3.4. Robustness of time constant estimates

The possible dependence of the TC estimates on the methods used for fitting was examined by measuring the extent to which the estimates changed when the methods were altered.

1. The data were fitted from the time of release, that is, about 10–20 ms before the time of peak velocity. The main effects of this change were to double the value of the shortest TC, to produce inconsistent effects (between animals) on the other TCs, and to double the RMS fitting error (median change in time constants, starting from shortest = 91%, 11%, −2%, −3%; median change in RMS fitting error = 100%). The original method of fitting from the time of peak velocity therefore avoided some of the problems associated both with the globe’s inertia, and with release not being instantaneous (see Section 2), without systematically biasing the longer TC estimates.

2. Since other studies have typically used shorter duration traces than those used here, we looked at the effects on TC estimates of varying maximum trace duration. Fig. 6A shows the duration of the shortest TC estimate for both two and four fitted TCs. It can be seen that if four TCs are fitted, then the value of the shortest TC remains relatively stable as maximum trace duration increases from 0.5 to 2.5 s, and is similar in all three animals. However, if only two TCs are fitted, the value of the shortest TC increases markedly over this range, and differences in value between the three animals become large. A similar pattern is observed for the second shortest TC (Fig. 6B): in this case the increase in mean value when only two TCs are fitted is ~5 fold. The figure thus shows that values for the shortest two TCs are very markedly affected by trace duration over the range 0.5–2.5 s when two TCs are fitted, but are relatively unaffected when four TCs are fitted. The third shortest TC (not shown) is also relatively stable when four TCs are fitted (from 403 ms with 0.7 s traces to 509 ms with 2.5 s traces), whereas the longest TC values are markedly variable at trace durations less than ~1.6 s.

3. Since almost all approaches to modelling the oculomotor plant assume that the system is linear, we assessed the linearity of the present data by carrying out principal component analysis (see Section 2). The first principal component accounted for more than 97.3–99.4% of the variance for three animals; the first two principal components together accounted for >99.7% of the variance in all three animals. This implies that, despite wide differences in initial conditions, all traces could be represented to high accuracy as a linear combination of just two components and this suggests that, over the amplitude range investigated, the plant is well-described as a linear system.

Fig. 6.

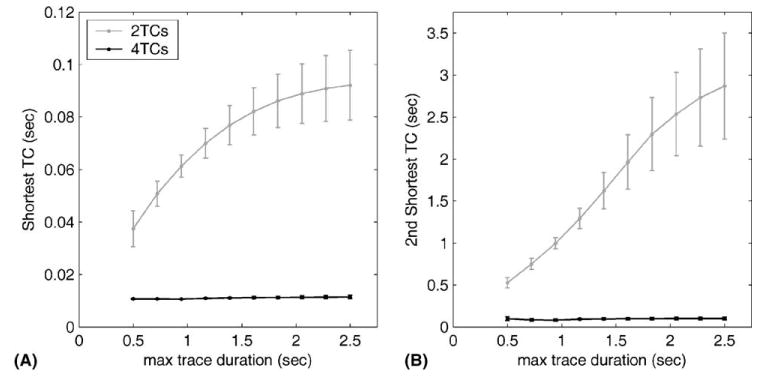
Effects of varying maximum trace duration on values of fitted TCs when either two or four TCs were fitted. Panel A: shortest TC, panel B: second shortest TC. Group means and standard errors are shown.

3.5. Properties of possible plant model

The implications of the present data for understanding eye-movement control can be more easily appreciated with the help of a plant model. A simple model to generate four TCs is four Voigt elements in series (cf. Fig. 1), but the TCs themselves do not provide the estimates of the elements’ elasticity and viscosity that are needed to build the model. This is because an element’s time constant is determined by the ratio of its viscosity to elasticity. The coefficients of the TCs would provide an estimate of the relative compliances of the elements, assuming (i) the mechanical influence of the EOMs can be neglected (see Section 4), and (ii) the system was in equilibrium before release (see Appendix A). These assumptions are made here, and the behaviour of the model is illustrated in Fig. 7.

Fig. 7.

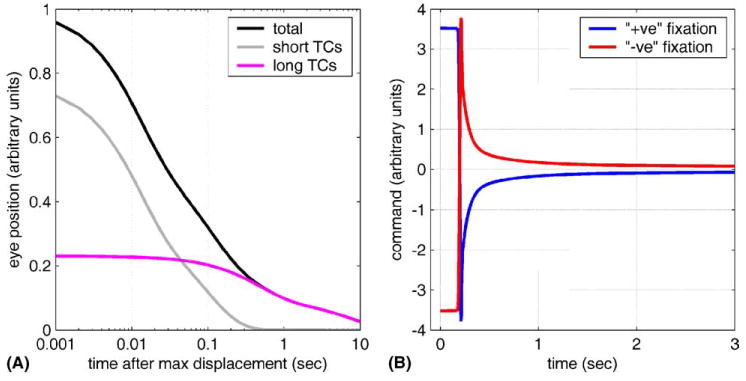
(A) Behaviour of a four Voigt-element model, with parameters derived from the mean TCs and their coefficients shown in Fig. 5. The simulated eye has been released after a maintained (30 s) displacement. The three curves show eye position (‘total’), the combined lengths of the elements with the two shortest TCs (‘short TCs’), and the combined lengths of the two longest TC elements (‘long TCs’). All are expressed as fractions of the original eye displacement (=1.0). (B) The commands required for a saccade to the primary position after maintained eccentric displacement for the same plant model as in A. The eccentric eye-position (10°) that preceded the saccade was maintained for 3 s, and was either in the positive’ (blue) or ‘negative’ (red) direction. The required commands differ, depending on the direction of the preceding saccade, for several seconds after the eye has stopped moving. This phenomenon has been termed hysteresis.

Fig. 7A shows the behaviour of the model following release after a displacement maintained for 30 s, sufficient to allow the long TC elements to reach equilibrium. The subsequent position of the eye and the contribution of the component Voigt elements are plotted. The two Voigt elements with the shortest TCs have been combined, as have the two elements with the longest TCs, and the time axis shown on a log scale, for clarity. It can be seen that the two short TC elements dominate behaviour for the first 300 ms (together they account for >90% of the change in eye position over this period). In contrast, the longer TC elements are responsible for almost all the change in eye position after ~400 ms. The actual proportion of total eye-position change that occurs after 400 ms depends on the relative compliance of long and short TC elements. The values used for the model were based on the assumption that the plant in the present study was in equilibrium before it was released: if, as is likely, the long TC elements were not in fact given sufficient time to reach their equilibrium lengths (see above), the model will underestimate their actual compliance.

Fig. 7B shows the commands required by the plant model to produce saccades that return the eye to the primary position after prolonged (3 s) eccentric fixation (see Appendix A). Immediately after a saccade the system is not in equilibrium, since the brief (<200 ms) saccadic pulse of force primarily extends the short TC elements alone (cf. Fig. 7A). Prolonged eccentric fixation however allows the long TC elements time to extend (‘creep’). This extension must then be compensated for when the system returns to primary position, as shown in Fig. 7B. The phenomenon demonstrated by the model is qualitatively similar to the hysteresis found for the firing rates of OMNs about 2–3 s postsaccade, and illustrated in Fig. 2 of Goldstein and Robinson (1986).

4. Discussion

The purpose of this study was to extend previous descriptions of oculomotor plant dynamics by systematic analysis of release trajectories, over longer periods than usually investigated. We found that the trajectories for each of three monkeys could be fitted by four exponential curves, with TCs of approximately 0.01, 0.1, 1 and 10 s. These curves correspond to the behaviour of four Voigt elements in series, and estimates of their relative compliances indicated that the two longer TC elements accounted for at least 25% of the total compliance of the plant. These findings indicate that the dynamics of the primate oculomotor plant need to be described over a wide range of time scales. The behaviour of a model derived from the estimates (shown in Fig. 7) supported this view: the presence of long TC elements allowed it to reproduce the qualitative pattern of OMN firing observed after prolonged eccentric fixation (Goldstein & Robinson, 1986). To our knowledge, this is the first model to do so.

The issues that arise from these findings concern (i) methodology, (ii) the physical basis of the four Voigt element model, and (iii) the significance of the improved plant description for understanding the neural control of eye movements.

4.1. Methodological issues

4.1.1. Linearity of plant

An important aspect of the methodology used here is the assumption that the oculomotor plant is approximately linear. This assumption has often been made in previous work on plant mechanics, sometimes without further examination. It was assessed here by use of principal component analysis. The outcome indicated that the present data are consistent with a linear model, an important finding since such models offer great advantages over nonlinear models in terms of tractability and applicability.

4.1.2. Recording technique

Eye movements were recorded with implanted scleral search coils, which have recently been shown to alter saccade dynamics in human subjects (Frens & VanderGeest, 2002). However, the effects found were small (<10%: coil inertia is ~5% that of the globe), and appeared to be of neural rather than mechanical origin. A second possible problem is that the coil used in the present study measured horizontal and vertical but not torsional eye position, so that release trajectories might have been affected by undetected torsional displacements. As stated in Section 2, care was taken to avoid vertical deviation by monitoring coil output, and this precaution would have restricted any torsional contribution.

4.1.3. Globe displacement

As in previous studies, the eyeball was displaced manually using forceps. A hitherto unsuspected drawback of this method is that the eyeball may not be released instantaneously, as suggested by the finding that the peak velocity of the return trajectory occurred 8–20 ms after release (a strictly viscoelastic plant produces peak velocity at the moment of release). It is possible that similar effects would have been observed in other studies using manual displacement. For example, Keller and Robinson (1971) measured return movements of the globe in awake rhesus monkeys, after displacement by rotation of an opaque contact lens. Our analysis of the averaged time course of 10 returns from a 10° medial displacement (Keller, 1971, Fig. 24) indicates that the globe continued to accelerate until ~60 ms after release, probably due to slippage of the suction contact lens. The present study, as far as we know, is the first to take account of this release problem. Trajectories were fitted from the time of peak velocity, and the resulting TCs compared with those obtained from fitting from the time of release. As indicated in Section 3, the main effect of fitting from the time of release appears to be a doubling of the value of the shortest TC, with small and unsystematic effects on other TCs. This comparison suggests that failure to fit from the time of peak velocity has probably contributed to the variations in TC estimates between previous studies and that more accurate measurements of the shortest TC will require an improved mechanical method for releasing the globe.

A second consequence of manual displacement is variability. This is not a problem if it is confined to the overall amplitudes of the globe displacements, because these are measured explicitly. Difficulties will arise, however, if the lengths of individual Voigt elements at the time of release vary relative to one another from trial to trial, since these cannot be measured directly. This possibility, apparently not addressed in previous studies, was allowed for here by use of a new fitting method that assumed the traces from a given animal reflected the same underlying TCs, but not necessarily the same starting lengths (Section 2, Appendix A). Thus, all traces from a given animal were fitted simultaneously with the same set of exponential curves. This fitting method derives directly from the underlying assumptions of a linear plant model, and allows estimation of TCs generated by manual (i.e., variable) globe displacements.

4.1.4. Statistical analysis and number of fitted TCs

As explained in Sections 2 and 3, certain features of the present data preclude straightforward application of conventional statistical methods. In particular the residual noise after fitting has structure, whereas statistical methods such as the F-test assume white noise (see Section 2). Therefore a combination of procedures was used to arrive at the best number of TCs for fitting.

1. A very conservative hierarchical F-test, using fewer than 1% of the original data points, still showed that the addition of a 4th TC significantly improved the fits for all three animals. Addition of a 5th TC, however, was significant for only one animal.

2. The error intervals of the TC estimates (as derived by the bootstrap procedure) were well separated for four TCs (Fig. 5A), but showed substantial overlap when five TCs were used.

3. The estimates of the two shortest TCs produced by fitting four TCs were stable with respect to trace duration over the range examined, whereas the estimates produced by fitting two TCs showed very marked changes. The curves for two fitted TCs shown in Fig. 6 are decisive evidence that the oculomotor plant cannot be adequately characterised by two Voigt elements, and illustrate why different values of the TCs are needed if a two Voigt element model is used to interpret firing-rate data for both fast and slow eye movements (see Section 1).

These findings suggest that the present data can be adequately approximated by four TCs. The physical interpretation of this approximation is discussed below.

4.2. Use of ketamine

Light ketamine anaesthesia allowed relatively long-duration release trajectories, essential for investigating the behaviour of the plant at long (1, 10 s) time scales. However, a methodological concern is that ketamine might have altered the plant dynamics characteristic of the alert animal to such an extent that the present results were misleading. Three pieces of evidence suggest that the effects of ketamine were in fact likely to have been modest.

1. Blanks, Volkind, Precht, and Baker (1977) concluded that “the use of Ketamine anesthesia [40 mg/kg i.p.] in our experiments had not significantly altered the functional state of the oculomotor system” (p. 392). This conclusion was based on comparison of the modulation of abducens motoneuron discharge induced by vestibular stimulation with that obtained in alert cats, and is consistent with evidence that tonic EMG activity in the cat lateral rectus muscle (King, Precht, & Dieringer, 1978, Fig. 1) persists after ketamine (20 mg/kg, i.m.).

2. Sklavos, Gandhi, Sparks, Porrill, and Dean (2002) fitted exponential curves to the return movements of the eye after displacements produced by electrical stimulation of the abducens nucleus in alert rhesus monkey. The return trajectories were typically 200–300 ms long before interruption by saccades, allowing two TCs to be estimated at 23 and 103 ms. The latter is very close to the estimates for the second shortest TC obtained here: the former is ~2× longer than the present estimate of the shortest TC, but it may have been affected by stimulation-induced muscle activation, which required the trajectories to be fitted 40 ms after the end of stimulation.

3. As mentioned in Section 3, the firing rates of OMNs show ‘hysteresis’ after prolonged (2–3 s) eccentric fixation (Goldstein & Robinson, 1986). This qualitative pattern of firing is reproduced by the four-element model (Fig. 8) that was derived from TC estimates obtained under ketamine. Thus, OMN hysteresis is indirect evidence in favour of long-TC elements in the oculomotor plant of alert animals.

Fig. 8.

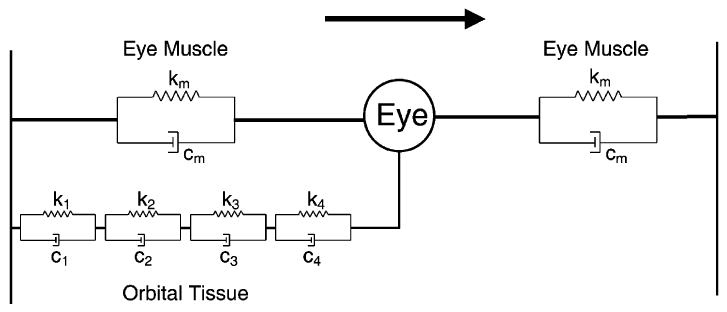
Schematic diagram of eyeball with attached eye muscles (each represented by a single Voigt element) and orbital tissue (represented by four Voigt elements). The arrow denotes direction of mechanical displacement.

In summary, therefore, it appears that the doses of ketamine used in the present experiment resulted in plant dynamics qualitatively similar to those found in alert animals, in the sense of requiring a broad range of time scales for their description. Where quantitative comparison is possible, it appears that the shortest but not second shortest TC may be different in alert animals. This issue is discussed further in the next section.

4.2.1. Reflex eye movements

A possible artefact would be the contamination of release trajectories observed in this and previous studies by active slow eye movements. However, in typical experiments the head is kept fixed so that vestibular induction of eye movements is precluded, and no targets are available for smooth pursuit. The possibility that mechanical disturbance itself induces reflex eye-movements was specifically investigated, and rejected, by Keller and Robinson (1971).

4.3. Physical interpretation of model

The model illustrated in Fig. 7 is a simplified representation of the underlying physical reality in at least two respects. One is that it lumps EOMs and orbital tissue together. The second is that it uses a discrete approximation (in this case with four elements) to what may in fact be a continuous distribution of viscoelastic properties. The issue of EOM properties is considered first.

4.3.1. Contribution of EOM properties to plant dynamics

The overall mechanics of the oculomotor plant depend on the properties of both orbital tissue and EOMs, which are usually considered to act in parallel on the globe (Fig. 8: cf. Robinson, 1964). Data from modelling and experimental studies can help separate out the contributions of orbital tissue and EOMs to overall system dynamics.

Modelling

If an EOM can be represented by a single Voigt element, the number of release TCs for the combined system is the same as that for orbital tissue alone (Appendix A). The values of the system’s release TCs are however affected by EOM stiffness and viscosity. For the present study plausible values for EOM stiffness range from that of passive muscle (i.e. the ketamine had a strong anaesthetic effect on muscle activation), to that of normally activated muscle (i.e. the ketamine had no effect). These two conditions are illustrated in Fig. 9, which plots the values of the TCs for the system as a whole against the value of the muscle TC, for either passive (Fig. 9A) or active (Fig. 9B) muscle.

Fig. 9.

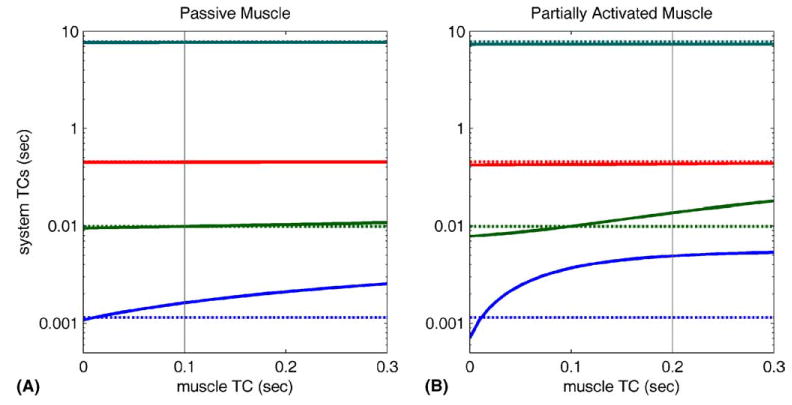
Overall system TCs for model shown in Fig. 8, plotted against the value of the eye muscle TC. Values for orbital tissue parameters were derived from present study (Appendix A) and from an estimate of 0.45 gf/deg for steady-state orbital stiffness (see text). (A) System TCs with passive muscle, here assumed to have a stiffness of 0.03 gf/deg. The broken lines show the values of the TCs for orbital tissue alone (not clearly visible for the two longest TCs). The vertical line corresponds to a muscle TC of 0.1 s. (B) System TCs for muscle activity generated by fixation at primary position, here assumed to produce a stiffness of 0.3 gf/deg. The broken lines show the values of the TCs for orbital tissue alone. The vertical line corresponds to a muscle TC of 0.2 s.

The passive condition (Fig. 9A) assumes a muscle stiffness of 0.03 gf/deg around the primary position, estimated from Fig. 4 of Fuchs and Luschei (1971). This value is small compared with that of ~0.45 gf/deg obtained for orbital tissue from measurements with force transducers (estimated from Fig. 7 of Miller, Bockisch, & Pavlovski, 2002), and 3 of the 4 system TCs are little affected by muscle TC over the range illustrated. The shortest TC does increase noticeably from its value assuming no EOM (dark blue broken line): if the TC for passive muscle is 0.1 s (measurements on cat lateral rectus muscle by Collins (1971)), the increase from orbital to system TC is ~40%.

In the active condition (Fig. 9B) muscle stiffness is assumed to have a value of 0.3 gf/deg (a possibly high value derived from measurements in humans (Collins et al., 1991; Roberts, Eaton, & Salt, 1991; Robinson, 1981; Simonsz & Spekreise, 1996)). Now both the two shortest TCs are clearly affected. There appear to be no direct measurements of the TC for ‘alert’ EOM; the value of 0.2 s shown in Fig. 9B is derived from modelling (Dean & Porrill, 2000) and from data on eye movements produced by abducens stimulation (Sklavos et al., 2002). For this value the shortest TC increases 330%, and the next shortest by 38%, from their orbital tissue values. The two longest TCs, however, are little altered.

Experimental data

Goldstein, Bockisch, and Miller (2000) used implanted force transducers in the tendons of primate medial and lateral rectus muscles to measure net muscle force during saccades. Comparison of force and eye position profiles indicated a two Voigt-element plant, with values corresponding to release TCs of 6 and 66 ms. Because of the positioning of the transducers, these estimates should be for orbital tissue on its own. However, the eye position records in the Goldstein et al.’s experiment were short (200 ms), so that characterisation of orbital-tissue behaviour at long time scales was not possible. Other, unsystematic, observations of orbital-tissue behaviour at long time scales have pointed to the existence of long TC elements. Robinson, O’Meara, Scott, and Collins (1969, p. 550) described the effects of an abrupt change in eye-position with the horizontal rectus EOMs detached: “The orbital tissue bed is also quite viscous. When the globe was rotated quickly (by hand as before) by a small increment, the tension rose initially to about twice the change in steady-state value and decayed with a time constant of about 8 s. It was necessary to wait almost 15 s after each globe rotation to be sure a new steady state had been reached”. Similarly, Collins (1971) recorded the movements of the human globe, with medial and lateral rectus muscles detached, by a photoelectric eye position transducer which tracked the limbus of the moving eye. The trace illustrated in Fig. 28 is said to have TCs of 0.02 and 1 s, but ~6 s after release the globe appears to have returned by only ~85% of the original displacement. Such behaviour requires a mechanical component with a TC substantially longer than 1 s, and is in fact consistent with a Voigt element with TC of 10 s and relative compliance of ~30%.

In summary, both simulation and measurement suggest that an important feature of oculomotor plant dynamics apparent in the present findings, namely the wide range of time scales needed for their description, is characteristic of orbital tissue on its own. The main effect of EOM tone appears to be a lengthening of the two shortest TCs. The precise magnitude of this lengthening is currently uncertain, since the TC estimates for orbital tissue alone (Goldstein et al., 2000) are at present only available for a single animal, but qualitatively the pattern of results suggests that EOM can be approximated by single Voigt elements with a TC of the order of 0.1–0.2 s. If so the model shown in Fig. 7, while useful for illustrating the effects of the long TC elements, would need the addition of elements representing the EOMs (as in Fig. 8) for better prediction of behaviour over short time periods.

4.3.2. Discrete approximation to continuous distribution

The viscoelastic behaviour of biological materials in response to sudden application of force (‘creep’) or its removal (‘relaxation’) is usually described in terms of a continuous spectrum of TCs, which can be modelled as arising from an infinite set of Voigt elements (Hall, 1968). As a biological material, the oculomotor plant is therefore likely to have such distributed viscoelastic properties. When the contribution to the total compliance of the elements with TCs between T and T + dT is represented as D(T)dT (so that the total compliance is ${\int }_0^{\infty }D(T)\hspace{0.17em}\text{d}T)$, the function D(T) is called the retardation spectrum of the material. Plotted as a function of log T, the retardation spectrum is typically smooth and slowly varying. In these circumstances, the continuous distribution of compliance can be well approximated by a small number of discrete T values spaced approximately an order of magnitude apart over the time scale of the behaviour under investigation.

The present results, which suggest that the relaxation behaviour of the globe over 1–10 s can be represented by four TCs of approximately 0.01, 0.1, 1 and 10 s, is consistent with this interpretation (cf. Anastasio, 1994; Buchthal & Kaiser, 1951; Stahl & Simpson, 1995).

4.4. Significance for data interpretation and modelling

Plant models feature in many studies of the oculomotor system (see Section 1). They are used, often implicitly, to interpret data relating neuronal firing rates to eye movements. They are also used explicitly in theoretical investigations of eye-movement control. The present findings are significant for both applications of plant models.

4.4.1. Interpretation of neuronal firing rates

Previous descriptions of the oculomotor plant have only allowed interpretation of data on OMN firing rates for limited sets of eye movements, in particular eye-movements made at a single frequency (Section 1). Stimulating any linear system with a fixed frequency sine wave produces a sine wave output of the same frequency, differing from the input only in gain and phase. Thus, no matter how complex the original system, its behaviour in these circumstances can be mimicked by a single Voigt element, whose two free parameters can be used to fit the observed gain and phase changes. Consequently for any linear plant the firing-rates of ocular motoneurons measured at a single frequency would always be consistent with a first-order plant model (Keller, 1981).

Characterisation of a higher order plant therefore requires measurements made at different frequencies. The firing rates of ocular motoneurons for smooth pursuit movements over 0.3–2.0 Hz appear to be consistent with a plant model with two Voigt-elements (Section 1). However, the parameters of this model in turn only stay fixed for a limited range of eye movements (cf. Fig. 6); the time constants required differ from those needed for ‘fast’ (saccadic) eye-movements (Goldstein & Reinecke, 1994; Goldstein & Robinson, 1984; Optican & Miles, 1985). This discrepancy has been made explicit in a recent study that identified the relevant best-fit parameters for a two-element model from OMN firing rates during both slow and rapid eye movements (Sylvestre & Cullen, 1999). “We …found that, for a given model, a single set of parameters could not be used to describe neuronal firing rates during both slow and rapid eye movements” (p. 2612).

The four-element plant model derived from the measurements of the present study has the potential to help resolve this problem, because its range of time constants covers both slow and fast movements (Fig. 7A). The model’s behaviour is dominated by the two short TC elements for the first 300 ms after disturbance because at high frequencies the long-TC elements are effectively rigid so that application of force for less than 300 ms, as in saccades, scarcely affects them. Slow movements, such as sinusoidal smooth pursuit or the vestibulo-ocular reflex at periods longer than 300 ms (equivalent to ~3 Hz) will, in contrast, engage the long TC elements. Thus, a quantitative model of both fast and slow eye movements must contain both fast and slow TC elements.

The scope of the new model is illustrated by its ability to account, at least qualitatively, for hysteresis (Fig. 7B). Prolonged eccentric fixation allows time for the long TC elements to lengthen (‘creep’), and for the system to near equilibrium (see Appendix A). In these circumstances, the muscle force and neural command required for the return saccade to primary position will depend on the location of the prior fixation. The command signals illustrated in Fig. 7B resemble actual OMN firing rates shown in Fig. 2 of Goldstein and Robinson (1986). The possibility that hysteresis might in principle be explained by long TC elements in the plant has been previously pointed out by Robinson (1981), though to our knowledge the present four-element plant model is the first that has done so.

4.4.2. Models of eye-movement control

Although all models of eye-movement control would seem to require an explicit description of the oculomotor plant, there is one type of model for which it is especially important. These are models of plant compensation, the process whereby command signals that specify eye velocity alone are translated to cope with the mechanics of the plant. The nature of the translation depends entirely on the nature of the plant. Thus, for a single Voigt-element plant part of the velocity signal must pass through an integrator (Skavenski & Robinson, 1973). For a two-element plant, an additional ‘slide’ term has to be added (Goldstein & Robinson, 1984; Optican & Miles, 1985). For the model derived here, a linear filter with additional components is needed (cf. Fig. 7B).

Oculomotor plant compensation is carried out by both the brainstem and the cerebellar flocculus (Optican & Miles, 1985; Optican, Zee, & Miles, 1986; Zee, Yamazaki, Butler, & Gücer, 1981). As such, it is a relatively well specified task with which to test general theories of cerebellar function. For example, a mechanism has been proposed whereby the flocculus can learn to compensate for complex plants with long TC elements (Dean et al., 2002, Dean, Porrill, & Stone, 2004; Porrill, Dean, & Stone, 2004). Comparing the predictions of plant compensation models with experimental data, such as Purkinje cell simple-spike firing rates in the flocculus (Yamamoto, Kobayashi, Takemura, Kawano, & Kawato, 2000, 2002), requires an accurate model of the plant.

4.5. Conclusions

The present findings suggest that the oculomotor plant of lightly anaesthetised rhesus monkeys can be modelled as four Voigt elements in series, with TCs of about 0.01, 0.1, 1 and 10 s. The presence of long TC elements may help to explain features of OMN firing such as its frequency-dependency in smooth pursuit, and the hysteresis observed at the primary position after prior, prolonged, eccentric fixation.

Further understanding of the primate oculomotor plant requires quantitative assessment of the separate contributions of its components, namely orbital tissue and EOMs. A number of experimental approaches could contribute to such an assessment, including measurements of (i) the plant dynamics in deeply anaesthetised animals with passive EOMs, (ii) the tendon force in alert animals (Miller et al., 2002; Miller & Robins, 1992), and (iii) the dynamic behaviour of isolated EOMs. These measurements are required for better models of the plant, and hence of oculomotor control in general, as was noted some time ago by Robinson (1981).

Appendix A

A.1. Behaviour of Voigt elements in series

The equation of motion for a single Voigt element (Fig. 1) is

$$F=kx+c\frac{\text{d}x}{\text{d}t}$$ (A.1)

where F is the external force acting on the element, x is its length (relative to resting length), dx/dt its velocity, k its stiffness and c its viscosity. In a release experiment, an external force pulls the element to length x₀, and then is abruptly removed (F = 0). Eq. (A.1) then becomes:

$$c\frac{\text{d}x}{\text{d}t}=-kx$$ (A.2)

which shows that the element shortens (indicated by negative sign) with a velocity proportional to its extension. Solving Eq. (A.2) for x gives:

$$x=x_0{\text{e}}^{-\frac{kt}{c}}=x_0{\text{e}}^{-\frac{t}{T}}$$ (A.3)

where T (=c/k) is the time constant of the element. For Voigt elements in series, the absence of inertia means that the force on each element is at all times equal to the external force, so the equations for each individual element are identical to those given above. Since element lengths sum, Eq. (A.3) becomes:

$$x=x_1(0){\text{e}}^{-\frac{k_{1}t}{c_1}}+\cdots +x_i(0){\text{e}}^{-\frac{k_{i}t}{c_i}}+\cdots +x_n(0){\text{e}}^{-\frac{k_{n}t}{c_n}}$$ (A.4)

where i refers to the ith of n elements, which has initial length x_i(0). The form of this equation is the same as that of Eq. (1) in Section 2, with x_i(0) equivalent to the ith coefficient A_i, and the ratio c_i/k_i equivalent to the ith time constant T_i. These may also be referred to as release or pole time constants.

If a series of Voigt elements is extended and held long enough for the individual elements to reach equilibrium (i.e., dx_i/dt = 0), Eq. (A.1) gives:

$$F=k_i{x}_i(0)$$

Thus x_i(0) ∝ 1/k_i, so that for a system released from equilibrium, the coefficients A_i will be in the ratio of the compliances of the corresponding Voigt elements. If a system is released after a rapid displacement, equilibrium will not be reached and the estimated compliances of the short TC elements will be greater than their true values.

A.2. Fitting method

Eye positions (x₁,…,x_m) from a single trace at times (t₁,…,t_m) are represented as a combination of n Voigt elements with time constants T_j and initial lengths A_j

$$x_i=\sum _j{A}_j{\text{e}}^{-\frac{t_i}{T_j}}+{\varepsilon }_i$$

where ɛ_i are fitting errors. This can be written as a matrix equation by introducing column vectors x = (x_i), a = (A_j), ɛ = (ɛ_i) and the m × n matrix E with elements E_ij = e^−t_i/T_j:

$$x=Ea+\varepsilon$$

The estimate of a which minimises the sum square error ɛ², as in multiple linear regression (Press et al., 1992), is then given by

$$\widehat{a}=E^{\#}x={(E^{t}E)}^{-1}{E}^{t}x$$

and has fitting error

$$\varepsilon =x-E\widehat{a}$$

The sum square fitting error for an animal’s entire data set given time constants T_j is obtained by summing the ɛ² for each individual trace for that animal.

The total error is then minimised over all the unknown T_j to estimate the time constants. Positive time constants can be guaranteed and improved convergence obtained if the time constants are re-parameterised as $T_j=1/w_j^2$; a standard minimisation routine (MATLAB^™ fminunc) is used to minimise over the weights w_j. Note that it is straightforward to include traces of different lengths in this fitting procedure.

A.3. Plant model

A convenient way to derive a plant model from estimates of Voigt element time constants and stiffnesses is to use Laplace transform to convert Eq. (A.1) to

$$F(s)=(k+cs)x(s)$$

where s is the Laplace complex frequency variable. For the 4 element model:

$$\begin{array}{l}x(s)=x_1(s)+x_2(s)+x_3(s)+x_4(s)\\ =\frac{F(s)}{k_1+c_{1}s}+\frac{F(s)}{k_2+c_{2}s}+\frac{F(s)}{k_3+c_{3}s}+\frac{F(s)}{k_4+c_{4}s}\end{array}$$

The transfer function H(s) of the plant for input F to angular eye position x is

$$\begin{array}{l}H(s)=\frac{x(s)}{F(s)}\\ =\frac{1}{k_1+c_{1}s}+\frac{1}{k_2+c_{2}s}+\frac{1}{k_3+c_{3}s}+\frac{1}{k_4+c_{4}s}\\ =\frac{a_1}{1+s{T}_1}+\frac{a_2}{1+s{T}_2}+\frac{a_3}{1+s{T}_3}+\frac{a_4}{1+s{T}_4}\end{array}$$ (A.5)

where a_i = 1/k_i (see above), and T_i = c_i/k_i. The numerical values for these terms in the model were the mean values of the time constants and coefficients (Fig. 5) for the three animals. Substituting these values in Eq. (A.5) and factorising into pole-zero form (e.g. by using the MATLAB Control System toolbox) gives the plant transfer function

$$H(s)=\frac{3(0.0612s+1)(0.395s+1)(7.04s+1)}{(0.0115s+1)(0.099s+1)(0.455s+1)(7.76s+1)}$$ (A.6)

where the coefficients of s in the numerator are the zero TCs of the system and those in the denominator are the pole TCs. After a prolonged step input this system will be in equilibrium (Eq. (A.4)). Abrupt removal of the input then generates the behaviour illustrated in Fig. 7A.

To determine the input F required for a particular eye-position trajectory x, the transfer function of Eq. (A.5) is inverted

$$F(s)=\frac{x(s)}{H(s)}$$

The desired eye position was derived from a saccadic velocity profile, represented by a Gaussian function with standard deviation chosen to produce a saccadic duration of about 30 ms (Fig. 7B).

A.4. Model of orbital tissues and eye muscle

If the transfer function of the orbital tissue shown in Fig. 8 is H_orb(s), and that of the two muscles is H_m(s), then the transfer function of the system as a whole H_sys(s) is given by

$$\begin{array}{l}{H}_{\text{sys}}(s)=1/\left(\frac{1}{H_{\text{orb}}(s)}+\frac{1}{H_{\text{m}}(s)}\right)\\ =\frac{H_{\text{orb}}(s)H_{\text{m}}(s)}{H_{\text{orb}}(s)+H_{\text{m}}(s)}\end{array}$$ (A.7)

From Eq. (A.6), H_orb(s) can be represented as

$$H_{\text{orb}}(s)=\frac{G_{\text{orb}}(1+s{T}_{\text{z}1})(1+s{T}_{\text{z}2})(1+s{T}_{\text{z}3})}{(1+s{T}_{\text{p}1})(1+s{T}_{\text{p}2})(1+s{T}_{\text{p}3})(1+s{T}_{\text{p}4})}$$ (A.9)

where G_orb is a gain term, the T_z are the zero TCs, and T_p the pole TCs. If the muscles can be approximated by single Voigt elements, then the transfer function H_m(s) for the two muscles in series is

$$H_{\text{m}}(s)=\frac{G_{\text{m}}}{1+s{T}_{\text{m}}}$$ (A.10)

where T_m is the muscle TC and G_m a gain term. Combining Eqs. (A.9) and (A.10) gives

$$\begin{array}{l}{H}_{\text{orb}}(s)H_{\text{m}}(s)\\ =\frac{G_{\text{orb}}{G}_{\text{m}}(1+s{T}_{\text{z}1})(1+s{T}_{\text{z}2})(1+s{T}_{\text{z}3})}{(1+s{T}_{\text{p}1})(1+s{T}_{\text{p}2})(1+s{T}_{\text{p}3})(1+s{T}_{\text{p}4})(1+s{T}_{\text{m}})}\end{array}$$ (A.11)

$$\begin{array}{l}{H}_{\text{orb}}(s)+H_{\text{m}}(s)\\ =\frac{G_{\text{orb}}(1+s{T}_{\text{z}1})(1+s{T}_{\text{z}2})(1+s{T}_{\text{m}})}{(1+s{T}_{\text{p}1})(1+s{T}_{\text{p}2})(1+s{T}_{\text{p}3})(1+s{T}_{\text{p}4})(1+s{T}_{\text{m}})}\\ +\frac{G_{\text{m}}(1+s{T}_{\text{p}1})(1+s{T}_{\text{p}2})(1+s{T}_{\text{p}3})(1+s{T}_{\text{p}4})}{(1+s{T}_{\text{p}1})(1+s{T}_{\text{p}2})(1+s{T}_{\text{p}3})(1+s{T}_{\text{p}4})(1+s{T}_{\text{m}})}\end{array}$$ (A.12)

The ratio of the expressions (A.11) and (A.12) is the transfer function for the system as a whole (Eq. (A.7)). Since the denominators of the individual expressions cancel out, the denominator of their ratio is the numerator of Eq. (A.12), which is a 4th order polynomial in s. Hence the number of poles in the system is 4, the same as in the model for orbital tissue alone. Actual evaluation of H_sys(s) was carried out using the MATLAB Control System toolbox. Parameter values for H_orb were those from Eq. (A.6) together with a gain term giving overall stiffness of 0.45 gf/deg. Parameter values for H_m were as described in the text.