X-APL: An Improved Family-Based Test of Association in the Presence of Linkage for the X Chromosome

Abstract

Family-based association methods have been developed primarily for autosomal markers. The X-linked sibling transmission/disequilibrium test (XS-TDT) and the reconstruction-combined TDT for X-chromosome markers (XRC-TDT) are the first association-based methods for testing markers on the X chromosome in family data sets. These are valid tests of association in family triads or discordant sib pairs but are not theoretically valid in multiplex families when linkage is present. Recently, XPDT and XMCPDT, modified versions of the pedigree disequilibrium test (PDT), were proposed. Like the PDT, XPDT compares genotype transmissions from parents to affected offspring or genotypes of discordant siblings; however, the XPDT can have low power if there are many missing parental genotypes. XMCPDT uses a Monte Carlo sampling approach to infer missing parental genotypes on the basis of true or estimated population allele frequencies. Although the XMCPDT was shown to be more powerful than the XPDT, variability in the statistic due to the use of an estimate of allele frequency is not properly accounted for. Here, we present a novel family-based test of association, X-APL, a modification of the test for association in the presence of linkage (APL) test. Like the APL, X-APL can use singleton or multiplex families and properly infers missing parental genotypes in linkage regions by considering identity-by-descent parameters for affected siblings. Sampling variability of parameter estimates is accounted for through a bootstrap procedure. X-APL can test individual marker loci or X-chromosome haplotypes. To allow for different penetrances in males and females, separate sex-specific tests are provided. Using simulated data, we demonstrated validity and showed that the X-APL is more powerful than alternative tests. To show its utility and to discuss interpretation in real-data analysis, we also applied the X-APL to candidate-gene data in a sample of families with Parkinson disease.

Family-based association methods are often used for localizing genes in complex diseases when family data are available; however, methodological developments have focused primarily on analysis of autosomal markers.^1–5 Linkage analyses have identified regions on the X chromosome for several diseases, such as Parkinson disease (PD [MIM 168600]),^6,7 autism (MIM 209850),^8,9 and early-onset cardiovascular disease.¹⁰ Although association analysis is often applied to further localize disease-susceptibility genes in linkage regions, fine mapping of such regions on the X chromosome has been slow, in part because of the lack of appropriate statistical methods for family-based association analysis on the X chromosome.

The X-linked sibling transmission/disequilibrium test (XS-TDT) and the reconstruction-combined TDT for X-chromosome markers (XRC-TDT), proposed by Horvath et al.,¹¹ are the first family-based association methods that test X-chromosome markers specifically. These are valid tests of association in family designs that include a single proband, such as triads or discordant sib pairs. For families with multiple affected offspring, these tests, which assume independent gamete transmissions from parents to affected siblings, can have an inflated type I error rate when linkage is present between a marker and the disease locus. This is the same problem faced by the original TDT and sibling TDT (S-TDT).² Because association analyses are often conducted in regions showing evidence of linkage, it is critical that family-based association tests allow for the presence of linkage under a null hypothesis of no association when multiple affected offspring are available.

More recently, the pedigree disequilibrium test (PDT), originally proposed for autosomal markers by Martin et al.,^2,3 was extended to markers on the X chromosome.¹² This approach, the XPDT, maintains the properties of the PDT—namely, it is a test of association in the presence of linkage (APL) in general pedigrees, is valid in stratified populations, and does not require specification of model parameters. However, in families with missing parental data, the XPDT uses only same-sex discordant sibships and, thus, may not have optimal power. Recognizing this possibility, Ding et al.¹² suggested a Monte Carlo approach for inferring missing parental data, the XMCPDT. They show that this approach generally has more power than the XPDT, and the power difference increases with an increasing amount of missing parental data. A limitation of the XMCPDT is that allele frequencies must be provided. Unknown allele frequencies are estimated from known parental (founder) genotypes, but the statistic does not account for variability in this estimate. Although the examples simulated by Ding et al.¹² show no inflation of type I error, the validity of the test with varying amounts of missing parental data has not been thoroughly examined.

Here, we extend the APL method,¹³ developed for autosomal markers, to the analysis of X-chromosome markers in nuclear families. Like the APL, our proposed procedure, which we refer to as “X-APL,” properly infers missing parental genotypes in regions of linkage by considering identity-by-descent (IBD) parameters for affected siblings. We use a bootstrap procedure to adjust for the variation in parameter estimates, which does not assume that allele frequencies are given. X-APL can perform both single-locus and haplotype association tests. Recognizing the existence of sex-limited traits, we introduce into the X-APL separate tests for males and females that allow inference about different effects in the sexes.

We used computer simulations to demonstrate the validity of the X-APL statistic and to examine robustness and power. We compared the power of the X-APL with the power of the XS-TDT, XPDT, and XMCPDT, under a range of models and sampling schemes. We compared the power of the X-APL test using all data with that of separate tests for males and females under sex-specific penetrance models. We then applied X-APL to a real data set containing families with PD. We tested markers in two X-linked genes, monoamine oxidase A and B (MAOA [MIM 309850] and MAOB [MIM 309860]), which have been examined elsewhere as candidate genes for PD.^14–18

Methods

The X-APL statistic is a modification of the APL statistic.¹³ The APL statistic is based on the difference between the observed number of copies of a specific allele in affected siblings and the expected number of copies conditional on parental genotypes, under the null hypothesis that there is no association or no linkage in nuclear families. When parental genotypes are missing, APL infers missing parental genotypes by using siblings’ genotypes and accounts for linkage by taking the IBD parameters into consideration (see the work of Martin et al.¹³ for details). The APL software can analyze families with up to three affected siblings and arbitrary numbers of unaffected siblings.¹⁹

X-APL Statistic

The X-APL is designed for nuclear families with one or more affected siblings. First, consider a sample of n families, each with two affected siblings. Markers are assumed to be biallelic, with alleles 1 and 2 on the X chromosome. We denote I_j as the number of copies of allele 1 in the affected siblings in the jth family. In the work of Martin et al.,¹³ the APL statistic T_j is the difference between I_j and the conditional expected value of I_j, E(I_j|G_pj), where the parental genotypes are represented by G_pj in the jth family. To extend the APL statistic to X-chromosome markers, we consider the sexes of the siblings when calculating the expected value of I_j. We define m as an affected male sibling, f as an affected female sibling, and “sex” as the combination of sexes of the affected siblings, which is (m,m) if both affected siblings are male, (m,f) if one affected sibling is male and the other is female, and (f,f) if both affected siblings are female.

Under the null hypothesis, the expected value of I_j can be estimated conditionally on the parental genotypes and sexes of the affected siblings:

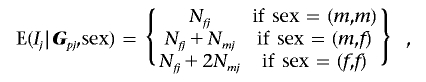where N_fj, the number of allele 1 in the female parent, takes value 0, 1, or 2 and N_mj, the number of allele 1 in the male parent, takes value 0 or 1 in the jth family. The expected value of I_j for a singleton family has a simpler form. E(I_j|G_pj,sex=m) is (1/2)×N_fj, and E(I_j|G_pj,sex=f) is (1/2)×N_fj+N_mj. We define the statistic T_j to be T_j=I_j-E(I_j|G_pj,sex) in the jth family. In complete pedigrees, N_fj and N_mj can be counted directly from the parental data, and the transmissions from male parent to affected siblings cancel in T_j; therefore, male parents provide no information for the X-APL statistic in complete pedigrees.

Although calculation of the statistic T_j is straightforward if the parental genotypes are available, parental genotypes are often missing for individuals with late-onset diseases. In that case, we must infer missing parental genotypes on the basis of the siblings’ genotypes. In equation (2) in the work of Martin et al.,¹³ the probability of a parental mating type, Pr(G_p|G,A), was estimated on the basis of siblings’ genotypes G and their affection status A. We modified this probability for X-APL by also conditioning on the sexes of the siblings. Like the APL for autosomes, the IBD parameters for an affected sibling pair are used to account for linkage between a marker and a disease locus when the missing parental genotypes are being inferred. The IBD for the alleles transmitted from the male parent is fully determined by the sexes of the affected sibling pair. That is, when we consider IBD sharing for alleles transmitted from the male parent, the affected siblings share 0 alleles IBD when sex=(m,m) or (m,f) and 1 allele IBD when sex=(f,f). Thus, only IBD status for alleles transmitted from the female parent needs to be estimated. The affected siblings share either 0 or 1 alleles IBD from the female parent.

When there is tight linkage and no association, the probability Pr(G_p|G,A,sex) is similar to equation (2) in the work of Martin et al.¹³ and can be written as

where μ_Gp is the unconditional probability of parental mating type G_p and z_k is the probability that the affected siblings share k alleles IBD from the female parent. Since disease penetrances are expected to be low for any particular locus for complex diseases, transmissions to the unaffected siblings are assumed to be independent of disease status. Then, IBD parameters for an unaffected sibling pair, or for a pair with one affected and one unaffected sibling, can be approximated by (z₀,z₁)=(1/2,1/2). Therefore, when there are unaffected siblings in a family, the probabilities Pr(G|G_p,IBD=k,sex) are multiplied by the Mendelian transmission probabilities for the unaffected siblings for given parental genotypes. The expectation-maximization (EM) algorithm is used to estimate the parameters μ_Gp and z_k. The procedures of the EM algorithm for estimating the mating-type and IBD parameters are similar to those used by Martin et al.¹³ For singleton families, the probability Pr(G|G_p,IBD=k,sex) reduces to Pr(G|G_p,sex), which depends only on Mendelian transmission probabilities. When parental genotypes are missing, the expectation of I_j is given by the expectation of E(I_j|G_pj,sex) with respect to the conditional distribution of parental genotypes, as follows:

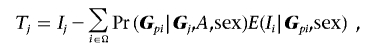where Ω is a set of all possible parental mating types. Partial parental genotypes can be used to improve estimation of the parental mating-type parameters, with use of the same methods discussed in the work of Martin et al.¹³ Let T_s be the sum of T_j over families; then, under the null hypothesis that there is no association or no linkage, the expected value of the statistic T_s is 0. The X-APL test is based on this summary statistic, T_s.

Variance Estimation

Martin et al.¹³ used a robust estimator to estimate the variance of the APL statistic. However, the estimator is difficult to implement in practice when various nuclear family structures exist in a data set. In the work of Chung et al.,¹⁹ a bootstrap variance estimator, which offers more flexibility for analysis of different family structures, was proposed to replace the original variance estimator. The bootstrap approach can be applied to the X-APL model as well. Families are resampled with replacement to form each bootstrap replicate, and a new T_s is calculated for each replicate. If B bootstrap replicates are performed, then the sample variance 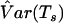can be obtained from the B values of T_s. When B is large, the sample variance will be asymptotically close to the variance of T_s.

Finally, the X-APL statistic takes the form

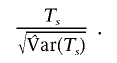Under the null hypothesis of no linkage or no association, this statistic is asymptotically normal, with a mean of 0 and a variance of 1.

Separate Tests for Males and Females

Disease loci can have different effects on males and females. Although a test using combined data could still find association between disease and markers, separate tests for males and females may be more powerful and informative for sex-specific effects. A straightforward approach to test association for males and females separately is to divide the transmissions from parents to affected siblings into separate transmissions to affected male and female siblings. They can be calculated using the parental mating-type and IBD parameters estimated by all data from both sexes. However, when a marker is in linkage disequilibrium (LD) with a disease locus, estimating parameters with the use of all data may not be appropriate for separate tests, particularly when the disease locus has an effect in only one sex. The parameters may not be estimated properly, since they are estimated under the null hypothesis that the marker alleles are not associated with the disease in either sex. Our simulation results showed that type I errors for the X-APL statistic for the sex with no disease-locus effect can be inflated when all data are used to estimate the parameters. A solution is to divide the data into two sets: one set that has only male affected siblings and another set that has only female affected siblings. The two sets may have overlapping families if some families have both affected male and female siblings. All unaffected individuals are retained in both sets. Then X-APL tests can be applied separately on the two sets with use of parameters estimated in their respective sets. We refer to the test using only male affected sibs and the test using only female affected sibs as “X-APL male” and “X-APL female,” respectively. Since both male and female tests can be performed simultaneously, multiple testing should be considered when we interpret the P values from the two tests. An adjustment for the P values, such as Bonferroni correction, may be required to interpret the P values properly.

Extension to Multiple-Marker Haplotype Analysis

To extend the X-APL test to a multiple-marker haplotype test, we assume that no recombination occurs between the markers within the families in the sample. The strategy of haplotype testing is analogous to a multiple-allele analysis for a single marker, but with haplotype phase not always known. Probabilities of consistent haplotype phases within each family are estimated jointly with the estimation of IBD parameters and haplotype frequencies, with the use of the EM algorithm. Only phase probabilities for females need to be estimated, since phase for the non-missing male is always known. A global test statistic, G, which follows an asymptotic χ² distribution under the null hypothesis that none of the haplotypes is associated with the disease locus, is calculated using the method described by Chung et al.¹⁹ to measure the overall haplotype effect, G=T^′_sΣ^-1T_s, where the vector T_s contains the X-APL statistics for each possible haplotype and Σ is the variance-covariance matrix of T_s. If h is the number of haplotypes tested, then the statistic G is asymptotically distributed as χ² with h-1 df.

A global test for all haplotypes can be more informative than individual haplotype tests, since it can capture multiple haplotype effects.²⁰ The global test also can have more power than individual haplotype tests because it does not have the multiple-testing issue faced when analyzing haplotypes individually.²¹ Moreover, in the X-APL test, IBD and parental mating-type parameters are estimated under the global null hypothesis that none of the haplotypes are in LD with a disease allele. It is not straightforward to estimate those parameters under a haplotype-specific null hypothesis. For these reasons, we base inference solely on the global test for haplotype analysis.

Hardy-Weinberg Equilibrium Assumption

Hardy-Weinberg equilibrium (HWE) for haplotype frequencies is assumed in X-APL for the haplotype test, to reduce the number of parameters estimated by the EM algorithm. The same assumption is also applied to the separate male and female tests. For single-marker analyses, we implement two versions of X-APL, one with and one without an HWE assumption. In real data analysis, genotyping errors, mutations, and population stratification may cause genotype frequencies to deviate from HWE. We used computer simulations to generate data sets with different degrees of deviation from HWE, by combining samples from two random-mating populations with different allele frequencies into one data set. To evaluate deviation from random mating, we generated data with two markers to evaluate the effect for haplotype tests. The HWE goodness-of-fit (GOF) test statistic, which has an asymptotic χ² distribution, was used to measure the degree of HWE deviation. Note that we can measure this deviation only in females, since males are haploid for the X chromosome. The HWE GOF statistic was calculated as

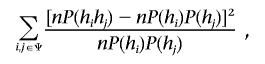where n is the number of female parents and P(h_i) and P(h_j) are the estimated allele frequencies from the mixed population for alleles h_i and h_j, respectively. For single-marker analyses, P(h_ih_j) is the estimated genotype frequency in the mixed population, and ψ is a set of all alleles for the marker. For haplotypes with two markers, P(h_ih_j) is the estimated haplotype frequency, and ψ is a set of all haplotypes between the two markers. Hence, the deviations from HWE in the data set were simulated with respect to haplotype frequencies for the two markers. We investigated the effects of deviations of allele or haplotype frequencies from HWE expectations with the X-APL test using all data and with the separate male and female tests.

Computer Simulations

Computer simulations were used to evaluate the type I error and power of X-APL. We used the SIMLA computer program²² to generate samples of families on the basis of different disease models. Family ascertainment included the following family structures: one affected offspring with one unaffected sibling (AU), one affected sibling pair (AA), and one affected sibling pair plus one unaffected sibling (AAU). No parental genotypes were available in these families, except as noted in the tables.

The SIMLA parameters used in our simulations are shown in table 1, which contains six recessive models (RecA, RecB, RecC, RecD, RecE, and RecF) and six multiplicative models (MultA, MultB, MultC, MultD, MultE, and MultF) with different prevalences and genotypic relative risks (GRRs).¹³ The null model, shown in table 1 with GRR=1, was used to simulate disease loci that have no effect on a specific sex. The GRR for females is the penetrance function for homozygous disease alleles (f_DD) divided by the penetrance function for homozygous normal alleles (f_dd). The GRR for males, assumed to be hemizygous, is the penetrance of the disease allele (f_D) divided by the penetrance of the normal allele (f_d). Hence, when GRR=1 for each sex, the disease loci do not contribute to the disease phenotype. When GRR>1, the disease alleles increase the risk of developing the disease phenotype. By default, we simulated samples in which males and females have the same prevalence and GRR; for example, GRR for females, f_DD/f_dd, is equal to GRR for males, f_D/f_d. The sex ratio of males to females is 1:1 because of the equal disease prevalence. Samples with different GRRs and prevalences for males and females were also generated to reflect disease loci with different effects in the different sexes. In cases of unequal prevalences in males and females, the sex ratio is determined by the prevalence in males to the prevalence in females.

Table 1. .

Genetic Models Used in Simulations

Model of Inheritance	Disease Marker-Allele Frequency	GRRa	Disease Prevalence
Recessive:
RecA	.25	5.00	.0063
RecB	.25	4.00	.0059
RecC	.25	3.00	.0056
RecD	.25	2.50	.0054
RecE	.25	2.00	.0053
RecF	.25	1.50	.0052
Multiplicative:
MultA	.15	7.50	.0064
MultB	.15	6.25	.0060
MultC	.15	4.00	.0053
MultD	.15	3.06	.0049
MultE	.15	2.25	.0046
MultF	.15	1.56	.0043
Null	.25	1.00	.0023

^aGRR for female = f_DD/f_dd. GRR for male = f_D/f_d. f is the penetrance function for disease allele D.

For type I error simulations, we assumed that disease and marker loci were tightly linked (there was no recombination between them), but there was no association between the disease and marker alleles, except as noted below (scenario 4). Four scenarios were simulated (scenarios 1, 2, 3, and 4), each with different family structures and disease models as described in table 2. In scenario 4, the marker and disease locus were in strong LD, but the GRR was 1 for one sex and >1 for the other. To evaluate type I error for multiple-marker haplotype tests, three markers were simulated with eight possible haplotypes. The haplotype frequencies were 0.512, 0.128, 0.128, 0.032, 0.128, 0.032, 0.032, and 0.008 for haplotypes 111, 112, 121, 122, 211, 212, 221, and 222, respectively. As indicated by Chung et al.,¹⁹ rare haplotypes may affect the validity of the global haplotype APL statistic. Rare haplotypes may also affect the X-APL statistic, particularly when samples are stratified into male and female tests. Hence, we increased the number of families to 1,000 in scenarios 1, 3, and 4 for haplotype analyses.

Table 2. .

Scenarios Simulated for Different Family Structures and Genetic Effects

Scenario	Samplea	Male:Female GRRb
For type I error:
1c	300 AAU (1,000 AAU)	Equal
2	250 AAU + 250 AAU*	Equal
3c	300 AAU (1,000 AAU)	Unequal
4c	300 AAU (1,000 AAU)	Sex-limited (GRR=1 in one sex)
For power:
5	250 AAU	Equal
6	250 AAU	Sex-limited (GRR=1 and lower disease prevalence in one sex)

^aAAU families have two affected and one unaffected sibling with parental genotypes missing. AAU* families are the same as AAU families but have genotype data available for one parent.

^bGRRs and prevalences are determined on the basis of the disease models in table 1.

^cFor haplotype analyses, 1,000 AAU families were used.

Power simulations assumed that the marker and disease alleles were in perfect LD for single-locus tests, so that the marker locus was, in fact, equivalent to the disease locus. The AU, AA, and AAU family structures with all parents missing were simulated. For multiple-marker haplotype tests, two markers were simulated as having four possible haplotypes—11, 12, 21, and 22—with frequencies 0.3, 0.3, 0.2, and 0.2, respectively. Haplotype 11 was set to be the risk haplotype and was the only haplotype positively associated with the disease allele.

To compare the power between the X-APL test using all data and the separate male and female tests, we simulated two additional scenarios (scenarios 5 and 6) as described in table 2. The two scenarios were simulated, with 250 AAU families with all parental genotypes missing, under the recessive model.

For comparison with X-APL, we used an SAS macro, which can be downloaded from Michael Knapp's Web site, to conduct the XS-TDT and XRC-TDT.¹¹ An R program provided by Ding et al. was used to conduct the XPDT and XMCPDT (MC-PDT Web site).¹² Asymptotic P values provided by the software were used to evaluate significance.

Results

Type I Error and Power

We first considered the effect of linkage on the XRC-TDT and XS-TDT as tests for association using computer simulations. Table 3 shows estimates of type I error for disease models RecA and MultA (from table 1) based on 5,000 replicate data sets with all parents missing. We found that, when multiple affected siblings are present, both XS-TDT and XRC-TDT have inflated type I error rates. For example, with significance level .05, XS-TDT has a type I error rate 0.062, and XRC-TDT has a type I error rate 0.088 for the 300 AAU families simulated under the disease model MultA. Unlike XS-TDT and XRC-TDT, the XPDT and XMCPDT allow for correlation among multiple affected siblings. In our simulations, we found that the type I error of the XPDT and the XMCPDT, with use of the true allele frequencies, are close to the nominal level (type I error estimates range from 0.045 to 0.054 at the nominal level of .05).

Table 3. .

Type I Error of XRC-TDT and XS-TDT for 5,000 Simulated Data Sets

	Type I Errora
	XS-TDT		XRC-TDT
No. of AAU Families and Inheritance Model	α=.05	α=.005	α=.05	α=.005
300:
RecA	.060	.006	.070	.011
MultA	.062	.006	.088	.016
600:
RecA	.060	.006	.077	.011
MultA	.060	.007	.078	.016

^aProportion of data sets with P⩽α.

We examined the impact of varying the sample size and the proportion of families with parental information on the XMCPDT, using allele frequencies estimated from the observed parental genotypes (table 4). When the proportion of families with parental information is small, we found that the type I error for XMCPDT can be inflated. For example, when there are 50 AAU families with parental information and 300 AAU families with no parental information, XMCPDT has a type I error rate 0.077 with a nominal significance level .05. This inflation of type I error was seen in both singleton and multiplex families. When the proportion of families with parental information increases, XMCPDT can have a reasonable type I error rate, though an upward bias is still evident (table 4).

Table 4. .

Type I Error of XMCPDT for 5,000 Simulated Data Sets

	Type I Errora
Family Structure	α=.05	α=.005
50 AUb + 300 AUc	.077	.011
50 AAUb + 300 AAUc	.077	.011
100 AAUb + 250 AAUc	.058	.006
250 AAUd + 250 AAUc	.059	.008

^aProportion of data sets with P⩽α.

^bBoth parental genotypes are available.

^cGenotypes are missing for both parents.

^dGenotype is missing for one parent.

Table 5 shows estimates of type I error for X-APL for single-marker and global haplotype tests. Type I error estimates for male and female tests are also shown. Under different disease models and family structures, the type I error rate is close to the nominal level of .05 for both single-marker and global haplotype tests. In scenario 4, where the marker and disease loci are in LD and the disease locus has an effect only in males, the female tests show correct type I error rates. In the reverse case—that disease locus has an effect only in females—the type I error rates for the male tests were also correct (data not shown). Type I error rates for a nominal level of .005 were also estimated, and they were also close to the nominal level (data not shown).

Table 5. .

Type I Error of the X-APL Tests for 5,000 Simulated Data Sets

	X-APL Type I Errora
	Single Marker			Global Haplotype
Scenario and Model of Inheritance	Allb	Malec	Femaled	Allb	Malec	Femaled
1:
RecA	.047	.052	.051	.056	.052	.051
RecB	.050	.054	.055	.057	.055	.057
MultA	.049	.049	.051	.049	.052	.056
MultB	.047	.053	.047	.053	.051	.054
2:
RecA	.046	.054	.044	.045	.051	.055
MultA	.046	.052	.047	.048	.053	.051
3:
RecA in male, RecC in female	.053	.045	.051	.048	.050	.055
MultA in male, MultC in female	.048	.045	.049	.048	.045	.053
4e:
RecA	…	…	.053	…	…	.048
MultA	…	…	.053	…	…	.052

^aProportion of data sets with P⩽.05.

^bX-APL test using all data.

^cX-APL male test.

^dX-APL female test.

^eDisease locus affects males but not females; thus, type I errors occur only in females.

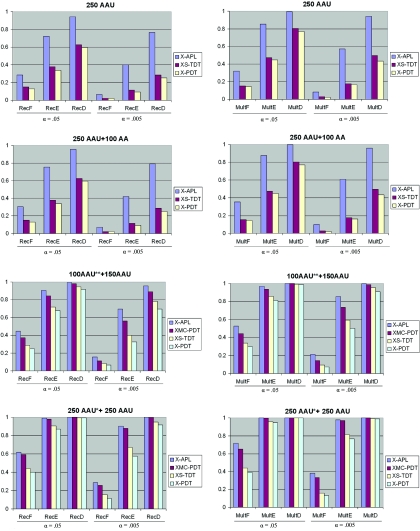
Even though, as a test for association, XS-TDT does not account for linkage when multiple affected siblings are present, its type I error rate is not severely inflated for the significance level (α=.05 and .005) in our simulations (table 3). Hence, we compared the power of X-APL with that of XS-TDT, as well as with that of XPDT, under different disease models and nuclear-family structures. Since the type I error rate is reasonable for XMCPDT when the proportion of families with parental information is large, we included power comparisons with XMCPDT in such cases. We considered two significance levels for power calculations: .05 and .005. Figure 1 shows that the X-APL outperforms XS-TDT, XPDT, and XMCPDT in the six disease models considered. We did not show the power for RecA, RecB, RecC, MultA, MultB, and MultC models in figure 1, since X-APL has a power of 1 for these models. For the data sets that have 250 AAU families without parental information, X-APL typically has substantially more power than XS-TDT and XPDT at significance level .005. As mentioned by Martin et al.,¹³ even families with no unaffected siblings and no parental information can add some power to the APL. We also observed that adding AA families to AAU families gives more information for the X-APL, whereas XS-TDT and XPDT maintain the same power because they do not use AA families (fig. 1). With a total sample size of 250 AAU families, we also simulated 100 AAU families with parental information and 150 AAU families with no parental information. Compared with the power for 250 AAU families with no parental information, the power for X-APL, XS-TDT, and XPDT is higher when some parental information is available. In the case of larger sample size (250 AAU with information for one parent and 250 AAU with missing parental information), we can see that all of the tests have increasing power. In examples with parental data, XMCPDT can have power comparable to that of X-APL. However, when the significance level is reduced to .005, X-APL shows notably more power than does XMCPDT. We also simulated 100 AU families with parental information and 150 AU families with no parental information, to evaluate the power for families with only a single proband. The same pattern as in figure 1 was also observed—namely, that X-APL still shows more power than do other tests (data not shown).

Figure  1. .

Power comparison for single-marker analysis. Power estimates for the single-marker X-APL, XS-TDT, XPDT, and XMCPDT were based on 2,000 simulated data sets. All families were simulated without parental data except AAU** families, which have both parents present, and AAU* families, which have one parental genotype missing. Power is calculated for both significance levels (α) of .05 and .005 for both the recessive and multiplicative models.

We also compared the power of the X-APL single-marker test using all data with that of the X-APL male and female tests for three cases—both sexes together and each sex separately. We applied a Bonferroni correction to the P values from male and female tests. We compared the power for the X-APL test using all data at significance level .05 with the power for male and female tests at significance level .025. Table 6 shows that the X-APL test using data for both sexes has more power than the separate tests for each sex have when the disease locus has effects on both males and females (scenario 5). However, when the disease locus affects only one sex (scenario 6), separate tests can be more powerful. From table 6, we can see (scenario 6) that separate tests have similar or more power than does the test using all data, even with the use of a conservative multiple-testing correction. We can also see that the type I error for the male or female test for the sex not affected by the disease locus is close to the .025 nominal level, as expected.

Table 6. .

Power Estimates for X-APL Test Using All Data and for Separate Tests for Males and Females

		X-APL Test Powerb
		All	Male	Female
Scenario and Model	Sex Ratioa (Male:Female)	α=.050	α=.025	α=.025
5:
RecD in both sexes	1:1	.944	.688	.140
6:
RecD in male, null model in female	7:3	.990	.997	.023c
Null model in male, RecD in female	3:7	.214	.023c	.218

^aSex ratio for males to females in the affected siblings is calculated by the prevalence of males to the prevalence of females in the population.

^bProportion of data sets with P⩽α.

^cEstimates of type I error for the test, since disease loci have no effect in the sex.

From table 6, we see that the power for the separate test in females is consistently lower than that for the separate tests in males, even when the same GRRs are specified in the two sexes. This is a consequence of the models selected and the constraints on model parameters. For example, in scenario 5, males and females have the same disease prevalence and GRR. This forces the phenocopy rate under a recessive model to be higher in females than in males, which, as a consequence, reduces power for the female test relative to the male test. Varying the relative disease prevalence in males and females also influences power because we have fixed the total sample size. For scenario 6, where the sex ratios are 7:3 and 3:7 and the genetic effect is present in the sex with the higher disease prevalence, the sex-specific test has more power than in scenario 5, where the sex ratio is 1:1.

HWE Effect

Table 7 shows type I error estimates for the single-marker X-APL test for data containing deviations from HWE. The version of the single-marker X-APL test that assumes HWE for genotype frequencies was tested. For different degrees of deviations from HWE, in table 7, type I error estimates are all close to the .05 nominal level. Thus, even in extreme cases where all parental information is missing and there are severe deviations from HWE in the data, the single-marker X-APL test is still valid at a significance level of .05. Another version of the X-APL test that does not assume HWE was also tested for the same data sets and has correct type I error as well (data not shown). Our power simulations showed that X-APL with the assumption of HWE has more power than X-APL without the HWE assumption, regardless of whether HWE really exists (data not shown). Table 7 also shows estimates of the type I error for the X-APL test for the global haplotype test. The type I error is inflated when deviations from HWE are present. More-severe departures from HWE cause more-liberal global haplotype tests.

Table 7. .

Type I Error of X-APL Tests with HWE Deviations^[Note]

	X-APL Type I Errorb
	Single Marker
HWE GOFa and Model	All	Male	Female	Global Haplotype
.036:
RecA	.052	.046	.043	.053
RecB	.048	.053	.047	.050
MultA	.047	.043	.046	.052
MultB	.052	.047	.057	.051
2.479:
RecA	.046	.048	.052	.073
RecB	.049	.047	.049	.068
MultA	.048	.046	.052	.075
MultB	.054	.045	.050	.070
5.055:
RecA	.053	.046	.050	.122
RecB	.043	.043	.048	.115
MultA	.043	.043	.052	.096
MultB	.052	.044	.048	.100

Note.— 300 AAU families without parental genotypes were simulated with HWE deviations for RecA, RecB, MultA, and MultB models.

^aLarger value means larger deviation from HWE.

^bProportion of data sets with P⩽.05.

MAO Genes for PD

We applied X-APL, XS-TDT, and XPDT to the data set used by Kang et al.¹⁸ A total of 774 families—558 singleton families and 216 multiplex families—were used for the overall X-APL test. Since 615 of these 774 families have no parental information, XMCPDT was not included for analysis. A total of 530 families—437 singleton families and 93 multiplex families—were used for the male test. A total of 329 families—288 singleton families and 41 multiplex families—were used for the female test. Table 8 shows the results for X-APL with all data and for separate male and female tests, as well as the results obtained by XS-TDT and XPDT. X-APL found that marker RS3027452, located in intron 5 in MAOB, was significant (P=.036) for the female test at significance level .05, whereas XS-TDT and XPDT did not show significant results. However, with a Bonferroni correction for multiple testing for the male and female test, P=.036 may not be considered a significant result. We also applied the X-APL global haplotype test to the markers in MAOA and MAOB but did not observe a significant haplotype association with PD.

Table 8. .

XS-TDT, XPDT, and X-APL Results for Gene Analysis

		P
Marker RS3027452	Na	XS-TDTb	XPDT	X-APL
Overall	774	.634	.676	.063
Male	530	.595	.673	.519
Female	329	.175	.349	.036

^aNumber of families.

^bAsymptotic P values for XS-TDT were used.

Discussion

We have developed the X-APL for testing association in family-based designs for markers on the X chromosome. Our simulation analyses show that X-APL has the correct type I error rate. This is not generally true for XS-TDT and XRC-TDT, which have inflated type I error when linkage is present and there are multiple affected siblings in the data. Inheriting the properties of PDT, XPDT does have the correct type I error rate in the linkage region for families with multiple affected siblings. XMCPDT, which can infer missing genotypes conditional on population allele frequency, relies on the availability of at least some parental genotypes to estimate population allele frequency. As demonstrated in our simulations, when the proportion of genotyped parents is low, XMCPDT may not be a valid test. It is also worth noting (table 3) that the type I error rate of XS-TDT is not substantially inflated and is much closer to the nominal level than is the type I error rate of XMCPDT.

Our simulation results showed that X-APL is more powerful than XS-TDT, XPDT, and XMCPDT for the six disease models used for single-marker analyses in our simulations. As mentioned by Horvath et al.,¹¹ the partition of siblings into same-sex groups can result in reduced power for XS-TDT. XPDT also requires that the discordant sib pairs be of the same sex.¹² X-APL does not require this partitioning, which contributes to its increased power. An unexpected observation was that XS-TDT consistently has more power than XPDT. This difference may be due to the hypergeometric distribution assumed in XS-TDT, which better approximates the distribution of the test statistic under the alternative hypothesis than the asymptotic distribution used by XPDT.

Our simulation results show that the X-APL test using data from both sexes can have more power than separate X-APL male and female tests when the X-linked disease locus contributes to disease risk for both sexes (scenario 5). On the other hand, when the X-linked disease locus affects only one sex, separate tests can have more power than the test using all data (scenario 6). However, some information may be lost when the data are divided into separate smaller data sets. Moreover, separate male and female tests give rise to a multiple-testing issue, and a correction may be required in assessing significance of the tests. We found that, even if we used a conservative Bonferroni correction for the P values from separate tests, the separate tests still have somewhat more power than the test using all data when disease loci affect only one sex. Therefore, we suggest that, in practice, tests using all data and separate male and female tests should be performed to capture the most information in the data. The same strategy for male and female tests can be applied to XPDT as well. Our expectation—that it would have less power—is, in fact, consistent with the previous real data analysis for the MAOB gene.¹⁸

We are not aware of any haplotype test other than X-APL for the X-chromosome markers. Consequently, we estimated power for the global haplotype test of X-APL, using computer simulation, and the results were reasonable. X-APL fills the gap for family-based haplotype association analysis on the X chromosome and will be very useful for haplotype analyses in real data applications. When compared with APL for autosomal markers, X-APL shows considerably more power for the global haplotype test using the same disease models and family structures (data not shown). One reason that we expect to find more power for haplotype analysis on the X chromosome compared with autosomes is that the phases for male haplotypes are determined explicitly for X-chromosome markers. Therefore, haplotype phases can be inferred more precisely in X-APL than in APL. When data from both parents are present, the haplotype phases can be exactly determined. When data from both parents are missing in a family, the haplotype of a male sibling determines one haplotype in the female parent. Moreover, the male parent is known to carry one Y chromosome, and the other haplotype in the male parent can be determined by a female sibling. Hence, there are fewer possible parental mating types that need to be considered compared with the autosomal data, which can reduce the variance of estimates of missing parental mating types. Although these observations are merely of academic interest, since a disease locus is either on the X chromosome or is not, they suggest that the X-APL haplotype test performance is consistent with expectations.

We also examined the robustness of X-APL for data containing deviations from HWE. Our simulation results showed that the X-APL test for single-marker analysis is robust to deviations from HWE in the data. Since the X-APL test with HWE assumption has more power than the X-APL test without HWE assumption for single-marker analysis, the version of X-APL with HWE assumption will be preferred for most real-data analyses. For global haplotype analyses, violations of HWE for haplotype frequencies can significantly inflate type I errors for X-APL. Therefore, haplotype analyses are not reliable in data sets deviating from HWE.

The monoamine oxidase genes MAOA and MAOB are located on the X chromosome and have been found to be associated with PD.^14–18 In Kang et al.,¹⁸ a total of 644 families with PD, consisting of both singleton and multiplex families, were used for association studies. The PDT,^2,3 developed for autosomal markers, was used by Kang et al.,¹⁸ who divided the whole data set into female and male siblings. The marker RS1799836, located in intron 13 in MAOB, showed significant association with PD in the data set containing only female siblings (P=.022). The X-APL female test showed significant association for marker RS3027452, located in intron 5, but, again, the effect was restricted to females. This suggests that the MAOB gene might have an effect for PD in females but not in males. Our results are not entirely consistent with the results obtained by Kang et al.,¹⁸ since different markers show significance in the different analyses. The inconsistency may be due to the fact that Kang et al.¹⁸ restricted analysis to same-sex discordant sib pairs from extended families, whereas X-APL calculated transmissions from parents to affected children only in nuclear families. Moreover, unaffected male and female siblings were used in X-APL sex-specific tests to estimate parameters, but, again, only same-sex unaffected siblings were considered in the Kang et al.¹⁸ analysis. Nevertheless, the associated SNPs show some LD (r²=0.23 between RS1799836 and RS3027452 in affected females),¹⁸ and both show effects limited to the female subset. Therefore, it may indicate that there is a yet-untested female risk variant in LD with the two SNPs.

In conclusion, we have developed X-APL as a powerful, robust, and versatile tool for family-based association analysis on the X chromosome. We demonstrated validity where other tests failed and showed that X-APL is more powerful than alternative tests, particularly when parental genotypes are unavailable, as for individuals with late-onset diseases. X-APL provides single-marker and global haplotype tests, as well as separate tests for males and females, allowing for evaluation of a variety of hypotheses. As presented here, X-APL uses nuclear families and allows for missing parental genotypes. XPDT and XMCPDT have the advantage of performing analyses for extended pedigrees. Similar approaches can be used to modify the APL and X-APL for extended pedigrees, and the bootstrap procedure to estimate the variance lends itself easily to this modification. We have implemented X-APL in a freely available software package. The X-APL software package is written in C++ and is available for use on several computer platforms. It can be publicly accessed at the Duke Center for Human Genetics Web site.