Experimental determination of object statistics from noisy images

Abstract

Modern imaging systems rely on complicated hardware and sophisticated image-processing methods to produce images. Owing to this complexity in the imaging chain, there are numerous variables in both the hardware and the software that need to be determined. We advocate a task-based approach to measuring and optimizing image quality in which one analyzes the ability of an observer to perform a task. Ideally, a task-based measure of image quality would account for all sources of variation in the imaging system, including object variability. Often, researchers ignore object variability even though it is known to have a large effect on task performance. The more accurate the statistical description of the objects, the more believable the task-based results will be. We have developed methods to fit statistical models of objects, using only noisy image data and a well-characterized imaging system. The results of these techniques could eventually be used to optimize both the hardware and the software components of imaging systems.

1. INTRODUCTION

Modern imaging systems rely on complicated hardware and sophisticated image-processing methods to produce images for evaluation. Owing to the complexity of the imaging chain, there are numerous variables in both the hardware and software that need to be determined. We and other groups advocate a task-based approach to measuring and optimizing image quality, i.e., optimizing imaging systems on the basis of the performance of an observer performing a specific task.^1–3 This type of analysis is especially important in medical imaging, where systems are inherently task driven, e.g., detection of tumors in images.

Tasks in medical imaging are either detection and classification tasks where the observer is classifying an image into two or more classes, or estimation tasks where the observer is attempting to estimate a particular quantity of interest.^1,4 In general, the types of observers that researchers can employ are ideal observers,³ human observers, or anthropomorphic observers (human-model observers).^5,6 The class of ideal observers includes the Bayesian observer,^3,7 which sets a theoretical upper limit on observer performance, and the Hotelling or ideal linear observer,¹ which sets an upper limit on the performance of an observer who performs only linear manipulations of the image data. Anthropomorphic observers attempt to predict the performance of a human observer reading the images for the specified task.

Numerous images are often required for computation of task-based measures of image quality and are thus infeasible with real patients. Researchers are forced to employ statistical models from which they can produce as many images as required. The stochastic nature of images is due to both detector noise and the randomness in the objects being imaged; e.g., patient anatomy differs greatly from person to person. Much of the current literature in this field has focused on generating image models that simulate a type of image produced with a particular imaging system.^8,9 Image models cannot be used to optimize imaging hardware, because they are specific to one imaging system.

It is desirable to have a model that takes both the object variability and the detector noise into account yet is independent of the imaging system. A statistical description of the objects being imaged is required, though we can observe objects only through a particular imaging system. We have developed methods to fit statistical models of objects that use only noisy image data, a well-characterized imaging system, and knowledge of the statistics of the noise. In this paper we will describe these methods and test them on a lumpy object model. In the future, we plan to use the results of these techniques to optimize both the hardware and the software components of imaging systems.

2. BACKGROUND

Imaging can be mathematically represented by

$$g=Hf+n,$$ (1)

where g is the M × 1 data vector, f is the continuous object being imaged, H is an operator representing the method in which an imaging system maps a continuous object to discrete data, and n is the measurement noise. Vectors are denoted by boldface type. (A note to the reader: Although f is a function, it still can be thought of as a vector in a Hilbert space, thus the vector notation.) The object f can represent, for example, the three-dimensional distribution of activity within an organ or the two-dimensional fluence of radiation impinging on a detector system. The vector g represents the data obtained from an imaging system that may be an image ready for viewing such as in projection x-ray imaging, or it may need processing before viewing, such as sinogram data from tomographic imaging systems.

The continuous-to-discrete operator H is often assumed to be linear and can be measured or modeled for a particular imaging system. We also assume that n is characterized by a known distribution—typically Poisson for gamma-ray imaging. We observe image data g, and thus it may be possible to experimentally determine the statistical properties governing g. However, little is known about the statistical properties of the objects f being imaged.

Because it is a random vector, the image data vector is governed by a probability density function (PDF), denoted pr(g). We could equivalently characterize the randomness in image data and objects by using the Fourier transform of the PDF or the characteristic function (CF). It is advantageous to represent the Fourier transform as an expectation over certain complex exponentials, defined for g as,

$${\mathrm{\Psi }}_g(\rho )={\langle exp(-2\pi i{g}^{†}\rho )\rangle }_{g.}$$ (2)

Here ρ is the Fourier conjugate of g, g^†ρ is the inner product of g and ρ, and 〈·〉_g represents an expectation over pr(g). The CF of the random process f has a similar definition,

$${\mathrm{\Psi }}_f(\xi )={\langle exp(-2\pi i{\xi }^{†}f)\rangle }_f,$$ (3)

where ξ is the infinite-dimensional Fourier conjugate of f. Because f is a random function, we will call Ψ_f(ξ) its characteristic functional (CFl).

Channels are often used in signal-detection tasks^5,10 to reduce the dimensionality of the image data vector g for computational purposes while retaining the salient information about the statistics of the image data. Specifically, Laguerre–Gauss channels have been employed successfully to approximate the ideal linear observer for complicated signal-detection tasks.¹⁰ A channel is a set of filters that are applied to an image to produce a vector of outputs v, i.e.,

$$v=Tg=T(Hf+n),$$ (4)

where T is the N × M linear channel matrix. The dimension (N) of v is much less than the dimension (M) of g; typically N is 6 to 15. Although we are not performing signal-detection tasks in this paper, the use of channels will aid in many of our computations.

3. OBJECT MODELS

In the past, researchers have focused on determining the statistical properties of the images^8,9 or assumed very simple nonrandom objects such as flat backgrounds. Both approaches essentially ignore the statistics of the objects that generate the images. Object variability, however, is known to have a substantial effect on observer performance and thus should not be ignored.^5,11 Characterizing the randomness of a continuous object function is difficult. In order to make the problem of determining the statistics of objects tractable, we will employ models of objects. We study two object models: lumpy objects¹¹ and clustered lumpy objects.¹²

A. Lumpy Objects

The first object model that we consider is the lumpy object model developed by Rolland and Barrett.¹¹ The lumpy object model is a continuous mathematical phantom designed to synthesize realistic objects such as those obtained in imaging biological tissue. For example, it is not uncommon to observe relatively few hot spots when one is imaging with nuclear medicine. The lumpy object model may be a good representation of such objects. Lumpy objects are generated by summing a random number of lump functions placed randomly in the field of view (FOV). Typically Gaussians are used as the lump functions, but other lump profiles could be used. Mathematically, a lumpy object is represented as

$$f=f(r)=\sum _{n=1}^N\mathrm{\Lambda }(r-c_n|a,s),$$ (5)

where r is a spatial coordinate in two or three dimensions, Λ(·) is the lump function, N is the number of lumps, c_n is the center of the nth lump function, a is the magnitude of the lump function, and s is the width parameter for the lump function.¹¹ The number of lumps N is a Poisson-distributed random variable with mean $\overline{N},$ c_n is uniformly distributed within the FOV, and both a and s are held constant. If we assume that the FOV and the lump function Λ(·) are given, then lumpy objects are characterized by the parameters $\overline{N},$ a, and s, which we will represent by the vector θ. Thus the CFl of f is conditional upon the parameter θ. Two examples of two-dimensional lumpy functions are shown in Fig. 1. The lumpy object model is fairly simple yet is an important starting point for this work. Note that although the lumps are Gaussian, the statistics governing this object model as a stochastic process are not Gaussian.

Fig. 1.

Examples of two-dimensional lumpy objects with different parameters θ.

The random variables N and {c_n} fully encompass the randomness of lumpy objects. Furthermore, as shown by Barrett and Myers,¹³ we can calculate the CFl for lumpy objects conditioned on the parameters characterizing the lumpy object model θ by substituting the definition of a lumpy object [Eq. (5)] into the CFl defined in Eq. (3):

$$\begin{array}{l}{\mathrm{\Psi }}_f(\xi |\theta )\\ ={\langle exp(-2\pi i{\xi }^{†}f)\rangle }_{f|\theta }\end{array}$$ (6)

$$={\langle exp\left[-2\pi i\int \xi (r)\sum _{n=1}^N\mathrm{\Lambda }(r-c_n|a,s)\text{d}r\right]\rangle }_{\left\{c_n\right\},N}$$ (7)

Here we have written out the L₂ inner product ξ^†f explicitly as ∫ξ(r)f(r)dr for a lumpy object. The expectation is taken with respect to {c_n} and N, the random variables that determine a lumpy object. The centers of the lumps, {c_n}, are uniformly distributed, and the number of lumps N is Poisson distributed. Simplifying the above expression, we have

$$\begin{array}{l}{\mathrm{\Psi }}_f(\xi |\theta )\\ =\langle {\prod _{n=1}^N{\langle exp\left[-2\pi i\int \xi (r)\mathrm{\Lambda }(r-c_n|a,s)\text{d}r\right]\rangle }_{c_n}\rangle }_N\end{array}$$ (8)

$$={\langle {\mathrm{\Psi }}_{\mathrm{\Lambda }}{(\xi |\theta )}^N\rangle }_N$$ (9)

$$=exp(-\overline{N})\sum _{N=0}^{\infty }\frac{{\overline{N}}^N}{N!}{\mathrm{\Psi }}_{\mathrm{\Lambda }}{(\xi |\theta )}^N$$ (10)

$$=exp\{-\overline{N}[1-{\mathrm{\Psi }}_{\mathrm{\Lambda }}(\xi |\theta )]\},$$ (11)

where $\overline{N}$ is the mean of N and Ψ_Λ(ξ|θ) is the characteristic functional of one randomly located lump given by

$${\mathrm{\Psi }}_{\mathrm{\Lambda }}(\xi |\theta )={\langle exp\left[-2\pi i\int \xi (r)\mathrm{\Lambda }(r-c|a,s)\text{d}r\right]\rangle }_c.$$ (12)

The computation of this function will be discussed in Section 6.

B. Clustered Lumpy Objects

In 1999, Bochud et al.¹² extended the lumpy object model to synthesize more complicated and realistic objects. Their model, known as clustered lumpy objects, clusters the lumps around certain cluster centers that are uniformly distributed within the FOV. This is represented mathematically for two-dimensional r as

$$f=f(r)=\sum _{n=1}^N\sum _{k=1}^{K_n}\mathrm{\Lambda }([R_{{\phi }_n}](r-c_n-{\mathrm{\Delta }}_{nk})|\alpha ),$$ (13)

where N is the number of clusters, K_n is the number of lump functions in the nth cluster, c_n is the center of the nth cluster, Δ_nk is the center of the kth lump function in the nth cluster, φ_n is the orientation of the lumps in the nth cluster, and α are the parameters characterizing the shape of the lumps. The rotation of the lumps is represented by the rotation matrix R_φn. Both N and K_n are Poisson distributed with means $\overline{N}$ and $\overline{K},$ respectively. The center of a cluster c_n is uniformly distributed over the FOV, and the lumps within a cluster are Gaussian distributed around c_n. That is, Δ_nk is sampled from a radially symmetric Gaussian distribution with width σ_Δ. The angle φ_n is, in general, uniformly distributed between 0 and 2π but may be distributed differently if desired. Again, assuming that the lump function Λ(·) is known, the parameters characterizing a clustered lumpy object are $\overline{N},\overline{K},$ σ_Δ, and α, which we combine to form the vector of parameters θ.

The function Λ(·) need not be a Gaussian function. Bochud used a two-dimensional asymmetric lump¹² given in polar coordinates as

$$\begin{array}{l}\mathrm{\Lambda }(r,\hspace{0.17em}\phi |\gamma ,\beta ,l_x,l_y)\\ =exp\left\{-\gamma r^{\beta }{\left[\frac{l_y^{2}cos{(\phi )}^2+l_x^{2}sin{(\phi )}^2}{l_x^2{l}_y^2}\right]}^{1/2}\right\}.\end{array}$$ (14)

This type of lump function was chosen because the resultant images approximated the texture of mammograms. Using this lump function results in seven parameters that characterize this object model, i.e., θ = { $\overline{N},\overline{K}$, σ_Δ, γ, β, l_x, l_y}. Examples of clustered lumpy objects are shown in Fig. 2.

Fig. 2.

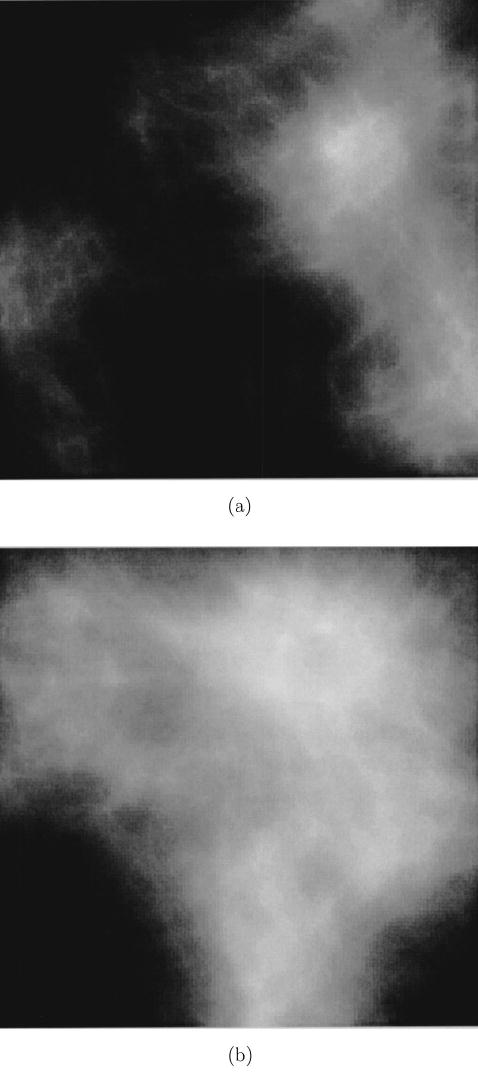
Examples of two-dimensional clustered lumpy objects with different parameters θ.

To calculate the CFl for the clustered lumpy object model, we rewrite the definition of a clustered lumpy object [Eq. (13)] as

$$f=f(r)=\sum _{n=1}^N\mathrm{\Omega }(r-c_n,\{{\mathrm{\Delta }}_{nk}\},{\phi }_n,K_n|\alpha ),$$ (15)

where

$$\begin{array}{l}\mathrm{\Omega }(r-c_n,\{{\mathrm{\Delta }}_{nk}\},{\phi }_n,K_n|\alpha )\\ =\sum _{k=1}^{K_n}\mathrm{\Lambda }([R_{\phi n}](r-c_n-{\mathrm{\Delta }}_{nk})|\alpha ),\end{array}$$ (16)

and {Δ_nk} is a list of K_n lump centers relative to the cluster center c_n. Equation (15) is similar to a lumpy object model with a more complicated lump function. Thus we will calculate the CFl of the clustered lumpy model in similar fashion. Beginning with

$${\mathrm{\Psi }}_f(\xi |\theta )=exp\{-\overline{N}[1-{\mathrm{\Psi }}_{\mathrm{\Omega }}(\xi |\theta )]\},$$ (17)

all that is left to compute is Ψ_Ω(·). The CFl for Ω can be expressed as

$${\mathrm{\Psi }}_{\mathrm{\Omega }}(\xi |\theta )={\langle exp\{-\overline{K}[1-{\mathrm{\Psi }}_{\mathrm{\Lambda }}(\xi |c,\hspace{0.17em}\phi ,\theta )]\}\rangle }_{c,\phi ,}$$ (18)

where Ψ_Λ(ξ|c, φ, θ) is the characteristic functional of a single randomly located lump with cluster center c and angle φ. The form of Ψ_Λ(·) is similar to Eq. (12) except that we now take the expectation over Δ instead of c. We are now able to write the final expression for the CFl of a clustered lumpy object model as

$$\begin{array}{l}{\mathrm{\Psi }}_f(\xi |\theta )=exp[-\overline{N}(1-\langle exp\{-\overline{K}[1\\ {-{\mathrm{\Psi }}_{\mathrm{\Lambda }}(\xi |c,\hspace{0.17em}\phi ,\hspace{0.17em}\theta )]\}\rangle }_{c,\phi })].\end{array}$$ (19)

We will discuss the computation of Ψ_f (ξ|θ) in Section 6.

4. TRANSFORMATION THROUGH IMAGING SYSTEMS

Both lumpy and clustered lumpy objects are characterized by the parameters θ. Our goal is to determine the parameters θ of the object model that best fit a set of image data {g_l}. The difficulty of this problem lies in that we can only observe g_l, and yet we wish to determine parameters that characterize the statistics of the objects f. We are further impeded because we do not know the PDF of g even though we have a model for f and a known imaging operator H. Maximum-likelihood estimation is thus not an immediate possibility. A different estimation approach is required that makes use of the knowledge we do have, namely, the CFl of the objects.

A complete description of the transformation of an object CFl through an imaging system is described by Clarkson et al.¹⁴ We summarize those results in Subsection 4.A.

A. Noiseless Imaging System

Let us assume that we know the CFl of the object distribution Ψ_f (ξ | θ). Let us, for now, envision a noiseless imaging system

$$\overline{g}=Hf$$ (20)

and analyze the characteristic function of $\overline{g}$. (The over-bar notation is used because $\overline{g}$ can be thought of as the noise-averaged image for a particular object f.) The characteristic function of $\overline{g}$ is

$${\mathrm{\Psi }}_{\overline{g}}(\rho |\theta )={\langle exp(-2\pi i{\rho }^{†}\overline{g})\rangle }_{\overline{g}|\theta }$$ (21)

$$=\int p(\overline{g}|\theta )\prod _{m=1}^{M}exp(-2\pi i{\rho }_m{\overline{g}}_m)\text{d}\overline{g},$$ (22)

which, by use of our noiseless imaging system [Eq. (20)] and using properties of the adjoint, can be rewritten as^13,14

$${\mathrm{\Psi }}_{\overline{g}}(\rho |\theta )={\langle exp(-2\pi i{(H^{†}\rho )}^{†}f)\rangle }_{f|\theta }$$ (23)

$$={\mathrm{\Psi }}_f(H^{†}\rho |\theta ).$$ (24)

Thus, if the CFl of f is known, then we also know the CF of any linear mapping of f by simply using the adjoint of the linear operator. Although we do not know the PDF of $\overline{g},$ we do know ${\mathrm{\Psi }}_{\overline{g}}(\rho |\theta )$ for either of our object models.

B. Noise

Thus far, we have dealt with noise-free imaging systems that are of little practical value. In order for the methods developed in this paper to be of practical interest, we must be able to compute the characteristic function of the image data $g=\overline{g}+n$ accounting for both object variability and noise. Two common noise models that researchers employ are Gaussian noise and quantum or Poisson noise.

The characteristic function for Gaussian noise with covariance K is known to be Gaussian as well, with the form

$${\mathrm{\Psi }}_n(\rho |K)=exp(-2{\pi }^2{\rho }^{†}K\rho ).$$ (25)

Because the noise is independent of the object being imaged, we know that the PDF of g is a convolution of the PDF of $\overline{g}$ and the PDF of n, which, using the Fourier-convolution theorem, yields

$${\mathrm{\Psi }}_g(\rho |\theta ,K)={\mathrm{\Psi }}_f(H^{†}\rho |\theta ){\mathrm{\Psi }}_n(\rho |K).$$ (26)

Poisson detector noise can also be incorporated into this framework. Poisson noise is conditional upon the mean image, i.e.,

$$\text{pr}(g|\overline{g})=\prod _{m=1}^{M}exp(-{\overline{g}}_m)\frac{{\overline{g}}_m{}^{g_m}}{g_m!},$$ (27)

where ${\overline{g}}_m$ denotes the mth component of the M vector $\overline{g}$. The PDF of g can then be obtained by marginalizing over the object $\overline{g}$,

$$\text{pr}(\text{g}|\theta )=\int \text{pr}(g|\overline{g})\text{pr}(\overline{g}|\theta )\text{d}\overline{g}$$ (28)

$$=\int \text{pr}(\overline{g}|\theta )\prod _{m=1}^{M}exp(-{\overline{g}}_m)\frac{{\overline{g}}_m{}^{g_m}}{g_m!}\text{d}\overline{g}.$$ (29)

By taking the expectation of the complex exponentials over the PDF given above, we arrive (after some manipulations described by Clarkson et al.¹⁴) at

$$\begin{array}{l}{\mathrm{\Psi }}_g(\rho |\theta )\\ =\int \text{pr}(\overline{g}|\theta )\prod _{m=1}^{M}exp[-{\overline{g}}_m+{\overline{g}}_{m}exp(-2\pi i{\rho }_m)]\text{d}\overline{g},\end{array}$$ (30)

which is close to the CF of $\overline{g}$ [Eq. (22)] except that the term in the exponent is not the same. We can relate the above expression to the CF of $\overline{g}$ by defining a nonlinear operator Γ(·) that maps an M vector to another M vector, by using the following equation for each component m,

$${[\mathrm{\Gamma }(\rho )]}_m=\frac{-1+exp(-2\pi i{\rho }_m)}{-2\pi i}.$$ (31)

Thus we can relate the CF of g to that of the noiseless CF of $\overline{g}$ that we previously related to the CFl of f, i.e.,

$${\mathrm{\Psi }}_g(\rho |\theta )={\mathrm{\Psi }}_{\overline{g}}(\mathrm{\Gamma }(\rho )|\theta )={\mathrm{\Psi }}_f(H^{†}\mathrm{\Gamma }(\rho )|\theta ).$$ (32)

In other words, because we know the CFl for our object models, we are able to use H^† and a known nonlinear operator to determine the CF for our noisy image data.

C. Channels

The channel operator, like the imaging system itself, is a linear operator, and thus if one wants to know the CF for the channel outputs v = Tg = T(H f + n), one needs only the adjoint T^†. That is,

$${\mathrm{\Psi }}_v(\omega |\theta )={\mathrm{\Psi }}_f(H^{†}\mathrm{\Gamma }(T^{†}\omega )|\theta ),$$ (33)

where ω is the Fourier conjugate of the channel outputs v.

5. ESTIMATION

One can determine exactly the CF of channel outputs Ψ_v(ω | θ) by using either of the two object models discussed. Given a database of L images {g_l}, we would like to estimate the parameters θ that characterize the object model that best fits the data, using channel outputs from these images v_l = Tg_l.

A standard maximum-likelihood or Bayesian approach to solving this problem is not computationally feasible. The likelihood of θ for an ensemble of images {g_l} is given by

$$\text{pr}(\{g_l\}|\theta )=\prod _{l=1}^L\int \text{d}f\hspace{0.17em}\text{pr(}{g}_l|f)\text{pr}(f|\theta ).$$ (34)

We would have to perform L high-dimensional integrals for a given θ. To optimize θ, we would have to compute these L integrals repeatedly as part of an iterative search. We present an estimation technique that relies on characteristic-function analysis to simplify the estimation of θ.

A. Empirical Characteristic Function

The characteristic function of a random variable or vector is an expectation value of the complex exponentials, i.e.,

$${\mathrm{\Psi }}_v(\omega )={\langle exp(-2\pi i{\omega }^{†}v\text{)}\rangle }_v.$$ (35)

Hence, given independent data sampled from pr(v) and denoted by v_l with l = 1 ... L, the characteristic function of v can be approximated by the sample average of the complex exponentials. That is, the empirical characteristic function is given by

$${\widehat{\mathrm{\Psi }}}_v(\omega )=\frac{1}{L}\sum _{l=1}^{L}exp(-2\pi i{\omega }^{†}{v}_l).$$ (36)

The empirical characteristic function is an unbiased estimate of the true characteristic function. We can further derive an expression for the covariance C(ω, ω ′) of this estimate:

$$C(\omega ,{\omega }^{\prime })={\langle {\widehat{\mathrm{\Psi }}}_v(\omega ){\widehat{\mathrm{\Psi }}}_v^{*}({\omega }^{\prime })\rangle }_{\left\{v_l\right\}}-{\mathrm{\Psi }}_v(\omega ){\mathrm{\Psi }}_v^{*}({\omega }^{\prime })$$ (37)

$$\begin{array}{l}=\frac{1}{L^2}\sum _{l=1}^L\sum _{l^{\prime }=1}^L\langle exp(-2\pi i{\omega }^{†}{v}_l)\\ {\times \hspace{0.17em}exp\hspace{0.17em}(2\pi i{{\omega }^{\prime }}^{†}{v}_{l^{\prime }})\rangle }_{v_l,v_{l^{\prime }}}\\ -{\mathrm{\Psi }}_v(\omega ){\mathrm{\Psi }}_v^{*}({\omega }^{\prime }).\end{array}$$ (38)

In the above double summation, there are L terms where l = l′ in which the inner expectation values become

$${\langle exp[-2\pi i{(\omega -{\omega }^{\prime })}^{†}{v}_l]\rangle }_{v_l}={\mathrm{\Psi }}_v(\omega -{\omega }^{\prime })$$ (39)

and L² − L terms where l ≠ l′ in which the inner expectation values become

$${\langle exp(-2\pi i{\omega }^{†}{v}_l)\rangle }_{v_l}{\langle exp(2\pi i{\omega }^{†}{v}_{l^{\prime }})\rangle }_{v_{l^{\prime }}}={\mathrm{\Psi }}_v(\omega ){\mathrm{\Psi }}_v^{*}({\omega }^{\prime }).$$ (40)

Equation (40) makes use of the independence of the two distinct samples v_l and v_l′. Thus our final expression for the covariance is

$$C(\omega ,\hspace{0.17em}{\omega }^{\prime })=\frac{1}{L}[{\mathrm{\Psi }}_v(\omega -{\omega }^{\prime })-{\mathrm{\Psi }}_v(\omega ){\mathrm{\Psi }}_v^{*}({\omega }^{\prime })].$$ (41)

By setting ω = ω ′ and noting that Ψ(0) = 1 by definition, we arrive at an expression for the variance V(ω) of the empirical estimate of the characteristic function,

$$V(\omega )=\frac{1}{L}[1-|{\mathrm{\Psi }}_v(\omega ){|}^2].$$ (42)

Note that the variance of the empirical characteristic function goes to 0 as ω approaches 0, so for most smoothly varying functions, the variance of the empirical characteristic function is small near ω = 0.

B. Cost Functions

We have yet to discuss potential cost function that could be employed to determine the object model parameters θ that best fit the available data. One obvious choice would be to apply weighted least-squares fitting of the characteristic functions. We are further aided by our knowledge of the variance of the empirical characteristic function as given in Eq. (42). The weighted least-squares solution is one that minimizes the weighted mean squared error,

$$\text{Wmse(}\theta \text{)}=\int \frac{|{\widehat{\mathrm{\Psi }}}_v(\omega )-{\mathrm{\Psi }}_v(\omega |\theta ){|}^2}{\frac{1}{L}[1-\hspace{0.17em}|{\mathrm{\Psi }}_v(\omega |\theta ){|}^2]}\text{d}\omega ,$$ (43)

where the denominator is an estimate of the variance of the empirical characteristic function [Eq. (42)]. Dividing by the variance of the empirical characteristic function has the effect of weighting regions with small variance more than those with large variance. We actually have a choice in Eq. (43) of using either Ψ_v(ω | θ) or $\widehat{\mathrm{\Psi }}(\omega )$ in the denominator for the variance expression.

The aforementioned cost function involves an integral over ω. Another approach to generating a cost function would be to approximate the inverse Fourier transform of Ψ_v(ω | θ) to obtain $\widehat{\text{p}}\text{r(}v|\theta )$ and then use maximum-likelihood estimation to choose the θ that maximizes

$$\lambda (\theta |\{v^{(l)}\})=\sum _{l=1}^{L}log[\widehat{\text{p}}\text{r(}{v}^{(l)}|\theta \text{)}]\text{.}$$ (44)

This also involves an integral over ω, but this integral turns out to be difficult to approximate.

6. COMPUTATIONAL ISSUES

Each of the cost functions [Eqs. (43) and (44)] requires an integral over ω that we calculate with Monte Carlo techniques. Monte Carlo techniques require a PDF in the integrand, something our cost functions lack. Importance sampling^15,16 provides the means to avert this lack of a PDF by multiplying and dividing by a user-defined PDF. It is advantageous to choose a PDF that would sample points around the important region of the integrand, i.e., nonzero values of the integrand. For example, Eq. (43) could be approximated by

$$\text{Wmse(}\theta \text{)}=\int \frac{|{\mathrm{\Psi }}_v(\omega |\theta )-{\widehat{\mathrm{\Psi }}}_v(\omega ){|}^2}{\frac{1}{L}[1-\hspace{0.17em}|{\mathrm{\Psi }}_v(\omega |\theta ){|}^2]}\text{d}\omega$$ (45)

$$=\int \frac{|{\mathrm{\Psi }}_v(\omega |\theta )-{\widehat{\mathrm{\Psi }}}_v(\omega ){|}^2}{\frac{1}{L}[1-\hspace{0.17em}|{\mathrm{\Psi }}_v(\omega |\theta ){|}^2]}\frac{\text{pr}(\omega )}{\text{pr}(\omega )}\text{d}\omega$$ (46)

$$~\frac{1}{J}\sum _{j=1}^J\frac{|{\mathrm{\Psi }}_v({\psi }_j|\theta )-{\widehat{\mathrm{\Psi }}}_v({\omega }_j){|}^2}{\frac{1}{L}[1-\hspace{0.17em}|{\mathrm{\Psi }}_v({\omega }_j|\theta ){|}^2]}\frac{1}{\text{pr}({\omega }_j)},$$ (47)

where ω_j is sampled from pr(ω).

The accuracy of the expression in Eq. (47) depends on J and the importance sampler pr(ω_j). Therefore a good choice of pr(ω_j) is needed. If we were to assume that the v_l were Gaussian distributed with covariance matrix ∑, then |Ψ_v(ω)| would be an unnormalized Gaussian with covariance matrix ∑⁻¹. Furthermore, the maximum of a characteristic function is 1 and occurs at ν = 0. Thus a reasonable choice for an importance sampler would be a Gaussian with zero mean and covariance ∑⁻¹. We measure the sample covariance $\widehat{\mathrm{\Sigma }}$for the channel outputs v_l and use ${\widehat{\mathrm{\Sigma }}}^{-1}$ as the covariance of our Gaussian importance sampler. The v_l are not Gaussian distributed, but this method provides a successful Gaussian sampler; i.e., the ω_j’s sampled lie near the peak of the integrand.

The term $\widehat{\mathrm{\Psi }}(\omega )$ in Eq. (47) is a straightforward computation. However, we have yet to describe how one calculates Ψ_v(ω_j | θ). Specifically, the term Ψ_Λ (·) shown in Eqs. (11) and (18) is computationally burdensome. For the lumpy object model, the characteristic functional of a single randomly located lump is given by

$${\mathrm{\Psi }}_{\mathrm{\Lambda }}(\xi |\theta )=\int p(c)exp\left(-2\pi i\int \text{d}r\xi (r)\mathrm{\Lambda }(r-c)\right)\text{d}c,$$ (48)

where p(c) is the PDF of the lump centers, which, as we described earlier, are uniformly distributed within the FOV for lumpy objects. Now, replacing ξ(r) with H_†Γ (T^†ω), we arrive at

$$\begin{array}{l}{\mathrm{\Psi }}_{\mathrm{\Lambda }}(\omega |\theta )=\int p(c)exp(-2\pi i\int \sum _{m=1}^M{h}_m(r)\mathrm{\Gamma }{(T^{†}\omega )}_m\\ \times \hspace{0.17em}\mathrm{\Lambda }(r-c)\text{d}r)\text{d}c\end{array}$$ (49)

$$\begin{array}{l}=\int p(c)exp(-2\pi i\sum _{m=1}^M\mathrm{\Gamma }{(T^{†}\omega )}_m\\ \times \hspace{0.17em}\int h_m(r)\mathrm{\Lambda }(r-c)\hspace{0.17em}\text{d}r)\text{d}c.\end{array}$$ (50)

This equation makes use of the adjoint of a continuous-to-discrete operator, i.e.,

$$H^{†}x=\sum _{m=1}^M{h}_m(r)x_m.$$ (51)

Also note that the inner integral in Eq. (50) is equivalent to transferring a lump centered at position c through the imaging system H and taking the inner product with the M vector Γ(T^†ω). We are aided in this computation because the M vector Γ(T^†ω_j) is fixed for a given importance sample ω_j. Thus, once we have our importance samples ω_j, we can precompute and store every element of this vector. In practice, we store this information in pieces because of computer memory limitations. We are still left with computing the outer integral over c. We again resort to Monte Carlo techniques to approximate this integral by sampling c_n uniformly in the FOV and averaging the integrand at each sampled point.

Similar techniques are applied to compute Ψ_Λ (·) for the clustered lumpy object model. The key difference is the increase in the number of random variables to integrate over: the angle of the lump, the cluster center, and the lump center. Again, Monte Carlo techniques can readily be employed for this computation because the densities are known for each of these parameters.

7. SIMULATIONS

The goal of our work is to determine parameters that characterize an object model by using only noisy images of the objects. To validate the methods presented in Section 3, we performed simulation studies using objects that match the model employed. We ran our simulations in parallel on five Pentium-based computers running Linux. The computers communicated by using the Parallel Virtual Machine (PVM) package. The optimization was performed with APPSPACK, a freely available optimization routine from Sandia National Laboratories.

We began by generating 100 64 × 64 images g_l, using the lumpy object model and a simulated imaging system. We then calculated the channel outputs v_l by using a channel operator T. We calculated Ψ_v(ω | θ) from our knowledge of Ψ_f (ξ | θ) for the lumpy object model and our knowledge of H, T, and the noise. We varied the parameters θ to match the data v_i by using the cost function shown in Eq. (43). Note that this cost function requires the empirical characteristic function determined from the data ${\widehat{\mathrm{\Psi }}}_v(\omega )$ [Eq. (36)].

The imaging system that we simulated was an idealized parallel-hole collimator system represented by

$${\overline{g}}_m=\gamma \int h_m(r)f(r)\text{d}r,$$ (52)

where h_m(·) is a Gaussian blur function centered at the mth pixel with a standard deviation of 1.5 pixels and γ is the amplitude of the system, which we set to 40. The images were generated by sampling a Poisson distribution for the mth pixel with parameter ${\overline{g}}_m$. For the lumpy object model with Gaussian lumps, there exists a closed-form expression for the integral in the imaging equation [Eq. (52)]. Example images used in the simulation are shown in Figs. 3(a)–3(c).

Fig. 3.

Simulation results for lumpy objects. (a)–(c) Three of the images used to fit the lumpy object model parameters. (d)–(f ) Three images generated by using the fitted model parameters. The top row of images are not meant to look exactly like the bottom row of images; they are simply meant to appear statistically similar.

The filter T that we used consisted of the first three Laguerre–Gauss functions.¹⁰ Laguerre—Gauss functions are circularly symmetric products of a Gaussian with Laguerre polynomials centered within the FOV. Because the lumps that we used in the lumpy object model are circularly symmetric and the statistical distribution of their positions is circularly symmetric and stationary (ignoring boundaries), the Laguerre–Gauss functions are a reasonable choice of channels to extract the salient statistical information about the object model. As we will show, we are able to get good estimates of our three object model parameters by using just three channels. It should be noted that computing the cost function becomes more and more computationally burdensome as the number of channels increases.

Note that we have run these simulations with the data-matching model in an attempt to verify our method. In this situation, we therefore have a great deal of prior knowledge about our objects that we exploit to limit the number of channels used. A more realistic situation is one in which the model does not perfectly match the data. Of course, it is difficult to verify that the method works properly if the true parameters θ are not known.

The parameters θ used to generate the 100 images g_l were $\overline{N}$ = 30, a = 1, and s = 5. The method returned an estimate of θ with parameter $\overline{N}$ = 26, a = 1.06, and s = 5.23, which are close to the true values. Using these fitted parameters, we then regenerated random images, using our simulated imaging system [shown in Figs. 3(d)–3(f )] that are statistically similar to the original images shown in Figs. 3(a)–3(c). Thus the method was able to determine the parameters that characterize the stochastic object model by using only channel outputs from 100 noisy and blurry images.

We reperformed this experiment ten times with different sets of images (100 each time) to obtain the average estimate of θ as well as the standard deviations of our estimates. The results of these ten runs in terms of the mean ± the standard deviation were $\overline{N}$ = 32.0 ± 6.2, a = 1.16 ± 0.28, s = 4.67 ± 0.77. Thus the method performs consistently over different sets of images.

8. DISCUSSION AND CONCLUSIONS

We have presented a method for fitting statistical object models to real image data produced by a well-characterized imaging system. With a statistical object model, one can readily simulate imaging systems and produce image data to be used in computing task performance. The method that we have presented addresses directly the variability in the objects being imaged and accounts for any blur or any degradation that may occur during imaging as well as the noise in the image data produced.

We presented and discussed our technique as it relates to two specific object models: the lumpy object model and the clustered lumpy object model. Our method, however, is general. All it requires is that the characteristic function of the object be computable. We showed that this condition is met for the lumpy and clustered lumpy object models. There are other object models based on filter-bank or wavelet analysis that might also be applicable to this technique.

The simulation study performed in this paper was a consistency test. That is, given that the model matches the data, does the method return parameters that are close to the true parameters? If one were to apply this technique to real images, then it would be impossible to say what the correct parameters were. The method for applying this technique to real images is exactly as presented in this paper. We will address the issues involved with matching statistical object models to real images in a future publication.

To ease computational complexity, we employed channel operators to reduce the dimensionality of the image data. Channels have been successfully employed in many signal-detection^5,17 and texture-analysis methods.⁸ However, we have not addressed the issue of the ideal or best filters to use for our method. This issue became particularly important when we applied our method to the clustered lumpy object model, because the lump functions for that model are asymmetric. It was difficult to determine the lump parameters by using symmetric Laguerre–Gauss channels. In particular, the parameters l_x and l_y that characterize the asymmetry in the lumps were never properly estimated with the Laguerre–Gauss channels. Channel selection is also an issue with sinogram image data, in which locally supported filters are not such an obvious choice.

We would like to compare different object models by measuring the performances of the corresponding ideal observers on real images of the real objects. The eventual goal of studying this technique is to perform hardware optimizations by using task-based measures of image quality. Specifically, we would like to compute ideal-observer performance for an imaging system by using one of our fitted object models. These topics will be addressed in future publications.