Evolutionary demographic models for mortality plateaus

Abstract

Plateaus in the age pattern of hazard functions at extreme ages have been discovered in large populations of medflies, Drosophila, nematodes, and people. Mueller and Rose [(1996) Proc. Natl. Acad. Sci. USA 93, 15249–15253] have proposed several age-structured demographic models to represent effects of mutation accumulation and antagonistic pleiotropy on randomly evolving schedules of demographic rates. They assert that “evolutionary theory [as embodied in their models] predicts late-life mortality plateaus.” This paper defines a class of Markovian models that includes those of Mueller and Rose and obtains a characterization of the possible limiting states. For the basic model, the result implies that schedules with late-life mortality plateaus above a minimal threshold are not limiting states. The models fail, but not for reasons previously conjectured. Transient states, visited early by the process, do display mortality plateaus. Other models from this class may have a role to play in reconciling observed plateaus with evolutionary theory.

The 1990s have brought the realization that there are a variety of species for which the widely observed acceleration of mortality rates with age abates or reverses at extreme ages. Documented cases include several million Mediterranean fruit flies, isogenic strains of Drosophila, nematode worms, and stationary-phase yeast. The highest quality data on human centenarians hint at this phenomenon in our own species as well (1–4).

These findings have catalyzed the emerging field of “biodemography” (5), because they do not fit neatly into the evolutionary theory of senescence pioneered by Sir Peter Medawar and George Williams (6–8). The diminishing contribution of older ages to net reproduction is supposed to shift the mutation-selection balance with respect to genes compromising late-age survival, implying a smooth increase in mortality rates with age late in reproduction. The accumulation of mutations with deleterious effects on survival solely at postreproductive, postnurturant ages logically would lead to accelerating mortality at these ages. Antagonistic pleiotropy, plausibly reflecting tradeoffs between reproduction and somatic maintenance, would be expected, on the face of it, to reinforce a pattern of ever-steepening mortality with age.

Contrary to these expectations, Mueller and Rose (9) announced that “evolutionary theory predicts late-life mortality plateaus.” They introduced several stochastic models for processes in which mutation accumulation and antagonistic pleiotropy induce long-term changes in age-specific demographic rates. The curves of mortality by age to which their models lead in the paper rise to moderately high levels and then flatten out, in the shape of plateaus.

Mueller and Rose have been challenged by Charlesworth and Partridge (10) and by Pletcher and Curtsinger (11). Both concentrate, as does the present paper, on the basic model (here called MR1A) simulated for figure 1A in ref. 9. Noting that the simulations, run for a finite time span, may not reveal the model’s long-term consequences, Charlesworth and Partridge conjecture that the true limiting states are trivially degenerate. Pletcher and Curtsinger conjecture that the MR1A process does approach a plateau-like equilibrium, but only because of certain specialized and unrealistic assumptions. All conclude that the Mueller–Rose models leave mortality plateaus unexplained.

This paper presents a mathematical analysis of a class of Markovian models for the genesis of mortality plateaus including those of Mueller and Rose. The chief result is a theorem characterizing the possible limit points for all processes in this class. Corollaries establish that limiting states of MR1A essentially never have the form of plateaus. These results also settle the conjectures of Charlesworth and Partridge and of Pletcher and Curtsinger, in the negative. The models fail, but not in the ways previously suggested. Despite these findings, the final section of this paper argues that this family of stochastic models may help in reconciling mortality plateaus with evolutionary theories of senescence.

Models

I begin by defining a class of Markovian models for changing schedules of demographic rates. All Mueller–Rose models are special cases. A schedule is a vector giving age-specific mortality and fertility rates at all ages. These rates are assumed to apply uniformly to all members of a population. The population dynamics determine the transition probabilities for the process of interest, namely, a series of step-by-step changes in the prevailing schedules. One step (one unit of time for the process) corresponds to a whole evolutionary episode in which (perhaps after a number of false starts and over many generations) an altered schedule is introduced and takes over throughout the population. Although a genetic interpretation is not essential to the mathematics, the readiest picture would be a dominant mutation, affecting mortality and fertility at specific ages, going to fixation.

Formally, I introduce the following structure:

The state space of allowable demographic schedules is a topological space S.

Fitness is measured by a bounded continuous real criterion function r : S → R.

A finite collection of continuous functions m : s → ms from S to S represent moves or mutations, one-step alterations in the demographic schedules.

The gain at state s from move m is r(ms) − r(s).

A starring move m*^s at state s is a move with maximal gain: r(m*^ss) = max_m r(ms).

The set of absorbing states is A = {s : r(ms) − r(s) ≤ 0 for all m}.

Define a Markov chain X_t, t = 1, 2, … starting at some state s₀.

If X_t is in A, X_t+1 = X_t.

If X_t = s is not in A, the permitted transitions are those moves s → ms for which r(ms) − r(s) > 0. The transition probabilities p_s(m) depend on the state s and need not be continuous functions of s.

The leading example is Mueller and Rose’s MR1A. The state space is S = [0, 1]¹¹⁰. The components of an element of s are indexed by ages x from 1 to 110, intended to represent days in a dipteran life cycle. (The model could be adapted to represent a human life cycle with ages in years.) The x component is the conditional probability q_x of dying between ages x and x + 1 given survival to x. In this model age groups 1–9 are juvenile, and all adult age groups from 10 to 110 are reproductive, with fertility rates f_x fixed at one per day. The criterion function r is Lotka’s intrinsic rate of natural increase, the real root of the equation

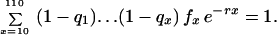The moves represent pleiotropic mutations of the adult survival schedule. There are 101² possible moves, indexed by a pair of adult ages b and g.

The mutation has a bad effect at age b, increasing the probability of dying q_b:

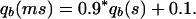It has a good effect at age g, decreasing q_g:

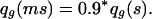Probabilities of dying at other ages remain unchanged.

The probability of the move m at a state s, the probability of fixation for the mutation, is a monotone function of the gain r(ms) − r(s) in fitness calculated from a formula representing effects of genetic drift. Only moves with positive gain are permitted. No neutral or deleterious mutations are allowed to go to fixation. If there is no move of positive gain, the Markov process halts. Because there are never more than 101² permitted moves, the monotonicity of the probabilities makes the probability of a starring move always greater than C = 101⁻².

Limit Characterization

Sample paths for models of this kind seem hard to characterize. In MR1A, mortality is allowed to go down at one age only if it goes up at another but only by so much as to leave a net gain in fitness overall. Deliberately finding moves to take the process toward high r would involve something like a chess game, sacrificing here and there to open up gains elsewhere. Stochastically, moves that block better, later moves are likely to occur.

The objects that do lend themselves to characterization are the absorbing states. The process need not converge to some single absorbing state, but one might hope that any limit points would have to be absorbing states. A condition is required to keep the process from taking, with positive probability, infinitely many wrong turns away from the vicinity of any absorbing state. The transition probabilities are not typically continuous functions, precluding quick arguments. But it turns out that there is a condition on the probabilities, satisfied by all the Mueller–Rose models, which does force all limit points to be absorbing states.

Theorem: If the infimum over all states s of the maximum probability p_s(m*^s) of a starring move for s equals some C greater than zero, then the limit points of X_t with respect to the topology on S belong to the set A of absorbing states with probability one.

Proof: The sample space can be identified with paths on a rooted tree in a usual way. Consider all infinite sequences of moves. Each initial segment of length t from a sequence corresponds to a node n of depth d(n) = t. The starting state s₀ is the root. The branches are the moves. A state s[n] is associated with each node n, namely the state reached from s₀ by taking the moves to that node. The same state may be associated with several distinct nodes, complicating the notation. The tree is pruned by removing all branches at and beyond any move with zero or negative gain, leaving finitely or countably many nodes. Each sample path ω then corresponds to a finite or infinite path up the tree starting from the root. The absorbing states are found at leaves or terminal nodes.

Define a real function h on the nodes of the tree by setting h(n) = r(m*^s[n] s[n]) − r(s[n]). Its value is the largest gain from any move starting at the state corresponding to the node.

Choose ɛ > 0. For any natural number T, define a set of nodes beyond T with potential for high-gain moves (exceeding ɛ) by

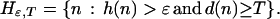Because the criterion function r is bounded, no sample path ω can take moves with gains greater than ɛ infinitely often. What is needed is the stronger claim that there is zero probability for the set of sample paths which visit nodes in H_ɛ,T infinitely often for any T. (These paths necessarily take moves other than the high-gain moves all but finitely often when leaving nodes in H_ɛ,T.)

Let V(n) be the set of sample paths ω that visit node n.

Let W(n, m) be the paths that visit node n and take move m away from node n.

Let X(n, ɛ) = {ω : ω in W(n, m) for some m such that r(ms[n]) − r(s[n]) > ɛ}.

These are the paths in V(n) that do take a high-gain move away from the node n.

For any node n in H (i.e. H_ɛ,T), the assumed lower bound on the probability of taking some starring move away from any state implies that

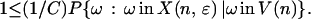Multiplying both sides by the probability of visiting the node,

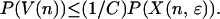This inequality holds separately for each node in H. To extend it to the union of V(n) over nodes in H requires constructing a partition. The collection of subsets V(n) is partially ordered by inclusion. All the paths that visit a given node coincide at nodes closer to the root of the tree, so any two subsets V(n) and V(n′) are either disjoint or included, one in the other. The maximal elements for the partial ordering therefore form a finite or countable collection of disjoint subsets of paths containing every path that visits any node in H. Call the collection of nodes indexing these subsets I. The index set I, strictly speaking I_ɛ,T, is a subset of H_ɛ,T. Because each W(n, m) is a subset of V(n), the W(n, m) as well as the V(n) are disjoint for different n in I. It follows that

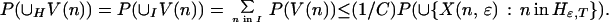The union set on the right-hand side consists of all paths ω that take a move with gain bigger than ɛ at one or more nodes at or beyond T from the root. The limit as T goes to infinity is zero, because the intersection over T is empty: the criterion function r is bounded, and no path can have gains greater than ɛ on infinitely many moves. Thus

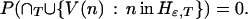In other words, there is zero probability that a path infinitely often visits nodes with high-gain moves. For any ɛ, there is probability one for the set of paths each of which, beyond some T, only visits nodes with h(n) less than or equal to ɛ. Choosing a sequence of epsilons converging to zero, I have shown that h(n) converges to zero along sample paths with probability one.

The continuity of the criterion function r and of every move m mapping S to S along with the finite size of the collection of moves make r(m*^ss) − r(s) a continuous function on S. The function h at a node n equals this difference evaluated at the state s[n] corresponding to the node.

The state s[n] belongs to the absorbing states A if and only if h(n) ≤ 0. Paths that terminate after visiting finitely many nodes necessarily terminate in A. A state s_l is a limit point of the Markov process if and only if there exists a finite or infinite subsequence n(1), n(2), ⋯ of the nodes visited by a sample path such that the limit as j → ∞ of s[n(j)] equals s_l. I have proved that h(n(j)) converges to zero with probability one, which is to say that the sequence of values of the difference function r(m*^ss) − r(s) evaluated at the states s[n(j)] converges to zero. The continuity of the difference function then implies that

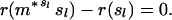I conclude that the limit points belong to A with probability one, Q.E.D.

Limiting States

The theorem allows us to determine whether a given state can be a limit point of the process by testing whether it belongs to the set A. A state s belongs to A if and only if the inequalities r(ms) ≤ r(s) are satisfied for each of the finitely many m. Like previous authors (10, 11), I concentrate on MR1A, which already displays the chief properties of all the Mueller–Rose models. For MR1A, starting from a state with probabilities of dying q_x and overall fitness r, the gain in fitness from a move with g ≤ b is positive if and only if

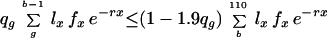with

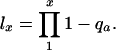A similar expression holds for b < g.

Fix q₁₁₀ = Q and r and take b = 110. The inequality supplies a recursion from which to calculate maximum allowable values for q_g for g = 109, 108, ⋯ 10, compatible with r. Tune r to agree with the q-values, and call the resulting schedule h_x(Q).

The first specific result for MR1A tests for the possibility of a terminal flat stretch of q-values among limiting states.

Corollary 1. For MR1A, no state with q_z = q_z+1 ⋯ = q₁₁₀ = Q and q_x < Q for 10 ≤ x < z is a limit point with positive probability unless Q ≤ h_z(1).

Corollary 1 only allows terminal flat stretches too miniscule to qualify as meaningful plateaus. The function h_x(1) is close to exp(−22.6779 + 0.1829x) except at the last few ages where q_x rises from q₁₀₁ = 0.0171 to q₁₀₉ = 0.3227. A plateau starting at age 70 would have all adult q_x less than 10⁻⁵.

If the process does not start (and immediately stop) in A, it takes some moves, and every move has a deleterious effect at some age b, leaving that q_b no less than 0.10. A limiting state in A can have such a large q-value only in the last few age groups:

Corollary 2. In MR1A, if s₀ is not in A, then with probability one, for every limit point of the process, the maximum value for the probability of dying is found within the oldest five age groups.

I now settle the Charlesworth–Partridge conjecture in the negative. They noted cogently that in “the Mueller and Rose pleiotropy model, the evolutionary process was run only for a finite amount of time.” They then conjectured “… presumably, late-life survival rates would approach zero as more evolutionary time elapsed, so again late survival is unexplained” (10).

If survival rates had to approach some constant limit, the limit would have to be one, not zero, because all Mueller–Rose models give positive fecundity to every adult age. There are no postreproductive age groups. It is true that the Mueller–Rose simulations were run too briefly to approach limiting behavior. But it is not true that, had they been run sufficiently long, the limit need be trivial.

Corollary 3. For MR1A, if the starting state has q_x > 2 ×  10⁻⁵ for all x, then with positive probability the process converges to a state with q_x increasing faster than exponentially with age.

Corollary 4. For MR1A, if the starting state has q_x > 2 ×  10⁻⁵ for all x, then, with positive probability, the limit points of the process include a state with q_x = 0 for x < 110.

These corollaries are proved by displaying a finite sequence of permitted moves that lead to the states described. The limit in corollary 3 can be taken to lie within a factor of 0.9 of h_x(10/19), an accelerating Gompertzian mortality schedule just the opposite of the flattening schedules that the models were invented to explain.

Pletcher and Curtsinger (11) discuss MR1A in depth. They endow the model with features that are not in the original, specifically with postreproductive age classes and positive probabilities for the fixation of neutral and deleterious mutations. It is true that moves that affect only late age classes are “essentially neutral” in the sense that their effects on the fitness criterion are tiny. But for Mueller and Rose (9) the difference between a tiny positive effect and a zero effect is decisive. The latter never spreads through the population. (The authors take initial allele frequencies for mutations as high as one in 10 for “[computational] convenience.” With an effective population size of 10,000, it seems better to regard one in 10 as a stage traversed en route to fixation starting from initial frequencies nearer 10⁻⁴.)

Pletcher and Curtsinger’s proposal that “there is an equilibrium mortality rate at all ages imposed by the proportional effects of mutation” (11) does not hold for MR1A, as corollaries 3 and 4 confirm. Their A5 is not, as asserted, an equation for expected survivorship at time t + 1 but for conditional expected survivorship at time t + 1 given actual survivorship at time t. The probabilities of fixation (π_d and π_b in A5) depend on the vector of actual survivorships and are not independent of the other factors. For MR1A, π_d vanishes for age x unless there is another age group with sufficiently high mortality that a mutation beneficial to it would overcome the loss in fitness from the effect at x. For variants for MR1A that allow essentially neutral mutations to go to fixation, however, the Pletcher-Curtsinger argument does give a useful approximation.

Allowing fixation in the face of small negative effects on fitness could turn MR1A into a process resembling a random walk with a stationary (equilibrium) limiting distribution. It is an interesting open question whether, as Pletcher and Curtsinger (11) suggest, “when mutational effects are small it [this process] will always tend to converge on these [equilibrium expected] values.” Solvable special cases studied so far show a diffuse probability distribution for the location of the process within S, wide excursions through state space, and vectors of q values at any given time that are typically irregular.

Transients

My analysis demonstrates that there is no accounting for mortality plateaus by appeal to limiting states of MR1A. (Similar arguments are believed to apply to all the Mueller–Rose models.) However, transient states, visited early by the process, do display mortality plateaus.

To explain plateaus by positing populations that are not in genetic equilibrium is unappealing (11). The interpretation of the starting state is problematic, and the time scale for relevant transient behavior is arbitrary.

Despite these general objections, the provisions by which the Mueller–Rose models are arranged to visit plateau-like transient states are of interest. There are three ingredients. First, via the equation for genetic drift, the probability of mutations in MR1A is a monotone function of the gain in fitness. Second, at ages still seeing both beneficial and deleterious effects with moderate frequency, the formulas provide a larger downward change for high q_x entries than for low ones, and vice versa, encouraging some equilibration (11). Third, early reductions in young adult mortality promote a high positive growth rate r and a stable age distribution tapering dramatically with age, leaving tiny gains in fitness from mutations affecting any but young adult ages. This occurs in all Mueller–Rose models except the one simulated for their figure 5, here called MR5, which has homeostatic regulation of population growth to stationary levels. However, even in MR5, the homeostatic mechanism is assumed to multiply each value of 1 − q_x by the same factor, as well as to multiply fecundity by this factor, leading to a highly skewed stable age distribution. The ratio of youngest to oldest age class in the stable age pyramid for MR5 is on the order of 10⁸.

Such a process, started at a state with moderate fairly flat mortality, typically will first see reductions in mortality at younger ages, so long as opportunities for large gains in fitness there remain. Scattered effects at old ages will tend to even out mild gradients without shifting the overall level very much. When mortality at young ages has dropped, the remaining mortality at old ages takes on the appearance of a plateau. Only when the scope for further gains at younger ages has been exhausted will older ages start to yield to mutation pressure. The sharper the stable age distribution and the higher the power of genetic drift to forestall the fixation of marginally favorable mutations, the more pronounced this sequence of transitions should be.

In moderate forms, the age discounting of selective advantage that drives this pattern underlies all evolutionary theories of senescence (6–8). The Mueller–Rose models have it in a very pronounced form. Growth rates for MR1A reach 0.182 per day. Even so, the transient plateaus are quite temporary and turn into transient states with adult probabilities of dying mostly concentrated around zero and one before proceeding toward their limit states.

Prospects

The analysis here substantiates the views of others (10, 11) that Mueller and Rose have failed to show that “evolutionary theory predicts late-life mortality plateaus.” What are the prospects for successful explanations?

Pletcher and Curtsinger (11) give an illuminating discussion of the experimental evidence. Tensions between the observations of plateaus and the theory of mutation accumulation might be alleviated by establishing the rarity of potential mutations whose effects on mortality rates are highly specific to older ages. On the other hand, the evolutionary theory of senescence needs mutations with fairly specific effects on mortality rates at less old ages to sustain the mutation part of the mutation-selection balance that is to account for the Gompertzian rise in hazards in middle age. Theories to keep such mutations frequent across middle age and make them progressively rarer with advancing age are a ticklish business. The gradient in rarity would seem eligible to substitute for the gradient in selective pressure derived from Lotka’s equation as an explanation of the Gompertzian rise, entailing further revisions to classical theory.

We are in the early stages of understanding mortality plateaus. Appealing ideas have been proposed along very different lines (4, 11, 12). However, the failure of the Mueller–Rose models need not be a reason to abandon the broader family of Markovian demographic models studied here.

Quite general processes that redistribute mortality by postponing but not eliminating deaths concentrated in some compact age range are well suited for representation by these models. The q_x values come down at certain ages and up at later adjacent ages, formally similar to effects of antagonistic pleiotropy.

A successful recipe for mortality plateaus using the present mathematical machinery would blend several ingredients. One could imagine an initial state with only moderate q_x entries at extreme ages. These would be latent probabilities; no population members in the wild would be surviving to these ages to experience them. However, such an initial state might be the implicit consequence of constraints on the engineering of organ systems with long-tailed distributions of waiting times to failure.

The key stochastic process would posit adaptations pushing back various concentrated modes of failure from younger to adjacent older ages, favored by net gains in fitness. The push-back process would tend to pile up deaths at a range of ages beyond those where selective pressure is strong. To halt the process at nontrivial limits, some small pervasive penalty analogous to friction might come into play. From such a combination, a Gompertzian escarpment bordering a flat or rounded plateau would be the landscape to expect.

Issues abound. Realism demands moderate rather than extreme versions of age discounting. Any appeal to limiting behavior demands a specification that radically broadens the class of absorbing states. The treatment of time needs rethinking; likewise the treatment of neutral and deleterious mutations and of homeostatic regulation. Polymorphisms deserve attention alongside mutations going to fixation. The randomness in demographic rates among dispersed members of a population should take its place alongside branching-process randomness when genetic drift is removing marginally favorable mutations.

In one combination or another, the ideas at stake figure in most speculations about senescence. What is of interest here is that they lend themselves to formal stochastic population models within an analytically tractable class. It remains to determine whether mortality plateaus like those revealed by the experimental evidence can appear as limiting states in a suitable stochastic formulation.