Abstract
Despite the clinical success of deep brain stimulation (DBS) for the treatment of movement disorders, many questions remain about its effects on the nervous system. We have developed a methodology to predict the volume of tissue activated (VTA) by DBS on a patient-specific basis. Our goals are to identify the intersection between the VTA and surrounding anatomical structures and to compare activation of these structures with clinical outcomes. The model system consists of three fundamental components: 1) a 3D anatomical model of the subcortical nuclei and DBS electrode position in the brain, each derived from magnetic resonance imaging (MRI); 2) a finite element model of the DBS electrode and electric field transmitted to the brain, with tissue conductivity properties derived from diffusion tensor MRI; 3) VTA prediction derived from the response of myelinated axons to the applied electric field, which is a function of the stimulation parameters (contact, impedance, voltage, pulse width, frequency). We used this model system to analyze the effects of subthalamic nucleus (STN) DBS in a patient with Parkinson’s disease. Quantitative measurements of bradykinesia, rigidity, and corticospinal tract (CST) motor thresholds were evaluated over a range of stimulation parameter settings. Our model predictions showed good agreement with CST thresholds. Additionally, stimulation through electrode contacts that improved bradykinesia and rigidity generated VTAs that overlapped the zona incerta / fields of Forel (ZI/H2). Application of DBS technology to various neurological disorders has preceded scientific characterization of the volume of tissue directly affected by the stimulation. Synergistic integration of clinical analysis, neuroimaging, neuroanatomy, and neurostimulation modeling provides the opportunity to address wide ranging questions on the factors linked with the therapeutic benefits and side effects of DBS.
INTRODUCTION
Deep brain stimulation (DBS) is an established therapy for the treatment of Parkinson’s disease (PD) (Obeso et al., 2001), essential tremor (Benabid et al., 1996) and dystonia (Vidailhet et al., 2005). It has also been used to treat various other neurological conditions including depression (Mayberg et al., 2005), obsessive-compulsive disorder (Gabriels et al., 2003) and epilepsy (Hodaie et al., 2002). Despite the general effectiveness of DBS, its clinical applications have preceded scientific understanding of its mechanism(s) of action (McIntyre et al., 2004a). In addition, a wide range of factors can influence the clinical response to DBS including the disease state of the patient, anatomical target selected for stimulation, location of the electrode within the target, electrode geometry and selection of the stimulation parameters (contact, voltage, pulse width, and frequency). Progress in understanding the effects of DBS has been limited by the inability to quantitatively characterize of the volume of tissue activated (VTA) during therapeutic and non-therapeutic stimulation. To address this limitation, we developed a methodology to evaluate the VTA on a patient-specific basis, with the goal of developing direct comparisons between the VTA, its overlap with specific brain regions, and the behavioral outcomes of DBS.
Stimulation of the subthalamic nucleus (STN) and surrounding areas for the treatment of PD represents the most common application of DBS technology. However, there is substantial debate regarding the optimal anatomical location for the DBS electrodes in the STN region (Saint-Cyr et al., 2002; Voges and J, 2002; Herzog et al., 2004; Zonenshayn et al., 2004; Kitagawa et al., 2005; Nowinski et al., 2005; Plaha et al., 2006). And, while guidelines exist on stimulation parameter settings that are typically effective (Volkmann et al., 2006), it is infeasible to clinically evaluate each of the thousands of stimulation parameter combinations that are possible. As a result, the therapeutic benefit achieved with STN DBS for PD is strongly dependent on the intuitive skill and experience of the clinicians treating the patient.
Given that the STN is a small structure surrounded by a number of different fiber pathways and gray matter areas, it is unclear which specific anatomical structures may be responsible for therapeutic effects or side effects when stimulated. Converging theoretical (Miocinovic et al., 2006b) and experimental (Hashimoto et al., 2003) results suggest that therapeutic STN DBS generates an excitatory effect on axons surrounding the electrode. While correlations between axonal activation and the therapeutic mechanisms of DBS remain controversial, one leading hypothesis is that high frequency stimulation overrides the underlying pathological neural activity patterns (Montgomery and Baker, 2000; McIntyre et al., 2004a). The fundamental goal of this project was to develop and test a methodology that would enable the prediction and visualization of the volume of axonal tissue activated during DBS on a patient-specific basis.
This study presents a patient-specific model of STN DBS for PD and the VTAs generated by a range of stimulation parameter settings. The overlap of the VTAs with local anatomical structures are quantified and compared with various clinical measurements. The patient-specific model consists of anatomical, electrical, and biophysical representations of DBS. The anatomical model was a 3D brain atlas (Schaltenbrand and Wahren, 1977) that was warped to the patient MRI using a non-linear warping algorithm (Christensen et al., 1997). The electrical and biophysical models rely on finite element models (FEM) of the electric field generated by DBS and theoretical predictions of the neural response to extracellular stimulation (McIntyre et al., 2004c; Butson and McIntyre, 2005; Butson et al., 2006a; Butson and McIntyre, 2006). In parallel with the model simulations, we collected clinical data from our research subject using two different protocols. The first used EMG recordings to quantify stimulation spread to the corticospinal tract (CST); the second examined the effects of stimulation on bradykinesia and rigidity. In both experiments we compared the stimulation effects with activation of specific anatomical sub-volumes. These results provide a new level of detail in predicting the effects of DBS and comparing them with patient outcomes.
MATERIALS & METHODS
We developed a computational system that integrates MRI-based patient-specific anatomy and FEMs of DBS that incorporate DTI-based tissue anisotropy into a single platform for simulation and visualization. The model system predicts the VTAs during DBS and these predictions are compared with clinical measurements. In this study we analyzed STN DBS for PD and evaluated the effects of stimulation on rigidity, bradykinesia and activation of the CST.
Image Coregistration & Brain Atlas Warping
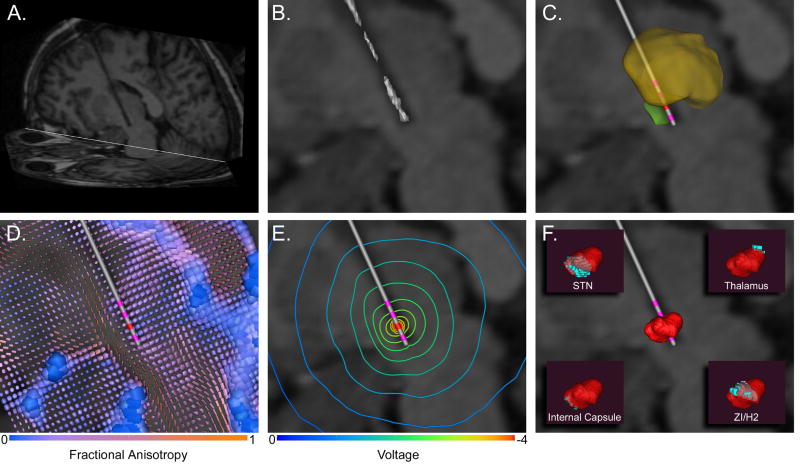
Three MRI data sets were used to construct the patient-specific DBS model. First, a pre-operative magnetization prepared rapid gradient echo (MPRAGE) image with 256 mm x 256 mm field of view and 1 mm3 isotropic voxels was acquired on a Siemens 1.5 T Magnetom Vision scanner. This image was used to warp a 3D brain atlas to the patient anatomy using software from Surgical Navigation Technologies (SNT) (Surgical Navigation Technologies (Medtronic Inc.), Boulder, CO). The 3D brain atlas used in the SNT software was originally produced by resampling a high-resolution volumetric spoiled gradient echo MRI to achieve 0.42 x 0.42 mm isotropic voxels. Outlines of the thalamus, caudate nucleus, putamen, globus pallidus, and nucleus accumbens were traced by hand on all three planes, and the outlines were smoothed to fit the boundaries of these structures as defined by changes in MR signal intensity. The 3D surface representing the thalamus was then imported into the graphical modeling program Rhinoceros (McNeal & Associates, Seattle, WA). Serial slices corresponding to stained histological sections from the Schaltenbrand and Wahren atlas (Schaltenbrand and Wahren, 1977) were overlaid and scaled to match 3D thalamic surface for each slice. Outlines of the thalamic sub-nuclei and the STN were created in each plane. These outlines were lofted to create a 3-D representation of the STN and thalamic sub-nuclei within the context of the 3D brain atlas. Forty landmarks were chosen on both the patient MRI and the 3D brain atlas MRI to serve as a starting point for the deformation. The patient MRI was then deformed to fit the 3D brain atlas MRI using a 3D non-linear warping algorithm (Christensen et al., 1997). A vector field describing the resulting deformation was applied to the 3D brain atlas surfaces, appropriately positioning them within the context of the patient MRI. The resulting deformed 3D surfaces were then used to represent the thalamus and STN in our patient-specific model of DBS (Figure 1).
Figure 1.
Modeling Methods. A) The post-operative MRI was used to identify the electrode location, as shown by the halo in the oblique sagittal slice. B) Intensity values around the electrode halo were isosurfaced with progressively lower values until the surface converged onto the electrode contacts. C) The anatomical surfaces from the 3D brain atlas warping were incorporated into the volume with the electrode location (thalamus – yellow; STN – green). D) The anatomical representation of the patient-specific DBS model was co-registered with a DTI atlas brain to account for the 3D tissue anisotropy and inhomogeneity. Each tensor is represented by a superquadric where the shape and size of the individual elements indicate principal direction and conductivity magnitude, while color indicates fractional anisotropy. E) The electric field is modulated by the 3D tissue conductivity tensors as shown in the voltage isolines. F) The VTA (red) is derived from the voltage distribution in the tissue medium. Its intersection with local anatomical volumes (blue) is shown in the insets.
A second MPRAGE MRI was acquired post-operatively on a Siemens 1.5 T Allegra scanner for DBS electrode localization. The acquisition sequence used in the post-operative MRI was designed to control for heating in accordance with safety studies conducted at the Cleveland Clinic (Baker et al., 2004). Detailed localization of the electrode lead and four contacts was performed by isosurfacing the halo around the electrode shaft in the postoperative MRI. At successively lower isovalues, the isosurface converged onto the four electrode contacts (Figure 1B). The position of the stimulating electrode in this patient was just medial to the STN, as defined by the 3D brain atlas. While the surgical goal is placement within the STN, the estimated electrode location in this patient-specific model is within the inherent error of the stereotactic neurosurgical procedure (Maciunas et al., 1994) and the brain atlas warping (Christensen et al., 1997; Nowinski et al., 2005).
The pre- and post-operative MPRAGE MRI volumes were co-registered with a diffusion tensor MRI (DTI) atlas brain (Wakana et al., 2004). The DTI atlas was acquired using single shot echo planar imaging sequence with an isotropic voxel size of 2.2 mm and b value of 700 mm2/sec. Analyze 6.0 (AnalyzeDirect, Lenexa, KS, USA) was used to co-register the pre- and post-operative MPRAGE volumes to a MPRAGE image of the DTI volume (acquired in parallel with the DTI acquisition for anatomic guidance) (Wakana et al., 2004). In all cases the ITK 3D-registration function in Analyze was used, followed by a manual adjustment to precisely match the positions of the anterior and posterior commissures. The ITK algorithm uses a gradient descent optimizer with the Viola-Wells mutual information metric (Viola and Wells, 1997). This method provided accurate co-registration as indicated by the closely aligned overlap of the STN surfaces from the individual SNT 3D brain atlas warpings of the pre-operative, post-operative and DTI MPRAGE volumes.
The fundamental purpose of the DTI data in our model was to define the 3D tissue electrical properties that surround the DBS electrode. The work of Tuch et al. (Tuch et al., 2001) defined relationships between diffusivity and conductivity within the brain. These concepts have subsequently been used in both forward and inverse analysis problems of electric fields within the human brain (Haueisen et al., 2002; McIntyre et al., 2004c). We converted the diffusion tensor atlas brain into a conductivity tensor atlas brain using a simple linear transform of each voxel (Haueisen et al., 2002):
where σ is the conductivity tensor, σe is the effective extracellular conductivity, D is the diffusion tensor and de is the effective extracellular diffusivity.
Bioelectric Field Model
We used the MRI data to construct a FEM of DBS with several important attributes. First, we used a variable-resolution meshing algorithm to adapt the mesh density to the gradient of the electric field, thereby maximizing the solution accuracy and minimizing the number of nodes in the mesh. The mesh was created using COMSOL 3.1 (Comsol, Inc, Burlington, MA). Second, we coupled the finite element mesh to the DBS electrode so that it could be moved to any position within the patient brain without repeating the time-consuming step of recreating the mesh. Third, we dynamically interpolated the DTI-based conductivity tensors onto the mesh such that the 3D conductivities were represented within the tetrahedral elements.
The active electrode contact was used as a voltage boundary condition for monopolar stimulation, while the outer surface of the brain was grounded. Once the conductivities and boundary conditions were specified, the forward field problem was solved using the Poisson equation with a Fourier FEM solver (Butson and McIntyre, 2005) to determine the time- and space-dependent voltage within the brain volume. The Fourier FEM solver incorporated the DTI-based tissue conductivities and the reactive components of the electrode-tissue interface into a single system of equations.
We have previously shown that high resistance tissue encapsulation surrounding the electrode lead can modulate VTA size by up to 50% (Butson et al., 2006a). To accurately account for the encapsulation layer, impedance measurements were taken from the Medtronic N’Vision programming device using the impedance review function, which conducts measurements during stimulation at 210 μsec, 30 Hz, −1.5 V. To account for the impedance measurements in our study participant, all VTAs in the results were calculated from a model with a 500 μm thick encapsulation layer with conductivity 0.07 S/m (Butson et al., 2006a).
VTA Prediction
The VTA for any given electrode location in the brain and stimulation parameter setting was determined from the voltage solution of the FEM with a series of post-processing steps. Detailed methodology for VTA prediction can be found in our previous publications (McIntyre et al., 2004c; Butson and McIntyre, 2005; Butson et al., 2006a; Butson and McIntyre, 2006). The patient-specific DBS model simulations were performed on an 8 processor SGI Prism (Silicon Graphics Inc., Mountain View, CA) with 36 GB of shared memory using BioPSE (Scientific Computing & Imaging Institute , University of Utah, Salt Lake City, UT). The FEM solution created a potential distribution (Ve) in the tissue medium that was dependent on the electrode location in the brain, the electrode-tissue interface (electrode capacitance, electrode impedance) and the stimulation parameter settings (voltage, pulse width, frequency and electrode contact). The neural response to extracellular stimulation is related to the second spatial derivative of the extracellular potential distribution along a given neural process (∂2Ve/∂x2) (McNeal, 1976; Rattay, 1986). Therefore, we performed thousands of simulations of the response of multi-compartment cable models of myelinated axons to the applied electric field generated by DBS electrodes. These simulations were used to develop quantitative relationships that describe the threshold ∂2Ve/∂x2 for axonal activation as a function of distance from the electrode. In turn, we calculated the ∂2Ve/∂x2 within the context of our patient-specific DBS FEM, and subsequently defined 3D surfaces that encompass the volume where ∂2Ve/∂x2 was suprathreshold for axonal activation for the given stimulation parameters.
Clinical evaluation
A 50 year old male PD patient (>10 year disease duration) with primary symptoms of freezing, rigidity, and bradykinesia underwent implantation of bilateral Medtronic 3387 DBS electrodes and Soletra pulse generators in August, 2003. Our clinical experiments were conducted approximately 1 year post-surgery. The Cleveland Clinic institutional review board approval and informed consent were obtained before patient evaluations. Data is reported for the left DBS electrode (measurements and recordings were made on the right arm and leg). The patient was evaluated in two clinical protocols. Each experiment was conducted in a single morning on separate days with the patient in the medication off state (last dose of medication taken at 9 pm the previous evening).
In the first experimental protocol, differential electromyogram (EMG) recordings were made from electrode pairs placed over the biceps, triceps, flexor carpi ulnaris, extensor carpi radialis, quadriceps, tibialis anterior and lateral gastrocnemius. During these experiments, 20 second recording epochs were gathered while the patient experienced low frequency, monopolar stimulation (2 Hz, 60 or 120 μsec pulse width, 0 to −10 V in −1 V increments) through each DBS electrode contact individually. EMG activity was recorded with a Biotop 6R12 amplifier with the following settings: low frequency filter 5 Hz; high frequency filter 1500 Hz; 1 mV/division. Signals were subsequently filtered with a 9th order Butterworth high pass filter with a cutoff frequency of 50 Hz to remove low frequency drift. Time-triggered average EMG signals were analyzed for a threshold response indicating a muscle twitch, which we interpreted as stimulation spillover into the internal capsule and activation of the CST. Trigger times were determined from the stimulus pulse, which was recorded from an electrode pair placed over the lead wire in the neck. Threshold responses were determined using time-triggered averages of the rectified EMG signal on a per-channel basis (Figure 3A). Two sections of the rectified EMG response were compared. First, the “noise” portion of the EMG was defined as the 10 msec epoch starting 3 msec after the end of the stimulus pulse. The “signal” portion of the EMG was defined as the 10 msec epoch centered around the maximum rectified EMG value. The mean and standard deviation of the difference between these two periods was determined, along with 95% confidence intervals. T-tests were performed to determine if a significant difference existed between the two time periods. The appearance of a significant difference indicated that a threshold event occurred at that stimulus amplitude. EMG thresholds are reported with muscles divided into arm (bicep, tricep, flexor carpi ulnaris, extensor carpi radialis) or leg (quadriceps, tibialis anterior, lateral gastrocnemius) groups.
Figure 3.
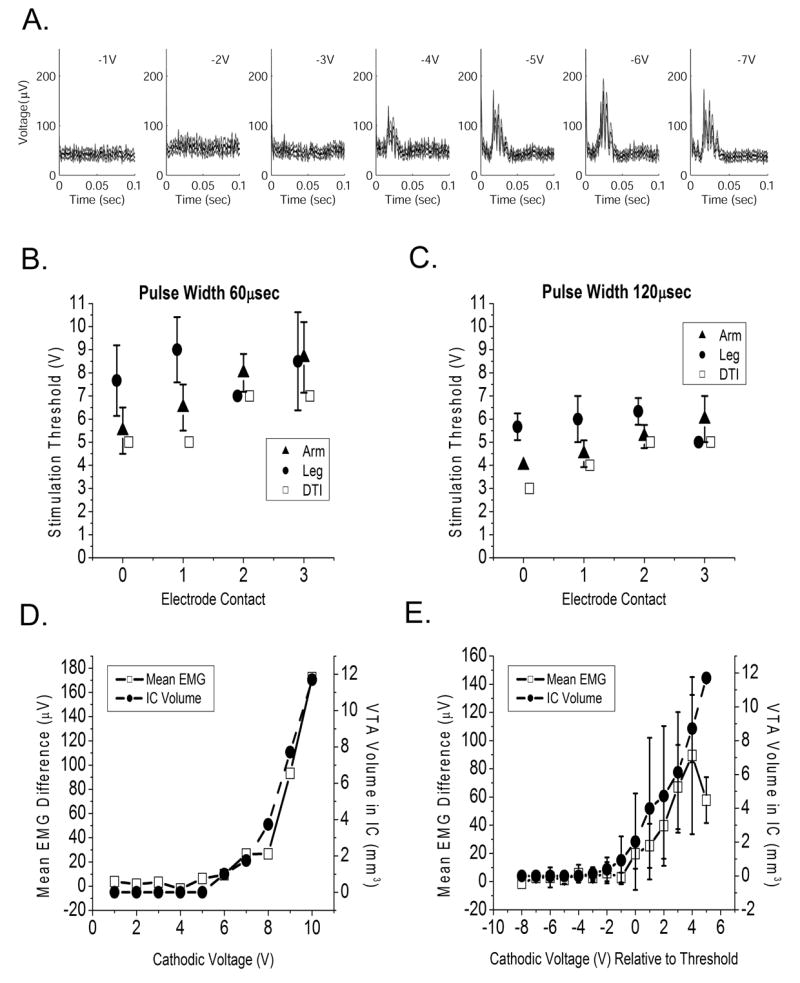
Corticospinal tract thresholds. A) EMG threshold detection during low frequency stimulation. Each graph shows time-triggered average signal (black line, stimulus occurs at time=0) with 95% confidence intervals (gray lines) for progressively higher magnitude cathodic stimulation as indicated. In this example the CST motor threshold occurred at −4 V. B, C) Average CST threshold voltages are shown for arm and leg muscle groups for stimulus pulse widths of 60 μsec and 120 μsec. Also shown are stimulus thresholds predicted by the patient-specific model by spread of the VTA into the IC. Data values are offset slightly along the x-axis to improve readability. D) Example mean EMG voltage difference (μV) for all stimulus pulses in a 20 second epoch for one channel at one electrode contact are shown as a function of stimulation voltage (V). Also shown is the VTA volume that intersects with internal capsule. E) These data are averaged across all channels and shifted relative to threshold voltage in this representative example for contact 0 at 60 μsec pulse width. The graph shows the mean EMG difference and IC volume +/− standard deviation relative to threshold; these measures were significantly correlated (Spearman coefficient 0.71, p<.01).
In a second experimental protocol a monopolar review of all four DBS contacts was performed with stimulation voltage varying from 0 to −4.5 V in an order randomized for voltage and contact (0.5 V resolution, 60 μsec pulse width, 130 Hz). Bradykinesia and rigidity were evaluated at each stimulation setting. Bradykinesia was measured with a finger tapping exercise where the patient was instructed to tap the index finger and thumb together as quickly and accurately as possible for 15 sec while keeping the magnitude of finger motion constant (Unified Parkinson’s Disease Rating Scale (UPDRS) item 23). Finger angular velocity was measured with solid state gyroscopes (model G-1, NeuroKinetics, Edmonton, Alberta, Canada), and bradykinesia was determined from the peak of the resulting power spectrum. The finger tapping trials were interleaved with rigidity measurements using a clinical impedance measurement device (model RA-1, NeuroKinetics) which has been validated against UPDRS item 22 (Patrick et al., 2001).
Data Analysis
VTAs generated in the patient-specific DBS model for each stimulation parameter setting were divided into sub-volumes based on their intersection with the STN, thalamus, zona incerta / Fields of Forel (ZI/H2), and internal capsule. The anatomical volumes representing the STN and thalamus were determined from the 3D anatomical nuclei warped to the MRI. Because the SNT 3D brain atlas does not explicitly include an anatomical volume representing ZI/H2 we co-registered the Mai et al. (Mai et al., 2004) human brain atlas to the patient MRI and created a separate surface to represent this highly important region for STN DBS. The internal capsule volume was segmented from the DTI dataset as the region lateral and ventral to the STN with a fractional anisotropy value of 0.44 or higher. For each VTA, the total volume and the sub-volume intersecting the four anatomical structures (thalamus, IC, ZI/H2, STN) was calculated. All statistical analysis was performed using SPSS 12.0 (SPSS Inc., Chicago, IL).
RESULTS
Volume of Tissue Activated by Deep Brain Stimulation
Previous efforts to calculate DBS electric fields have concentrated on models that assume a homogenous and isotropic bulk tissue medium (McIntyre et al., 2004b; Butson and McIntyre, 2005; Hemm et al., 2005; Astrom et al., 2006; Butson et al., 2006a; Butson and McIntyre, 2006). However, the STN is surrounded by a range of gray and white matter structures, resulting in an inhomogeneous and anisotropic environment that distorts the shape of the DBS electric field and subsequent neural response to stimulation (Butson et al., 2004; McIntyre et al., 2004c; Sotiropoulos and Steinmetz, 2004). We compared the size and shape of the VTAs generated in our patient-specific model of STN DBS with various representations of the surrounding tissue medium. Figure 2 shows example VTAs generated with either an isotropic bulk tissue medium or a medium with 3D tissue electrical properties defined by DTI. In each case the DBS electrode was surrounded by a high resistance tissue encapsulation sheath that regulated the electrode impedance (Butson et al., 2006a). We found that regardless of tissue medium representation, the VTA volume was modulated by voltage and pulse width. However, the shape of VTAs created with DTI-based tissue conductivities were often distorted compared to their spherical counterparts created with the isotropic tissue conductivity. The geometric asymmetries of the DTI-based VTAs often resulted in differential activation spread into the local anatomical structures.
Figure 2.
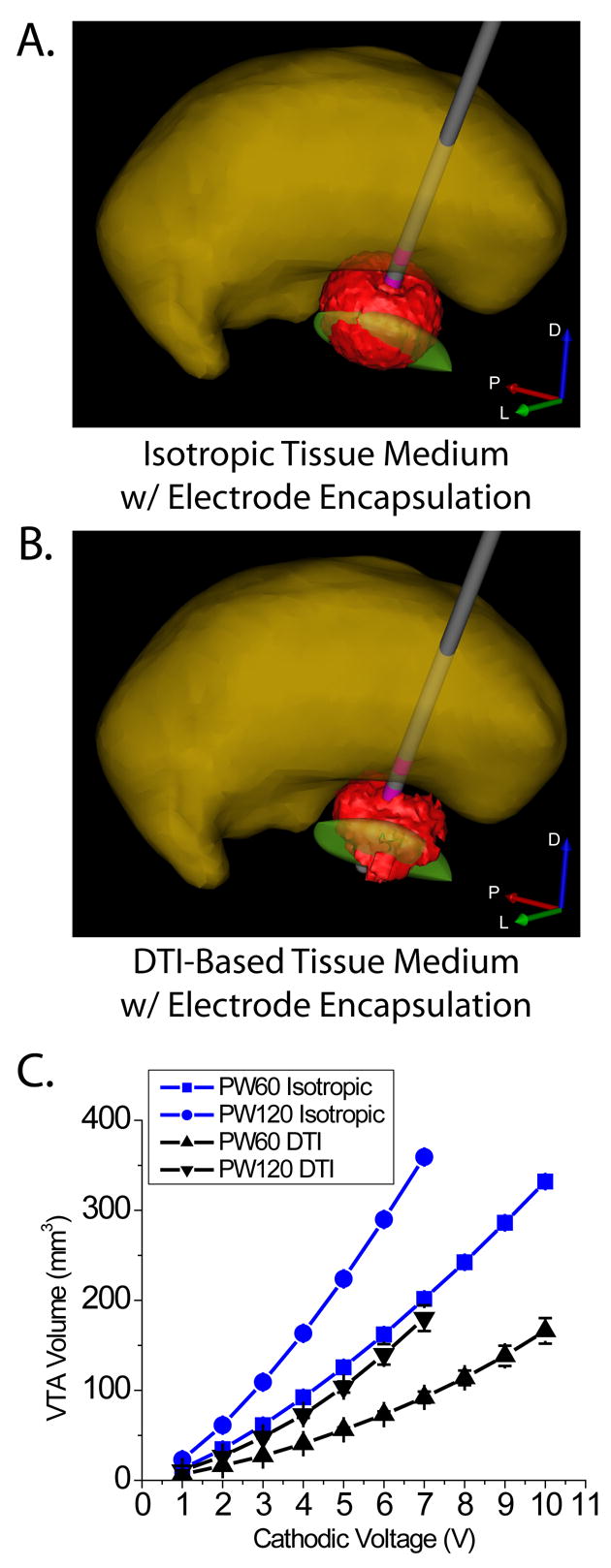
Volume of tissue activated by deep brain stimulation. VTA shape and size differed between isotropic (A) and DTI-based (B) tissue mediums, resulting in differential activation of surrounding anatomical structures. Both models included a tissue encapsulation layer around the electrode shaft, and volumes generated under the two conditions were matched for electrode impedance. C) Average VTA volume +/− standard deviation for all electrode contacts as a function of stimulus voltage for stimulus pulse widths of 60 μsec and 120 μsec.
Corticospinal Tract Thresholds
CST threshold voltages were modulated by the active electrode contact and stimulation parameters. A univariate ANOVA yielded significant CST threshold voltage effects for muscle group (arm versus leg, F=11.68, p<0.001), electrode contact (F=6.95, p<0.001) and stimulation pulse width (F=53.16, p<0.001). Arm thresholds were usually lower than leg thresholds, and longer pulse widths had lower thresholds than shorter pulse widths. Further, we found good agreement between the clinically measured CST thresholds and the model predicted stimulation spread into the IC when we used DTI-based tissue conductivities (Figure 3B, C). Lastly, we found that mean peak EMG values were correlated with activation of the IC (example shown in Figure 3D) as measured by the average VTA volume in the IC relative to the stimulation threshold voltage (Figure 3E, Spearman coefficient 0.71, p<0.01).
Stimulation Spread into Anatomical Structures
Following verification that our model could accurately capture clinically identified spread of stimulation into the IC, we turned our attention to the anatomical structures activated with therapeutic stimulation parameter settings. We quantified the degree of bradykinesia and rigidity as a function of the active electrode contact and stimulus voltage (Figure 4A, B). As the stimulus amplitude increased, VTAs generated from the various contacts spread into the STN, ZI/H2, and thalamus (Figure 4C, D). Stimulation parameters that showed improvement in both bradykinesia and rigidity were centered around −2 V through either contact 1 or 2. When comparing those two VTAs (contact 1 at −2 V or contact 2 at −2 V) the common volume resided in ZI/H2. We also found a significant linear regression for rigidity as a function of voltage (F=6.60,p<0.001) with significant coefficients for stimulation spread into thalamus (p<0.001), and ZI/H2 (p<0.02), but not STN (p>0.84). While contact 0 was adjacent to the STN, it was also close to the substantia nigra and oculomotor nerve. In turn, the lack of improvement in motor symptoms and the presence of stimulation induced side effects made this contact ineffective from a clinical perspective.
Figure 4.
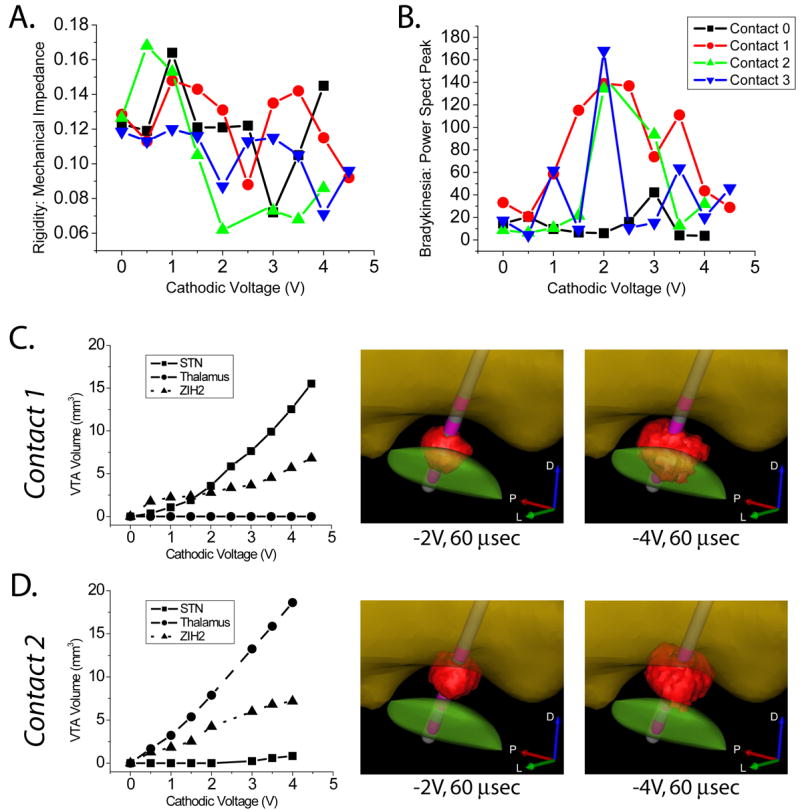
Clinical Measures and Stimulation Spread. We observed effects of activation on A) rigidity (lower scores indicate therapeutic improvement) and B) bradykinesia (higher scores indicate therapeutic improvement). Parts A and B share a legend. For both of these measures, the clinical outcome was dependent on the stimulation voltage and the electrode contact. Rigidity improved roughly motonically with voltage, while bradykinesia showed optimal improvement at a distinct voltage which was dependent on the electrode contact, with worsening effects beyond the optimal voltage. C, D) VTA volume within STN, thalamus, and ZI/H2 for contact 1 and contact 2 as a function of the stimulus voltage. Also shown are example VTAs at -2 V and -4 V.
DISCUSSION
The fundamental goal of this study was to integrate neuroimaging, neuroanatomy, neurostimulation modeling, and clinical analysis to improve our understanding of the effects of DBS on the nervous system. Substantial clinical effort has been invested in determining optimal stimulation parameters for STN DBS for PD (Limousin et al., 1998; Rizzone et al., 2001; Moro et al., 2002; Volkmann et al., 2006). These studies have resulted in general guidelines on the selection of stimulation parameters, as well as clinical algorithms for programming the devices. Imaging studies have developed correlations between stimulation parameters and markers of brain activity (Hershey et al., 2003; Haslinger et al., 2005; Phillips et al., 2006; Trost et al., 2006), and identified the location of therapeutic DBS electrode contacts (Saint-Cyr et al., 2002; Voges and J, 2002; Herzog et al., 2004; Zonenshayn et al., 2004; Kitagawa et al., 2005; Nowinski et al., 2005; Plaha et al., 2006). Modeling studies have characterized the theoretical effects of DBS electric fields on the underlying neural tissue (McIntyre et al., 2004b; Miocinovic et al., 2006b). However, individual analysis of modeling, imaging, or physiological measures alone does not provide sufficient insight or explain the variability of the effects of DBS on a per-patient basis. In turn, we developed a novel computational system that enables integration of multiple data types for the creation of patient-specific models of DBS.
Defining the effects of DBS on neural activity remains an area of active research around the world. Our goal in this study was to apply our previously developed techniques of VTA prediction as a marker for stimulation spread within the anatomy of the patient. It should be noted that our predictions of axonal activation are based on theoretical analysis, and have not been explicitly validated experimentally. However, we attempted to provide a gross level of model validation by comparing our model predictions to clinical measures of CST activation (Figure 3). The CST is a major fiber pathway within the internal capsule, which defines the lateral border of the STN. Consequently, motor evoked responses from activation of the CST can be elicited with relatively low thresholds during STN DBS. Clinically, CST activation is an unwanted side-effect of the stimulation. However, the generation of muscle contractions via stimulation of the CST represents a direct link between STN DBS, known neural substrates, and clinically measurable behaviors. Our model system predicted stimulation spread into the IC; but we did not attempt to explicitly define the CST within the IC. In turn, our model predicted IC thresholds should be lower than the clinically measured CST thresholds because of the more general definition of the anatomical entity stimulated in the model. Indeed, the model and experimental threshold measurements were very close at each electrode contact and pulse width, with the model slightly underestimating the experimental data. In turn, we believe that our DBS model system can accurately account for the various factors that influence the VTA (electrode location and stimulation parameters).
Following characterization of CST activation we turned our attention to the effects of DBS on bradykinesia and rigidity. Rigidity usually responds within seconds to STN stimulation and can be reliably examined even if patient cooperation is poor (Volkmann et al., 2006). In contrast, bradykinesia and tremor in PD may respond with a variable time delay to effective STN DBS, and their severity may be influenced by confounding factors such as fatigue, patient comfort or training. Bradykinesia can be subdivided into two main categories. First is generalized bradykinesia, which is comprised of generalized slowness and paucity of spontaneous movements. The second category is impairment in performance of cyclical rapid alternative movements (such as finger tapping) which can be impaired via either decreased frequency, decreased amplitude or both. One of the problems with measuring frequency and amplitude of rapid alternating movements is that the patient makes a tradeoff between the two. While analyzing the finger-tapping data we looked at the frequency and magnitude of the peaks in the power spectral density recordings and found the latter to vary robustly with stimulator settings. This is also compelling because to some extent, the height of the peak can be a proxy for frequency changes. For example, if tapping frequency is irregular due to hesitations, drifts or fatigue then the height of the peak is reduced because some of the power has shifted to other frequencies. The inverted U-shaped result for bradykinesia for contacts 0, 1 and 2 with a peak at −2 V (Figure 4B) is intriguing, and we have observed a similar effect in other patients. One possible explanation for this effect is that the increase in voltage causes activation of different anatomical structures with opposite effects on bradykinesia. This hypothesis is supported by our data showing differential activation of surrounding structures (Figure 4C, D).
Integrated analysis of neuroimaging, neuroanatomy, neurostimulation, and behavioral data has the potential to shed new light on many scientific and clinical questions related to DBS. However, it should be noted that there are several possible sources of variability in our modeling approach for VTA prediction. First, the co-registration of multiple images and atlas representations of the patient creates spatial variability that can not be ignored. We attempted to minimize co-registration error by using easily identifiable landmarks such as the anterior and posterior commissures (for MRI/DTI volumes) and widely accepted co-registration algorithms (ITK 3D registration in Analyze). Second, due to signal-to-noise considerations, the DTI brain atlas used in this study was acquired with relatively large voxel sizes (Wakana et al., 2004). In turn, our electric field model only provides a gross estimate of the local 3D tissue conductivities surrounding the DBS electrode. However, we believe this is a substantial improvement over traditional techniques that assume a homogeneous isotropic bulk tissue medium (Fig. 2). Third, the VTA prediction functions are based on the activation of straight, relatively large diameter (5.7 μm) myelinated axons (McIntyre and Grill, 2002; Butson and McIntyre, 2006), and may not be representative of the response of other neuron types surrounding the electrode (local projection neurons, local interneurons, afferent inputs, etc.). Given that myelinated axons are considered the most excitable neuron type to extracellular electrical stimulation (Ranck, 1975), our VTA predictions should be considered a worst case scenario in terms of stimulation spread.
While our patient-specific model system suffers from a number of limitations, the comparisons with our clinical measurements are consistent with previous studies on location of therapeutically effective electrode contacts (Saint-Cyr et al., 2002; Voges and J, 2002; Herzog et al., 2004; Zonenshayn et al., 2004; Kitagawa et al., 2005; Nowinski et al., 2005; Plaha et al., 2006). The results of this study, though limited to a single patient, suggest that the therapeutic volume of tissue to activate is centered on ZI/H2 (Fig. 4). However, it should be noted that in this patient the DBS electrode was slightly medial to the STN. To better define the therapeutic target VTA, our next goal is to use the methodology presented in this study to develop voxel-based, probabilistic maps of VTAs and their corresponding behavioral outcomes from a large cohort of patients. This fundamental concept was pioneered by Nowiniski et al. (Nowinski et al., 2005) who developed probabilistic maps of the location of therapeutic electrode contacts. We believe integration of stimulation spread into these probabilistic maps will find utility in the surgical targeting for electrode implantation (Miocinovic et al., 2006a), identification of optimal stimulation parameter settings following implantation (Butson et al., 2006b), and design of DBS electrodes customized to generate VTAs that best match the anatomical and electrical constraints of the target region (Butson and McIntyre, 2006).
Acknowledgments
This work was supported by grants from the American Parkinson Disease Association, the Ohio Biomedical Research and Technology Transfer Partnership, and the National Institutes of Health (NS-50449 & NS-52042). The authors would also like to thank Susumu Mori for providing the diffusion tensor image brain atlas, Christopher Maks and Ashu Chaturvedi for assistance with the model simulations, and Barbara Wolgamuth for assistance with the clinical data collection.
References
- Astrom M, Johansson JD, Hariz MI, Eriksson O, Wardell K. The effect of cystic cavities on deep brain stimulation in the basal ganglia: a simulation-based study. J Neural Eng. 2006;3:132–138. doi: 10.1088/1741-2560/3/2/007. [DOI] [PubMed] [Google Scholar]
- Baker KB, Tkach JA, Nyenhuis JA, Phillips M, Shellock FG, Gonzalez-Martinez J, Rezai AR. Evaluation of specific absorption rate as a dosimeter of MRI-related implant heating. J Magn Reson Imaging. 2004;20:315–320. doi: 10.1002/jmri.20103. [DOI] [PubMed] [Google Scholar]
- Benabid AL, Pollak P, Gao D, Hoffmann D, Limousin P, Gay E, Payen I, Benazzouz A. Chronic electrical stimulation of the ventralis intermedius nucleus of the thalamus as a treatment of movement disorders. J Neurosurg. 1996;84:203–214. doi: 10.3171/jns.1996.84.2.0203. [DOI] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation. Clin Neurophysiol. 2005;116:2490–2500. doi: 10.1016/j.clinph.2005.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Role of electrode design on the volume of tissue activated during deep brain stimulation. J Neural Eng. 2006;3:1–8. doi: 10.1088/1741-2560/3/1/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, Maks CB, McIntyre CC. Sources and effects of electrode impedance during deep brain stimulation. Clin Neurophysiol. 2006a;117:447–454. doi: 10.1016/j.clinph.2005.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, Hall J, Henderson JM, McIntyre CC. Patient-specific models of deep brain stimulation: 3D visualization of anatomy, electrode and volume of activation as a function of the stimulation parameters. Society for Neuroscience. 2004;30:1011.11. [Google Scholar]
- Butson CR, Noecker AM, Maks CB, McIntyre CC. StimExplorer: Deep Brain Stimulation Parameter Selection Software System. In: Sakas DE, Simpson B, Krames E, editors. Neuromodulation. New York: Springer-Verlag; 2006b. [DOI] [PubMed] [Google Scholar]
- Christensen GE, Joshi SC, Miller MI. Volumetric transformation of brain anatomy. IEEE Trans Med Imaging. 1997;16:864–877. doi: 10.1109/42.650882. [DOI] [PubMed] [Google Scholar]
- Gabriels L, Cosyns P, Nuttin B, Demeulemeester H, Gybels J. Deep brain stimulation for treatment-refractory obsessive-compulsive disorder: psychopathological and neuropsychological outcome in three cases. Acta Psychiatr Scand. 2003;107:275–282. [PubMed] [Google Scholar]
- Hashimoto T, Elder CM, Okun MS, Patrick SK, Vitek JL. Stimulation of the subthalamic nucleus changes the firing pattern of pallidal neurons. J Neurosci. 2003;23:1916–1923. doi: 10.1523/JNEUROSCI.23-05-01916.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haslinger B, Kalteis K, Boecker H, Alesch F, Ceballos-Baumann AO. Frequency-correlated decreases of motor cortex activity associated with subthalamic nucleus stimulation in Parkinson's disease. Neuroimage. 2005;28:598–606. doi: 10.1016/j.neuroimage.2005.06.034. [DOI] [PubMed] [Google Scholar]
- Haueisen J, Tuch DS, Ramon C, Schimpf PH, Wedeen VJ, George JS, Belliveau JW. The influence of brain tissue anisotropy on human EEG and MEG. Neuroimage. 2002;15:159–166. doi: 10.1006/nimg.2001.0962. [DOI] [PubMed] [Google Scholar]
- Hemm S, Mennessier G, Vayssiere N, Cif L, El Fertit H, Coubes P. Deep brain stimulation in movement disorders: stereotactic coregistration of two-dimensional electrical field modeling and magnetic resonance imaging. J Neurosurg. 2005;103:949–955. doi: 10.3171/jns.2005.103.6.0949. [DOI] [PubMed] [Google Scholar]
- Hershey T, Revilla FJ, Wernle AR, McGee-Minnich L, Antenor JV, Videen TO, Dowling JL, Mink JW, Perlmutter JS. Cortical and subcortical blood flow effects of subthalamic nucleus stimulation in PD. Neurology. 2003;61:816–821. doi: 10.1212/01.wnl.0000083991.81859.73. [DOI] [PubMed] [Google Scholar]
- Herzog J, Fietzek U, Hamel W, Morsnowski A, Steigerwald F, Schrader B, Weinert D, Pfister G, Muller D, Mehdorn HM, Deuschl G, Volkmann J. Most effective stimulation site in subthalamic deep brain stimulation for Parkinson's disease. Mov Disord. 2004;19:1050–1054. doi: 10.1002/mds.20056. [DOI] [PubMed] [Google Scholar]
- Hodaie M, Wennberg RA, Dostrovsky JO, Lozano AM. Chronic anterior thalamus stimulation for intractable epilepsy. Epilepsia. 2002;43:603–608. doi: 10.1046/j.1528-1157.2002.26001.x. [DOI] [PubMed] [Google Scholar]
- Kitagawa M, Murata J, Uesugi H, Kikuchi S, Saito H, Tashiro K, Sawamura Y. Two-year follow-up of chronic stimulation of the posterior subthalamic white matter for tremor-dominant Parkinson's disease. Neurosurgery. 2005;56:281–289. doi: 10.1227/01.neu.0000148167.49105.a3. [DOI] [PubMed] [Google Scholar]
- Limousin P, Krack P, Pollak P, Benazzouz A, Ardouin C, Hoffmann D, Benabid AL. Electrical stimulation of the subthalamic nucleus in advanced Parkinson's disease. N Engl J Med. 1998;339:1105–1111. doi: 10.1056/NEJM199810153391603. [DOI] [PubMed] [Google Scholar]
- Maciunas RJ, Galloway RL, Jr, Latimer JW. The application accuracy of stereotactic frames. Neurosurgery. 1994;35:682–694. doi: 10.1227/00006123-199410000-00015. discussion 694–685. [DOI] [PubMed] [Google Scholar]
- Mai JK, Assheuer J, Paxinos G. Atlas of the human brain. 2nd Edition. Amsterdam ; Boston: Elsevier Academic Press; 2004. [Google Scholar]
- Mayberg HS, Lozano AM, Voon V, McNeely HE, Seminowicz D, Hamani C, Schwalb JM, Kennedy SH. Deep brain stimulation for treatment-resistant depression. Neuron. 2005;45:651–660. doi: 10.1016/j.neuron.2005.02.014. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM. Extracellular stimulation of central neurons: influence of stimulus waveform and frequency on neuronal output. J Neurophysiol. 2002;88:1592–1604. doi: 10.1152/jn.2002.88.4.1592. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Savasta M, Walter BL, Vitek JL. How Does Deep Brain Stimulation Work? Present Understanding and Future Questions. Journal of Clinical Neurophysiology. 2004a;21:40–50. doi: 10.1097/00004691-200401000-00006. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM, Sherman DL, Thakor NV. Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. J Neurophysiol. 2004b;91:1457–1469. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Mori S, Sherman DL, Thakor NV, Vitek JL. Electric field and stimulating influence generated by deep brain stimulation of the subthalamic nucleus. Clin Neurophysiol. 2004c;115:589–595. doi: 10.1016/j.clinph.2003.10.033. [DOI] [PubMed] [Google Scholar]
- McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans Biomed Eng. 1976;23:329–337. doi: 10.1109/tbme.1976.324593. [DOI] [PubMed] [Google Scholar]
- Miocinovic S, Maks CB, Noecker AM, Butson CR, McIntyre CC. Cicerone: Stereotactic Neurophysiological Recording and Deep Brain Stimulation Electrode Placement Software System. In: Sakas DE, Simpson B, Krames E, editors. Neuromodulation. New York: Springer-Verlag; 2006a. [DOI] [PubMed] [Google Scholar]
- Miocinovic S, Parent M, Butson CR, Hahn PJ, Russo GS, Vitek JL, McIntyre CC. Computational analysis of subthalamic nucleus and lenticular fasciculus activation during therapeutic deep brain stimulation. J Neurophysiol. 2006b;96:1569–1580. doi: 10.1152/jn.00305.2006. [DOI] [PubMed] [Google Scholar]
- Montgomery EB, Jr, Baker KB. Mechanisms of deep brain stimulation and future technical developments. Neurological Research. 2000;22:259–266. doi: 10.1080/01616412.2000.11740668. [DOI] [PubMed] [Google Scholar]
- Moro E, Esselink RJ, Xie J, Hommel M, Benabid AL, Pollak P. The impact on Parkinson's disease of electrical parameter settings in STN stimulation. Neurology. 2002;59:706–713. doi: 10.1212/wnl.59.5.706. [DOI] [PubMed] [Google Scholar]
- Nowinski WL, Belov D, Pollak P, Benabid AL. Statistical analysis of 168 bilateral subthalamic nucleus implantations by means of the probabilistic functional atlas. Neurosurgery. 2005;57:319–330. doi: 10.1227/01.neu.0000180960.75347.11. [DOI] [PubMed] [Google Scholar]
- Obeso JA, Olanow CW, Rodriguez-Oroz MC, Krack P, Kumar R, Lang AE. Deep-brain stimulation of the subthalamic nucleus or the pars interna of the globus pallidus in Parkinson's disease. N Engl J Med. 2001;345:956–963. doi: 10.1056/NEJMoa000827. [DOI] [PubMed] [Google Scholar]
- Patrick SK, Denington AA, Gauthier MJ, Gillard DM, Prochazka A. Quantification of the UPDRS Rigidity Scale. IEEE Trans Neural Syst Rehabil Eng. 2001;9:31–41. doi: 10.1109/7333.918274. [DOI] [PubMed] [Google Scholar]
- Phillips MD, Baker KB, Lowe MJ, Tkach JA, Cooper SE, Kopell BH, Rezai AR. Parkinson disease: pattern of functional MR imaging activation during deep brain stimulation of subthalamic nucleus–initial experience. Radiology. 2006;239:209–216. doi: 10.1148/radiol.2391041990. [DOI] [PubMed] [Google Scholar]
- Plaha P, Ben-Shlomo Y, Patel NK, Gill SS. Stimulation of the caudal zona incerta is superior to stimulation of the subthalamic nucleus in improving contralateral parkinsonism. Brain. 2006;129:1732–1747. doi: 10.1093/brain/awl127. [DOI] [PubMed] [Google Scholar]
- Ranck JB. Which elements are excited in electrical stimulation of mammalian central nervous system: A review. Brain Res. 1975;98:417–440. doi: 10.1016/0006-8993(75)90364-9. [DOI] [PubMed] [Google Scholar]
- Rattay F. Analysis of models for external stimulation of axons. IEEE Trans Biomed Eng. 1986;33:974–977. doi: 10.1109/TBME.1986.325670. [DOI] [PubMed] [Google Scholar]
- Rizzone M, Lanotte M, Bergamasco B, Tavella A, Torre E, Faccani G, Melcarne A, Lopiano L. Deep brain stimulation of the subthalamic nucleus in Parkinson's disease: effects of variation in stimulation parameters. Journal of Neurology, Neurosurgery & Psychiatry. 2001;71:215–219. doi: 10.1136/jnnp.71.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saint-Cyr JA, Hoque T, Pereira LC, Dostrovsky JO, Hutchison WD, Mikulis DJ, Abosch A, Sime E, Lang AE, Lozano AM. Localization of clinically effective stimulating electrodes in the human subthalamic nucleus on magnetic resonance imaging. J Neurosurg. 2002;97:1152–1166. doi: 10.3171/jns.2002.97.5.1152. [DOI] [PubMed] [Google Scholar]
- Schaltenbrand G, Wahren W. Atlas for stereotaxy of the human brain. 2nd Edition. Stuttgart: Thieme; 1977. [Google Scholar]
- Sotiropoulos SN, Steinmetz PN. A biophysical model of deep brain stimulation of the subthalamic nucleus. Society for Neuroscience. 2004:1011.5. [Google Scholar]
- Trost M, Su S, Su P, Yen RF, Tseng HM, Barnes A, Ma Y, Eidelberg D. Network modulation by the subthalamic nucleus in the treatment of Parkinson's disease. Neuroimage. 2006;31:301–307. doi: 10.1016/j.neuroimage.2005.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch DS, Wedeen VJ, Dale AM, George JS, Belliveau JW. Conductivity tensor mapping of the human brain using diffusion tensor MRI. Proc Natl Acad Sci U S A. 2001;98:11697–11701. doi: 10.1073/pnas.171473898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidailhet M, Vercueil L, Houeto JL, Krystkowiak P, Benabid AL, Cornu P, Lagrange C, Tezenas du Montcel S, Dormont D, Grand S, Blond S, Detante O, Pillon B, Ardouin C, Agid Y, Destee A, Pollak P. Bilateral deep-brain stimulation of the globus pallidus in primary generalized dystonia. N Engl J Med. 2005;352:459–467. doi: 10.1056/NEJMoa042187. [DOI] [PubMed] [Google Scholar]
- Viola P, Wells WMI. Alignment by maximization of mutual information. IJCV. 1997;24:137–154. [Google Scholar]
- Voges J, Vea J. Bilateral high-frequency stimulationin the subthalamic nucleus for the treatment of Parkinson's disease: correlation of therapeutic effect with anatomical electrode position. J Neurosurgery. 2002;96:269–279. doi: 10.3171/jns.2002.96.2.0269. [DOI] [PubMed] [Google Scholar]
- Volkmann J, Moro E, Pahwa R. Basic algorithms for the programming of deep brain stimulation in Parkinson's disease. Mov Disord. 2006;21:S284–S289. doi: 10.1002/mds.20961. [DOI] [PubMed] [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher LM, van Zijl PC, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Zonenshayn M, Sterio D, Kelly PJ, Rezai AR, Beric A. Location of the active contact within the subthalamic nucleus (STN) in the treatment of idiopathic Parkinson's disease. Surg Neurol. 2004;62:216–225. doi: 10.1016/j.surneu.2003.09.039. [DOI] [PubMed] [Google Scholar]