Emergence of homeostasis and “noise imprinting” in an evolution model

Abstract

Homeostasis, the creation of a stabilized internal milieu, is ubiquitous in biological evolution, despite the entropic cost of excluding noise information from a region. The advantages of stability seem self evident, but the alternatives are not so clear. This issue was studied by means of numerical experiments on a simple evolution model: a population of Boolean network “organisms” selected for performance of a curve-fitting task while subjected to noise. During evolution, noise sensitivity increased with fitness. Noise exclusion evolved spontaneously, but only if the noise was sufficiently unpredictable. Noise that was limited to one or a few stereotyped patterns caused symmetry breaking that prevented noise exclusion. Instead, the organisms incorporated the noise into their function at little cost in ultimate fitness and became totally noise dependent. This “noise imprinting” suggests caution when interpreting apparent adaptations seen in nature. If the noise was totally random from generation to generation, noise exclusion evolved reliably and irreversibly, but if the noise was correlated over several generations, maladaptive selection of noise-dependent traits could reverse noise exclusion, with catastrophic effect on population fitness. Noise entering the selection process rather than the organism had a different effect: adaptive evolution was totally abolished above a critical noise amplitude, in a manner resembling a thermodynamic phase transition. Evolutionary adaptation to noise involves the creation of a subsystem screened from noise information but increasingly vulnerable to its effects. Similar considerations may apply to information channeling in human cultural evolution.

In the biosphere, great delicacy coexists with turmoil. The ability to exclude external fluctuations is a hallmark of living organisms, one whose survival value is usually taken to be self evident. This belief rests on two implicit assumptions: (i) stability is more conducive to functioning than chaos, and (ii) natural selection is able to recognize and favor such stability. The first assumption, although intuitively plausible, is unproven; more precisely, it is not obvious that the strategy of excluding noise from the organism, though simple to describe, is actually the most likely way for the “blind watchmaker” of evolution to maximize fitness in a noisy environment. The second assumption may be challenged if the noise varies unpredictably on a time scale longer than the generation time of the organism, so that there is no direct competition between individuals based on noise resistance.

Here, I report results of numerical experiments to test these assumptions by determining whether noise exclusion would evolve spontaneously in a simple computational model of evolution: a population of (initially) random Boolean networks (logical circuits) selected for performance of a curve-fitting task while subjected to noise. Noise that was identical in every generation was never excluded, but was incorporated into the computation, despite its complexity and lack of relation to the desired output, so that the network became “imprinted” with that particular noise pattern and required it to function. The noise sensitivity of the network increased as evolution proceeded. Noise that was completely random from generation to generation was eventually excluded from the output and most network elements causally connected to the output (usually after a period of increasing noise sensitivity), forming a “protected subsystem” to compute the output function. The transition between these two regimes was not smooth: if the noise varied gradually over several generations, evolution toward noise exclusion was punctuated by “information catastrophes,” during which fitness was abruptly lost by maladaptive selection events that reintroduced noise information. This behavior was insensitive to the details of the model. Noise entering the selection process rather than the organism had still a different effect: evolution was totally abolished above a critical noise intensity, in a manner resembling a thermodynamic phase transition.

Cell differentiation and morphogenesis involve highly nonlinear dynamic interactions among many genes, with combinatorial specification of cell fate by several gene products (1). Random Boolean networks have been proposed as a model of this process (2–6), although I do not demand this concrete interpretation here—they may also be a useful model of the more complex processes of cultural evolution. The model is a simple example of a highly nonlinear dynamical system defined by a collection of digital information (“genome”), which can be tested for fitness in performing a task—computing a specified (but arbitrary) target function. As such, it is an example of a genetic algorithm (7). Over the past few years, there has been an extensive development of this field of computer science (8–11). Most of this work has been directed toward the development of practical computer programs that attack optimization problems by using methods suggested by biological evolution and to understanding how these programs function and may be improved. These methods have also been applied to aid in the understanding of natural molecular and prebiotic evolution (12–15). In contrast, the present model was chosen for its ability to display explicitly the flow of information within the organism, to examine the impact of noise information entering the machinery of the organism directly from the environment. As an open statistical-mechanical system, an organism must be subject to such inputs unless excluded by an active process; however, the role this plays in evolution seems not to have been examined previously. This approach was made possible by the great increase in computer power since earlier studies of Boolean network evolution (16, 17).

METHODS

The model consists of a (simulated) population of M organisms, each of which is a network, initially randomly connected, of n = ≈100 Boolean circuit elements, each element having two inputs, x and y, and one output, z (Fig. 1). The output of an element is given by z_t = f(x_t−1, y_t−1), where f stands for one of the 16 possible Boolean functions of two variables, and t is the discrete time. In the notation of Kauffman (18), the organism is an NK Boolean network, with K = 2.† A random Boolean time series (“noise”) is connected to the first input terminal of each of several (typically 4–20) elements (the second input terminals of those elements, as well as both inputs of all other elements, receive the outputs of other network elements). The “phenotype” output of the network is an integer time series obtained from a subset of m elements (“output elements,” not otherwise distinguished from the others) by counting the number of elements in the TRUE state (0 … m). In each generation, each network was developed through 100 time steps, and the “fitness” F determined as the negative of the mean squared difference between the network output and the target function. [The word “develop” is used to refer to changes over the dynamical time of a single network (by analogy to development of an organism), whereas “evolve” always refers to evolutionary time (generations).] The population was expanded by replicating each organism R times, allowing mutations, and then reduced to its original size by selecting the best M networks ranked by fitness. Each mutation consisted of either (i) randomly moving one of the input connections of a randomly chosen element, (ii) randomly changing the Boolean function of a randomly chosen element, (iii) deleting an element, or (iv) adding an element. Mutations that disconnected a noise input were not allowed. The numbers of mutants per generation and mutations per mutant were binomially distributed on the basis of a fixed mutation rate μ per network element. A relatively large mutation rate was used in some of the simulations shown in the figures to speed convergence; qualitatively similar results were obtained with a lower more realistic mutation rate, over a larger number of generations. Including mutations of types (iii) and (iv) did not seem to increase the adaptability of the model or introduce any novel phenomena, so most of the results displayed below were obtained with a fixed value of N, with mutations of types (i) or (ii) selected at random with probability 0.5. Recombination was not considered in the model, to avoid an arbitrary choice about how to recombine two different Boolean networks. M and R determine the effective intensity of selection; a particularly simple case is strong selection (M = 1, R = 2), in which a single “wild type” is compared with a single mutant in each generation, the network of greater fitness replacing the parent in the following generation. (There are a total of R⋅M replicates, including wild type and mutants, therefore R = 2, rather than 1 for the case where a single wild type is compared with a single mutant.)

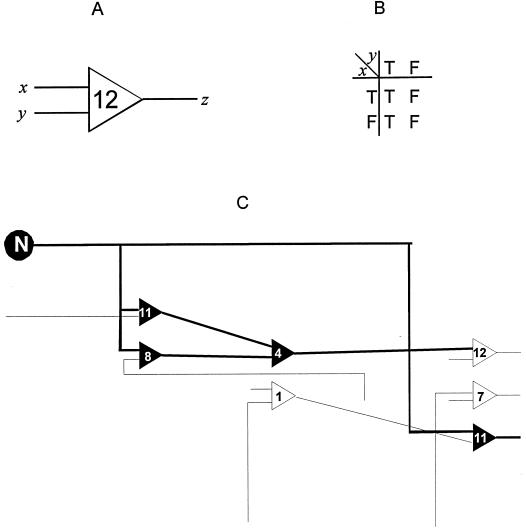
Figure 1.

(A) A Boolean circuit element. There are 16 possible element types, numbered 0–15. The Boolean function of the element is determined by interpreting its inputs (x, y) as a 2-bit binary number and using this as a pointer to a bit in the binary representation of the element number, giving the output z (0 = FALSE, 1 = TRUE). (B) Truth table describing Boolean function 12. (C) Fragment of a Boolean network, showing the propagation of injected noise information in bold. Note that the noise information is blocked at element 12, because Boolean function 12 is independent of its x input, as seen from the truth table.

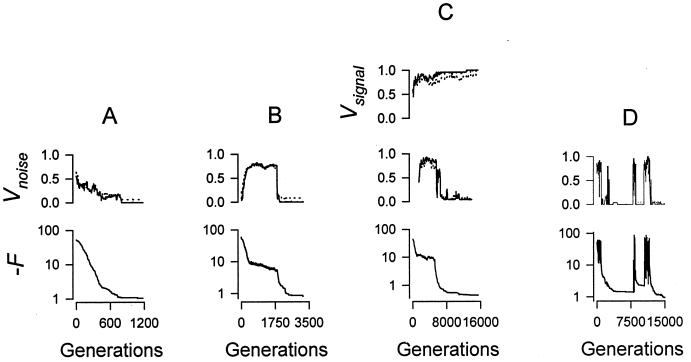
In all of the figures, fitness is represented by the population average of the mean-squared error in fitting the target function, denoted by −F. When the noise realization was different for each organism and generation (Fig. 3), the plotted value is expected or “long-term” fitness (in the sense of Fig. 4B), which was obtained by exercising each of the M networks in each generation with multiple random noise realizations (10–100, depending on computation time constraints, only one of which was the “real” one used for determining selection) and averaging the results. With the exception of Fig. 5, each curve represents the result of a single evolution run; all are highly representative of reproducible behavior of the model, although quantitative details (e.g., the duration of the plateau phase in Fig. 3B, the number and location of information catastrophes, etc.) varied from run to run. The “noise vulnerability” (Fig. 3) denoted by V_noise was determined as follows: (i) in each generation, the networks in the population were exercised with multiple independent random noise realizations; (ii) noise-sensitive network elements were identified as those whose output state differed, at any time step, between developments in the presence of different noise realizations; (iii) the number of noise-sensitive elements was expressed as a fraction of the number N of elements in the network, and the number of noise-sensitive output elements was expressed as a fraction of the number m of output elements; (iv) the resulting fractions were averaged over the M networks in the population. The resulting quantity is therefore a measure of how widely noise information is propagated in the network. An analogous quantity, V_signal, was computed for the model in which an information bit was included in the input that predicted which of two target functions would be used (Fig. 3C), by exercising the networks with both values of this bit and counting the number of elements whose states were affected by its value.

Figure 3.

Evolution histories in the presence of random noise, different in each generation, showing noise vulnerability (see Fig. 2 and text) and fitness; M = 100, R = 2 (A–C), or 4 (D). (A) Fitness improves as noise is steadily excluded from parts of the network, leading to a network with a protected subsystem consisting of noise-free output elements (Upper, solid) and the elements that compute the output (Upper, dotted). (B) The more common pattern in which the restructuring of the network by evolution initially increases the dissemination of noise information, despite the selective advantage that would accrue from its elimination. During this period, fitness slowly improves as a result of adaptations that “filter” the noise, reducing noise-related output variance. This is followed by a phase of rapid irreversible noise exclusion, which allows further evolution to maximum fitness. (C) The target function was randomly switched between step functions at t = 30 and t = 70, and a bit predicting which step function would be used was intercalated into the even time bins of the noise input, while the odd bins contained only random noise. A network evolved that was able to decode the inputs, creating a protected subsystem from which the noise was excluded (Middle) while the predictive signal was widely distributed (Top). (D) Noise correlated over a number of generations was produced by randomly resetting one randomly chosen bit of the noise array in each generation. In this environment, noise exclusion evolves, but can be reversed by maladaptive selection events (see Fig. 4), causing “information catastrophes” during the latter stages of evolution.

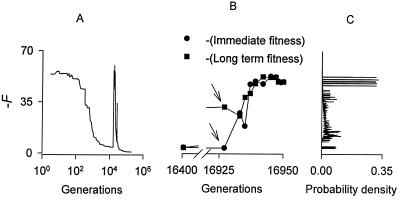
Figure 4.

Mechanism of the information catastrophe, studied in the strong selection model (M = 1, R = 2) in which it occurs even with uncorrelated random noise. Note logarithmic scale of generations. (A) Evolution interrupted by a typical information catastrophe. (B) Leading edge of the information catastrophe at high resolution. It begins with a maladaptive selection event (arrows) in which a mutation that recouples noise into the protected subsystem is accepted because it increases fitness (decreases error) with the particular noise realization present in that generation, although its long-term fitness (expected fitness over all noise realizations) is poor. In subsequent generations, with other noise realizations, the short-term fitness is also poor, allowing the acceptance of many mutations that damage the previously evolved structure of the network, producing a cascade of maladaptive selections. (C) The distribution of fitness of the maladaptive network over all noise realizations is extremely nonnormal, allowing it to subvert the selection process by appearing highly fit in a small fraction of noise environments.

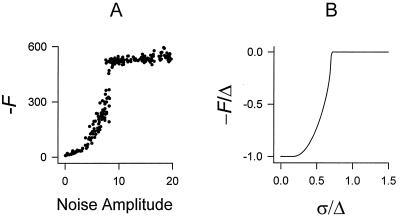
Figure 5.

Critical behavior caused by selection noise. (A) Uniformly distributed white noise was added to the target function. Each point represents an independent evolution history under strong selection (M = 1, R = 2, 1,000 elements/organism), showing the (negative of) fitness at the end of 10⁵ generations. Above the critical noise amplitude, no adaptive evolution takes place. (B) Fitness as a function of selection-noise amplitude for the two-genotype analytical model used to derive Eq. 1, with μ₂₁ = 0.47.

The analytical model of selection noise effects (see below and Fig. 5) was analyzed as follows: assuming the limit of a large population, the distribution of apparent fitness will be the sum of two Gaussian with centers ±Δ/2 and weights p and 1 − p, where p is the fraction of the population of the high-fitness genotype. The mean fitness is then F = −(1 − 2p)Δ/2. The effect of one generation of selection can be found by first readjusting p to take into account the effects of mutation and then integrating the two Gaussians from M to infinity to obtain the fractions of the population in each genotype after selection. This procedure gives a recurrence relation (not shown) for the new value p′ in terms of p. This recurrence has two fixed points, one stable and the other unstable; iteration over many generations will cause the population to converge to the stable one. In the absence of mutation, the fixed points are p₁ = 0 and p₂ = 1, corresponding to fixation of the low- and high-fitness genotypes, respectively, with the latter stable. If μ₁₂ is ignored, p₁ remains zero; solving for the critical stability of this point by dp′/dp = 1| _{p = 0} gives Eq. 1. The other fixed point, p₂, crosses zero at the critical point and becomes stable; its location was determined by numerically iterating the recurrence and is plotted in Fig. 5B.

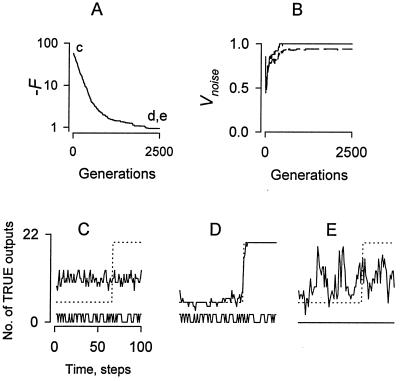
Adaptation to Stereotyped Noise: Noise Imprinting. To determine whether an evolving organism would exclude noise on the basis of its complexity and lack of relationship to the task, the same single random sequence of 100 noise bits was injected into all organisms in all generations. This “stereotyped noise” may be regarded as representing a stable complex feature of the environment, not necessarily temporal, that carries no useful information about the task that the organism must carry out to ensure its survival. Intuition suggests that evolving the ability to compute accurately the target function must involve the creation of some kind of order in the network structure, which would be severely disrupted by the noise. Nevertheless, population fitness improved steadily over two orders of magnitude (Fig. 2A), regardless of what noise realization was present (including none). The network output, initially random (Fig. 2C), evolved to a good approximation of the target function (Fig. 2D). Intuitively, the simplest way to achieve this would be to ignore (i.e., exclude) the noise information, but this was never observed. Instead, the fraction of elements whose states depended on noise information increased to nearly 100% over the course of evolution (Fig. 2B), apparently because of the increased functional connectivity required to carry out the task. As a result, the network became dependent on the noise and failed completely if it was removed (Fig. 2E).

Figure 2.

Evolution in the presence of stereotyped noise. M = 100, R = 2, μ = 0.005/element/generation. (A) Fitness improves steadily over two orders of magnitude. Labels c, d, and e indicate the generations used to generate the corresponding lower panels. (B) Noise vulnerability V_noise, defined as the population mean of the fraction of network elements whose states depend on noise information, for the 25 output elements (solid) and the set of all elements causally connected to the output (dashed). V_noise invariably increases to near unity as evolution progresses, indicating that the network structure that evolves has higher functional connectivity than the randomly constructed starting network. (C) Random output of the starting network (solid), the target function (dotted), and the fixed randomly chosen binary noise pattern (Lower). (D) The network evolved after 2,500 generations generates a good approximation of the target function. (E) The same network as in D but operated in the absence of noise fails completely, indicating that the evolved network has been “imprinted” by the arbitrary noise sequence present during its evolution and requires it to function.

This surprising result may be explained as follows. Because noise enters the network at several points, multiple mutations are required to exclude it. The advantage of any one mutation is likely to be small, because the quasichaotic nonlinear dynamics will amplify the remaining noise. Simultaneously, evolution is restructuring the network to perform the task, and any adaptation that makes incidental use of noise information will create a fitness barrier to future removal of that information. The result is a symmetry breaking‡ that commits the organism to retaining the noise, leading to “noise imprinting.” This phenomenon may be analogous to a spontaneous breaking of inversion symmetry that has been observed in the evolution of computation by cellular automata (19). Remarkably, if each organism in each generation was randomly assigned to one of a few different stereotyped noise environments, this commonly resulted in simultaneous imprinting to all environments (one of which then had to be present for the organism to function) rather than noise exclusion. The existence of noise imprinting shows that organisms can evolve to become “adapted” to, and dependent on, features of the environment that have no direct influence on fitness—an important consideration when trying to understand the (apparent) adaptations seen in nature.

Adaptation to Unpredictable Noise: Noise Exclusion and Information Catastrophe. In addition to complexity and irrelevance, a third characteristic of most noise is unpredictability. To examine its effect, the model was operated with a different random noise realization for each organism in each generation. In this case, noise exclusion evolved reliably. In some cases, the number of network elements influenced by noise decreased more or less steadily, as in Fig. 3A. More commonly, there was an initial period of increasing noise dissemination, superficially similar to that observed with stereotyped noise (Fig. 3B). Surprisingly, fitness continued to improve slowly during this period. Detailed examination of element statistics showed that this was because of adaptations that decreased noise-related variance of the output function by delaying the buildup of noise at the output elements and anticorrelating their states (not shown).§ This “noise-filtering” effect was invariably followed by actual noise exclusion. Once this exclusion began, it proceeded rapidly, over ≈20 generations. Noise information was excluded completely from the output elements,¶ as well as from the great majority of elements causally connected to the output elements, creating a noise-free subsystem to compute the output function. Noise exclusion was essentially irreversible—only minor effects of noise on fitness were observed in subsequent generations. The noise-exclusion process was able to separate noise from useful information even when both were random and unpredictable and both entered through the same inputs (Fig. 3C).

An intermediate case between stereotyped and totally random noise is noise that varies gradually over a number of generations. This noise produced a feature not seen in either extreme case: episodes of catastrophic loss of fitness because of reversal of noise exclusion (Fig. 3D). These information catastrophes were caused by maladaptive selection events in which a mutation that permitted noise information to enter the protected subsystem was accepted because it appeared beneficial in a particular noise environment that happened to be present in that generation (Fig. 4). Full-scale catastrophes were seen only if the noise correlation time was longer than the time required for the maladaptive mutation to capture the population, roughly log(M)/log(R) generations. This expression is zero for M = 1, and information catastrophes occurred in the strong selection model even when the noise was totally randomized between generations. For difficult problems, such as exclusion of many noise inputs or extraction of a predictive signal from noise, the population model (M = 100) was much more powerful than the strong selection model (M = 1), both because it prevented mutants that were viable in only a fraction of noise environments from producing information catastrophes, and because it was able to retain them as raw material for future evolution. While these problems were being worked on, the population model maintained a high degree of genetic diversity, which then collapsed to a few genotypes after an optimal solution had been found. This diversity appeared to make a major contribution to evolvability, despite the absence of recombination from the model. This behavior is of interest in relation to the recent observation of prolonged persistence of a high degree of genetic diversity in experimental evolution of steady-state bacterial cultures (20, 21). The importance of population size for the effectiveness of genetic algorithms, particularly in the presence of selection noise (see below), is well recognized (22). However, its origins are subtle and have been shown to depend critically on the relationship between genomic representation and phenotype, and on the precise definition of evolvability (23). Most analyses have assumed (explicitly or implicitly) a linear genome with recombination by crossing over and a substantial correlation between the fitnesses of neighboring genotypes, characteristics that are absent or dubious in the Boolean network model. The effects of noise entering the organism itself (e.g., information catastrophes) have not been considered previously. Because of the slow logarithmic dependence on M, information catastrophes are likely to remain a significant feature in populations too large to simulate.

Critical Effect of Selection Noise.

Noise entering the fitness measurement rather than the organism had a different effect. Steady-state fitness was degraded, as has been described for other genetic algorithms (24, 25), but above a critical noise amplitude all adaptive evolution was lost (Fig. 5). This appears to be because of an “error catastrophe” similar to that in theories of molecular evolution (26, 27), but involving errors of selection rather than replication. It can be explained qualitatively by a simple analytical model. Assume a population comprised of two genotypes, 1 and 2, with the latter having a fitness that is greater by an amount Δ, and mutation rate μ_ij per generation per organism from genotypes i to j. The two genotypes must be understood as representing ensembles of genotypes of low or high fitness. Because there are many more of the former than the latter, μ₂₁ ≫ μ_12. In each generation, select those organisms whose apparent fitness, including Gaussian noise of standard deviation σ, is greater than the population mean. It is relatively straightforward (see Methods) to show that this process will converge to a population consisting almost entirely of the less fit genotype, unless (neglecting μ₁₂):

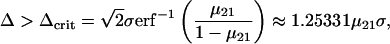1

where the far right-hand side is the first-order approximation for small mutation rate. The combined effects of deleterious mutation and erroneous selection therefore set a fitness threshold limiting the ability of evolution to capture a “shallow” ecological niche, i.e., one whose contribution to mean fitness is small compared with the fluctuations of overall fitness. This may be considered as a (negative) entropic component of fitness.

DISCUSSION

As a physical system, a living organism is bombarded by information from its environment. We can classify this information into several categories. The first is selection pressure. The taller giraffe can reach more leaves, so it is more likely to survive; in this way, the information that trees are tall is conveyed to the evolving population. This is the kind of interaction most often considered in evolutionary biology. Information also enters the individual organism directly. Some of this information may be useful for survival (there are leaves at the top of this tree). Most is irrelevant, at best useless, and more than likely to interfere with the adaptive functions of the organism. Teleologically, we would expect the organism to exclude this noise. These simulations of an evolution model in which information flow is explicit were undertaken to determine whether Darwinian selection makes these distinctions and, if so, how. The results show that the idea of homeostasis can be extended from the simple regulation of analog variables (e.g., body temperature, pH, electrolyte concentrations) to the creation of subsystems from which “digital” forms of irrelevant information are excluded. This may be important in the most nonlinear parts of biology: development/morphogenesis, behavior/neurobiology, and cultural evolution. For fundamental thermodynamic reasons, excluding noise information always has a cost. The fact that organisms are willing to pay this cost confirms our intuition that increasingly complex adaptations require machinery that is increasingly vulnerable to disruption. However, the criteria by which evolution identifies irrelevance are more subtle than might have been expected and are subject to error, sometimes catastrophic, for reasons that may be fundamental.

Two such error phenomena emerged, unexpectedly, from the simulations. Noise imprinting, which was very robust, may be a prototype of a general form of symmetry breaking that leads to the evolution of structures that are suboptimal and unnecessarily dependent on fortuitous features of the environment. Recognizing it unambiguously in the evolutionary record will be complicated by the fact that nature, unlike the model, does not provide us with an a priori partitioning of the physical interactions between organism and environment into selective forces and noise. It might also be found in experimental evolution; as a gedanken experiment, one might imagine that flies reared for many generations in a container with polka-dot wallpaper become unable to orient in its absence. However, the symmetry breaking probably occurs early in the evolution of a new adaptive trait and might not affect one that is already established.

Information catastrophe is a manifestation of the difficulty faced by evolution in recognizing noise by its unpredictability. No single organism is aware of this unpredictability—it sees only one realization of the noise—and, depending on the rate of fluctuation of the noise, no single generation may be aware of it either. Evolution must integrate information over time and population to recognize and exclude the noise, and it makes mistakes. This behavior was unchanged if the model was altered in various ways: (i) by using a fixed number of network elements; (ii) by using only mutations of types i or ii individually; (iii) by connecting an independent noise source to each of the input elements in a network; (iv) by introducing noise only by randomly initializing the states of the input elements; (v) by generating the noise endogenously by the chaotic dynamics of part of the network which was not reinitialized in each generation; (vi) by interpreting the states of the output elements as bits of a binary number, rather than counting them; (vii) by using only two Boolean functions: f₈(x, y) = x&y and f₅(x, y) = not x; (viii) by using Boolean networks with K > 2. Because any finite automaton can be represented as a Boolean network, this qualitative behavior may be generic to a broad class of highly nonlinear systems. The crucial element appears to be internal dynamics sufficiently chaotic to cause a wide dispersion of fitness in different noise environments (Fig. 4C). In the Boolean network model, this noise sensitivity is induced by evolution itself (Figs. 2B, 3B).‖ Thus, the evolution process becomes a competition between the increasing noise sensitivity that is a side effect of the adaptations required for more accurate performance of the task and the improving noise exclusion. Real physical evolving systems are dissipative thermodynamic structures in which a subsystem cannot be physically disconnected from the parent, because the latter supplies the free energy to drive its irreversible processes. It therefore remains vulnerable to corruption by information from the parent system, with potentially catastrophic consequences. I give this paradox the name “dynamic irony.”

Several questions invite further study using the Boolean network model. The detailed structural mechanisms involved in noise imprinting and in the progressive exclusion of unpredictable noise (Figs. 2B, 3B) are not known. The effects of recombination need to be explored. Random recombination might prevent the maladaptive symmetry breaking manifested as noise imprinting; this might be an additional reason for the great evolutionary success of sexual reproduction. It is also of interest to ask whether the phenomena discussed above have a parallel in cultural evolution, which probably proceeds in large part by replication of information with random innovation and selection (28). One possibility is that the creation of specialized institutions with their own values and belief systems is an analog of the protected subsystem. The compartmentation of information required to maintain the stability of such institutions would then represent a generalized form of homeostasis, subject, perhaps, to some of the same weaknesses revealed in the model.