Single Molecule Energetics of F₁-ATPase Motor

Abstract

Motor proteins are essential in life processes because they convert the free energy of ATP hydrolysis to mechanical work. However, the fundamental question on how they work when different amounts of free energy are released after ATP hydrolysis remains unanswered. To answer this question, it is essential to clarify how the stepping motion of a motor protein reflects the concentrations of ATP, ADP, and P_i in its individual actions at a single molecule level. The F₁ portion of ATP synthase, also called F₁-ATPase, is a rotary molecular motor in which the central γ-subunit rotates against the α₃β₃ cylinder. The motor exhibits clear step motion at low ATP concentrations. The rotary action of this motor is processive and generates a high torque. These features are ideal for exploring the relationship between free energy input and mechanical work output, but there is a serious problem in that this motor is severely inhibited by ADP. In this study, we overcame this problem of ADP inhibition by introducing several mutations while retaining high enzymatic activity. Using a probe of attached beads, stepping rotation against viscous load was examined at a wide range of free energy values by changing the ADP concentration. The results showed that the apparent work of each individual step motion was not affected by the free energy of ATP hydrolysis, but the frequency of each individual step motion depended on the free energy. This is the first study that examined the stepping motion of a molecular motor at a single molecule level with simultaneous systematic control of ΔG_ATP. The results imply that microscopically defined work at a single molecule level cannot be directly compared with macroscopically defined free energy input.

INTRODUCTION

In many biological ATP-driven motor proteins, stepping motion (linear or rotary) is observed at a single molecule level. In these cases, the free energy liberated by ATP hydrolysis (ΔG_ATP) is the energy input, and the mechanical step motion is the apparent output. This gives rise to an intriguing question: how does the change in ΔG_ATP affect the stepping motion? For example, how do molecular motors behave at a very low ΔG_ATP? As free energy is a macroscopically defined quantity and stepping motion of a single molecule is a microscopic feature, the above question is asking how to relate the law of the macroscopic world to observation in the microscopic world.

At first, the following may be considered as the possible behaviors:

1. The stepping velocity depends on ΔG_ATP; therefore, there is a change in the mechanical work done by the individual step motion.

2. The motor generates a step motion of a fixed size and velocity, irrespective of the ΔG_ATP input. However, when the chemical energy input (ΔG_ATP) becomes lower than the mechanical energy output in one step, it simply stops all step motions except those required for thermal fluctuation.

3. It might be possible that when one ATP is hydrolyzed, constant mechanical work is derived irrespective of the ΔG_ATP. However, the frequency of the forward step motion decreases as ΔG_ATP decreases and the back step increases due to the reverse reaction.

However, each of the three possibilities stated above has its limitations. In the case of possibility 1 or 2, a single motor molecule has to detect ΔG_ATP, which is a function of [ATP], [ADP] and [P_i] in a bulk medium. In addition, the mechanism of changing or stopping the stepping motion in response to ΔG_ATP remains unclear. Alternatively, in the case of possibility 3, it might be possible that the constant mechanical work exceeds the ΔG_ATP input; this seems to violate the law of thermodynamics.

The simple abovementioned question on the action of molecular motors has remained unanswered due to many experimental difficulties. For example, myosin II easily detaches from an actin filament, preventing the continuous observation of a single molecule under different conditions. Myosin V or kinesin's step motions yield a relatively low mechanical energy. Moreover, in the presence of a high concentration of ADP or P_i, which is required for controlling ΔG_ATP, carrying out a single molecule motility assay for these linear motors is quite difficult. This study aims to experimentally answer the above question by using a rotary molecular motor, namely, F₁-ATPase.

F₁-ATPase, a water-soluble portion of ATP synthase (1), is a rotary molecular motor in which the central γ-subunit rotates against the α₃β₃ cylinder, hydrolyzing ATP (2). The rotation is stepwise. When one ATP molecule is hydrolyzed, the γ-subunit makes a 120° step (anticlockwise, viewed from the F_o side) (3). The structure of this motor is highly stable, giving rise to a continuous, processive stepping rotation. In addition, the torque generated is considerably high (2–6). These features are ideal to explore the relationship between free energy input and mechanical work output. The only drawback is that this motor protein is severely inhibited by ADP. This ADP inhibition, also known as ADP-Mg inhibition, is not a simple product inhibition. Extensive kinetic analyses of ADP-Mg inhibition have lead to the conclusion that when ADP-Mg is formed during ATP hydrolysis or if it binds from the external medium, then the enzyme enters an inhibited state, which barely releases the bound ADP-Mg (7–9). Due to this specific inhibition, it has been practically impossible to observe continuous rotations while controlling ΔG_ATP by adding high concentrations of ADP. To overcome this problem, we introduced several mutations in α₃β₃γ, the minimal subcomplex of F₁ that shows ATP-catalyzed rotation (Fig. 1). Using the mutant, termed as GT mutant, we investigated the relationship between ΔG_ATP and the stepping motion against viscous load. This is the first report in which the stepping motion of a molecular motor was examined at a single molecule level while ΔG_ATP was systematically controlled.

FIGURE 1.

Mutations specifically introduced in the β-subunit of the GT mutant. Mutations common to the previous mutants used in the rotation assay are not shown.

MATERIALS AND METHODS

Protein

The mutant of the α₃β₃γ subcomplex resistant to ADP-Mg inhibition was derived from F₁-ATPase of a thermophilic Bacillus PS3 by introducing the following mutations: β-G181A (10) and β-T165S (11) for minimizing ADP-Mg inhibition; α-C193S, γ-S107C, and γ-I210C for specific biotinylation of the γ-subunit (12); β-His₁₀ at the amino terminus (2); α-W463F and β-Y341W (13) (Fig. 1). The mutant was named as GT mutant. In this manuscript, we call α-W463F / β-Y341W mutant as wild-type F₁. The protein was expressed and purified by the conventional method described in Dou et al. (14). The purified enzyme hardly retained bound nucleotides (<0.05 mol/mol of enzyme).

ATP hydrolysis was measured as a decrease in the absorbance of NADH at 340 nm at 25°C by using an ATP-regenerating system. Since the GT mutant showed a lag phase in its ATPase activity, the maximum rate of ATP hydrolysis was determined several minutes after the start of the reaction.

Rotation assay

Carboxy-modified polystyrene beads (0.35 μm in diameter; Polysciences, Warrington, PA) were modified with 0.5 mg·ml⁻¹ biotin-X cadaverine (Molecular Probes, Eugene, OR) and 2.5 mg·ml⁻¹ 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide hydrochloride (EDC, Pierce, Rockford, IL) at room temperature for 2 h in dark; unreacted biotin was removed by centrifugation. Next, 1 mg ml⁻¹ NeutrAvidin or streptavidin (Sigma, St. Louis, MO) was added, and the excess avidin was washed off. Biotin (BiotinPEAC₅maleimide; Dojindo, Kumamoto, Japan) was coupled to Cys residues in the γ-subunit of F₁ by a 30-min incubation at room temperature at 1∼8 μM of F₁ at F₁/biotin = 1:2. To observe the rotation, ∼100 pM F₁ in buffer A was infused into a flow chamber that comprised of two glass coverslips. The volume of the chamber was ∼15 μl.

F₁ tended to attach to the glass surface in a nonspecific manner. After 2 min, the chamber was washed with 20 mM MOPS-KOH, 10 mM MgCl₂, 10 mg·ml⁻¹ BSA, 0.1 M potassium phosphate at pH 7, and the avidin-coated beads at 0.1% concentration were then infused. Avidin on the beads specifically attached to the γ-subunit in a single F_1, while α₃β₃ was immobilized on the surface. Stepping between α₃β₃ and γ was visualized as bead displacement. The buffer system used for the rotation assay contained 20 mM MOPS-KOH, 10 mM MgCl₂, 10 mg·ml⁻¹ BSA, 0.1 M potassium phosphate at pH 7, and 2 or 10 μM ATP. To change the ΔG_ATP, ∼40 or 60 μl of the buffer containing different concentrations of ADP was infused at least twice.

In this study, [ATP] was fixed at 2 or 10 μM, [P_i] was fixed at 0.1 M, and [ADP] was varied from 0.2 to 1000 μM to change ΔG_ATP. The reason that we chose only [ADP] as a variable to control ΔG_ATP was that we wanted to maintain ionic strength (nearly) constant by keeping high [P_i] constant. Change in the ionic strength may cause change in friction between beads probe and glass surface. Addition of other salts to adjust the ionic strength might change enzymatic activity of F₁-ATPase. The stock solution of ADP was treated with hexokinase and glucose to remove any contaminating ATP. The level of ATP contamination after treatment was measured using a luciferase assay and was found to be <0.05%. ΔG_ATP was calculated by the following equation according to Nicholls (15).

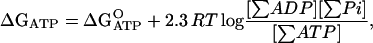at pH 7.0, 10 mM Mg²⁺.

Here, R is the gas constant (8.3 J·mol⁻¹·K⁻¹), and T is the absolute temperature (300 K). In the calculation of the mass-action ratio, the sums of different ionic species of ATP, ADP, and P_i are used and apparent equilibrium constant (K′) of 10⁵ is applied. Therefore, here. The rotation of the same F₁ molecule was compared at different ΔG_ATP levels defined above. Observations were recorded at room temperature (25 ± 2 °C).

RESULTS

Enzymatic activity and resistance to ADP-Mg inhibition of the GT mutant

The GT mutant was made by introducing several mutations to get resistant to ADP-Mg inhibition as described in Materials and Methods (Fig. 1). It is known that initial rate of ATP hydrolysis by wild-type F₁ is severely inhibited by preincubation with ADP due to the ADP-Mg inhibition. But in case of the GT mutant, which has a lag phase in the initial rate of ATP hydrolysis, it was activated by ADP preincubation rather than inhibited (Fig. 2). The initial rate and steady-state rate after ADP preincubation are plotted against ADP concentration in Fig. 3. The causes of the lag phase in ATP hydrolysis of the GT mutant and elimination of it with ADP preincubation (Fig. 2) are not clear. We suspect nucleotide binding to noncatalytic sites is necessary for full activity of ATP hydrolysis for the GT mutant, but further investigation is required on this point.

FIGURE 2.

Effect of ADP preincubation on the GT mutant and wild-type F₁. Wild-type F₁ and GT mutant were preincubated with or without 100 μM ADP for 10 min and aliquots were injected into an ATPase assay mixture containing ATP regenerating system at the time indicated by the arrow. The hydrolysis of ATP was monitored as the oxidation of NADH (decrease in the absorbance at 340 nm). ATP concentration was 4 mM. (Left panel, wild-type; right panel, GT mutant).

FIGURE 3.

Effect of ADP preincubation on the initial and steady-state rate of the ATPase activity of GT mutant GT mutant was preincubated with various concentrations of ADP and ATPase activity was measured as in Fig. 2. Initial rate (open circle, determined from the slope between 3 and 8 s after injection) and steady-state rate (solid square, determined several minutes after injection) were plotted against ADP concentration during preincubation.

The V_max was estimated at 250 ± 20 (SE) s⁻¹ and the K_m was estimated at 37 ± 10 μM at 25°C; these values are comparable to 247 s⁻¹ and 19 μM, which are the values for wild-type F₁ in the presence of lauryl dimethylamine oxide (LDAO). LDAO is known to reduce ADP-Mg inhibition in wild-type F₁. However, the GT mutant did not require LDAO for hydrolysis measurement because of the absence of ADP-Mg inhibition.

NaN₃, a potent inhibitor of F₁-ATPase, which inhibits F₁ by stabilizing ADP-Mg inhibited state had significantly less effect on the GT mutant than the wild-type (Fig. 4). These results together indicate that the GT mutant is highly resistant to ADP-Mg inhibition. Thus, it was possible to observe rotation with ADP at a concentration 500 times higher than ATP in this mutant.

FIGURE 4.

Inhibitory effect of NaN₃ on wild-type F₁ and GT mutant. Wild-type F₁ and GT mutant were injected into an ATPase assay mixture containing 4 mM ATP at the indicated arrow. Then 10 mM NaN₃ was injected at the indicated arrow. (Upper line, wild-type; lower line, GT mutant).

Rotation assay at different ΔG_ATP levels

After the mutant subcomplex was attached to a glass surface, a duplex of beads (0.35 μm in diameter) coated with streptavidin was attached to the γ-subunit that had been biotinylated at two engineered Cys residues. Relatively large beads were used so that the viscous friction against the beads was the major rate-limiting factor during step motions. ΔG_ATP was controlled by perfusing different media and the rotation of the same bead duplex (the same F₁ molecule) was compared at different ΔG_ATP levels.

First of all, we attempted to examine the rotation at a relatively high ATP concentration (10 μM) with 100 mM P_i and various concentrations of ADP (1 μM to 1000 μM); this corresponds to ΔG_ATP of −64∼−37 pN·nm/ATP. Fig. 5 a shows the time course of the rotation. Under these conditions, clear step rotation could not be resolved, and the average rate of rotation was plotted as a function of ΔG_ATP in Fig. 5 b. Due to data scattering, we are not sure if the relation is linear or not. Nevertheless, Fig. 5 b clearly indicates a correlation between the average rotational rate and ΔG_ATP. If we regard the average rotational rate ×120° as proportional to the mechanical work done by the hydrolysis of one ATP molecule, it indicates that the mechanical work done by one ATP molecule appeared to change as a function of ΔG_ATP when our time resolution was low.

FIGURE 5.

Rotation of the GT mutant at 10 μM ATP and various ΔG_ATP levels. (a) Rotation at 10 μM ATP, 100 mM P_i and 10, 100, or 1000 μM ADP. Nominally calculated ΔG_ATP values are −37, −46, and −55 pN·nm/ATP, respectively. (b) Average rotation speed was plotted against −ΔG_ATP. In this case, ΔG_ATP initially increased from −64 pN·nm/ATP to −37 pN·nm/ATP and then decreased again to −55 pN·nm/ATP. The same F₁ molecule (beads duplex) was observed throughout the experiment. The beads flowed away before the last observation at −64 pN·nm/ATP. The straight line was drawn by least square fitting.

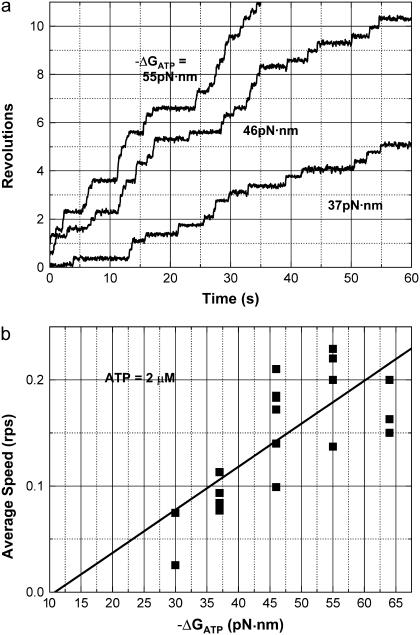
Next, we attempted to reduce the ATP concentration to resolve the individual step motions. At 2 μM ATP, we observed the step motions as shown in Fig. 6 a. The average rotational rate showed a similar tendency observed at a concentration of 10 μM ATP (Fig. 6 b). Fig. 7 shows the analysis of the rate of rise of individual steps and the dwell time between them. Fig. 7, b–e, indicates that the dwell time increases as ΔG_ATP increases. In contrast, Fig. 7, f–i, shows that the rate of rise in individual steps barely depended on ΔG_ATP. The decrease in the average velocity was attributed to the increase in dwell time. Due to the difficulties in repeated perfusion of different media for the same specimen, we could examine an ADP concentration range of 0.2–1000 μM (nominal ΔG_ATP was −64 to −30 pN·nm/ATP.) in only six independent experiments. ADP concentration ranges of 0.2–200 μM and 2–1000 μM were examined in one experiment. In all the experiments, the rate of rise in individual steps did not demonstrate significant ΔG_ATP dependency. The rate of rise at −30 pN·nm/ATP of ΔG_ATP ([ADP] = 1000 μM) was 92% ± 9.9% (average ± SD) of the rate at −64 pN·nm/ATP of ΔG_ATP ([ADP] = 0.2 μM) for the six experiments. The apparent “work” per 120° step motion was calculated using the viscosity of bulk water and rate of rise in individual steps for each experiment. The values varied with each experiment, probably due to the difficulty in determining the precise rotation radius. At −30 pN·nm/ATP of ΔG_ATP, the experimentally obtained minimum and maximum value was 19.3 pN·nm/step and 36.1 pN·nm/step, respectively. The average (±SD) was 27.1 (±6.0) pN·nm/step. As described in Discussion, the “work” associated with the step motion, estimated by using the viscosity of bulk water, is the minimum limit of its true value. Based on these results, we conclude that the rate of rise in each step motion and hence the apparent work per 120° step motion is essentially independent of the free energy input, i.e., ΔG_ATP.

FIGURE 6.

Rotation of the GT mutant at 2 μM ATP and at various ΔG_ATP levels. (a) Rotation at 2 μM ATP, 100 mM P_i, and 2, 20, or 200 μM ADP. Nominally calculated ΔG_ATP values are −37, −46, and −55 pN·nm/ATP, respectively. (b) Average rotation speed was plotted against −ΔG_ATP. In this case, ΔG_ATP initially increased from −64 to −30 pN·nm/ATP by perfusing different solutions containing different concentrations of ADP. The same F₁ molecule (beads duplex) was observed throughout the experiment and average speed was defined in the time courses where very long pauses were not included. Therefore, we plotted more than one point at the same ΔG_ATP in panel d. The straight line was drawn by least-square fitting.

FIGURE 7.

Statistical analyses of the rotation of the GT mutant at 2 μM ATP and at various ΔG_ATP. (a) Rates of rise and dwell time that were analyzed are shown along the time course of rotation. (b–e) Analyses of dwell time between steps. The time constant was deduced by fitting with a single exponential curve to the dwell time histogram (b–d) and plotted against the −ΔG_ATP in panel e. (f–i) Analyses of the rate of rise at the step. The rate of rise was estimated for every step motion, and the histograms were constructed (f–h). The mean and standard errors were plotted against −ΔG_ATP in panel i. In panel i, 3.0 rps corresponds to the mechanical “work” of 27 pN·nm/step without the correction of the viscosity increase near the glass surface. See text for details.

DISCUSSION

The results in Figs. 6 and 7 clearly demonstrated that the apparent “work” in a single step motion, which was defined as the rate of rise (=angular velocity) × frictional drag coefficient × step angle (=2/3 π), was almost constant, irrespective of the free energy input (ΔG_ATP). Therefore, the possibility 1 proposed in the Introduction is disproved. The apparent “work” was almost the same or occasionally higher than the lowest value of −ΔG_ATP that was examined (30 pN·nm/ATP). But the value of the apparent “work” seems to be underestimated for the following reasons: In the above calculation, the frictional drag coefficient of bulk water was used. When the increase in viscosity near the glass surface is considered, the value of the frictional coefficient should be approximately twice of that in bulk water (16). Alternatively, when the actin filament attached to the γ-subunit was used as a spring balance, the torque was estimated to be 50 ± 6 pN·nm (17) rather than 40 pN·nm estimated by simple hydrodynamic calculation using a viscosity of the bulk water (3,18). The result indicates that the true value of the torque should be at least 1.2 times larger than that estimated above. Thus, the true value of the apparent “work” plus ΔG_ATP easily becomes positive with either of these corrections. Therefore, possibility 2 also appears unlikely. Possibility 3 predicted that constant mechanical work is derived in a one-step motion even with an increase in the ADP concentration, and that partial product inhibition or back reaction by ADP and P_i occurs. In this study, the ΔG_ATP-independent rate of rise in Fig. 7 B agrees with this prediction. Further, the increase in the dwell time observed in Fig. 7 A agrees with the predicted product inhibition; however, a clear increase in the back step was not observed. But the apparent absence of full back steps (120° back step) was anticipated because when considering the equilibrium constant of 10⁵ M for ATP hydrolysis, the ratio of the forward reaction to the backward reaction is in the order of 1000 even at the lowest −ΔG_ATP examined in this study (2 μM ATP, 1000 μM ADP, and 100 mM P_i).

From the viewpoint of enzyme kinetics, this result would be expected because increases in [ADP] will cause product inhibition of the forward reaction. Previous single molecule work has established that the individual ATP-triggered steps occur rapidly. If ADP dissociation was required before ATP could bind, then high ADP would increase the dwell time, but not influence the rise time once it was gone and ATP had bound. This would be true even if ADP dissociated from a different subunit than the one to which ATP bound. However, if we think of the balance between input free energy (ΔG_ATP) and output mechanical work, there is still a problem to be clarified. In fact, if we define the energy transduction efficiency as the ratio of the apparent work of individual steps to −ΔG_ATP, these results indicate this apparent efficiency will exceed 100%. From this result, one may conclude that the biological molecular motor can violate the law of thermodynamics. This conclusion, of course misdirected, is based on a misinterpretation of the law of thermodynamics. The problem resides in the definition of “work”. A simple reasoning may be explained as follows: the reason that the maximum work is limited by the free energy input is that if it exceeds the free energy, it would result in an entropy decrease of the whole system. A prerequisite for this statement is that the thermodynamically defined work does not contribute to entropy production in any way (19). In this situation, however, the apparent “work” is done against viscous load and hence dissipated as heat. Therefore, it eventually contributes to the increase in entropy. Thus, the apparent “work” against viscous load is different from thermodynamically defined work. Therefore, even if the apparent “work” defined for the individual rate of rise exceeds the magnitude of input free energy (−ΔG_ATP), it does not violate the law of thermodynamics. This outcome reflects statistical nature of thermodynamics.

To compare the work done by a molecular stepping motor with thermodynamic parameters such as ΔG_ATP, Wang and Oster theoretically proposed that it is necessary to average the rotation speed over a long time including interstep dwells (20). The efficiency calculated using the averaged speed (Stokes efficiency) is limited to 100% even if the work is done against frictional load (20). In this case, averaging the speed is a type of statistical treatment by which work and chemical potential can be compared.

In a sense, it can be said that thermodynamic parameters are defined macroscopically with low spatial and temporal resolutions. The low resolution data in Fig. 5 in which we cannot discriminate individual steps matches the chemical potential rather than the data in Fig. 6. In Fig. 5, our temporal resolution was not high enough to resolve individual steps at 10 μM ATP and we could only get information on the average rotational velocity. But using this rotational velocity, we could calculate apparent work that showed clear correlation with ΔG_ATP (Fig. 5 b). At 2 μM ATP (Figs. 6 and 7), the temporal resolution was relatively higher than at 10 μM ATP and we could resolve each step motion. Then, the apparent “work” calculated from the rate of rise of individual steps lost correlation with ΔG_ATP. Instead, time-averaged velocity that was obtained indirectly after statistical treatment, showed correlation with ΔG_ATP (Fig. 6 b). As our temporal and spatial resolution get higher, we can observe single molecule events microscopically. At such a high resolution, what we observe is a single molecular motor exchanging thermal energy to and from the environment to achieve its function. Then the results of our observation can be related to macroscopically defined thermodynamic parameters after appropriate statistical treatment. At the high resolution, the field of microscopic vision shows us a world where ambient noise cannot be reduced, and what is directly seen is not directly compared with macroscopically defined thermodynamics (21).