Multiscale Modeling of Nucleosome Dynamics

Abstract

Nucleosomes form the fundamental building blocks of chromatin. Subtle modifications of the constituent histone tails mediate chromatin stability and regulate gene expression. For this reason, it is important to understand structural dynamics of nucleosomes at atomic levels. We report a novel multiscale model of the fundamental chromatin unit, a nucleosome, using a simplified model for rapid discrete molecular dynamics simulations and an all-atom model for detailed structural investigation. Using a simplified structural model, we perform equilibrium simulations of a single nucleosome at various temperatures. We further reconstruct all-atom nucleosome structures from simulation trajectories. We find that histone tails bind to nucleosomal DNA via strong salt-bridge interactions over a wide range of temperatures, suggesting a mechanism of chromatin structural organization whereby histone tails regulate inter- and intranucleosomal assemblies via binding with nucleosomal DNA. We identify specific regions of the histone core H2A/H2B-H4/H3-H3/H4-H2B/H2A, termed “cold sites”, which retain a significant fraction of contacts with adjoining residues throughout the simulation, indicating their functional role in nucleosome organization. Cold sites are clustered around H3-H3, H2A-H4 and H4-H2A interhistone interfaces, indicating the necessity of these contacts for nucleosome stability. Essential dynamics analysis of simulation trajectories shows that bending across the H3-H3 is a prominent mode of intranucleosomal dynamics. We postulate that effects of salts on mononucleosomes can be modeled in discrete molecular dynamics by modulating histone-DNA interaction potentials. Local fluctuations in nucleosomal DNA vary significantly along the DNA sequence, suggesting that only a fraction of histone-DNA contacts make strong interactions dominating mononucleosomal dynamics. Our findings suggest that histone tails have a direct functional role in stabilizing higher-order chromatin structure, mediated by salt-bridge interactions with adjacent DNA.

INTRODUCTION

Most eukaryotic DNA is associated with histone proteins to form highly compact structures. This complex of DNA and histones, called nucleosomes (1), forms the fundamental repeating subunit of chromatin. Such hierarchical packaging of DNA is of fundamental importance to eukaryotic organisms. The central core of nucleosomes, called the nucleosome core particle (NCP) is composed of a histone octamer having four pairs of the core histone proteins: H2A/H2B-H4/H3-H3/H4-H2B/H2A wrapped around by 1.65 turns of 147 basepairs of nucleosomal DNA (2,3) (italicized and non-italicized core histones refer to structurally distant sets of H2A/H2B-H4/H3 tetramers). The NCP crystal structure has been reported at 1.9 Å resolution (Protein DataBank: 1kx5)(4). The structure of the constituent eight core histones is also well resolved, and consists of many basic Arginine and Lysine residues (Fig. 1, a and b). It is also known that the N-terminal histone tails are flexible and disordered in the crystal structure (2,5,6) and their reversible posttranslational modifications—methylation, acetylation, phosphorylation, ubiquitination, and ADP-ribosylation—trigger specific functions (7,8) critical for nucleosome stability. The high-resolution crystal structures of the nucleosome core particle show histone tails as having extended random-coil topology, lacking secondary structure (2,9). Whereas the proximal ends of H2A histone tails pass through the minor-groove DNA between superhelical gyres, the distal ends are spatially segregated from the nucleosomal DNA (2,4). Although many in vitro and in vivo assays demonstrate the role of conserved histone tail modifications in transcriptional regulation (7,10), a structural understanding of how the histone tail dynamics mediates chromatin organization is poorly understood.

FIGURE 1.

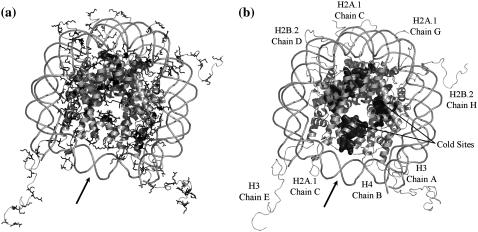
(a) Basic residues in the nucleosome core particle. Crystal structure of the nucleosome core particle (Protein DataBank ID 1kx5) (4). Basic residues, lysine (dark gray) and arginine (black), present in the histone octamer assembly are shown. Strong salt-bridge interactions are formed between basic histone side chains and the phosphate backbone of nucleosomal DNA. (b) Snapshot of cold sites in the nucleosome. Cold sites are those histone residues that maintain more of their contacts throughout simulations than other residues. In discrete molecular dynamics simulations of histone-octamer assembly, we observe that these sites are present within the core of the nucleosome. A and B are aligned for comparison of cold sites against regions rich in basic lysine and arginine residues. Bold arrow indicates the nucleosomal dyad axis of symmetry.

How nucleosomes become organized and packaged into discrete domains such as euchromatin and heterochromatin in eukaryotic cells has been an intriguing puzzle for many years (11–13). Yet the precise control of chromatin structure is essential for all DNA-templated processes, such as replication, recombination, repair, and transcription (14,15). At the heart of chromatin structure is the NCP, whose structure has been solved at the atomic resolution (4) and is composed of DNA and histone proteins. Many biophysical experiments have provided key insights into higher-order chromatin organization (16). Although information obtained from crystal structures, as well as others containing histone variants, has been exceedingly informative, it is insufficient to explain the complex dynamics of nucleosomes and the nature of nucleosome-nucleosome interactions that are essential for creating higher-order chromatin structure in cells.

Although the structure of histone fold domains are highly conserved across genomes (17), a key element missing in our understanding of chromatin structure and function has been the lack of information pertaining to the histone tails, which are dynamic, disordered (18), and not resolved in many crystal structures. Increasing evidence indicates a fundamental role for histone tails and their covalent modifications in higher-order chromatin organization. However, how these tails and their posttranslational modifications contribute to the packaging and organization process of chromatin is not well understood, but likely involves a combination of activities including the control of nucleosome stability, nucleosome-nucleosome interaction and the precise recruitment of protein machineries that organize discrete chromosomal domains. Chromatin organization is a highly complex process involving multiple steps and layers of regulation. Combining high-resolution computational modeling of nucleosomes with long-timescale discrete molecular dynamics (DMD) simulation enables a detailed understanding of the complex and dynamic nature of nucleosomes and how histone tail modifications affect nucleosome stability.

Molecular dynamics approaches have provided important insights into our understanding of the dynamics of proteins (19–25) and nucleic acids (25–27). Theoretical studies of chromatin fiber and the NCP have been performed using coarse-grained (CG) physical models (28,29). Computational approaches that employ conventional all-atom molecular dynamics simulations (30) using molecular mechanics and quantum mechanics force fields (25,31) provide detailed information on the local dynamics of molecules. However, because of the large size of the NCP (>16,850 heavy atoms in mononucleosome crystal structure) and the vast dimensionality of feasible conformations of nucleosomes, all-atom molecular dynamics simulations have severe limitations on the timescales and lengthscales (32) on which nucleosomal dynamics can be studied. An alternative approach for improving the conformational sampling efficiency is using simplified structural models of protein and DNA. In these simplified models, amino acids and nucleotides are coarse-grained to the level of effective particles (beads), where each bead represents the center of mass or geometric centroid of a group of atoms. Local fluctuations among atoms constituting the beads are ignored and the interaction potentials between these beads are derived from the native crystal structure of NCP.

In this study, we examine the dynamics of NCP using fixed-temperature DMD simulations. We further investigate the structural dynamics of our model nucleosome and the determinants of nucleosome stability using essential dynamics analysis and frequencies of interhistone and histone-DNA contacts found in DMD trajectories. The results presented here show that in mononucleosomes, histone tails form strong salt-bridge interactions with adjacent nucleosomal DNA, suggesting their direct functional role in stabilizing higher-order chromatin structure. We identify a small fraction of histone core residues, termed “cold sites”, having significantly low fluctuations in multiple constant-temperature simulations. We postulate a functional role of cold sites in mediating nucleosome stability. Our structurally detailed simulations show interactions of distal ends of histone tails with nucleosomal DNA due to the formation of hydrogen bonds between terminal lysines/arginines and DNA phosphates. Also, based on our simulations, we report the presence of cold sites, residues responsible for structural stability of the nucleosome core. The presence of such cold sites is significant, since variant nucleosomes found in eukaryotic genomes (having H2A.Z/CENP variant histones) may incorporate variant histones in cold sites, resulting in alterations in the stability of the NCP core.

MATERIALS AND METHODS

Geometric description of a model histone octamer

Amino acids in the histone octamer assembly are modeled by two effective beads per residue (33): C_α beads representing the coordinates of backbone α-carbon atoms and C_β beads representing the effective coordinates of side-chain β-carbon atoms (for glycine, the C_α and C_β beads coincide) (34,35). Each amino acid is assigned an index i, corresponding to its position in the sequence from the N-terminus (i = 1) to the C-terminus (i = N, number of residues). The geometry of histones is modeled by four types of bonds: 1), covalent bonds between C_αi and C_βi; 2), peptide bonds between C_αi and C_α(i±1); 3), effective bonds between C_βI and C_α(i±1) and 4), effective bonds between C_αi and C_α(i±2). Effective bond lengths for bond types 3 and 4 are determined by computing the standard deviation of distances between carbon pairs in 10³ representative globular proteins obtained from Protein DataBank, as described in Ding et al. (33).

Geometric description of model nucleosomal DNA

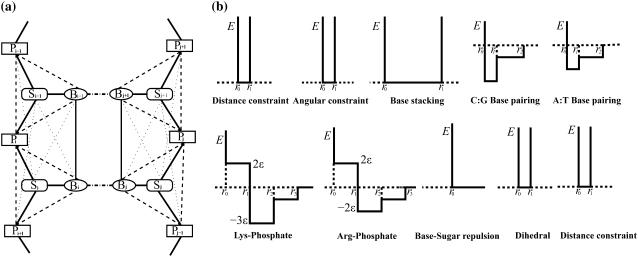
Each nucleotide in the 147-bp DNA fragment is modeled as three beads (Fig. 2): one bead each for the sugar, phosphate, and base. These beads represent the effective coordinates of sugar, phosphate, and base portions of the nucleotide. The sugar bead S_i of the ith nucleotide is positioned at the centroid of its constituent C1′, C2′, C3′, C4′, and O4′ atoms, the phosphate bead P_i at the centroid of P, O1P, O2P, and O5P atoms, and the base bead B_i is positioned at the centroid of N1, C2, N3, C4, C5, and C6 atoms. The average bond-length parameters of beads and their standard deviations of nucleosomal DNA were obtained from the available high-resolution NCP structure (4). The structural parameters used in the model are listed in Supplementary Materials (Table S1).

FIGURE 2.

(a) Interactions between the model DNA beads. Consecutive nucleotides in the DNA double helix are shown. The sugar, phosphate and base beads are indicated by S_i, P_i and B_i, respectively. Covalent interactions between these beads are shown by (dark solid lines) and noncovalent interactions by dashed lines: angular constraints (dotted lines), basepairing (dash-dotted line), base stacking (thin solid lines), and dihedral constraints . (b) Interaction potentials used in the DNA model. Each interaction is modeled as a coarse-grained square-well potential. Lysine-phosphate and arginine-phosphate interactions have a weaker long-range attractive shoulder to simulate the effects of solvent-mediated hydrogen bonds. Steric repulsion between sugar and base beads is modeled as hardcore repulsion. Constraints for distance, angular, dihedral, and base stacking are infinitely high potential wells whose breadth depends on the nature of the interacting species. The depths of potential wells for A-T and C-G basepairs are proportional to their corresponding strength of interaction: 2:3. The radial separations (such as r₀, r₁, and r₂) at which these constraints are applicable are based on mean separation and fluctuations of corresponding beads observed in the crystal structure of the nucleosome core particle.

Simulation potentials

Interactions in the histone octamer assembly CG model are modeled as two-body potentials. These interactions include covalent bonds between Cα_i and Cβ_i, peptide bonds between Cα_i and Cα_(i+1), angular constraints between Cβ_i and Cα_(i+1), and dihedral constraints between Cα_i and Cα_(i+2) beads (34). These additional bonds model angular and dihedral constraints between side chains and backbones. Effective bonds (two-body) are used to mimic the tetrahedral constraints of amino acids and the planar constraints of peptide bonds. Permanent bonds are realized by infinitely high potential wells, as described in Peng et al. (34) and Ding et al. (36), whereas hard-core repulsions are modeled by infinitely high square-well potentials.

In nucleosomal DNA, covalent interactions between sugar, phosphates, and bases are modeled as infinitely high potential wells: V_i,j = 0 if r_i,j lies within one standard deviation (σ_i,j) of the mean bond length (D_i,j) between beads i and j and V_i,j = ∞, otherwise. Noncovalent interactions are modeled as discrete attractive/repulsive potentials: DNA base-pairing interactions are attractive and the base-stacking interactions along the chain incur steric repulsions. The interactions between core histones and the DNA are modeled as nonspecific electrostatic attractions between the basic side chains of lysine and arginine residues and the acidic phosphates present in the DNA backbone. Interactions between histone amino acids and nucleotide bases are dominated by direct and solvent (water)-mediated electrostatic attractions (hydrogen bonds) between basic arginine and lysine side chains and DNA backbone phosphates (4). Because of negative charges present on DNA backbone phosphates, the interactions of nucleosomal DNA with acidic and nonpolar amino acids are relatively infrequent and are disregarded in the model. Simulation interaction potentials used for the DNA model are shown in Fig. 2 a.

The structural parameters required for the model are mean bond lengths and standard deviations for each pair of model interactions (Fig. 2). The structure of nucleosomal DNA is remarkably different from that found in nonhistone protein-DNA complexes or canonical B DNA (37). These structural parameters, derived from the high-resolution NCP structure (2), are used in all the simulations. The numerical values of each of the r₀, r₁, r₂, and r₃ interaction radii used in the model are listed in Table S1. The DMD potential for purine-pyrimidine interactions are scaled as −3ɛ and −2ɛ for G-C and A-T basepairing, according to the relative strengths of these basepairs: three hydrogen bonds are formed in the G-C basepair, whereas two hydrogen bonds are formed in the A-T pair. Similarly, the interactions between DNA and lysine/arginine are also scaled according to the number of potential hydrogen bonds formed with the DNA.

DMD algorithm

Using simplified square-well potentials as interparticle interactions, we apply the discrete time molecular dynamics simulations approach (32,34,38) to study the dynamics of the NCP. In this approach, the beads move with a constant velocity until an elastic or inelastic collision occurs. Upon collision, the interaction potential of the beads changes, thereby changing the kinetics of colliding beads. DMD maintains a set of possible collisions and the current state of each bead. After each collision, DMD updates the set of possible collisions and the state for colliding beads. It then determines the pair of beads undergoing the earliest subsequent collision. Since every collision needs to update the state of only the colliding pair of beads, this approach samples a vast dimensionality of histone and DNA conformations. DMD simulations of two-bead-per-residue protein models may be performed using the iFold server (http://ifold.dokhlab.org) (39). Each 1 × 10⁵-time unit (t.u.) run of NCP simulations takes ∼30 days on a single 2.4-GHz Intel Pentium 4 computer.

Essential dynamics of the nucleosome core particle

The essential dynamics (40) of a multiparticle system separates large concerted structural rearrangements from irrelevant uncorrelated fluctuations. In this method, we compute the normalized covariance matrix (NCM):

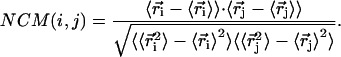(1)

Here, r_i and r_j represent the cartesian coordinates of the ith and jth beads, respectively, and the bracketed values represent averages over the entire trajectory. The covariance matrix describes the correlation of the positional fluctuations of α carbon beads for the histone core and of phosphate beads for nucleosomal DNA. To verify the validity of calculated correlation coefficients, we perform covariance analysis over two 3 × 10⁴ t.u. of nonoverlapping DMD subtrajectories and observe that the two covariance matrices thus obtained are nearly identical to the matrix obtained for the entire trajectory. We then diagonalize the covariance matrix of fluctuations of atoms (beads in the case of the coarse grained model) along the trajectory, yielding eigenvectors as directions in the 3N-dimensional subspace (where N represents the total number of C_α and P beads in the system). Most of the topological fluctuations cluster in correlated motions in a subspace of a few degrees of freedom, whereas the other degrees of freedom represent independent uncorrelated fluctuations. The eigenvalues are a measure of the mean-squared fluctuations of the constituent beads along the corresponding eigenvectors, and are computed using the QL algorithm of Numerical Recipes in C (41). The eigenvalues are sorted in descending order, and the corresponding first eigenvalue represents the largest topological fluctuation and a majority of the fluctuations are restricted to first few eigenvectors.

Heavy-atom reconstruction of histone, DNA conformations

Using the reconstruction procedure, the CG model (two-bead) trajectories of histones obtained from DMD simulations are transformed into a heavy-atom representation (N, C, O, CA, and CB). The method of heavy-atom reconstruction used for histones is described in Ding et al. (42). A four-bead representation of each residue is generated by adding N and C′ atoms into the simulated two-bead (C_α–C_β) model. The conformation of this four-bead model was then relaxed to the lowest energy state and the secondary-structure elements were refined using short discrete molecular simulations. The side-chain and backbone oxygen structures are added according to the most stable (C_α, C_β, N, C′) conformation. Backbone and side-chain rotamers are optimized using Monte Carlo-based simulated annealing procedure using the Dunbrack and Cohen backbone-dependent rotamer library (43).

DNA reconstruction is used to generate a heavy-atom trajectory of DNA from three-bead trajectories generated by DMD. For each nucleotide present in the crystal structure of nucleosomal DNA, we generate coordinates of the corresponding sugar (S_i), phosphate (P_i), and base (B_i) beads, and the coordinates of preceding sugar (S_i−1) and succeeding phosphate (P_i+1) beads, forming a five-bead nucleotide conformation template Tⁱ = [S_i, P_i, B_i, S_i-1, P_i+1]. We then classify these conformation templates according to nucleotide type—adenine, cytosine, guanine, or thymine—yielding a library of CG nucleotide conformations present in the native state. Each snapshot of the simulation trajectory is then reconstructed as follows: for the jth nucleotide of the snapshot, the target conformation T^j = [S_j, P_j, B_i, S_j−1, P_j+1] is structurally superimposed with each of the templates of corresponding nucleotide type using the Kabsch algorithm(44). The template T^k = [S_k, P_k, B_k, S_k−1, P_k+1] minimizing root-mean-square deviation with target T^j is chosen and the rotation matrix R^k→j transforming template T^k to target structure T^j is computed. This rotation matrix R is then applied to the crystal structure coordinates of the nucleotide corresponding to the k^th template to yield the heavy-atom structure of the jth nucleotide of the snapshot.

Analysis of conserved contacts: interhistone and histone-DNA contact frequencies

Frequencies of interhistone and histone-DNA contacts reveal key contacts conserved in the course of simulation. We define two histone residues to be in contact if the separation between their corresponding C_β beads is <7.5 Å. Mean frequencies of interhistone contacts are evaluated by averaging the contacts formed over the entire simulation trajectory. A comparison of mean frequencies of interhistone contacts against the contacts present in the native state reveals key histone-histone interactions conserved in the simulation, thereby ascertaining the flexibility of the contact. We propose that interactions having high frequencies of histone-DNA contacts in the constant-temperature simulations specify key interactions responsible for nucleosomal stability. A large fraction of histone-DNA contacts in the NCP are solvent-mediated salt bridges and hydrogen bonds (45) between the backbone phosphate of DNA and basic histone side chains. Thus, we define a contact between histone residue and DNA nucleotide if the separation between the corresponding C_β and phosphate beads is <11.5 Å. We plot the frequencies of histone-DNA contacts formed in constant-temperature DMD simulations performed over a range of temperatures.

Estimation of the DMD simulation timescales

Evolution of DMD trajectories does not require Verlet integration; rather, it computes iterative solutions of the ballistic equations of motion under soft square-well potential. Longer timescales are accessible by DMD simulations due to integration of available degrees of freedom in CG models and use of soft square-well potentials/implicit solvation in DMD simulations. The classical equipartition principle divides thermal motions of nucleosomes into translational, rotational, and vibrational degrees of freedom. However, high-frequency vibrations, such as hydrogen vibrations, are typically uncoupled from the mean-field dynamics of the system. The effective mean-field interactions in CG models reduce the classical degrees of freedom.

Nielson et al. (46) have estimated the effective timescales accessed by CG models for dimyristoyl phosphatidylcholine in water (13 beads/molecule), calibrating diffusion coefficients for CG models against all-atom simulations and experiments. There is a 100-fold increase in timescales for translational and rotational diffusions between atomistic versus CG simulations. The CG model for DNA incorporates nucleotides as three beads/nucleotide (∼20 heavy atoms and 14 hydrogen atoms, 1:11 reduction) and proteins are coarse-grained as two beads/residue (∼10 heavy atoms and 12 hydrogen atoms, 1:11 reduction). We estimate a 100-fold increase in translational and rotational diffusional timescales for CG nucleosomes. In addition, the use of soft square-well potentials in simulations allows another 10- to 100-fold increase in simulation timesteps (47). In the worst-case scenario, there is at least a three-orders-of-magnitude reduction in time steps due to the use of soft potentials and implicit solvation in CG models.

To incorporate the effect of time-step discreteness we compute the fundamental DMD time unit along with the effective scaling 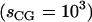due to reduced degrees of freedom in the CG model. The timescales for CG models in DMD are given by: [T_CG] ≈ s_CG[L]([M]/[E])^1/2. For NCP simulations, the effective mass of each coarse-grained bead is ∼100 g mol⁻¹, the unit length of simulation is 1 Å, and the DMD unit energy is 1 kcal mol⁻¹. This leads to the estimate: [T_CG] ≈ 0.5 ns. Thus, one time unit in CG-DMD simulations of nucleosomes corresponds to ∼0.5 ns of physical time. Consequently, our coarse-grained NCP and histone octamer simulations of 1 × 10⁵ t.u. correspond to simulating dynamics for roughly 50 μs of experimental time. Zhou et al. (48) have also used a coarse-grained model to investigate the timescales of CG simulations. The authors have translated the simulation timescales to physical timescales by comparing the dynamics observed in their simulations to experimental results. They conclude that the reduced simulation time unit corresponds to 1 ns of physical time (48); thus, our time unit is also of the order computed by Zhou et al.

RESULTS

To understand the role of DNA in nucleosome stability, we first describe the comparison of DMD simulations of NCP with simulations of the histone octamer complex. We then describe essential dynamics analysis of the NCP to study the large-scale dynamics of nucleosomes. We then present the frequencies of interhistone and histone-DNA contacts and analyze contacts mediating nucleosome stability. Throughout this study, the temperature is measured in DMD units of energy ɛ divided by Boltzmann's constant, ɛ/k_B (see Materials and Methods). The reduced temperature 0.7 ɛ/k_B corresponds to approximately the ambient temperature (T^amb = 300 K).

DMD simulations of nucleosomes display cold sites in the nucleosome core

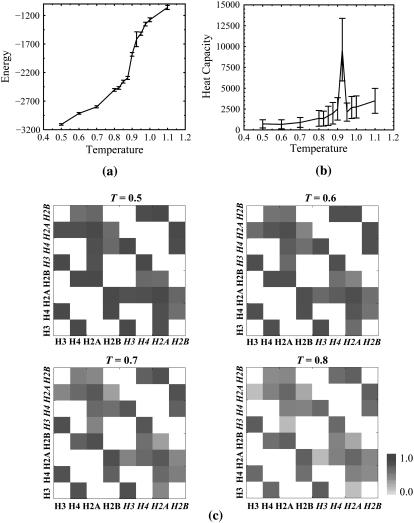
Our simulations of the histone octamer complex reveal that in the absence of nucleosomal DNA, histone tails are highly mobile in nature, and often adopt random-coil conformations. We study the equilibrium behavior of the histone octamer complex and NCP by measuring the heat capacity and the average potential energy as a function of temperature. Based on our constant-temperature simulations, we define the unfolding temperature of the histone octamer assembly to be T_f = 0.8 ɛ/k_B (Supplementary Materials, Fig. S4). For nucleosomes, we performed constant-temperature DMD simulations over a temperatures range T = 0.1–2.8 for 1 × 10⁵ t.u. At each sampled temperature, we start with the native-state (crystal structure) conformation and perform DMD simulations for 5 × 10⁴ t.u. simulation to equilibrate the system, followed by an additional 5 × 10⁴ t.u. for recording the simulation trajectory (see Materials and Methods). The dependence of average potential energy and related heat capacity versus temperature for the NCP is shown in Fig. 3, a and b, respectively. We find that the NCP folding temperature is 0.92ɛ/k_B (Fig. 3 b). The heat capacity is computed from the relation

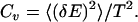FIGURE 3.

(a) Thermodynamics of the nucleosome core particle. The dependence on temperature of the energy, E, is shown. The error bars represent a standard deviation of energy fluctuations. (b) Variation of the constant-volume heat capacity, C_v, of the nucleosome core particle with temperature. The error bars are the standard deviation of C_v fluctuations. NCP unfolding occurs at temperature T = 0.92. (c) Temperature dependence of frequencies of interhistone contacts. Histone chains making contacts in constant-temperature simulations of the histone-octamer complex are shown for temperatures T = 0.3–0.8. Frequencies of interhistone contacts are color-coded from white (contact frequency of 0) to black (contact frequency of 1). Under high-temperature conditions, the frequencies of contact are significantly reduced; however, novel interhistone contacts are not observed, indicating the absence of intranucleosome domain swap.

In simulations performed at low temperatures (T = 0.1–0.5 ɛ/k_B), the core histone octamer is rigid, while the histone tails are flexible. Under high-temperature conditions, the histone octamer is destabilized, thereby contributing to increased flexibility of histone tails. We characterize specific regions present in the histone core (cold sites) (Fig. 1), where residues retain a majority of their contacts throughout simulations compared to other residues (trajectory-normalized contact frequency >0.7). We find that many cold sites are composed of hydrophobic residues, clustered as domains of five of more adjacent residues, and are present in the core of the nucleosome. Large fractions of cold sites are clustered in the interface between H3-H3 histones formed by the C-terminal helices of H3 histone fold domains: (His-113A, His-113E, Ala-114A, Ala-114E, Leu-126A, Leu-126E, Ala-127A, Ala-127E, Arg-131A, Arg-131E, and Ile-130E). Interhistone interactions between the H3-H3 interfaces are essential for fastening the two H2A/H2B-H4/H3 NCP tetramers. This H3-H3 interface thereby mediates the dynamics of these halves of the NCP. Cold sites are also localized between the two H4-H2A and H4-H2A interfaces: (Thr-96B, Leu-97B, Tyr-98B, Gly-99B, Val-100G, Thr-101G, Ile-102G, Ala-103G) and (Thr-96F, Leu-97F, Tyr-98F, Val-100C, Thr-101C, Ile-102C, Ala-103). As opposed to the H3-H3 histone fold, the interface of each of these two domains is formed by small stretches of parallel interhistone β-sheets (H4-H2A and H4-H2A).

We posit that these cold sites are essential for the stability of histone octamer complex and that the presence of clusters of cold sites at interhistone interface suggests that domains containing cold residues may have a direct functional role in stabilizing the corresponding interactions at interhistone interfaces. During transcription elongation, the interactions at these interhistone cold sites may need to be weakened in part, resulting in significant destabilization of the nucleosomes. We find less abundance of cold sites in the histone fold domains of H2A, H2B, and H4 histones, suggesting that within the NCP, the globular histone fold domains of these histones have relatively greater flexibility than H3 histones. The frequency of contacts between H3-H2A, H3-H2B interfaces is low, indicating that these contacts have weak interactions in the NCP. The enhanced rigidity of selective interhistone interfaces by cold sites also suggests an order of histone release during nucleosome dissociation, whereby weakly interacting H2B and H2A histones are dislodged before the release of strongly bound H3, H4 histones.

Essential dynamics of nucleosome and histone octamer assembly

To elucidate the global dominant motions within the NCP, we use essential dynamics approach (40) on DMD trajectories to generate the principal components of nucleosome dynamics during constant temperature simulations. In this approach, the collective concerted fluctuations in the NCP are projected onto the principle-components subspace (see Materials and Methods). In the principal-components subspace, eigenvectors and eigenvalues of the covariance matrix represent the direction and amplitudes, respectively, of the essential motions of nucleosome. We perform separate essential dynamics analyses on the DMD trajectories of the histone octamer and the NCP. We find that in both cases, the largest principal component of nucleosome dynamics corresponds to flagellar motions of flexible histone tails. This behavior is conserved over a wide range of temperatures examined (T = 0.1–1.1). Normalized correlation maps depict correlations between motions of all pairs of histone-histone, histone-DNA, and DNA-DNA beads (cf. Materials and Methods). By comparing the normalized correlation maps of the NCP and the core histone octamer, we find that in the absence of nucleosomal DNA, dynamics of intrahistone residues are strongly correlated, whereas dynamics of interhistone residues are largely uncorrelated. The subsequent component of histone-octamer dynamics consists of bending of the two [H3-H4-H2A-H2B] tetramers relative to each other about the H3-H3 interface. This observation is consistent with our previous result: the cold sites found at the H3-H3 interface mediate large-scale dynamics of the NCP.

Temperature dependence of the normalized correlation map of the nucleosomes over a range of temperatures (T = 0.1–1.2 ε/k_B) demonstrates that in the presence of DNA, the fluctuation of histone tails is suppressed by hydrogen-bonded interactions with nucleosomal DNA (Fig. S1). Within the histone octamer core, the H3 and H4 core histones belonging to the same H2A/H2B-H4/H3 histone tetramer undergo mutually correlated dynamics, whereas these motions are uncorrelated with the motion of H2A, H2B histones and H3 and H4 histones belonging to the other H2A/H2B-H4/H3 tetramer. However, the two H2A and H2B histone pairs belonging to the same histone tetramer are mutually correlated. This result suggests that the dynamics of the two histone tetramer halves of the NCP are largely uncoupled with each other; however, their constituent histones have strongly correlated dynamics.

We find that in high-temperature simulations, nucleosomal DNA collapses into the histone octamer assembly. Because of base-pairing interactions, relative motions between the DNA strands are strongly correlated with each other. Under high temperature regimes (T = 0.8–1.2 E/k_B), the motion of DNA is significantly anti-correlated with motion of H2A and H2B histones and is largely uncorrelated with motion of H3 and H4 histones. This finding suggests presence of fluctuating DNA-histone interactions formed with H2A and H2B, which may impart conformational flexibility and thereby assist in stabilizing the NCP. Also, absence of correlated motions between H2A/H2B and H3/H4 heterodimers at elevated temperatures shows that the contacts between the two heterodimers are weakened under these conditions.

Contact frequencies reveal key interhistone and histone-DNA interactions

Frequencies of interhistone and histone-DNA contacts reveal key contacts conserved in the course of simulation. We plot the frequencies of interhistone contacts in Fig. 3 c. Intrahistone and histone-DNA contact frequencies are shown in Figs. S2 and S3, respectively. Under low-temperature conditions, interhistone contacts are persistent throughout the simulation and mimic contact space of the native conformation. Contacts between histone pairs H3/H4, H2A/H2B, H3/H4, and H2A/H2B occur more frequently than other interhistone contacts (Fig. 3 c).

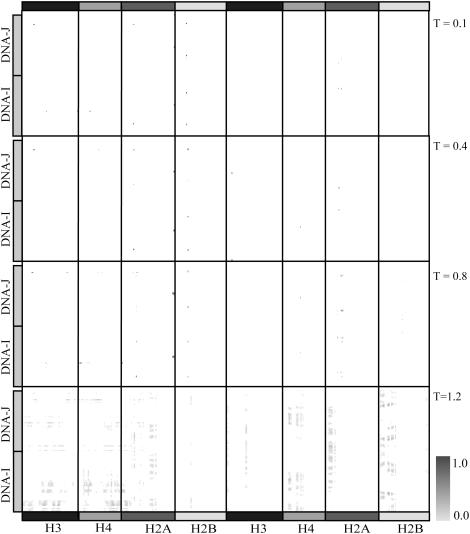
We calculate contact frequencies for all histone-DNA contacts formed at a range of temperatures from DMD simulations. The contact frequency map shows frequencies of histone-DNA interactions formed, averaged over the simulation trajectory. We have generated the map of contact frequencies for histone-DNA contacts formed during simulations at temperatures T = 0.1, 0.8, and 1.2 (Fig. 4). We find that under low-temperature conditions (T = 0.1), fewer histone-DNA contacts are formed relative to high-temperature conditions (T = 0.8 and 1.2), which is a characteristic of higher conformational rigidity of DNA under low-temperature conditions. A high frequency of histone-DNA contacts specifies key salt-bridge interactions persistent in the constant-temperature DMD simulations. We observe that a large number of histone-DNA contacts are long-range interactions and the frequencies of intrahistone contacts decreases monotonically as the temperature is increased from 0.1 (below unfolding temperature), through 0.9 ɛ/k_B (∼T_f) to 1.2 ɛ/k_B (above the unfolding temperature). We also find that all long-range contacts have frequencies close to zero. Our coarse-grained histone-DNA interaction potentials mimic the first-order simplification of specificity among amino acid-base interactions as demonstrated by Luscombe et al. (49,50). We have generated a detailed map illustrating frequencies of inter- and intrahistone contacts formed in the presence of DNA (Fig. S2). We find that in the presence of DNA, there is an increase in the number of interhistone contacts formed, suggesting that in the NCP, histones are tightly embraced by nucleosomal DNA.

FIGURE 4.

Temperature dependence of histone-DNA contact frequencies. The frequencies of contact are color-coded from white (contact frequency of 0.0) to black (contact frequency of 1.0). Few contacts are populated in the low-temperature condition (T = 0.1), indicating that the nucleosome core particle is energetically trapped in a local energy minimum. Under high temperature conditions, T = 0.4 and 0.8, we observe a substantial increase in highly frequent histone-DNA contacts formed. Under very high temperature conditions (T = 1.1), the nucleosome core particle is unfolded and the frequency of histone-DNA contacts becomes uniform over the contact-space.

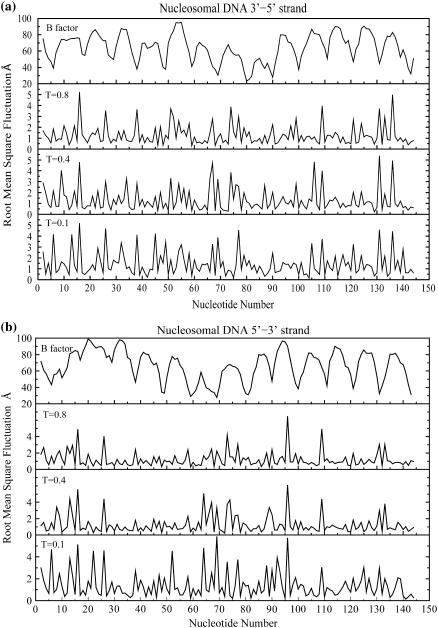
A plot of per-nucleotide fluctuations of the two nucleosomal DNA strands observed in constant-temperature DMD simulations performed at temperatures T = 0.1–0.8 ɛ/k_B (folded state) is shown in Fig. 5. Fluctuations are computed as standard deviations of phosphate beads, relative to their initial conformation, averaged over the last 3 × 10⁴ t.u. of the total time (10⁵) of simulation trajectory. Nucleotides having low fluctuations (<1.0 Å RMSD) impart structural rigidity to the nucleosomal DNA and are conformationally constrained by interactions with the histone octamer assembly. These fluctuations in nucleosomal DNA are specific to the DNA sequence context and significant variations in the magnitude of fluctuations among neighboring nucleotides are observed in our simulations. DNA fragments making strong contacts with neighboring nucleotides have low mean fluctuations (Fig. 5). The dynamics of the two DNA strands are cross-correlated with each other over the range of temperatures used in the simulation; however, the extent of correlation is diminished at the elevated temperature (T = 1.2 ɛ/k_B), indicating that the standard Watson/Crick basepairing is conserved in simulations performed at elevated temperatures. The crystallographic temperature factors for corresponding phosphorus atoms in the two strands are also shown (Fig. 5, top panel). We observe that these experimentally observed temperature factors correlate with the extent of fluctuations of the phosphate beads. Localized sequence specificity of these DNA fluctuations is essential for the nucleosome positioning code (51) and is expected to be a conserved feature for nucleosomal DNA across genomes.

FIGURE 5.

Fluctuations in nucleosomal DNA conserved over a range of temperatures. Root-mean-square deviations (in Ångstroms) with respect to the initial conformation of the phosphate beads along the two nucleosomal DNA strands: 3′-5′ (a) and 5′-3′ (b) are shown at temperatures T = 0.1, 0.4, and 0.8 ɛ/k_B. Crystallographic temperature factors for corresponding phosphorus atoms derived from the crystal structure (Protein DataBank 1kx5) are also shown. The extent of these fluctuations is observed by averaging the fluctuations in the last 3 × 10⁴ t.u. of the corresponding constant-temperature DMD simulation trajectories. The fluctuations in nucleosomal DNA are sequence-specific and are correlated (correlation coefficient 0.55) over the shown range of temperatures (0.1–0.8 ɛ/k_B). These crystallographic temperature factors are also correlated with these fluctuations in phosphate beads. The simulation data is averaged over three independent constant-temperature DMD simulation runs performed at temperatures from 0.1 to 0.8 ɛ/k_B.

Modulating DMD histone-DNA interaction potentials simulates salt effects

The electrostatic environment of the NCP is known to have a significant effect on its dynamics (52,53). We performed constant-temperature simulations of mono-nucleosomes with varying strengths of interaction between histone side chains and DNA over a range of temperatures. In our model, DNA backbone phosphates have attractive (electrostatic) interactions with histone lysine and arginine residues (see Materials and Methods). A coarse-grained phase-space plot of histone-DNA interactions is shown in Fig. 6. Since salt and ionic environment are known to mediate the stability of histone-DNA contacts (54–57), varying the strengths of these histone-DNA contacts qualitatively models the variations in salt concentration around the nucleosome. Calibration of histone-DNA interaction strengths enables us to recapitulate the effects of salt on the stability of NCP (56,57). We have performed high-temperature simulations (T = 1.2–2.8 ɛ/k_B) to estimate the NCP phase-space behavior. We observed that the ensemble of NCP conformations found at T = 1.2 was qualitatively similar to the conformational ensemble at significantly higher temperatures, with progressively increased amounts of DNA-end fraying. However, temperatures above T = 1.2 are physically unrealistic and are unlikely to be attained under normal physiological conditions.

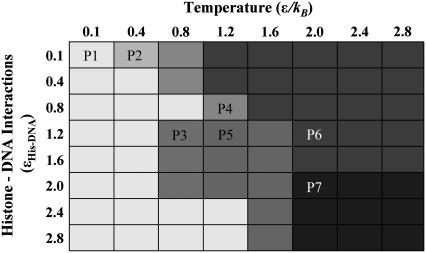
FIGURE 6.

Phase space of the nucleosome core particle. This coarse-grained phase space of the nucleosome core particle is generated by performing discrete molecular dynamics simulations of the nucleosome core particle over a range of simulation temperature (T = 0.–2.8 ɛ/k_B, step size of 0.4 ɛ/k_B) and also over a range of histone-DNA interaction potentials: ɛ_His-DNA = 0.1–2.8 k_BT^amb, with step size ɛ = 0.4 k_BT^amb. Interactions between lysine side chains and DNA backbone phosphate correspond to −3 ɛ_His-DNA, whereas interactions between arginine side chains and DNA backbone phosphate correspond to −2 ɛ_His-DNA. Independent sets of constant-temperature DMD simulations are performed at each of these interaction potentials and over this range of temperatures to obtain the nucleosome behavior under varying physical conditions. Differences in grayscale intensities (labeled P1 to P7) correspond to variations in equilibrium NCP conformations observed over the range of temperatures, and histone-DNA contact potentials. P1), Histone tails bind to DNA; NCP is stable. P2), DNA segregated from histones; histone octamer is intact. P3), Nucleosomal end-fraying: terminal DNA base-pairing is disrupted, histone octamer is intact. P4), Nucleosome intact, histone tails bind DNA; H2A histones extruded from the NCP and the H3-H3 interhistone interactions stabilizing the NCP are disrupted. P5), DNA ends unfurl, collapse on histones; histone octamer unfolds. P6), DNA base-pairing is segregated and the histone octamer unfolds. P7), DNA collapses onto the histone octamer, and the H3-H3, H3-H4, and H2A-H2B contacts unfold.

The number of histone-DNA contacts formed in the simulations enumerates the stability of the NCP. We observe that under conditions of low interaction strength, the interactions between histones and DNA are predominantly local and weak salt bridges, which are often disrupted by thermal fluctuations or in simulations at higher temperatures. Under conditions of moderate attraction between histones and DNA, (ɛ_His-DNA = 0.4–1.2 k_BT^amb), the NCP is stable over a range of temperatures. Under very large values of histone-DNA interaction strengths (ɛ_His-DNA = 1.2–2.8 k_BT^amb), interhistone interactions become significantly weaker than histone-DNA interactions. In this phase, the wrapped nucleosomal DNA entwines and presses against the histone octamer assembly. We characterize ɛ_His-DNA = 0.8 k_BT^amb as the histone-DNA interaction strength for the physiologically relevant scale of histone-DNA contacts.

DISCUSSION

In our simulations, we observe persistent salt-bridge interactions formed between histone tails and nucleosomal DNA at low temperatures, whereas thermal fluctuations disrupt these contacts in high-temperature conditions. These interactions include direct (short-range) and solvent-mediated (long-range) contacts and mediate the stability of the NCP. Experimental evidence suggests that histone tails are highly mobile in the NCP and often adopt random-coil structures (4). Luger et al. (18) have proposed that histone tails essentially assemble nucleosomes into chromatin fibers. Transcriptional regulation by covalent histone tail modifications is well established in literature (6,7,10,14), with many histone acetyltransferases being transcriptional coactivators (58). In our NCP simulations, we observe that the histone tails are highly mobile and they bind to proximal nucleosomal DNA. These strong electrostatic interactions between DNA phosphates and histone tails are conserved even in simulations performed at elevated temperatures. This finding supports our hypothesis that histone tails may have a direct structural role in stabilizing higher-order chromatin structure, and suggests a structural mechanism for stabilizing higher-order chromatin organization (59), whereby histone tails bind to neighboring nucleosomal DNA and this binding is destabilized by histone tail modifications leading to nucleosome remodeling. Our findings of strong interactions between histone tails and nucleosomal DNA are in agreement with the work done by Ausio et al. (60), where the authors report that under physiologically relevant salt conditions (<0.7 M NaCl), nucleosomal tails play a significant role in maintaining the thermal stability of mononucleosomes. We attribute this effect to the strong electrostatic interactions between histone tails and DNA. In our simulations, the histone tails do not behave as strictly random coils, in polymer physics sense (61). However, we report the absence of extended secondary/tertiary structures for histone tails in our DMD simulation trajectories. Our simulations suggest that binding of elongated histone tails to nucleosomal DNA imparts structural stability to the tails. During chromatin condensation, the histone tails may adopt an ordered secondary structure and make structurally conserved interactions with adjacent nucleosomes.

In the context of long nucleosomal arrays, with large conformational flexibility accessible to histone tails, the propensity to form internucleosomal histone-DNA interactions competes against intranucleosomal histone-DNA interactions. This equilibrium between intra- and internucleosomal interactions is attributed to the stability during condensation of chromatin fibers. Studies of small-angle x-ray scattering (SAXS) for NCPs also support our results: SAXS data from Mangenot et al. (56) shows salt-dependent binding of histone tails to neighboring nucleosomes. Zheng et al. (62–64) investigated inter- and intranucleosomal interactions in a model dinucleosomal array and observed that upon salt-dependent folding and oligomerization of nucleosomes, H3 tail interactions reorganize to engage in primarily internucleosome interactions. Positively charged N-terminal tails of H3 histones are longest among all core histone tails, and therefore have significantly greater conformational flexibility available to form strong interactions with neighboring nucleosomes and its own nucleosomal DNA. Preferential binding to neighboring nucleosomes at higher salt concentrations is expected due to weakening of intranucleosome histone tail-DNA interactions. Predictions of Zheng et al. that alterations in H3 histone tail interactions may elaborate different structural and functional states of chromatin is also in agreement with our simulations: Low-temperature DMD simulation trajectories (Fig. S3) show stabilization of nucleosome upon binding of histone tails with nucleosomal DNA, while under higher-temperature conditions, thermal fluctuations hinder histone tails binding to DNA, leading to a higher energy conformation.

Evidently, below the folding transition temperature (i.e., T = 0.5–0.875 ɛ/k_B), DMD simulations achieve equilibration by 4 × 10⁴ t.u., whereas the simulations performed above the folding temperatures are equilibrated by 6.5 × 10⁴ t.u. Subtle equilibrium between intramolecular interactions and entropic contributions is sufficient to fold a protein into its specific tertiary structure. The approach used in our model, i.e., DMD simulations of two-bead/residue models, has previously been applied successfully to study the protein-folding transition-state ensemble of the C-Src SH3 domain (33) and the amyloidogenesis mechanism for Src SH3 domain proteins (65). Similar DMD approaches have been extensively applied to successfully capture the essential elements of structural stability, encompassing important biological processes: protein folding, unfolding, and aggregation (32,34,36,66–69). Thus, we believe that our DMD model captures relevant elements of structural stability for the NCP. Coarse-graining the structural details of NCP results in underestimation of histone side-chain entropic contributions. Due to the enormous structural complexity of nucleosomes, an accurate estimation of side-chain entropy is unfeasible. The coarse-grained approximation in the DMD model allows us to sample longer-timescale conformations at the expense of structural detail. By generating an all-atom representation of corresponding coarse-grained trajectories (using the heavy-atom reconstruction method, cf. Materials and Methods), we can generate atomic-resolution trajectories for NCP, giving an estimate of the loss of entropic contributions in CG models.

CG models have integrated degrees of freedom in comparison to the corresponding all-atom models. We have used the coordinates of C_α and C_β atoms as our beads for investigating the dynamics of corresponding histone residues. Hence, in our unified-atom model, the masses of these beads (m_C) are independent of the nature of the histone residue. Accurate estimation of physical timescales from CG models is difficult (46). We have provided a method to scale the DMD-simulation timescales to experimental timescales (Materials and Methods). Due to coarse-graining of the system, intrabead fluctuations occurring at small timescales, such as hydrogen vibrations, are not manifested in DMD simulations. Notably, DMD simulations of the NCP enable us to sample longer conformational dynamics of NCP, accessing experimentally relevant timescales (70,71) with near atomic-resolution detail.

We postulate a functional role of cold sites in the nucleosomes. The interface between H2A-H4 and H2A-H4 β-sheets are found to be rich in clusters of cold sites, and make stable interactions throughout the DMD simulations. Santisteban et al. (72) showed that disruption of H2A-H4 and H2A-H4 β-sheet interactions by H4-Y98G mutants leads to disruption of H2A-H3-H4, H2A-H3-H4 molecular clusters and H4-H2B interactions, thereby causing nucleosome dissociation. Wood et al. (73) showed the presence of significant H2A-H4 and H2A-H4 β-sheet interactions in their high-resolution (1.9-Å) crystal structure of the histone octamer assembly. Based on solvent-accessibility analysis and residue conservation, they postulated that the region of histone octamer binding transcription elongation factors and other histone-binding compounds involved in transcription is present in the β-sheet interaction region. Thus, studies by Santisteban et al. (72) and Wood et al. (73) also support a functional role of H2A-H4, H2A-H4 cold sites in transcription elongation.

We also observe that the magnitude of local structural fluctuations in nucleosomal DNA is sequence-dependent in nature. Although the extent of these fluctuations increases monotonically with temperature; the sequence dependence is conserved across a wide range of temperatures (correlation coefficient of 0.55 for T = 0.1, 0.4, and 0.8 ɛ/k_B), as shown in Fig. 5. Local fluctuations in nucleosomal DNA vary significantly along the DNA sequence, suggesting that only a fraction of histone-DNA contacts make strong interactions and dominate the dynamics of nucleosomal DNA. This observation is in agreement with the observations by Luger et al. (2), where x-ray crystal structure of the NCP shows 14 contact points between DNA and the histone.

Histone-DNA interactions have previously been studied using DNase I digestion (74), protein-DNA cross-linking (75,76), and immunoprecipitation (77). In our constant-temperature DMD simulations, under low-temperature conditions (T = 0.1 ɛ/k_B), histone tails form few contacts with nucleosomal DNA, whereas at higher temperatures (T = 0.4–0.8 ɛ/k_B), we observe frequent contacts formed between the C-terminus of one H2A (chain C) and the dyad axis of nucleosomal DNA (Fig. 4). These results support earlier experimental work (78) where the authors used covalent protein-DNA cross-linking experiments to demonstrate that in the absence of linker DNA, the C-terminal domain of histone H2A contacts the dyad axis, and showed the ability of the H2A C-terminal domain to rearrange. These interactions of positively charged histone tails with negatively charged nucleosomal DNA stabilizes the histone tails and its secondary structure may change from random coils to α-helices, which is consistent with previously reported results on a similar increase in α-helical content upon acetylation of histone tails (79). Other dominant histone-DNA interactions include contacts with H2B histone. Under very high temperature conditions (T = 1.2 ɛ/k_B), the histone octamer assembly is unfolded and the DNA basepairing is lost at the termini. We find that the frequency of histone-DNA contacts found in the native state is significantly reduced, with contacts largely interspersed. We expect that transient histone-DNA hydrogen-bond interactions having low contact frequency in DMD simulations will be weaker and have a smaller contribution to nucleosome stability.

The elastic nature of free DNA has been characterized using several biophysical experiments (80–82) and theoretical models (83–87). Bending properties of DNA have been extensively studied for prokaryotic (88) as well as eukaryotic (89,90) cells. Protein-induced DNA bending (91) is shown to be necessary for transcription activation (92). It is proposed that the intrinsic curvature and flexibility of nucleosomal DNA mediates nucleosome stability (93). In our simulations, we observe that due to the preferential attraction of DNA strands toward core histones, significant bending deformations are observed in nucleosomal DNA. Strong electrostatic interactions with histones stabilize the bent state of DNA, and this conformation persists throughout the simulation. However, in mononucleosomes, elongated conformations are preferred for base-pairings present at the ends of nucleosomal DNA. Stopped-flow FRET experiments demonstrate spontaneous unwrapping of nucleosomal DNA (71,71,94). Recent work by Li et al. (71) demonstrates rapid rates for unwrapping (∼4 s⁻¹) and rewrapping (20–90 s⁻¹) of nucleosomal DNA from the histone octamer assembly. Our simulations suggest that for nucleosome remodeling, the resulting rate-limiting step of nucleosomal DNA unwrapping is mediated in part by spontaneous disruption of these interactions between histone tails and core histones and nucleosomal DNA. Since the kinetics of nucleosomal transcription, which occurs at longer timescales (∼1.4 kb/min (95)), is limited by the rate of DNA rewrapping (71), the aggregate number of local contacts formed between histone tails and nucleosomal DNA, which enhance DNA rewrapping, may mediate the kinetics of transcription at nucleosome-rich DNA fragments.

CG models using effective potentials are also known to reproduce gyration-radius and distribution functions of constituent CG variables over a wide range of temperatures (96). Our approach of performing DMD simulations on near-atomic-resolution CG models of the NCP, with heavy-atom trajectory reconstruction, may be extended to simulations of naturally occurring variant nucleosomes (having a Cse4-containing H3-variant or Htz1-containing H2A-variant), dinucleosomes, and other higher-order nucleosomal arrays having linker histones, for deciphering the functionality of histone variants (97–100), histone tail modifications (101), and linker DNA (102) on the stability of NCP and the higher-order organization of chromatin structure. Existing approaches for modeling the NCP using coarse-grained electrostatic models (70,103) and Monte Carlo simulations of the chromatosome particle (104) have been successful in predicting gross chromatin dynamics. All-atom simulations of simplified nucleosome models lacking histone tails (105,106) have yielded important insights into higher-order chromatin organization. However, the presence of histone tails is critical in ascertaining the structural organization of chromatin fibers (6,7). Complementing models of higher-order chromatin dynamics with our higher-resolution DMD simulations based on NCP structural models, a detailed insight on large-scale chromatin structure and dynamics is accessible.

CONCLUSIONS

In summary, using DMD simulations, we show that our simplistic model recapitulates the stability and simulates the dynamics of NCP for experimentally relevant timescales. We find that in our simulations of mononucleosomes, histone tails form strong salt-bridge interactions with nucleosomal DNA, suggesting their direct role in forming higher-order chromatin structure. Based on constant-temperature discrete molecular dynamics simulations, we find that bending across the H3-H3 interface is a prominent mode of nucleosome dynamics. The dynamics of the NCP is dominated by histone tails with subsequent normal modes composed of large-scale interhistone motions. Analysis of frequencies of histone-DNA contacts formed in constant-temperature DMD simulations shows persistent contacts formed with C-terminal H2A and the nucleosomal dyad axis, thereby suggesting functional roles of the H2A C-terminal domain. We determine a coarse-grained phase space of the NCP under altering potentials of histone-DNA interactions. Our approach of amalgamating rapid conformation sampling techniques like DMD with coarse-grained models of nucleosome may be useful for analyzing the effects of histone variants and the effects of DNA sequence on nucleosome positioning.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.