Abstract
Catch bonds, whose lifetimes are prolonged by force, have been observed in selectin-ligand interactions and other systems. Several biophysical models have been proposed to explain this counterintuitive phenomenon, but none was based on the structure of the interacting molecules and the noncovalent interactions at the binding interface. Here we used molecular dynamics simulations to study changes in structure and atomic-level interactions during forced unbinding of P-selectin from P-selectin glycoprotein ligand-1. A mechanistic model for catch bonds was developed based on these observations. In the model, “catch” results from forced opening of an interdomain hinge that tilts the binding interface to allow two sides of the contact to slide against each other. Sliding promotes formation of new interactions and even rebinding to the original state, thereby slowing dissociation and prolonging bond lifetimes. Properties of this sliding-rebinding mechanism were explored using a pseudoatom representation and Monte Carlo simulations. The model has been supported by its ability to fit experimental data and can be related to previously proposed two-pathway models.
INTRODUCTION
Complex formation between macromolecules (e.g., proteins and carbohydrates) involves many noncovalent interactions, including electrostatic interactions, van der Waals forces, hydrogen (H) bonds, and dipole-dipole interactions. Although each of these can be well described by established theories in physical chemistry, as implemented in the force fields for molecular dynamics (MD) simulations, predicting the collective properties of many such interactions distributed over a binding interface of complex geometry represents a major challenge no less than that of predicting protein folding. Usually these interactions work cooperatively, as suggested by the observation that binding and unbinding between macromolecules usually proceed as rapid state transitions, which can be described by a kinetics framework originally developed for chemical reactions. George Bell recognized this by modeling specific receptor-ligand binding that mediates cell-cell adhesion with this kinetics framework (1). Thus researchers in the field refer to a macromolecular complex as a “bond” and characterize the respective association and dissociation of receptor-ligand bonds using a pair of on-rate and off-rate constants, or simply their ratio—the binding affinity—to describe the overall binding propensity, which omits the details of the atomic-level interactions and their changes during the process of rapid transitions. Bell recognized one more complication, however. A cell is usually subjected to mechanical forces applied to it from the environment or exerted by it to the environment. These forces are transmitted from one cell to another or from a cell to the extracellular matrix via adhesion bonds, which regulate their binding kinetics. Bell proposed the first model for force dependence of off-rate, which is an exponentially increasing function of force (see Eq. 1 below) (1). This model is intuitive and has been widely supported by experiments.
Dembo et al. proposed several alternative models: off-rate could be an exponential function of force and/or the square of force (2). In his derivation based on the transition state theory, Dembo et al. realized a theoretical possibility that off-rate could be a decreasing function of force in addition to being an increasing function of force as originally proposed by Bell. Different types of bonds were classified according to how their off-rates respond to increasing force: slip bonds if off-rates are increased, catch bonds if off-rates are decreased, and ideal bonds if off-rates are the same (2). Evans and Ritchie (3) derived the Bell model from Kramers' kinetic rate theory (4). Dissociation was treated as a thermally activated diffusive escape over an energy barrier (the top of which is the transition state) from an energy well that trapped the interacting molecules in the bound state. The applied force tilted the energy landscape and lowered the energy barrier, thereby accelerating dissociation. This treatment considered the system to be far from thermodynamic equilibrium, which was thought to be more appropriate than the equilibrium treatment employed in the derivation of catch bonds by Dembo et al. Under the assumption of a single dissociation pathway, such a simple physical picture only allowed slip bonds. Thus, although the catch bond concept was intriguing and sparked some debates in the field, it was generally dismissed because it was unusual and counterintuitive.
Using atomic force microscopy, biomembrane force probes and flow chamber experiments, catch bonds have recently been demonstrated for P-selectin (5) and L-selectin (6–8) dissociating from P-selectin glycoprotein ligand 1 (PSGL-1) at low forces. At high forces they transition to slip bonds like those previously observed (9,10). Catch-slip transitional bonds have also been reported for other systems, including the bacteria adhesin FimH interacting with mannose ligands (11,12) and myosin interacting with actin (13). Several theoretical articles have modeled the catch-slip transitional bonds (12,14–19). Most of these models extended the topology of the assumed energy landscape from a one-dimensional curve to a two-dimensional surface and the assumed number of dissociation pathways from one to two. The external force was assumed to lower the energy barrier along an individual pathway, but it was also assumed to switch dissociation from a fast to a slow pathway, thereby generating the catch-bond behavior. Thus, although along each pathway dissociation might behave as a slip bond on its own right, the force-induced redistribution of relative proportions of dissociation along the two pathways resulted in catch bonds at low forces, which then transitioned to slip bonds at high forces. Different models made different assumptions regarding whether there were one or two internal bound states, whether the internal bound states were in rapid equilibrium or were slowly converted from one to another, whether one of the pathways had to be a catch bond by itself or both could be slip bonds, and/or whether the energy landscape was rigid or could be deformed by force in addition to being tilted by force. Although all were capable of curve-fitting the experimental data, these data are insufficient to validate or rank the models. A major deficiency of the published models is that they neither take into account the structure of the interacting molecules nor explain how noncovalent interactions at the atomic level give rise to two dissociation pathways.
The purpose of this article is to address this gap by exploring how simple kinetic properties assumed for atomic-level interactions can cooperate to generate catch-bond behavior at the level of unbinding of macromolecular complexes. Using crystallography data and MD simulations we analyzed selectin:ligand structures, their possible conformational changes, the network of noncovalent interactions distributed over the binding interface, and their dynamic changes over time in the absence of force and in the presence of a pulling force that was applied to induce conformational change and/or unbinding. Based on the insights obtained from these observations, we proposed a sliding-rebinding mechanism for catch bonds, related it to the two-pathway models, examined the properties of our model, and tested it against experimental data.
METHODS
Molecular dynamics simulations
The crystal structures of the lectin and epidermal growth factor (EGF) domains of unliganded P-selectin (Protein Data Bank (PDB) code, 1G1Q) and P-selectin liganded with sialyl Lewis x (sLex) (PDB code, 1G1R) or with the N-terminal portion of PSGL-1 (PDB code, 1G1S) (20) were used as starting coordinates. In some simulations, only the lectin domain was used by deleting the EGF domain from residues 121–158. The molecules were solvated in rectangular water boxes and neutralized by adding Ca2+ and Cl− ions to create a ∼50 mM calcium concentration known to be required for selectin-ligand binding. The largest system had 52,213 atoms (including 7 Ca2+ and 9 Cl−) in a water box of 120 × 64 × 72 Å3. Free dynamics and steered molecular dynamics (SMD) simulations (21) were performed using the NAMD program (22) with the CHARMM22 all-atom force field for proteins (23). The sugar force field was modified from a carbohydrate solution force field (CSFF) (24). Missing parameters for 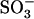 group of sulfated tyrosine,
group of sulfated tyrosine, 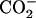 carboxyl group of sialic acid (NeuNAc), as well as N-acetyl group of N-acetyl-d-galactosamine (GalNAc), N-acetyl-d-glucosamine (GlcNAc), and sialic acid were adopted from the CHARMM22 parameters of the groups with similar topologies. Periodical boundary condition was used along with particle mesh Ewald method for electrostatic interaction and a 12-Å cutoff for van der Waals interaction. The system was energy-minimized by 10,000 steps with heavy atoms fixed first and then another 10,000 steps with all atoms free. After energy minimization, the system was heated up from 0 to 300 K in 100 ps and then equilibrated for 1.5–2 ns with pressure and temperature control. The temperature was held at 300 K using Langevin dynamics and the pressure was held at 1 atm by Langevin piston method. Free dynamics or SMD simulations were then run on the equilibrated system. For SMD, the O1 atom of residue GlcNAc (N-acetyl-O-methyl-d-glucosamine) of sLex or the Cα atom of residue Pro-18 of PSGL-1 was pulled through a spring with a spring constant of 70 pN/Å at a constant speed of 5, 10, or 50 Å/ns. The Cα atom of Gly-147 of the EGF domain or of Ala-120 of the lectin domain was constrained to its equilibrated position. Constraining Gly-147 instead of the C-terminal residue reduced the likelihood for the EGF domain to be unfolded during simulation. The interdomain angle was quantified as the angle between two lines, respectively, connecting the respective centers of masses of the lectin domain (residues 1–119) and majority of the EGF domain (residues 122–141) to that of the hinge (residues 120 and 121). Simulation data were sampled at a frequency of 1012 Hz unless stated otherwise. New interaction formation was defined by an interatomic distance of <3.5 Å that lasted for >25, 25, or 5 ps for pulling speeds of 5, 10, or 50 Å/ns, respectively. All protein structures are drawn with visual molecular dynamics (25).
carboxyl group of sialic acid (NeuNAc), as well as N-acetyl group of N-acetyl-d-galactosamine (GalNAc), N-acetyl-d-glucosamine (GlcNAc), and sialic acid were adopted from the CHARMM22 parameters of the groups with similar topologies. Periodical boundary condition was used along with particle mesh Ewald method for electrostatic interaction and a 12-Å cutoff for van der Waals interaction. The system was energy-minimized by 10,000 steps with heavy atoms fixed first and then another 10,000 steps with all atoms free. After energy minimization, the system was heated up from 0 to 300 K in 100 ps and then equilibrated for 1.5–2 ns with pressure and temperature control. The temperature was held at 300 K using Langevin dynamics and the pressure was held at 1 atm by Langevin piston method. Free dynamics or SMD simulations were then run on the equilibrated system. For SMD, the O1 atom of residue GlcNAc (N-acetyl-O-methyl-d-glucosamine) of sLex or the Cα atom of residue Pro-18 of PSGL-1 was pulled through a spring with a spring constant of 70 pN/Å at a constant speed of 5, 10, or 50 Å/ns. The Cα atom of Gly-147 of the EGF domain or of Ala-120 of the lectin domain was constrained to its equilibrated position. Constraining Gly-147 instead of the C-terminal residue reduced the likelihood for the EGF domain to be unfolded during simulation. The interdomain angle was quantified as the angle between two lines, respectively, connecting the respective centers of masses of the lectin domain (residues 1–119) and majority of the EGF domain (residues 122–141) to that of the hinge (residues 120 and 121). Simulation data were sampled at a frequency of 1012 Hz unless stated otherwise. New interaction formation was defined by an interatomic distance of <3.5 Å that lasted for >25, 25, or 5 ps for pulling speeds of 5, 10, or 50 Å/ns, respectively. All protein structures are drawn with visual molecular dynamics (25).
Monte Carlo simulations
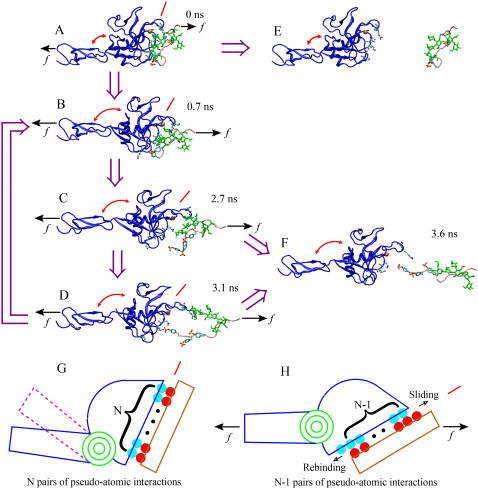
In a recent study, we formulated a minimal model for the sliding-rebinding mechanism with only two pairs of pseudoatoms (8). Here we formulated a more general model with an arbitrary number (N) of pseudoatom pairs. Both models were solved using Monte Carlo simulations but the detail implementations were different. This simulation had N stages. In the Ith stage (1 ≤ I ≤ N), I pairs of pseudoatoms were capable of interacting and the association and dissociation kinetics of each pair were simulated. At the end of the Ith stage when all I pairs of pseudoatomic interactions dissociated, sliding and rebinding were simulated. Sliding moved the simulation forward to the (I − 1)th stage (or dissociation of the entire complex if I = 1) whereas rebinding brought the simulation backward to the (I + 1)th stage (for I < N) (see Fig. 5, G and H).
FIGURE 5.
Pathways of sliding-rebinding mechanism. (A–D and F) Sequential SMD simulated structures of PSGL-1 (pink for the peptide and green for the glycan) dissociating from P-selectin lectin-EGF domains (blue) at indicated times. The simulation is the same as that shown in Figs. 3 A and 4 and the structural elements are marked the same way as in Fig. 4. (E) Separate structures of P-selectin lectin-EGF domains and PSGL-1 N-terminal fragment indicating complete dissociation. The thick purple arrows indicate the hypothetical sequence of events along dissociation pathways. The interdomain angles are marked by arched double-sided red arrows. The inclinations of the binding interface are marked by inclined red lines. (A) The initial bound state. (B) Force-induced opening of the hinge angle. (C) Rupture of preexisting interactions. (D) Sliding and formation of new interactions. (E) Dissociation from fast pathway 1. (F) Dissociation from slow pathway 2. When a small force f (short black arrows) is applied, the complex may detach by dissociation of all noncovalent interactions that preexisted in the bound state. An intermediate force (long black arrows) may open the hinge angle, tilt the binding interface, and promote sliding of PSGL-1 over the lectin binding interface after preexisting atomic-level interactions dissociate. This provides an opportunity for new interactions to form, which would replace those that are disrupted, or for the original interactions to reform, which would return the system back to its previously bound state, before the ligand fully dissociates. (G and H) Pseudoatom representation of the sliding-rebinding mechanism for catch bonds. The lectin domain (blue half-ellipse) connects to the EGF domain (blue rectangle for open-angle and mauve dashed rectangle for closed-angle conformations as in Fig. 1 A) through an interdomain hinge modeled as a rotational spring (green coiled-coil). The hinge angle conformation is multistable and can be regulated by force. The ligand (brown rectangle) interacts with the selectin through pseudoatoms (some shown explicitly as cyan and red circles; others are not shown but implicated by small black circles). The closed-angle system in G has N pairs of interacting pseudoatoms. Force (f, black arrows) induces the opening of the interdomain angle in H and induces sliding (shown by dislocation of the cyan and red circles to dock new partners) to a new stage that has N − 1 pairs of interacting pseudoatoms (shown by one red circle from the PSGL-1 moving outside of the interface from the upper-right side, one cyan circle from the lectin moving outside of the interface from the lower-left side, and one less small black circle inside the interface). Further sliding will take the system to the next stage with N − 2 pairs of interacting pseudoatoms. Rebinding will bring the system back to the previous stage with N pairs of interacting pseudoatoms.
Simulations started from the Nth stage assuming that all N pseudoatomic interactions were in the bound state initially at the first step. Each stage had many steps. It was assumed that all pseudoatomic interactions in a macromolecular complex were identical, were independent from each other, and followed first-order kinetics with a constant on-rate k+1 and a force-dependent off-rate that obeyed the Bell equation (1):
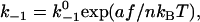 |
(1) |
where 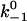 and a are model parameters, f is the current level of applied force, kB is Boltzmann constant, T is absolute temperature, and n is the number of bound pseudoatomic interactions in the present step. The fate of each pseudoatomic interaction was governed by a survival possibility,
and a are model parameters, f is the current level of applied force, kB is Boltzmann constant, T is absolute temperature, and n is the number of bound pseudoatomic interactions in the present step. The fate of each pseudoatomic interaction was governed by a survival possibility, 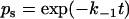 , or a binding probability,
, or a binding probability, 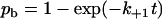 , depending on whether that pseudoatomic interaction was bound or free in the immediate-past step. A random number uniformly distributed between 0 and 1 was generated for the value of ps or pb to allow calculation of the survival time,
, depending on whether that pseudoatomic interaction was bound or free in the immediate-past step. A random number uniformly distributed between 0 and 1 was generated for the value of ps or pb to allow calculation of the survival time,
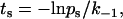 |
(2) |
or the time-to-bind,
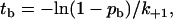 |
(3) |
for that interaction in the present step. A previously intact pseudoatomic interaction would dissociate if it had the shortest ts among all intact pseudoatomic interactions in the present step or it would remain intact. A previously dissociated pseudoatomic interaction would bind if its tb was shorter than the shortest survival time or it would remain dissociated. The shortest ts or tb was taken as the lifetime of the complex in the present step, and the simulation would proceed to the next step. The above procedures were repeated in many steps until all pseudoatomic interactions dissociated. The cumulative lifetimes in all steps were taken as the lifetime of the complex in this stage.
After all pseudoatomic interactions in the current stage dissociated, the system entered the next stage to simulate sliding and formation of new interactions. Sliding made it difficult for the original pseudoatom pairs to interact but created opportunities for the newly paired pseudoatoms to interact. Rebinding of pseudoatoms at the edge of the contact surface was treated differently because their partners on the other side of the interface had dislocated (see next paragraph). Excluding the edge pseudoatoms reduced the number of possible new interactions. The number of reductions depends on the shape of the interface and the spatial distribution of the pseudoatoms assumed. Here the pseudoatoms were assumed to align along a straight line such that dislocation at the interface by one sliding step only reduced a single pair of pseudoatoms (cf. Fig. 4, G and H). In other words, only one pseudoatom on one side of the interface moved ahead of the contact and one pseudoatom on the other side of the interface moved behind the contact. The rest of the pseudoatoms remain in contact but were now paired with new partners for possible interactions. Whether any one of them actually did interact was determined by comparing a random number (uniformly distributed between 0 and 1) to a probability for formation of new interaction that depends on the current level of force,
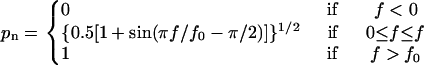 |
(4) |
If the random number was smaller than pn, a new interaction would be formed between that pair of pseudoatoms; otherwise they remained dissociated. Equation 4 represents a simple monotonically increasing function that smoothly spans the full range of probability (0 ≤ pn ≤ 1) in a force range between 0 and f0. It was chosen to approximate the shape of the interdomain angle versus force curve (cf. Fig. 1 C) to account for the observation that opening of the interdomain angle promotes sliding and formation of new interactions. It differs from and has one less parameter than that used in our recent study (8); but the particular form of the equation is not essential. The constant f0 in Eq. 4 sets the force level beyond which new interaction will form with 100% certainty. Note that no new interaction will form when the force vanishes; therefore, stage N simulation with f = 0 calculates the stress-free lifetime for the complex. If none of the pseudoatomic pairs formed new interactions, the molecular complex would dissociate. If at least one pair of pseudoatoms formed a new interaction, all “inner” pairs of pseudoatoms would be subjected to the same kinetics simulations as in the previous stage.
FIGURE 4.
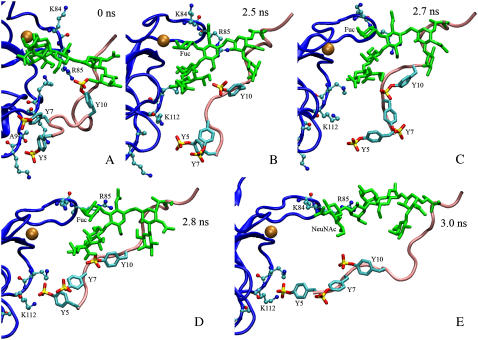
Sequential snapshots of SMD simulated structures at indicated times. The simulation is the same as that shown in Fig. 3 A. The binding interface of the lectin domain (blue) as well as the peptide segment (pink) and the glycan (green) of PSGL-1 are shown. Calcium is shown as a golden sphere. Three sulfated tyrosines (indicated) are highlighted as cyan sticks with yellow (sulfur) and red (oxygen) ends on the side chains. (A) Initial conformation for SMD simulation. The interactions seen in the crystal structure were well maintained after equilibration except for PSGL-1 sulfated Tyr-5, whose sulfate on the side chain was not observed in the crystal structure but now formed an H-bond with the backbone nitrogen of Ala-9 (indicated). Sulfated Tyr-10 was observed to interact with Arg-85. (B) Immediately before dissociation of all preexisting interactions. The Ca2+ coordination bond with Fuc was the last preexisting interaction present. (C) Immediately postdissociation of the PSGL-1 Fuc and the lectin calcium. PSGL-1 began to slide over the lectin binding interface and Fuc formed a new interaction with P-selectin Arg-85. (D) Sulfated Tyr-5 formed a new interaction with the backbone as well as side chain of P-selectin Lys-112. Fuc slid over Arg-85. (E) Sulfated Tyr-5 maintained interactions with Lys-112. NeuNAc slid over lectin Lys-84 and then Arg-85 and formed interactions. These and several other briefer new interactions halted the rapid drop in force seen in Fig. 3 A.
FIGURE 1.
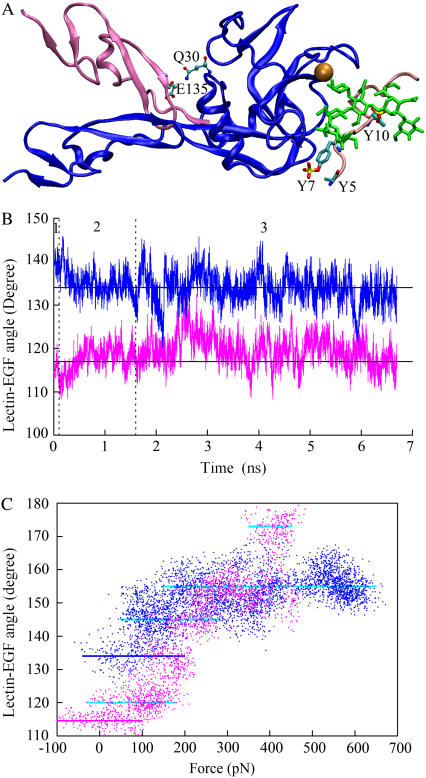
(A) Cocrystal structures of P-selectin complexed with ligands. The open-angle structure of P-selectin (blue, lectin and EGF domains) liganded with PSGL-1 is shown by ribbon representation (PDB code 1G1S). The closed-angle structure of P-selectin (mauve, only EGF domain shown) liganded with sLex (not shown) is superimposed (PDB code 1G1R). The two lectin domains have been aligned and only the one that was liganded with PSGL-1 is shown. An H-bond between Gln-30 and Glu-135 (shown by sticks and balls) was observed in the closed-angle but not the open-angle structure. A calcium ion is shown as a golden sphere. The PSGL-1 peptide is shown in pink. Three sulfated tyrosines (indicated) are highlighted as cyan sticks with yellow (sulfur) and red (oxygen) ends on the side chains of Tyr-7 and Tyr-10. The side chain of sulfated Tyr-5 is not shown because it was missing from the crystal structure. Glycan is shown in green. (B) Simulated time courses of lectin-EGF interdomain angles. MD simulations started from the closed-angle unliganded P-selectin structure (mauve) (see supplementary video 1) or the open-angle liganded P-selectin structure (blue) (see supplementary video 2) after deleting the PSGL-1. The two horizontal lines indicate the corresponding angles observed in the crystal structures. Separated by dotted vertical lines, regions 1, 2 and 3 mark, respectively, times for heat-up, equilibration, and free dynamics simulations. (C) Interdomain angle versus pulling force plots. Data from two SMD simulations are overlaid: a 3.6-ns simulation starting from the closed-angle structure of P-selectin liganded with sLex (mauve dots) (see supplementary video 3) and a 3.75-ns simulation starting from the open-angle structure of P-selectin liganded with PSGL-1 (blue dots) (see supplementary video 4). The closed and open angles observed in the crystal structures are marked by a mauve and a blue line, respectively. Other stable conformations are indicated with cyan lines. Data were sampled at 1012 Hz.
From the (N − 1)th stage onward, the possibility for the pseudoatoms that just moved out of the interface (to enter into the present stage) to rebind was treated by calculating the time-to-rebind,
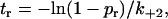 |
(5) |
from a random number pr (uniformly distributed between 0 and 1) where k+2 is a constant rebinding rate. If tr was smaller than the lifetime of that stage, rebinding would occur and the system would return to the previous stage with one more pair of pseudoatomic interaction. Otherwise rebinding would not occur and the system would slide to the next stage with one less pair of pseudoatomic interaction (cf. Fig. 4 H). The same procedures were then repeated. Thus, the system would slide or rebind. At the end of the Nth stage only sliding was allowed but not rebinding. At the end of the first stage (with only one pair of pseudoatoms capable of interacting) only rebinding was allowed but no sliding. The receptor-ligand complex would dissociate at the end of any stage if sliding did not result in any new interaction and rebinding did not occur. The cumulative lifetimes of all stages before dissociation were taken as the lifetime of the complex in that simulation run, which was repeated 500,000 times for a given force to obtain an ensemble of lifetimes at that force from which distribution and statistics were calculated. In particular, the survival probability at time t for the selectin-ligand bond was estimated from the fraction of simulations that yielded lifetimes >t.
RESULTS
Lectin-EGF interdomain angle has multistable conformations regulated by force
Six selectin (lectin and EGF domains) crystal structures have been obtained: unliganded E-selectin (20,26), P-selectin (20), and L-selectin (P. Mehta, V. Oganesyan, S. Terzyan, T. Mather, and R. P. McEver, personal communication, 2004), E-selectin and P-selectin, respectively, liganded with sLex (20), and P-selectin liganded with the N-terminal fragment of PSGL-1 (20). We examined these structures to search for a mechanistic basis for catch bonds, which have been observed for P-selectin interacting with PSGL-1 (5) and L-selectin interacting with PSGL-1 (6–8) and with 6-sulfo-sLex (8). We used MD simulations to study these structures dynamically in the absence (free dynamics) and presence of a pulling force (SMD). The lectin-EGF interdomain angle of P-selectin was crystallized in two conformations. An “open-angle” conformation was observed in the structure of P-selectin liganded with PSGL-1 where the interdomain angle was 139.3° (Fig. 1 A). By comparison, a “closed-angle” conformation was observed in the structure of P-selectin liganded with sLex where the EGF domain bent toward the lectin domain with an interdomain angle of 114.6° (Fig. 1 A; only the EGF domain is shown), which is the conformation also observed in the other four selectin structures. Although the EGF domain is attached to the end of lectin domain opposite to where PSGL-1 binds, it has been shown experimentally to regulate ligand binding (8,27–30). In a recent study using free dynamics simulations, we observed that L-selectin, whose crystal structure aligns well with the closed-angle crystal structure of P-selectin (P. Mehta, V. Oganesyan, S. Terzyan, T. Mather, and R. P. McEver, personal communication, 2004), could transition to an open-angle conformation that aligns well with the open-angle crystal structure of P-selectin, although such transition was observed in only two of seven simulations (8). In this study we performed free dynamics simulations using the closed-angle (three 5-ns simulations, supplemental video 1, Supplementary Material) or the open-angle (three 5-ns simulations, supplemental video 2) P-selectin as a starting structure. Although the interdomain angle fluctuated about the original position (either closed or open), transition to the other conformation was not observed (Fig. 1 B), suggesting that the structure may be stable in both conformations and/or the average time required for conformational transition may be much longer than our simulation times. An H-bond between Gln-30 of the lectin domain and Glu-135 of the EGF domain was observed in the closed-angle but not the open-angle crystal structure, which may stabilize the closed-angle conformation (Fig. 1 A). Ile-137 in the EGF domain packed hydrophobically with residues in the lectin domain differently in the open and closed-angle conformations, which may stabilize both conformations because conformation transition may require Ile-137 to unpack and repack.
Can the interdomain angle opening be induced by a pulling force that applies a moment about the hinge? If so, is this related to catch bonds? We used SMD simulations to address these questions. In these simulations, the O1 atom of GlcNAc of sLex or the Cα atoms of Pro-18 of PSGL-1 was pulled by a spring (spring constant ∼70 pN/Å) that moved at a constant speed (5, 10, or 50 Å/ns). The Cα atom of Gly-147 of the EGF domain was constrained. In Fig. 1 C, the lectin-EGF angles are plotted against force for the respective simulated structures of P-selectin liganded with sLex (mauve) and PSGL-1 (blue). The plots are busy as there were significant fluctuations in both force and angle. However, a sigmoidal trend correlating the increasing force with increasing angle is evident. It is also evident that the plots appear as alternating regions of dense and sparse data points. Because data were collected every picosecond, regions with dense data points represent relatively stable conformations (marked by horizontal lines in Fig. 1 C) whereas regions with sparse data points reveal more rapid transitions. The simulated structural changes in time are shown in supplementary videos 3 and 4 (Supplementary Material). The angle of the P-selectin:sLex structure fluctuated about the close conformation (114.6°, marked by a solid mauve line) until the force exceeded 100 pN after which it increased by ∼5o (Fig. 1 C). Note that this new interdomain angle (∼120°, marked by a cyan line) was also observed in free dynamics simulations (Fig. 1 B). In the SMD simulation, the structure fluctuated about that angle for the next ∼100 pN of force increase and then jumped ∼14° to an angle of ∼134° slightly smaller than the open-angle (139.3°) conformation observed in the P-selectin:PSGL-1 cocrystal structure (Fig. 1 C, marked by a blue line). Note that this 134° angle was also observed in free dynamics simulations with the open-angle structure after equilibration (Fig. 1 B). Interestingly, force induced further opening of the interdomain angle in both structures (although by different amounts due to a difference in the point where the pulling forces were applied) (Fig. 1 C). These observations suggest that force regulates the interdomain angle by applying a moment to overcome the bending rigidity of the hinge at its stable conformations that may be stabilized by noncovalent interactions at the atomic level.
Unbinding by force induces sliding of interface and formation of new interactions
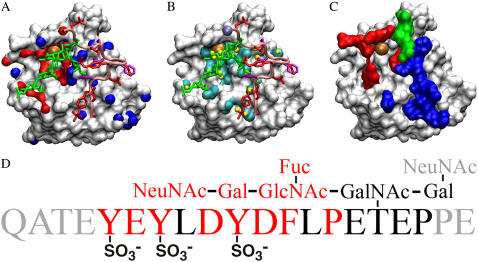
P-selectin binds PSGL-1 in a stereospecific manner, as previously described (20,31,32). The binding surface on the lectin domain fits that of PSGL-1 with high degree of electrostatic complementarity. Shown in Fig. 2 A using electrostatic potential surface representation, the positively charged residues (whose nitrogen atoms are shown in blue) are mostly located on one side where the peptide segment of PSGL-1 (pink tube) docks whereas the H-bond acceptor/donor residues (whose oxygen atoms are shown in red) are located mostly on the other side where the glycan (green sticks) docks. The first 20 amino acids of the PSGL-1 peptide is highly negatively charged, with seven acidic residues and three negatively charged sulfated tyrosines (seven of which are observed in the cocrystal structure and shown as red sticks in Fig. 2, A and B), which can potentially form electrostatic interactions with the basic residues on the lectin. The glycan of the PSGL-1 N-terminal region has a large number of oxygen atoms, which can potentially form H-bonds with H-bond acceptor/donor residues on the lectin. However, only some of these potential interactions were observed in the cocrystal structure, as shown in Fig. 2 B where the interacting atoms from the lectin and PSGL-1 are, respectively, colored cyan and yellow, which are distributed over a broad and shallow interface.
FIGURE 2.
(A) Top view of the binding surface. The lectin domain is shown by electrostatic potential surface representation. The nitrogen atoms of the positively charged residues are colored in blue and the oxygen atoms of the H-bond donor/acceptor residues are colored in red. PSGL-1 glycan is shown in green, peptide is shown in pink with the side chains of the negatively charged residues shown in red and those of the hydrophobic residues shown in purple. The calcium ion is shown as a large golden sphere. (B) Noncovalent interactions between the lectin atoms (cyan) and PSGL-1 atoms (yellow). The Cα atom of PSGL-1 Pro-18 where the pulling force was applied is marked by an ice-blue sphere. (C) New interaction map. Residues that formed new interactions with the PSGL-1 peptide, glycan, or both are, respectively, colored in blue, red, or green. (D) Sequence of the PSGL-1 N-terminal segment. The residues that were not observed in the crystal structure (and also not used in MD simulations) are shown in gray. The residues that were observed to form new interactions in SMD simulations are shown in red.
Unbinding of PSGL-1 from P-selectin was simulated using 5, 10, and 50 Å/ns pulling speeds with both the lectin and EGF domains (e.g., supplemental video 4) or with the lectin domain alone after deleting the EGF domain (e.g., supplemental video 5). Similar to a recent report (33), the EGF domain was observed to unfold before the lectin domain unbinds from PSGL-1 in most simulations. Unfolding of globular domains has been observed in SMD simulations (34,35), even in those that were intended to unbind receptor:ligand complexes (36). Because lowering pulling speed resulted in unbinding of CD2:CD58 complex without unfolding, unfolding was suggested to be an artifact of the unrealistically high-speed pulling to accelerate dissociation that takes place in millisecond-to-second laboratory timescales to the nanosecond timescale achievable by MD simulations (36). To reduce unfolding, we constrained the Cα atom of the Gly-147 instead of C-terminal residue of the EGF domain (cf. supplemental video 4). We also used periodic boundary conditions to treat electrostatic interaction more accurately. In one of 24 simulations performed, unbinding was observed without unfolding of either the lectin or EGF domain, allowing us to quantify the interdomain angle changes during unbinding and their relationship with force and other events that occurred concurrently at the binding interface (Figs. 1 C, 3 A, 4, 5 A–D and F, and supplemental video 4).
FIGURE 3.
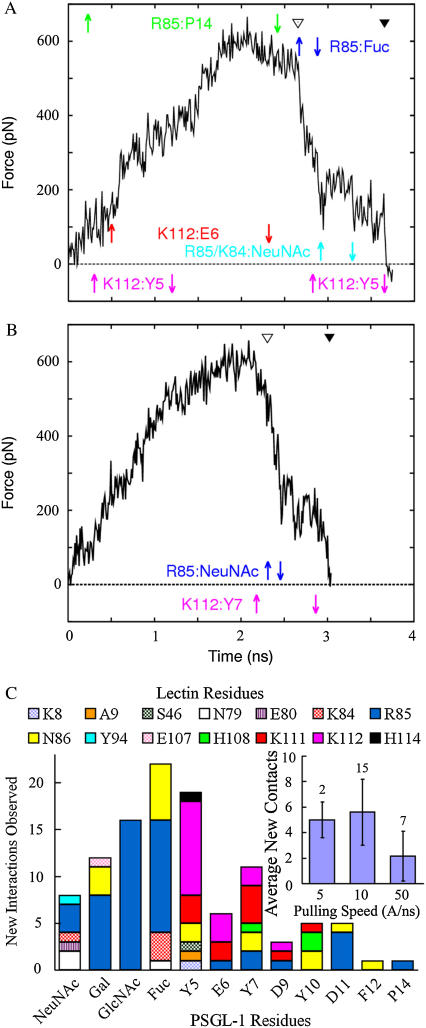
(A and B) Force-time courses of SMD simulated unbinding of PSGL-1 from P-selectin lectin and EGF domains (A) or lectin domain only after deleting the EGF domain (B). The Cα atom of Gly-147 of the EGF domain (A) or Ala-120 of the lectin domain (B) was constrained, and a force was applied through a spring (spring constant = 70 pN/Å) with one end attaching to the Cα atom of PSGL-1 Pro-18 (A) or the O1 atom of sLex GlcNAc (B) and the other end moving at a constant speed of 10 Å/ns. Complete rupture of all preexisting interactions (indicated by an open arrowhead) resulted in a sudden drop in force, but the complex remained bound for ∼1 ns of time and sustained ∼200 pN of force due to sliding and formation of new interactions. Some long lasting new interactions are shown by color-matched paired arrows, with up arrows indicating their formation and down arrows indicating their dissociation. The residue pairs involved in the new interactions are indicated at the same level as the arrows using matched colors with P-selectin residues on the left and PSGL-1 residues on the right. New interaction between Lys-112 and sulfated Tyr-5 was observed to form and dissociate multiple times in a single simulation run. Final dissociation of the complex is marked by a closed arrowhead. (C) Number of new interactions observed in 24 SMD simulations versus PSGL-1 residue involved in new interaction formation. The contributions from various lectin residues are indicated. (Inset) Mean ± SE of the number of new interactions observed per simulation is plotted versus pulling speed. The number of simulations for each of the three pulling speeds is indicated.
The time course of force at the spring where the Cα atom of PSGL-1 Pro-18 was attached is shown in Fig. 3 A for this unbinding simulation. The force increased steadily until ∼2.1 ns when the interaction between sulfated Tyr-10 and Arg-85 began to break, which initiated the dissociation of the complex. The force decreased slowly as this and other interactions ruptured, but abruptly after the calcium coordination bond with Fuc ruptured at ∼2.6 ns, when almost all preexisting interactions observed in the cocrystal structure had broken. Interestingly, new interactions were observed to form as PSGL-1 slid over the lectin surface. Six durable new interactions are shown by color-matched paired arrows in Fig. 3 A, with the up arrows indicating when a new interaction was formed and the down arrows indicating when that interaction was ruptured. The residue pairs involved in the new interactions are indicated with matched colors, with P-selectin residues on the left and PSGL-1 residues on the right (Fig. 3 A). Snapshots of the binding interface at various simulation times during dissociation are shown in Fig. 4. The continuous changes in the complex structure along the dissociation pathway are shown in supplementary video 4 and snapshots at several simulation times are shown in Fig. 5, A–D and F. After dissociation of all preexisting interactions, the PSGL-1 glycan slid over the basic residue Arg-85 and the PSGL-1 peptide slid over the basic residue Lys-112 (Fig. 4). It was these and other interactions (summarized in Fig. 3 C) that held the P-selectin:PSGL-1 complex together, slowed the rapid decline in force and even caused a small increase in force, and prolonged dissociation for ∼1 ns (Fig. 3 A).
In this simulation, a majority of the new interactions were observed after all preexisting interactions had dissociated to allow interface sliding. Of the six shown in Fig. 3 A, three were formed and broken before all preexisting interactions dissociated at ∼2.6 ns. The other three were formed after that time. Three more new interactions were also observed after dissociation of all preexisting interactions, but are not shown in Fig. 3 A due to their short durations (<0.1 ns). It is intuitive that sliding would promote new interaction formation because the two sides of the interface exhibit broad electrostatic complementarity, as previously discussed (Fig. 2 A), which may allow binding with multiple partners when sliding brings them into close proximity. Indeed, sliding and formation of new interactions was repeatedly observed in different simulations, including those that unfolded the EGF domain and those that deleted the EGF domain. Although unfolding of the EGF domain resulted in a force history different from that shown in Fig. 3 A (see Lü and Long (33)), the observations that sliding promoted new interaction formation and that new interactions slowed force decline and prolonged dissociation were similar. Simulations with a lectin:PSGL-1 structure that deleted the EGF domain were performed to obtain clearer force histories not obscured by unfolding of the EGF domain. One such simulation is shown in Fig. 3 B and supplementary video 5, where all new interactions (total of four, only two durable ones are shown) were observed after all preexisting interactions had dissociated. It is evident from Fig. 3 B that new interactions delayed dissociation of the lectin:PSGL-1 complex. Depending on the pulling speed and direction, different new interactions were observed in different simulations. A residue on one side of the interface might form multiple new interactions with multiple residues on the other side in a single simulation or in different simulations. Counting only those formed after all preexisting interactions had dissociated, a total of 109 new interactions were observed in a total of 24 SMD simulations (totaling >70 ns) performed to unbind the P-selectin:PSGL-1 complex. The number of new interactions observed per simulation is shown in Fig. 3 C (inset) for the three pulling speeds tested. In Fig. 3 C, the number of new interactions is plotted against the PSGL-1 residue involved, which is broken down among the lectin residues with which they interacted. These residues are mapped onto the lectin surface in Fig. 2 C where those that interacted with the peptide, glycan, or both were, respectively, colored in blue, red, or green. The PSGL-1 residues involved in new interaction formation are colored in red in the PSGL-1 N-terminal sequence shown in Fig. 2 D. New interaction formation was often observed to involve multiple atoms from the same residue.
The fucose, which participated in the calcium coordination in the cocrystal structure (20), stood out as the PSGL-1 residue that was most frequently observed to form new interactions with four lectin residues (total of 22 new interactions; Fig. 3 C). Three other residues on the PSGL-1 glycan (NeuNAc, Gal, and GlcNAc) were also frequently observed to form new interactions. The residues with which they interacted mostly came from a loop comprising residues Asn-83–Asp-89. Remarkably, Arg-85 was most frequently observed to form new interactions (total of 48). This lectin residue made contact with sulfated Tyr-10 in the cocrystal structure (20) (Fig. 4 A), but SMD simulations revealed that, during unbinding, it could interact with 10 other PSGL-1 residues—the largest number of new partners with which any lectin residue was observed to interact (Fig. 3 C).
Eight residues from the PSGL-1 peptide were observed to form new interactions, including the three sulfated tyrosines. Among these, sulfated Tyr-5 was most frequently observed to form new interactions (total of 19; Fig. 3 C). Interestingly, sulfated Tyr-5 was not visualized in the crystal structure, suggesting that it was flexible and did not interact with P-selectin under the crystallization condition (20). This was puzzling because the functional importance of sulfated Tyr-5 has been demonstrated experimentally by mutagenesis (37) and biochemical studies (20,31,32). We modeled sulfated Tyr-5 by assigning several initial positions. During equilibration, it formed an H-bond with the backbone nitrogen of Ala-9 (Fig. 4 A) and/or a salt bridge with Lys-8 of P-selectin. In the SMD simulations, sulfated Tyr-5 was observed to form new interactions with seven lectin residues (Fig. 3 C). These results provide an explanation for the apparent discrepancies between crystallographic data and functional data.
Significantly, the frequency of new interaction formation appears to correlate with the opening of the interdomain angle, as no new interaction was observed to form before the interdomain angle opened. In simulations without the EGF domain, pulling on PSGL-1 induced a rotation of the lectin domain about the Ala-120 Cα atom that was constrained in the simulation, which was similar to the rotation about the interdomain hinge in simulations with the EGF domain when the angle was forced to open. It is intuitive that the binding interface would be tilted by the lectin domain rotation to better align with the force direction (Fig. 5), which would promote the sliding of the PSGL-1 across the binding surface. Furthermore, before final rupture, atomic-level interactions, regardless of whether they were previously or newly formed, were often observed to dissociate and rebind repeatedly, giving rise to the fluctuating appearance in the force time courses (Fig. 3, A and B). For example, sulfated Tyr-5 firstly formed a new interaction with Lys-112 at 0.3 ns, then dissociated from it at 1.2 ns, rebound it at 2.8 ns despite the fact that sulfated Tyr-5 was some distance away from Lys-112 between 2.5 and 2.7 ns (Fig. 4, B and C), and finally dissociated from it at 3.6 ns (Fig. 3 A). This is also intuitive, as residues that made atomic-level contacts were held in close proximity to their interacting partners for certain periods of time even after dissociation because the complex was held together by other interactions.
Sliding-rebinding mechanism
Due to limited computational resources, any of the above simulations was run for only several nanoseconds. To observe selectin-ligand dissociation that takes a fraction of a second to occur in the laboratory in nanosecond simulations, the processes had to be accelerated by pulling the molecules with six orders of magnitude higher speeds using springs three orders of magnitude stiffer than those used in experiments, resulting in rupture forces two orders of magnitude greater than those measured in the laboratory. Nevertheless, it seems reasonable to assume that many of the features observed in the MD simulations, including multistable interdomain conformations, force-induced interdomain angle opening, binding interface tilting/sliding, formation of new interactions, and repeated dissociation and rebinding of atomic-level interactions, would also occur in reality during single-molecule experiments of forced unbinding of selectin:ligand complexes. In particular, formation of new interactions and repeated dissociation and rebinding of the atomic-level interactions would seem likely because the much slower selectin:ligand dissociation in laboratory experiments pulled by much slower speeds, much softer springs, and much smaller forces would likely make it much easier for these events to occur, which also likely last much longer. Indeed, the number of new interactions observed per simulation was more than doubled when the pulling speed was reduced from 50 to 10 Å/ns (Fig. 3 C, inset). This doubling likely underestimates the increase in the number of new interactions because new interaction formation was defined by an interatomic distance of <3.5 Å that lasted for >5 ps for pulling speed of 50 Å/ns but >25 ps for pulling speed of 10 Å/ns (so that the pulling spring would move the same distance). By this definition, new interactions observed in the 10 Å/ns pulling simulations also lasted much longer than those observed in the 50 Å/ns pulling simulations. We further assume that rebinding can also occur between atomic contacts that are dissociated in the previous steps, i.e., returning back to their previous binding partners after they have slid away and formed new interactions with new binding partners. That such events were not observed was hypothesized to be an artifact of the MD simulations that unrealistically speeded up unbinding by excessive forces. In addition, we assume that ligand can bind a selectin in the open-angle as well as in the closed-angle conformation, as E-selectin and P-selectin liganded with sLex were observed in a closed-angle conformation in their respective cocrystal structures (20).
The above assumptions form the basis for a mechanistic model for catch bonds observed experimentally for P-selectin and L-selectin dissociating from their ligands (5,6). We termed this a “sliding-rebinding” mechanism, which is schematically shown in Fig. 5 using simulated structures observed during unbinding of PSGL-1 from P-selectin, but is assumed applicable to unbinding of PSGL-1 or 6-sulfo-sLex from L-selectin as well (8). In the model, the various multistable conformations of the lectin-EGF interdomain angle are in dynamic equilibrium with or without ligand binding. The fraction of time for the structure to stay in any conformation and the frequency of transition from one state to another are both regulated by externally applied force, such that it is mostly in the closed conformation in the absence of force but more likely to transition to and to stay in more open conformations when a force is applied to unbind the selectin:ligand complex. Thus, dissociation at low force would occur along a pathway indicated by the purple horizontal arrow pointing rightward from panel A to panel E in Fig. 5. Because the binding interface would be more perpendicular to the force direction, dissociation would occur without much sliding and rebinding, which is along a fast dissociation pathway with short lifetimes. When a higher force is applied, the dynamic equilibrium between the two interdomain angles would shift toward having a higher fraction of time in the open conformation observed in the liganded P-selectin crystal structure (20) and in the MD simulated L-selectin structure (8) or an even larger opening angle as that observed in Fig. 1 C. The rotation of the lectin domain resulting from the interdomain angle opening would tilt the binding interface to better align with the direction of force, thereby promoting sliding. This would provide an opportunity for new interactions to form, which would replace those that are disrupted, or for the original interactions to reform, which would return the system back to its previously bound state, before the ligand fully dissociates, thereby slowing dissociation and prolonging lifetime. This would represent a switch to a slow dissociation pathway, as shown by the purple vertical arrow pointing downward from panel A to panel B and by other purple arrows indicating possible subsequent events from panel B to panels C, D, F, and/or back to panel B in Fig. 5. Such a force-induced deceleration of dissociation is a hallmark of catch bonds (5,6). Thus, the model assumes that force applies a moment to the multistable interdomain hinge between the lectin and EGF domains to allosterically elicit catch bonds with ligand by sliding and rebinding. Once the interdomain angle is fully opened, the probability for new bond formation and rebinding reaches maximum; further increases in force can no longer prolong bond lifetimes. Instead, force would accelerate dissociation of each individual atomic-level interaction, thereby resulting in transition from catch bonds to slip bonds.
Pseudoatom representation
We have formulated mathematical models using reduced representation for the network of noncovalent interactions to test the sliding-rebinding mechanism. This can be done in many different ways depending on how detailed the atomic-level interactions one wishes to describe. To test the basic idea and key elements of the sliding-rebinding mechanism, we constructed a tractable model using pseudoatomic interactions to simplify the real noncovalent interactions (Fig. 5, G and H). This formulation idealizes the binding interface geometry, assumes identical kinetic properties for all pseudoatomic interactions, only considers new interaction formation after all preexisting interactions dissociate, and can be easily implemented with Monte Carlo simulations. The simulation assumed N pairs of pseudoatoms and proceeded in N stages (Fig. 5 G). In the starting stage all N pseudoatom pairs interact according to simple kinetic laws and dissociate as ordinary slip bonds independent to each other, except that they share the applied force equally. After all N initial interactions dissociate the interface may slide if it is tilted by a force-induced opening of the interdomain angle. Sliding provides equal opportunities for N − 1 pairs of pseudoatoms to interact (Fig. 5 H); but if none forms new interactions the whole complex would dissociate. After all N − 1 pseudoatomic interactions dissociate, the system may rebind and return to the previous stage with N pseudoatomic interactions, further slide into the next stage where N − 2 pseudoatom pairs can interact, or dissociate. Stage by stage, sliding separates the two molecules while rebinding brings them back, as indicated by the arrows in Fig. 5 H. Bond lifetime is prolonged by two mechanisms: forming new interactions after sliding and returning to the previous stage after rebinding. The detailed implementation of this model in Monte Carlo simulations is described in the Methods section.
Parametric analysis
Assuming that the rebinding rate and the probability for forming new interaction are independent of the stage in which the system currently resides, the Monte Carlo model requires only five parameters regardless of the number of pseudoatom pairs assumed. These include a constant on-rate k+1 for association of any individual pseudoatomic interaction, a force-free off-rate 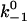 and an energy well width a for force-dependent dissociation of any individual pseudoatomic interaction that follows the Bell equation (Eq. 1 in Methods), a constant rebinding rate k+2, and a force scale f0 above which the interdomain angle will be fully opened (see Methods).
and an energy well width a for force-dependent dissociation of any individual pseudoatomic interaction that follows the Bell equation (Eq. 1 in Methods), a constant rebinding rate k+2, and a force scale f0 above which the interdomain angle will be fully opened (see Methods).
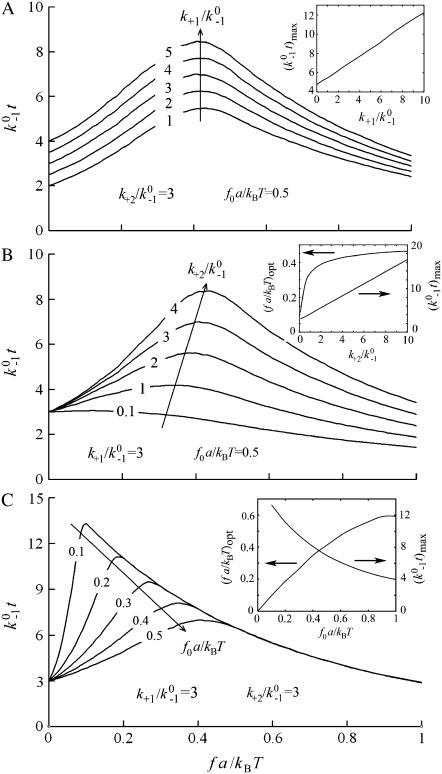
It is evident from Fig. 6 that the sliding-rebinding mechanism (as implemented by this pseudoatom representation and parameterized by the present Monte Carlo simulation algorithm) can generate theoretical curves that mimic experimentally measured single molecule catch-slip bonds data published to date (5–8,13). To illustrate how various aspects of the model behavior depend on the parameter values, a dimensionless bond lifetime 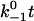 is plotted against a dimensionless force fa/kBT for ranges of three dimensionless parameters,
is plotted against a dimensionless force fa/kBT for ranges of three dimensionless parameters, 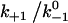 (Fig. 6 A),
(Fig. 6 A), 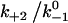 (Fig. 6 B), and f0a/kBT (Fig. 6 C). Increasing
(Fig. 6 B), and f0a/kBT (Fig. 6 C). Increasing 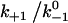 upshifts the
upshifts the 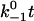 vs. fa/kBT curve toward longer lifetimes (Fig. 6 A). The linear increase of the maximum
vs. fa/kBT curve toward longer lifetimes (Fig. 6 A). The linear increase of the maximum 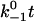 value with increasing
value with increasing 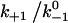 over a wider range is shown in Fig. 6 A (inset). These results are intuitive because
over a wider range is shown in Fig. 6 A (inset). These results are intuitive because 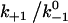 is the force-free binding affinity for an individual pseudoatomic interaction.
is the force-free binding affinity for an individual pseudoatomic interaction.
FIGURE 6.
Parametric analysis. Monte Carlo simulated solutions of the sliding-rebinding model (with two pairs of pseudoatoms) are shown as families of curves of dimensionless lifetime 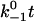 versus dimensionless force fa/kBT for indicated values of three dimensionless parameters. (A) Changing
versus dimensionless force fa/kBT for indicated values of three dimensionless parameters. (A) Changing 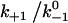 while keeping the other two constant. (B) Changing
while keeping the other two constant. (B) Changing 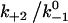 while keeping the other two constant. (C) Changing f0a/kBT while keeping the other two constant. In the insets, the maximum of the lifetime versus force curve (
while keeping the other two constant. (C) Changing f0a/kBT while keeping the other two constant. In the insets, the maximum of the lifetime versus force curve (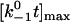 ) and/or the force where lifetime reaches maximum ([fa/kBT]opt) are plotted against
) and/or the force where lifetime reaches maximum ([fa/kBT]opt) are plotted against 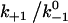 (A),
(A), 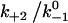 (B), and f0a/kBT (C) for constant values of the other two parameters (indicated in the corresponding main panels).
(B), and f0a/kBT (C) for constant values of the other two parameters (indicated in the corresponding main panels).
Increasing 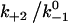 augments catch bonds by lengthening lifetime and widening the force range of catch bonds (Fig. 6 B). As shown in Fig. 6 B (inset) over a wider range of
augments catch bonds by lengthening lifetime and widening the force range of catch bonds (Fig. 6 B). As shown in Fig. 6 B (inset) over a wider range of 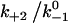 values, the force where lifetime reaches maximum (optimal force) increases initially with increasing
values, the force where lifetime reaches maximum (optimal force) increases initially with increasing 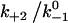 then approaches a plateau. The maximum lifetime, however, increases linearly with increasing
then approaches a plateau. The maximum lifetime, however, increases linearly with increasing 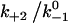 values. Because
values. Because 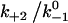 represents a dimensionless rebinding rate, these results demonstrate that rebinding can indeed provide a mechanism in the model to produce catch bonds.
represents a dimensionless rebinding rate, these results demonstrate that rebinding can indeed provide a mechanism in the model to produce catch bonds.
Decreasing f0a/kBT also augments catch bonds by lengthening lifetime at smaller force but narrows the force range for catch bonds instead of widening it (Fig. 6 C). In Fig. 6 C (inset), the force where lifetime reaches maximum (optimal force) is shown to be an increasing function of f0a/kBT, whereas the maximum lifetime is shown to be a decreasing function of f0a/kBT. This is intuitive because the dimensionless force scale f0a/kBT reflects the bending rigidity of the interdomain hinge. The smaller the f0a/kBT, the more flexible the lectin-EGF hinge, the smaller the force required to induce interdomain angle opening, sliding, and formation of new interactions, thereby prolonging bond lifetimes at smaller force and left-shifting the optimal force where lifetime reaches maximum. This parameter has no impact on the slip bonds.
Comparison with experiments
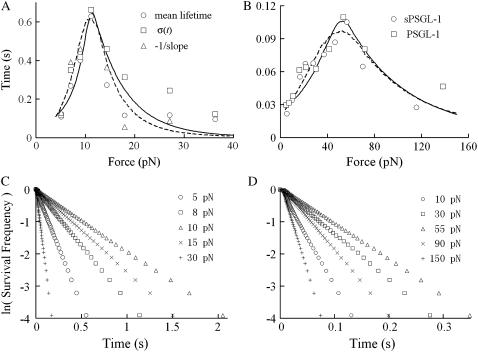
We fitted the published bond lifetime versus force data for soluble (s) PSGL-1 dissociating from P-selectin (Fig. 7 A) (5) and L-selectin (Fig. 7 B) (6) by the simplest model with only two pairs of pseudoatoms (N = 2, solid curves) and a less simplified model with three pairs of pseudoatoms (N = 3, dashed curves). Both models fit the data equally well (Fig. 7, A and B), which is expected from the general properties of the sliding-rebinding model (Fig. 6). The fitting parameters are summarized in Table 1. These appear reasonably ranged except for k+2, which seems too large. As discussed in a separate study (8), the unrealistically large k+2 may result from an overly reduced representation, namely, representing a large number of noncovalent interactions with too small a number of pseudoatomic interactions and assuming the same kinetic properties for all pseudoatomic interactions regardless of whether they were preexisted or newly formed. This view is supported by the finding that the fitting parameters of the model with three pairs of pseudoatoms (i.e., N = 3) were similar to the corresponding parameters of the model with two pairs of pseudoatoms (i.e., N = 2) except for k+2, which is much smaller and more realistic (Table 1).
FIGURE 7.
Comparison with experiments. (A and B) Monte Carlo simulated solution of the sliding-rebinding model with two (solid curve) or three (dashed curve) pairs of pseudoatoms was fit to the lifetime measure versus force data of soluble (s) PSGL-1 dissociating from P-selectin (A) (5) or of two forms of PSGL-1 dissociating from L-selectin (B) (6). The fitting parameters are listed in Table 1. (C and D) Semilog plots of survival frequency versus time for indicated levels of constant forces. Data were generated using parameters that fitted the bond lifetime versus force data for P-selectin-sPSGL-1 interaction by the model with two pairs of pseudoatoms (C) or L-selectin-sPSGL-1 interaction by the model with three pairs of pseudoatoms (D) (cf. Table 1).
TABLE 1.
Summary of fitting parameters
| Model interaction |
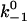 (1/s) (1/s) |
kBT/a (pN) | k+1 (1/s) | k+2 (1/s) | f0 (pN) |
|---|---|---|---|---|---|
| Two pseudoatom pairs P-selectin-sPSGL-1 | 30 | 12 | 30 | 1300 | 12 |
| Three pseudoatom pairs P-selectin-sPSGL-1 | 90 | 11 | 30 | 630 | 13.5 |
| Two pseudoatom pairs L-selectin-(s)PSGL-1 | 70 | 91 | 30 | 500 | 59.5 |
| Three pseudoatom pairs L-selectin-(s)PSGL-1 | 110 | 91 | 30 | 150 | 70 |
The experimental data in Fig. 7, A and B, were fitted using mean lifetimes. Each Monte Carlo simulation resulted in a random lifetime. It was repeated 500,000 times at each force to generate an ensemble from which the survival probabilities as functions of time can be calculated for various force levels. For the two models tested (N = 2 and 3), these appear as straight lines in semilog plots (Fig. 7, C and D), as would be predicted from first-order dissociation kinetics. Furthermore, the reciprocal negative slopes of these lines agree well with the means and standard deviations of lifetimes for each force level, just as single exponential decays would predict. Thus, the experimentally observed apparent first-order dissociation kinetics can be reproduced by our sliding-rebinding model via cooperation of the multiple pseudoatomic interactions (38).
DISCUSSION
The goal of this work was to explore the structural basis for catch bonds. Although several crystal structures of selectins with or without complexing with ligands have been solved, which served as a foundation for this study, not enough insights could be obtained from analyses of these static structures to reveal a basis for catch bonds. Analysis of protein sequences alone is also unlikely to uncover the structure basis of catch bonds (39). A likely reason is that catch bonds are unusual kinetic properties emerging from many dynamic interactions at the atomic level over time. Furthermore, catch bonds represent changing kinetic properties in response to an externally applied force. However, no one has grown protein crystals under tension, much less under different tensile forces. Thus, the structural bases for catch bonds are unlikely to be understood without MD simulations. In particular, SMD can be used to study the effects of force on structures over time. However, although MD simulations can reveal dynamic changes of the molecular structure in atomic detail at intervals on the femtosecond timescale, our computational resources only allow us to compute processes in the nanosecond timescale for molecules of the size of selectin lectin-EGF domains (molecular weight is ∼20,000). Unrealistically large forces had to be used to accelerate P-selectin:PSGL-1 unbinding that takes place on subsecond timescale in laboratory experiments, which is likely the reason why the EGF domain was unfolded in most of the simulations. Nevertheless, interesting features were observed from these simulations, including multistable interdomain hinge conformations, force-induced opening of hinge angle, sliding of molecular contacts over a tilted binding interface, formation of new interactions, and repeated dissociation and reassociation of noncovalent interactions. These observations form the basis of the proposed sliding-rebinding mechanism for catch bonds, which was modeled mathematically using reduced representation for noncovalent interactions.
Although more involved, the pseudoatom representation of the sliding-rebinding mechanism can be related to the previous two-pathway models (6,12,14–17). Our Monte Carlo simulation algorithm has N (≥2) stages if N pairs of pseudoatoms are assumed. The system in the Ith stage can either slide to the (I − 1)th stage, rebind to the (I + 1)th stage, or dissociate (Fig. 5 H). This can be considered as a model of N internal bound states and N dissociation pathways. Each stage can be thought of as an internal bound state. The only difference is that the Ith bound state includes I (1 ≤ I ≤ N) pairs of interacting pseudoatoms instead of just one. To illustrate this point, we formulated a set of kinetic equations for the minimal sliding-rebinding model that contains two pairs of pseudoatoms (i.e., N = 2). Such a system has four possible states. Let p11 denote the probability for the molecular complex to be bound with both pairs of pseudoatoms, p10 denote the probability for the molecular complex to be held by either pseudoatom pair (the other pair has dissociated) in its original position without sliding, p01 denote the probability for the molecular complex to remain bound by the newly formed interaction between a switched pseudoatomic pairing after sliding, and p00 denote the probability of dissociation. Their rates of changes are described by the following master equations:
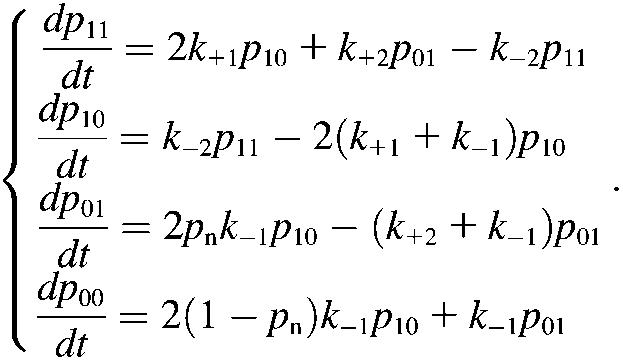 |
(6) |
As in the Monte Carlo simulations, the on-rate k+1 and rebinding rate k+2 are constants. The off-rate k−1 is given by Eq. 1 (with n = 1) and k−2 = 2k−1(f/2) because each pseudoatomic interaction is assumed to be identical and share the force equally. The probability for new interaction formation pn is given by Eq. 4. Under the initial conditions p11 = 1 and p10 = p01 = p00 = 0, solutions to Eq. 6, which can be obtained analytically when force is kept constant, should yield the same results as Monte Carlo simulations. In particular, ln(1 − p00) versus t curves at different levels of constant force should yield the same nearly linear plots as those shown in Fig. 7 C.
Equation 6 differs from previous catch-bond models (6,12,14–17) in two aspects. First, in the third equation a force-dependent probability pn is introduced to provide the opportunity for new interaction formation after dissociation from state (1,0), i.e., the state at which the molecular complex is held by either pseudoatom pair in its original position. Only when no new interaction forms (probability 1 − pn) will the complex dissociate to the free state (0,0) in the fourth equation. Second, the introduction of a new state (0,1) by the formation of a new interaction provides the opportunity for rebinding, allowing the system to return to state (1,1) in the first equation. Both aspects contribute to the catch-bond behavior of the system.
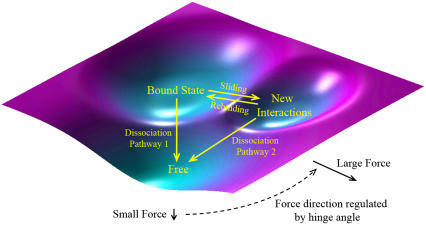
The previous models conceptualize two-pathway dissociation from an abstract viewpoint of energy landscape without considering the structure of the interacting molecules and the atomic-level noncovalent interactions involved. Following Eq. 6, we can construct a conceptual energy landscape for the sliding-rebinding model with two pairs of interacting pseudoatoms (Fig. 8). Complex formation should result in a low energy well as indicated by the bound state, which represents the sum of states (1,1) and (1,0) in Eq. 6. At low forces, dissociation may occur mostly as diffusive escape from this energy well along pathway 1 to the free state (0,0) (Fig. 8). Initial increases in force may open the interdomain angle, which may tilt the selectin:ligand interface to better align with the direction of force, thereby promoting interface sliding and new interaction forming. This may steer the force direction away from the direction of pathway 1, thereby limiting the effect of force-accelerated dissociation along this pathway, and toward the direction of sliding, thereby enhancing transition from the bound-state energy well to a neighboring energy well. This neighboring energy well, which represents state (0,1) in Eq. 6, may allow two things to happen. First, it may slow dissociation as dissociation now takes pathway 2. Second, it may provide an opportunity for rebinding to occur, which brings the system back to the bound-state energy well, thereby further prolonging bond lifetimes. The relative ease with which the system dissociates along pathway 1 or slides into the new interaction energy well may increase with force as it increases in magnitude and turns in direction, thereby giving rise to the catch bond behavior. After exceeding a certain level, further increase in force may not be able to increase the likelihood of sliding any further, thereby turning the catch bond to a slip bond. By relating this model to the previous models (12,14,16,17) through an energy landscape description, the hypothesis of two internal bound states proposed in previous models (12,14,16,17) has been supported by structural evidence obtained by our SMD simulations. For a sliding-rebinding model with N pairs of interacting pseudoatoms, we can conceptualize N − 1 new interaction energy wells in series with the bound-state energy well and N pathways for dissociation. The Ith energy well (counting from the outermost one inward) represents the collective interactions of I pairs of pseudoatoms.
FIGURE 8.
Energy landscape for sliding-rebinding mechanism. Starting from the energy well marked bound state, the molecular complex can dissociate to the free-state along pathway 1 or slide into a neighboring energy well resulted from formation of new interactions. From the new interaction energy well the system can dissociate to the free state along pathway 2 or rebind back to the bound-state energy well. As the magnitude of force increases, its direction also turns from the direction of pathway 1 to the direction of sliding as the interdomain angle opens by the force, such that sliding into the new interaction energy well increases as force increases from low to intermediate levels. Sliding into the new interaction energy well and rebinding back to the bound-state energy well prolong bond lifetime, thereby giving rise to catch bonds. At high forces all energy barriers are suppressed and dissociation is accelerated despite sliding and rebinding, which transitions the catch bonds to slip slips.
The above energy landscape description provides another avenue to further develop the sliding-rebinding model. For example, the kinetics of I pseudoatomic interactions in the Ith energy well can be simplified as a single interaction. The rebinding on-rate can be formulated as a decreasing function of force because the tilted energy landscape may lower the Ith energy well more than the (I + 1)th energy barrier, which would slow rebinding.
Force regulation of a multistable interdomain hinge is a crucial element of the sliding-rebinding mechanism for catch bonds. Parametric analysis predicts that increasing the hinge flexibility would augment catch bonds by prolonging bond lifetimes at small forces but narrow the catch bond force range by left-shifting the force of catch-slip transition toward a smaller value (Fig. 6 C). This prediction has been supported by a recent experiment in which the lectin-EGF interdomain hinge of L-selectin was made more flexible by eliminating an H-bond that stabilizes the hinge by a single residue mutation (8). Similarly, stiffening the interdomain hinge is predicted to diminish catch bonds by shortening bond lifetimes at low forces but widen the catch-bond force range by right-shifting the force of catch-slip transition toward a larger value. Fixing the interdomain hinge is predicted to eliminate the catch-bond behavior.
Many proteins consist of multiple domains connected by interdomain hinges. The sliding-rebinding mechanism proposed herein may be applicable to other systems. For example, recent single molecule experiments have demonstrated that the actomyosin interaction exhibited catch-slip transitional bonds (13). The globular motor domain of the myosin head is connected to an α-helical extension of the heavy chain, or neck. Concomitant with phosphate release, rotation of the neck causes a 5.5-nm step “working stroke” and a 3–4 pN isometric force (13,40). Thus, it seems reasonable to assume that the neck may serve as a bistable hinge whose conformational change can generate force as well as be regulated by force. Consistent with this consideration, the sliding-rebinding model can readily fit the published catch-slip bond data of the actomyosin interaction. However, mutations in the neck region and on the binding interface are required to rigorously test the sliding-rebinding mechanism, as the same data can be equally well fitted by other models (13).
Interactions between bacteria adhesin FimH and mannose ligands have also been reported to exhibit catch-slip bonds (11,12). The mannose-binding lectin domain of FimH is connected to the pilin domain via a linker. SMD simulations based on an unliganded lectin domain crystal structure showed that pulling on the mannose binding site in SMD simulations induced linker extension (11,12). Mutations to weaken the linker were found to enhance mannose binding. A recently published cocrystal structure of FimH containing both the lectin and pilin domains liganded with mannose reveals an interdomain angle similar to that of the closed-angle selectins (41). It seems reasonable to predict that pulling on the mannose would extend the linker, open the lectin-pilin angle, and rotate the lectin domain. In the cocrystal structure, the mannose sugar docks into a pocket on one end of the lectin opposite to the lectin-pilin hinge, although this bent angle may be influenced by a chaperone protein included in the structure (41). Interestingly, two loops from the lectin surface (Tyr-48–Ile-52 and Asn-135–Asp-140) are seen just outside the pocket but do not make contact with the mannose, although they may interact with structures to which the mannose sugar may attach. However, rotation of the lectin domain may provide opportunities for these loops to form new interactions with the mannose as it slides out from the binding pocket. These observations suggest that a sliding-rebinding mechanism may also operate in the FimH-mannose interaction to elicit catch bonds.
We should emphasize that the sliding-rebinding mechanism is only one of many possible mechanisms for catch bonds. For example, another possible mechanism may be force induced-fit of the binding interface. Multiple mechanisms may cooperate to produce catch bonds in a single system.
Acknowledgments
We thank P. Mehta and R. P. McEver for sharing their unpublished data of the L-selectin crystal structure, M. Long and S. Lü for sharing their version of sugar force field, and R. P. McEver and S. C. Harvey for helpful discussion. The computational resources for MD simulations were provided by the Interactive High Performance Computing Laboratory of the College of Computing and by the High Performance Computing Centre of the Office of Information Technology, Georgia Institute of Technology.
This work was supported by National Institutes of Health grant AI44902.
References
- 1.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 2.Dembo, M., D. C. Torney, K. Saxman, and D. Hammer. 1988. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 234:55–83. [DOI] [PubMed] [Google Scholar]
- 3.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kramers, H. A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica (Utrecht). 7:284–304. [Google Scholar]
- 5.Marshall, B. T., M. Long, J. W. Piper, T. Yago, R. P. McEver, and C. Zhu. 2003. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 423:190–193. [DOI] [PubMed] [Google Scholar]
- 6.Sarangapani, K. K., T. Yago, A. G. Klopochi, M. B. Lawrence, C. B. Fieger, S. D. Rosen, R. P. McEver, and C. Zhu. 2004. Low force decelerates L-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 279:2291–2298. [DOI] [PubMed] [Google Scholar]
- 7.Yago, T., J. Wu, C. D. Wey, A. G. Klopochi, C. Zhu, and R. P. McEver. 2004. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 166:913–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lou, J., T. Yago, A. G. Klopochi, P. Metha, W. Chen, V. I. Zarnitsyna, N. V. Bovin, C. Zhu, and R. P. McEver. 2006. Flow-enhanced adhesion regulated by a selectin interdomain hinge. J. Cell Biol. 174:1107–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. [DOI] [PubMed] [Google Scholar]
- 10.Alon, R., S. Chen, K. D. Puri, E. B. Finger, and T. A. Springer. 1997. The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling. J. Cell Biol. 138:1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thomas, W. E., E. Trintchina, M. Forero, V. Vogel, and E. V. Sokurenko. 2002. Bacterial adhesion to target cells enhanced by shear force. Cell. 109:913–923. [DOI] [PubMed] [Google Scholar]
- 12.Thomas, W., M. Forero, O. Yakovenko, L. Nilsson, P. Vicini, E. Sokurenko, and V. Vogel. 2006. Catch-bond model derived from allostery explains force-activated bacterial adhesion. Biophys. J. 90:753–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gao, B., and W. H. Guilford. 2006. Mechanics of actomyosin bonds in different nucleotide states are tuned to muscle contraction. Proc. Natl. Acad. Sci. USA. 103:9844–9849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Evans, E., A. Leung, V. Heinrich, and C. Zhu. 2004. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 101:11281–11286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pereverzev, Y. V., O. V. Prezhdo, W. E. Thomas, and E. V. Sokurenko. 2005. Distinctive features of the biological catch bond in the jump-ramp force regime predicted by the two-pathway model. Phys. Rev. E. 72:010903. [DOI] [PubMed] [Google Scholar]
- 16.Pereverzev, Y. V., O. V. Prezhdo, M. Forero, E. V. Sokurenko, and W. E. Thomas. 2005. The two-pathway model for the catch-slip transition in biological adhesion. Biophys. J. 89:1446–1454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Barsegov, V., and D. Thirumalai. 2005. Dynamics of unbinding of cell adhesion molecules: transition from catch to slip bonds. Proc. Natl. Acad. Sci. USA. 102:1835–1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu, F., Z. C. Ou-Yang, and M. Iwamoto. 2006. Dynamic disorder in receptor-ligand forced dissociation experiments. Phys. Rev. E. 73:010901. [DOI] [PubMed] [Google Scholar]
- 19.Pereverzev, Y. V., and O. V. Prezhdo. 2006. Force-induced deformations and stability of biological bonds. Phys. Rev. E. 73:050902. [DOI] [PubMed] [Google Scholar]
- 20.Somers, W. S., J. Tang, G. D. Shaw, and R. T. Camphausen. 2000. Insights into the molecular basis of leukocyte tethering and rolling revealed by structures of P- and E-selectin bound to SLe(X) and PSGL-1. Cell. 103:467–479. [DOI] [PubMed] [Google Scholar]
- 21.Isralewitz, B., M. Gao, and K. Schulten. 2001. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 11:224–230. [DOI] [PubMed] [Google Scholar]
- 22.Phillips, J. C., R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale, and K. Schulten. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.MacKerell Jr., A. D., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, et al. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 24.Kuttel, M., J. W. Brady, and K. J. Naidoo. 2002. Carbohydrate solution simulations: producing a force field with experimentally consistent primary alcohol rotational frequencies and populations. J. Comput. Chem. 23:1236–1243. [DOI] [PubMed] [Google Scholar]
- 25.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD-visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 26.Graves, B. J., R. L. Crowther, C. Chandran, J. M. Rumberger, S. Li, K. S. Huang, D. H. Presky, P. C. Familletti, B. A. Wolitzky, and D. K. Burns. 1994. Insight into E-selectin/ligand interaction from the crystal structure and mutagenesis of the lec/EGF domains. Nature. 367:532–538. [DOI] [PubMed] [Google Scholar]
- 27.Kansas, G. S., K. B. Saunders, K. Ley, A. Zakrzewicz, R. M. Gibson, B. C. Furie, B. Furie, and T. F. Tedder. 1994. A role for the epidermal growth factor-like domain of P-selectin in ligand recognition and cell adhesion. J. Cell Biol. 124:609–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dwir, O., G. S. Kansas, and R. Alon. 2000. An activated L-selectin mutant with conserved equilibrium binding properties but enhanced ligand recognition under shear flow. J. Biol. Chem. 275:18682–18691. [DOI] [PubMed] [Google Scholar]
- 29.Dwir, O., A. Solomon, S. Mangan, G. S. Kansas, U. S. Schwarz, and R. Alon. 2003. Avidity enhancement of L-selectin bonds by flow: shear-promoted rotation of leukocytes turn labile bonds into functional tethers. J. Cell Biol. 163:649–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Phan, U. T., T. T. Waldron, and T. A. Springer. 2006. Remodeling of the lectin-EGF-like domain interface in P- and L-selectin increases adhesiveness and shear resistance under hydrodynamic force. Nat. Immunol. 7:883–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Leppänen, A., S. P. White, J. Helin, R. P. McEver, and R. D. Cummings. 2000. Binding of glycosulfopeptides to P-selectin requires stereospecific contributions of individual tyrosine sulfate and sugar residues. J. Biol. Chem. 275:39569–39578. [DOI] [PubMed] [Google Scholar]
- 32.Leppänen, A., T. Yago, V. I. Otto, R. P. McEver, and R. D. Cummings. 2003. Model glycosulfopeptides from P-selectin glycoprotein ligand-1 require tyrosine sulfation and a core 2-branched O-glycan to bind to L-selectin. J. Biol. Chem. 278:26391–26400. [DOI] [PubMed] [Google Scholar]
- 33.Lü, S., and M. Long. 2005. Forced dissociation of selectin-ligand complexes using steered molecular dynamics simulation. Mol Cell Biomech. 2:161–177. [PubMed] [Google Scholar]
- 34.Lu, H., B. Isralewitz, A. Krammer, V. Vogel, and K. Schulten. 1998. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 75:662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gao, M., D. Craig, O. Lequin, I. D. Campbell, V. Vogel, and K. Schulten. 2003. Structure and functional significance of mechanically unfolded fibronectin type III1 intermediates. Proc. Natl. Acad. Sci. USA. 100:14784–14789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bayas, M. V., K. Schulten, and D. Leckband. 2003. Forced detachment of the CD2–CD58 complex. Biophys. J. 84:2223–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ramachandran, V., M. U. Nollert, H. Qiu, W. J. Liu, R. D. Cummings, C. Zhu, and R. P. McEver. 1999. Tyrosine replacement in P-selectin glycoprotein ligand-1 affects distinct kinetic and mechanical properties of bonds with P- and L-selectin. Proc. Natl. Acad. Sci. USA. 96:13771–13776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhu, C., M. Long, S. E. Chesla, and P. Bongrand. 2002. Measuring receptor/ligand interaction at the single-bond level: experimental and interpretative issues. Ann. Biomed. Eng. 30:305–314. [DOI] [PubMed] [Google Scholar]
- 39.Dima, R. I., and D. Thirumalai. 2006. Determination of network of residues that regulate allostery in protein families using sequence analysis. Protein Sci. 15:258–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Finer, J. T., R. M. Simmons, and J. A. Spudich. 1994. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 368:113–119. [DOI] [PubMed] [Google Scholar]
- 41.Hung, C. S., J. Bouckaert, D. Hung, J. Pinkner, C. Widberg, A. DeFusco, C. G. Auguste, R. Strouse, S. Langermann, G. Waksman, and S. J. Hultgren. 2002. Structural basis of tropism of Escherichia coli to the bladder during urinary tract infection. Mol. Microbiol. 44:903–915. [DOI] [PubMed] [Google Scholar]