Interaction of Glycolysis and Mitochondrial Respiration in Metabolic Oscillations of Pancreatic Islets

Abstract

Insulin secretion from pancreatic β-cells is oscillatory, with a typical period of 2–7 min, reflecting oscillations in membrane potential and the cytosolic Ca²⁺ concentration. Our central hypothesis is that the slow 2–7 min oscillations are due to glycolytic oscillations, whereas faster oscillations that are superimposed are due to Ca²⁺ feedback onto metabolism or ion channels. We extend a previous mathematical model based on this hypothesis to include a more detailed description of mitochondrial metabolism. We demonstrate that this model can account for typical oscillatory patterns of membrane potential and Ca²⁺ concentration in islets. It also accounts for temporal data on oxygen consumption in islets. A recent challenge to the notion that glycolytic oscillations drive slow Ca²⁺ oscillations in islets are data showing that oscillations in Ca²⁺, mitochondrial oxygen consumption, and NAD(P)H levels are all terminated by membrane hyperpolarization. We demonstrate that these data are in fact compatible with a model in which glycolytic oscillations are the key player in rhythmic islet activity. Finally, we use the model to address the recent finding that the activity of islets from some mice is uniformly fast, whereas that from islets of other mice is slow. We propose a mechanism for this dichotomy.

INTRODUCTION

Glucose metabolism plays a key signaling role in pancreatic β-cells, the insulin-secreting cells located in the islets of Langerhans. In addition to the ubiquitous role that the metabolic product adenosine triphosphate (ATP) plays in providing energy to the cell, metabolism in β-cells is also the means through which information about the blood glucose level is transmitted to the cell, ensuring the appropriate level of insulin secretion. ATP-sensitive K⁺ channels (K(ATP) channels) in the plasma membrane are activated by ADP and inactivated by ATP, so the ratio of these nucleotides determines the fraction of open K(ATP) channels (1,2). When the ATP/ADP ratio is elevated there is a reduction in the number of open K(ATP) channels. This results in membrane depolarization, causing voltage-dependent Ca²⁺ channels to open. The resulting Ca²⁺ influx evokes insulin secretion (3). In vivo and in vitro measurements of insulin levels show that insulin secretion is typically oscillatory, consisting of fast oscillations with a period of <1 min, or slow oscillations with period of 2–7 min, or a combination of the two (4–9). The slow insulin oscillations appear to have a physiological function, and are lost in patients with type II diabetes (10,11).

It has been suggested that oscillations in the cytosolic adenine nucleotide levels are largely responsible for oscillatory insulin secretion. Some authors have suggested that these oscillations are due to Ca²⁺ feedback onto ATP production (12,13) or ATP consumption (14), whereas others have suggested that they are due to oscillations in glycolysis (9,15). In another current model, oscillations in Ca²⁺ and nucleotides are secondary to oscillations driven by the Na⁺/K⁺ exchanger (16). Although these mechanisms can explain some features of the islet data, each has limitations. For example, each mechanism by itself is unable to explain the compound bursting oscillations that are observed in both single β-cells and islets (discussed below). Our central hypothesis is that Ca²⁺ feedback is responsible for the fast component of insulin oscillations, whereas glycolytic oscillations are responsible for the slow component (17). In this article we develop a mathematical model that combines a recent model of mitochondrial metabolism (18) with models for glycolytic oscillations, plasma membrane electrical activity, and Ca²⁺ handling in the cytosol and the endoplasmic reticulum (17). We demonstrate the explanatory power of this combined model by using it to interpret several recent experimental findings.

For many years, in vitro electrical recordings from islets exhibited fast bursting patterns, with periods of <1 min (2,19–21). Similar fast oscillations have been observed in in vitro measurements of the Ca²⁺ concentration and insulin secretion, including studies where two of the three variables (membrane potential, Ca²⁺ concentration, and insulin) were recorded simultaneously (7,8,22–24). There are, however, numerous examples of islet Ca²⁺ oscillations with much longer periods of up to 2–7 min (6,22,25,26). Finally, there is a growing number of examples where the membrane potential (27–29) or Ca²⁺ concentration (22,25,30) combine fast and slow oscillations. We call these “compound oscillations”. Other reports have shown slow oscillations in the islet oxygen tension (31,32) or the NAD(P)H concentration (33). Some of these O₂ oscillations also appear to be composed of fast and slow oscillations, i.e., they appear to be compound oscillations (32,34). These fast, slow, or compound oscillations in islet membrane potential, Ca²⁺ concentration, O₂, and NAD(P)H concentration are likely responsible for parallel oscillations in insulin secretion.

The first goal of this article is to demonstrate that the combined model can account for the time courses described above. A key parameter in the model is the activity level of the enzyme glucokinase, which is the glucose sensor in β-cells (35). This provides input to the key enzyme for glycolytic oscillations, phosphofructokinase (PFK). The M-type isoform of PFK is known to be responsible for glycolytic oscillations in muscle extracts (36). In the model, for small or large values of glucokinase activity the glycolysis is stationary and the only oscillations produced are due to Ca²⁺ feedback onto metabolism and Ca²⁺-activated K⁺ (K(Ca)) ion channels. The resulting oscillatory pattern is typically fast with only small amplitude metabolic oscillations. For intermediate values of the glucokinase activity level glycolytic oscillations are produced. These provide the slow (2–7 min) component of islet activity. In some cases, Ca²⁺ feedback produces fast bursting oscillations that superimpose with the slower rhythm produced by glycolytic oscillations, yielding compound oscillations.

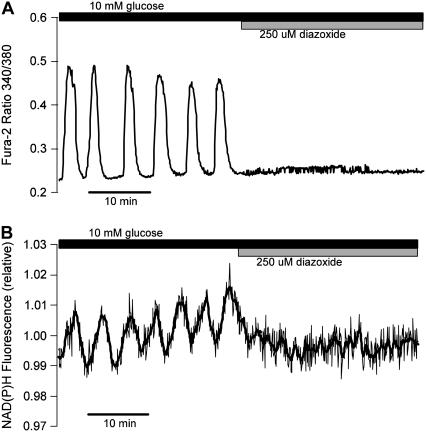
The second goal of the article is to address data that have been interpreted to argue against a role for glycolytic oscillations in the production of slow metabolic oscillations. In one report, the O₂ level was measured in a stimulatory (10 mM) concentration of glucose with an O₂-sensing electrode. This was shown to oscillate, with a period of 6–7 min. The oscillations were terminated almost immediately upon application of the K(ATP) channel activator diazoxide, which hyperpolarizes the islet and reduces the intracellular Ca²⁺ concentration to a basal level (34). These data were interpreted as evidence that Ca²⁺ acting on metabolism and ion channels drives the metabolic rhythm, and not the other way around. In another report, a similar protocol was used, but this time the islet NAD(P)H and Ca²⁺ levels were recorded simultaneously (33). It was shown that application of diazoxide terminated slow oscillations in Ca²⁺ and NAD(P)H, the latter a marker for metabolism. Additional data are presented here (Fig. 5). In the current article we demonstrate that these experimental findings do not argue against a role for glycolytic oscillations. Rather, we suggest that the termination of the oscillations produced by reduction of the intracellular Ca²⁺ concentration is evidence of cross talk between the glycolytic and aerobic metabolic pathways in β-cells.

FIGURE 5.

(A) Oscillations in the islet Ca²⁺ concentration are terminated and the concentration is maintained at a low level after application of 250 μM diazoxide. (B) Parallel islet NAD(P)H measurements. Slow oscillations in NAD(P)H are terminated when the islet is hyperpolarized with diazoxide.

The final goal of the article is to provide a plausible explanation for data from a recent study that combined in vivo insulin measurements from a mouse and subsequent in vitro Ca²⁺ recordings from islets of the same mouse (6). It was shown that insulin oscillations from the mouse and Ca²⁺ oscillations from its islets have a similar period. It was also shown that Ca²⁺ oscillations in islets from a single mouse almost all have either a short period of <2 min (“fast mice”) or a long period of 2–7 min (“slow mice”). This was surprising since it was expected that some islets from a mouse would be fast whereas others would be slow; it was not expected that they would all fall into one category. We provide a plausible explanation for this dichotomy, based on the relative expression levels of phosphofructokinase isoforms.

MATERIALS AND METHODS

Islet isolation and culture

Islets were isolated from the pancreases of 7–12-week-old C57BL/6 mice by collagenase digestion and subsequently cultured overnight in Gibco RPMI 1640 media containing 10 mM glucose and supplemented with 100 μU ml⁻¹ penicillin, 100 μg ml⁻¹ streptomycin, and 10% fetal calf serum (pH 7.4 with NaOH) at 37°C and 5% CO₂. The following day, islets were handpicked, transferred to glass coverslips in groups of 4–8 and allowed to adhere in culture for 48 h before they were used for imaging.

Islet [Ca²⁺]_i and NAD(P)H autofluorescence measurements

For measurement of [Ca²⁺]_i, intact islets were loaded for 30 min in RPMI media with 5 μM of the ratiometric Ca²⁺-indicator fura-2/AM. (Fura-2/AM was purchased from Molecular Probes, Eugene, OR) and other chemicals were from Sigma (St. Louis, MO).) The cover slips were then transferred to a chamber of volume 1 ml, which was mounted on a temperature-controlled stage (Medical Systems, Bothell, WA) on an inverted microscope (Eclipse TE300, Nikon, Tokyo, Japan) equipped with a 10× S Fluor objective (Nikon). Islets were continuously perfused at 2.5 ml min⁻¹ by Ringer's solution containing (in mM): NaCl 144, KCl 5.5, MgCl₂ 1, CaCl₂ 2, Hepes 20 (adjusted to pH 7.35 by NaOH), and 10 mM glucose. Before the onset of either [Ca²⁺]_i or NAD(P)H measurements, islets were perifused for 30 min to wash out excess dye and allow them to reach a steady state.

Excitation wavelengths were controlled by means of excitation filters (Chroma Technology, Brattleboro, VT) mounted in a Lambda DG-4 wavelength switcher (Sutter Instrument, Novato, CA). NAD(P)H autofluorescence was excited at 365 nm, and the fluorescence emission was filtered using a DAPI/FITC/TxRed polychroic beamsplitter and triple band emission filter (Chroma Technology). Fura-2 was excited ratiometrically at 340 and 380 nm, and its fluorescence collected through a D510/80m wide band emission filter. Changes in [Ca²⁺]_i are expressed as the ratio of fluorescence emission intensity (F₃₄₀/F₃₈₀). Images were collected every 5 s by a CoolSNAP HQ monochrome 12-bit digital camera (Roper Scientific, Tucson, AZ), and both image acquisition and analysis were controlled by Metafluor software (Universal Imaging, West Chester, PA).

NAD(P)H recordings were corrected for the slow downward trend due to photobleaching. The trend was projected by an exponential best fit to the full time series, and removed by division of the raw data by the estimated function. Hence, the NAD(P)H changes are expressed relative to the mean fluorescence. Data processing and plotting were done using the program Igor Pro (Wavemetrics, Portland, OR).

The mathematical model

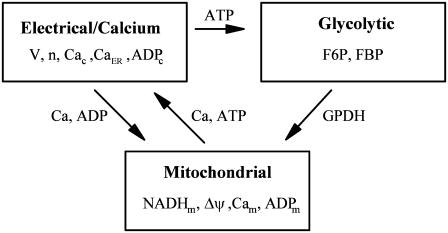
The model consists of a glycolytic component, a mitochondrial metabolism component, and an electrical and cytosolic/endoplasmic reticulum (ER) Ca²⁺ component. The variables defined in each component and their interaction pathways are illustrated in Fig. 1, and differential equations, functional expressions, and explanations are given in the Appendix.

FIGURE 1.

Model components and interconnections.

The glycolytic component describes the enzymatic reaction of the M-type (muscle-type) isoform of phosphofructokinase (PFK), which is responsible for glycolytic oscillations in muscle extracts (37) and is the isoform whose activity level is dominant in β-cells (38). PFK is an allosteric enzyme that converts substrate fructose 6-phosphate concentration (F6P) into product fructose 1,6-bisphosphate concentration (FBP). Oscillations in glycolysis are produced by the positive feedback of the product FBP, which produces acceleration of PFK activity with an eventual crash due to substrate depletion. A constant influx of F6P to the system through the actions of the glucokinase (GK) enzyme eventually replenishes the substrate concentration, reactivating PFK. This model was developed by Smolen based on data from muscle extracts (39), and was used in two of our previous β-cell models (17,40).

In these models (17,40) mitochondrial metabolism was described in an extremely simple way, using a single differential equation to describe ATP production. This minimal description was used originally by Keizer and Magnus (12). We are now interested in the dynamics of the mitochondrial variables, since these variables are measurable with imaging techniques and since we believe that these dynamics can help us understand the bursting mechanism in β-cells. For this reason, in this report we modify the mitochondrial component of the β-cell model by replacing the minimal model for mitochondrial metabolism with a much more detailed model.

A detailed model of mitochondrial metabolism, the Magnus-Keizer (M-K) model, was developed previously (13,41). This has the advantage of being based on first principles, so one can calibrate it to different cell types. However, this strength is also a weakness, as it is very complex and the functional forms of the reaction terms are not transparent. In a recent publication we developed a simplified version of the model, greatly reducing the number of parameters and complexity of the mathematical expressions (18). This simplification was achieved by fitting curves for simpler functions to those of the original functions. One should of course be cautious when using a model based on curve fitting, as such a model would not be valid when large parametric changes occur in the biological system. We use this simplified model as the mitochondrial component of the full combined β-cell model since we have found that it produces the same behavior as the original Magnus-Keizer model in the relevant parameter regimes.

The mitochondrial model has four variables: the NADH, ADP, and Ca²⁺ concentrations (NADH_m, ADP_m, Ca_m, respectively), and the inner membrane potential (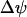). The oxygen consumption (J_O) is also a quantity of interest determined by the model. Full equations and descriptions are given in the Appendix. A derivation of the model can be found in Bertram et al. (18).

The final compartment of the β-cell model describes the electrical activity of the plasma membrane (variables V and n), the Ca²⁺ concentrations in the cytosol and the endoplasmic reticulum (Ca_c and Ca_ER), and the ADP concentration in the cytosol (ADP_c). The model for this compartment was developed by us in a previous publication (17). The equations and a description of the model are given in the Appendix.

As illustrated in Fig. 1, there is communication between the three compartments of the β-cell model. The output of the glycolytic compartment, the glyceraldehyde 3-P dehydrogenase reaction rate (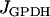) serves as the input to the mitochondrial compartment. The ATP produced in the mitochondrial compartment enters the electrical/calcium compartment, whereas ADP from the electrical/calcium enters the mitochondrial compartment. Calcium flows between these two compartments. Finally, the ATP concentration in the electrical/calcium compartment affects the glycolytic compartment through its negative effect on the PFK reaction rate.

The differential equations were solved numerically with the variable step size CVODE method with tolerance 10⁻⁹ implemented in the XPPAUT software package (42). Computer codes for the model can be downloaded from http://www.math.fsu.edu/∼bertram or http://mrb.niddk.nih.gov/sherman.

RESULTS

Fast, slow, and compound bursting

Electrical recordings of islet membrane potential and measurements of the free Ca²⁺ concentration in islets demonstrate that one of three types of oscillatory behavior typically occurs. Oscillations may be fast with periods ranging from ∼15 s to ∼2 min, or they may be slow with periods ranging from ∼2 min to ∼7 min, or they may consist of fast oscillations superimposed on slower oscillations (22,30). Each type corresponds to electrical bursting, which we refer to as fast, slow, or compound, respectively (17). We have previously suggested that slow bursting and the slow component of compound bursting are due to oscillations in glycolysis, and that during fast bursting glycolysis is nonoscillatory (17). In this section, we demonstrate that the model can produce the different types of bursting, and illustrate how key variables change in time during these oscillations.

In our model, glycolytic oscillations occur only for intermediate values of the glucokinase rate parameter J_GK. That is, there is a lower threshold and an upper threshold, and glycolytic oscillations occur only if J_GK is between these thresholds (43). Fast bursting is shown in Fig. 2. To obtain this, J_GK is set to a value, J_GK = 0.7 μM ms⁻¹, which is past the upper threshold for glycolytic oscillations. Fast electrical bursting is reflected in the burst-like Ca_c time course, with burst period of ∼30 s (Fig. 2 A). The FBP concentration is relatively constant since glycolysis is in a nonoscillatory state (Fig. 2 B). However, there are small fluctuations in FBP, due to the effect of ATP_c feedback onto PFK. These small fluctuations are present, but attenuated, in NADH_m, which is nearly constant at a high level (Fig. 2 C).

FIGURE 2.

Fast bursting driven by Ca²⁺ feedback. There are no glycolytic oscillations, only small fluctuations due to the feedback of ATP onto PFK. .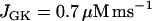

In the model, calcium influx across the mitochondrial membrane has two effects on the mitochondrial membrane potential. One is to increase activation of dehydrogenases, leading to an increase in mitochondrial membrane polarization. The other effect is to depolarize the membrane due to the influx of the Ca²⁺ ions. (A third effect, observed in cardiac cells and not present in the model, is to directly increase the activity of the F₁F₀ ATP synthase (44). This would increase the production of ATP by the mitochondria.) We have shown previously that either effect may be dominant, depending on the choice of parameter values (18). With the values used here, the primary effect of Ca²⁺ influx across the mitochondrial membrane is membrane depolarization (Fig. 2 D). This depolarization is accompanied by an increase in O₂ consumption (Fig. 2 E) because it is easier for the electron transport chain to pump protons across the mitochondrial membrane, raising the rate of oxidation of NADH_m (13). Finally, the rate of ATP synthesis, and thus the mitochondrial ATP concentration, decline during each burst due to the reduction in the proton gradient. As a result, less ATP is transported out of the mitochondria into the cytosol through the adenine translocator, so the cytosolic ATP concentration declines during each burst (Fig. 2 F). A second factor contributing to the decline in ATP_c during a burst is the hydrolysis of ATP by Ca²⁺ pumps in the plasma and ER membranes (14,45). When Ca²⁺ is elevated the activity of these pumps is increased, resulting in a reduction in ATP_c due to increased hydrolysis (Eq. 28).

The decline in ATP_c (and, more important, the increase in ADP_c) during a burst results in an increase in the K(ATP) current, causing the plasma membrane to hyperpolarize. Another ionic current that contributes to membrane hyperpolarization is the Ca²⁺-activated K⁺ current, which increases during bursting due to the elevation of Ca_c. Together, I_K(ATP) and I_K(Ca) are responsible for driving fast bursting in this model (17,46).

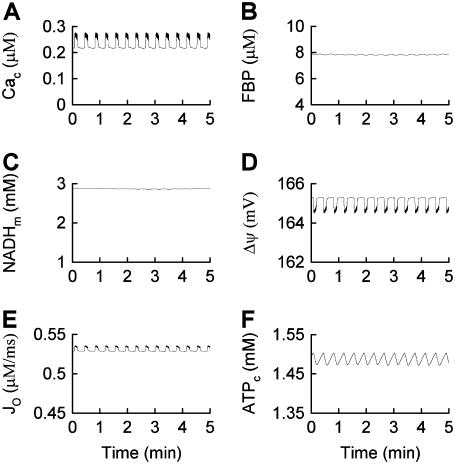
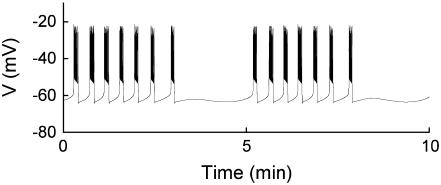
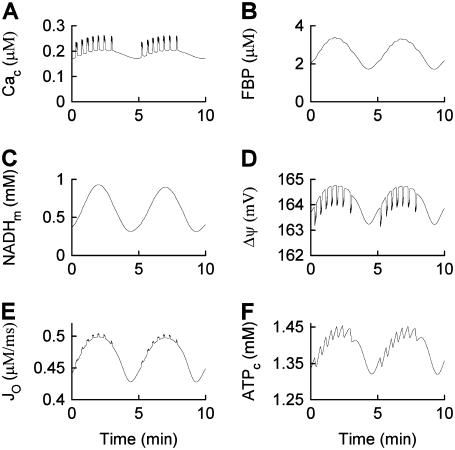
To produce compound oscillations (Figs. 3 and 4), J_GK is reduced to a value between the lower and upper thresholds for glycolytic oscillations, 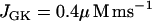. The fast component is due to bursts of action potentials (Fig. 3), whereas the slow component is due to oscillations in glycolysis. The glycolytic oscillations are reflected most directly in the variable FBP (Fig. 4 B). In contrast to the small fluctuations shown in Fig. 2 B, the oscillations in FBP in Fig. 4 B have large amplitude and period, with small faster fluctuations superimposed. The large, slow oscillations are due to oscillations in glycolysis, whereas the small, fast fluctuations are due to ATP feedback onto PFK. Each pulse of FBP provides fuel to the mitochondria in the form of NADH, so that NADH_m oscillates in phase with FBP (Fig. 4 C). When NADH_m is elevated during an oscillation the rate of electron transport is increased, increasing O₂ consumption (Fig. 4 E) and the proton gradient, resulting in hyperpolarization of the mitochondrial membrane (Fig. 4 D). The hyperpolarized mitochondrial membrane leads to increased ATP production, and consequently an increase in ATP_c (Fig. 4 F). The additional cytosolic ATP closes K(ATP) channels in the plasma membrane, depolarizing the membrane and consequently increasing the influx of Ca²⁺ through Ca²⁺ channels. This results in the slow Ca_c envelope shown in Fig. 4 A.

FIGURE 3.

Compound bursting. Fast bursts of action potentials are grouped into episodes. .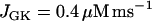

FIGURE 4.

Time courses of variables during compound bursting. The slow component is due to glycolytic oscillations. The fast component is due to Ca²⁺ feedback. The mitochondrial membrane potential, oxygen consumption, and cytosolic ATP concentration all exhibit teeth, reflecting the effects of Ca²⁺ .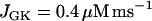

The fast component of the compound oscillations appears as fast, small oscillations in Ca_c (Fig. 4 A). These elevations in Ca_c depolarize the mitochondrial membrane (Fig. 4 D), as in Fig. 2 D. The small deflections, or “teeth”, are superimposed on the slower oscillations produced by glycolytic oscillations. The downward teeth in produce upward teeth in J_o (Fig. 4 E) and downward teeth in the cytosolic ATP concentration (Fig. 4 F) as described above for Fig. 2. The ATP teeth are amplified by the increased hydrolysis of Ca²⁺ pumps during Ca_c bursts.

One feature of the compound oscillations produced by the model is that O₂ consumption is high during an episode of bursts in Ca_c, and low between episodes. Since insulin secretion occurs when Ca_c is elevated, the model suggests that oscillations in insulin secretion should be roughly in phase with oscillations in O₂ consumption. Stated another way, the model shows that insulin oscillations should be 180° out of phase with external oxygen tension (the quantity that is typically measured experimentally). This has been verified in prior simultaneous measurements of insulin release and O₂ tension in islets (31). The model also shows that the O₂ tension should be characterized by slow oscillations with superimposed fast fluctuations or teeth. This has also been verified in prior measurements of O₂ tension in islets (9,32).

Slow bursting, like the slow component of compound bursting, is driven by oscillations in glycolysis in our model (see Bertram et al. (17)). We can obtain this using the same glucokinase rate as in compound bursting, but with different values for the K(Ca) and K(ATP) current conductances (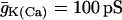, 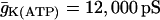). The slow components of the time courses for metabolic variables are similar to those for compound bursting.

Plasma membrane hyperpolarization can terminate metabolic oscillations

If, as we propose, glycolytic oscillations drive Ca²⁺ oscillations during compound or slow bursting, then what happens if the Ca²⁺ oscillations are terminated? Do metabolic oscillations continue? This question was addressed by Kennedy et al. (2002). They measured slow O₂ oscillations in mouse islets in 10 mM glucose, and then hyperpolarized the islets by adding diazoxide (Dz) to the bath, which opens K(ATP) channels. The large O₂ oscillations were rapidly terminated, and the O₂ level approached and maintained an elevated value (Fig. 5 A in Kennedy et al. (34)). These data demonstrated that metabolic oscillations stop and O₂ consumption declines when Ca²⁺ is maintained at a low level.

In accordance with the O₂ recordings, we also found that metabolic oscillations, as measured by the NAD(P)H level, stop when the plasma membrane is hyperpolarized with Dz (Fig. 5 and Luciani et al. (33)). Fig. 5 shows robust oscillations in both islet Ca²⁺ and NAD(P)H in 10 mM glucose (variables were measured in parallel recordings, not simultaneously). When Dz was added to the bath the Ca²⁺ concentration stopped oscillating and approached a low value (Fig. 5 A), as expected when the plasma membrane is hyperpolarized. The oscillations in NAD(P)H were also terminated by Dz, and NAD(P)H went to a low level (Fig. 5 B), demonstrating that the plasma membrane hyperpolarization stopped the metabolic oscillations.

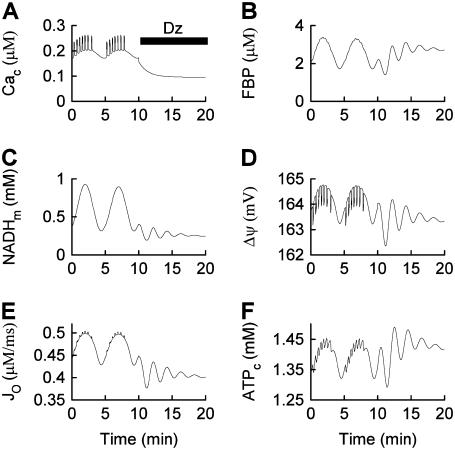
One could interpret these two sets of data as evidence against a glycolytic mechanism for slow oscillations. After all, if glycolytic oscillations drive Ca²⁺ oscillations, and not the other way around, then terminating Ca²⁺ oscillations should have little effect on the glycolytic oscillations. We show in Fig. 6, however, that in the combined model plasma membrane hyperpolarization can terminate glycolytic oscillations, due to the nucleotide dependence of PFK activity. Initially the model produces compound oscillations, as in Fig. 3. When application of Dz is simulated, by setting the fraction of open K(ATP) channels to 1, the model cell hyperpolarizes and Ca_c approaches a low value (Fig. 6 A). This reduces the amount of work that must be done by plasma membrane and SERCA pumps, so there is less hydrolysis of cytosolic ATP. As a result, ATP_c increases (Fig. 6 F). The critical enzyme for glycolytic oscillations, PFK, is inhibited by ATP (47). In our simulation, the increase in ATP_c inhibits PFK sufficiently to terminate glycolytic oscillations (Fig. 6 B). In this state NADH_m is low (Fig. 6 C), and respiration is reduced compared with its level before Dz application. Therefore, O₂ consumption is reduced (Fig. 6 E), so the extracellular O₂ level would be elevated, consistent with the data from Kennedy et al. (34). The low value of NADH_m after simulated Dz application is consistent with the data in Fig. 5 B. We also simulated the effect of adding the L-type Ca²⁺ channel blocker nifedipine, by reducing the channel conductance 10-fold (from 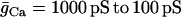). Like simulated application of diazoxide, this terminated the metabolic oscillations (not shown), consistent with what was observed in islets by Jung et al. (32).

FIGURE 6.

Model simulation demonstrating that the metabolic oscillations that drive compound bursting can be terminated by plasma membrane hyperpolarization. Application of diazoxide (Dz) is simulated by setting the fraction of open K(ATP) channels to 1, at the arrow. The reduction in Ca_c reduces ATP hydrolysis by Ca²⁺ pumps, increasing ATP_c. This inactivates the key glycolytic enzyme PFK, terminating the metabolic oscillations.

A mechanism for fast and slow mice

We have previously demonstrated that Ca²⁺ and insulin oscillations in some mice were primarily fast (period <2 min) whereas in other mice they were primarily slow (period >2 min) (6). This finding was surprising, since we had expected islet periods to be mixed in each mouse. According to our model, glycolytic oscillations occur when J_GK is between a lower and an upper threshold. It is highly unlikely that for most islets of a slow mouse the J_GK parameter falls between the thresholds, whereas for a fast mouse J_GK falls outside of the thresholds. A much more reasonable hypothesis is that for a fast mouse there is no J_GK parameter region where glycolytic oscillations occur. That is, for slow mice there is an oscillatory parameter regime, whereas for fast mice there is not. In this section we discuss one natural mechanism through which this may occur.

It has been shown that three isoforms of PFK are expressed in β-cells (38). The M-type isoform is responsible for glycolytic oscillations in muscle extracts, and has the highest activity level in islets (38). Parameter values used in the simulations above reflect this isoform. The C-type isoform is typically found in the brain, and the L-type isoform is found in the liver. These two types have a lower affinity for FBP (48) and a higher affinity for ATP (49,50). It is likely that the higher affinity for inhibitory ATP is responsible for the lower activity levels of C- and L-type PFK in β-cells, relative to the activity level of M-type PFK (38). It is also likely that the low affinity for the product FBP is the reason that oscillations in C- and L-type PFK activity do not occur.

We include the contribution of C- and L-type PFK in the model by adding a second PFK reaction term. This reaction (which we call PFK-C to distinguish from PFK-M, the M-type) is described by Eqs. 4 and 5 as before, but the value of the parameter k₂ is increased to account for the lower affinity for FBP, and the value of the parameter k₄ is decreased to account for the higher affinity for ATP (these changes are only qualitative). As a result, the reaction rate of PFK-C is lower than that of PFK-M for the same value of the input F6P. Also, whereas PFK-M activity is oscillatory for a wide range of values of J_GK, the PFK-C activity is never oscillatory. The total PFK activity is then

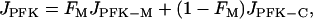(32)

where F_M is the fraction of PFK that is M-type, J_PFK-M is the PFK-M reaction rate, and J_PFK-C is the combined PFK-C and PFK-L reaction rates (we combine these since both are nonoscillatory). The two PFK flux terms see the same F6P concentration. The new J_PFK term is used in the differential equations for F6P and FBP (Eqs. 2–3).

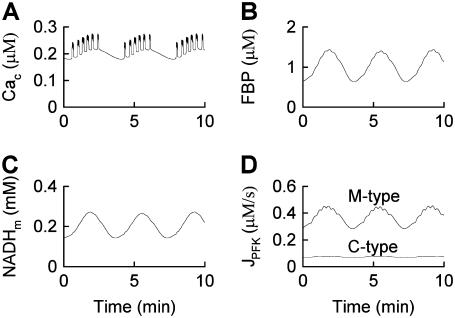
Fig. 7 shows compound bursting when 40% of the PFK expressed is C-type and 60% is M-type 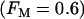. This figure demonstrates that the model produces glycolytic oscillations (and compound bursting) even if a significant fraction of the PFK is of the nonoscillatory type. The figure also shows that the M-type PFK activity is oscillatory, whereas the C-type activity only exhibits small fluctuations as a result of the effect of oscillatory PFK-M activity on the F6P concentration.

FIGURE 7.

Compound bursting driven by glycolytic oscillations occurs even if only 60% of the PFK is of the oscillatory M-type (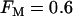). This is representative of a slow mouse. , .

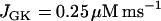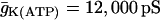When the fraction of M-type PFK is reduced to 30% (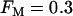) the situation is quite different (Fig. 8). In this case, glycolytic oscillations do not occur for any value of J_GK. When 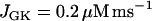the glycolytic flux is so low that the cell is inactive. That is, the K(ATP) current keeps the plasma membrane hyperpolarized. When the reaction rate is increased to 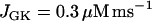the cell becomes active, producing fast bursting. However, there are no large oscillations in J_PFK-M, as were present in Fig. 7 and indicative of glycolytic oscillations. Increasing J_GK further to 0.4 μM ms⁻¹ simply speeds up the fast bursting oscillations, due to the increased glycolytic flux. Thus, we hypothesize that Fig. 8 corresponds to an islet from a fast mouse, whereas Fig. 7 corresponds to an islet from a slow mouse.

FIGURE 8.

When the percentage of M-type PFK is reduced to 30% (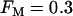) glycolytic oscillations do not occur for any value of J_GK. Increasing J_GK converts a silent cell to a fast bursting cell, or increases the burst frequency, but the large, slow oscillations in J_PFK-M that are characteristic of glycolytic oscillations do not occur. This is representative of a fast mouse. .

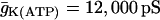Although the combined model has three interacting components, the dynamic mechanism for the effects of varying F_M lies entirely within the glycolytic component. We demonstrate this by isolating the glycolytic component (Eqs. 2–5) and holding the nucleotide concentrations (which are inputs to the glycolytic component) fixed. Specifically, we set 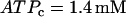and 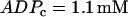, which are typical values of the variables during compound bursting. 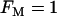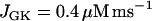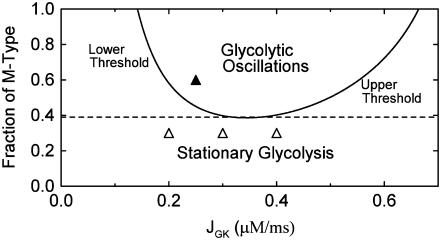When all of the PFK is of M-type () and , the same conditions that produce compound bursting in the full model (Fig. 3), the isolated glycolytic component produces oscillations. When the M-type fraction is reduced to 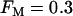, slow oscillations never occur, regardless of the value of J_GK. Fig. 9 shows the regions of the two-dimensional J_GK-F_M parameter space where glycolysis is stationary and where it is oscillatory. From this figure, we see that glycolytic oscillations do not occur for any value of J_GK when F_M is <∼0.4 (open triangles represent the parameter values used in Fig. 8). When 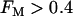, glycolytic oscillations do occur, but only for “intermediate” values of J_GK (the solid triangle represents the parameter value used in Fig. 7). For 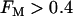there are lower and upper J_GK thresholds for the existence of oscillations, and the distance between the thresholds increases as F_M is increased. Islets from fast mice remain fast when the glucose concentration is changed (43), corresponding to a change in J_GK. Thus, for such islets, no horizontal shift in Fig. 9 (say, from one open triangle to another) can enter the oscillatory region. For islets from a slow mouse, on the other hand, it should be possible for changes in the glucose concentration to initiate glycolytic oscillations, so it should be possible for a horizontal shift to enter the oscillatory region. Therefore, our hypothesis is that the region of this two-dimensional parameter space below the dashed line in Fig. 9 is representative of fast mice, whereas the region above the dashed line is representative of slow mice.

FIGURE 9.

Two-parameter diagram showing the regions in parameter space where the glycolytic component of the model is stationary or oscillatory. The solid curve denotes the threshold between stationary and oscillatory activities. The solid triangle corresponds to the parameter values used in Fig. 7, whereas the open triangles correspond to the parameter values used in Fig. 8. Parameter combinations falling below the dashed line correspond to fast mice, whereas those above the dashed line correspond to slow mice. Nucleotide concentrations are fixed at 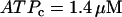and .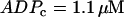

DISCUSSION

We have described a mathematical model of the pancreatic β-cell that can account for the fast (period <2 min) and slow (period 2–7 min) oscillations in insulin and Ca²⁺ concentration that are typically observed in islets. The model consists of a glycolytic component that can produce slow oscillations in glycolysis, a mitochondrial component that converts the glycolytic input to ATP output, and an electrical/calcium component that responds to ATP from the mitochondria by changing the pattern of electrical activity. The model produces a compound bursting pattern when glycolysis is oscillatory and the electrical/calcium component generates fast bursts. During compound bursting (Fig. 4), the O₂ consumption time course is similar to what has been observed experimentally (9,32), with slow large oscillations in O₂ consumption (or O₂ tension) superimposed with faster and smaller “teeth”. In our model, the large oscillations are due to glycolytic oscillations, whereas the teeth are due to Ca²⁺ feedback onto metabolism and ATP consumption by Ca²⁺ pumps in the plasma membrane and ER. The model is also consistent with in vitro islet data showing that O₂ tension was ∼180° out of phase with insulin concentration (31), and with in vivo data showing that O₂ tension was 180° out of phase with portal vein insulin levels in anesthetized rats (51). Since insulin is released when the cytosolic Ca²⁺ concentration is high, this suggests that O₂ tension and Ca²⁺ concentration are 180° out of phase (so that O₂ consumption and Ca²⁺ concentration are in phase), as predicted by the model.

Another important set of data reproduced by the model is from experiments showing that plasma membrane hyperpolarization can terminate oscillations in O₂ (34) and NAD(P)H (Fig. 5 and (33)). These data had previously been interpreted as evidence against glycolytic oscillations, but our model simulations (Fig. 6) indicate that the data are in fact consistent with a mechanism whereby metabolic oscillations are driven by PFK-mediated glycolytic oscillations. The key here is that the reduction in the intracellular Ca²⁺ concentration that results from membrane hyperpolarization reduces the pumping action of plasma membrane and ER Ca²⁺ pumps. Thus, the pumps use less ATP and the cytosolic ATP level increases, inhibiting PFK and terminating the PFK-mediated oscillations.

In an earlier article we made the opposite prediction, that metabolic oscillations could persist even if the plasma membrane were hyperpolarized (17). This prediction was recently confirmed, where membrane hyperpolarization was accomplished by reducing the glucose concentration or reducing the glucokinase activity (43). In both cases slow, subthreshold oscillations in Ca²⁺ persisted. Since these were not due to electrical activity, the most likely explanation is that the subthreshold Ca²⁺ oscillations were due to metabolic oscillations. This remains to be tested directly, however.

In the model, the key determining factor for whether or not plasma membrane hyperpolarization terminates glycolytic oscillations is the affinity of PFK for its inhibitor ATP (reflected in the parameter K₄). When 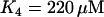, the default value used here, the ATP affinity is relatively high, so the ATP level reached during hyperpolarization is sufficient to terminate PFK-mediated oscillations. When 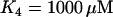, the value used in Bertram et al. (17), the ATP affinity is relatively low, so the ATP level reached during hyperpolarization does not sufficiently inhibit PFK to terminate oscillations. It may be that the ATP level reached during hyperpolarization differs from islet to islet, explaining why hyperpolarization terminates metabolic oscillations in some, but not all, islets.

Another variable reflecting mitochondrial activity is the inner membrane potential, 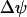. Our model predicts that during slow and compound bursting the mitochondrial membrane potential becomes more polarized during the upstroke of a glycolytic oscillation (i.e., when FBP is elevated, Fig. 4). The elevated glycolytic flux provides fuel for mitochondrial respiration, polarizing the inner membrane. Concurrent with this, the cytosolic Ca²⁺ concentration is elevated due to the increase in the cytosolic ATP level. Thus, the model predicts that 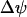becomes more polarized during the peaks of the slow Ca²⁺ oscillations (Fig. 4). One recent study in which the Ca²⁺ concentration and mitochondrial membrane potential in islets were measured simultaneously is consistent with this model prediction (Fig. 5 in Kindmark et al. (52)). That is, during slow Ca²⁺ oscillations, 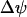became more polarized during the Ca²⁺ peaks and less polarized between peaks.

The combined model that we have described is built partly from earlier modeling work by Magnus and Keizer (12,13). Our model differs in two major ways from the Magnus-Keizer models. First, it treats fast, slow, and compound bursting, whereas the M-K models treat only fast bursting. Second, it treats the dynamics of glycolysis and glycolytic oscillations, whereas the M-K model assumes that glycolysis is at steady state.

Finally, we have presented a potential mechanism for the recent observation that islets from some mice are mostly fast, whereas those from other mice are mostly slow. We postulate that this reflects relative expression levels of the M-type isoform of PFK, which is capable of producing glycolytic oscillations, and C- and L-type isoforms that are not. If the percentage of PFK that is M-type is too low (40% in the model), then glycolytic oscillations, and compound oscillations, will not occur regardless of the glucose concentration. This leads to the testable prediction that islets from fast mice have a lower percentage of M-type PFK than do islets from slow mice.

APPENDIX

The glycolytic model

The glycolytic model describes the action of the M-type isoform of phosphofructokinase, which is responsible for glycolytic oscillations in muscle extracts (37) and is the isoform whose activity level is dominant in β-cells (38). In our model, the output of the PFK reaction is the output of the glycolytic component, since the remainder of the glycolytic process leading to pyruvate production is not included because those steps are assumed to be in equilibrium with PFK. PFK converts fructose 6-phosphate (F6P) to fructose 1,6-bisphosphate (FBP), which is a substrate for glyceraldehyde 3-P dehydrogenase (GPDH). Following Tornheim (53), we assume that the GPDH reaction is at rapid equilibrium, and the reaction rate is:

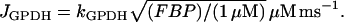(1)

This is the output of the glycolytic model.

A detailed description of the glycolytic model, which is based on Smolen (39), can be found in a previous publication (40). The model has two differential equations, one for glucose 6-phosphate (G6P) and one for FBP. G6P is assumed to be in rapid equilibrium with F6P (F6P=0.3 G6P), so either G6P or F6P is representative of input to the PFK reaction, whereas FBP is the output of the reaction. The differential equations are:

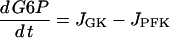(2)

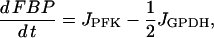(3)

where J_PFK is the PFK reaction rate, J_GPDH is given by Eq. 1, and J_GK is the glucokinase reaction rate, which we treat as a model parameter. This rate would depend on the glucose concentration, as well as other factors (such as the GLUT-2 glucose transporter expression and activity level, and the glucokinase expression level). In simulations presented here we use different values of this parameter to highlight different model behaviors. Our model predicts that at low and high values of J_GK glycolysis is stationary, whereas at intermediate values of J_GK it is oscillatory. The oscillatory behavior is due to the positive feedback of the product FBP onto the M-type isoform of PFK (38,39). The adenine nucleotides AMP and ATP also feed back onto this isoform of PFK: AMP is stimulatory whereas ATP is inhibitory (47). It is this feedback that allows the mitochondrial metabolism to influence glycolysis. Since glycolysis influences mitochondrial metabolism through the GPDH activity, there is a two-way interaction or cross talk between these stages of metabolism. In a prior publication, we demonstrated that this cross talk may contribute to synchronization of glycolytic oscillations throughout an islet (40). The PFK reaction rate was developed in Smolen (39) and is given by:

(4)

where i, j, k, and l take on the values 0 or 1, and

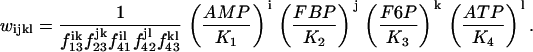(5)

Parameter values for the glycolytic model are given in Table 1.

TABLE 1.

Parameter values for the glycolytic compartment

kGPDH = 0.0005 μM ms−1	Vmax = 0.005 μM ms−1	λ = 0.06	K1 = 30 μM
K2 = 1 μM	K3 = 50,000 μM	K4 = 220 μM	f13 = 0.02
f23 = 0.2	f41 = 20	f42 = 20	f43 = 20

The mitochondrial model

The model that we use for mitochondrial metabolism was developed in Bertram et al. (18), based on the detailed Magnus-Keizer model of mitochondrial metabolism (13,41). Our model uses curve fitting to simplify the functional expression of the Magnus-Keizer reaction terms.

Pyruvate dehydrogenase (PDH) produces the coenzyme NADH from NAD⁺ and pyruvate. In addition to this, there are several dehydrogenases in the citric acid cycle, all producing NADH and all upregulated by mitochondrial Ca²⁺. We assume that the reaction rates of citric acid dehydrogenases are proportional to that of PDH, and thus use the reaction rate J_PDH to represent the total dehydrogenase activity. This is, of course, only a simplifying approximation, and the inclusion of dynamics for the citric acid cycle could have a significant impact on the dynamics of the metabolic system. Since we do not explicitly include pyruvate in the glycolytic model, J_GPDH (which should be proportional to pyruvate concentration), is used as input for the PDH reaction. The PDH reaction rate is:

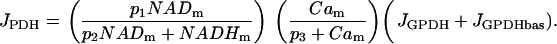(6)

The values of the parameters 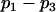and all other mitochondrial parameters are given in Table 2. Values of all parameters except 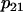and 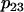are identical to those calibrated in Bertram et al. (18). The 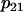parameter is increased from 0.01 μM⁻¹ms⁻¹mV⁻¹ to 0.04 μM⁻¹ms⁻¹mV⁻¹ and the 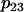parameter is increased from 0.001 ms⁻¹ to 0.01 ms⁻¹ to produce faster mitochondrial Ca²⁺ dynamics.

TABLE 2.

Parameter values for the mitochondrial compartment

p1 = 400	p2 = 1	p3 = 0.01 μM	p4 = 0.6 μM ms−1
p5 = 0.1 mM	p6 = 177 mV	p7 = 5 mV	p8 = 7 μM ms−1
p9 = 0.1 mM	p10 = 177 mV	p11 = 5 mV	p13 = 10 mM
p14 = 190 mV	p15 = 8.5 mV	p16 = 35 μM ms−1	p17 = 0.002 μM ms−1 mV−1
p18 = −0.03 μM ms−1	p19 = 0.35 μM ms−1	p20 = 2	p21 = 0.04 μM−1 ms−1 mV−1
p22 = 1.1 μM−1 ms−1	p23 = 0.01 ms−1	p24 = 0.016 mV−1	JGPDHbas = 0.0005 μM ms−1
fm = 0.01	NADm,tot = 10 mM	Am,tot = 15 mM	Cm = 1.8 μM mV−1

The first factor in Eq. 6 reflects the positive effect of NAD_m and the negative effect of NADH_m on the PDH reaction rate. In addition, the activity level is increased by mitochondrial Ca²⁺, Ca_m, as reflected in the second factor. Finally, PDH activity is driven by glycolytic flux, as represented by J_GPDH and J_GPDHbas, a constant parameter that represents a small basal level of glycolytic flux.

Equation 6 is used in the differential equation for NADH_m:

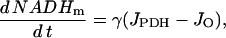(7)

where J_O is the O₂ consumption at the final stage of the electron transport chain, during which NADH is converted to NAD⁺. Both J_PDH and J_O have units of μM/ms, whereas we express NADH_m in units of mM. The factor 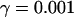makes the conversion from μM to mM. The expression for O₂ consumption in our model is:

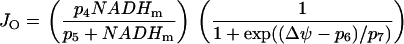(8)

From this we see that J_O is an increasing function of NADH_m, since NADH is an electron donor. The O₂ consumption rate declines with increased polarization of the mitochondrial inner membrane potential (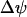), since it is more difficult to pump protons against a large potential gradient (metabolic control). Finally, we assume nucleotide conservation:

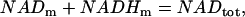(9)

where NAD_tot is the total concentration (in mM).

The mitochondrial inner membrane potential changes over time according to:

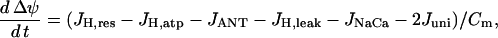(10)

where C_m is the mitochondrial inner membrane capacitance. We use the convention that the membrane potential is positive if the inner membrane is hyperpolarized. The first term in this equation, 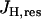, represents flux through respiration-driven proton pumps. Since this pumping is driven by O₂ consumption, its mathematical expression is similar to that for J_O:

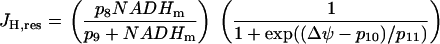(11)

The F₁F₀ ATP synthase phosphorylates ADP to form ATP. The expression for this reaction rate is:

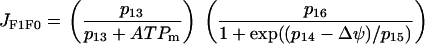(12)

The first factor reflects the fact that mitochondrial ATP opposes the action of the synthase (and can even make the synthase run backwards, however, this possibility is not included in Eq. 12), whereas the second factor reflects the positive action of membrane polarization on the synthase activity.

The phosphorylation is driven by proton flux. Three protons move through the F₁F₀ ATP synthase for each ATP molecule produced. Hence,

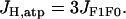(13)

Protons also enter the mitochondria through leakage down the proton gradient. We assume that the leakage depends linearly on the membrane potential:

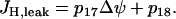(14)

The ATP produced in the mitochondria is transported to the cytosol through the adenine nucleotide translocator. This moves ATP out of and ADP into the mitochondria. Flux through the translocator, J_ANT, is given by:

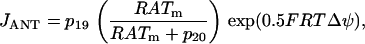(15)

where 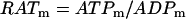and 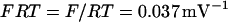is Faraday's constant divided by the gas constant and the temperature. With this expression, an increase in the mitochondrial ATP concentration activates the translocator, whereas an increase in ADP deactivates the transporter.

Calcium ions enter the mitochondria through Ca²⁺ uniporters. Flux through the uniporters, J_uni, is given by:

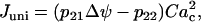(16)

where Ca_c is the cytosolic Ca²⁺ concentration. This reflects the positive dependence on the membrane polarization and Ca²⁺, the substrate for the uniporter. Calcium is transported from the mitochondria to the cytosol by Na⁺/Ca²⁺ exchangers, with flux J_NaCa:

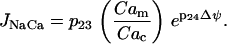(17)

This reflects the dependence of the exchangers on Ca²⁺ both within the mitochondria and within the cytosol. It also assumes that the mitochondrial Na⁺ concentration remains constant (balanced by Na⁺/K⁺ exchangers). The mitochondrial Ca²⁺ concentration then changes according to:

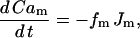(18)

where 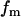is the fraction of Ca²⁺ that is free and .

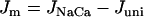The final differential equation for the mitochondrial dynamics describes the ADP concentration (in mM), ADP_m:

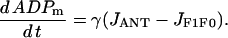(19)

This reflects the increase in ADP_m when ATP is transported out and ADP transported in by the translocator, and the decrease in ADP_m when ADP is phosphorylated by the ATP synthase.

Finally, we assume conservation of the adenine nucleotides:

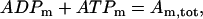(20)

where 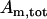is the total concentration. This conservation equation is used to determine the concentration of mitochondrial ATP.

The electrical/calcium model

Equations for this model are from Bertram and Sherman (46). Four ionic currents determine the plasma membrane potential. Calcium and delayed rectifier K⁺ currents, I_Ca and I_K, are responsible for action potentials, and both are gated by voltage (V). There is also a Ca²⁺-activated K⁺ current, I_K(Ca), which is activated by cytosolic Ca²⁺. Finally, there is an ATP-sensitive K⁺ current, I_K(ATP), which is activated by cytosolic ADP and inactivated by cytosolic ATP. Incorporating the membrane capacitance, C, the voltage is then described by the differential equations:

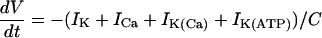(21)

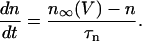(22)

The variable n is the activation variable for the delayed rectifying K⁺ channels. The ionic currents are 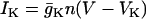, , 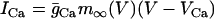, 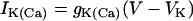and 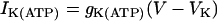, where 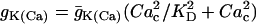, 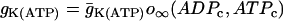. The steady-state function for n is 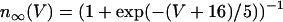. Activation of the Ca²⁺ current is assumed to be instantaneous, with equilibrium function 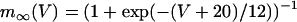. The K(ATP) conductance is also assumed to adjust instantaneously to changes in nucleotide levels, and is (13):

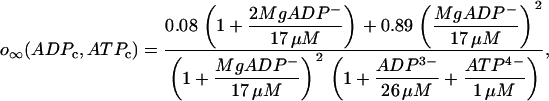(23)

where ADP_c and ATP_c are cytosolic concentrations. As discussed in Magnus and Keizer (13), the nucleotide concentrations are related to the concentrations of ADP_c and ATP_c by

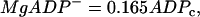(24)

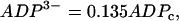(25)

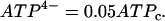(26)

The cytosolic ADP concentration (in μM), ADP_c, is given by:

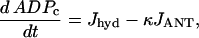(27)

where κ is the mitochondria/cytosol volume ratio. The term J_hyd represents cytosolic hydrolysis of ATP. Much of this hydrolysis has been shown to be due to Ca²⁺ pumps in the endoplasmic reticulum (SERCA) and the plasma membrane (45). We model both types of pumps as linear functions of Ca_c, so the hydrolysis rate is also linear in Ca_c. A basal level of hydrolysis, k_hyd,bas, is also included to account for other sources of hydrolysis:

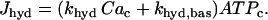(28)

The cytosolic adenine nucleotide concentration is assumed to be conserved:

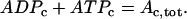(29)

The AMP concentration is fixed, while there is cycling of nucleotides between ADP and ATP due to hydrolysis and flux through the mitochondrial adenine translocator. Adenine nucleotide conservation is used to determine the cytosolic ATP concentration (in μM), ATP_c.

The cytosolic Ca²⁺ concentration is determined by the flux of Ca²⁺ across the plasma membrane, J_mem, the flux out of the endoplasmic reticulum, J_er, and the flux out of the mitochondria, J_m. The differential equation for the free cytosolic Ca²⁺ concentration is:

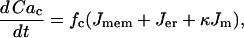(30)

where f_c is the fraction of free Ca²⁺ in the cytosol. The flux across the plasma membrane is 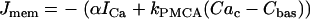, where α converts current to flux, 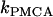is the plasma membrane pump rate, and 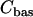is a constant basal Ca²⁺ parameter. Flux out of the mitochondria, 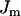, is scaled by the mitochondria/cytosol volume ratio, κ. Flux out of the ER is assumed to occur only through leakage (IP₃ receptors are not activated), 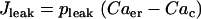. Flux into the ER from the cytosol is through SERCA pumps, 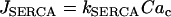. Thus, 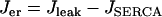and the differential equation for the Ca²⁺ concentration in the ER is:

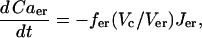(31)

where f_er is the fraction of free Ca²⁺ in the ER, and V_c, V_er are the volumes of the cytosolic and ER compartments, respectively. All parameter values for this model component are given in Table 3. Most parameter values are the same as those used in previous publications (17,40,46). The parameters 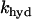, , 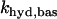κ, and 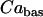are new to the model and have been set to produce reasonable nucleotide (54) and Ca²⁺ concentration (22) time courses.

TABLE 3.

Parameter values for the electrical/calcium compartment

C = 5300 fF	τn = 20 ms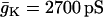
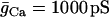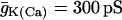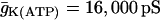		VK = −75 mV	VCa = 25 mV
KD = 0.5 μM	khyd = 5 × 10−5 ms−1μM−1	khyd,bas = 5 × 10−5 ms−1	κ = 0.07
Ac,tot = 2500 μM	AMPc = 500 μM	α = 4.5 × 10−6μM ms−1	kpmca = 0.1 ms−1
pleak = 2 × 10−4 ms−1	kSERCA = 0.4 ms−1	fc = fer = 0.01	Vc/Ver = 31
Cabas = 0.05 μM