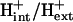Thermodynamics-Based Metabolic Flux Analysis

Abstract

A new form of metabolic flux analysis (MFA) called thermodynamics-based metabolic flux analysis (TMFA) is introduced with the capability of generating thermodynamically feasible flux and metabolite activity profiles on a genome scale. TMFA involves the use of a set of linear thermodynamic constraints in addition to the mass balance constraints typically used in MFA. TMFA produces flux distributions that do not contain any thermodynamically infeasible reactions or pathways, and it provides information about the free energy change of reactions and the range of metabolite activities in addition to reaction fluxes. TMFA is applied to study the thermodynamically feasible ranges for the fluxes and the Gibbs free energy change, Δ_rG′, of the reactions and the activities of the metabolites in the genome-scale metabolic model of Escherichia coli developed by Palsson and co-workers. In the TMFA of the genome scale model, the metabolite activities and reaction Δ_rG′ are able to achieve a wide range of values at optimal growth. The reaction dihydroorotase is identified as a possible thermodynamic bottleneck in E. coli metabolism with a Δ_rG′ constrained close to zero while numerous reactions are identified throughout metabolism for which Δ_rG′ is always highly negative regardless of metabolite concentrations. As it has been proposed previously, these reactions with exclusively negative Δ_rG′ might be candidates for cell regulation, and we find that a significant number of these reactions appear to be the first steps in the linear portion of numerous biosynthesis pathways. The thermodynamically feasible ranges for the concentration ratios ATP/ADP, NAD(P)/NAD(P)H, and 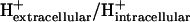are also determined and found to encompass the values observed experimentally in every case. Further, we find that the NAD/NADH and NADP/NADPH ratios maintained in the cell are close to the minimum feasible ratio and maximum feasible ratio, respectively.

INTRODUCTION

Thermodynamics have been applied to many areas of analysis of biological systems (1–5), but thermodynamics have yet to be applied to a rigorous examination of entire metabolic networks. This has been primarily due to a scarcity of thermodynamic data on metabolic reactions, a lack of rigorous models of metabolic chemistry, and the absence of any extensive databases, which bring all of this information together. However, the availability of thermodynamic data has increased over time, and group contribution methodologies for estimating thermodynamic properties have also been introduced (6–9). Furthermore, several rigorous models of the metabolic chemistry of a variety of microorganisms have been developed including some genome-scale models (10–13). Recently, the application of thermodynamics to study the feasibility of metabolic pathways has been revisited. Beard, Qian, and co-workers have conducted studies on the topic of eliminating internal flux cycles from flux balance analysis solutions (14–16). These are sets of reactions such as A→B→C→A. According to the first law of thermodynamics, the overall thermodynamic driving force through these cycles must be zero, meaning that no net flux is possible through these cycles. Beard and Qian have also used nonlinear thermodynamic and enzyme activity constraints to determine the concentration profiles of metabolites in the central carbon chemistry of a hepatocyte cell (17). Maskow and Stockar used the pathway analysis method of Mavrovouniotis (18,19) to study the thermodynamic feasibility of the lactic acid fermentation pathway, and they found that without careful consideration of ionic strength of solution, uncertainty in thermodynamic data, and cell pH, feasible pathways can be falsely labeled as infeasible or vice versa (20). However, these previous studies were performed on relatively small-scale pathways due to a lack of thermodynamic data for genome-scale models and utilized nonlinear optimization criteria to determine fixed values for the activities of the metabolites under an isolated set of conditions.

In a previous article, we utilized the group contribution method (7,8) to estimate the standard Gibbs free energy change, Δ_rG′°, of the reactions in a genome-scale model of Escherichia coli, and we used these estimates to assess the thermodynamic feasibility of the reactions in the model (21). We called this model iHJ873, which is based on the iJR904 model developed by Palsson and co-workers. The iHJ873 model was derived from the iJR904 model by removing all of the reactions in the iJR904 model that contain compounds for which the standard Gibbs free energy change of formation, Δ_fG′°, could not be estimated and replacing these reactions with lumped reactions. The iHJ873 model contains fewer reactions than the iJR904 model (873 vs. 931, respectively), but Δ_rG′° of every reaction in the iHJ873 can be estimated. The thermodynamic studies of the iHJ873 model focused on the individual reactions in the model that were found to have a large positive Δ_rG′° in the direction of flux. We simulated the impact of removing these unfavorable reactions on the growth of the cell, and we considered the biological implications that these particular reactions were thermodynamically unfavorable. In this article, we take this work a significant step forward by examining the metabolite concentrations required for every reaction essential for optimal growth to be simultaneously thermodynamically feasible. We propose a new methodology that we call thermodynamics-based metabolic flux analysis (TMFA) for integrating thermodynamic data and constraints into a constraints-based metabolic model to ensure that flux distributions produced by the model are thermodynamically feasible and to provide data on the thermodynamically feasible metabolite activity ranges for the metabolites in the cell. TMFA can also be used for the analysis of unmodified models that are lacking some thermodynamic data to allow for direct analysis of models such as iJR904 without first creating lumped models like the iHJ873. We apply TMFA to analyze the iJR904 model using new thermodynamic data estimated from an updated and expanded implementation of the group contribution method (M. D. Jankowski, C. S. Henry, L. J. Broadbelt and V. Hatzimanikatis, unpublished); we assess the sensitivity of TMFA to changes in Δ_rG′° due to uncertainty and ionic strength; and we examine the thermodynamically feasible ranges for biologically important concentrations ratios such as ATP/ADP, NAD(P)/NAD(P)H, and 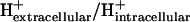. Finally, we utilize the Δ_rG′ ranges calculated for the iJR904 reactions with TMFA to identify candidate reactions for cell regulation as it has been previously proposed (2).

METHODS

Metabolic flux analysis (MFA)

TMFA uses at its core the mass balance constraints of metabolic flux analysis (MFA) (13,23–25). MFA defines the limits on the metabolic capabilities of a model organism under steady-state flux conditions by constraining the net production rate of every metabolite in the system to zero as

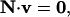(1)

where N is an m × r matrix of the stoichiometric coefficients for the r reactions and m metabolites in the model, and v is an r × 1 vector of the steady-state fluxes through the r reactions in the model. MFA is combined with optimization to determine the limits on the ability of the cell to produce biochemicals such as ethanol (26,27), to predict the maximum possible growth yields of the cell (28–30), and to predict the responses to gene knockouts and additions (31,32).

The introduction of thermodynamics-based constraints in MFA will enforce the exclusion of thermodynamical infeasibilities from flux distribution solutions. One example of these infeasibilities would be flux distributions involving flux through the thermodynamically infeasible internal flux loops mentioned earlier. In addition, these constraints will allow the quantification of the ranges in the gradients of metabolite activities required to drive reactions in the direction of flux reported in all calculated flux distributions. Knowledge of the permissible ranges of metabolite activities is essential for the development of kinetic models of metabolism and metabolic control analysis (33–38).

Estimation of Δ_rG′° of reactions in the iJR904 metabolic model

Formulation of the thermodynamic constraints in TMFA requires knowledge of Δ_rG′° of the reactions in the model, and it must either be estimated or measured experimentally. Experimental data is available for only a small fraction of the reactions involved in a genome-scale metabolic model such as iJR904. Fortunately, the group contribution method provides a means of estimating Δ_rG′° of nearly every reaction (7,8). In a previous article (21), the group contribution method was used to estimate Δ_rG′° of 808 of the 931 reactions in the iJR904 model. Recent improvement and expansion of the group contribution method (M. D. Jankowski, C. S. Henry, L. J. Broadbelt and V. Hatzimanikatis, unpublished) based on a refitting of the group contribution values using the thermodynamic data gathered in the NIST Standard Reference Database (39) and other literature (40–42) have allowed the estimation of Δ_fG′° for 576 (92%) of the compounds and Δ_rG′° for 891 (96%) of the reactions in the iJR904 model. In addition, we have been able to quantify the ranges of uncertainty in the estimated energy values due to variances in experimental measurements and the fitting method. All new estimated thermodynamic data for the iJR904 model are provided in the Supplementary Material.

In contrast, experimental Δ_rG′° measurements taken within 10 K and one pH unit of the standard conditions of 298 K and a pH of 7 exist for only 52 (5.6%) of the 931 reactions in iJR904. The estimated Δ_rG′°, 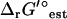, for these 52 reactions agree well with the measured Δ_rG′° (Fig. 1). Literature values exist for Δ_fG′° of 68 (11%) of the compounds in iJR904, and the Δ_fG′° values from the literature are nearly identical to the estimated Δ_fG′° (Fig. 2). In all but three cases, the measured Δ_rG′° values fall within the uncertainty of the estimated Δ_rG′°. All of the experimental Δ_rG′° and Δ_fG′° data shown in Figs. 1 and 2 were part of the dataset to which the group contribution energies were fit using multiple-linear regression (M. D. Jankowski, C. S. Henry, L. J. Broadbelt and V. Hatzimanikatis, unpublished).

FIGURE 1.

Comparison of estimated Δ_rG′° to experimentally measured Δ_rG′°. Estimated Δ_rG′° values (solid diamonds) are shown and compared to experimentally measured Δ_rG′° values (shaded squares) for every reaction in the iJR904 model for which data exists in the NIST database (39) within the temperature and pH limitations (288–308 K and pH of 6–8). In some cases, multiple data points existed in the NIST database at the suitable conditions. In these cases, the average Δ_rG′° is shown along with the standard deviation in the data (shaded error bars). The uncertainty in the estimated Δ_rG′° (solid error bars) calculated from the group contribution method (22) is also shown verifying that all but three of the measured Δ_rG′° fall within the range of uncertainty of the estimated Δ_rG′°.

FIGURE 2.

Comparison of estimated Δ_fG′° to Δ_fG′° available in the literature. Estimated Δ_fG′° values (solid diamonds) are shown and compared to literature values of Δ_fG′° (shaded squares) for every compound in the iJR904 model for which literature data was found (40–42). The uncertainty in the estimated Δ_fG′° (solid error bars) calculated from the group contribution method (22) are also shown verifying that all but one of the literature Δ_fG′° values fall within the range of uncertainty of the estimated Δ_fG′°.

In our previous article (21), all of the reactions in iJR904 for which the value Δ_rG′° could not be estimated were lumped to produce a set of net reactions for which the value Δ_rG′° could be estimated. We then removed the reactions with unknown Δ_rG′° and replaced them with the net reactions to produce the iHJ873 model. In the work presented here, although we still lump together the 40 reactions for which Δ_rG′° cannot be estimated, we do not remove these 40 reactions from the model stoichiometry. Instead, these reactions are treated in the manner discussed in the formulation of the thermodynamic constraints in TMFA described in a following section.

Adjustment of Δ_rG′° for ionic strength

All TMFA studies performed in this article are in terms of metabolite activities instead of concentrations, making the results of these studies independent of ionic strength. However, ionic strength will have an effect on the Δ_rG′° value of the reactions, and the zero ionic strength reference state upon which the estimated Δ_rG′° values are based differs significantly from the ionic strength of the cytosol in which these reactions take place, between 0.15 and 0.20 M (20). We explore the sensitivity of Δ_rG′° of the reactions in the genome-scale model to ionic strength using the extended Debye-Hückel equation (43,44),

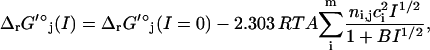(2)

where I is the ionic strength of the solution, c_i is the charge of species i, and A and B are parameters of the extended Debye-Hückel equation with universally applicable values of 0.5093 mol^1/2/L^1/2 and 1.6 mol^1/2/L^1/2, respectively (45). The charge used for each metabolite in the ionic strength studies performed is the charge of the predominant ionic form of each metabolite at pH 7 determined using pK_a estimation software (MarvinBeans pKa estimation plug-in, Ver. 4.0.3, ChemAxon, Budapest, Hungary). This dramatically simplifies the calculation, although it might result in less accuracy.

Calculation of Δ_rG′_i for reactions involving transmembrane ion transport

As discussed in a previous article (21), the standard conditions of pH 7 solution and zero ionic strength upon which all values are based is applied to both the extracellular and intracellular environment when calculating 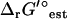for reactions involving the transport of metabolites across the cellular membrane. As a result, 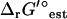for these reactions is based on the assumption that the electrochemical potential, Δψ, and the pH gradient, ΔpH (pH_{intracellular} − pH_{extracellular}), across the cell membrane is zero. For example, the ATP synthase reaction in E. coli is typically written in as

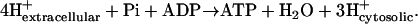(3)

The 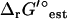calculated from the group contribution method only applies to the portion of this reaction that takes place inside the cell, ,

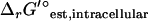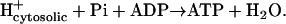(4)

The energy contribution of the transmembrane transport portion of the ATP synthase reaction, Δ_rG′_transport,

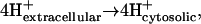(5)

is the sum of the driving force of ΔpH across the membrane for the transport of H⁺ into the cell, Δ_ΔpHG, and the energy associated with the transport of an ion across the membrane, Δ_ΔψG_est,

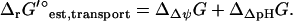(6)

The overall 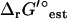of a reaction energetically coupled to the transport of an ion across the cell membrane such as ATP synthase is

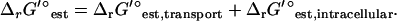(7)

Under physiological conditions Δψ, and 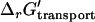depend on ΔpH. Δ_ΔψG_est depends upon 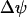, which in turn depends on ΔpH according to the equations (47)

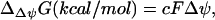(8)

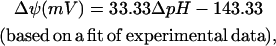(9)

where c is the net charge transported from outside the cell into the cell, and F is the Faraday constant in kcal/mV mol. Δ_ΔpHG depends only on ΔpH according to the equation (47)

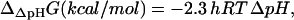(10)

where h is the number of protons transported across the membrane. While 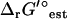used in the TMFA constraints for every reaction involving the transport of ions across the cell membrane will involve a Δ_rG′_transport term according to Eq. 7, the nature of the Δ_rG′_transport term depends on the ion being transported. If protons are transported across the cell membrane as in ATP synthase, Δ_rG′_transport will involve a contribution from both Δ_ΔpHG and Δ_ΔψG_est according to Eq. 6. If any other ions are being transported across the membrane, Δ_rG′_transport is equal to Δ_ΔψG_est.

Thermodynamics-based metabolic flux analysis (TMFA)

To produce flux distributions that are free of thermodynamic infeasibilities and to allow the exploration of feasible metabolite activities and reaction driving force, TMFA augments the mass balance constraints of MFA with additional thermodynamic constraints. Linear thermodynamics-based constraints have already been proposed and utilized with MFA to eliminate thermodynamically infeasible flux loops (14–16), and nonlinear constraints have been proposed to eliminate flux distributions that utilize reactions that cannot be thermodynamically feasible under physiological conditions (17). However, these constraints and methods have never been applied on a genome scale, and the nonlinear constraints make application to large-scale systems computationally challenging. In the proposed TMFA, the following mixed integer linear constraints are used to produce flux distributions free of any thermodynamic infeasibilities and provide data on feasible metabolite activity profiles and Δ_rG′,

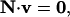(11)

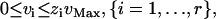(12)

(13)

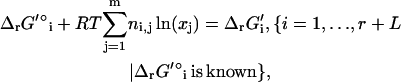(14)

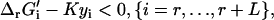(15)

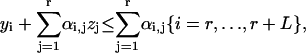(16)

where N is the m × r stoichiometric matrix, v is the r × 1 flux vector, r is equal to the total number of reactions in N, and m is equal to the total number of metabolites. The value r is larger than the number of reactions in any model being used because each of the reversible reactions in the model must be split into separate irreversible forward and backward component reactions during the formation of N. This separation is performed so that the flux through each reaction i can be constrained to be greater than or equal to zero. A binary use variable, z_i, is also associated with each reaction i specified in the stoichiometric matrix N. The value of z_i is equal to one if the flux through reaction i, v_i, is positive, and z_i is equal to zero if v_i is zero. This condition is enforced by the constraint described in Eq. 12. The v_Max in Eq. 12 is the upper limit on the flux through any reaction typically set to a physiologically reasonable value such as 100 mmol/gm DW/h. Equations 11 and 12 represent the mass balance constraints carried over from MFA with the only difference being the separation of reversible reactions into forward and backward component reactions.

The new thermodynamic constraints of TMFA begin with Eq. 13, which ensures that the activity profiles and flux distributions generated by TMFA adhere to the second law of thermodynamics; a reaction flux cannot be positive unless Δ_rG′_i is negative. The K in Eq. 13 is a constant selected to be large enough that Eq. 13 is always satisfied if v_i and z_i are zero. The terms involving K in Eq. 13 ensure that the constraint is only applied to reactions with a non-zero flux. Equation 14 is the Gibbs free energy equation used to set the value of Δ_rG′_i for reaction i given the metabolite activities. In Eq. 14, ln(x_j) is the natural logarithm of the activity of compound j, and n_i,j is the stoichiometric coefficient of compound j in reaction i. In Eq. 14, the energy contribution for any transport of ions across the cell membrane is accounted for in the Δ_rG′° term as described in Eq. 7.

As Δ_rG′° of a reaction must be known to formulate the thermodynamic constraints for a reaction, the constraints described by Eqs. 13 and 14 are not applied to the reactions in the model with unknown Δ_rG′°. Instead, these reactions are lumped into overall reactions with known Δ_rG′°, and special thermodynamic constraints are applied to the reactions for which Δ_rG′° is unknown; these constraints are described by Eqs. 14–16. In these equations, L is the number of lumped reactions, and α_i,j is a coefficient equaling one if reaction j is one of the original reactions with unknown Δ_rG′° that makes up the lumped reaction i. When Eq. 14 is applied to a lumped reaction, it sets the value for Δ_rG′_i of the lumped reaction. Equation 15 is the thermodynamic feasibility constraint for the lumped reactions similar to Eq. 13 except that the binary use variable for each lumped reaction, y_i, is set to zero when the reaction is thermodynamically feasible and one when the reaction is infeasible. Equation 16 excludes flux distributions that involve flux through the set of reactions that comprise an infeasible lumped reaction. The continuous independent variables of this optimization problem are ln(x_j), v_i, and Δ_rG′_i, and the binary independent variables are z_i, and y_i.

In the TMFA of the iJR904 model, the 40 reactions with unknown 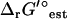are lumped into 20 reactions with known 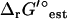. An additional two internal flux loops were found within the stoichiometry of the reactions with unknown 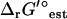. Being internal flux loops, the Δ_rG′ of these reactions is constrained to zero, i.e., Eqs. 15 and 16 constrain the flux through these loops to zero. All 20 lumped net reactions and the two internal flux loop reactions are listed in the Supplementary Material.

TMFA with uncertainty in thermodynamic data

The values of Δ_rG′° used in the thermodynamic constraints of TMFA can be based on either group contribution estimates or experimental observations, and they are subject to some uncertainty due to the error allowed when fitting group contribution energy values or in measuring Δ_rG′° experimentally. The TMFA must account for this uncertainty to avoid overconstraining the ranges of possible values for metabolite activities and reaction Δ_rG′ due to inaccurate Δ_rG′° values. This uncertainty can be accounted for by allowing the Δ_rG′° values used in the TMFA constraints to vary within the range of the uncertainty.

For example, when the Δ_rG′° values used in TMFA are estimated using the group contribution method, the potential variance in 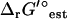due to uncertainty is captured by allowing the energy contributions of the molecular substructures used in the group contribution method to vary. The error in the energy contribution of molecular substructure i, E_g,i, is introduced as a new variable in the TMFA formulation, and E_g,i is allowed to vary within two standard errors, σ, reported for the group contribution energies in the new group contribution scheme (M. D. Jankowski, C. S. Henry, L. J. Broadbelt and V. Hatzimanikatis, unpublished),

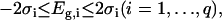(17)

where q is the number of molecular substructures used in the group contribution scheme, and σ_i is the standard error reported for the group contribution value of molecular substructure i. The thermodynamic constraint specified in Eq. 14 is now altered to include terms accounting for the uncertainty in ,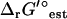

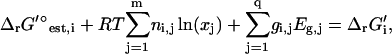(18)

where g_i,j is the number of occurrences of molecular substructure j being created or destroyed during reaction i.

RESULTS

Optimization of aerobic growth on glucose using TMFA

We applied TMFA to determine the maximum growth yield achievable in the iJR904 genome-scale model. In our TMFA analysis, we chose to study aerobic growth on glucose as a carbon source. The concentrations of the extracellular compounds used as nutrient sources in the model were fixed to the typical concentrations found in growth media (48). These concentrations are listed in Table 1. The concentrations of all intracellular species were restricted within the ranges observed in the cell (between 10⁻⁵ M and 0.02 M) (49) with the following exceptions. The concentration of H⁺ in the cell was held constant at 10⁻⁷ M, or a pH of 7. Because the oxygen concentration selected for the media is 8.2 × 10⁻⁶ M (Table 1) and the oxygen concentration in the cell cannot exceed the concentration in the media, the bounds on the oxygen concentration in the cell were set from 10⁻⁷ M to 8.2 × 10⁻⁶ M. The extracellular pH was allowed to vary between a pH of 4 and 11 to allow for exploration of the thermodynamically feasible extracellular pH ranges for E. coli. Specifics on metabolite uptake and secretion constraints used in the analysis are listed in the Appendix.

TABLE 1.

Concentrations of nutrients in media

Molecules	Concentration
Phosphate	0.056 M
Sulfate	0.0030 M
Ammonium	0.019 M
Sodium	0.16 M
Potassium	0.022 M
Fe2+	0.062 M
CO2	0.00010 M
Oxygen	8.2 × 10−6 M
Glucose	0.020 M
	pH 4–11

Initially, uncertainty was not accounted for and σ_i in Eq. 17 was set to zero. With zero uncertainty, the maximum growth yield determined from TMFA was zero, suggesting that growth was not feasible due to the thermodynamic infeasibility of one or more essential reactions. Under these conditions, the reaction dihydroorotase,

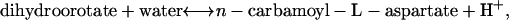(19)

which must operate in the reverse direction for any biomass production to occur, is thermodynamically infeasible with a 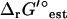of 4.7 kcal/mol in the reverse direction. Because E. coli is capable of growing on glucose, this reaction must be thermodynamically feasible under physiological conditions. One possible way to overcome the infeasibility of this reaction is to allow for a wider range of values for the activities of the reactants and the products in this reaction. While the activities of water and H⁺ are both lumped into Δ_rG′° and thereby fixed, expanding the minimum and maximum bounds on the activities of dihydroorotate and n-carbamoyl-L-aspartate to 0.8 × 10⁻⁵ M and 0.025 M, respectively, allows sufficient driving force to exist for dihydroorotase to be thermodynamically feasible. Performing TMFA on the model with the bounds on the activities of dihydroorotate and n-carbamoyl-L-aspartate set to these expanded values results in an optimal growth yield of 0.0923 g biomass/mmol glucose. This is the same optimal growth yield observed for the iJR904 model using mass balance constraints alone (50). Under these conditions, only dihydroorotase is sensitive to the thermodynamic constraints; there are no other active thermodynamic bounds.

However, another potential explanation for the infeasibility of dihydroorotase is inaccuracy in 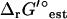, the estimated values of Δ_rG′°. Allowing the error in the group contribution values to vary within the range of two standard deviations for the group contribution energies, the optimal growth yield for the iJR904 model is achievable within the original selected activity range of 1 × 10⁻⁵ M and 0.02 M. While experimental evidence does verify that dihydroorotase is a thermodynamically unfavorable reaction, the experimentally observed Δ_rG′° is 1.4 kcal/mol, or 3.3 kcal/mol 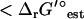. This deviation is within the range of two standard deviations for 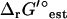of dihydroorotase, which is 4.7 ± 4.6 kcal/mol. These results suggest the importance of accounting for uncertainty in 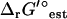, since ignoring uncertainty can lead to feasible reactions being incorrectly labeled as infeasible. Although dihydroorotase can be thermodynamically feasible in the direction required for growth at the experimentally observed Δ_rG′° of 1.4 kcal/mol, this reaction is still less favorable than 91% of the reactions in the iJR904 model. Interestingly, while dihydroorotase is not part of a multienzyme complex in E. coli (51), dihydroorotase is a part of a multienzyme complex in mammalian cells (52) indicating that mammalian cells could be utilizing substrate channeling as a means of overcoming the unfavorable Δ_rG′° of this reaction without the use of large concentration gradients.

Essential, substitutable, and blocked reactions

Under optimal growth conditions, reactions in E. coli may be classified as essential (requiring a non-zero flux for optimal growth to occur), substitutable (capable of carrying zero or non-zero flux at optimal growth), or blocked (do not carry any flux at optimal growth). Flux variability analysis (FVA) (53) was used to classify the reactions involved in the maximum production of biomass from glucose in E. coli. In FVA, the flux of each reaction in the stoichiometric matrix is individually minimized and maximized subject to the mass balance constraints on the metabolites (Eq. 11) and the growth conditions being analyzed (optimal aerobic growth on glucose). When the reversible reactions are expressed as separate forward and backward component reactions, reactions with a positive minimum flux are essential; reactions with a minimum and maximum flux of zero are blocked; and reactions with a zero minimum flux and positive maximum flux are substitutable. When maximizing growth in the iJR904 model using only mass balance constraints, 272 (29%) reactions are essential, 83 (9%) reactions are substitutable, and 576 (62%) reactions are blocked. When maximizing growth in the iJR904 model using mass balance and thermodynamic constraints, 272 (29%) reactions are essential, 53 (6%) reactions are substitutable, and 606 (65%) reactions are blocked. The addition of thermodynamic constraints causes 30 of the reactions that were classified as substitutable using FVA alone to become blocked. These reactions are all part of thermodynamically infeasible flux loops in the iJR904 model, demonstrating the effectiveness of the thermodynamic constraints in restricting the net flux through these loops to zero while still allowing flux through the individual reactions involved in the loops. Overall, every reaction involved in aerobic growth of E. coli on glucose that is not participating in an internal flux loop is indeed thermodynamically feasible under the activity conditions studied. These results hold true whether or not uncertainty in 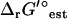is accounted for as long as the expanded bounds on the activities of dihydroorotate and n-carbamoyl-L-aspartate are used.

Sensitivity of TMFA to the ionic strength reference state

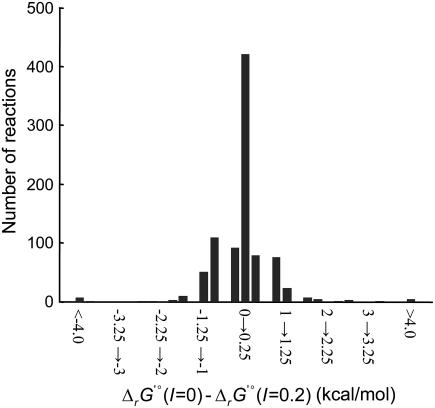
A reference state of zero ionic strength is not an accurate representation of the intracellular environment in E. coli, as the ionic strength of the cytosol in E. coli is known to range between 0.15 and 0.20 M (20). To determine the effect of the high intracellular ionic strength on 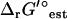, we utilized Eq. 2 to adjust the reference ionic strength of 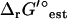for all of the reactions in the iJR904 model to a new reference state of 0.2 M. The effect of ionic strength on 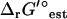was found to be very small for most reactions. For 95% of the reactions in iJR904, the difference between 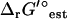(I = 0) and 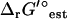(I = 0.2 M) is <1 kcal/mol (Fig. 3). There are six exceptional reactions in the iJR904 model for which 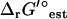(I = 0.2 M) is >10 kcal/mol 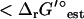(I = 0). However, these six reactions also have 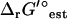(I = 0) values that are all <−80 kcal/mol, and these reactions are all large lumped reactions involved in membrane lipid metabolism.

FIGURE 3.

Effect of ionic strength on Δ_rG′°. A histogram of the differences between Δ_rG′° at an ionic strength of zero (Δ_rG′° (I = 0)) and Δ_rG′° at an ionic strength of 0.2 M (Δ_rG′° (I = 0.2 M)) for all of the reactions in the iJR904 model. The bin sizes in the histogram are all 0.25 kcal/mol. Greater than 95% of the differences are within 1 kcal/mol of zero.

In the case of thermodynamic bottleneck reactions such as dihydroorotase, even the small change to 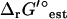that results from the adjustment for ionic strength is sufficient to make a reaction become infeasible. For dihydroorotase, 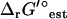(I = 0.2 M) is 0.73 kcal/mol higher than 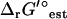(I = 0). While this is sufficient to make this reaction infeasible under the concentration ranges studied when the uncertainty is set to zero, this is not sufficient to make this reaction infeasible when the uncertainty is accounted for. Overall, the variation in 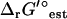due to the ionic strength of solution falls well within the uncertainty in .

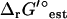Thermodynamic variability analysis (TVA): ranges of the Gibbs free energy

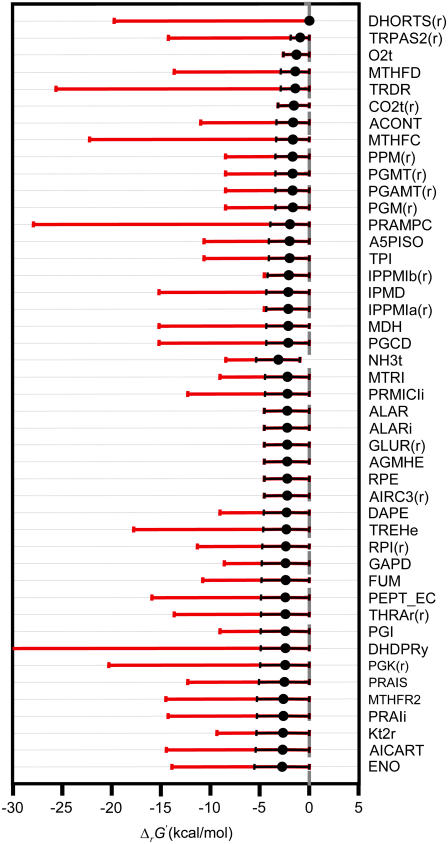
The permissible ranges of the new system variables of metabolite activity and Δ_rG′ introduced in TMFA can be explored using linear optimization in a methodology we call thermodynamic variability analysis (TVA), which is analogous to FVA. In TVA, the activity of each metabolite and Δ_rG′ of each reaction are minimized and maximized subject to the thermodynamic and mass balance constraints. TVA allows for the identification of the thermodynamic bottlenecks in the metabolic network. Thermodynamic bottlenecks are reactions for which Δ_rG′ is constrained to be approximately zero, meaning these reactions must operate very close to equilibrium. Any small decrease in the concentrations of the reactants or increase in the concentrations of the products in these reactions is sufficient to force the flux to zero (18,19).

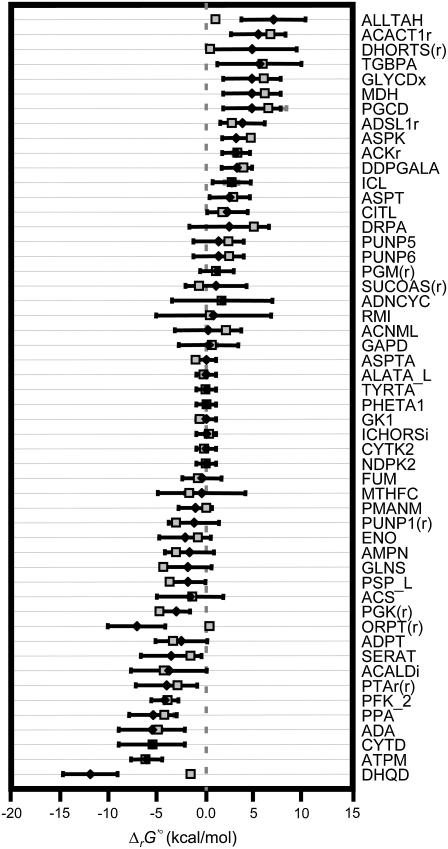
We first studied the system in the absence of uncertainty, i.e., TVA was performed with the uncertainty set to zero while using the expanded bounds on the dihydroorotase reactants and the default bounds on the remaining metabolite activities (black error bars in Fig. 4). Under these conditions, the Δ_rG′ values of the reactions are constrained by the ranges of the values of the metabolite activities that allow every reaction required for optimal growth to be simultaneously thermodynamically feasible (Fig. 5 and Table 2). Only one reaction, dihydroorotase, has a Δ_rG′ that is constrained to near zero, indicating that this reaction is the only thermodynamic bottleneck under these conditions.

FIGURE 4.

Ranges for Δ_rG′ of required and substitutable reactions. The thermodynamically feasible ranges for Δ_rG′ of the 45 essential and substitutable reactions with the narrowest feasible Δ_rG′ range. The ranges are the widest when the uncertainty in Δ_rG′° is accounted for by allowing the group contribution energy values to vary within their standard errors (red error bars). If the uncertainty is assumed to be zero, the feasible ranges for Δ_rG′ decrease significantly (black error bars), and Δ_rG′ of the reaction dihydroorotase becomes constrained to near zero. When the two error bars do not overlap completely, the larger error bar always corresponds to the range calculated, accounting for uncertainty.

FIGURE 5.

Thermodynamically feasible activity ranges. The thermodynamically feasible metabolite activity ranges are shown for all of the compounds with a feasible range that is less than the bounds placed on the metabolite activities (0.01–20 mM with the exception of the compounds listed in Table 1, n-carbamoyl-L-aspartate and dihydroorotate). When the uncertainty in the estimated Δ_rG′° values is assumed to be zero, the metabolite activities are the most tightly constrained (black error bars). Tightly constrained metabolites include the main reactant and product of the bottleneck reaction dihydroorotase, n-carbamoyl-L-aspartate (cbasp) and dihydroorotate (dhor), respectively. When the uncertainty in the estimated Δ_rG′° values is accounted for, the feasible activity ranges increase significantly (red error bars). When the two error bars do not overlap completely, the larger error bar always corresponds to the range calculated, accounting for uncertainty.

TABLE 2.

Most thermodynamically constrained reactions

Abbreviation	Reaction name
DHORTS(r)	Dihydroorotase (reverse)
TRPAS2(r)	Tryptophanase (reverse)
O2t	O2 transport via diffusion
MTHFD	Methylenetetrahydrofolate dehydrogenase
TRDR	Thioredoxin reductase
CO2t(r)	CO2 transport via diffusion (reverse)
ACONT	Aconitase
MTHFC	Methenyltetrahydrofolate cyclohydrolase
PPM(r)	Phosphopentomutase (reverse)
PGMT(r)	Phosphoglucomutase (reverse)
PGAMT(r)	Phosphoglucosamine mutase (reverse)
PGM(r)	Phosphoglycerate mutase (reverse)
PRAMPC	Phosphoribosyl-AMP cyclohydrolase
A5PISO	Arabinose-5-phosphate isomerase
TPI	Triose-phosphate isomerase
IPPMIb(r)	2-isopropylmalate hydratase (reverse)
IPMD	3-isopropylmalate dehydrogenase
IPPMIa(r)	3-isopropylmalate dehydratase (reverse)
MDH	Malate dehydrogenase
PGCD	Phosphoglycerate dehydrogenase
NH3t	Ammonia reversible transport
MTRI	5-methylthioribose-1-phosphate isomerase
PRMICIi	Phosphoribosyl imidazolecarboxamide isomerase
ALARi	Alanine racemase
GLUR(r)	Glutamate racemase (reverse)
AGMHE	ADP-glycero-manno-heptose epimerase
RPE	Ribulose 5-phosphate 3-epimerase
AIRC3(r)	Phosphoribosylaminoimidazole carboxylase (reverse)
DAPE	Diaminopimelate epimerase
RPI(r)	Ribose-5-phosphate isomerase (reverse)
GAPD	Glyceraldehyde-3-phosphate dehydrogenase
FUM	Fumarase
PEPT_EC	Ethanolamine phosphotransferase
THRAr(r)	Threonine aldolase (reverse)
PGI	Glucose-6-phosphate isomerase
DHDPRy	Dihydrodipicolinate reductase
PGK(r)	Phosphoglycerate kinase (reverse)
PRAIS	Phosphoribosylaminoimidazole synthase
MTHFR2	5,10-methylenetetrahydrofolate reductase
PRAIi	Phosphoribosylanthranilate isomerase
AICART	Phosphoribosylaminoimidazolecarboxamide formyltransferase
S7PI	Sedoheptulose 7-phosphate isomerase
HCO3E	HCO3 equilibration reaction
FBA	Fructose-bisphosphate aldolase
ENO	Enolase

We next performed TVA with the uncertainty in Δ_rG′° accounted for by allowing the error in the group contribution energies to vary according to Eq. 17. The expanded bounds on activities of the metabolites in the dihydroorotase reaction were also used to keep the conditions consistent with the TVA study conducted with uncertainty set to zero and allow for comparison of the results. Due to the relatively large uncertainty ranges in Δ_rG′°, all of the reactions can achieve a wide range of Δ_rG′ values, and none of the Δ_rG′ values are constrained near zero, indicating that no reactions behave as thermodynamic bottlenecks under these conditions (red error bars in Fig. 4).

Thermodynamic variability analysis (TVA): ranges of metabolite activity

TVA was also used to study the ranges of the activities of the metabolites. When TVA was performed with the uncertainty in 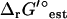set to zero, the activities of the metabolites involved in the bottleneck reaction dihydroorotase were highly constrained (black error bars in Fig. 5). The activity of the primary product of the reaction, dihydroorotate, is fixed at the minimum concentration while the primary reactant, n-carbamoyl-L-aspartate, is fixed at the maximum concentration. When the uncertainty in 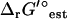is accounted for, concentrations of most compounds are nearly unconstrained (red error bars in Fig. 5). One important exception is oxygen. As mentioned earlier, the intracellular oxygen concentration is always fixed to the very low concentration range of <10⁻⁵ M because the intracellular oxygen concentration must be lower than the extracellular concentration for diffusion into the cell to occur. Interestingly, this limitation does not have a large effect on the cell as only two essential reactions require oxygen as a reactant, cytochrome oxidase bo3 and 2,3-diketo-5-methylthio-1-phosphopentane degradation, and these reactions have very negative 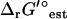values of −36.8 and −124 kcal/mol, respectively, ensuring thermodynamic favorability despite small reactant concentration.

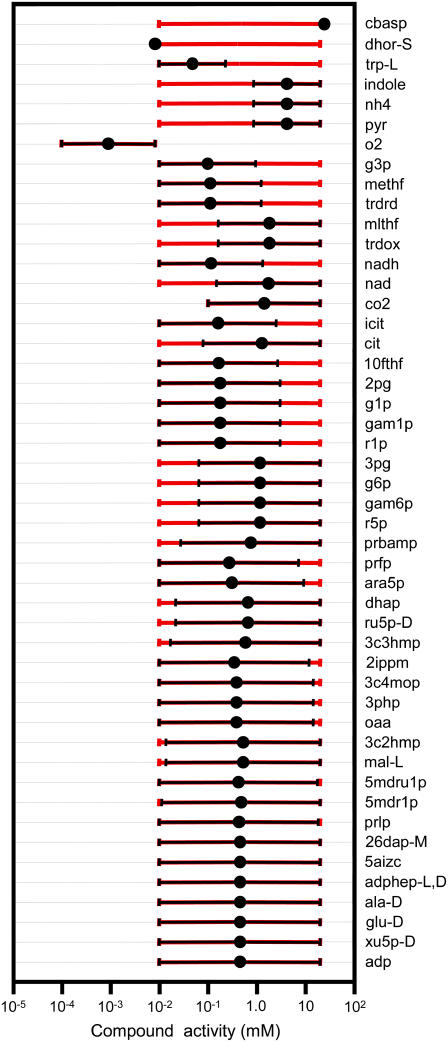
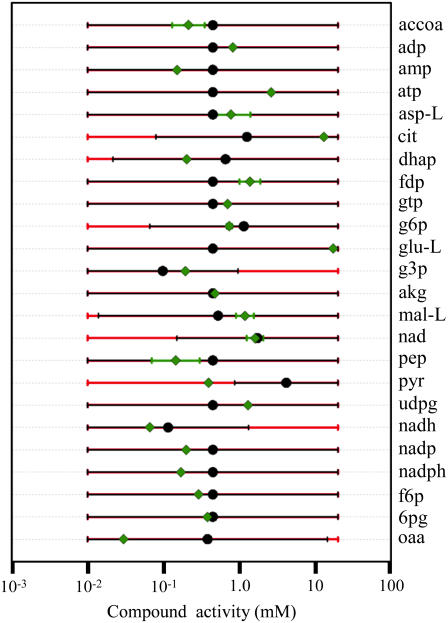
Experimentally measured metabolite concentrations are available from a variety of literature sources (49,54,55) for 24 (3.8%) of the metabolites in iJR904. These concentrations are compared with the thermodynamically feasible activity ranges determined from TMFA (Fig. 6), and for all but one metabolite (pyruvate) the experimentally measured concentration data falls within the thermodynamically feasible activity range when uncertainty in 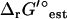is set to zero. Pyruvate falls within the thermodynamically feasible activity range when 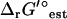is allowed to vary within the uncertainty. Surprisingly, the measured metabolite concentrations fall near the logarithmic mean (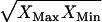) of the minimum and maximum feasible activities determined from TMFA with zero uncertainty for a significant number of important metabolites. In particular, 6pg, f6p, NADH, NAD⁺, akg, g3p, g6p, GTP, asp, and ADP all fall on or near the logarithmic mean of the minimum and maximum feasible activities. This is of particular significance because the concentrations of the metabolites NADH, NAD, and ADP are all under strict regulatory control. One purpose for maintaining the concentrations of these metabolites near the center of the thermodynamically feasible range could be to maximize flexibility. The activity of these metabolites can deviate significantly from the intrinsic value before any of the reactions in which the metabolites are involved become infeasible.

FIGURE 6.

Comparison to metabolic concentrations reported in the literature. Experimentally measured concentration ranges (green diamonds and green error bars) reported in the literature (49,54,55) are shown along with the thermodynamically feasible activity ranges for the same metabolites found using TMFA with no uncertainty (black circles and error bars). The black circles show the logarithmic mean for the feasible activity range (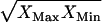). The feasible activity ranges for the metabolites found using TMFA accounting for uncertainty in estimated Δ_rG′° values are also shown (red error bars). When the two error bars do not overlap completely, the larger error bar always corresponds to the range calculated, accounting for uncertainty.

Predicting candidate reactions for regulation based on thermodynamics

As it has been recently proposed (2), the magnitude of Δ_rG′ of a reaction has some implications for the possibility that this reaction is subject to regulation. It has been proposed that reactions with a Δ_rG′ that is close to zero (the reactions we refer to as thermodynamic bottlenecks) have only limited potential for regulation as these reactions are very sensitive to minor perturbations in the concentrations of their reactants. In contrast, reactions with a highly-negative Δ_rG′ have the thermodynamic potential to serve as regulatory control points for the pathways in which they participate because enzyme regulation will be the dominant mechanism for control of the flux through these reactions. The Δ_rG′ range data generated by TVA can be used with this proposed criterion to determine all of the reactions in the genome-scale iJR904 model that have the potential to be regulatory control points. Specifically, we identified the reactions in the iJR904 model for which the maximum possible Δ_rG′ as calculated with TVA is <−1.0 kcal/mol, meaning none of these reactions can reach equilibrium under the concentration ranges studied (Table 3). In our analysis of candidate reactions for regulation, we utilized the Δ_rG′ range data produced assuming the uncertainty in 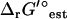is zero, because we want to focus the analysis on the range of Δ_rG′ values possible given variations in metabolite concentrations alone. While the analysis presented previously (2) focuses solely on the central carbon pathways, we find candidates for regulation in a variety of pathways in the cell. Because the metabolite concentration ranges that we explore are much larger than those used previously (2), we do not identify as many candidate reactions for regulation in central carbon (we find six of the 14 reactions reported in Kummel et al. (2), only three of which carry flux; the rest do not carry flux in our analysis because the operating conditions used to generate our flux distributions are different from those used in (2)) .

TABLE 3.

Candidate reactions for regulation

Reaction	Pathway	Reaction	Pathway
GLYCTO2	Alternate carbon metabolism	C160SN*	Membrane lipid metabolism
GLYCTO3	Alternate carbon metabolism	C181SN*	Membrane lipid metabolism
GLYCTO4	Alternate carbon metabolism	C141SN*	Membrane lipid metabolism
PPA	Anaplerotic reactions	C161SN*	Membrane lipid metabolism
MDRPD	Arginine and proline metabolism	PSD_EC	Membrane lipid metabolism
DKMPPD	Arginine and proline metabolism	CYSTL*	Methionine metabolism
G5SADs	Arginine and proline metabolism	RNDR1	Nucleotide salvage pathways
ORNDC*	Arginine and proline metabolism	RNDR2	Nucleotide salvage pathways
ADMDCr*	Arginine and proline metabolism	RNDR4	Nucleotide salvage pathways
PPTGS†	Cell envelope biosynthesis	RNDR3	Nucleotide salvage pathways
UDCPDP	Cell envelope biosynthesis	RNTR1	Nucleotide salvage pathways
KDOPP	Cell envelope biosynthesis	RNTR2	Nucleotide salvage pathways
KDOPS*	Cell envelope biosynthesis	RNTR3	Nucleotide salvage pathways
UAPGR	Cell envelope biosynthesis	RNTR4	Nucleotide salvage pathways
USHD	Cell envelope biosynthesis	TMDS*	Nucleotide salvage pathways
PPCDC	Cofactor and prosthetic biosynthesis	CYTBO3	Oxidative phosphorylation
GTPCI*	Cofactor and prosthetic biosynthesis	FDH2	Oxidative phosphorylation
QULNS	Cofactor and prosthetic biosynthesis	FDH3	Oxidative phosphorylation
ASPO3*	Cofactor and prosthetic biosynthesis	HYD1	Oxidative phosphorylation
ASPO4*	Cofactor and prosthetic biosynthesis	HYD2	Oxidative phosphorylation
ASPO5*	Cofactor and prosthetic biosynthesis	PGL‡	Pentose phosphate cycle
NNDPR	Cofactor and prosthetic biosynthesis	GLUPRT*	Purine and pyrimidine biosynthesis
DNTPPA*	Cofactor and prosthetic biosynthesis	IMPC(r)	Purine and pyrimidine biosynthesis
ADCL	Cofactor and prosthetic biosynthesis	PRFGS	Purine and pyrimidine biosynthesis
ASP1DC*	Cofactor and prosthetic biosynthesis	DHORD2	Purine and pyrimidine biosynthesis
GTPCII2*	Cofactor and prosthetic biosynthesis	DHORD5	Purine and pyrimidine biosynthesis
DB4PS*	Cofactor and prosthetic biosynthesis	OMPDC†	Purine and pyrimidine biosynthesis
DHPPDA2*	Cofactor and prosthetic biosynthesis	DHDPS*	Threonine and lysine metabolism
RBFSa	Cofactor and prosthetic biosynthesis	DAPDC†	Threonine and lysine metabolism
RBFSb	Cofactor and prosthetic biosynthesis	GLCpts*	Extracellular transport
SULR(r)‡	Cysteine metabolism	DHQS	Aromatic amino acid metabolism
CYSS†	Cysteine metabolism	CHORS	Aromatic amino acid metabolism
SULabc*	Cysteine metabolism (transport)	DHQD	Aromatic amino acid metabolism
GCALDD†	Folate metabolism	DDPA*	Aromatic amino acid metabolism
FTHFD	Folate metabolism	PPNDH*	Aromatic amino acid metabolism
PDH‡	Glycolysis/gluconeogenesis	CHORM*	Aromatic amino acid metabolism
GLCS1	Glycolysis/gluconeogenesis	IGPS	Aromatic amino acid metabolism
IGPDH*	Histidine metabolism	ANS*	Aromatic amino acid metabolism
HISTD†	Histidine metabolism	THRD_L*	Val, Leu, and isoleu metabolism
IG3PS	Histidine metabolism	ACLS*	Val, Leu, and isoleu metabolism
PRATPP	Histidine metabolism	DHAD2	Val, Leu, and isoleu metabolism
C140SN*	Membrane lipid metabolism	DHAD1	Val, Leu, and isoleu metabolism
C120SN*	Membrane lipid metabolism	OMCDC	Val, Leu, and isoleu metabolism

^*Reaction is the first step in the pathway leading to the pathway end-product.

^†Reaction is the final step in the pathway producing pathway end-products.

^‡Reaction also identified in the literature (2) as a candidate for regulation.

Typically, a key step for regulation in a metabolic pathway in the cell is the first step of a linear pathway (56). Therefore, we studied the locations of the candidate reactions for regulation identified based on thermodynamics, and 30 of the 86 reactions serve as the first step in the pathways in which they participate while five reactions serve as the final step. For example, in aromatic amino-acid biosynthesis, DDPA is the first step in the pathway that produces chorismate; CHORM is the first step in the pathways that produce phenylalanine and tyrosine; PPNDH is the first step of the pathway that produces only phenylalanine; and ANS is the first step of the pathway that produces tryptophan. All of these reactions belong to branching nodes in the aromatic amino-acid biosynthesis pathways (56), and all four of these reactions were identified as candidates for regulation using TVA.

The analysis presented here has three advantages over the analysis performed in Kummel et al. (2). First, the thermodynamic data used in our analysis is far more complete, covering 891 of the reactions in the iJR904 model as opposed to 132 in Kummel et al. (2). This allows for the identification of candidates for regulation in every known metabolic pathway in addition to central carbon. Second, TMFA combines the quantification of the fluxes in the cell metabolism with the assessment of thermodynamic feasibility in a single step. Thus no flux distributions are produced that must later be corrected due to thermodynamic infeasibilities found. Finally, the metabolite concentration ranges used in our analysis are far less constrained, allowing a more complete exploration of the potential ranges for Δ_rG′ of the reactions in the model.

Exploring the limits on physiologically important concentration ratios

Thermodynamically unfavorable reactions required to take place in cell metabolism are typically driven by hydrolysis of the triphosphate bond in ATP to generate ADP. As such, the ratio of the ATP activity to the ADP activity is an important and carefully regulated quantity in the cell (54), and Δ_rG′ of many reactions in the cell metabolism depend on this ratio. Similarly, oxidation and reduction reactions taking place in cell metabolism typically utilize NAD(P)⁺ as electron sinks and NAD(P)H as electron sources. The Δ_rG′ of these oxidation and reduction reactions depend on the ratio of NAD+ to NADH and NADP+ to NADPH, and these ratios have also been found to be under strict regulatory control (54).

We utilized TVA to determine if the physiological levels of the concentration ratios ATP/ADP, NAD/NADH, and NADP/NADPH maintained inside the cell are due to thermodynamic constraints by exploring the range of thermodynamically feasible values for these ratios. We also used TVA to study the limits on the ratio of the intracellular pH to the extracellular pH as all transport of ions across the cell membrane depends on this ratio. The minimum and maximum ratios found are shown in Table 4 along with the values for these ratios found in the literature (47,49,54). We found that without accounting for uncertainty in the group contribution method, all of the ratios found in the literature nearly fit within the thermodynamically feasible ranges for the ratios. Interestingly, the physiologically observed ratio for NAD/NADH is very close to the minimum ratio predicted by TVA, whereas the physiologically observed ratio of NADP/NADPH is very close to the maximum ratio predicted by TVA. This suggests that the values of these physiologically important quantities at optimal growth conditions are determined by the constraints imposed by the thermodynamic properties of the entire metabolic network. When accounting for uncertainty, the estimated ratios NADP/NADPH and NAD/NADH span the entire range of values possible given the concentration limits of 10⁻⁵ M and 0.02 M, whereas the ratios ATP/ADP and 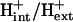remain close to the ranges estimated by the analysis without uncertainty.

TABLE 4.

Thermodynamically feasible physiologically important concentration ratios

	Ratio reported in literature	Min ratio with no uncertainty	Max ratio with no uncertainty	Minimum ratio	Maximum ratio
ATP/ADP	3.2*	0.17	2.0 × 103§	0.022	2.0 × 103§
NAD/NADH	19†	15	2.0 × 103§	0.00050¶	2.0 × 103§
NADP/NADPH	1.2†	0.0086	1.1	0.00050¶	2.0 × 103§
	0.025–6.3‡	0.0010¶	5.0	0.0010¶	7.1

^*From Albe et al. (49).

^†From Andersen and Meyenburg (54).

^‡From Neidhardt and Curtiss (47).

^¶Equal to the minimum ratio possible given the bounds on the concentrations of these species.

^§Equal to the maximum ratio possible given the bounds on the concentrations of these species.

The minimum value for the ATP/ADP ratio is constrained by thermodynamics because Δ_rG′ of every kinase reaction in the cell depends on this ratio. As the ATP/ADP ratio decreases, Δ_rG′ of every reaction driven by the dephosphorylation of ATP increases. This includes the many essential phosphorylase and kinase reactions in the nucleotide salvage pathway responsible for the production of all the other triphosphate nucleotides in the cell. All of these reactions transfer one phosphate from ATP to another nucleotide such as GDP, UDP, or CDP to create ADP and either GTP, UTP, or CTP, respectively. Because the energies of the triphosphate bonds being created and destroyed in these reactions are essentially identical, Δ_rG′° of these reactions are all approximately zero. Therefore, these reactions must be driven entirely by the concentration gradient between the reactants and products. Driving the ATP/ADP ratio to very low levels also drives the ratios GTP/GDP, UTP/UDP, CTP/CDP, and nearly every other triphosphate/diphosphate pair in the cell, to even lower levels to maintain a favorable concentration gradient. A low ATP/ADP ratio results in an unfavorable concentration gradient for every kinase reaction in the cell, reducing the energy generated by the kinase reactions.

The maximum 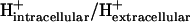ratio is constrained by thermodynamics because Δ_rG′ of every reaction involving the transport of ions across the cell membrane depends on this ratio. Many transport reactions in E. coli, most notably ATP synthase, are powered by the transport of H⁺ across the cell membrane. As the extracellular H⁺ concentration decreases, the transmembrane proton concentration gradient becomes more unfavorable reducing the power generated by the transport of the proton into the cell until insufficient power is provided to drive these reactions in the direction required for growth.

DISCUSSION

The addition of thermodynamic constraints to MFA results in both improved accuracy and expanded applicability of flux balance analysis methods. The flux distributions generated using TMFA do not involve flux through any thermodynamically unfavorable flux loops, and no thermodynamically unfavorable reactions given the concentration ranges found in the cell are utilized. Furthermore, TVA allows the exploration of the thermodynamically feasible values for Δ_rG′ of the reactions and the metabolite activities. Some differences do exist between the results presented here and the results presented in the previously published article on this topic (21). These differences are a result of the combination of improvements in the thermodynamic estimates and an improved ability of TMFA to assess the feasibility of reactions by accounting for all possible metabolite concentrations rather than just mM concentrations used in the previous article.

Uncertainty remains an issue when utilizing the group contribution method to analyze the effect of thermodynamic constraints on metabolite activities and reaction Δ_rG′. All of the feasible ranges for the metabolite activity ratios studied in this article with no uncertainty allowable in Δ_rG′° encompassed the values observed in literature. When uncertainty in 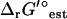is accounted for, nearly all of the metabolite activities are completely unconstrained, and all of the experimentally measured metabolite activities fall within the range of possible values obtained from TVA. The feasible ranges for Δ_rG′ and metabolite activities determined from TVA accounting for uncertainty in Δ_rG′° are far larger than the true feasible ranges for these quantities. The ranges determined from TVA with no uncertainty allowable are much closer to the true feasible ranges.

Regardless of uncertainty in 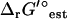, very few of the metabolites in E. coli are affected by the thermodynamic constraints at all. The majority of the reactions in E. coli are thermodynamically favorable, allowing the reactions to remain active under a wide variety of metabolite concentrations and granting the cell a large degree of versatility. While this thermodynamic flexibility prevents the determination of exact values for Δ_rG′ of the reactions, the estimated magnitudes of Δ_rG′ are determined, which can provide valuable insight for the potential of a reaction to undergo regulation. To tightly constrain metabolite activities and reaction Δ_rG′ based on thermodynamic constraints, either a thermodynamic optimization objective must be utilized as done in the work by Beard and Qian (17), or additional nonlinear constraints involving kinetics must be added to the TMFA formalism.

The activity ratio study performed does demonstrate that while the values for the activities of single metabolites have a wide range of feasible values, constraints do exist on the activity ratios of some metabolites of physiological significance. Important metabolite pairs that appear together in many different reactions such as ATP and ADP, NAD and NADH, NADP and NADPH, and intracellular and extracellular protons become thermodynamically coupled to the activity ratios of many other metabolites in the cell. This coupling results in a thermodynamic constraint on these ratios. Interestingly, while the physiological concentrations of key metabolites in the cell are maintained near the middle of the feasible activity range, the NAD/NADH ratio is maintained near the minimum feasible value while the NADP/NADPH ratio is maintained near the maximum feasible value.

While ionic strength can have a large effect on metabolite activities causing the activity of a metabolite to differ from the concentration of the metabolite by over 20%, ionic strength has a much smaller impact on Δ_rG′° of the reactions. Therefore, the thermodynamic feasibility of reactions can often be accurately assessed from Δ_rG′° of the reactions based on a reference ionic strength of zero. The difference between Δ_rG′° (I = 0) and Δ_rG′° (I = 0.2 M) is also typically much smaller than the uncertainty involved in Δ_rG′° (I = 0) making uncertainty the more important factor to take into account. However, these adjustments are based on the extended Debye-Hückel equation, which is applicable for solutions with an ionic strength of <0.1 M. Applying this relationship to adjust Δ_rG′° to an ionic strength of 0.2 M may affect some of the reported results. The extent of these differences is the subject of ongoing investigations.

Finally, it is important to note that neither the key thermodynamic bottleneck dihydroorotase nor most of the candidates for regulation identified were a part of the central carbon chemistry of the cell. This emphasizes the importance of applying thermodynamic analysis to large-scale genome-based models to account for the highly coupled nature of thermodynamic constraints.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: MFA CONDITIONS

MFA studies were performed under a specific set of constraints on the metabolites the cell could uptake from or excrete to the cell surroundings. The ability of E. coli to grow optimally under aerobic conditions was studied using glucose as a primary carbon source. The uptake of glucose and oxygen from the environment into the cell was restricted to 0.01 and 0.02 Mol/g dw h, respectively (29). The uptake and excretion of sulfate, phosphate, and ammonium, CO₂, water, and hydrogen ion were left unrestricted and the ATP maintenance requirement was fixed at 7.6 mmol/g dw h (24,30,57). Under these conditions, the optimal growth on glucose was found to be 0.923 g biomass/g dw h, with a yield of 0.0923 gram biomass per mmol of glucose uptake (0.512 g biomass/g glucose). This optimal growth yield agrees well with the optimal growth yields for E. coli under similar conditions reported in the literature from MFA and experiments (30).