On the Characterization of Protein Native State Ensembles

Abstract

Describing and understanding the biological function of a protein requires a detailed structural and thermodynamic description of the protein's native state ensemble. Obtaining such a description often involves characterizing equilibrium fluctuations that occur beyond the nanosecond timescale. Capturing such fluctuations remains nontrivial even for very long molecular dynamics and Monte Carlo simulations. We propose a novel multiscale computational method to exhaustively characterize, in atomistic detail, the protein conformations constituting the native state with no inherent timescale limitations. Applications of this method to proteins of various folds and sizes show that thermodynamic observables measured as averages over the native state ensembles obtained by the method agree remarkably well with nuclear magnetic resonance data that span multiple timescales. By characterizing equilibrium fluctuations at atomistic detail over a broad range of timescales, from picoseconds to milliseconds, our method offers to complement current simulation techniques and wet-lab experiments and can impact our understanding and description of the relationship between protein flexibility and function.

INTRODUCTION

It is well established that, while an experimentally determined structure may reveal a protein's functional regions, structural fluctuations under native conditions can modulate function (1–3). Experiments, simulations, and theory indicate that a detailed description of function (encompassing enzymatic reactions, electron transfer, protein ligand binding, and protein/protein interactions) requires the characterization of a protein's native state as an ensemble of conformations (4–7). Such a characterization involves describing in detail the structural and thermodynamic properties over all conformations of the native state ensemble.

Obtaining this description has proven challenging. While nuclear magnetic resonance (NMR) spectroscopy describes picosecond-millisecond timescale dynamics through relaxation phenomena (1,8,9), the characterization of all the conformations constituting the native state at atomistic detail remains an active area of research (10). Molecular dynamics (MD) and Monte Carlo (MC) methods, especially when combined with enhanced sampling techniques and massive parallelization (11–14) or when conducted in low-dimensional configuration spaces (15–17), are powerful complements to characterize the native state ensemble (18). However, the computational demand of these methods makes it challenging to explore longer timescales (19–21). Efforts to explore native state ensembles with no timescale limitations have recently focused either on obtaining native thermodynamic propensities of amino acids (22) or on generating conformations of the native state ensemble by guiding MD or MC with explicit information from NMR measurements (10,23,24).

In this context, we have recently developed the Protein Ensemble Method (PEM) (25) to exhaustively characterize the native state ensemble of a protein at atomistic detail with no inherent timescale limitations. PEM obtains all-atom conformations of the native state in a multiscale fashion combining geometric and energetic considerations. On the generated conformations, PEM measures thermodynamic averages in a statistical mechanics framework and so allows a direct quantitative comparison with wet-lab experimental measurements. We have shown that PEM is intrinsically parallel, efficient in generating large ensembles, and able to characterize equilibrium fluctuations of both loop segments and polypeptide chains (25,26).

In this work, we show the generality of PEM by using the method to characterize native state ensembles of proteins of different sizes and folds. We present the PEM-obtained native state ensembles of eglin c, the SH3 domain of Fyn tyrosine kinase (FynSH3), the 10th type III domain of fibronectin (FNfn10), and the Peptostreptococcus magnus albumin-binding second GA module of PAB (ALB8-GA). These proteins are 70, 58, 90, and 53 aa long, of α + β, mainly β, all β, and all α-folds, respectively. We show that for all these proteins the PEM-obtained native fluctuations agree remarkably well with NMR data such as order parameter and three-bond scalar coupling data. In addition, for ALB8-GA, where side-chain NMR data are presently not available, we present our prediction on equilibrium side-chain fluctuations.

MATERIALS AND METHODS

We first briefly review the main components of PEM. A more detailed discussion of the method can be found in Shehu et al. (26).

Generation of native state ensembles

PEM employs the following multi-scaling approach to generate the native state ensemble of a protein:

1. Starting from the topology of an initial native structure (used as a reference), the method first divides the polypeptide chain into consecutive long segments of significant overlap.

2. For each segment, an extensive ensemble of relevant backbone configurations is obtained through a geometric exploration of conformational space that combines uniform sampling of the backbone dihedral degrees of freedom of the segment with an efficient inverse kinematics procedure known as cyclic coordinate descent (27).

3. Optimal side-chain configurations are then added onto each backbone configuration, and a short energy minimization of each of the resulting all-atom conformations is finally performed. A generated conformation is deemed low-energy and added to the native state ensemble if its energy is no higher than 20 kcal/mol from the energy of the initial structure employed.

Equilibration of solution structures

For the proteins presented here, an initial native structure is obtained by equilibrating an NMR solution structure. NMR ensembles of solution structures of eglin c (28), FynSH3 (29), FNfn10 (30), and ALB8-GA (31) are available in the PDB (32) under codes 1egl, 1nyg, 1ttf, and 1gab. The solution structure that is reported as the best, representative, or the average of the NMR ensemble for each protein is subjected to a short energy minimization. The average structures of the NMR ensembles of FynSH3, FNfn10, and ALB8-GA are reported under PDB codes 1nyf, 1ttg, and 1prb. When a best, representative, or average structure is not reported in the PDB, which is the case for eglin c, the first structure of the NMR ensemble is chosen to be subjected to an energy minimization procedure.

The energy of a structure is measured through the CHARMM all-atom force field (33). The energy minimization procedure involves a conjugate gradient descent in the energy landscape. The minimization of a structure is considered converged if during the last 300 steps of the conjugate gradient descent the improvement in energy is <2.0 kcal/mol. Equilibrated structures of eglin c, FynSH3, FNfn10, and ALB8-GA differ from their corresponding solution structures by all-atom RMSDs of 1.8, 1.7, 2.0, and 2.5 Å, respectively (the effect of the equilibration of PDB-obtained structures on the native state ensembles generated by PEM is discussed in full in Shehu et al. (26)).

PEM divides the polypeptide chain of each of these proteins into segments of 30 aa long with an overlap with each other of 25 aa. The values for the segment length and overlap are chosen by a general and automated procedure. Optimal segment length and overlap result in consistent amino acid fluctuations as measured over the ensembles generated for overlapping segments enclosing each amino acid (see (26) for details and for values to all parameters used by PEM).

Measurement of thermodynamic averages

PEM measures thermodynamic averages over the segment ensembles in a statistical mechanics framework. Each PEM-generated conformation C with energy E(C) is weighted by its Boltzmann probability 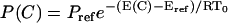, where E_ref is the energy of the equilibrated solution structure (taken as reference), R is the gas constant, and T₀ is room temperature of 300 K. The constant P_ref is the probability of the reference structure and can be set to 1 without loss of generality. Let X_i(C) indicate the value of an observable X, at position i, measured on conformation C; the thermodynamic average of this quantity over the generated ensemble is measured as 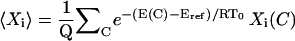, where Q refers to the partition function. Averages measured over ensembles of neighboring segments are then combined to obtain structural and thermodynamic observables of the native state. Since a conformation C with energy E(C) higher than 20 kcal/mol from the reference energy E_ref has an associated relative Boltzmann probability 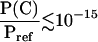, its contribution to ensemble averages 〈X_i〉 is practically negligible. Therefore, only conformations whose energies are no higher than a cutoff of 20 kcal/mol from the reference energy E_ref are considered in the ensembles.

The thermodynamic observables calculated over the PEM-obtained ensembles consist of amide and methyl order parameter (S²) data that measure the reorientational averaging of amide and methyl bonds, respectively, and three-bond scalar coupling (³J) data that measure side-chain rotamer averaging. These average values can be directly compared to the corresponding values measured in NMR experiments and quantify native fluctuations of a protein at varying timescales. While amide S² data measure picosecond-nanosecond timescale fluctuations, methyl S² and ³J data can span up to millisecond timescales (1,8,9).

S² data for a bond are measured by averaging over the distribution of vectors assumed by the bond in a generated ensemble (23). The calculation of S² data is based on the Lipari-Szabo model-free formalism (34) that does not assume a particular model of internal motions. The model-free formalism allows for a direct comparison of calculated S² values with experimental order parameters under the assumption that motions of the methyl symmetry axis and of the protons about this axis are decoupled (35). A thorough discussion on the model-free formalism can be found in the literature (34,35). Based on the Lipari-Szabo model-free formalism (34), the order parameter 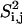for a bond between atoms i and j is calculated through the formula

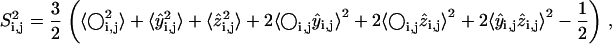where 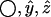denote the components of the unit vector along the bond. Since bond lengths remain essentially unchanged from their equilibrium values during PEM's execution, the above formula can be simplified as in Best and Vendruscolo (23) to

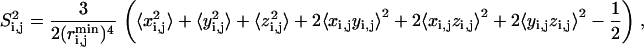where 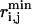refers to the equilibrium length of the bond connecting atoms i and j. The ensemble-averaged S² for a particular bond is thus obtained by Boltzmann-averaging over the distribution of x, y, z components of vectors assumed by the bond. S² = 1 indicates no heterogeneity in the distribution of these vectors, whereas S² = 0 is indicative of a uniform distribution. Similarly, ³J data are measured over the distribution of assumed rotamers (36). The calculation of these quantities and their comparison with NMR data allows us to quantitatively assess the agreement between the PEM-generated and the actual native state ensembles.

Additional measurements presented in this work consist of probabilities of contacts and hydrogen bonds, which are similarly Boltzmann-weighted. Two amino acids are considered in contact with one another if the Euclidean distance between two of their atoms is no more than 4.5 Å. A hydrogen bond is considered formed if the OH distance is <2.4 Å and the maximum NHO angle for the hydrogen bond alignment is 2.44 rad.

The computational uncertainty associated with the thermodynamic observables calculated over the PEM-generated ensembles is obtained by measuring differences in the observables when alternative implementation decisions are made in PEM. Therefore, the error bars associated with the PEM-calculated thermodynamic observables measure the inherent error, hence the robustness, of PEM (see (26) for a list of all implementation decisions).

The Pearson correlation R² and reduced χ² are used to quantify the agreement between calculated and experimental thermodynamic averages. They are measured as defined in Bevington and Robinson (37).

Computational cost

For each of the proteins in this study, ∼13,000 conformations with energy within 20 kcal/mol from the reference structure are generated for each 30 aa segment. Of these, ∼5000 conformations per segment have energies no higher than 5 kcal/mol from the energy of the equilibrated solution structure used as reference. All results presented here were obtained on the Rice University Terascale cluster of 900 MHz Intel Itanium2 processors (Intel, Santa Clara, CA) and on the Rice University ADA cluster of 2.2 GHz AMD Opteron processors. The calculations for each protein required <100 CPU hours.

RESULTS

Figs. 1 a, 2 a, 4 a, and 6 a, show the obtained conformational ensembles for eglin c, FynSH3, FNfn10, and ALB8-GA, respectively. Figs. 1 b, 2 b, 4 b and c, and 6 b, show that correlations between the S² and ³J data calculated over the ensembles obtained for eglin c, FynSH3, and FNfn10 ( and ³J_calc) and the NMR S² and ³J data (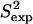 and ³J_exp) are >92%. This result is particularly significant when considering the low correlations, 37–50%, between the 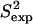, ³J_exp data and the corresponding quantities measured over the NMR ensembles (28–31) available for these proteins. Results for each protein are discussed in the following.

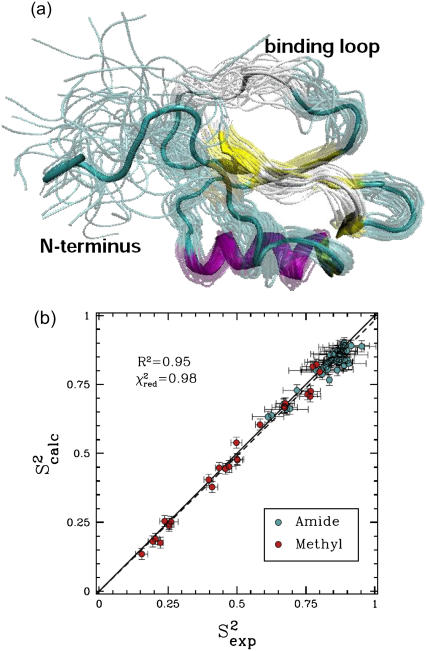
FIGURE 1.

(a) Eglin c conformations with energy no higher than 5 kcal/mol from the equilibrated solution structure, shown as opaque, are drawn in transparent representation. (b) Calculated amide and methyl S² data (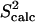 on the y axis) are compared to NMR S² data ( 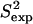on the x axis). The dashed line indicates the linear least squares regression fit on the data sets. The solid line is the identity line.

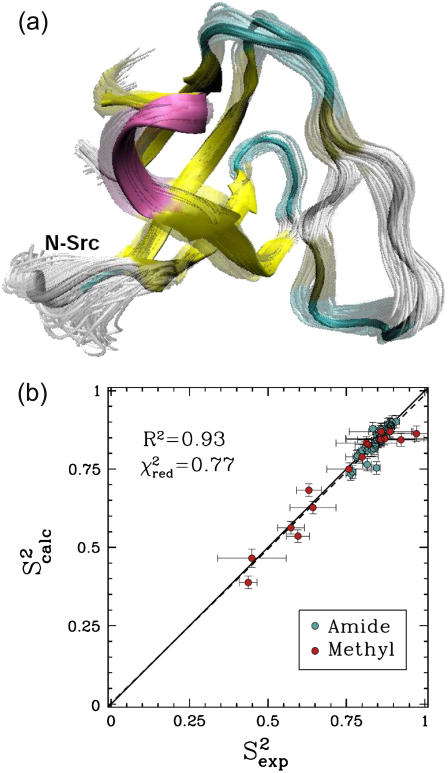
FIGURE 2.

(a) Fyn SH3 conformations with energy no higher than 5 kcal/mol from the equilibrated solution structure, shown as opaque, are drawn in transparent representation. (b) Calculated amide and methyl S² data (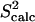 on the y axis) are compared to NMR S² data ( 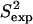on the x axis). The dashed line indicates the linear least squares regression fit on the data sets. The solid line is the identity line.

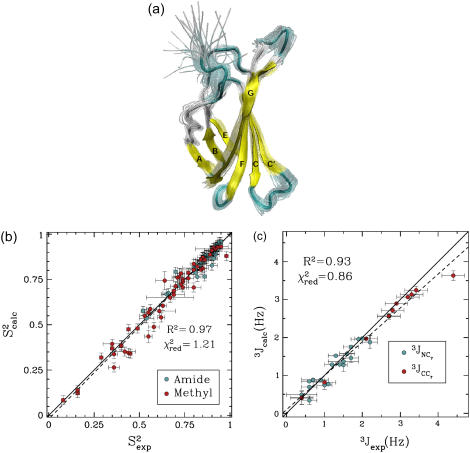
FIGURE 4.

(a) FNfn10 conformations with energy no higher than 5 kcal/mol from the equilibrated solution structure, shown as opaque, are drawn in transparent representation. (b) Calculated amide and methyl S² data (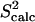 on the y axis) are compared to NMR S² data ( 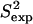on the x axis). (c) Calculate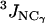d and 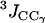(³J_calc on the y axis) are compared to NMR ³J data (³J_exp on the x axis). (b and c) The dashed black line indicates the linear least-squares regression fit on the data sets. The continuous line is the identity line.

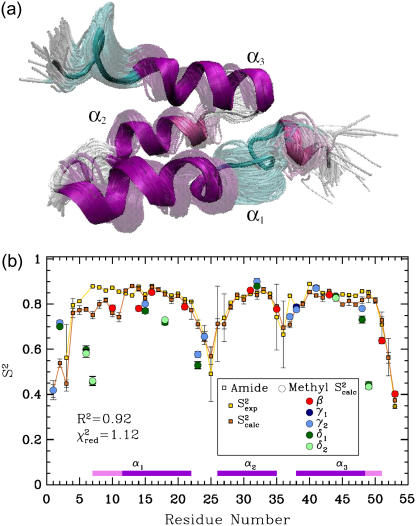
FIGURE 6.

(a) ALB8-GA Conformations with energy no higher than 5 kcal/mol from the equilibrated solution structure, shown as opaque, are drawn superimposed in transparent representation. (b) Calculated amide 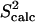data (orange squares), are compared to NMR 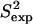data (yellow squares). PEM-obtained methyl 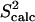data are shown in colored circles (no NMR data are available for comparison). Horizontal bars on the x axis show the position of the three α-helices on the amino acid sequence of ALB8-GA. The parts of these bars drawn in lighter colors indicate amino acids that are found in unfolded configurations as well.

Analysis of PEM-generated native state ensemble of eglin C

Fig. 1 a shows the native state ensemble obtained by PEM for eglin c. Fig. 1 a clearly shows the heterogeneity of this ensemble. The largest equilibrium fluctuations obtained for this protein are located in the Thr¹-Gly¹⁵ N-terminus, which is practically disordered. Interestingly, the protease-binding loop, encompassing amino acids Ser⁴¹-Arg⁴⁸, is also very mobile. Of all the amino acids of the loop, Val⁴³-Leu⁴⁷ are the most mobile. The mobility of the entire loop is also reflected in the low average of 0.7 of the amide 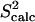data corresponding to the amide bonds of the loop's amino acids.

The entire amide and methyl 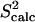data computed over the ensemble obtained for eglin c are shown in Fig. 1 b. Fig. 1 b shows that 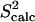agree with 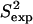data (38) with a Pearson correlation of 95% and reduced χ² of 0.98. Methyl 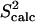data measured over the generated native state ensemble of eglin c are on average as low as 0.49. This is mostly due to the disordered Thr¹-Gly¹⁵ N-terminus.

Analysis of PEM-generated native state ensemble of Fyn SH3

The obtained native state ensemble of FynSH3 is shown in Fig. 2 a. In contrast to the ensemble obtained for eglin c, Fig. 2 a shows that the obtained equilibrium fluctuations for FynSH3 are prevalently small-scale. The largest fluctuations are located in the N-Src loop, which encompasses amino acids Asn¹¹³-Trp¹¹⁹. Interestingly, the N-Src loop discriminates between class I and class II ligands binding to FynSH3 (29). Of all this loop's amino acids, its central amino acid, Glu¹¹⁶ is the most mobile.

The obtained equilibrium fluctuations of FynSH3 are validated by comparing 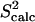data to the corresponding 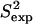NMR data (39). Fig. 2 b shows that 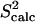and 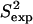data (39) for FynSH3 agree with a Pearson correlation of 93% and reduced χ² of 0.77. The small-scale fluctuations qualitatively shown in Fig. 2 a are reflected in the 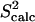data: amide and methyl 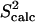data have high averages of 0.84 and 0.72. This result agrees with experimental findings that large amplitude microsecond-millisecond motions are unlikely in the FynSH3 native state (39).

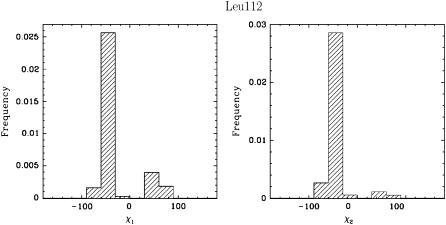
An interesting instance is represented by amino acid Leu¹¹², located at the border between a β-sheet and the beginning of the N-Src loop. The methyl 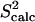values associated with the χ₁ and χ₂ angles of Leu¹¹² are the lowest in the whole protein, even though the backbone fluctuations at this position are limited. Fig. 3 shows the distribution of the side-chain χ₁ and χ₂ angles in Leu¹¹² and reveals that the low methyl 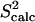data result from averaging over multiple rotameric states populated by the side chain of Leu¹¹² in the ensemble.

FIGURE 3.

Distributions of χ₁ and χ₂ angles (χ₁ and χ₂ correspond to the dihedral angles associated with the 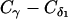and the 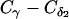bonds, respectively) for Leu¹¹² in FynSH3 reveal that Leu¹¹² prefers more than one rotameric state.

Analysis of PEM-generated native state ensemble of FNfn10

The native state ensemble obtained for FNfn10 is shown in Fig. 4 a. The N-terminal amino acids appear disordered, while the seven β-strands of FNfn10, A, B, C, C′, E, F, and G, are well defined and practically rigid. The surface loops connecting the β-sheets (AB, BC, CC′, C′E, EF, and FG), however, are shown to be mobile. The PEM-obtained mobility for these loops agrees with the hypothesis that motions of these loops play a role in the induced-fit recognition of FNfn10 by multiple receptors (40). In particular, the most mobile amino acids, Val²⁷, Ser⁴³, and Arg⁷⁸, are located in the BC, CC′, and FG loops. Interestingly, the FG loop, which includes the RGD cell-adhesion motif, encompassing amino acids Arg⁷⁸-Asp⁸⁰ (40), is the most flexible of all the surface loops in FNfn10.

Fig. 4, b and c, show that 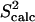and ³J_calc for FNfn10 agree with 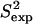and ³J_exp data (41) with Pearson correlations of 97% and 93%, and reduced χ²s of 1.21 and 0.86, respectively. Amide S² data with a high average of 0.86 indicate small-scale fluctuations and a practically rigid hydrophobic core. This result agrees with the findings reported in Carr et al. (40), where microsecond-millisecond motions in FNfn10 are not observed.

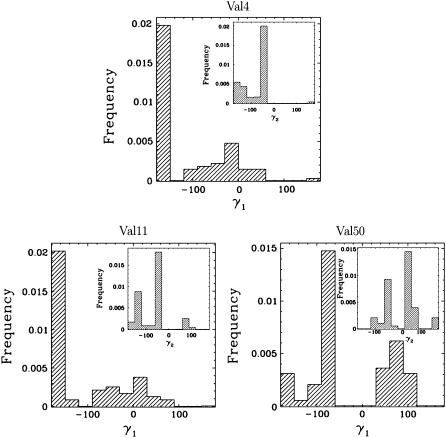
While most side chains have a single staggered rotamer, Val⁴, Val¹¹, and Val⁵⁰ have unusually low ³J values, indicative of rotamer averaging. Distributions of the side-chain γ₁ and γ₂ angles in these amino acids are measured over the obtained native state ensemble of FNfn10 and shown in Fig. 5. Fig. 5 confirms that Val⁴, Val¹¹, and Val⁵⁰, while preferring one rotamer, are found on average in 4–5 rotamers.

FIGURE 5.

Distributions of γ₁ and γ₂ angles for Val⁴, Val¹¹, and Val⁵⁰ in FNfn10 reveal that these amino acids visit an average of 4–5 other rotamers. The distributions of γ₂ angles are shown inside the distributions of the γ₁ angles. Averaging over the rotameric states explains these amino acids' unusually low ³J data, even though only small-scale backbone fluctuations are detected in FNfn10.

Analysis of PEM-generated native state ensemble of ALB8-GA

The native state ensemble obtained by PEM for ALB8-GA is shown in Fig. 6 a. Fig. 6 b shows the amide and methyl 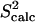measured over the obtained ensemble. Amide 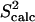and 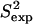data (42) for ALB8-GA agree with a Pearson correlation of 92% and reduced χ² of 1.12. Since NMR methyl S² data are currently not available for comparison, in Fig. 6 b we show our prediction of methyl S² data as obtained by PEM.

The ensemble drawn in Fig. 6 a shows that the second α-helix of ALB8-GA, α₂, is tightly packed between the other two helices, α₁ and α₃. Fig. 6 b shows that obtained backbone fluctuations of α₂ are small (amide S² data >0.8). This result supports the loss of conformational flexibility resulting from selective pressure on α₂, which has evolved to bind human serum albumin with high affinity (42).

In contrast, we observe disorder in the N-terminus of α₁. We find that amino acids Leu⁷-Lys¹¹ located at the beginning of the α₁ helix of the solution structure of ALB8-GA (31) are highly mobile. These amino acids' high fluctuations can be seen in Fig. 6 b. Moreover, we find that Leu⁷-Lys¹¹ can populate both helical and coil configurations. Indeed, while occasionally populating helical configurations in the PEM-obtained ensemble, these amino acids have a high probability to visit unfolded coil-like configurations.

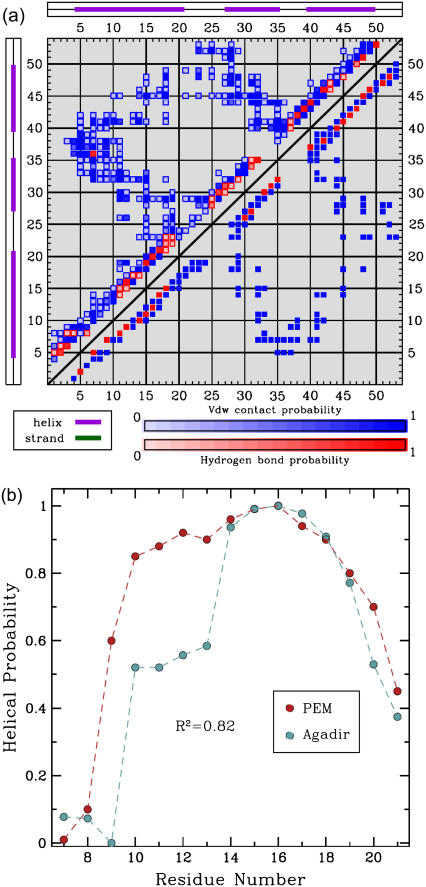
The low helical content of these amino acids in the PEM-generated ensemble can be seen in Fig. 7 a. Fig. 7 a shows a square symmetric matrix where a blue square at position (i, j) indicates the presence of a contact between amino acid i and amino acid j, and a red square indicates the formation of a hydrogen bond between amino acids i and j. Fig. 7 a contrasts the contacts and hydrogen bond network as present in the PEM-generated ensemble, shown top left, with the network present in the representative NMR structure of ALB8-GA, shown bottom right. The bottom right half of the map reveals that in the NMR structure hydrogen bonds are present for amino acids Leu⁷-Lys¹¹ to be in helical configurations. On the other hand, the top left half of the map shows both the scarcity and the low probabilities for hydrogen bonds in this region, indicating that amino acids Leu⁷-Lys¹¹ visit coil-like configurations in the PEM-generated ensemble with high probability.

FIGURE 7.

(a) The contact map is drawn as a 53 × 53 square symmetric matrix (there are 53 aa in ALB8-GA). The formation of a contact between amino acids i, j is indicated with a blue square at position (i, j). The formation of a hydrogen bond between i, j is indicated with a red square at position (i, j). Shades of blue and red indicate different formation probabilities, with dark blue and dark red indicating a probability of 1, and lighter shades indicating lower probabilities. The top left half of the matrix shows the formation probabilities of contacts and hydrogen bonds in the PEM-generated ensemble. For reference, the bottom right of the matrix shows the contacts and hydrogen bonds in the representative NMR structure of ALB8-GA. The hydrogen bonds in the NMR structure indicate that amino acids Leu⁷-Lys¹¹ are in helical configurations. The PEM-generated map shows that there are either missing or less probable hydrogen bonds in this region, indicating that Leu⁷-Lys¹¹ visit unfolded configurations in the PEM-generated ensemble. (b) The probabilities for amino acids Leu⁷-Ala²¹ to be part of α₁ are shown in red. These probabilities are measured over the ensemble conformations obtained by PEM. The secondary structure assignment for each conformation of the ensemble is computed with the STRIDE program (43) in the Tcl/TK environment of VMD (48). The normalized helicity scores predicted for each amino acid by Agadir (44) are shown in blue.

The relative populations of helical and coil configurations visited by amino acids Leu7-Lys¹¹ can be quantified by measuring the probabilities of the N-terminus amino acids Leu7-Ala²¹ to be in helical configurations in the ALB8-GA ensemble obtained by PEM. Secondary structure assignment for these amino acids on every conformation of the ensemble is computed with STRIDE (43). The measured probabilities are shown in Table 1(b). We have compared these probabilities with the helicity scores produced by Agadir (44), a program that predicts the helical behavior of polypeptide chains given only amino acid sequence information. The complete amino acid sequence of Leu⁷-Ala²¹ is shown in Table 1(a). The helicity scores predicted by Agadir are shown in Table 1(c).

TABLE 1.

(a)	L	K	N	A	K	E	D	A	I	A	E	L	K	K	A
(b)	0.01	0.10	0.60	0.85	0.88	0.92	0.90	0.96	0.99	1.00	0.94	0.90	0.80	0.70	0.45
(c)	4.7	4.6	3.0	14.4	14.4	15.2	15.8	23.5	24.7	24.9	24.4	22.9	19.9	14.6	11.2

The ALB8-GA sequence of amino acids 7–21 is shown in row a. The probability of each amino acid to be part of the first α-helix in the ALB8-GA ensemble obtained by PEM is measured over the ensemble conformations and shown in row b. The helicity scores predicted for each amino acid by Agadir (44) are shown in row c.

The helicity scores predicted by Agadir agree with our prediction that amino acids Leu⁷-Lys¹¹ of α₁ have lower probabilities of being found in helical configurations in the native state of ALB8-GA compared to amino acids Lys¹²-Lys¹⁹. This can be seen in Fig. 7 b, where we plot and correlate the probabilities measured over the PEM-obtained ensemble with the Agadir-predicted scores. Although the comparison with the Agadir-predicted scores can only be interpreted at a qualitative level (the two data sets measure different quantities), the Pearson correlation with these scores is interestingly high, 82%. This agreement further supports our claim that these five amino acids (Leu⁷-Lys¹¹) at the beginning of the α₁ helix in ALB8-GA have indeed a high probability to visit unfolded configurations under native conditions.

Since helix/coil transitions happen on timescales longer than nanoseconds (45), the unfolding observed for amino acids Leu⁷-Lys¹¹ cannot be detected by the NMR amide 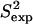data (42). The native state ensemble obtained by PEM for ALB8-GA may contain additional information to what is present in the available NMR data. It would be interesting to devise wet-lab experiments that can observe native fluctuations of α₁ over longer timescales. In this particular case, by capturing helix-coil transitions, such experiments could allow to test our prediction of low helical content for Leu⁷-Lys¹¹.

DISCUSSION AND CONCLUSION

In summary, we have shown that PEM fully characterizes native local fluctuations of small- to medium-size proteins at atomistic detail. The remarkably good agreements between the available NMR data for these proteins and the thermodynamic properties measured over the PEM-obtained ensembles show that PEM efficiently characterizes native state ensembles in detail, at least for the proteins presented here.

Unlike in trajectory-based simulation techniques, the native conformations obtained by PEM are not correlated to one another. It is this feature that gives PEM its inherent lack of timescale limitations and makes the method intrinsically parallel. The massive parallelism together with the efficient sampling and geometric techniques employed to generate each all-atom conformation of the native state, make PEM an efficient method to obtain extensive native state ensembles of thousands of conformations.

It is worth stressing that the agreement obtained between PEM-calculated and experimental order parameter and scalar coupling data is still a challenge for MD or MC simulation techniques, since slow side-chain rotations may take up to milliseconds (46). In addition, the rotameric averaging measured in the scalar couplings may take from picoseconds to few hundredths of a second (47).

As a sampling-based approach with no inherent timescale limitations, PEM can complement current simulation techniques in highlighting structural and thermodynamic properties of the native state. In particular, as demonstrated for ALB8-GA, PEM can also complement experimental techniques and formulate hypotheses that can be tested through wet-lab experiments.

It is worth stressing that PEM is primarily intended for application on proteins with nonconcerted motions, as for instance the proteins studied in this article. By obtaining conformations of one segment at a time while maintaining the rest of the protein in a reference conformation, as a first-order approximation method, PEM does consider the possibility of correlated motions of segments far away in sequence. We are currently investigating higher-order approximations (25) to extend PEM to proteins with concerted motions and, more generally, to larger and more complex systems. The results presented in this work lead us to believe that PEM represents a significant first step toward improving our characterization and understanding of protein function at a microscopic scale.