Skip to main content
PMC home page
Applied and Environmental Microbiology logoLink to Applied and Environmental Microbiology
. 2006 Nov 10;73(1):250–258. doi: 10.1128/AEM.00351-06

Estimation of Microbial Contamination of Food from Prevalence and Concentration Data: Application to Listeria monocytogenes in Fresh Vegetables▿

Amélie Crépet 1,*, Isabelle Albert 1, Catherine Dervin 1, Frédéric Carlin 2
PMCID: PMC1797144  PMID: 17098926

Abstract

A normal distribution and a mixture model of two normal distributions in a Bayesian approach using prevalence and concentration data were used to establish the distribution of contamination of the food-borne pathogenic bacteria Listeria monocytogenes in unprocessed and minimally processed fresh vegetables. A total of 165 prevalence studies, including 15 studies with concentration data, were taken from the scientific literature and from technical reports and used for statistical analysis. The predicted mean of the normal distribution of the logarithms of viable L. monocytogenes per gram of fresh vegetables was −2.63 log viable L. monocytogenes organisms/g, and its standard deviation was 1.48 log viable L. monocytogenes organisms/g. These values were determined by considering one contaminated sample in prevalence studies in which samples are in fact negative. This deliberate overestimation is necessary to complete calculations. With the mixture model, the predicted mean of the distribution of the logarithm of viable L. monocytogenes per gram of fresh vegetables was −3.38 log viable L. monocytogenes organisms/g and its standard deviation was 1.46 log viable L. monocytogenes organisms/g. The probabilities of fresh unprocessed and minimally processed vegetables being contaminated with concentrations higher than 1, 2, and 3 log viable L. monocytogenes organisms/g were 1.44, 0.63, and 0.17%, respectively. Introducing a sensitivity rate of 80 or 95% in the mixture model had a small effect on the estimation of the contamination. In contrast, introducing a low sensitivity rate (40%) resulted in marked differences, especially for high percentiles. There was a significantly lower estimation of contamination in the papers and reports of 2000 to 2005 than in those of 1988 to 1999 and a lower estimation of contamination of leafy salads than that of sprouts and other vegetables. The interest of the mixture model for the estimation of microbial contamination is discussed.

Quantitative microbial risk assessment (QMRA) is in rapid development in the area of food safety. To obtain a quantitative exposure assessment or a quantitative risk characterization for a given food and a given food-borne pathogen, statistical distributions of microbial concentrations are used as input values (such as bacterial concentrations in raw food materials subjected to further process) and/or as output values (predicted contamination in foods after processing and/or storage) (35, 75). Microbial contaminations in foods are expressed in two forms: (i) prevalence data (percentage of positive samples in a given study, i.e., growth/no growth of a target pathogen after enrichment in an appropriate broth of an aliquot of a food sample) and (ii) concentration data expressed as CFU per gram or CFU per milliliter. Data on the concentration of pathogenic bacteria in foods, while scarce, are essential to QMRA.

Previous works on QMRA did not consider low levels of concentrations, i.e., concentrations below the threshold of detection of microbiological methods (6, 15, 44, 53). However, low concentration estimates in raw materials subjected to further processing and storage are necessary for proper QMRA. Finding low initial numbers of bacteria does not mean that the bacteria will not increase to reach numbers critical for human health.

The objective of this work is to estimate bacterial concentration levels from prevalence and concentration data using two statistical methods: (i) a determination of the parameters of a normal distribution on the logarithm base 10 (log) of microbial concentrations and (ii) a mixture model of two normal distributions on the logarithm base 10 of microbial concentrations using a Bayesian approach (37). The methods are both based on the most-probable-number (MPN) theory to estimate bacterial concentrations from prevalence data (10, 11, 28) and allow modeling of both prevalence and concentration data in a single frame. In the method for determining the parameters of the normal distribution, the mean of the distribution was estimated from the MPN estimates and its standard deviation was estimated from the concentration data. The assumption of the mixture model is to consider that the concentrations are distributed by two normal distributions, one representing low concentrations (below the threshold of detection) and one representing high concentrations (higher than the threshold of detection). Using a probabilistic approach of the MPN theory on prevalence data, the low concentrations and the variability of concentrations between studies were estimated. High concentrations and variability of concentrations between samples representing the variability within studies were directly estimated from the concentration data. The estimations were carried out as in a variance component model and by using a hierarchical Bayesian approach (12).

In a Bayesian framework (37), model parameters are random variables and are firstly described by a prior distribution. When information about parameters is absent or poor, uninformative or vague prior distributions are used. In contrast, available expert knowledge may contribute to more-informative prior distributions. Posterior distributions over all parameters are computed using Bayes' theorem, which combines prior distributions and information available in the data set. From these posterior distributions, distributions of predicted quantities of interest can be computed. Hierarchical Bayesian models use an additional level on parameters, i.e., observations are modeled conditionally on certain parameters of interest, which themselves are given distributions that conditionally lead to further parameters, known as hyperparameters. In these models, hyperprior distributions are assigned to hyperparameters. Through the hyperprior distributions, hierarchical Bayesian models account for the variability and the uncertainty of the parameters of interest (23, 58, 61).

The two statistical methods were applied to the estimation of the contamination of vegetables with the food-borne pathogenic bacterium Listeria monocytogenes. L. monocytogenes has caused several recognized outbreaks of food-borne infections in which vegetables were implicated; it is regularly isolated from fresh vegetables and can survive and grow even at low temperatures (7, 8, 34, 54, 65). L. monocytogenes is therefore a major hazard for fresh and minimally processed vegetables. Its prevalence in vegetables is rather well documented and monitored by the food industry, facilitating the collection of a significant amount of data from international literature or from food companies, along with a comparison of concentration levels of different categories of vegetables, periods of publications, degrees of processing, and geographical origins of vegetables. In addition, the methods of detection of food-borne pathogens show various sensitivities (78, 80), and their influence was tested by taking advantage of the flexibility of the Bayesian approach. However, the prevalence of L. monocytogenes in vegetables is generally below 5% and concentration data are scarce and relevant for the highest microbial concentrations. Establishing the distribution of contamination from such structured data requires proper methods, and these are tested in the present work.

MATERIALS AND METHODS

Data related to L. monocytogenes prevalence and concentration in vegetables.

Data related to L. monocytogenes contamination of fresh unprocessed or minimally processed vegetables were extracted from the scientific literature, the FSTA database (Food Science Technology Abstracts; IFIS Publishing, Reading, United Kingdom), reports from the French food inspection service DGCCRF (Direction Générale de la Concurrence, de la Consommation et de la Répression des Fraudes, Paris, France) (19), and food companies (69). Papers and reports not using proper methods for L. monocytogenes detection or confirmation or those containing ambiguous information about the number of samples analyzed or L. monocytogenes prevalence or concentrations were excluded. Only fresh unprocessed (undressed and uncooked) or minimally processed (trimmed, cut or shredded, or washed) vegetables were considered. Data were kept in the format of the bibliographic source. Consequently, for each paper or report, several studies of different vegetables may have been analyzed. From 51 selected papers and reports, J (=165) prevalence studies (absence/presence of L. monocytogenes) were identified (Table 1). For each study, the number of analyzed samples (n), the number of positive samples (r), and the analyzed quantity (q) were recorded. A number J0 (=15) out of the J (=165) studies and reports gave concentrations of L. monocytogenes in class intervals (counts in CFU L. monocytogenes per gram), which were also recorded. For instance, in the paper of Sagoo et al. (64), L. monocytogenes prevalence data are n, r, and q equal 3,849, 90, and 25, respectively, and, out of 90 positive samples, the concentrations are lower than 20 CFU/g for 88 samples, between 20 and 99 CFU/g for 1 sample, and between 100 and 999 CFU/g for 1 sample.

TABLE 1.

Number of studies extracted from the 51 papers and reports on the contamination of fresh and minimally processed vegetables with L. monocytogenes per type of product with total, minimum, and maximum numbers of samples analyzed

Product No. of studies
No. of samplesd
References
Total Prevalence only Prevalence and concn Total Min Max
Minimally processed vegetablesa,c 48 42 6 8,511 1 2,934 1, 3-5, 9, 16, 17, 19, 26, 29, 39, 42, 46-50, 55, 60, 62, 63, 69
Minimally processed leafy salad vegetablesb,c 15 10 5 7,511 3 3,849 4, 16, 19, 22, 25, 42, 46, 62, 64, 69, 70, 72
Sprouts and germinated seed, mung bean, alfalfa, and bean sprouts 12 10 2 785 6 276 3, 16, 19, 51, 71
Unprocessed vegetablesa 67 66 1 3,934 1 425 1, 3, 8, 9, 13, 14, 18, 20, 21, 24, 26, 27, 31, 36, 38, 39, 42, 47-49, 51, 56, 57, 59, 66, 67, 69, 71, 72, 74, 78, 81
Unprocessed leafy salad vegetablesb 23 22 1 4,337 10 2,966 9, 13, 21, 25, 27, 32, 38, 41, 42, 45, 57, 67, 69, 71, 78
Total 165 150 15 25,078 1 3,849
Open in a new tab
a

Vegetables included beets, carrots, cabbage, cauliflower, celery, cucumber, roots, bulbs, tomato, spinach, broccoli, leek, various herbs, and mixed vegetables.

b

Vegetables included lettuce, rocket, lamb's lettuce, and endive.

c

Vegetables were trimmed, cut or shredded and washed.

d

Min, minimum; max, maximum.

To generate concentration values from the class interval of concentration, we used the following procedure. For each study j of the J0, k = 1, … , rj concentration values, noted as cj,k, were randomly selected in each class interval by a triangular distribution: triangular(minj,k, modj,k, maxj,k), where the minj,k and the modj,k were assumed to be the lower bound of the interval containing the concentration of the sample k of the study j, and the maxj,k was its upper bound. Afterwards, the randomly selected concentration values cj,k were considered to be observed concentrations for the mixture model. All data were stored in a Microsoft Excel spreadsheet.

Determination of the parameters of a normal distribution to establish the distribution of the contamination. (i) MPN calculations.

The MPN estimation, based on the assumption of a Poisson distribution of the bacterial numbers in a volume, was used to determine the concentrations from prevalence studies (10, 11, 28). Let nj denote the number of analyzed samples for the study j, rj the number of positive samples, and qj the quantity in grams of analyzed samples. Let mj denote the mean concentration expressed in MPN per gram of the samples for the study j. With the Poisson assumption, the probability that a sample of the study j is contaminated is

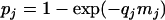graphic file with name M1.gif (1)

This probability can be estimated as rj/nj, and therefore, the mean concentration of the samples of the study j is

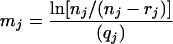graphic file with name M2.gif (2)

Further calculations will use L. monocytogenes counts expressed as CFU per gram or MPN per gram. These counts will be equally designated as viable L. monocytogenes bacteria per gram.

(ii) Determination of the parameters of normal distribution.

L. moncytogenes mean log concentrations were estimated for the J prevalence studies by using equation 2. The logarithms base 10 of these concentrations were assumed to be independently and identically normally distributed as proposed by Jarvis (37). No positive sample (rj = 0) was detected in 100 out of the 165 analyzed studies. For these studies, mj was 0 and consequently an overestimated value of one positive sample (rj = 1) was attributed to make possible the determination of a log(mj) value. The mean M of the J log(mj) values gave the mean of the normal distribution. Concentrations given by the J0 concentration studies were higher than MPN estimates and therefore were assumed to be part of the high percentiles of the contamination distribution. The standard deviation of the normal distribution (S) was derived from the proportion α of concentration values higher than a fixed value log(d), corresponding to the high percentiles of the contamination distribution. The log(d) values of 1 and 2 log viable L. monocytogenes organisms per gram, which are the highest and the most common limits of detection of L. monocytogenes counts in studies reviewed in this work, were chosen to determine the standard deviation.

Estimation of the distribution of the contamination using a mixture model.

The mixture model is based on the assumption that the distribution of the concentrations noted log(c) is a mixture of two normal distributions and can be represented by

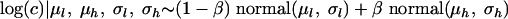graphic file with name M3.gif (3)

where μl and μh are the means of the low and the high log concentrations, respectively, and σl and σh are the standard deviations of the low and the high log concentrations, respectively, and β denotes the proportion of high concentrations from the normal(μh, σh). Assuming that all of the positive samples are contaminated at levels comprised in the distribution of the observed concentrations, an estimation of the proportion β can be expressed as the equation 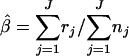Inline graphic.

The parameters of the distribution of low log concentrations were estimated in the following way. Consider J independent prevalence studies, with study j estimating the random parameter pj from the number nj of analyzed samples and from the number rj of positive samples following a binomial distribution:

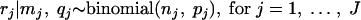graphic file with name M5.gif (4)

The parameter pj, which is the probability for a sample of study j being positive, is expressed as a function of the concentration mj of study j, and qj is expressed as the quantity in grams of analyzed samples by equation 1.

A hierarchy is included in the model to account for the variability between studies. Let mpj be log(mj); the mpj values are viewed as a sample from a common normal distribution with hyperparameters (μp, σp)

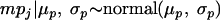graphic file with name M6.gif (5)

where μp and σp are the common mean and the standard deviation, respectively, of the log concentrations of the studies, with σp denoting the variability between studies. Then the mean and the variance of the low log concentrations are given by the equations μl = μp and σl2 = σp2 + s2, respectively, where s is the standard deviation of the sample log concentrations estimated from observed concentrations (see below).

The parameters of the distribution of high log concentrations were estimated as follows. Let a number J0 of studies indexed by j =1, … , J0 out of the J studies, with observed concentrations. The logarithms base 10 of these concentrations, log(cj,k), are then supposed to be normally distributed as follows:

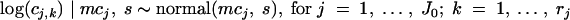graphic file with name M7.gif (6)

where s is the standard deviation of the sample log concentrations denoting the variability within studies and the parameter mcj is the log concentration of the study j. As for low log concentrations, a hierarchical level is considered and therefore the mcj values are distributed by a common normal distribution with hyperparameters (μc andσc)

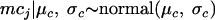graphic file with name M8.gif (7)

where μc and σc are the common mean and the standard deviation, respectively, of log concentrations of the studies with observed concentrations, with σc denoting the variability between studies. Then the mean and the variance of the high log concentrations are given by the equations μh = μc and σh2 = σc2 + s2, respectively.

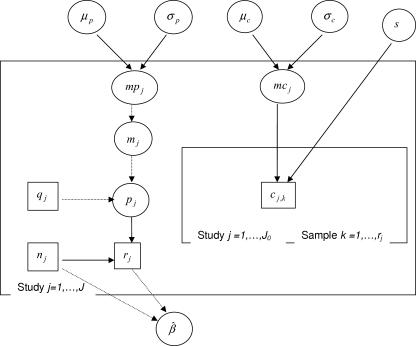
A graphical representation of the model and of its conditional dependences is shown in Fig. 1.

FIG. 1.

FIG. 1.

Open in a new tab

Directed acyclic graph of the model estimating the mixture component parameters. All model quantities are presented as nodes. Data are denoted by rectangles, and parameters and hyperparameters are denoted by ellipses. Arrows run between nodes from their direct influence (“parents”) to the “descendants,” indicating the conditional dependence assumptions of the model: given its parent nodes, each node is independent of all other nodes in the graph except its “descendants.” A solid arrow indicates probabilistic dependences while dashed arrows indicate logical functions. Probabilistic and logical links are described in Materials and Methods. The mixture process to estimate the distribution of predicted concentrations is described in the “Distribution of predicted concentrations” section of Materials and Methods.

Posterior distributions of the hyperparameters and the parameter.

Vague distributions were used to assign hyperprior distributions for the hyperparameters μp, σp, μc, and σc and the parameter s: a normal(0, 106) for each mean μp, μc, and a uniform(0, 103) for each standard deviation, σp, σc, or s.

The analytical calculations of posterior distributions are often difficult, especially for models including many parameters, but computer-intensive techniques, such as those for the Markov chain Monte Carlo method, are powerful for the generation of chains of simulated values for parameters converging to the posterior distribution of interest. With these techniques for each hyperparameter, μp, σp, μc, or σc, and the parameter, s, a vector of a number of B simulated posterior values was computed.

Distribution of predicted concentrations.

The distribution of predicted (pred) concentrations given the observed data (c, r, q, and n) is obtained by simulating B log concentrations from the mixture of the two normal distributions

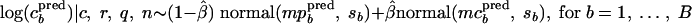graphic file with name M9.gif (8)

Their means, mpbpred and mpcpred, are the realizations obtained by

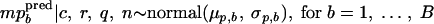graphic file with name M10.gif (9)
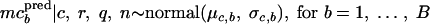graphic file with name M11.gif (10)

Introduction in the mixture model of a rate of sensitivity for the detection methods.

A rate of sensitivity of the method was introduced in the mixture model to account for the inability of any method to detect all contaminated samples. Let tj denote the updated number of positive samples of the study j. tj was introduced in the mixture model by rj | vj ∼ binomial(tj, vj), for j = 1, … , J, where rj is the observed number of positive samples of study j, and vj is the rate of sensitivity attributed to study j. This sensitivity rate was assumed either to be fixed or to be variable and distributed as a triangular distribution to account for the unpredictability of the sensitivity rate expressed in the equation vj ∼ triangular(minv, modv, maxv).

The parameters minv and maxv of the triangular distribution represent the lowest and the highest value of v, respectively, and the parameter modv represents the most probable value of v.

Then expression 4 is replaced with tj|mj, pj ∼ binomial(nj, pj) and the parameter β is estimated as the equation 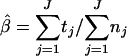Inline graphic.

Integration of qualitative variables in the mixture model.

Let (Xj) with j = 1, … , J denote a qualitative variable representing the product category, publication period, degree of processing, or geographical origin of the studies. Given a vector of one input variable with M modalities (Xj = Xj,0, … , Xj,m, … , Xj,M−1), the output log concentrations mpj and mcj are estimated by replacing expressions 5 and 7 with Inline graphic and Inline graphic, where αp,m and αc,m are the coefficients of the modality m and Xj, m takes the value 1 if the study j has the modality m and 0 otherwise. For m = 0, Xj,m is always equal to 1. For the coefficients αp,m and αc,m, the vague hyperprior distribution normal(0, 106) was attributed.

Computing tools.

Bayesian calculations were performed using OpenBUGS software (MRC Biostatistics Unit, Cambridge, United Kingdom, Department of Epidemiology and Public Health, Imperial College, London, United Kingdom, and Department of Mathematics and Statistics, University of Helsinki, Helsinki, Finland) (68). A triangular distribution function was developed to complete the proposed distribution functions. The convergence of the Markov chain Monte Carlo algorithm was checked by visual analysis of three independent chains and was obtained after 2,000 iterations. Other B (=10,000) iterations were carried out to obtain posterior values of the hyperparameters μp, σp, μc, and σc and the parameter s and predicted concentrations.

RESULTS

Distribution of the contamination using a normal distribution.

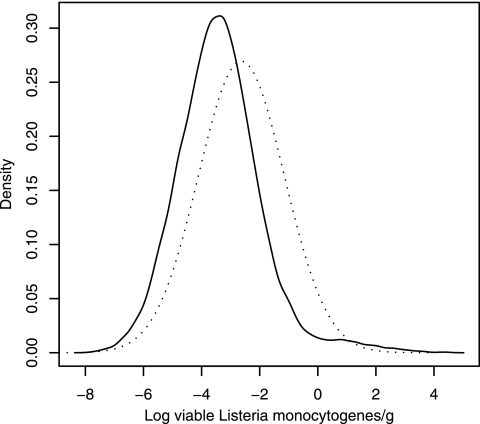
The predicted mean of the normal distribution of the logarithms of viable L. monocytogenes organisms per gram in fresh vegetables was −2.63 log viable L. monocytogenes organisms/g. The percentage of concentration data higher than log(d) = 2 log viable L. monocytogenes organisms/g was α = 0.09% (11 samples out of 12,451 samples tested). The value of the standard deviation of the normal distribution, S, was estimated as 1.48 log viable L. monocytogenes organisms/g (Table 2 and Fig. 2). The percentage of concentration data higher than log(d) = 1 log viable L. monocytogenes organisms/g was α = 1.09% (104 samples out of 9,517 samples tested), and the derived standard deviation S was 1.56 log viable L. monocytogenes organisms/g. In conclusion, selecting log(d) values of 1 or 2 log viable L. monocytogenes organisms/g (and consequently different α values) had almost no influence on the estimation of the contamination distribution using a normal distribution.

TABLE 2.

Descriptive statistics of the log concentrations of vegetables with L. monocytogenes determined by a normal distribution and by the mixture modela

Method Mean SD 2.5th percentile Median 97.5th percentile
Normal distribution −2.63 1.48 −5.53 −2.63 0.28
Mixture model −3.38 1.46 −5.97 −3.45 0.07
Open in a new tab
a

Results are expressed as log viable L. monocytogenes organisms per gram.

FIG. 2.

FIG. 2.

Open in a new tab

Density of log concentrations (expressed as log viable L. monocytogenes organisms per gram) of fresh unprocessed and minimally processed vegetables with L. monocytogenes determined by a normal distribution (dotted line) with an S value of 1.48 log viable L. monocytogenes organisms/g [corresponding to an α value of 0.09% of samples with log(d) counts higher than 2 log viable L. monocytogenes organisms/g], or predicted by a mixture model (solid line).

Distribution of the contamination using a mixture model.

The percentage of positive samples calculated for all studies is expressed as β̂ = 3.01% (754 positive samples out of 25,078 tested samples of fresh unprocessed and minimally processed vegetables). Table 3 shows statistics of the posterior distributions of the hyperparameters. The posterior means of the mean, μp, and the standard deviation, σp, of the log concentrations, estimated from prevalence data, were −3.51 log viable L. monocytogenes organisms/g and 1.10 log viable L. monocytogenes organisms/g, respectively. Therefore, the future log concentrations mppred had a mean of −3.51 log viable L. monocytogenes organisms/g and a 95% credible interval of [−5.70; −1.33] log viable L. monocytogenes organisms/g, i.e., the log concentrations had a probability of 95% to belong to this interval (Table 4). The posterior means of the hyperparameters estimated with concentration data were 1.01 log viable L. monocytogenes organisms/g for the mean μc and 1.03 log viable L. monocytogenes organisms/g for the standard deviation σc of the log concentrations estimated from studies with observed concentrations. Therefore the predicted log concentrations mcpred had a mean of 1.03 log viable L. monocytogenes organisms/g and a 95% credible interval of [−1.12; 3.22] log viable L. monocytogenes organisms/g (Table 4). The posterior mean of the standard deviation of the sample concentrations was 0.57 with a very low standard deviation of 10−4 (Table 3). The variability between studies of prevalence and studies with observed concentrations was quite similar and was higher than the variability within studies.

TABLE 3.

Descriptive statistics of the empirical posterior distributions of hyperparameters and parameter of the mixture modela

Hyperparameter and parameter of the mixture model Value Mean SD 2.5th percentile Median 97.5th percentile
μp Mean −3.51 0.13 −3.79 −3.50 −3.27
μc 1.01 0.28 0.46 1.02 1.57
σp SD 1.10 0.11 0.90 1.09 1.34
σc 1.03 0.23 0.69 1.00 1.58
s 0.57 0.0001 0.54 0.57 0.61
Open in a new tab
a

Results are expressed as log viable L. monocytogenes organisms per gram.

TABLE 4.

Descriptive statistics of the predicted mean log concentrations of vegetables with L. monocytogenes estimated by the mixture modela

Mean log concn type Mean SD 2.5th percentile Median 97.5th percentile
mppred −3.51 1.11 −5.70 −3.50 −1.33
mcpred 1.03 1.10 −1.12 1.02 3.22
Open in a new tab
a

Results are expressed as log viable L. monocytogenes organisms per gram.

Table 2 and Fig. 2 show that the predicted log concentrations of vegetables with L. monocytogenes had a mean of −3.38 log viable L. monocytogenes organisms/g and a 95% credible interval of [−5.97; 0.07] log viable L. monocytogenes organisms/g. The model predicts probabilities of 1.44, 0.63, and 0.17% of samples of fresh unprocessed and minimally processed vegetables to be contaminated with concentrations higher than 1, 2, and 3 log viable L. monocytogenes organisms/g, respectively.

Influence of the sensitivity of the detection methods.

Considering previous works performed on naturally contaminated or artificially spiked samples (2, 30, 40, 43, 73, 77-80), the percentage of sensitivity of the methods (samples testing positive/samples known to be contaminated with L. monocytogenes) ranges from 40 to 100%, being commonly close to 80%. In the absence of specific tests, these values were assumed to be the same for the detection of L. monocytogenes in vegetables and the triangular(40, 80, 100) was used for a variable sensitivity rate.

Introducing a fixed sensitivity rate of 80 or 95% in the mixture model had a small effect on the estimation of the contamination (Table 5). In contrast, introducing a low fixed sensitivity rate (40%) resulted in marked differences in the distribution, especially for high percentiles. The predicted mean log concentration was −2.74 log viable L. monocytogenes organisms/g and the 97.5th percentile was 1.56 log viable L. monocytogenes organisms/g (Table 5), while these values were −3.38 log viable L. monocytogenes organisms/g and 0.07 log viable L. monocytogenes organisms/g, respectively, when no sensitivity rate was used (which corresponds to a sensitivity rate of 100%) (Table 2). With a variable sensitivity rate distributed by a triangular distribution, the predicted mean log concentration and the 97.5th percentile were between those obtained with a sensitivity rate of 40% and those obtained without introducing a rate of sensitivity. Because of an increase in the proportion β̂ of concentrations from the distribution of high concentrations, most differences appeared on the estimate of the 97.5th percentile, but not on the 2.5th percentile, the median, or the mean. For instance, a marked increase from β̂ at 3.01% to β̂ at 7.52% resulted from the introduction of a level of sensitivity of 40% (Table 5).

TABLE 5.

Descriptive statistics of the log concentrations of vegetables with L. monocytogenes estimated for different values of the sensitivity rate of the methods of detectiona

Level of sensitivityb (%) Proportion β̂ of high concn (%)c Mean SD 2.5th percentile Median 97.5th percentile
40 7.52 −2.74 1.61 −5.39 −2.91 1.56
80 3.76 −3.22 1.46 −5.73 −3.32 0.55
95 3.16 −3.33 1.41 −5.77 −3.41 0.10
Triangular (40; 80; 100) 4.12 −3.21 1.56 −5.95 −3.30 0.69
Open in a new tab
a

Results are expressed as log viable L. monocytogenes organisms per gram unless otherwise indicated.

b

A rate of sensitivity of 100% corresponds to estimations made without the introduction of a sensitivity level in the calculation and is found in Table 2.

c

See Materials and Methods for details.

Influence of qualitative variables.

Table 6 shows the descriptive statistics of the concentrations of vegetables with L. monocytogenes estimated with the mixture model for the different qualitative variables which are the type of product (three levels, leafy salads, sprouts, and other vegetables), the process degree (two levels, unprocessed vegetables, minimally processed vegetables), the period of publication (two levels, 1988 to 1999 and 2000 to 2005), and the geographical origin of the studies (three levels, North America, Europe, and other regions). The coefficients of the variables “type of product” and “period of publication” were significantly different from zero (with a credible interval of 95%). Leafy salads, with a mean log concentration of −3.36 log viable L. monocytogenes organisms/g and a 95% credible interval of [−5.99; −0.17] log viable L. monocytogenes organisms/g, showed lower predicted concentrations than those of sprouts and other vegetables, which had means of log concentrations of −3.09 and −3.43 log viable L. monocytogenes organisms/g, respectively, and 95% credible intervals of [−5.88; 0.74] and [−6.10; 0.69] log viable L. monocytogenes organisms/g, respectively. Concentrations of L. monocytogenes in fresh vegetables recorded in publications issued between 1988 and 1999, with a mean log concentration of −2.79 log viable L. monocytogenes organisms/g and a 95% credible interval of [−5.30; 1.49] log viable L. monocytogenes organisms/g, were higher than those from publications issued between 2000 and 2005 with a mean log concentration of −3.94 log viable L. monocytogenes organisms/g and a 95% credible interval of [−6.34; −1.23] log viable L. monocytogenes organisms/g.

TABLE 6.

Descriptive statistics of the log concentrations of the vegetables with L. monocytogenes by the type of product, the process degree, the period of publication, and the geographical origin of the studiesa

Qualitative variable Modality No. of studies Mean SD 2.5th percentile Median 97.5th percentile
Type of product Leafy salads 38 −3.36 A 1.42 A −5.99 A −3.41 A −0.17 A
Sprouts 12 −3.09 B 1.55 B −5.88 B −3.17 B 0.74 B
Other vegetables 115 −3.43 B 1.55 B −6.10 B −3.53 B 0.69 B
Process degree Unprocessed 91 −3.40 1.47 −6.01 −3.48 0.11
Minimally processed 74 −3.37 1.53 −6.03 −3.47 0.57
Period of publication 1988-1999 80 −2.79 C 1.53 C −5.30 C −2.93 C 1.49 C
2000-2005 85 −3.94 D 1.31 D −6.34 D −3.97 D −1.23 D
Geographical origin North America 33 −3.73 1.39 −6.32 −3.78 −0.80
Europe 95 −3.45 1.50 −6.05 −3.53 0.30
Other countries 97 −3.07 1.38 −5.67 −3.12 −0.13
Open in a new tab
a

For each variable, significant differences at the 95% credible interval between modalities are indicated by different letters. Results are expressed as log viable L. monocytogenes organisms per gram unless otherwise indicated.

DISCUSSION

Previous works on quantitative microbial risk assessment stuck strictly to prevalence and concentration data but treated them separately. Such an approach results in a nonestimation of low concentration levels. The method that we proposed to determine the parameters of a normal distribution using prevalence and concentration data can give an easy-to-apprehend estimate of a distribution of contamination. However, it leads to an intrinsic overestimation of the mean concentration because of the artificial consideration of one contaminated sample in studies in which all samples are in fact negative. In contrast, the mixture model offers a framework simultaneously accounting for both prevalence and concentration data. The mixture model using a probabilistic approach of the MPN theory offers an appropriate treatment of studies with all negative samples which are, however, worth considering. It allows an estimation of concentrations that are below the threshold of detection of microbiological methods, but that nevertheless have a high significance for QMRA. The overestimation of the normal distribution relative to the mixture model distribution can be seen on Fig. 2, showing the densities of the two distributions. The mixture model satisfactorily accounts for high concentrations. There are slight differences between the values predicted by the model and those generated by the random selection in the triangular distribution. For instance, the model predicts 1.44% of samples with more than 1 log viable L. monocytogenes organism/g and 0.63% of samples with more than 2 log viable L. monocytogenes organisms/g against 1.87 and 0.61%, respectively, for generated data. However, the differences between concentration data in class intervals (1.09 and 0.09% of observed samples with more than 1 and 2 log viable L. monocytogenes organisms/g, respectively) and predicted high concentrations are due to the constraint of data generation using a triangular distribution, which is nevertheless the most appropriate procedure. Parameters of a triangular distribution can be determined unambiguously from the format of the data, and the distribution accounts for a decrease in probability of high concentrations. The estimation process could be improved using methods adapted to class interval data, such as those for censored data (but with an increased complexity of the model) (33), or with a better availability of defined concentration data. Anyway, in the current situation, the estimation process is likely slightly conservative for high percentiles and therefore keeps its interest for risk assessors or risk managers.

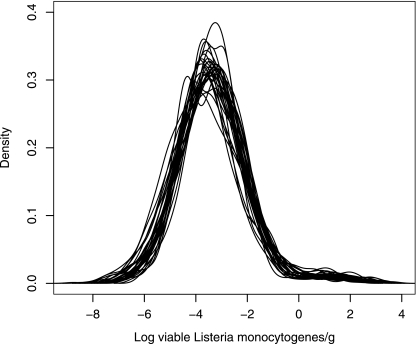
Integrating variability and uncertainty presents great interest when output distributions have to be used as input values for further modeling, such as for further QMRA (52, 76). The hierarchical structure of the mixture model makes possible the introduction in modeling of the “between” and the “within” variability and the uncertainty on the hyperparameters. The variability of the contaminations of fresh unprocessed and minimally processed vegetables between studies is higher than the variability within studies. To approach the overall variability of contaminations, a large number of studies from different contexts (time period, origin, and product) are necessary to reflect the variability of the contaminations, assuming that the variability due to the methods of detection has a minor contribution to the overall variability. The results of the mixture model shown in Table 3, i.e., the mean posterior values of the hyperparameters μp, σp, μc, and σc and the model parameter s can be used in expressions 8, 9, and 10 to simply establish a distribution of L. monocytogenes in fresh unprocessed and minimally processed vegetables. However this computation does not account for the uncertainty of the hyperparameters and parameter. The Bayesian approach makes possible the introduction of several distributions of contamination in simulation processes, including QMRA, determined from a random selection (accounting for the correlations between the hyperparameters and the parameter) of the values of the hyperparameters μp, σp, μc, and σc, and the parameter s in their posterior distributions. Figure 3 shows the diversity of distributions of contamination of fresh vegetables with L. monocytogenes generated by variables μp, σp, μc, σc, and s, reflecting the importance of considering variability and uncertainty. In contrast, Fig. 2 represents the distributions of contamination of fresh unprocessed and minimally processed vegetables with L. monocytogenes, when all variability and uncertainty are integrated, i.e., when all of the distributions of the hyperparameters and the parameter are used.

FIG. 3.

FIG. 3.

Open in a new tab

Diversity of the distributions of predicted log concentrations of fresh vegetables with L. monocytogenes generated by variables μp, σp, μc, σc, and s in the mixture model. Fifty values were randomly selected among the B posterior values of each hyperparameter and parameter. Each curve represents one of the 50 derived density functions of log(cbpred) b = 1, … 50.

No statistically significant difference was observed between vegetables from different origins or between unprocessed and minimally processed vegetables. In contrast, studies of 2000 to 2005 showed lower levels of L. monocytogenes contamination than did the previous ones starting in 1988. This decrease could be attributed to improved management of risk as a consequence of the improved knowledge of the biology and ecology of L. monocytogenes since the first recognized food-borne outbreaks in the early 1980s. This suggests use of the most recent data for QMRA whenever sufficient data are available. In the same way, leafy salads also showed significantly lower numbers of predicted contaminations than sprouts and other vegetables and this suggests the preferential use of disaggregated data or of data relevant to the type of vegetable of interest.

Most studies report the presence-absence of L. monocygenes in series of food samples. As shown in this work, these data have a strong influence on the estimation of the mean concentration but are of limited interest in the estimation of the highest levels of concentration, precisely where major uncertainty lies. Studies combining prevalence and concentration data represent a much heavier and more tedious analytical effort, but have a tremendous impact on the quality of the estimation of the distribution of L. monocytogenes contamination. In addition, the sensitivity of the methods of detection must be high enough (80% showed to be quite satisfactory in this work) to limit high rates of false-negative samples, which may markedly alter the quality of the prediction. The transformation of data obtained by the food microbiologist into a statistical distribution is of fundamental interest to the risk assessor who needs such structured data as input values for risk assessment (75). The mixture model developed in this work is a generic tool responding to the expectations of the risk assessors. It can be applied to contamination data in foods of other major food-borne pathogens, such as Salmonella, Escherichia coli O157:H7, and Clostridium botulinum, which have the same characteristics (majority of prevalence data with a low frequency of positive samples and scarce concentration data) as those of L. monocytogenes in vegetables.

Acknowledgments

Amélie Crépet received a grant from INRA (Paris, France), the Ministry of Agriculture (Paris, France), and ACTIA (Paris, France) (Association de Coordination Technique pour l'Industrie Agro-alimentaire) under contract 03-13 through Aérial, Technology Resource Centre (Illkirch 67, France).

We thank Olivier Gouze for developing the triangular distribution and Valérie Stahl, Catherine Denis, Véronique Huchet, Olivier Cerf, Laurent Rosso, Jean-Jacques Daudin, and Jessica Tressou for stimulating discussions.

Footnotes

▿

Published ahead of print on 10 November 2006.

REFERENCES

  • 1.Arnold, G. J., and J. Coble. 1995. Incidence of Listeria species in foods in NSW. Food Aust. 47:71-75. [Google Scholar]
  • 2.Art, D., and P. Andre. 1991. Comparison of three selective isolation media for the detection of L. monocytogenes in foods. Zentbl. Bakteriol. 275:79-84. [DOI] [PubMed] [Google Scholar]
  • 3.Arumugaswamy, R. K., R. R. A. Gulam, and N. B. A. H. Siti. 1994. Prevalence of Listeria monocytogenes in foods in Malaysia. Int. J. Food Microbiol. 23:117-121. [DOI] [PubMed] [Google Scholar]
  • 4.Beaufort, A., G. Poumeyrol, and S. Rudelle. 1992. Fréquence de contamination par Listeria et Yersinia d'une gamme de produits de 4e gamme. Rev. Gen. Froid. March 1992:28-31. [Google Scholar]
  • 5.Beckers, H. J., P. H. In't-Veld, P. S. S. Soentoro, and E. H. M. Delfgou van Asch. The occurrence of Listeria in food. Foodborne listeriosis. Proceedings of a symposium on September 7, 1988 in Wiesbaden. Behr's Verlag, Hamburg, Germany.
  • 6.Bemrah, N., H. Bergis, C. Colmin, A. Beaufort, Y. Millemann, B. Dufour, J. J. Benet, O. Cerf, and M. Sanaa. 2003. Quantitative risk assessment of human salmonellosis from the consumption of a turkey product in collective catering establishments. Int. J. Food Microbiol. 80:17-30. [DOI] [PubMed] [Google Scholar]
  • 7.Beuchat, L. R. 2002. Ecological factors influencing survival and growth of human pathogens on raw fruits and vegetables. Microbes Infect. 4:413-423. [DOI] [PubMed] [Google Scholar]
  • 8.Beuchat, L. R. 1996. Listeria monocytogenes: incidence of vegetables. Food Control 7:223-228. [Google Scholar]
  • 9.Bind, J. L. 1992. La listériose. Bull. Group Tech. Vet. 89:59-77. [Google Scholar]
  • 10.Blodgett, R. 2001. Bacteriological analytical manual online, appendix 2, most probable number from serial dilutions. http://www.cfsan.fda.gov/∼ebam/bam-a2.html.
  • 11.Blodgett, R. J., and W. E. Garthright. 1998. Several MPN models for serial dilutions with suppressed growth at low dilutions. Food Microbiol. 15:91-99. [Google Scholar]
  • 12.Box, G. E. P., and G. C. Tiao. 1973. Bayesian inference in statistical analysis. Addison-Wesley, Reading, MA.
  • 13.Breer, C., and A. Baumgartner. 1992. Vorkommen un Verhalten von Listeria monocytogenes auf Salaten und Gemüsen sowie in frischgepreßten Gemüsesäften. Arch. Lebensmittelhyg. 43:108-110. [Google Scholar]
  • 14.Breer, C., and K. Schopfer. 1989. Listerien in Nahrungsmitteln. Schweiz. Med. Wochenschr. 119:306-311. [PubMed] [Google Scholar]
  • 15.Cassin, M. H., A. M. Lammerding, E. C. Todd, W. Ross, and R. S. McColl. 1998. Quantitative risk assessment for Escherichia coli O157:H7 in ground beef hamburgers. Int. J. Food Microbiol. 41:21-44. [DOI] [PubMed] [Google Scholar]
  • 16.Cho, S. Y., B. K. Park, K. D. Moon, and D. H. Oh. 2004. Prevalence of Listeria monocytogenes and related species in minimally processed vegetables. J. Microbiol. Biotechnol. 14:515-519. [Google Scholar]
  • 17.de Curtis, M. L., O. de Franceschi, and N. de Castro. 2002. Listeria monocytogenes in vegetables minimally processed ready-to-use. Arch. Latinoam. Nutr. 52:282-288. [PubMed] [Google Scholar]
  • 18.de Simón, M., C. Tarrago, and M. D. Ferrer. 1992. Incidence of Listeria monocytogenes in fresh foods in Barcelona (Spain). Int. J. Food Microbiol. 16:153-156. [DOI] [PubMed] [Google Scholar]
  • 19.DGCCRF. 2002. 1993-1996 and 1997-2001. Plan de surveillance de la contamination des aliments par Listeria monocytogenes. Internal report. DGCCRF, Paris, France.
  • 20.Dhanashree, B., S. K. Otta, I. Karunasagar, W. Goebel, and I. Karunasagar. 2003. Incidence of Listeria spp. in clinical and food samples in Mangalore, India. Food Microbiol. 20:447-453. [Google Scholar]
  • 21.Farber, J. M., G. W. Sanders, and M. A. Johnston. 1989. A survey of various foods for the presence of Listeria species. J. Food Prot. 52:456-458. [DOI] [PubMed] [Google Scholar]
  • 22.Garcia-Gimeno, R. M., G. Zurera-Cosano, and M. Amaro-Lopez. 1996. Incidence, survival and growth of Listeria monocytogenes in ready-to-use mixed vegetable salads in Spain. J. Food Saf. 16:75-86. [Google Scholar]
  • 23.Gelman, A., J. B. Carlin, H. S. Stern, and D. B. Rubin. 2004. Bayesian data analysis, 2nd ed. Chapman & Hall, Boca Raton, FL.
  • 24.Gohil, V. S., M. A. Ahmed, R. Davies, and R. K. Robinson. 1995. Incidence of Listeria spp. in retail foods in the United Arab Emirates. J. Food Prot. 58:102-104. [DOI] [PubMed] [Google Scholar]
  • 25.Gombas, D. E., Y. Chen, R. S. Clavero, and V. N. Scott. 2003. Survey of Listeria monocytogenes in ready-to-eat foods. J. Food Prot. 66:559-569. [DOI] [PubMed] [Google Scholar]
  • 26.Guerra, M. M., J. McLauchlin, and F. A. Bernardo. 2001. Listeria in ready-to-eat and unprocessed foods produced in Portugal. Food Microbiol. 18:423-429. [Google Scholar]
  • 27.Gunasena, D. K., C. P. Kodikara, G. Kumuda, and S. Widanapathirana. 1995. Occurrence of Listeria monocytogenes in food in Sri Lanka. J. Natl. Sci. Counc. Sri Lanka 23:107-114. [Google Scholar]
  • 28.Halvorson, H. O., and N. R. Ziegler. 1933. Applications of statistics to problems in bacteriology. I. A means of determining bacterial population by the dilution method. J. Bacteriol. 25:101-121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Harvey, J., and A. Gilmour. 1993. Occurrence and characteristics of Listeria in foods produced in Northern Ireland. Int. J. Food Microbiol. 19:193-205. [DOI] [PubMed] [Google Scholar]
  • 30.Hayes, P. S., L. M. Graves, G. W. Ajello, B. Swaminathan, R. E. Weaver, J. D. Wenger, A. Schuchat, and C. V. Broome. 1991. Comparison of cold enrichment and U.S. Department of Agriculture methods for isolating Listeria monocytogenes from naturally contaminated foods. Appl. Environ. Microbiol. 57:2109-2113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Heisick, J. E., F. M. Harrel, E. H. Peterson, S. McLaughlin, D. E. Wagner, I. V. Wesley, and J. Bryner. 1989. Comparison of four procedures to detect Listeria spp. in foods. J. Food Prot. 52:154-157. [DOI] [PubMed] [Google Scholar]
  • 32.Heisick, J. E., D. E. Wagner, M. L. Nierman, and J. T. Peeler. 1989. Listeria spp. found on fresh market produce. Appl. Environ. Microbiol. 55:1925-1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Helsel, D. R. 2004. Nondetects and data analysis: statistics for censored environmental data. Statistics in practice. Wiley, New York, NY.
  • 34.Ho, J. L., K. N. Shands, G. Friedland, P. Eckind, and D. W. Fraser. 1986. An outbreak of type 4b Listeria monocytogenes involving patients from eight Boston hospitals. Arch. Intern. Med. 146:520-524. [PubMed] [Google Scholar]
  • 35.Hoornstra, E., and S. Notermans. 2001. Quantitative microbiological risk assessment. Int. J. Food Microbiol. 66:21-29. [DOI] [PubMed] [Google Scholar]
  • 36.Inoue, S., A. Nakama, Y. Arai, Y. Kokubo, T. Maruyama, A. Saito, T. Yoshida, M. Terao, S. Yamamoto, and S. Kumagai. 2000. Prevalence and contamination levels of Listeria monocytogenes in retail foods in Japan. Int. J. Food Microbiol. 59:73-77. [DOI] [PubMed] [Google Scholar]
  • 37.Jarvis, B. 2000. Sampling for microbiological analysis, p. 1691-1733. In B. M. Lund, A. C. Baird-Parker, and G. W. Gould, The microbiological quality and safety of food, volume 2. Aspen Publishers, Gaithersburg, MD.
  • 38.Johannessen, G. S., S. Loncarevic, and H. Kruse. 2002. Bacteriological analysis of fresh produce in Norway. Int. J. Food Microbiol. 77:199-204. [DOI] [PubMed] [Google Scholar]
  • 39.Kaneko, K., H. Hayashidani, Y. Ohtomo, J. Kosuge, M. Kato, K. Takahashi, Y. Shiraki, and M. Ogawa. 1999. Bacterial contamination of ready-to-eat foods and fresh products in retail shops and food factories. J. Food Prot. 62:644-649. [DOI] [PubMed] [Google Scholar]
  • 40.Kornacki, J. L., D. J. Evanson, W. Reid, K. Rowe, and R. S. Flowers. 1993. Evaluation of the USDA protocol for detection of Listeria monocytogenes. J. Food Prot. 56:441-443. [DOI] [PubMed] [Google Scholar]
  • 41.Laine, K., and J. Michard. 1988. Fréquence et abondance des Listeria dans des légumes frais découpés prêts à l'emploi. Microbiol. Alim. Nutr. 6:329-335. [Google Scholar]
  • 42.Levre, E., P. Valentini, and G. Caroli. 1995. Prodotti orticoli e contaminazione da Listeria. Ig. Mod. 103:475-486. [Google Scholar]
  • 43.Liming, S. H., Y. Zhang, J. Meng, and A. A. Bhagwat. 2004. Detection of Listeria monocytogenes in fresh produce using molecular beacon-real-time PCR technology. J. Food Sci. 69:M240-M245. [Google Scholar]
  • 44.Lindqvist, R., and A. Westöö. 2000. Quantitative risk assessment for Listeria monocytogenes in smoked or gravad salmon and rainbow trout in Sweden. Int. J. Food Microbiol. 58:181-196. [DOI] [PubMed] [Google Scholar]
  • 45.Little, C., D. Y. Roberts, E. Youngs, and J. DeLouvois. 1999. Microbiological quality of retail imported unprepared whole lettuces: a PHLS food working group study. J. Food Prot. 62:325-328. [DOI] [PubMed] [Google Scholar]
  • 46.Little, C. L., H. A. Monsey, G. L. Nichols, and J. de Louvais. 1997. The microbiological quality of refrigerated salads and crudites. An analysis of the results from the 1995 European Community Coordinated Food Control Programme for England and Wales. PHLS Microbiol. Dig. 14:142-146. [Google Scholar]
  • 47.MacGowan, A. P., K. Bowker, J. McLauchlin, P. M. Bennett, and D. S. Reeves. 1994. The occurrence and seasonal changes in the isolation of Listeria spp. in shop bought food stuffs, human faeces, sewage and soil from urban sources. Int. J. Food Microbiol. 21:325-334. [DOI] [PubMed] [Google Scholar]
  • 48.McLauchlin, J., and R. J. Gilbert. 1990. Listeria in food. PHLS Microbiol. Dig. 7:54-55. [Google Scholar]
  • 49.Messi, P., C. Casolari, A. Fabio, G. Fabio, C. Gibertoni, G. Menziani, and P. Quaglio. 2000. Occurrence of Listeria in food matrices. Ind. Aliment. 39:151-157. [Google Scholar]
  • 50.Monge, R., and M. L. Arias. 1996. Presencia de microorganismos patogenos en las hortalizas de cosumo crudo en Costa Rica. Arch. Latinoam. Nutr. 46:293-294. [PubMed] [Google Scholar]
  • 51.Murase, M., T. Miyata, H. Kimata, and M. Kurokawa. 2002. Investigation of the actual conditions of pathogenic bacteria among imported fresh vegetables and fruits. Jpn. J. Food Microbiol. 19:71-75. [Google Scholar]
  • 52.Nauta, M. J. 2000. Separation of uncertainty and variability in quantitative microbial risk assessment models. Int. J. Food Microbiol. 57:9-18. [Google Scholar]
  • 53.Nauta, M. J., S. Litman, G. C. Barker, and F. Carlin. 2003. A retail and consumer phase model for exposure assessment of Bacillus cereus. Int. J. Food Microbiol. 83:205-218. [DOI] [PubMed] [Google Scholar]
  • 54.Nguyen-the, C., and F. Carlin. 2000. Fresh and processed vegetables, p. 620-684. In B. M. Lund, A. C. Baird-Parker, and G. W. Gould, The microbiological quality and safety of food. Aspen Publishers, Gaithersburg, MD.
  • 55.Nørrung, B., J. K. Andersen, and J. Schlundt. 1999. Incidence and control of Listeria monocytogenes in foods in Denmark. Int. J. Food Microbiol. 53:195-203. [DOI] [PubMed] [Google Scholar]
  • 56.Pacini, R., L. Panizzi, E. Quagli, R. Galassi, L. Malloggi, and R. Morganti. 1993. Diffusione di Listeria monocytogenes. Ind. Aliment. 32:1086-1089. [Google Scholar]
  • 57.Porto, E., and M. N. Uboldi Eiroa. 2001. Occurrence of Listeria monocytogenes in vegetables. Dairy Food Environ. Sanit. 2:282-286. [Google Scholar]
  • 58.Pouillot, R., I. Albert, M. Cornu, and J. B. Denis. 2003. Estimation of uncertainty and variability in bacterial growth using Bayesian inference. Application to Listeria monocytogenes. Int. J. Food Microbiol. 81:87-104. [DOI] [PubMed] [Google Scholar]
  • 59.Prazak, A. M., E. A. Murano, I. Mercado, and G. R. Acuff. 2002. Prevalence of Listeria monocytogenes during production and postharvest processing of cabbage. J. Food Prot. 65:1728-1734. [DOI] [PubMed] [Google Scholar]
  • 60.Previdi, M. P., L. Tomasoni, and B. Bondi. 2000. Minimally processed and frozen vegetables: microbiological quality and incidence of pathogens in commercial products. Ind. Conserve 75:383-391. [Google Scholar]
  • 61.Robert, C. P. 2001. The Bayesian choice, 2nd ed. Springer, New York, NY.
  • 62.Sagoo, S. K., C. L. Little, and R. T. Mitchell. 2001. The microbiological examination of ready-to-eat organic vegetables from retail establishments in the United Kingdom. Lett. Appl. Microbiol. 33:434-439. [DOI] [PubMed] [Google Scholar]
  • 63.Sagoo, S. K., C. L. Little, and R. T. Mitchell. 2003. Microbiological quality of open ready-to-eat salad vegetables: effectiveness of food hygiene training of management. J. Food Prot. 66:1581-1586. [DOI] [PubMed] [Google Scholar]
  • 64.Sagoo, S. K., C. L. Little, L. Ward, I. A. Gillespie, and R. T. Mitchell. 2003. Microbiological study of ready-to-eat salad vegetables from retail establishments uncovers a national outbreak of salmonellosis. J. Food Prot. 66:403-409. [DOI] [PubMed] [Google Scholar]
  • 65.Schlech, W. F., III, P. M. Lavigne, R. A. Bortolussi, A. C. Allen, E. V. Haldane, A. J. Wort, A. W. Hightower, S. E. Johnson, S. H. King, E. S. Nicholls, and C. V. Broome. 1983. Epidemic listeriosis—evidence for transmission by food. N. Engl. J. Med. 308:203-206. [DOI] [PubMed] [Google Scholar]
  • 66.Sizmur, K., and C. W. Walker. 1988. Listeria in prepacked salads. Lancet i:1167. [DOI] [PubMed] [Google Scholar]
  • 67.Soriano, J. M., H. Rico, J. C. Molto, and J. Manes. 2001. Listeria species in raw and ready-to-eat foods from restaurants. J. Food Prot. 64:551-553. [DOI] [PubMed] [Google Scholar]
  • 68.Spiegelhalter, D. J., A. Thomas, N. Best, and D. Lunn. 2005. OpenBUGS version 2.10, user manual. MRC Biostatistics Unit, Cambridge, United Kingdom; Department of Epidemiology and Public Health, Imperial College, London, United Kingdom; and Department of Mathematics and Statistics, University of Helsinki, Helsinki, Finland.
  • 69.Stahl, V., C. Denis, and V. Huchet. Survey on the contamination of minimally processed fresh salads with major foodborne pathogens. Internal report. ACTIA 03.13. AERIAL, Illkirch, France.
  • 70.Szabo, E. A., K. J. Scurrah, and J. M. Burrows. 2000. Survey for psychrotrophic bacterial pathogens in minimally processed lettuce. Lett. Appl. Microbiol. 30:456-460. [DOI] [PubMed] [Google Scholar]
  • 71.Thunberg, R. L., T. T. Tran, R. W. Bennett, R. N. Matthews, and N. Belay. 2002. Microbial evaluation of selected fresh produce obtained at retail markets. J. Food Prot. 65:677-682. [DOI] [PubMed] [Google Scholar]
  • 72.Tiwari, N. P., and S. G. Aldenrath. 1990. Occurrence of Listeria species in food and environmental samples in Alberta. Can. Inst. Food Sci. Technol. J. 23:109-113. [Google Scholar]
  • 73.Twedt, R. M., A. D. Hitchins, and G. A. Prentice. 1994. Determination of the presence of Listeria monocytogenes in milk and dairy products: IDF collaborative study. J. AOAC Int. 77:395-402. [PubMed] [Google Scholar]
  • 74.Villari, P., G. Greco, and I. Torre. 1997. Listeria spp. in ready-to-eat foods. Ig. Mod. 107:403-410. [Google Scholar]
  • 75.Vose, D. 1998. The application of quantitative risk assessment to microbial food safety. J. Food Prot. 61:640-648. [DOI] [PubMed] [Google Scholar]
  • 76.Vose, D. 2000. Risk analysis: a quantitative guide, 2nd ed. John Wiley and Sons, Chichester, United Kingdom.
  • 77.Waak, E., W. Tham, and M. L. Danielsson-Tham. 1999. Comparison of the ISO and IDF methods for detection of Listeria monocytogenes in blue veined cheese. Int. Dairy J. 9:149-155. [Google Scholar]
  • 78.Walsh, D., G. Duffy, J. J. Sheridan, I. S. Blair, and D. A. McDowell. 1998. Comparison of selective and nonselective enrichment media for the isolation of Listeria species from retail foods. J. Food Saf. 18:85-99. [Google Scholar]
  • 79.Warburton, D. W., J. M. Farber, A. Armstrong, R. Caldeira, T. Hunt, S. Messier, R. Plante, N. P. Tiwari, and J. Vinet. 1991. A comparative study of the ‘FDA’ and ‘USDA’ methods for the detection of Listeria monocytogenes in foods. Int. J. Food Microbiol. 13:105-117. [DOI] [PubMed] [Google Scholar]
  • 80.Westöö, A., and M. Peterz. 1992. Evaluation of methods for detection of Listeria monocytogenes in foods: NMKL collaborative study. J. AOAC Int. 75:46-52. [Google Scholar]
  • 81.Wong, H. C., W. L. Chao, and S. J. Lee. 1990. Incidence and characterization of Listeria monocytogenes in foods available in Taiwan. Appl. Environ. Microbiol. 56:3101-3104. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Applied and Environmental Microbiology are provided here courtesy of American Society for Microbiology (ASM)

RESOURCES