Aggregation during Fruiting Body Formation in Myxococcus xanthus Is Driven by Reducing Cell Movement

Abstract

When starved, Myxococcus xanthus cells assemble themselves into aggregates of about 10⁵ cells that grow into complex structures called fruiting bodies, where they later sporulate. Here we present new observations on the velocities of the cells, their orientations, and reversal rates during the early stages of fruiting body formation. Most strikingly, we find that during aggregation, cell velocities slow dramatically and cells orient themselves in parallel inside the aggregates, while later cell orientations are circumferential to the periphery. The slowing of cell velocity, rather than changes in reversal frequency, can account for the accumulation of cells into aggregates. These observations are mimicked by a continuous agent-based computational model that reproduces the early stages of fruiting body formation. We also show, both experimentally and computationally, how changes in reversal frequency controlled by the Frz system mutants affect the shape of these early fruiting bodies.

Myxococcus xanthus is a rod-shaped gram-negative bacterium that grows in soil, animal dung, or other natural environments rich in organic matter (2). The bacteria move by gliding over solid surfaces, periodically reversing their direction of movement. Gliding motility in this bacterium is driven by two motors: social or S-motility is driven by the extension, adhesion, and retraction of type IV pili (12, 22, 23). Adventurous or A-motility depends on—and may be driven by—slime secretion (21, 25). Gliding reversals are controlled by the Frz chemosensory system; some Frz mutants show greatly reduced or increased reversal rates (1). When nutrients are abundant, myxobacteria form colonies a few cell layers thick in which the cells locally align into domains (14). Under these conditions they swarm away from the center of a colony towards new areas where they retrieve nutrients from prey that are lysed by their secreted exoenzymes (15). When nutrients are scarce, the bacteria undergo a developmental change: cells migrate inward, forming fruiting bodies in which the cells later sporulate. The myxospores are dormant cells, capable of surviving long periods of unfavorable conditions (10, 17).

The behavioral changes of individual bacterial cells during starvation are not always obvious: the variations are very large between the alignment, speed, and reversal frequencies of individual cells. However, multicellular movements are much more striking. Several hours after placing the bacteria under starvation conditions, the cells aggregate into distinct mounds of about 100,000 cells each. In M. xanthus, the process of fruiting body formation terminates with dome-shaped aggregates, as the cells sporulate within the mounds. In related myxobacteria, such as Stigmatella aurantiaca or Chondromyces crocatus, cells aggregate into lobe-shaped fruiting bodies that are highly branched structures, with sporulation occurring within sporangia (2). Several speculative mechanisms have been proposed to describe cell movements leading to fruiting body formation. For example, elasticotaxis, wherein cells follow stress line cues in the substratum, was suggested as a possible mechanism that can direct cells to aggregate into fruiting bodies (3). Alternatively, it has been suggested that streaming can lead to fruiting body formation, since M. xanthus cells frequently form networks of aligned cells that gather into streams, the reversal frequency of cells in streams is reduced, and aggregation centers form where the streams intersect (8, 19). A computational model utilizing cellular automata with nonreversing, self-aligning cells showed that cell alignment and the resulting stream formation could create structures reminiscent of myxobacterial fruiting bodies (11, 20). The observed reduction in reversal frequency of cells in streams as well as the role of the Frz chemosensory system in regulating reversals suggested that chemotaxis may direct cell movements during fruiting body formation. This hypothesis was supported by the finding that the frz mutants cannot form discrete fruiting bodies and that at least two secreted compounds, C-signal and exopolysaccharide (EPS), both cause some reduction in the reversal frequency and have properties suitable for an inducer of this process (7, 8, 19; W. Shi, personal communication). According to this hypothesis, an inducer (EPS, C-signal, or some other unidentified signal) accumulates in and around cell aggregates, where it increases to a high level that is maintained by the increased cell density. This would create a gradient in cell reversal frequency, causing aggregates to grow until all the cells are absorbed.

In this paper we investigated cell movements during the early stages of fruiting body formation, before the onset of sporulation, to validate these models. Our observations suggest a different explanation for cell aggregation based on changes in the velocity of cells instead of reversal frequency. Our model explains various observations on the fruiting body formation process and the phenotypic defects in Frz system mutants. The relationship of the mechanism to previous models is also discussed.

MATERIALS AND METHODS

The strain DK1622 (4) and DK10547, its derivative with green fluorescent protein (GFP) transcriptionally fused to the highly active pilA promoter (26), were used for the wild-type cells. The strain DZ4548, a ΔfrzCD deletion mutant in a DK1622 background, as well as the same strain with the GFP insert moved to strain DZ4548 from DK10547, were used for ΔfrzCD mutants. The cells were grown in nutrient-rich liquid medium (CYE, 1% Casitone [Difco], 0.5% yeast extract [EMD], 8 mM MgSO₄ [EMD] in 10 mM morpholinepropanesulfonic acid [MOPS] buffer [Sigma]; pH 7.6) to mid-exponential phase (between Klett 50 and 100 or 3.8 × 10⁸ to 5.6 × 10⁸ cells/ml). These bacteria were diluted in CYE medium to Klett 20 and plated in coverglass-bottomed chambers (no. 1 glass, one-well; Nunc) at 2 ml per chamber. They were allowed to grow for 24 h at 32°C, when the cells attached to the glass bottom, and then they were washed and the medium was replaced with starvation medium (8 mM MgSO₄ in 10 mM MOPS buffer, pH 7.6). The suspensions of the nonfluorescent cells were mixed with fluorescent cells in proportions of 50:1 or 100:1 depending on the experiment. The cells were kept at 32°C during development, including the period when they were imaged.

The high-resolution images were taken using an Applied Precision Deltavision Spectris DV4 microscope. Pairs of fluorescence and differential interference contrast (DIC) images were taken at 30-s intervals for 2 to 8 h. The low-resolution images were taken with a Zeiss Lumar dissection microscope. The images were postprocessed by image contrast enhancement and spatial band filtering. Individual fluorescent cells were tracked semiautomatically using homemade software written in the Matlab programming language where manual tracking was required for tracking touching cells. Cell speeds were computed by measuring the shifts in cell positions of randomly chosen cells in ∼10 consecutive frames at different stages of development. The cell orientations were measured by capturing the “front” and the “back” of each cell in the specified area. The front and the back were considered equivalent in still pictures; in movies they were distinguished by their direction of motion. The boundaries of the fruiting bodies were determined from the DIC images.

RESULTS

Tracking individual cells as they form fruiting bodies.

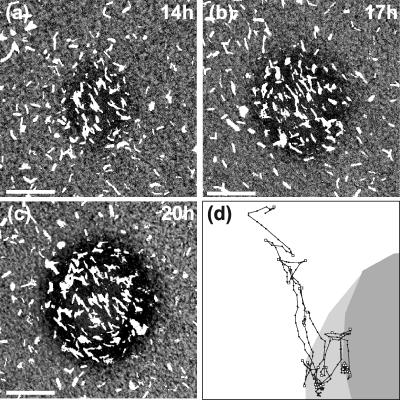
Our experiments consisted of carefully following the movements of cells during fruiting body formation by time-lapse video microscopy. The experiments were conducted in a submerged culture on a glass surface. These conditions were chosen since cells can be imaged in this culture for long periods of time at high resolution. Moreover, this setup eliminates elasticotaxis effects. In these experiments, cells were grown in rich medium until they formed a layer approximately two to three cells thick, at which time the cells were arranged in domains of coaligned cells. The growth medium was then replaced with a medium lacking nutrients. Under these cultural conditions, it usually took 13 to 14 h for the first aggregates to become visible (Fig. 1a to c) and an additional 8 h for the aggregates to form fruiting bodies. The fruiting bodies at 20 to 22 h contained fully motile rod-shaped cells that had not yet begun to sporulate. These fruiting bodies were essentially complete in that they contained approximately the same morphology and number of cells observed in older fruiting bodies. (The number of cells was determined by counting the average cell density outside of the fruiting bodies. At these times, the cell density was stable.) We refer to the period between 10 and 20 h of starvation as the early stage of fruiting body formation. Sometimes cells left outside of fruiting bodies, the peripheral rods, moved in accordion waves called “ripples,” although ripples were not well pronounced under the plating conditions used in this study. Figure 2a shows the arrangement and morphology of the fruiting bodies. These fruiting bodies are hemispherical, about 80 μm in diameter, distributed randomly at a density of ∼10 to 15 fruiting bodies/mm². Since it is very difficult to follow the motility of individual cells in a large group, we spiked the cultures with fluorescently labeled cells (1 to 2%) before beginning the experiments. These cells could easily be tracked using a fluorescence microscope. This setup allowed us to observe the layer about 5 μm thick on top of the glass surface that contained all cells before fruiting bodies formed and lower layers of the fruiting bodies as they grew taller (after 15 to 16 h of starvation). A few images from one series are shown in Fig. 1a to c, and the track of one such cell is shown in Fig. 1d. The most noticeable difference between the cells inside and outside of fruiting bodies was their velocity: cells inside fruiting bodies moved much slower than ones outside (Table 1; see also movie S1 in the supplemental material). Surprisingly, we observed no noticeable difference in the average rates of cell reversals inside and outside of the fruiting bodies. Single cells were observed leaving and reentering the nascent fruiting bodies many times over the course of an experiment (Fig. 1d).

FIG. 1.

Growth of a fruiting body, showing the distribution of cells. (a to c) Different stages of formation of the same fruiting body. Approximately 1/50 of the cells are labeled with GFP; they appear as white regions on the image. These images are taken from the sequences used to compute the motion parameters of individual cells. A movie constructed from the entire sequence, along with the corresponding computational movies, can be downloaded from the supplemental material. Bars, 20 μm. (d) Example of an individual cell track for a representative cell. The fruiting body shapes at the beginning and at the end of the tracking period are shown as shaded areas: the dark gray indicates its initial shape, and light gray indicates its final shape. Locations of the cell on each frame are shown as dots; the frames are separated by 30-s time intervals. The cell started the motion at the top left corner and finished at the bottom point of the track. Automatically determined reversal points are shown with squares. The reduction in the distances between cell positions in consecutive frames shows the velocity decrease.

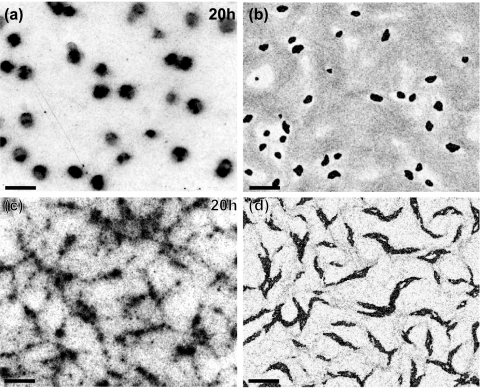
FIG. 2.

Comparison of experimentally observed and computed fruiting bodies. (a) Low-resolution bright field image of formed fruiting bodies. The image is taken 20 h after the beginning of starvation. (b) Corresponding image computed from the model. The image was taken at approximately 10 h of cell time (i.e., the time of the simulated cells, as opposed to computer time) after the beginning of the simulation corresponding to the time for panel a. (c) Image of the ΔfrzCD mutant under the same conditions as described for panel a. (d) Corresponding computed image. Bars, 200 μm.

TABLE 1.

Motility parameters inside and outside of fruiting bodies^a

Strain	Location	Velocity (μm/s)	Time between reversals (min)
Wild type	Outside	0.12 ± 0.04	7.5 ± 3
Wild type	Inside	0.023 ± 0.01	7.5 ± 3
ΔfrzCD	Outside	0.13 ± 0.04	>60
ΔfrzCD	Inside	0.056 ± 0.03	>60

^aIndicated errors combine statistical errors of the mean and variability between different cells or samples.

Cell densities were not uniform: the cells formed a network containing regions of aligned cells at higher cell density. The first aggregations appeared in these areas of higher density; these groupings acquired a circular shape, with the interior cells aligned parallel to one another (Fig. 1a). At this stage, most cells entering a nascent fruiting body remained in the aggregate, but cells that escaped usually joined the randomly moving cells outside. As fruiting body aggregates grew, the alignment of cells changed. First, the cells on the periphery aligned tangential to the fruiting body, but by 20 h the fruiting body contained cells in parallel in the central area and tangential cells on the periphery. The proportions differed in individual fruiting bodies (Fig. 3a, c, and e).

FIG. 3.

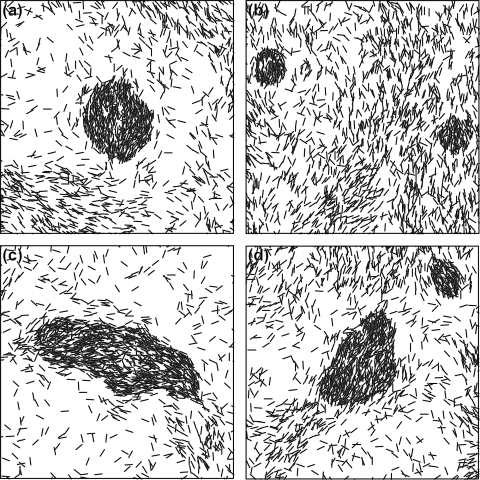
Orientations of cells inside a typical fruiting body at different times. Left panels show the experimental data for the same fruiting body, and right panels show the corresponding frames in the simulations. The time of development is indicated on the panels. Each cell shown (1 out of 50, as in Fig. 1) is represented by a line segment of the actual cell length both on the experimental and computed images. Dashed lines are the fruiting body boundaries, defined as a line of equal total density determined from DIC images on the experimental figures, and from total density on the simulated figures. In the earliest aggregates the cells are mostly coaligned; they acquire tangential orientations later as the cell density on the periphery becomes higher than in the interior of the nascent fruiting body. Bars, 20 μm.

Because cell reversal rates are important for fruiting body formation, we examined the ΔfrzCD mutant, since it is defective at reversing. This mutant does not form discrete fruiting bodies but forms “frizzy” aggregates with greatly elongated shapes, as shown in Fig. 2c. The individual cell tracking results are presented in Table 1. As with the wild type, the mutant also showed significant differences in speed between cells inside and outside the aggregates.

Computational results.

To quantify the behavioral rules that govern aggregation patterns of wild-type and mutant cells, we constructed a computational model to describe the behavior of individual myxobacteria. The model is based on several assumptions that are supported by previous experimental observations and by the experiments described above.

(i) Isolated cells glide back and forth autonomously, implying the existence of an internal biochemical cycle, or clock (6). The exact nature of this clock is not important for our present analysis.

(ii) Neighboring cells align with each other, i.e., cells are found coaligned in domains, presumably by steric constraints. This is in agreement with our observations and those of others (14).

(iii) Cell reversals in a particular cell are independent of reversals in other cells. This assumption is based on our experiments that showed that the reversal rates of different cells are independent. This rule may not be true under all conditions, and the effect of signal exchange-dependent reversals is investigated in the Appendix.

(iv) Cells reduce their velocity in regions of high density. This is reflected by our observations that the speed of cells in large aggregates under developmental conditions is significantly slower than outside.

Based on these assumptions we constructed an agent-based model of cell behavior. In this type of model each cell is represented as an individual object moving on a continuous two-dimensional surface. An agent model is more suitable for our system than a mean-field or a cellular automata model because more experimental information can be taken into account and we can be fairly certain that the effects we observe are not numerical artifacts arising because of discretization errors and instabilities. In the model, each cell is characterized by its spatial coordinates in the plane, its speed, and its direction of motion (Fig. 4a). The equations of motion consist of a force balance between a constant driving force and the viscous drag that increases with cell density and a density-dependent torque balance that promotes steric alignment of each cell with the cells in its neighborhood but perpendicular to the local cell density gradient. The exact forms of the equations are given in the Appendix, below.

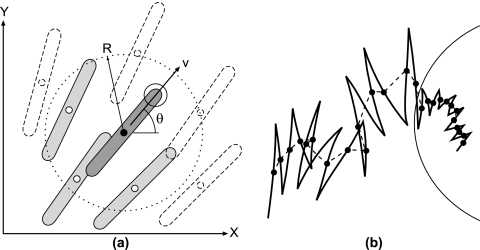
FIG. 4.

(a) Schematic representation of the computational model showing the computational variables. The cell under consideration is shown with a black center. Each cell is represented by its center coordinates (x and y), its direction of motion, θ, and its scalar speed, v. The cell aligns to its neighbors whose centers are located within a certain interaction range, R; the corresponding area is indicated by the dotted line. The cells transmit a density signal to each other when their centers are located within the same range, R. If rippling signaling is taken into account (see Appendix), a cell also transmits a collision signal when its head is located within the interaction regions (indicated by a solid circle) around the head of another (shaded) cell. (b) Illustration of a random walk performed by a cell in the model. The cell track is represented by a solid line. The mid-points between reversals (black dots) can be treated as an object performing a random walk with an anisotropic diffusion coefficient. The equivalent path of a cell is indicated by the dotted line. The diffusion coefficient in the fruiting body decreases because of the reduction in the cell's velocity.

The simulation parameters were determined directly from the experimental data, wherever possible. Those parameters not determined directly were selected to fit the observed properties of the cellular patterns (see Table A1, below). The simulations always started with random cell distributions and orientations and ran for an experimental time of approximately 10 h of starvation conditions. To select a computational picture corresponding to an experiment, a picture was taken at the corresponding cell time minus 10 h.

TABLE A1.

Parameters used in the simulations

Parameter	Name	Value	Source
ρ	Average/initial density	0.3 μm−2	Estimates from counting fluorescent cells or high-resolution imaging
ρO	Threshold density	0.7 μm−2	Fitted to obtain correct no. of fruiting bodies
v0 = Fspτv	“Fast” velocity	0.1 μm/s	Cell speed measurements using time-lapse imaging and cell tracking
vs = Fsp(τv + τρ)	“Slow” velocity	0.02 μm/s
D	Diffusion coefficient	3 × 10−6 μm2/s
Dθ	Angular diffusion coefficient	3 × 10−6 rad2/s	Fitted to obtain correct alignment/streams
Dφ	Phase diffusion coefficient	10−4 rad2/s	Determined from the variance of the time between reversals
τν	Speed correlation time	50 s	Estimate from cell tracking
τθ1	Alignment to neighbors	1,000 s	Fitted to obtain streaming pattern at early stages and correct timing
τθ2	Alignment to aggregate boundary	1,000 s	Fitted to obtain correct late structure
go	Minimum aligning gradient	0.3 μm	Visual observations/estimate
ω	Phase speed	0.0009 rad/s	Cell tracking, time between reversals (T ≈ π/ω ≈ 400 s)
L	Cell length	5 μm	Microscopic observations, L ∼ 3-6 μm
R	Interaction distance for alignment and streaming signaling	5 μm	R ∼ L
Rc1	Interaction distance for collision signaling	1 μm	About two cell diameters, ∼0.5 μm
α	Collision signaling coefficient	0a, 5 μm−2	Fit from reference 18
ρ	Streaming signaling coefficient	0b, 2.5 μm−2	Estimated to reduce the reversal rate by half
Δt	Time step	3 s	Numerical parameter, should be less than any other time scale

^aIn the text, α = 0; in Fig. A1b and d, α = 5 μm⁻².

^bIn the text, ρ = 0; in Fig. A1c and d, ρ = 2.5 μm⁻².

In the simulations, cell streams formed early on, resembling those seen previously(19). These streams develop purely due to steric alignment of cells (see Fig. A3, below). The final pattern formed in the simulations is presented in Fig. 2b, which is a frame from the movie available in the supplemental information. The number and size of the fruiting bodies are well reproduced. The major parameter that cannot be determined from the data is the density threshold after which cells slow down. When this parameter is small, a larger number of smaller fruiting bodies form and the process is accelerated. Adjusting the value of this parameter allows the model to reproduce the correct growth rate of the fruiting bodies. In the simulations, it takes ∼10 h to form fruiting bodies (corresponding to 10 to 20 h of starvation in the experiments). A depletion region of lower cell density immediately surrounding the fruiting bodies formed, similar to that seen in the experiments (data not shown). These pattern characteristics were quite insensitive to the reduction in cell velocity.

FIG. A3.

Streams formed at very early stages of the simulated process (1 h of cell time). Cells form a network of streams. However, since there is no change in the frequency of cell reversals, there is no net convective motion in these streams: they are a result of steric alignment of the cells.

The orientations of the cells were also similar to those observed experimentally. Cells in early fruiting bodies were all aligned, although the overall shapes of the fruiting bodies were already spherical. Later fruiting bodies acquired tangentially orientated cells around their periphery. The fraction of cells on the periphery depended on the adjustable coefficient of alignment to the fruiting body edge (Fig. 3).

The same model was used to simulate the patterns formed by the ΔfrzCD mutant, as shown in Fig. 2d. In these simulations the mutants were assumed to differ from the wild-type cells only by their reversal rates, which were significantly smaller. That this modification alone is sufficient to model fruiting bodies in a mutant with a severe defect in the reversal rate suggests that the fruiting body formation process is not caused—at least initially—by varied reversal rates. Early-stage fruiting bodies developed elongated shapes which grew into a network of aggregates, very similar to the patterns observed experimentally.

DISCUSSION

In this paper, we studied the mechanisms that initiate fruiting body formation in M. xanthus. This process—central in the life cycle of M. xanthus—is quite robust, taking place under a wide range of conditions. We have focused primarily on the earliest stages, when the size and number of fruiting bodies are determined. Our analyses used high-resolution time-lapse imaging to track the position and orientation of individual cells labeled with GFP within fruiting bodies. These experiments determined the shape and size of the nascent fruiting bodies, the timing of the process, and the cell velocities and orientations inside and outside aggregates. Our results clearly showed that during aggregate formation, cells slowed down; moreover, they oriented themselves in parallel inside fruiting bodies and circumferentially around the periphery.

Some of our observations differ significantly from previous studies. For example, we rarely observed ripples, and even when ripples were seen, they were not very distinct (for a description of ripples see references 6, 16, 18, and 24). Ripples were only observed under very specific conditions of cell density, cell orientation, and nutrition. Cells outside fruiting bodies that we studied were not suitable for this process. Under these conditions the times between cell reversals were independent of cell density.

In order to investigate the basic rules of cell behavior that are important for fruiting body formation, we constructed an agent-based model that incorporated the cell alignment and reduced cell velocities observed experimentally. This model was sufficient to generate fruiting body-like aggregates that reproduced most of the observed features of myxobacterial fruiting bodies. A central ingredient in the model was decreasing cell velocity in regions of high cell density. We assumed that there is a density threshold beyond which the cells reduce their velocity in proportion to the local cell density. By varying this threshold, we were able to simulate fruiting bodies containing from a few hundred to a hundred thousand cells. Experimentally, fruiting bodies form under a wide range of cell densities. This suggests that the threshold for reducing cell velocity drops to a low level during development.

Cell alignment also plays a prominent role in fruiting body formation. Although cells aggregate over a wide range of alignment parameters, a very high or very low alignment coefficient prevents cells from aggregating. The model also reproduces the streams observed during the very early stages of development, when the aggregations are just beginning to form. These streams are shown below in Fig. A3 of the Appendix; they resemble those seen previously (19). However, these streams arise only from cell alignment and, because cells continue to reverse at their normal frequency, there is no net convective flow of cells. Thus, the term stream is misleading and is used here only for consistency with previous descriptions (“columns” might be a more descriptive term). Diffusive flux is possible, however, if there is a cell density gradient along the stream. The fact that the streams were only observed under developmental conditions could be explained by a change in the mutual adhesiveness of the cells, by a change in density that makes them more visible, or because the streams develop dynamically and become visible slightly later. In any case, stream formation may not be necessary for fruiting body formation, since fruiting bodies still form in simulations when the alignment coefficient is low enough so that streams never form. Indeed, stream formation is less pronounced on glass surfaces in our experiments than on agar (19).

In the models described by Kiskowski and Alber (11) and by Sozinova et al. (20), the cells were assumed to be nonreversing, based on the observations of Jelsbak and Søgaard-Anderson (9). Those models explain how suppression of reversals can lead to fruiting body formation. In our model, C-signaling-mediated alignment used in those works can be replaced by steric alignment. Our experiments showed that the reduction in cell reversals is insignificant during the developmental stages when fruiting body formation takes place. Thus, the above-referenced models can explain the fruiting body formation process only under particular conditions, which are not universal. In addition, the observed reduction in velocity makes unnecessary the reversal suppression mechanism mediated by C-signaling.

Using the parameters given in Tables 1 and A1, below, the simulated aggregates had approximately the correct shape, timing, and number of cells as seen in authentic fruiting bodies. Moreover, the relative cell positions and orientations within the aggregates resembled our experimental observations. For example, in both experimental and simulated early aggregations, cells did not cycle around nascent fruiting bodies, but cyclical cell motions appeared in later aggregates.

We tested the model further by applying it to a population of ΔfrzCD mutants whose reversal rates are extremely reduced. These cells accumulated as a network of elongated “frizzy” fruiting bodies, strikingly different from the wild type. Because the Frz system controls reversals, we hypothesize that this mutant has defects only in the reversals rate, and not in cell density-dependent velocity changes, whatever may be the mechanism. With these assumptions, we obtained simulated patterns closely resembling those observed experimentally.

Two types of signaling have been proposed for M. xanthus: (i) a “streaming” signaling that slows cells' reversal clock so that they reverse less often (7, 19), and (ii) head-to-head “collision” signaling that speeds up the reversal clock and is necessary for ripple formation (6, 18). It was not necessary to include collision-induced effects on reversal frequency, as was necessary to explain the rippling phenomenon (6, 18). The cells in the experiments reported here showed little variation in their reversal frequencies. This could be the result of the two signaling effects compensating for each other. However, similar results were obtained when signaling effects were included. This is discussed in more detail in the Appendix, below.

This study highlights the importance of cell orientation and reductions in cell velocity in fruiting body formation. We found that over long time scales and in the absence of signaling everywhere except in the immediate vicinity of a fruiting body, cell movements can be treated as a random walk (see Fig. 4b for a schematic explanation). Thus, fruiting bodies appear to form by simple diffusion driven aggregation, i.e., as if cells simply diffuse down their density gradient. Cell absorption by fruiting bodies is explained simply by a reduction in the effective diffusion coefficient. Thus, the aggregation process is somewhat analogous to condensation of liquids from vapors. In this process, higher-density fluctuations that arise because random effects in addition to stream formation serve as initial nucleation centers for aggregation. Fruiting body formation may still require chemotactic behavior. However, good agreement between the simulations and the experimental observations suggests that chemotaxis probably plays a secondary role during the early stages of fruiting body formation.

The random distribution of fruiting bodies on the surface in the areas of uniform cell density provides additional evidence for aggregation being mainly due to diffusion. This is shown below in Fig. A2, where this is discussed further. Under other experimental conditions, fruiting bodies may form in regularly spaced arrays. For example, in the submerged culture of Welch et al. (24), fruiting bodies were arrayed linearly around the periphery of the culture and spaced apart twice the wavelength of the ripple field in the adjacent annular region of the culture (5). The reason for this is that the interface between the slime gel and the aqueous medium forced the cells at the colony periphery to be parallel to the boundary. This enforced alignment led to the regular spacing of the fruiting bodies (6, 18). Under the conditions studied here, there was no global alignment or density gradient. Thus, steric alignments were only local, and so the fruiting bodies were distributed nearly randomly. We say “nearly” because the depleted zone around each fruiting body formed a hard core that created a somewhat nonrandom packing of the fruiting bodies (see the Appendix, below).

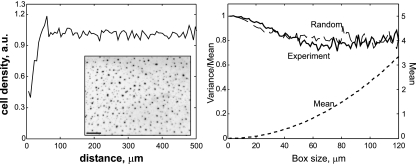
FIG. A2.

Test for randomness of fruiting body distribution. (Left) Radial density distribution of experimentally observed fruiting bodies (for a sample containing ∼1,000 fruiting bodies). The initial increase is determined by the size of the fruiting bodies and the depletion region around each one. The approximately constant dependence and absence of oscillations indicate the absence of a fundamental length scale or wavelike distribution of the dense regions, characteristic of patterns based on Turing instabilities. (Inset) Fragment of a plate with multiple fruiting bodies. Bar, 200 μm. (Right) Variance to mean ratio for the fruiting bodies and for the same number of randomly distributed points with the excluded area (circle of radius 15 μm, with mean distance between fruiting bodies of 49 μm).

What triggers the cell density-dependent reduction in cell velocity required for aggregation? It could involve a reduction in the propulsive force of the A and/or S gliding motors or an increase in the frictional drag on each cell due to increased cell and/or slime density. Since fruiting body formation depends on a broad set of signals expressed only during starvation, we favor explicit signaling over a general increase in drag, but we cannot rule out the latter. Candidates for signaling agents might include extracellular polysaccharide or exposure to C-signal.

Finally, the pattern formation mechanism at work here is completely different from those generated by Turing instabilities (13).

APPENDIX

Computational methods.

In the computational model, each bacterial cell is specified by four real-valued variables: the coordinates of its center, x and y, the cell orientation angle, θ, and the scalar speed, v (see Fig. 4a in the main text). The laws of motion are Newtonian with unit mass, so that the variables change according to the following equations:

Coordinates

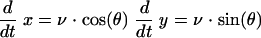(1)

Speed

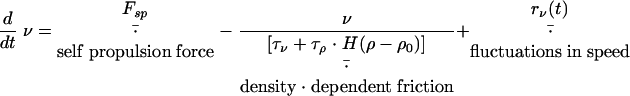(2)

Orientation

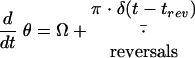(3)

Angular velocity

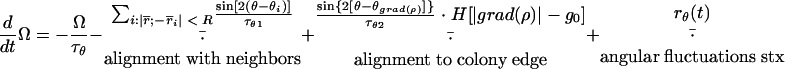(4)

Here, the speed, v, changes under the action of the self-propulsion force, F_sp, which is opposed by friction. The friction force consists of a density-independent term determined by the relaxation time, τ_v, and a density-dependent term determined by τ_ρ · H(ρ − ρ₀), where H(x) is the Heaviside step function. The orientation angle, θ, changes with angular velocity Ω and changes by π (to the opposite direction) when the cell reverses at times t_rev. A test cell orients with a relaxation time τ_θ1 to (or opposite to) the average of all the cells located within a distance R from the test cell and along sharp aggregate boundaries with relaxation time τ_θ2. Here, θ_grad(ρ) is the angle of the density gradient computed as the direction of the vector from the center of the test cell to the center of mass of the cells within a distance R from the test cell. The angular velocity decays with relaxation time τ_θ (usually, τ_θ = τ_v). Random white noise terms r_v(t) and r_θ(t) are added to both velocity and orientation angle equations; if Δt is the time step of the simulations, then r_v(i · Δt) = (6D · Δt)^1/2 · r and r_θ(i · Δt) = (6D_θ · Δt)^1/2 · r, where r is a uniformly distributed random number between −1 and 1, i is an integer number, and D and D_θ are diffusion coefficients.

The reversals were determined by an internal clock characterized by a phase variable, φ. In the absence of intercellular signaling, φ(t) evolves according to the following equation:

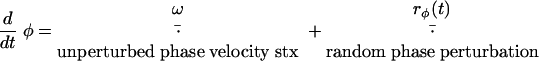(5)

Here, r_φ(t) is a random noise term, r_φ(t + Δt) = r_φ(t) + (6D_φ · Δt)^1/2 · r. A cell reverses when the phase crosses 0, π, 2π,… for the first time. In the simulations that took into account reversal regulation, a more complicated formulation was used (see also the supplemental information).

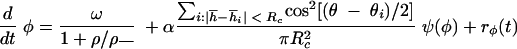(6)

Here, the phase speed increases with collisions and decreases in high-density areas with a coefficient, ρ_, having the dimensions of density. Collisions were counted when the “heads” of two cells were separated by no more than a constant distance R_c. The cell heads were defined as points located at a half-length of a cell (L/2) in the direction of motion from the center of a cell. Here, α is the collision signaling strength and ψ(φ) is the resetting map of the Frizilator limit cycle [see reference 18 for additional details of the method and the shape of ψ(φ)].

A second-order explicit Euler method was used to solve the equations. At each step, the neighbors were determined by dividing the area into squares of size dx × dy, such that dy ∼ dx > L, L/2 ∼ R > R_c. The separation was computed for the cells in the same and neighboring squares, and the torques and the signals were computed only for cells separated by no more than R or R_c, respectively. The computations were performed on a Pentium 4 3-GHz desktop computer. Simulation of a 1-mm² area for the entire time of fruiting body formation took ∼200 h.

Effect of signaling-induced reversals.

The model described in the main text treats cells that reverse at approximately equal time intervals, independent of other cells. This was true in our experiments, but it may not be true under other experimental conditions. In previous publications we showed ripple formation requires a collision-induced speed up of the internal clock at the moment of collision with other cells (6, 16, 18), which we will call here “rippling signaling.” However, the existence of a slowing down effect on the reversal clock in high-density areas has also been proposed, which we will call here “streaming signaling.” This was based on observations of cell streams, as well as of tangentially aligned cells on the periphery of mature fruiting bodies, where cells noticeably reduce their reversal rates (19; W. Shi, personal communication). We extended the model to include the two signaling effects described above in order to understand the effect of signaling-dependent reversals on the patterns formed and to explore the possibility that different effects may compensate each other (Table A1). As expected, weak signaling does not produce any effect; the effect of a higher level of signaling is shown in Fig. A1. Rippling signaling essentially produces an effect opposite to Escherichia coli chemotaxis, working against aggregation. Consequently, fruiting body formation is delayed, and the fruiting bodies seen in Fig. A1b (5 h of simulations) are smaller than for nonsignaling cells (Fig. A1a). The streaming signaling becomes especially strong in high-density areas, where the reversal rates are significantly decreased. The result is reminiscent of the ΔfrzCD phenotype, which produced elongated fruiting bodies (Fig. A1c). These signaling effects, when combined in the model, effectively compensate each other and produce fruiting bodies almost identical to the nonsignaling morphology (Fig. A1d).

FIG. A1.

Effect on fruiting body formation in the computational model where head-to-head signaling resets the internal clock. The images are taken after 5 h of cell time (i.e., time in the simulations) in the early stages of fruiting body formation. (a) No signaling. (b) Strong collision signaling speeds up the clock (as in references 5, 6, and 18). Fruiting body formation is delayed, and as a result we can see small early aggregates. (c) Strong density-dependent slowing of the clock (possibly the effect of EPS and/or C-signal). The fruiting bodies are elongated, similar to the Frz deletion mutants, wherein the reversal rates are reduced. (d) Combination of both signaling effects. In combination, these effects effectively compensate each other, leading to fruiting bodies similar to those in panel a.

Our conclusion is that these signaling effects usually take place in different developmental stages, probably with rippling signaling acting earlier in development and streaming signaling acting on cells close to spores at a later developmental stage. During fruiting body formation, these signals are either weak or partially compensate each other, so that the process of fruiting body formation is not altered significantly by them.

Spatial distribution of fruiting bodies.

One test of the model's validity is the distribution of the fruiting bodies on the plane. In a simplified case, all fruiting bodies can be considered nucleating very fast from loci of local density fluctuations that are distributed randomly. These nucleation centers soon absorb enough cells so that large fluctuations are impossible in other places. This produces fruiting bodies only at loci of the original density fluctuations, which ensures that the distribution of these fruiting bodies is random. This approximation is true everywhere except in the proximity of the fruiting bodies: a nucleating fruiting body recruits, and thus depletes, cells in its surrounding area, thus inhibiting new ones from forming in its vicinity. In addition, larger fruiting bodies absorb younger and smaller neighbors that develop subsequently. The radial distribution function is defined as the average fruiting body density at all distances from each fruiting body. This function should grow from zero to its maximum value within the average distance between fruiting bodies and then stay constant (Fig. A2, left panel). In the case of Turing instabilities—typical of patterns generated by reaction-diffusion equations—the radial distribution function will oscillate several times about its average value.

Another test is to split the area into boxes of various sizes and compute the ratio of the variance to the mean number of fruiting bodies per box. For a Poisson distribution, this ratio should be unity. If there is a depletion region around each aggregation, this ratio will decrease to a somewhat smaller value (Fig. A2, right panel). Figure A3 also shows these distributions in the experiments, in which the distribution of the fruiting bodies clearly showed no regular pattern.