Breaking proteins with mutations: threads and thresholds in evolution

A common high school science experiment involves anchoring one end of a rubber band to a desk and then attaching a small weight to the other end. The weight stretches the rubber band, and adding another weight causes the rubber band to dangle even lower. More weights can be added, and each one pulls the rubber band a little further towards the floor. Now, instead imagine attaching the weights to a thread. The thread stretches only slightly; so the first couple of weights have just a small effect. But if you add enough weights, the thread suddenly breaks and the weights fall to the floor. In the first case, each additional weight stretches the rubber band by the same amount, whereas in the second, it is the combination of several weights that breaks the thread. Mutating proteins is like adding weights, as mutations eventually ‘break' the individual proteins, dragging down the fraction of proteins that still function (this fraction is the average fitness).

The question becomes, does each mutation decrease the average fitness by the same amount (like weights on a rubber band), or are several mutations worse than their combined individual effects (like weights on a thread)? The latter situation is called ‘negative epistasis,' and measuring the extent of epistasis is important for understanding evolution. If mutating a protein is like stretching a rubber band, then there is no epistasis and each random mutation has the same probability ν of leaving a protein's function intact. So the average fitness W₍₁₎ after each protein is mutated once is ν, as this is the fraction of proteins that are still functional. Because there is no epistasis, the second mutation is just as likely as the first to inactivate the protein; so the average fitness W₍₂₎ after each protein is mutated twice is ν². After n mutations, the average fitness is just

where α is defined to be −ln ν. In this equation, larger values of ν (corresponding to smaller values of α) indicate an increased robustness of the protein towards mutations. Indeed, several studies (Shafikhani et al, 1997; Guo et al, 2004) have reported that average protein fitness declines roughly exponentially with the number of mutations, in accordance with equation (1).

On the other hand, if mutating proteins resembles stretching a thread, then the second mutation may inactivate a larger fraction of proteins than the first mutation, owing to the additional damage from combining mutations. One equation that captures how such negative epistasis might affect the mutational decline in average fitness is (Charlesworth, 1990)

This equation differs from equation (1) by its inclusion of an epistasis parameter β that causes the average fitness to decline more than exponentially as additional mutations accumulate. Small values of α still indicate that the proteins are robust to the first few mutations, but large values of the epistasis parameter β cause an increasingly steep drop in average fitness for more mutations.

In a recent paper in Nature, Bershtein et al (2006) report randomly mutating TEM-1 β-lactamase proteins and testing whether the changes in average fitness are better described by equation (1) or (2). When they test their lactamases with high concentrations of the antibiotic ampicillin, they find that mutations sharply decrease the average fitness in a fashion that is well described by equation (1), indicating that there is not only little epistasis but also little robustness to initial mutations. When they test their lactamases with low concentrations of antibiotic, they find them initially to be quite robust to mutations. But with more mutations, the average fitness drops steeply. Bershtein et al argue that this situation is better described by equation (2), indicating the presence of negative epistasis. They also suggest that robustness and epistasis are linked, with proteins that are highly robust to initial mutations displaying more negative epistasis. The underlying explanation offered by Bershtein et al is that the lactamases have an extra margin of function and stability beyond the threshold imposed by the low antibiotic concentration. The first few mutations are buffered by this extra margin, but once the margin is exhausted the mutants begin to cross the threshold, and the average fitness declines sharply.

This finding has a parallel to our own work on lactamase (Bloom et al, 2005). We mutated two lactamase variants with different stabilities and tested them at the same antibiotic concentration. We found that the more stable lactamase variant was more robust to mutations, an effect that we attributed to an extra margin of stability (Bloom et al, 2005) (and subsequently also confirmed for a different protein, cytochrome P450 (Bloom et al, 2006)). Therefore, increasing protein stability (as we did) or decreasing the antibiotic concentration (as done by Bershtein et al, 2006) has the same effect of providing the lactamase with an extra margin that increases its initial mutational robustness. We found that in our data, the decline in average fitness was consistent with a simple stability threshold model that assumes that once the stability margin is exhausted, the protein unfolds and loses function (Bloom et al, 2005). However, our stability threshold model predicts negative epistasis for only the first few mutations, until the stability margin is exhausted. Beyond this point, average fitness is predicted to decline exponentially (Bloom et al, 2005; Wilke et al, 2005). On the other hand, equation (2) used by Bershtein et al (2006) suggests that negative epistasis eventually causes the average fitness to decline more than exponentially. Another important difference is that we tested all our lactamases at the same antibiotic concentration, whereas Bershtein et al tested a range of concentrations. Their work therefore adds an additional dimension to the fitness space: in this setting, the fitness of a mutant depends on the extent to which it confers resistance. An interesting question for future research is whether the simple stability threshold model can be quantitatively extended to the more complex situation studied by Bershtein et al.

The analogy with the weights on a thread can help us visualize how a threshold can cause both robustness and epistasis in proteins. Protein chemists often think of epistasis as being caused by specific interactions between mutated residues. However, if two mutations combine to exhaust a stability margin that is sufficient to buffer either of them individually, there is negative epistasis even in the absence of a direct interaction. The thread is robust to the first few weights, as they do not exceed its threshold strength. But just as weights will eventually combine to snap the thread, enough mutations will eventually exceed a protein's capacity to withstand them (Figure 1).

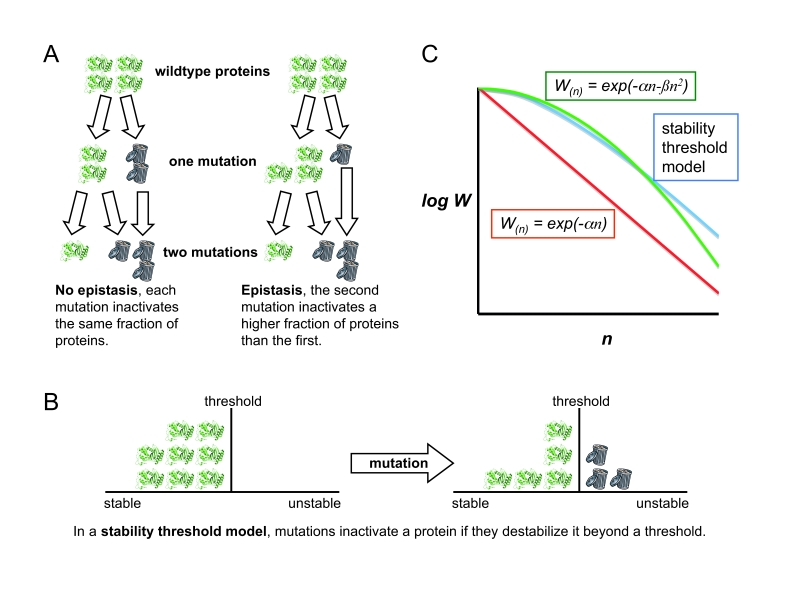
Figure 1.

(A) Without epistasis, each random mutation inactivates the same fraction of the remaining functional proteins. In the negative epistasis model used by Bershtein et al (2006), each subsequent mutation inactivates a larger fraction of proteins. (B) In a stability threshold model (Bloom et al, 2005), a protein is inactivated if it is destabilized beyond a threshold. Proteins are robust to the first few mutations, if they have high stability (Bloom et al, 2005, 2006). (C) Without epistasis, the average fitness (W) decreases exponentially with the number of mutations (n), as described in Shafikhani et al (1997) and Guo et al (2004) (red line). The negative epistasis equation used by Bershtein et al (2006) predicts that proteins are robust to the first few mutations, but that mutations decrease their average fitness faster than exponentially (green line). A stability threshold model predicts that stable proteins are robust to the first few mutations before their fitness begins to decrease exponentially (blue line, plot is of equation [1] of Bloom et al, 2005). Note that a direct comparison of Bershtein et al (2006) with Shafikhani et al (1997), Guo et al (2004) and Bloom et al (2005) is complicated by the fact that the former fails to account for the fact that each library has a distribution of mutations. However, accounting for this mutational distribution using the method of Shafikhani et al (1997) leads to only modest parameter changes that do not affect the conclusions of Bershtein et al (2006).