Refinement and expansion of signaling pathways: The osmotic response network in yeast

Abstract

The analysis of large-scale genome-wide experiments carries the promise of dramatically broadening our understanding on biological networks. The challenge of systematic integration of experimental results with established biological knowledge on a pathway is still unanswered. Here we present a methodology that attempts to answer this challenge when investigating signaling pathways. We formalize existing qualitative knowledge as a probabilistic model that depicts known interactions between molecules (genes, proteins, etc.) as a network and known regulatory relations as logics. We present algorithms that analyze experimental results (e.g., transcription profiles) vis-à-vis the model and propose improvements to the model based on the fit to the experimental data. These algorithms refine the relations between model components, as well as expand the model to include new components that are regulated by components of the original network. Using our methodology, we have modeled together the knowledge on four established signaling pathways related to osmotic shock response in Saccharomyces cerevisiae. Using over 100 published transcription profiles, our refinement methodology revealed three cross talks in the network. The expansion procedure identified with high confidence large groups of genes that are coregulated by transcription factors from the original network via a common logic. The results reveal a novel delicate repressive effect of the HOG pathway on many transcriptional target genes and suggest an unexpected alternative functional mode of the MAP kinase Hog1. These results demonstrate that, by integrated analysis of data and of well-defined knowledge, one can generate concrete biological hypotheses about signaling cascades and their downstream regulatory programs.

Genome-wide expression profiles (Gasch et al. 2000; Hughes et al. 2000) have paved the way to systems biology approaches that aim to elucidate system architecture by large-scale data analysis. A variety of sophisticated computational methods have been developed toward this goal (Eisen et al. 1998; Ihmels et al. 2002; Beer and Tavazoie 2004; Friedman 2004). An essential and important part of these analyses is the biological interpretation of the computational results based on knowledge available in the literature. The common practice is to first perform the computational analysis and then to explain the results using prior knowledge (Tavazoie et al. 1999). However, several studies have shown the advantage of integrating the existing knowledge as part of the analysis (Ideker et al. 2001; Gardner et al. 2003; Covert et al. 2004; Gat-Viks et al. 2004). In this study we propose a new method that aims to achieve a better understanding of a signaling pathway by integrated analysis of genome-wide datasets and prior knowledge, in a way that improves that knowledge systematically. The method suggests new hypotheses which can be validated by additional focused experiments.

We formalize the current information on the studied biological system in a mathematical model. Cellular signaling networks are characterized by signal transduction pathways that are triggered by environmental stimulation and control the cellular response. For such biological systems, a large body of qualitative knowledge is available today, both on the structural and on the logical relations between the components. In many cases, the information is still informal and thus not amenable to mathematical manipulation. For example, many transcription factors have been established as activators or repressors, but their stoichiometric coefficients are unknown. To properly formalize such qualitative knowledge, we use Bayesian networks, a probabilistic framework for modeling complex systems such as signaling cascades (Sachs et al. 2002; Friedman 2004). Our model formalizes the current knowledge about the structure (“topology”) of the network, i.e., which system components interact, and its logic, which dictates the level of each component based on the level of its upstream effectors (Gat-Viks et al. 2006). The topology tells “which component acts on which other components” and the logic tells “how that action takes place.”

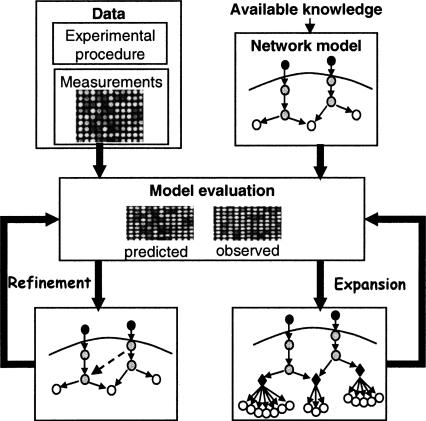
The model predicts the levels of the system's variables (genes, proteins, etc.) under each condition and is improved systematically in a process that seeks structural and logical changes that increase the fit between predicted and observed variable levels. In particular, we propose two methods for model improvement (Fig. 1): The first refines the model by adding interactions and modifying logics, without adding variables. The second expands the model to include additional variables beyond the original model. We focus on the identification of regulatory modules, i.e., sets of coregulated genes that are regulated by the same model components via a common logic. In the standard clustering approach, after identifying a group of coregulated genes, the regulating transcription factors are revealed by overrepresentation of their DNA binding motifs, or by enrichment in chip-ChIP data (Beer and Tavazoie 2004). In contrast, using our methodology, the newly discovered modules are added to the model, and thus their regulators and the logic of their regulation are determined as part of the analysis. Consequently, the expression of the modules is directly explained by the model.

Figure 1.

Overview of the model improvement methodology. Model formalization: The current qualitative knowledge on the studied biological system is formalized as a Bayesian network (top right; see also Fig. 2). The illustrated model contains several molecular types: environmental stimulations (dark gray), signaling proteins and transcription factors (light gray), and mRNAs (white). The refinement and expansion procedures take as input the network model and high throughput measurements on network's components (top left), and search systematically for model improvements that maximize a probabilistic improvement score. The score measures the increase of fit between the model predictions and the observed data. The model refinement procedure (middle left) seeks structural and logical changes in existing model components, which attain the best score. Structural refinements are marked by dashed connections. The model expansion procedure (middle right) assigns systematically new target genes to regulatory modules, based on their fit to the predicted expression of the module. In the illustration, three regulatory modules were formed. They contain known and novel target genes (white circles). All genes in the same module share the same logic (black diamonds).

We have chosen to apply our methodology in the analysis of the cellular response of Saccharomyces cerevisiae to hyper-osmotic and calcium stresses. This response is mediated by a signaling network that involves the PKA signaling pathway, the HOG and mating/pseudohyphal growth MAPK cascades, and the calcineurin pathway. Based on 106 transcription profiles (Gasch et al. 2000; Harris et al. 2001; Yoshimoto et al. 2002; O'Rourke and Herskowitz 2004), the refinement procedure suggests three missing cross-talk connections in the network, which all have independent support in the literature. The expansion procedure was applied to six known regulatory modules and 78 putative sets of regulators and yielded 10 statistically significant modules. We discover both HOG pathway-dependent induced and repressed novel modules, and show that these modules are distinct from the known HOG pathway-dependent response. Remarkably, our analysis indicates that Hog1 MAP kinase acts in several distinct functional modes. The expanded network contains many transcriptional regulatory feedback and feedforward loops. This rich circuitry is probably part of the osmotic adaptation and provides rapid and transient response to osmotic changes.

Several features distinguish our computational methodology from extant network reconstruction methods. Recently, a few advanced methods sought to improve system models systematically, both for quantitative metabolic networks (Klipp et al. 2005; Herrgard et al. 2006) and for physical interaction networks (Calvano et al. 2005; Yeang et al. 2005). Our approach differs in that it uses informal qualitative knowledge, including regulatory logics, which is crucial for modeling of the activation and down-regulation of signaling cascades. Bayesian networks were used for de novo reconstruction of system models (Friedman 2004). In contrast, here the Bayesian network represents the existing well-characterized system model, and the analysis seeks its improvement. In addition, we use a discriminative improvement score, rather than a classical Bayesian score, in order to identify significant and specific model changes. Concerning modules identification, extant methods approximate the regulator's protein activity by its mRNA expression (Bar-Joseph et al. 2003; Segal et al. 2003; Tamada et al. 2003). A key advantage of our methodology is that we use the model to predict the activity of the regulators, and then use these levels to identify the modules. Since the transcription factor activity levels are more directly related to their targets’ expression, better module identification is possible.

Overall, the results show that, by formalizing the qualitative knowledge available and analyzing the system model jointly with relevant large-scale data, it is possible to extend the current understanding on biological systems and to analyze regulatory mechanisms in a new level of detail.

Results

We selected for our analysis 106 gene expression profiles from four large-scale microarray studies in yeast (Gasch et al. 2000; Harris et al. 2001; Yoshimoto et al. 2002; O'Rourke and Herskowitz 2004). The profiles measure the yeast response to osmotic and calcium stresses and the effect of genetic perturbations in the osmotic response pathways. Originally, these studies applied clustering algorithms on the data. The following results show that, by integrated analysis of the data and the model, we find regulatory relations and mechanisms that could not be revealed using the data alone.

The computational approach

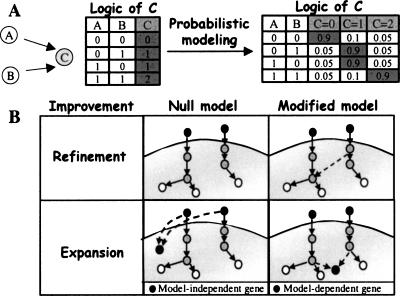
We formalize the biological knowledge in a Bayesian network model (Gat-Viks et al. 2006), which represents dependencies among interacting components. The components, or variables, are mRNAs, proteins, external inputs, etc. The model provides a structure and a logic for each variable. The structure (or topology) is represented by a graph diagram, where the nodes represent the variables, and arcs represent influence among variables (e.g., transcription factor binding to a gene promoter, phosphorylation by a kinase, etc.). For each graph node, the nodes that have arcs directed into it are its regulators, or its regulatory unit. Each variable can be in one of several discrete states, indicating, for example, the activity of a protein variable, or the expression level of a mRNA variable. In the logic component of the model, a variable’s state is determined by the combination of states of its regulators according to its specified discrete function, which might represent a complex relationship among multiple regulators. The logic is formulated probabilistically in order to allow for uncertainty about the available biological knowledge (Fig. 2A).

Figure 2.

The computational approach. (A) Modeling the current knowledge. Nodes represent the variables of the model and arcs are known regulatory relations. Here, the state of variable C depends on the states of its regulators A and B according to a specific logic. In the combinatorial logic of C (left), the state of C is 1 if, and only if, at least one of its regulators has state 1. In the probabilistic modeling (right), each possible state of C is assigned a probability depending on our confidence in the current biological knowledge (here, 90% confidence). (B) Improving the model. The model refinement and expansion procedures look for model changes that improve the model significantly. The improvement score compares between the fit of a possible modified model and that of the null (original) model. The plots are a schematic representation of these two models in cases of refinement (top) and expansion (bottom). In expansion, when adding a new gene, the null model assumes that the gene expression can be explained sufficiently by the environmental stimulation. The alternative hypothesis is a model-dependent gene, i.e., the gene is regulated by our signaling network. We expand the model only if the improvement score is significant, i.e., the signaling network explains the expression much better than the environmental stimulation only.

In order to allow formulation of the available qualitative knowledge, we have chosen to model the logics as discrete functions using discrete states. However, the actual cellular concentrations are continuous levels, and hence our model must transform continuous levels into discrete logical states. The observed level (or observation) is the result of a measurement in a biological experiment, e.g., the measured concentration of mRNAs or a metabolite, or the measured phosphorylation of a protein which indicates its activity. The predicted level is the probabilistic expectation of the variable given the model and the experimental procedure applied (i.e., the genetic perturbations and the environmental stimulation performed in the experiment). Hence, the predicted levels of protein activities (predicted activities) constitute additional information that is not available from microarray experiments. The predicted levels of mRNA variables (predicted expression) are compared to the observed expression, and reveal important information on the quality of the model. In particular, points of disagreement between observed and predicted expression levels indicate where our understanding of the biological system is lacking. Mathematically, the quality of the model is evaluated by a Bayesian score, which measures the closeness of the observations to the predicted levels (see Methods).

Naively, the model can be improved by searching in the space of all possible model improvements (i.e., either refinements or expansions) for the model with the best Bayesian score. However, in order to propose only trustable hypotheses, we introduce here a new improvement score, which measures the difference between the Bayesian scores of the modified and the original model. Hence, we seek model improvements with significantly high improvement scores. In the case of model refinement, the improvement score compares the Bayesian score before and after introducing the logical or structural changes (Fig. 2B). In the more complicated case of model expansion, among all genes that respond to the environmental changes, we wish to identify specifically the model-dependent genes, which are affected by model components. We wish to exclude other responding genes (model-independent genes), such as ribosomal proteins, which respond to the environmental stimuli, but probably independently of our model and through another signaling pathway. Both types respond to the environmental changes, but only the model-dependent responding genes are influenced by genetic perturbations in model components. Hence, the expansion improvement score compares the scores of adding a gene in a model-dependent and in a model-independent fashion (Fig. 2B). A gene with a significant improvement score is considered a model-dependent gene and is assigned to the module (i.e., regulatory unit and logic) that obtained the highest improvement score (see Methods).

The osmotic response network model in yeast

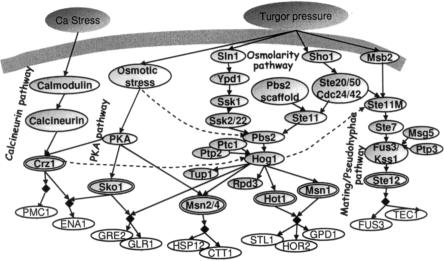
Building on literature reports, we modeled the response of yeast cells to calcium and hyper-osmotic stresses. The model formalizes the HOG, mating/pseudohyphae growth, calcineurin, and the PKA signaling pathways. The signaling cascades act together to affect the activity of many regulators (Hog1, Sko1, Msn1, Hot1, Msn2/4, Crz1, Ste12) that govern the complex expression of target genes by diverse combinatorial logics. For each pathway, our model includes the environmental stresses, the signaling cascades, the transcription factors, and their known targets (Fig. 3). Each variable has three to five possible states. Supplement A catalogs all variables, connections, and logics in the model, along with their source in the literature. All the literature sources used for the modeling do not rely, directly or indirectly, on the 106 profiles that we use here. Note that the mating and pseudohyphal growth pathways are modeled together. Since they share most of their components (up to the Kss1/Fus3 MAPKs and their upstream activators; O'Rourke and Herskowitz 1998), and our dataset does not include any experiment that can distinguish between them, a separate modeling of the pathways will not improve our results. In practice, our joint modeling of mating/pseudohyphae pathways reduces model size and thus increases efficiency and accuracy.

Figure 3.

A model of the yeast response to osmotic and calcium stress. The model contains (left to right) the calcineurin pathway, PKA signaling pathway, the HOG MAPK pathway, including its Sln1–Ssk1 and Sho1–Ste11 upstream branches, and the mating/pseudohyphal growth pathways. The network, constructed based on literature reports, contains environmental conditions (dark gray), signaling components (light gray ovals), transcription factors (double ovals) and their transcriptional targets (white ovals). Targets sharing the same regulatory logics (i.e., in the same module) are indicated by black diamonds. Arrows are well-established relations (solid lines) or relations predicted by the refinement procedure (dashed lines). The logic by which each component is governed by its regulators is described in Supplement A. The dual role of the MAPKKK Ste11 in the HOG and mating pathways is formalized by refining two different model variables called Ste11 and Ste11^M, respectively.

Network refinements

Given the dataset of 106 transcription profiles and the osmotic response model, the refinement procedure looks for structure and logic modifications with high improvement scores. Three new connections providing the most significant improvement (marked as dashed arcs in Fig. 3) indicate cross talk in the model. The three predicted connections are not well-established, and thus were not included in the original model, but each has an independent support in the literature (Supplemental Table S1). First, the model predicts a down-regulation of the HOG pathway by the calcineurin pathway (Crz1⫞Pbs2/Hog1, improvement score P-value < 0.0005, see Methods). Indeed, Shitamukai et al. (2004) support this claim by showing that calcium ions induce Hog1 hyperphosphorylation in crz1 mutants. Calcium ions activate Crz1 through the calcineurin pathway and activate Hog1 through the HOG pathway. Crz1 down-regulates Hog1 and thus there is hyperphosphorylation of Hog1 in a strain lacking Crz1. Second, Hog1 prevents osmolarity-induced activation of the mating/pseudohyphae pathway. The predicted inhibitory connection is directed from Hog1 to the mating MAPKKK Ste11 or to its downstream mating components, but not to the osmosensor Sho1 (P-value < 0.005). Indeed, the data show strong inhibition of the mating/pseudohyphae targets in sho1 mutant (Supplemental Fig. S1A), and thus the refinement procedure could not predict that the inhibition is directed to Sho1, but only to its downstream components. O'Rourke and Herskowitz (1998) suggested this cross talk based on measurements of morphological changes and mating phenotypes.

Third, an alternative mechanism is proposed for HOG pathway activation in severe osmotic shock. Significant improvements (P-value < 0.0005) were obtained for the connections: Osmotic Stress → Ssk2/22 and Osmotic Stress → Pbs2. The HOG pathway is still active in ssk1sho1, ssk1ste11 mutants, but not in pbs2 or hog1 mutants (Supplemental Fig. S1B), and thus a third input to Ssk2/22 or Pbs2 was added by the refinement procedure. Van Wuytswinkel et al. (2000) provide an independent support for the existence of such additional input to Pbs2. Note that O'Rourke and Herskowitz (2004) already observed this effect in their dataset, but here we succeed to identify it automatically.

The model expansion process

A regulatory module is a set of genes that are regulated by the same regulatory unit via the same logic. To expand the network model, we focused on identifying such modules whose regulatory units are part of the original model. In principle, the space of possible modules is huge: All subsets of variables in the model may participate in a regulatory unit with any possible logic. In practice, we tested putative regulatory units of one or two variables, including the six known units depicted in Figure 3. Altogether, the number of tested units was 78, among them 72 putative units, each with up to 3⁹ = 19,683 possible discrete logics, and six known units, each with its known logic (see details in Supplemental Fig. S2). All 5700 measured yeast genes were considered as possible targets, each with three possible states.

For each target gene, the expansion procedure searches heuristically for the unit and logic that best predict its expression as a function of the predicted activity of the regulators. The predicted activities represent the post-transcriptional effects that are formalized in our model, such as the regulator’s phosphorylation (and hence activation) by the MAPK Hog1. An alternative approach is to approximate activity with expression levels (Friedman et al. 2000; Tamada et al. 2003), but this approach cannot handle the major post-translational regulation events in the osmotic signaling cascade (Supplemental Fig. S3).

As described above, in order to avoid inclusion of nonspecific targets, the expansion procedure computes the improvement score and thus discriminates between model-dependent responding genes and model-independent responding genes (see Methods and Fig. 2B). According to this analysis, while about 71% of the yeast genes respond to the osmotic stress, only 15% are specifically dependent on the model. On the other hand, the fact that a fifth of the stress response is characterized as model-dependent highlights the important role of the osmotic-specific stress mechanisms in the general cellular machinery of response to stress.

Since small modules could have been generated at random given the large space of regulatory units and logics searched, we focused further analysis on novel modules containing at least 20 genes, and known modules of at least 10 genes. Five novel modules and five known ones passed this filter. When performing expansion using randomly shuffled condition labels (experimental procedures), no module with more than three genes was found (Supplemental Fig. S5), indicating that it is unlikely to obtain our large modules at random.

Transcriptional modules discovered

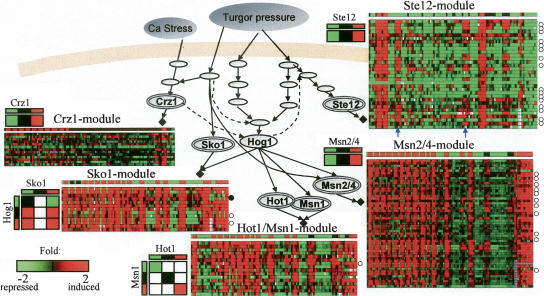
The known regulatory units of Msn2/4, Ste12, Hot1/Msn1, Crz1, and Sko1 attained modules containing 52, 32, 15, 13, and 12 genes, respectively (Fig. 4; Supplement C). The Crz1–Sko1 unit was assigned only its known ENA1 target gene. We discovered three novel modules regulated by Hog1 with different logics (referred to as Hog1A, B, and C), one module controlled by both Hog1 and calmodulin (called Hog1/Ca), and one module regulated by Ssk2/22 or Ssk1, called Ssk2/22 (Supplement C).

Figure 4.

Expansion of the osmotic network model. The expansion algorithm assigns known and novel target genes to known modules (black diamonds). Each module is represented by a matrix showing the expression of its target genes (rows) across the 106 conditions (columns). Known target genes that were assigned to their module correctly/incorrectly are marked with white/black circles to the right of the corresponding row (known targets were excluded from the model before expansion, to allow validation and to avoid circularity). The predicted expression levels in each condition appear as a separate row above the matrix. The logic of each module, obtained by the refinement procedure, appears near the matrix. We show in color only logic entries with significant improvement score. In general, there is high agreement between model predictions and observed levels. The few cases of disagreement (e.g., columns marked by blue arrows in the Ste12 module) highlight our incomplete understanding (and hence modeling) of the biological system. The full details on each module appear in Supplement C, including lists of correct/incorrect target genes, and their sources in the literature.

The predicted regulatory units do not necessarily control their target genes directly. For example, the Msn2/4-module contains YAP4, (currently known as CIN5), GCY1, and DCS2, but, actually, Msn2 regulates the YAP4 gene, which encodes a transcription factor; the up-regulation leads to increased activity of Yap4, which in turn up-regulates transcription of GCY1 and DCS2 (Nevitt et al. 2004). Calmodulin and Ssk2/22 probably affect their targets indirectly, since they are cytoplasmatic kinases and have no DNA binding domain. The prediction that their regulatory effect does not involve downstream elements in the model has some support in the literature (Ohya et al. 1991; Yuzyuk et al. 2002).

A key advantage of our methodology is that the activity of the modules can be predicted by the model and compared with the observed levels. Cases of disagreement between the predicted and observed levels are of particular interest, since they highlight spots of incomplete understanding in the biological system. For example, the Ste12 module shows inconsistency in the case of ssk1sho1 mutants exposed to 0.5 M KCl and the ssk1 mutants exposed to 0.125 M KCl (marked in Fig. 4; an extended version of this module appears in Supplement C). An increase in transcription is observed, in contrast to the predicted reduction. The inaccurate modeling is probably due to incomplete understanding of the inhibitory effect of Hog1 on the mating/pseudohyphal growth pathway.

Transcriptional modules evaluation

A unique feature of our methodology is that a module and its regulators are identified together in the same process. In order to evaluate the methodology, we excluded all known transcriptional targets from the model and then constructed the modules. We then tested the accuracy of assigning known targets to modules. An extended collection of 126 known targets and their literature sources is available in Supplement C. Among them, 37 genes were assigned to modules, and 17 additional genes were assigned to very small modules which were filtered from in our analysis. Out of the 37 genes assigned to modules, 30 genes were assigned correctly to their known regulators, and one gene was assigned incorrectly (marked in Fig. 4). Six additional Msn2/4 targets were assigned to the Hog1A novel module, which is also hypothesized to be regulated by Msn2/4 (see below). Hence, we obtain 97% specificity (correct/assigned = 36/37; see Supplemental Table S2). To get such high specificity, we pay the cost of low (29%) sensitivity (correct/known = 36/126).

In another evaluation of the predicted modules and their regulators, we tested each module for enrichment in transcription factor (TF) binding using TF-DNA binding profiles (Harbison et al. 2004). For each TF whose binding profile in relevant conditions is available, the enrichment test supports the predicted regulatory unit (Supplemental Fig. S6A): The Ste12 module is bound by Ste12, Dig1, Mcm1, and Tec1 in mating/PH growth induction (pheromone and Butanol treatment); the Msn2/4 module is bound by the Msn2/4 in stress conditions (acidic and H₂O₂ treatment); and the Sko1 module is bound by Sko1 in YPD medium. Indeed, Sko1-dependent repression is constitutively active (bound) under normal conditions and derepressed under osmotic shock. In addition, for the modules of Ste12 and Msn2/4, sequence analysis shows that the known TF binding site motifs are highly enriched in the promoters of the genes in the predicted module (Supplement D).

To validate the biological significance of the predicted gene sets, we tested the functional coherence and separation of gene sets. We used 87 gene expression profiles of 10 stress conditions from Gasch et al. (2000) that were not included in the set of 106 profiles used for constructing the modules (stationary phase, heat shock, Diamide, Menadione, H₂O₂, amino acid starvation, nitrogen depletion, hypo-osmotic shock, DTT, and various carbon sources). We found significant coregulation of the genes in each module and significant separation between modules (Supplemental Fig. S6B,C). The module predicted to be regulated by Msn2/4 shows strong coregulated response in all stress conditions, in agreement with the known general stress functionality of the Msn2/4 transcription factors.

Separating gene sets that differ only in a few experiments using standard clustering algorithms is a hard task, since the minor expression differences might be the result of noise. A unique feature of our approach is the ability to separate genes using both data and prior model, rather than data only. Hence, if the model can predict two modules with slight differences, these differences become significant, and the targets will be partitioned into two modules. For example, the targets of Hog1B module and Ssk2/22 module were separated by the model, even though they are very similar according to our data (Supplemental Fig. S6D). The separation is corroborated using independent data of heat shock stress (Gasch et al. 2000), in which the expression patterns of these two gene sets are significantly different (KS-test P-value < 10⁻³; Supplemental Fig. S6E). Another example for separation of two similar Msn2/4 modules is given below.

The transcription factors Msn2/4 regulate two distinct modules

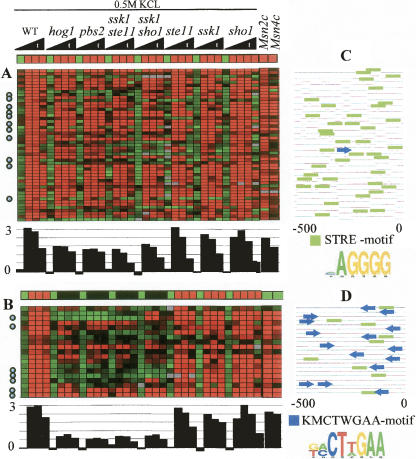
In our analysis, we identified the known Msn2/4 module (Fig. 5A). In addition, several indications suggest that Hog1A, one of the novel modules (Fig. 5B), is also regulated through Msn2/4. First, Hog1A is enriched in Msn2/4 targets: Among 24 module genes known to be Msn2/4 targets (based on expression experiments in Msn2/4 knockout mutants from Rep et al. 2000), 11 are in the Msn2/4 module, and seven are targets of the Hog1A module (Fig. 5A,B, hyper geometric enrichment P-value < 10⁻¹⁷, 10⁻¹², respectively), and the rest were assigned to various other logics. Second, a significant enrichment in binding of Msn4 to the promoters of Hog1A module genes was observed in ChIP experiments (Harbison et al. 2004) (P < 10⁻⁷; Supplemental Fig. S6A). Third, the Hog1A module is highly expressed in strains overexpressing Msn4 (Gasch et al. 2000) (two right columns in Fig. 5A; KS-test P-value < 10⁻¹²). Fourth, Hog1A exhibits highly significant response in all stress conditions (Supplemental Fig. S6B), in agreement with the central role of Msn2/4 in general stress response. Finally, the Msn2/4 STRE binding motif was highly enriched in the Hog1A module (P-value < 10⁻⁵; Fig. 5D).

Figure 5.

Expression profiles of two modules associated with Msn2/4. (A) The known Msn2/4 module. (B) The novel Hog1A module. The conditions are time series measurements in response to 0.5 M KCl osmotic shock. Below the predicted expression vector and the observed expression matrix (the same presentation as in Fig. 4), the average fold induction of the module is shown. Both modules are hypothesized to be regulated by Msn2/4 and include many known Msn2/4 targets (marked with circles). However, their expression patterns are clearly distinct: The Hog1A module depends much more strongly on the presence of Hog1 in severe osmotic shock. In wild type (WT), the expression level in both modules is ∼3, but in hog1, pbs2, ssk1ste11, and ssk1sho1 the expression levels differ significantly: ∼0.5 in Hog1A and ∼2 in Msn2/4 module (KS-test P-value < 10⁻⁴). The two rightmost columns in A and B show the expression level of the modules in Msn2 and Msn4 overexpression mutants. Although the predicted expression in these conditions is low in the Hog1A module, the observed level in both modules is high, indicating that both modules are regulated by Msn2/4. (C,D) Promoter analysis. Each line represents the 500-bp sequence upstream of the transcription start site for the gene in that row. Green boxes represent occurrences of the STRE motif (a known Msn2/4 binding site); blue arrows represent the new motif KMCTWGAA discovered in this analysis. This motif exhibits a non-uniform distribution along the promoter in terms of location and orientation. The novel motif supports the separation of the Msn2/4 targets into two distinct modules.

To provide additional evidence that the two transcriptional modules are distinct, we performed promoter sequence analysis. Remarkably, a new motif was discovered to be highly enriched only in the novel module (KMCTWGAA, enrichment P-value < 10⁻¹⁴) and it may contribute to the unique behavior of the module (Fig. 5C,D). This novel motif exhibits a very strong bias in orientation and distance from the transcription start site of the regulated genes (hyper geometric P-value < 2 × 10⁻⁴).

HOG pathway-dependent repression of genes

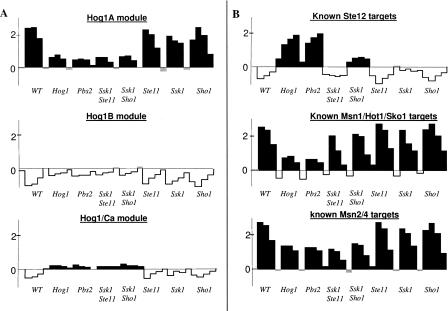
It was previously demonstrated that Hog1-dependent genes are either induced or repressed in hog1 mutants. The prevalent view in the literature is that the genes induced by hog1 mutants are associated with pheromone response and pseudohyphal growth (O'Rourke and Herskowitz 2004). Indeed, among nineteen genes that are specifically up-regulated in hog1 mutants (Rep et al. 2000), all 11 genes with high score (improvement score > 0.05) were assigned to the module of the mating/pseudohyphae TF Ste12. Surprisingly, our results revealed four additional modules that increase specifically in the hog1 mutant (Fig. 6A; Supplement C). In contrast with the Ste12 targets (Fig. 6B), the novel modules respond neither to pheromone nor to perturbation in the mating/pseudohyphal growth pathway (Supplemental Fig. S7) and are not bound by the TFs Ste12, Tec1, or Dig1/2 (Supplemental Fig. S6A). Taken together, these observations suggest that Hog1 plays an additional role in inhibiting expression that is not related to the cross talk between the HOG and mating/pseudohyphae pathways.

Figure 6.

HOG pathway-dependent repression of genes, and multiple functional modes of Hog1. Each plot shows the average fold induction (in log2 scale) of novel gene modules (A) or known targets of TFs (B) in wild type (WT) and seven HOG pathway mutants exposed to 0.5 M KCl. Black/white coloring indicates average fold induction above/below 0.1. (A) The novel modules Hog1A, Hog1B, and Hog1/Ca (the Hog1C and Ssk2/22 modules [data not shown] are similar to Hog1B in this view). (B) The known target genes of Ste12 (KSS1, TEC1, FUS1, FUS3, MSG5, KAR4, CLN1, PGU1), Hog1 (HOR2, GRE2, STL1, ENA1, GLR1, GPD1, HAL1, CHA1, AHP1, YGR043C, YGR052W (reserved name FMP48), YML131W; Hohmann 2002), and Msn2/4 (Rep et al. 2000). Expression of the novel modules Hog1B and Hog1/Ca (A, middle and bottom) increases in the absence of Hog1. Although the whole Hog1-dependent inhibition response is known to be regulated by Ste12, one can clearly see that these novel modules differ significantly from the Ste12 targets (B, top), indicating existence of Hog1-dependent in spite of Ste12-independent inhibition. The known Hog1/Msn1/Sko1 and Msn2/4 targets (B, middle and bottom) have distinct expression pattern (KS-test P-value < 10⁻⁵): The Msn1/Hot1/Sko1 targets have higher expression in the ssk1ste11 and ssk1sho1 mutants compared to hog1 and pbs2 mutants, indicating that Hog1 can be activated also by a third additional input. In contrast, the Msn2/4 targets have a similar expression pattern in all four of these mutants, indicating that Hog1 is dependent on the two upstream branches of the HOG pathway. Surprisingly, the novel modules' expression pattern (A) also suggests dependency on the two HOG branches. One can clearly see that two of these modules (Hog1B and Hog1/Ca) differ significantly from the known Msn2/4 targets (the distinction between Msn2/4 and the third module Hog1A is discussed in Fig. 5). Taken together, this suggests that Hog1 has two distinct functional modes that involve a different combination of transcription factors. An extended version of the novel modules appears in Supplement C.

Multiple functional modes of Hog1

The refinement procedure suggested the existence of an alternative third mechanism that activates the HOG pathway in severe osmotic stress, in addition to the two known upstream branches of the pathway (Sho1–Ste11 and Sln1–Ssk1; Fig. 3). This refinement was suggested since the transcription of some of the classical HOG pathway targets (regulated by Hot1, Msn1, and Sko1) does not depend on the two upstream branches in 0.5 M KCl (Fig. 6B). However, the transcription level of the known Msn2/4 targets does depend on the two branches (Fig. 6B). This suggests that Hog1 has two different activity modes, and that one of the modes is only functional while interacting with Msn2/4. To test this prediction computationally, we added to the model, in addition to a Hog1 variable that is controlled by three inputs (the two HOG pathway upstream branches, and a third uncharacterized input), an additional variable called Hog1⁽²⁾, which is controlled solely by the two HOG pathway upstream branches (Supplemental Fig. S2). We applied the module identification process on this extended model.

Remarkably, although the classical HOG pathway targets seem to be activated by a third input, four novel modules (Hog1A, Hog1B, Hog1C, and Hog1/Ca) are predicted to be regulated by Hog1⁽²⁾ and indeed seem to be dependent on the two upstream branches, similarly to Msn2/4 (Fig. 6; Supplement C). Several indications suggest that one of these modules, Hog1A, is actually regulated through Msn2/4 (as detailed above; Fig. 5). But surprisingly, the Hog1B, Hog1C, and Hog1/Ca modules are not enriched according to any of these criteria, and thus it seems that their regulation does not involve Msn2/4. Therefore, there is a strong indication that Hog1 has multiple functional modes that probably go beyond its functionality in particular combinatorial regulation with Msn2/4. Supporting this new hypothesis, some of these functional modes have opposite effects (there are both repressed and induced Hog1⁽²⁾-dependent modules). The Hog1 functional modes can be explained in many ways, such as distinct Hog1 activity as a TF (in the nucleus) and as a kinase (in the cytoplasm), or differences in activity of other mediators, e.g., nuclear translocators or phosphatases.

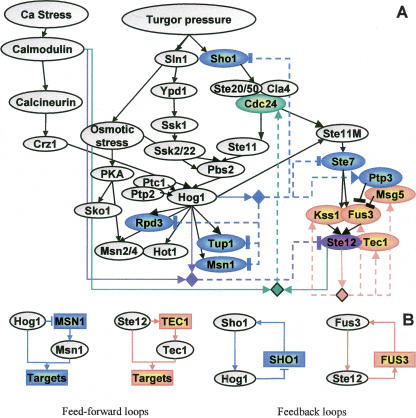
Transcriptional feedback in the osmotic response network

Many components of the osmotic and mating MAPK pathways were included in modules, thereby forming both feedback and feedforward loops (Fig. 7). The algorithm predicts that the expression of SHO1 is down-regulated by the MAPK Hog1, suggesting down-regulation of one arm of the HOG pathway upon osmotic shock. In the nucleus, active Hog1 interacts with the Msn1 transcription activator, the Rpd3 histone deacetylase, and the Tup1 transcriptional cofactor, all important for activation of the response to osmotic shock (Proft and Struhl 2002; De Nadal et al. 2004). The feedforward loop predicted between Hog1 and each of these factors (exemplified in Fig. 7B on MSN1) may encourage transient activation signals, allowing rapid system shutdown (Shen-Orr et al. 2002).

Figure 7.

Complex transcriptional feedback in the yeast osmotic network model. (A) We highlight in color model variables whose corresponding genes were included in a module. Regulatory units are shown as diamonds, where the incoming arcs indicate the regulators they contain, and outcoming dashed arcs indicate their (direct or indirect) targets. For each regulatory unit, we use a different color for its target genes and the relevant edges. For example, the unit of Ste12 (orange) has TEC1, FUS3, KSS1, and MSG5 among its targets. Unlike previous maps, the same diamond might represent several different regulatory logics, and the arcs distinguish between positive (→) and negative (⫞) feedback. The rich circuitry observed is probably part of the cellular adaptation and provides rapid and transient response to osmotic stress. (B) A few network motifs discovered in A. Rectangles indicate target genes, and ovals are proteins.

From the refinement results described above, we concluded that Hog1 somehow prevents cross talk with the mating/pseudohyphae pathway. Consistent with this observation, the STE7, STE12, and SHO1 genes, which are translated into components of that pathway, are down-regulated by Hog1. On the other hand, the phosphatase Ptp3 inactivates the mating kinase Fus3, and its gene PTP3 is up-regulated by Hog1. These predictions suggest that transcription regulation is part of the mechanism by which Hog1 prevents cross talk between the MAP kinase pathways.

Ste12 up-regulates the FUS3 and KSS1 genes, forming a positive feedback loop (exemplified in Fig. 7B on FUS3) that can increase stability and reduce response time to environmental stimuli (Shen-Orr et al. 2002). We also identified a negative feedback loop via Ste12 up-regulation of MSG5, indicating that the pathway has also an autoregulatory deactivation mode. Note that, upon osmotic shock, all the predicted targets that are components of the mating/pseudohyphae pathway (SHO1, CDC24, STE7, KSS1, FUS3, MSG5, PTP3, STE12, and TEC1) behave similarly: They are expressed only in the absence of active Hog1. Yet, the expansion procedure identifies SHO1, STE7, PTP3, and STE12 as Hog1-dependent, while CDC24, KSS1, FUS3, MSG5, and TEC1 are identified as Ste12-dependent. Indeed, experimental results not used in the computational process support these predictions: Only the predicted Ste12-dependent genes are up-regulated by pheromone that specifically activates the mating pathway (Supplemental Fig. S8). Several mechanisms for the adaptive regulation of the osmolarity pathway have been described (Hohmann 2002). The results here provide additional insight on the way transcriptional regulation might take part in the osmotic adaptation.

Discussion

Signaling and transcriptional networks are intertwined and influence each other in a complex manner. In this study, focusing on the osmotic response system in S. cerevisiae, we show that, by modeling together the available knowledge on signaling cascades and transcriptional regulation, we could improve our understanding of both systems in two important ways: The signaling pathways are refined based on known transcriptional regulation effects, and transcriptional regulatory modules are generated using known cascades of events along signaling pathways.

A large amount of curated qualitative knowledge on biological systems is available today. The formulation of such knowledge is shown here to be surprisingly instrumental in improving our biological understanding. Our computational framework enables modeling of the existing knowledge in the presence of feedback loops in the network, formalization of the uncertainty in this knowledge, and integration of high throughput data. In addition, the model can accommodate partial noisy measurements of diverse biological entities (Gat-Viks et al. 2006). We make major modeling simplifications: The regulatory relations are discrete logical functions, and the model describes the steady state of the system. As expected, the prediction and improvement processes that we propose here also have limitations: They are sensitive to the size and complexity of the model (e.g., number of variables, interactions, and feedback loops), the certainty in the logics, and the amount of data available. The robustness of our methods to these parameters still needs further exploration. We do have strong positive indication for the robustness of the prediction process and logical refinement procedure on small networks (Gat-Viks et al. 2006; www.cs.tau.ac.il/~rshamir/metareg). The robustness of the expansion procedure is yet needed to be systematically explored, although the biological validations in this study are highly promising. In the future, we hope this study will lead to creation of more sophisticated mathematical models and robust improvement algorithms for the analysis of genome-wide datasets.

A key advantage of our module identification approach is that we use a discriminative scoring scheme which specifically identifies modules along with their model regulators. Consequently, we can detect modules on a finer level than was previously possible (for example, novel HOG pathway-dependent repressed modules). Our method outperforms extant methods mainly because it exploits prior knowledge on the signaling pathways and on the experimental procedure. This prior knowledge helps to detect minute expression differences that are the result of distinct regulatory mechanisms, and thus the method can discard better differences that are due to noise. The main limitation in our module identification approach is that it requires high quality of prior knowledge on the signaling pathways, whereas many biological systems are only partially known. To overcome this obstacle, the model should be corrected by applying a refinement procedure before elucidating the modules. In the current study, we did not allow refinement steps that cause global effects, such as novel feedbacks or disconnected networks. We hope that, within the formalism of our model, it will be possible to develop techniques to handle those cases as well.

Although there is much to be developed both in the modeling and the algorithmic parts, by extending the concepts derived here, it is clear that simultaneous analysis of qualitative knowledge with high throughput data is a useful approach. The approach is applicable to other types of perturbations, such as siRNA, to other environmental conditions, such as pharmaceutical agents, and to other molecular data, such as protein activity levels measured by microarrays. High throughput phosphorylation measurements might allow an automated construction of kinase signaling modules using known signaling pathways. As new databases of curated knowledge on signaling pathway are developed (such as BioModels [Le Novere et al. 2006], Reactome [Joshi-Tope et al. 2005], and SPIKE [www.cs.tau.ac.il/~spike]), it will be easier to obtain the prior information on many biological systems and apply the methodology to them.

Methods

Model formalization

Our model consists of variables and relations among them, formulating prior knowledge. The model variables X₁. . .X_n express diverse biological entities (e.g., mRNAs, proteins, metabolites, and phenotypes), and arcs between variables represent biological regulations (e.g., transcription and translation regulation, post-translational modifications). Each variable X_i is regulated by a regulatory unit Pa_i, i.e., the set of variables that have arcs into X_i. Each variable in Pa_i is called a regulator of X_i. Each variable can be in one of several (typically three) discrete states, and its state in any condition is assumed to be determined by its logic, i.e., a discrete function of its regulators’ states in that condition. Note that this assumption implies that the relevant conditions are in steady state. In order to model our uncertainty about the prior knowledge, the logic of a variable X_i is formulated probabilistically as our belief that the variable attains a certain state given the state of its regulatory unit. It is represented by the conditional probability θⁱ(X_i | Pa_i). This approach allows us to model uncertainty in prior biological knowledge and to distinguish between regulatory logics that are known at high level of certainty and those that are more speculative. In practice, biological experiments provide continuous observations and we do not know in advance how to translate them into discrete states. Hence, each logical variable X_i is associated with an observed real-valued variable Y_i, and the conditional distribution ψⁱ (X_i | Y_i) specifies the probability of the variable X_i to attain a certain state given its observed real value. In this work, we discretize the observed values using a mixture of Gaussians model.

Our probabilistic model defines a Bayesian score, which evaluates the fit of the model predictions to the data, measured as the log likelihood of the data given the model:

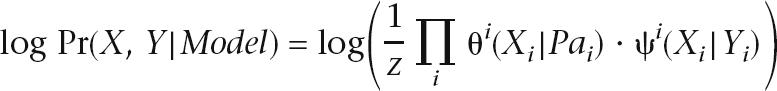where Z is a normalization constant. The conditional probabilities θⁱ are known from our prior knowledge on the biological system, and ψ is determined by maximizing a likelihood score using an EM-procedure. The ψⁱ parameters depend strongly on the particular model, and thus we reoptimize them during each step of the improvement procedures. Given the probabilistic model, we predict the levels of variables (e.g., the activity level of proteins, the expression levels of mRNAs) using a standard probabilistic inference method called Loopy Belief Propagation (Kschischang and Loeliger 2001). As described in Gat-Viks et al. (2006), the above model is represented by a Bayesian network in case of acyclic dependencies, or by factor graph (Kschischang and Loeliger 2001), in the more general case where feedback loops, that are essential in many biological systems, are present.

Expression profiles

We compiled a dataset of 106 relevant transcription profiles selected from four large-scale studies (Gasch et al. 2000; Harris et al. 2001; Yoshimoto et al. 2002; O'Rourke and Herskowitz 2004). In addition to gene expression measurements, for each profile the experimental procedure is recorded, i.e., the environmental conditions and the genetic perturbations in the experiment. This information is used for generating model predictions. The complete list of conditions and their experimental procedures are available in Supplement B. The analysis was applied on 5700 genes that were measured in at least 100 of the conditions.

Model refinements

The refinement procedure searches for a structure modification (an added arc in the network with an accompanying logic) that improves the model significantly. Each such modified model is evaluated by the fit of its predictions to the data, measured by the Bayesian score. The score is computed by an EM-algorithm that locally maximizes the free parameters of the model: the discretization parameters ψⁱ and the logic of the new regulation (Gat-Viks et al. 2006). To evaluate the significance of the improvement achieved by a particular modification to the model, we compared the likelihood scores distributions (across the 106 profiles) of the original and the modified model. The null hypothesis assumes that both models provide equal scores in each condition. The alternative hypothesis suggests higher scores for the modified model. The improvement score is the P-value generated using non-parametric paired Wilcoxon test. All P-values presented are Bonferroni corrected. The same improvement score was used for learning the regulatory logics of the six known modules.

Identification of transcriptional modules

We consider all possible regulatory units of one or two regulators out of twelve candidate regulators. These regulators include two environmental stimuli variables (Calcium stress and Turgor pressure) and 10 signaling network variables (Supplement Fig. S2). Note that the regulatory units are of two types: Variables governed by units that consist only of environmental stimuli are not affected by genetic perturbations in the model, and thus will be called model-independent modules (and their genes will be called model-independent genes). In contrast, the model-dependent modules (which contain model-dependent genes) are controlled by at least one signaling network regulator and thus influenced by genetic perturbations of model components (Fig. 2B).

Our expansion procedure seeks for each candidate gene the unit that governs it based on an improvement score. In particular, given a target gene and its candidate regulatory unit, the procedure applies a greedy search in the space of regulatory logics and discretization parameters using an EM-like procedure in order to achieve a locally maximum Bayesian score. When assigning genes to regulatory units, one should take caution about model dependence decision. Many of the reactions observed in stress and perturbation conditions can be attributed to general stress response, even if they match model predictions (Supplemental Fig. S4). To specifically discriminate model-dependent genes from model-independent genes, we require that they should be predicted significantly better by some model-dependent module than using model-independent ones. Mathematically, we define the improvement score obtained by a gene assignment to a regulatory unit as the difference between its original Bayesian score and the best model-independent Bayesian score obtained for the same gene. This approach can be viewed as hypothesis testing, where the null hypothesis is a model-independent response, and we reject it only if the alternative model-dependent hypothesis is much more convincing.

In practice, 71% of the genome (4051 genes) attained significant Bayesian score in either a model-dependent fashion (68.2%, 3887 genes) or a model-independent one (51.5%, 2935 genes) (we used a cutoff of 0.1 computed based on the shuffled data, see Supplemental Fig. S4); 876 genes (15.3%) that obtained improvement score ≥10 were used to construct model-dependent modules.

Our analysis is focused on model-dependent modules, but the expansion algorithm outputs also model-independent modules. Supplemental Figure S9 exemplifies one such module, which is strongly repressed by hyper-osmotic stress and enriched with ribosomal proteins. Indeed, the expression of the module genes appears by and large unaffected by the genetic perturbations in our dataset.

Module significance

To evaluate modules’ significance, we tested for enrichment (hyper-geometric P-value) of each module’s genes in each of the sets of TF targets (identified at P < 0.01) reported in Harbison et al. (2004) (Supplemental Fig. S6A). In addition, enrichment was computed on up-regulated and down-regulated gene sets in independent expression profiles from Gasch et al. (2000) (excluding the conditions included in the training data, and all other hyper-osmotic conditions and genetic perturbations in model variables, Supplemental Fig. S6B). Separation between modules was computed by KS-test for the difference in the expression profile distributions of each module across the same independent conditions (Supplemental Fig. S6C). All P-values presented are Bonferroni corrected.

Promoter analysis

We performed promoter analysis on the set of target genes in each module, aiming to find regulatory signals and putative transcription factor binding sites. For each set we searched the 500 bp upstream of the transcription start site in each gene using Amadeus motif finder (Halperin et al. 2006). Amadeus performs de novo search for enriched motifs and also compares the motifs found to the known ones in the TRANSFAC version 8.3 database (Matys et al. 2003). The discovered motifs are listed in Supplement D.