Near-native structure refinement using in vacuo energy minimization

Abstract

One of the greatest shortcomings of macromolecular energy minimization and molecular dynamics techniques is that they generally do not preserve the native structure of proteins as observed by x-ray crystallography. This deformation of the native structure means that these methods are not generally used to refine structures produced by homology-modeling techniques. Here, we use a database of 75 proteins to test the ability of a variety of popular molecular mechanics force fields to maintain the native structure. Minimization from the native structure is a weak test of potential energy functions: It is complemented by a much stronger test in which the same methods are compared for their ability to attract a near-native decoy protein structure toward the native structure. We use a powerfully convergent energy-minimization method and show that, of the traditional molecular mechanics potentials tested, only one showed a modest net improvement over a large data set of structurally diverse proteins. A smooth, differentiable knowledge-based pairwise atomic potential performs better on this test than traditional potential functions. This work is expected to have important implications for protein structure refinement, homology modeling, and structure prediction.

The field of protein structure prediction concerns itself with the generation of models of protein structures that approximate the true, native protein structure as accurately as possible. These methods are intended to augment, or even replace, the experimental determination of a protein structure in cases where the structure is either highly derivative (such as a protein with a close relative of known structure) or experimentally difficult to obtain (as with integral membrane proteins). It has been estimated that the generation of an experimental protein structure costs, on average, between U.S. $250,000 (1) and $300,000 (2). Improved methods in structure prediction, therefore, hold the promise of shifting some of the cost burden from experimentalists to (relatively) cheap computations, allowing experimentalists to focus on those structures of particular interest.

The most recent Critical Assessment of Protein Structure Prediction (CASP5 and CASP6) experiments have shown that significant progress has been made in two of the three main CASP prediction categories: template-free modeling (or ab initio prediction), in which the fold is either new or fairly unique, and fold recognition (or threading), in which a similar fold has been solved experimentally but the sequence homology between the target and the experimental structure is very weak.

In the third category, comparative modeling (or homology modeling) (3), in which an experimental structure exists with significant sequence similarity to the protein of interest, improvement has been less forthcoming since the CASP experiments began in 1994 (4). In these types of modeling applications, the related structure is typically within the 1- to 3-Å Cα root mean square deviation (rmsd) range of the true structure (5). Traversing this seemingly tiny distance, however, from a near-native structure model (NNSM) to the native structure (NS) has proven to be extremely challenging. The protein structure refinement problem, therefore, has proven to be a major bottleneck to further improvement in structure prediction. Recently, there has been some very encouraging progress toward solving this problem by using techniques that involve either optimization of new potential functions (5, 6) or inclusion of contact restraints from homologous proteins (7). The search methods used in refinement techniques, however, can be highly computationally intensive. We decided to test whether a technique using more modest computational resources [potential energy minimization (PEM)] could be applied to the refinement problem.

Potential functions used in structure prediction and refinement are typically grouped into two general classes: traditional “physical” molecular mechanics (MM) potentials and statistically derived “knowledge-based” (KB) potentials. In both cases, the energy of the system is defined as the sum over energetic terms that are themselves functions of the 3D coordinates of the atoms. The ENCAD potential, an example of a traditional MM force field, has the following functional form:

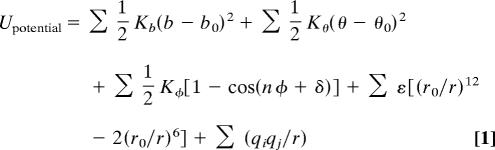The first three terms represent the energetic contributions of bonded interactions: bond stretches, bond angle bends, and torsion angle twists, respectively. The final two terms represent the nonbonded interactions: the first, a Lennard–Jones style potential representing van der Waals interactions, and the second, a Coulombic term representing electrostatic interactions. Nonbonded terms are weaker than bonded terms, but there are many more such terms, and they are more likely to contain systematic errors resulting from the neglect of quantum mechanical interactions between atoms (8).

PEM was one of the earliest search methods applied to protein structure refinement (9, 10). Since that time, it has been a primary tool in the refinement of protein structures in crystallography, NMR, and protein structure prediction and modeling. The central assumption in PEM is that the NS of a protein should be at the global minimum of the potential energy surface of an MM force field. In this article, our aim was to test the central assumption of PEM vis-à-vis MM force fields. We compare and contrast the ability of a number of MM force fields to move the 3D atomic coordinates of an NNSM closer to those of the experimentally determined NS. In an effort to simplify this comparison (and limit the scope of this article), we focus on a single refinement technique that is commonly used in molecular modeling: that of PEM in vacuo. One attractive feature of PEM is the lack of ambiguity at the end point of the process; given a potential function and a starting structure, PEM will find at least a local minimum on the potential surface, and for each run, there is a single structure output.

Definition of Testing Criteria

In testing the in vacuo refinement utility of some common force fields, it is necessary to set up some criteria for comparison as follows:

1. The refinement process should not significantly perturb the atomic coordinates of the NS.

2. The refinement process should move NNSMs closer to the NS.

Both of these comparison criteria derive directly from the assumption that the NS represents a minimum of the potential energy surface. Criterion 1 is a direct restatement of this assumption, but it also assumes that the energy surface is smooth and that the search method is able to reach the closest local minimum. Criterion 1, therefore, is weak; a nonconvergent minimization method will seem to not perturb the NS even if it is not near an energy minimum. Criterion 2, however, puts more stringent demands on the search technique (positive movement must be observed to satisfy it) and gives a more global picture of the shape of the potential in the region around the NS.

In this work we introduce a method for generating sets of NNSMs for a set of 75 test proteins. These NNSM sets can be arbitrarily large and seem to cover the conformational space near the NS uniformly. We then test the MM force fields AMBER99 (11, 12), OPLS-AA (13), GROMOS96 (14), and ENCAD (15), and 3 hybrid KB/MM force fields for performance by using the above-listed testing criteria. The MM force fields tested in this work were chosen because they are freely available and have all been implemented for use with the GROMACS molecular dynamics package.

Hybrid KB/MM force fields (16) are generated by using a differentiable KB energy function in place of the nonbonded energy term of an MM force field. We tested three different KB/MM potentials that vary in the width of distance bins with which statistics were initially gathered. In tests based on criteria 1 and 2, a KB/MM hybrid works better than all other potentials assessed here. In particular, it is able to move the NNSMs of almost all test proteins closer to the native state.

Results

Generating NNSMs to Map the Energy Surface.

To ensure that the results herein are general, a database of 75 native protein structures and structure fragments was compiled to represent the larger set of all known protein folds. A detailed discussion of the database-building procedure can be found in Materials and Methods.

To test a series of force fields for their ability to draw NNSMs toward the NS, we then generated sets of NNSMs that closely resembled what might result from a series of well-built fold-recognition models or homology models. For each test protein, a set of 729 NNSMs was generated by perturbing the NSs along the six lowest-frequency quasiorthogonal normal modes in a combinatorial manner by using the method of Tirion (17). The mean of the 〈rmsd〉 values over all near-native sets was 1.06 ± 0.14 Å. This procedure is described in detail in Materials and Methods and is represented visually in Fig. 1.

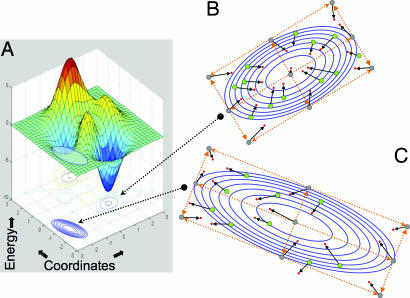
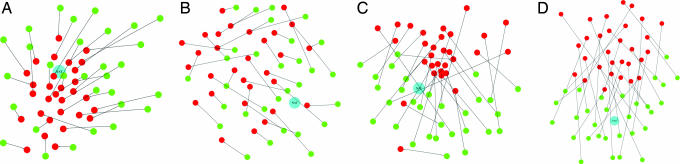
Fig. 1.

Cartoon showing energy vs. conformation. (A) A hypothetical protein energy hypersurface is projected onto two spatial dimensions that denote changes in structure. (B and C) Conventional normal modes are calculated from a quadratic expansion about an exact minimum of the energy surface (B), whereas the Tirion modes are calculated about an arbitrary point on the energy surface (C). The orange dotted lines represent the orthogonal normal-modes eigenvector directions, and the gray points represent conformations formed by combining amplitudes perturbation of (−1, 0, 1) along these two directions. Green dots represent conformations produced by similar perturbation along other, out-of-plane eigenvectors. The black vectors from these green circles represent the change of conformation that occurs as a result of energy minimization. (B and C) As expected, in the expansion about the exact minimum (B), the vectors point to the single minimum at the center of the quadratic expansion, whereas in the expansion about an arbitrary point (C), energy minimization does not cause such concerted shifts.

Generating KB/MM Hybrid Potentials.

A series of three pairwise, atomic potentials of mean force (PMFs) were derived by using counting bins with widths of 0.5, 0.2, and 0.1 Å with 167 residue-specific protein heavy atom types, as defined in Samudrala's RAPDF potential (Fig. 2) (18). Energies were derived and a repulsive term was added as described in Materials and Methods. The KB/MM hybrids were generated by replacing the nonbonded terms of the ENCAD potential with quintic spline fits to the KB potentials. The KB/MM potential derived at 0.5-Å widths is termed KB_0.5, etc.

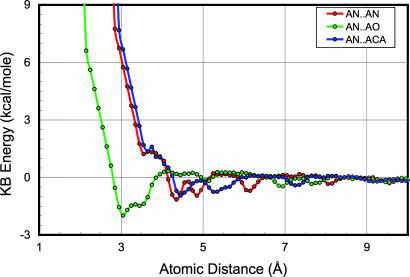
Fig. 2.

Atomic pairwise KB PMF. For each of the 167 atom types used here, a pairwise PMF was derived to describe its energy of interaction with every other atom type. Shown here are three such energy profiles: AN is the alanine backbone nitrogen, AO is the alanine backbone carbonyl oxygen, and ACA is the alanine α carbon. This set of curves was initially discretized into 0.1-Å bins. A repulsive part is added in the region of low distance to account for steric overlap, and the curves are fit to a quintic spline function to give a continuous, smoothly differentiable energy term for use in ENCAD. The symbols shown are the energies from the PMF derivation, and the fit shown is a simple smooth curve fit in Excel, not the quintic spline as generated in ENCAD.

Criterion 1: Energy Minimization of the NS.

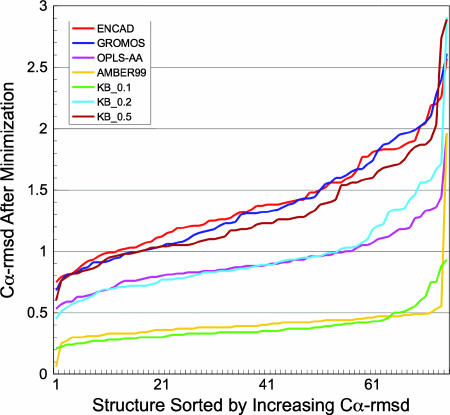
To test criterion 1, dealing with perturbation of the NS, we performed energy minimization by using the NS as the starting point. Fig. 3 shows that the AMBER99 potential showed the smallest mean deviation in rmsd (0.41 ± 0.20 Å) of the MM potentials tested, followed by OPLS-AA, GROMOS96, and ENCAD with values of 0.92 ± 0.23, 1.36 ± 0.42, and 1.39 ± 0.39 Å, respectively. Our three KB/MM potentials, derived at 0.5, 0.2, and 0.1 Å bin widths, were also tested. The best performer by a significant margin was KB_0.1 (0.38 ± 0.14 Å rmsd), followed by KB_0.2 and KB_0.5 (0.96 ± 0.36 and 1.29 ± 0.41 Å, respectively). It is interesting to note that all of the potentials can be grouped into three categories on the basis of their performance in this test. In the “highest-performing” category are KB_0.1 and AMBER99, followed by KB_0.2 and OPLS-AA in the “middle-performing” category, with KB_0.5, GROMOS96, and ENCAD in the “lowest-performing” category.

Fig. 3.

PEM of NSs. For each MM energy function tested here, the 75 native conformations were minimized to convergence by using the Limited-Memory Broyden-Fletcher-Goldfarb-Shanno algorithm in vacuo. The rmsd of the resulting minimum-energy structure relative to the NS was calculated. For each energy function, the rmsd values were sorted from lowest to highest and plotted against the rank of the sort (along the x axis). Thus, the protein at rank 1 in the OPLS-AA series is not necessarily the protein at rank 1 with the AMBER99 series, etc. It can be clearly seen that the KB_0.1 potential and AMBER99 cause the least perturbation of the NS relative to both the other KB/MM potentials tested and the other MM potentials.

Criterion 2: Energy Minimization of Near-Native Structures.

To test criterion 2, dealing with the ability of refinement to draw an NNSM toward the NS, we performed minimization on all 729 NNSMs for each of the 75 test proteins. The mean of the rmsd to the NS over the 729 NNSMs for a particular set is denoted as 〈rmsd〉, and the double mean over all 75 test proteins is denoted as ≪rmsd≫. Before minimization, the value of ≪rmsd≫ was 1.06 ± 0.14 Å. Values obtained after minimization depend on the force field used for the minimization and provide the most rigorous test of the different potentials.

Of the traditional MM potentials, the best performance again is shown by AMBER99 (≪rmsd≫ = 1.03 Å), which is a slight improvement over the original NNSMs (≪rmsd≫ = 1.06 Å). The best-performing KB/MM potential, KB_0.1, showed a larger improvement in ≪rmsd≫ relative to the starting structures (≪rmsd≫ = 0.95 Å). The other potentials tested showed a net degradation, moving NNSMs further away from their native states with ≪rmsd≫ values of 1.17, 1.48, and 1.51 Å for OPLS-AA, GROMOS96, and ENCAD, respectively.

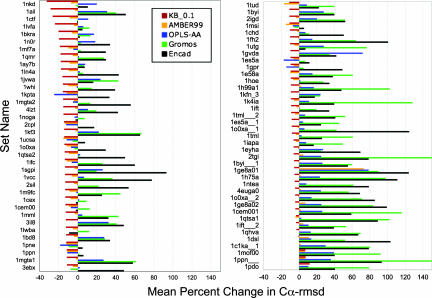
Fig. 4 shows the percent improvement in 〈rmsd〉 for individual NNSM sets, defined as PI = (〈rmsd〉_min − 〈rmsd〉_start)/〈rmsd〉_start (PI < 0 denotes improvement). As expected from the ≪rmsd≫ values presented above, the KB_0.1 potential performs best. More surprising is its high consistency, in that only three NNSM sets showed degradation (PI > 0). With AMBER99, the top-performing MM potential, 15 sets showed a percent mean degradation. OPLS-AA produced an improvement in only 18 of the 75 sets, and GROMOS96 and ENCAD showed improvement for only 9 and 5 sets, respectively. The correlation between the PI values obtained with KB_0.1 and AMBER99 is 0.35, showing that good performance with one potential on an NNSM set does not necessarily imply good performance with another.

Fig. 4.

PEM of near-native structures. The PI caused by energy minimization is shown for all of the 75 test proteins and a selection of the energy functions. PI is calculated as described in the text. If minimization improves the structure overall so that 〈rmsd〉_min is less than 〈rmsd〉_start, then PI is negative. The test proteins are ordered as best to worst with respect to the KB_0.1 energy function. Of the traditional MM potentials, the best performance again is shown by AMBER99 (with a mean PI of −3% over all decoy sets of all test proteins). The best-performing statistical potential, KB_0.1, showed a larger PI of −11%. All of the other energy functions moved the decoys away from the NS with PI values of 11%, 40%, and 44% for OPLS-AA, GROMOS96, and ENCAD, respectively. Although both KB_0.1 and AMBER99 do improve decoy structures, proteins that do well with one energy function do not generally do well with the other energy function.

The best-performing MM potential, AMBER99, showed a mean PI of −3.0% over all NNSM sets. The best-performing KB/MM potential, KB_0.1, showed a much better PI of −11%. The other potentials tested showed a mean degradation, namely, PI = 11%, 40%, and 44% for OPLS-AA, GROMOS96, and ENCAD, respectively.

To visualize the shape of the potential surface in the region near the NS, we further examined a randomly selected subset of 30 NNSMs for two proteins, 1CTF and 1PDO, chosen because they are representative of the best and worst cases with respect to performance of the KB_0.1 potential. We considered the starting and minimized confirmations of each NNSM as well as the native state and calculated a 61 × 61 matrix of pairwise rmsd values. The program GRAPHVIZ (41) was then used to generate a projection of the high-dimensional configuration space into two dimensions (Fig. 5). For a given protein and energy function, we were able to visualize whether a basin of attraction exists in conformation space (and, by inference, in the shape of the energy surface). It also allowed us to determine whether such a basin is situated about the NS. We see in Fig. 5A that, for test protein 1CTF, a basin of attraction exists around the native state when using the KB_0.1 potential. Such a basin is not present for protein 1PDO (Fig. 5B), which is a poor performer (Fig. 4), and there seem to be few correlated shifts, suggesting a rough energy surface. When using the ENCAD potential (Fig. 5 C and D), which performs badly for these test proteins, there is a basin situated further from the native state than the ensemble of starting points.

Fig. 5.

Directionality of movement caused by minimization. Shown are matrices of the rmsd distances between all pairs of structures in a random subset of 30 decoys before and after minimization (including the NS). We map the data into a 2D space to visualize the attraction basin around the native state (or the lack thereof). Each decoy starts at a green point and, after minimization, moves to a red point; the shift is shown as an arrow between these two states. (A) The presence of an attraction basin is most apparent. Shown is the performance of the KB_0.1 potential on the set 1CTF. In this case, the vectors point radially inward toward the NS. (B) For the protein 1PDO, the vectors seem to be pointing toward an area in the upper left region of the plot (although most seem to be unable to fully reach that area), and there is no apparent attractor near the native state. (C and D) When the same decoys minimized by using the ENCAD potential are considered [1CTF (C) and 1PDO (D)], an attraction basin seems to be present, but, unfortunately, it appears in an area of configuration space far from the native state. This figure was generated by using the open-source program GRAPHVIZ (41).

Discussion

At present, the protein structure refinement problem is one of the most challenging and important areas in the field of protein structure prediction (4). The accuracy of the backbone trace of a protein structure model has a profound impact on the ability to accurately predict the side-chain placement (19), and, as a result, places constraints on what can be achieved with structure-based drug design (20), prediction of multimeric protein complexes (21), and structure-based protein function prediction (22).

In this work, we set out to test how well an MM force field is able to refine near-native protein structures by using the technique of PEM in vacuo. We considered two important questions in our testing: Does the native state represent at least a local minimum of the potential function, and does the shape of the potential surface in the area near the native state allow for downhill searching toward native? A force field with these properties is of considerable utility for refinement applications in both structure prediction and the model-building procedure of experimental structure determination. Such tests might also allow us to suggest improvements to current force fields.

The Near-Native Chain Set.

To test for the presence and position of an attraction basin near the native state, it was necessary to (i) choose a set of nonredundant protein chains for testing so that our results were not protein-dependent, and (ii) generate a set of NNSMs for each chain to sample the configuration space as widely as possible about the native state. Our method, which involved perturbation of the chains by using Tirion-style normal modes expanded about the native state, generated a diverse set of NNSMs. This method generated a set of NNSMs that retained the bulk of the secondary structure present in the NS, akin to what one might find when generating an initial protein model from homology modeling or threading. An added benefit of this technique is its generality; generation of the normal modes need not occur at a deep energy minimum (a constraint present in most other normal-mode generation techniques), allowing such configurational sampling about any point in protein conformation space.

Creating NNSMs by combining Cartesian coordinate shift vectors, however, can generate atomic clashes and highly strained bond lengths and angles. With PEM, such stereochemical deformations quickly correct themselves (9), but this may not be true as we begin to explore other methods of searching configuration space. An ideal NNSM-generation method would combine the torsion angle shift vectors directly; a more complex process because increasing a torsion angle produce changes in Cartesian coordinates that do not lie on a straight line and are not monotonically increasing.

Potential Function Performance.

Of the MM potentials tested, AMBER99 showed the best performance when performing PEM on native protein structures, causing the smallest perturbation on average from the experimental structure. In our tests of NNSM minimization, AMBER99 was the only MM potential tested that was able to show a mean improvement in rmsd after PEM averaged over all NNSM sets. After AMBER99, OPLS-AA was the best performer on both tests, followed by GROMOS96 and ENCAD. It is interesting to note that both AMBER99 and OPLS-AA are potentials parameterized for use with explicit solvent, whereas the versions of the GROMOS96 and ENCAD potentials tested were parameterized for vacuum calculations. Thus, the performance ranking seen herein is contrary to our intuition before this work was begun, which indicates the need for careful, NNSM-based testing of energy functions.

It is interesting to consider at this point what upper limit of refinement performance is to be expected; this has been addressed in recent work in which structures of the same proteins have been structurally compared in different experimental crystal-packing arrangements. Eyal et al. (23) estimated the “accuracy limit” of crystal structures to be 0.8 Å rmsd, and Vriend and coworkers (5) estimated an accuracy limit of 0.48 Å for rmsd and 0.95 Å for all heavy atoms. If we assume that a model within 0.8 Å rmsd is indistinguishable from native, the seemingly modest improvements of 3% and 11% of rmsd attributed to AMBER99 and KB_0.1, respectively, for NNSMs with a mean of 〈rmsd〉 of 1.06 Å become much more substantial.

It would be satisfying at this point to state specifically why one potential works better than another in these tests. Because the energy for a given configuration is a sum over many hundreds, and often thousands, of individual energy contributions, and because a single bad contact along a trajectory can have a much larger contribution to the overall energy than a large number of small, favorable interactions, teasing out the energetic differences between potentials is an exceedingly difficult task. We have not yet fully resolved this issue to our satisfaction.

It is possible that the reductionist viewpoint, stated in the preceding paragraph, may not be sufficient to explain our results: the shapes of the energy landscapes encoded by the potentials are far more important than the individual interactions themselves. The ruggedness of the energy landscape may also be important.

It is gratifying to note that use of criteria 1 and 2 give the same overall ranking of force-field performance: KB_0.1 works best, followed by AMBER99, KB_0.2, OPLS-AA, KB_0.5, GROMOS96, and ENCAD. Individual test proteins that perform well under PEM with a particular energy function from the native state (criterion 1) do not necessarily score well when the same energy function is used to attempt to move NNSMs closer to the NS (criterion 2). Specifically, there is no correlation whatsoever between scores of individual protein under criterion 1 with the scores of the same proteins under criterion 2.

Use of KB Potentials in Refinement.

Our secondary aim was to test whether a statistical KB/MM hybrid potential could perform as well as, or better than, traditional MM potentials in refinement applications. We found that a force field in which the nonbonded terms of ENCAD have been replaced by a smoothed KB potential derived with bin widths of 0.1 Å showed the best performance of any of the potentials tested in this work. Two other statistical potentials derived with bin widths of 0.2 and 0.5 Å were tested also, but their performance lagged significantly behind that of KB_0.1.

KB PMFs are derived by using statistics culled from the 3D structures of known proteins. Clearly, the widths of the distance bins into which pairwise atomic interactions are sampled from the database have a significant impact on the resultant PMF's performance in our tests. There are two factors that likely contribute to this impact: (i) the more accurate placement of energy minima in the energy-vs.-distance curves, and (ii) the more accurate placement of the repulsive “overlap” segments of each curve.

An underlying assumption when deriving pairwise PMFs is that the frequencies of atom-pair contacts are statistically independent from one another. We (24) and others (25–27) have pointed out that this assumption is not valid for proteins, given the complex bonding topology of the atoms in amino acids. Phantom, cooperative interactions can turn into explicit, “real” favorable interactions in this treatment (26). It may be precisely this effect that enables the KB/MM potentials in this work to draw NNSMs closer to native via minimization. Also, the formulation of a PMF implicitly contains the effects of solvent, because all of the experimental structures in our derivation database are folded.

Finally, our choice of a PMF-derivation scheme (28) was made at a very early stage in this work. Each of the currently used PMF derivations (18, 28–30) differs primarily in the method used to calculate the expected pairwise atomic distributions, which affects the energies assigned to each distance bin in the energy profiles.

Materials and Methods

Choice and Generation of NNSM Test Set.

Test proteins were selected to be accurately determined and have a broad, representative set of folds. First, all 27,570 coordinate files in the Protein Data Bank (release 23, August 2004) were sorted by decreasing Summary Protein Data Bank ASTRAL Check Index (SPACI) (31, 32) score, and all structures with prosthetic groups or heteroatoms other than SO₄, Mg, Ca, Cl, Na, K, NO₃, and NH₄ were removed. Starting at the top of the list, we selected one representative of each Structural Classification of Proteins (SCOP) (33) fold to give a list of 99 domains. If some of these domains were split parts of a single chain, we also included the entire chain in our test set. We included additional domains if CATH (34) or our domain parsing split a chain that was treated as a single domain by SCOP, which gave us a list of 122 protein chains and domains. This list was pruned further on the basis of preliminary minimization using the ENCAD potential: chains that showed poor behavior upon minimization of the NS (rmsd > 2.0 Å) were discarded, leaving 77 chains in total.

Generation of sets of near-native, structurally perturbed variants of each chain was performed by our method of normal-mode perturbation. This method involves calculating quasielastic modes of each NS by using the single-bond torsion angles as degrees of freedom. We generated the required V and T matrices by using numerical differentiation (35) with the Tirion-like (17) energy function, U_ij = 90·(r² − R²)²/{R⁴·[aR⁴ + (1 − a)r⁴]}, where r is the separation of atoms i and j, R is the constant separation of the same atoms in the NS, and the constant a is set to 0.2. With this function, the energy and its first derivative are zero at the NS (r = R), and its second derivative, which is always positive, decreases as R⁻⁶.

Eigenvectors derived in torsion-angle space are straight-line Cartesian coordinates. We use the shifts of atomic positions caused by a very small shift along a torsional mode denoted as v_ij for the ith Cartesian coordinate of the kth mode. These shift vectors are not necessarily orthogonal in Cartesian coordinates (Σv_ikv_ij ≠ 0). Adding components from such vectors can fail to span the subspace of K modes properly. We dealt with this by selecting the lowest frequency mode and then testing the next lowest-frequency modes in order of increasing frequency. A new mode is selected if the largest value of its dot product to modes already selected is <0.4. This procedure is continued until 6 quasiorthogonal modes have been selected. We use these six modes with a value of m = 1 (amplitudes of −δ, 0, and δ) to give a total of 3⁶ = 729 NNSMs.

In this initial test, modes were generated only for the heavy atoms and polar hydrogen atoms. Normal-mode generation succeeded in 75 of the 77 cases; this set of 75 chains is analyzed in this work.

Derivation of Continuous KB Potentials.

Proteins from the Top500 Database were used for the counting of pairwise atomic contact frequencies. With a total of >74,000 nonhydrogen atoms, it was possible to use all of the 167 atom types used before in Samudrala's RAPDF KB potential (18). Interactions between pairs of atoms in the same residue or in residues adjacent along the sequence were ignored. The ≈250 million pairwise interactions were counted in bins centered at distances of i·S, where S is the bin width (Å), and i is the bin number, starting with 0. Each pairwise count is fractionally assigned to the two bins on either side of the exact interatomic distance. Specifically, for a pair of atoms at an interatomic distance, d, where i·S ≤ d < (i + 1)·S, the count of bin i is incremented by [1 − (d − i·S)/S] and the count of bin (i + 1) is incremented by [(i + 1)·S − d]/S. These counts are converted to an energy value by using the formalism of Lu and Skolnick (28).

The repulsive close-contact portion of each pairwise interaction was calculated by using

Here i_L is the index and E(i_L) is the knowledge-based energy of the first distance with at least a fractional count, and i_0c (zero counts) is the immediately preceding bin. i_0c-0.5 is the index of the bin in which the r(i_0c) distance is decreased by 0.5 Å, i_0c-1.0 is the index of the bin in which the r(i_0c) distance is decreased by 1.0 Å, and E_z is the plateau energy value [80 kcal/mol (1 kcal = 4.18 kJ)] used for smaller distances.

Each distance-dependent pairwise curve was then fit to a quintic spline function. These differentiable KB potentials were used together with the bonded terms of the ENCAD force field by replacing all nonbonded energy terms in ENCAD with the corresponding KB terms. The KB/MM hybrid potential was smoothly truncated to 0 kcal/mol between 9 and 11 Å.

Minimization Protocol.

Proteins were minimized in vacuo by using the Limited-Memory Broyden-Fletcher-Goldfarb-Shanno (36) minimizer in either GROMACS (37–39) or ENCAD (15, 40). In every case, the minimizer was set to run for 10,000 steps of minimization or until convergence to machine precision. In minimizations using the ENCAD potential, a force-shifted truncation method was used with nonbonded (Lennard–Jones and Coulomb) cutoff values of 6 Å. When using GROMOS96, AMBER99, and OPLS-AA, the simple nonbonded cutoff scheme of GROMACS was used for long-range force truncation beyond 9 Å. In all cases, the dielectric constant was set to 1, and the hydrogen atoms were built by the program used for energy minimization to produce neutrally charged side chains. The version for the GROMOS96 potential used was GROMOS96 43b1, which was parameterized for vacuum simulations, as was the ENCAD potential.

Abbreviations

CASP

Critical Assessment of Protein Structure Prediction

NNSM

near-native structure model

NS

native structure

PEM

potential energy minimization

MM

molecular mechanics

KB

knowledge-based

PI

percent improvement

PMF

potential of mean force.

Note.

Our method of PEM with KB_0.1 was tested in the “Physics-Based Refinement” section of CASP7. For the eight near-native structures released, our minimized submissions showed a mean rmsd improvement of 0.05 Å and PI of −3.2%. We expect more robust search methods to improve this performance.