Dynamic use of multiple parameter sets in sequence alignment

Abstract

The level of conservation between two homologous sequences often varies among sequence regions; functionally important domains are more conserved than the remaining regions. Thus, multiple parameter sets should be used in alignment of homologous sequences with a stringent parameter set for highly conserved regions and a moderate parameter set for weakly conserved regions. We describe an alignment algorithm to allow dynamic use of multiple parameter sets with different levels of stringency in computation of an optimal alignment of two sequences. The algorithm dynamically considers various candidate alignments, partitions each candidate alignment into sections, and determines the most appropriate set of parameter values for each section of the alignment. The algorithm and its local alignment version are implemented in a computer program named GAP4. The local alignment algorithm in GAP4, that in its predecessor GAP3, and an ordinary local alignment program SIM were evaluated on 257 716 pairs of homologous sequences from 100 protein families. On 168 475 of the 257 716 pairs (a rate of 65.4%), alignments from GAP4 were more statistically significant than alignments from GAP3 and SIM.

INTRODUCTION

Sequence alignment programs are tremendously useful in analysis of DNA and protein sequences (1–10). Those programs are efficient variations of alignment algorithms that produce an optimal global alignment of two sequences or an optimal local alignment between two sequences under a given set of parameter values (11–19). An alignment algorithm can be run multiple times, each with a different set of parameter values, and a set of parameter values that leads to a largest-scoring alignment is selected along with the alignment (20,21). Algorithms based on Bayesian statistics are recently developed to compute the posterior distribution of all alignments over several sets of parameter values, where every alignment is scored by using each of the parameter sets (22–24).

The level of conservation between two homologous sequences often varies among sequence regions; functionally important domains are more conserved than the remaining regions. Thus, any one set of parameter values may not be the most appropriate one for all sequence regions. A stringent set of parameter values should be used for a highly conserved region, whereas a moderate set of parameter values should be used for a weakly conserved region.

We present a global alignment model that uses sets of parameter values with different levels of stringency to address sequences with different levels of conservation among regions. We design a dynamic programming algorithm for computing an optimal alignment of two sequences with proper assignment of a parameter set to each section of the alignment. For two sequences of lengths m and n, and p parameter sets, the algorithm runs in time proportional to pmn, and in space proportional to p(m+n). The algorithm is implemented in a computer program named GAP4 (Global Alignment Program Version 4). We also describe changes to the global alignment algorithm to produce a local alignment algorithm with the dynamic use of multiple parameter sets. The local alignment algorithm is also available in GAP4 as an option.

The local alignment algorithm in GAP4, the local alignment algorithm in its predecessor GAP3 (19), and an ordinary local alignment program SIM (17) were evaluated on 257 716 pairs of homologous sequences from 100 protein families. On 168 475 of the 257 716 pairs (a rate of 65.4%), alignments from GAP4 were more statistically significant than alignments from GAP3 and SIM. The results show that the dynamic use of multiple parameter sets is more effective than the static use of each parameter set. In addition, every alignment from GAP4 contains annotations of conservation level. Results from a motif finding program on five pairs of protein sequences show that many motifs are located in highly conserved regions found by GAP4.

Our algorithm goes one step further than the existing alignment algorithms that use multiple parameter sets. Every existing alignment algorithm selects a parameter set at the alignment level, where every alignment is scored by using each parameter set alone, and a parameter set that yields a largest-scoring alignment is selected. All sections of the largest-scoring alignment are scored with the selected parameter set. Our algorithm, on the other hand, selects a parameter set at the section level. The algorithm uses multiple parameter sets to score each candidate alignment simultaneously. For every section of the candidate alignment, a parameter set that yields the maximum score for the section is selected for the section. An alignment produced by the algorithm is optimal in partition of the alignment into sections, and in selection of a largest-scoring parameter set for each section.

MATERIALS AND METHODS

We first define a global alignment model and present a dynamic programming algorithm for computing the score of an optimal alignment. Then we describe a space-efficient algorithm for computing an optimal alignment of two sequences. Next we show how to compute an optimal local alignment between two sequences.

Alignment model

We define a global alignment model to handle sequences with different levels of conservation among regions. Let A = a₁a₂ … a_m and B = b₁b₂ … b_n be two sequences of lengths m and n. A global alignment of A and B consists of three types of configurations: substitutions, gaps, and difference blocks. A substitution associates a residue of A with a residue of B. A gap consists only of residues from one sequence with each residue associated with the symbol −. There are two kinds of gaps. A deletion gap with respect to sequence A consists only of residues from A and an insertion gap with respect to sequence A consists only of residues from B. A difference block consists of residues from one or two sequences with each residue associated with the symbol + (19). There are three types of difference blocks. A difference block of type 1 consists only of residues from A, a difference block of type 2 consists only of residues from B, and a difference block of type 3 consists of residues from both A and B.

Parameter value sets with different levels of stringency are used to score alignments. Let p be the number of parameter sets. For each k between 1 and p, let < σ_k, q_k, r_k, d_k, c_k> denote parameter set k, where σ_k is a substitution matrix, nonnegative number q_k is a gap-open penalty, nonnegative number r_k is a gap-extension penalty, nonnegative number d_k is a difference block penalty and nonnegative number c_k is a parameter set change penalty. If a configuration of an alignment is mapped to parameter set k, then the score of the configuration is calculated by using parameter set k. For example, σ_k(a,b) is the score of a substitution involving residues a and b that is mapped to parameter set k, the score of a gap of length l mapped to parameter set k is −(q_k + l × r_k), and the score of a difference block mapped to parameter set k is − d_k. We require that adjacent difference blocks be combined into one difference block that can be mapped to only one parameter set. The same requirement is also placed on adjacent deletion gaps and adjacent insertion gaps. In addition, a difference block and a gap that are adjacent to each other are combined into a larger difference block, which results in no loss of score.

An alignment is mapped to the parameter sets if each configuration of the alignment is mapped to one of the parameter sets. A section of a mapped alignment is a largest part of consecutive configurations that are mapped to the same parameter set. The parameter set change score of a section mapped to parameter set k is −c_k. The score of a mapped alignment is the sum of scores of each mapped substitution, each mapped gap, and each mapped difference block in the alignment, plus the sum of parameter set change scores of each mapped section in the alignment. As an example, an initial part of a mapped alignment is shown in Figure 1. An optimal mapped alignment has the maximum score of all mapped alignments.

Figure 1.

An initial part of a global alignment from GAP4 on two protein sequences (SwissProt accession nos Q9NTI2 and Q9Y2G3). A difference block is indicated by the plus sign +. Each column of the alignment is marked with one of the three letters: l, m and h, which indicates one of the three parameter sets used to score the column.

We develop a dynamic programming algorithm for computing an optimal mapped alignment of A and B. Let A_i = a₁a₂ … a_i and B_j = b₁b₂… b_j be initial segments of lengths i and j of A and B. Define Z(i, j) to be the maximum score of mapped alignments of A_i and B_j. Then Z(m, n) is the score of an optimal mapped alignment of A and B. For each k with 1 ≤ k ≤ p, define S_k(i, j) to be the maximum score of mapped alignments of A_i and B_j that end with a configuration mapped to parameter set k. Then Z(i, j) is the maximum score of S_k(i, j) for each k with 1 ≤ k ≤ p. For each k with 1 ≤ k ≤ p, to compute the matrix S_k efficiently, three additional matrices are introduced. Define H_k(i, j) to be the maximum score of mapped alignments of A_i and B_j that end with a difference block mapped to parameter set k. Similarly, define D_k(i, j) for mapped alignments that end with a deletion gap mapped to parameter set k and I_k(i, j) for mapped alignments that end with an insertion gap mapped to parameter set k. The following recurrences for computing the matrices are derived from the definitions of the matrices. Assume that any expression with −∞ is less than any expression without it.

$$Z(0,0)=0,$$

$$Z(i,j)=\text{max}\left\{S_k\right(i,j\left)\right|1\le k\le p\}\hspace{1em}\text{for}\hspace{1em}i>0\hspace{1em}\text{or}\hspace{1em}j>0.$$

$$S_k(0,0)=Z(0,0)-c_k,$$

$$S_k(i,0)=\text{max}\left\{D_k\right(i,0),H_k(i,0\left)\right\}\hspace{1em}\text{for}\hspace{1em}i>0,$$

$$S_k(0,j)=\text{max}\left\{I_k\right(0,j),H_k(0,j\left)\right\}\hspace{1em}\text{for}\hspace{1em}j>0,$$

$$D_k(0,0)=S_k(0,0)-q_k,$$

$$D_k(0,j)=-\infty \hspace{1em}\text{for}\hspace{1em}j>0,$$

$$D_k(i,0)=D_k(i-1,0)-r_k\hspace{1em}\text{for}\hspace{1em}i>0,$$

$$I_k(0,0)=S_k(0,0)-q_k,$$

$$I_k(i,0)=-\infty \hspace{1em}\text{for}\hspace{1em}i>0,$$

$$I_k(0,j)=I_k(0,j-1)-r_k\hspace{1em}\text{for}\hspace{1em}j>0,$$

$$H_k(0,0)=S_k(0,0)-d_k,$$

$$H_k(0,j)=H_k(0,j-1)\hspace{1em}\text{for}\hspace{1em}j>0,$$

$$H_k(i,0)=H_k(i-1,0)\hspace{1em}\text{for}\hspace{1em}i>0,$$

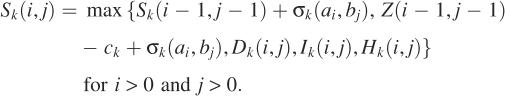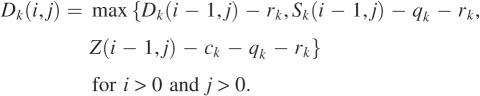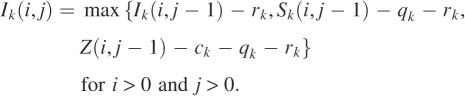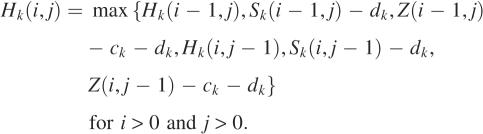In Supplementary Data, we justify the recurrences for the matrix S_k and for the matrix D_k for any k with 1 ≤ k ≤ p. The matrices are computed according to the recurrences in order of rows. The computation is performed by saving only the most recent row of each matrix. This is possible because each of the matrices observes the property that the score at an entry depends only on scores at its neighbor entries. For each entry (i, j), it takes time proportional to p to compute all matrix scores at the entry; it takes time proportional to p to compute Z(i, j), and for each k from 1 to p, it takes constant time to compute each of S_k(i, j), D_k(i, j), I_k(i, j) and H_k(i, j). An optimal mapped alignment is computed in linear space by an algorithm described in the next subsection.

Algorithm

We develop a space-efficient algorithm for computing an optimal mapped alignment of A and B. A divide-conquer technique is developed by Hirschberg (25) for computing a longest common subsequence of two sequences. The Hirschberg technique is applied to global alignment models (15,19,26,27). Here the Hirschberg technique is applied to the new alignment model. The main idea of the space-efficient algorithm is to determine a middle pair of positions on an optimal mapped alignment in linear space. Then the portions of the optimal mapped alignment before and after the middle pair of positions are constructed recursively. Let imid be ⌊m / 2⌋, where ⌊y⌋ is the largest integer less than or equal to y. We first consider a procedure for finding a position jmid such that the pair of positions imid and jmid is on an optimal mapped alignment of A and B.

Partition the mapped alignments of A and B into four groups. Group 1 consists of mapped alignments with a difference block containing a residue a at position imid of A and another residue immediately to the right of a. In other words, a mapped alignment is in group 1 if, upon splitting the alignment into two parts immediately after the residue a, the first part ends with a difference block mapped to a parameter set and the second part begins with a difference block mapped to the same parameter set. Group 2 consists of mapped alignments with a deletion gap containing residues at positions imid and imid + 1 of A, with the deletion gap mapped to a parameter set. Group 3 consists of mapped alignments with a substitution involving a residue at position imid of A, with the substitution and the configuration immediately to its right mapped to the same parameter set. Group 4 consists of all the remaining mapped alignments. Note that a residue at position imid of A can not be inside any insertion gap and hence that there is no need to consider this case. We consider computing the score of and a middle pair of positions on a largest-scoring mapped alignment in each group.

Let R(A,B) denote a largest-scoring mapped alignment of A and B in group 1. Split R(A,B) into two parts immediately after position imid of A. Let jh be the largest position of B in the first part. Let $A_i^s$ denote the suffix a_i+1a_i+2 … a_m of A. Notation $B_j^s$ is similarly defined. Then the first part of R(A,B) is an alignment, denoted by R₁(A_imid, B_jh), of A_imid and B_jh and the second part is an alignment, denoted by $R_2(A_{imid}^s,B_{jh}^s)$, of $A_{imid}^s$ and $B_{jh}^s$. Note that for some k with 1 ≤ k ≤ p, R₁(A_imid,B_jh) ends with a difference block mapped to parameter set k and that $R_2(A_{imid}^s,B_{jh}^s)$ begins with a difference block mapped to parameter set k. Define ${\overline{H}}_k$(i,j) to be the maximum score of mapped alignments of $A_i^s$ and $B_j^s$ that begin with a difference block mapped to parameter set k. It follows from the definition of R(A,B) that the score of R₁(A_imid,B_jh) is H_k(imid,jh) and the score of $R_2(A_{imid}^s,B_{jh}^s)$ is ${\overline{H}}_k$(imid,jh). Moreover, the score of R(A,B), denoted by hk, is

$$hk=H_k(imid,jh)+{\overline{H}}_k(imid,jh)+d_k+c_k,$$

where including the terms d_k and c_k on the right-hand side ensures that the mapped difference block containing a residue at position imid of A is charged for difference block penalty exactly once and the section containing the mapped difference block is charged for parameter set change penalty exactly once. Observe that for each k with 1 ≤ k ≤ p and each j with 0 ≤ j ≤ n, H_k(imid, j) + ${\overline{H}}_k$(imid, j) + d_k + c_k is the score of a mapped alignment of A and B in group 1. Combining the observations together, we obtain

$$hk=\text{max}\left\{H_k\right(imid,j)+{\overline{H}}_k(imid,j)+d_k\hspace{1em}+c_k|1\le k\le p,0\le j\le n\}.$$

Note that jh is a position j at which the maximum score hk is obtained. Thus, the score of and a middle pair of positions on a largest-scoring mapped alignment in group 1 can be obtained using middle rows of the matrices H_k and ${\overline{H}}_k$.

The score of and a middle pair of positions on a largest-scoring mapped alignment in group 2 and those in groups 3 and 4 can be obtained similarly. Define ${\overline{D}}_k$(i, j) to be the maximum score of mapped alignments of $A_i^s$ and $B_j^s$ that begin with a deletion gap mapped to parameter set k. Define ${\overline{S}}_k$(i,j) to be the maximum score of mapped alignments of $A_i^s$ and $B_j^s$ that begin with a configuration mapped to parameter set k. Define $\overline{Z}(i,j)$ to be the maximum score of mapped alignments of $A_i^s$ and $B_j^s$. Then the score of a largest-scoring alignment in group 2, denoted by df, is

$$df=\text{max}\left\{D_k\right(imid,j)+{\overline{D}}_k(imid,j)+q_k\hspace{1em}+c_k|1\le k\le p,0\le j\le n\}.$$

Let jd be a position j at which the maximum score df is obtained. Then (imid, jd) is a middle pair of positions on a largest-scoring alignment in group 2.

In group 3, the score of a largest-scoring alignment, denoted by st, is

$$st=\text{max}\left\{S_k\right(imid,j)+{\overline{S}}_k(imid,j)\hspace{1em}+c_k|1\le k\le p,0\le j\le n\}.$$

Let js be a position j at which the maximum score st is obtained. Then (imid, js) is a middle pair of positions on a largest-scoring alignment in group 3.

In group 4, the score of a largest-scoring alignment, denoted by zy, is

$$zy=\text{max}\left\{Z\right(imid,j)+\overline{Z}(imid,j\left)\right|0\le j\le n\}.$$

Let jz be a position j at which the maximum score zy is obtained. Then (imid, jz) is a middle pair of positions on a largest-scoring alignment in group 4.

The recurrences for computing the matrices ${\overline{D}}_k$, ${\overline{I}}_k$, ${\overline{H}}_k$, ${\overline{S}}_k$ and $\overline{Z}$ are developed in the same way as those for D_k, I_k, H_k, S_k and Z. The score of an optimal mapped alignment of A and B is max{df, hk, st, zy}. Let jmid be the corresponding one of jd, jh, js and jz. Then the pair of positions imid and jmid is on an optimal mapped alignment of A and B.

An algorithm for computing an optimal mapped alignment of A and B in linear space consists of the following steps. If m is small enough, compute an optimal mapped alignment of A and B using a traceback procedure. Otherwise, determine a pair of positions imid and jmid on an optimal mapped alignment of A and B, and recursively compute the portions of the alignment before and after the pair of positions.

The positions imid and jmid are determined as follows. Set imid = ⌊m/2⌋. Compute the matrices D_k, I_k, H_k and S_k, 1 ≤ k ≤ p, and the matrix Z from row 0 to row imid, and save D_k(imid, j), H_k(imid, j), S_k(imid, j) and Z(imid, j) for 0 ≤ j ≤ n. Compute the matrices ${\overline{D}}_k$, ${\overline{I}}_k$, ${\overline{H}}_k$ and ${\overline{S}}_k$, 1 ≤ k ≤ p, and the matrix $\overline{Z}$ from row m down to row imid, and save ${\overline{D}}_k$(imid, j), ${\overline{H}}_k$(imid, j), ${\overline{S}}_k$(imid, j) and $\overline{Z}(imid,j)$ for 0 ≤ j ≤ n. Compute the values df, hk, st and zy. Let jd be a position at which the maximum score df is obtained, jh a position at which the maximum score hk is obtained, js a position at which the maximum score st is obtained and jz a position at which the maximum score zy is obtained. If df > hk, df > st, and df > zy, then set jmid = jd. Otherwise, if hk > df, hk > st and hk > zy, then set jmid = jh. Otherwise, if st > df, st > hk and st > zy, then set jmid = js. Otherwise, set jmid = jz.

It can be proved that for two sequences of lengths m and n, and p parameter sets, the algorithm runs in time proportional to pmn, and in space proportional to p(m + n). The proof is similar to one from Huang (28).

The algorithm presented above is for the simple scoring scheme where a parameter set change penalty is always charged even if the whole alignment is mapped to one parameter set. In a more realistic scoring scheme, no parameter set change penalty is charged for the first use of a parameter set. For any change from one parameter set to another parameter set, the change penalty for the second parameter set is charged. The realistic scoring scheme is implemented by using proper boundary values for the matrices and passing them as parameters to a recursive alignment procedure. Implementation details can be found in the source code of the GAP4 program.

Local alignment

A local mapped alignment between A and B is a mapped alignment of a region of A and a region of B. An optimal local mapped alignment between A and B is one with the maximum score. An optimal local mapped alignment between A and B is computed by applying the technique of Smith and Waterman (12) to the new alignment model. Specifically, the value zero is included in the recurrence for Z(i, j), and the term σ_k(a_i,b_j) is included in the recurrence for S_k(i, j). Thus, if Z(i−1, j−1) is less than c_k, then the term σ_k(a_i,b_j) is larger and hence better than the term Z(i−1, j−1)−c_k + σ_k(a_i,b_j) for computing S_k(i, j). In other words, the change allows a local mapped alignment to start at every entry without charging any parameter set change penalty for the first mapped substitution of the alignment.

Let (ie, je) be an entry with the maximum score in the matrix Z. Then (ie, je) is the end point of an optimal local mapped alignment between A and B, and its score is Z(ie, je). The start point (is, js) of the optimal local mapped alignment is found by performing the computation in right-to-left order with initial segments A_ie and B_je, where (is, js) is an entry with the maximum score in the matrix. The optimal local mapped alignment is obtained by using the algorithm of the previous subsection to compute an optimal global mapped alignment of segments a_is+1 a_is+2 … a_ie and b_js+1 b_js+2 … b_je.

RESULTS

The new algorithms are implemented in a computer program named GAP4; the global alignment algorithm is available in GAP4 with the −g 1 option (default), and the local alignment algorithm is available in GAP4 with the −g 0 option. The GAP4 program can handle both DNA and protein sequences. The program takes as input two sequences in FASTA format and a file of parameter sets. Each line of the parameter file contains a complete set of parameter values in the following order: a single character for representing the parameter set on the alignment output, the name of a substitution matrix file, gap open penalty, gap extension penalty, difference block penalty, and parameter set change penalty.

We tested GAP4 on protein sequences with the following three sets of parameter values in the parameter file:

• l BLOSUM45 12 2 90 10

• m BLOSUM62 14 3 95 10

• h BLOSUM100 16 4 100 10

The BLOSUM62 matrix was selected as it is commonly used (29). The BLOSUM45 matrix was selected as its stringency level is sufficiently lower than that of BLOSUM62, whereas the BLOSUM100 matrix was selected as its stringency level is sufficiently higher than that of BLOSUM62. The three BLOSUM matrices were on the same scale of 1/3 bit units. The gap open and extension penalties in each parameter set were selected according to Pearson (30–32). The difference block penalty in each parameter set was set to a value above the scores of similarity blocks between random sequences (19). The parameter set change penalty is new. We used various values between 1 and 15 for this parameter and found that using a value of 10 keeps a balance between too frequent changes and no changes in use of parameter sets. The value 10 was also selected in another test given below to assess the effect of the parameter set change penalty on the statistical significance of alignments from GAP4.

The three sets of parameter values have low, medium and high levels of stringency, as represented by the three letters l, m and h. The low parameter set is often best for scoring regions with percent identity ∼20%, the medium parameter set for scoring regions with percent identity ∼30% and the high parameter set for scoring regions with percent identity >45%. We selected those three parameter sets because protein sequences with an overall percent identity between 15 and 30% are hard to align accurately by sequence alignment programs. The stringency levels of the three sets of parameter values suggest that we should select pairs of protein sequences with an overall percent identity between 25 and 40%, which are likely to have regions suitable for each of the three parameter sets.

An alignment from GAP4 with the three parameter sets contains four types of sections: sections of different sequence regions (marked with the sign +), sections of similar regions scored with the low parameter set (marked with the letter l), sections of similar regions scored with the medium parameter set (marked with the letter m) and sections of similar regions scored with the high parameter set (marked with the letter h). An initial part of a GAP4 alignment is shown in Figure 1. For each parameter set, GAP4 reports the total length and overall percent identity of all alignment sections that are scored with the parameter set. The GAP4 program finds sequence regions with different levels of conservation and scores each section of regions by using the most appropriate parameter set.

Global alignment examples from GAP4

The global alignment algorithm in GAP4 was used on five randomly selected pairs of long protein sequences with an overall percent identity ∼40%. For each pair of sequences, the GAP4 program was run with the three parameter sets given above and with each of the other combinations of the three parameter sets. The seven combinations of the three parameter sets are represented by the strings l, m, h, lm, lh, mh and lmh, where the letters in each string denote the parameter sets in the combination. For each pair of sequences, seven global alignments were produced by GAP4, one alignment for each of the seven combinations. As expected, for each pair of sequences, the alignments from GAP4 with the single-parameter set combinations (the l, m and h combinations) are identical both in score and configuration to the alignments from GAP3 with the static use of each of the three parameter sets, respectively.

For each pair of sequences, the seven alignments have different similarity scores, and the alignment for the lmh combination has the largest score. In addition, some of the seven alignments are different in gap or difference block positions. For each pair of sequences, the seven alignments were compared by configuration, and alignments identical in configuration were placed in the same group. Table 1 shows the alignment groups for each pair of sequences. For example, on sequence pair one, six out of the seven alignments are different from one another in gap positions. As another example, on pair four, the alignment for the lmh combination has two difference blocks with a total of 144 residues, and the alignment for the mh combination has two difference blocks with a total of 188 residues. Each difference block along with its weakly aligned boundary region in the lmh alignment became a difference block in the mh alignment because of lack of the l parameter set in the mh combination. Those results indicate that alignments from GAP4 may be different in both score and configuration when different parameter set combinations are provided to GAP4.

Table 1.

Groups of identical alignments from GAP4 with seven combinations of parameter sets on five pairs of SwissProt protein sequences

Accession of sequence A	Length	Accession of sequence B	Length	Alignment groupsa
Q9NY15	2570	Q8R4U0	2559	{l} {m, mh} {h} {lm} {lh} {lmh}
O12990	1153	Q62120	1129	{l, lm} {m} {h} {lh, lmh} {mh}
Q9H7F0	1130	Q9NQ11	1180	{l, lh, lmh} {m, mh} {h} {lm}
Q82Z40	1207	Q9XPS7	1076	{l} {m} {h} {lm} {lh, lmh} {mh}
Q9NTI2	1076	Q9Y2G3	1177	{l, lh, lmh} {m, mh} {h} {lm}

^aEach alignment is denoted by the parameter set combination used to produce the alignment. Each parameter set combination is indicated by the letters for the parameter sets in the combination, with the letter l for the low parameter set, m for the medium parameter set and h for the high parameter set.

We used an independent method to show that motifs are likely to be located in highly conserved sections found by GAP4. The alignments from GAP4 with the lmh combination on the five pairs of sequences were selected for this illustration. Each of the ten sequences was run through a motif finding program named eMATRIX-Scan with the default parameter settings (33,34). For each sequence, the start and end coordinates of all motifs in the sequence from eMATRIX-Scan were transformed into coordinates with respect to the corresponding GAP4 alignment. We report in Table 2, for each alignment, the proportions of the motif residues in the l, m and h sections of the alignment, respectively, and the proportions of the alignment positions in the l, m, and h sections of the alignment, respectively. Table 2 also shows the proportions for motif residues and alignment positions for all alignments, where the total number of motif residues is 2219 and the total number of alignment positions is 7497. Many of the motifs have an overlap with an h section.

Table 2.

Proportions of the motif residues in the l, m and h sections of the alignment, respectively, and proportions of the alignment positions in the l, m and h sections of the alignment, respectively, for each alignment and for all alignments

Alignment	Proportions of motif residues			Proportions of alignment positions
	Type l	Type m	Type h	Type l	Type m	Type h
1	0.06	0.43	0.51	0.25	0.44	0.31
2	0.10	0.04	0.86	0.39	0.03	0.58
3	0.00	0.00	1.00	0.43	0.05	0.52
4	0.01	0.02	0.97	0.42	0.19	0.39
5	0.12	0.00	0.88	0.49	0.06	0.45
All	0.06	0.20	0.74	0.37	0.21	0.42

Evaluation of GAP4

We assessed the biological purpose of making the dynamic use of multiple parameter sets by comparing the local alignment algorithm in GAP4 with the local alignment algorithm in GAP3 (19), and the Smith–Waterman local alignment algorithm in SIM (17) on a large number of homologous protein sequences. Local alignment algorithms, instead of global alignment algorithms, are often used on sequences with local similarities, and the Smith–Waterman algorithm is shown to be more sensitive than other fast alignment methods (30–32). The SIM program produces an ordinary local alignment called a similarity block, and GAP3 produces an ordered list of similarity blocks separated by difference blocks. Both SIM and GAP3 use one parameter set at a time, whereas GAP4 extends GAP3 by making the dynamic use of multiple parameter sets.

We browsed the Pfam protein families at http://pfam.wustl.edu and focused on large families with an average sequence length of at least 200 residues and with an average percent identity between 25 and 40%. By following the links from the Pfam families to SwissProt, we selected 100 families of homologous protein sequences with a total of 7092 sequences from release 50.4 of the SwissProt protein database.

The three programs were evaluated by assessing the statistical significance of alignments from the programs. The statistical significance of an optimal local alignment produced by the Smith–Waterman algorithm with one set of parameters is estimated with the equation

$$P(S\ge x)=1-exp(-Kmn{e}^{-\lambda x}),$$ 1

where x is the similarity score of the alignment, m and n are the lengths of the two sequences, and K and λ are statistical parameters dependent on the set of alignment parameters and the amino acid compositions of the sequences (35–38). Values for the statistical parameters are obtained by fitting Equation 1 to an empirical distribution of scores of alignments between randomly shuffled versions of the two sequences (36,38).

In the rest of this subsection, we first show how to find values for statistical parameters K and λ in Equation 1 in order to estimate the statistical significance of alignments from each of the three programs with the three parameter sets. Then we describe how to compute the standard error of probability estimate for each of the three programs. Those standard errors of probability estimate are useful in showing that Equation 1 can also be used to estimate the statistical significance of optimal local alignments from GAP3 and GAP4, with the same level of accuracy as from SIM. Finally we present evaluation results on the statistical significance of alignments from the three programs.

A million pairs of random sequences are generated from a real protein sequence by reversing the sequence to produce a second sequence, by shuffling each of the two sequences a number of times to produce a first pair of random sequences, and by shuffling each of the two sequences in the first pair a number of times to produce a second pair of random sequences, and so on. Then for each of the three programs with each, two, or all of the three parameter sets, an optimal alignment is computed by the program on each pair of random sequences, and an empirical distribution of scores of a million alignments is generated. Let f_1,h(x) be the observed frequency of getting the optimal alignment score above x in the empirical distribution of a million alignment scores from SIM with the parameter set h. Similarly, introduce f_1,l(x) for SIM with l, f_1,m(x) for SIM with m, f_3,l(x) for GAP3 with l, f_3,m(x) for GAP3 with m, f_3,h(x) for GAP3 with h, f_4,m,h(x) for GAP4 with m and h and f_4,l,m,h(x) for GAP4 with l, m and h. As to be explained below, for some pairs of sequences, alignments from GAP4 with m and h are more statistically significant than alignments from GAP4 with l, m and h.

For SIM with h, let K_1,h and λ_1,h denote the K and λ parameters in Equation 1, and obtain their values by fitting Equation 1 to the empirical data f_1,h(x). For GAP3 with h, obtain K_3,h and λ_3,h values by fitting Equation 1 to f_3,h(x). Similarly, obtain values for K_1,l and λ_1,l, K_3,l and λ_3,l, K_1,m and λ_1m, and K_3,m and λ_3,m. For GAP4 with m and h, obtain K_4,m,h and λ_4,m,h values by fitting Equation 1 to f_4,m,h(x). Similarly, obtain K_4,l,m,h and λ_4,l,m,h values. There are eight pairs of K and λ values: three pairs for SIM, three pairs for GAP3 and two pairs for GAP4.

Let p_1,h(x) be the probability of getting an optimal local alignment score above x from SIM with h. The probability is estimated by Equation 1 with the pair of K_1,h and λ_1,h values. Similarly, define p_1,l(x) for SIM with l, p_1,m(x) for SIM with m, p_3,l(x) for GAP3 with l, p_3,m(x) for GAP3 with m, p_3,h(x) for GAP3 with h, p_4,m,h(x) for GAP4 with m and h and p_4,l,m,h(x) for GAP4 with l, m and h. Those probabilities are estimated by Equation 1 with the corresponding pairs of K and λ values.

The standard error of estimate for each probability from Equation 1 is computed as follows. Generate another million pairs of random sequences. For each pair (A,B) of random sequences, two alignments are computed by SIM, one with l and the other with h. Let $s_{1,l}^{A,B}$ denote the score of the alignment with l, and $s_{1,h}^{A,B}$ denote that with h. Let Q be the set of all pairs (A,B) of sequences with $0.00005\le f_{1,l}\left(s_{1,l}^{A,B}\right)\le 0.01$ and $0.00005\le f_{1,h}\left(s_{1,h}^{A,B}\right)\le 0.01$. The use of the upper bound 0.01 and the lower bound 0.00005 ensures that the pairs of sequences in the set Q have accurate and useful empirical frequencies; a frequency above 0.01 is less useful and a frequency below 0.00005 is less accurate. The set Q is used to compute the standard error of probability estimate for each of the three programs with each, two, or all of the parameter sets. The standard error of probability estimate for SIM with h on the set Q of sequence pairs is defined as

$$s{e}_{1,\pm h}=\sqrt{\left({\displaystyle \sum _{(A,B)\in Q}}{\left[p_{1,h}\right(s_{1,h}^{A,B})\hspace{0.17em}-\hspace{0.17em}{f}_{1,h}(s_{1,h}^{A,B}\left)\right]}^2\right)/(N_Q-2)},$$

where N_Q is the number of sequence pairs in the set Q. Using the denominator N_Q − 2, instead of N_Q, is a standard practice in regression analysis. The standard errors se_1,l, se_1,m, se_3,l, se_3,m, se_3,h, se_4,m,h and se_4,l,m,h are similarly defined by using the same set Q. There are eight standard errors: three for SIM, three for GAP3 and two for GAP4.

Next we present evaluation results on the statistical significance of alignments from the three programs with the three parameter sets. A real protein sequence (SwissProt accession no. Q8R016) was randomly selected as a source sequence from one of the 100 families of homologous sequences. From this source sequence, eight pairs of K and λ values and eight standard errors were computed by using the method given above. Those values, marked from above with the corresponding parameter names, are given below:

The number of sequence pairs in the set Q was 796. Note that the statistical parameter values of GAP3 are identical to those of SIM, respectively. Because the standard errors for GAP4 are similar to those for SIM, Equation 1 can be used to estimate the statistical significance of alignments from GAP4 at a similar level of accuracy as it is for SIM. The λ_1,m value of 0.202 (for BLOSUM62 in 1/3 bit units) given above is smaller than a λ value of 0.305 for BLOSUM62 in 1/2 bit units from Altschul and Gish (38).

An important observation about the λ values is that the λ_4,l,m,h value is close to the λ_1,l value, and the λ_4,m,h value is close to the λ_1,m value. It follows by Equation 1 that if GAP4 with l, m and h produces an alignment of sufficiently larger score than SIM with l on a pair of sequences, then the alignment from GAP4 is more statistically significant than the alignment from SIM. Similarly, if GAP4 with m and h produces an alignment of sufficiently larger score than SIM with m on a pair of sequences, then the alignment from GAP4 is more statistically significant than the alignment from SIM. In addition, the λ_4,m,h value is not far below the λ_1,h value, so an alignment of much larger score from GAP4 with m and h may be more statistically significant than an alignment from SIM with h. On the other hand, the λ_4,l,m,h value is much smaller than the λ_1,m value, so an alignment of much larger score from GAP4 with l, m and h may be less statistically significant than an alignment from SIM with m. Because the K_4,l,m,h value is larger than the K_1,l value, an alignment from GAP4 with l, m and h is less statistically significant than an alignment of the same score from SIM with l.

Different values for the parameter set change penalty c were used to see its effect on λ_4,m,h in relation to λ_1,m. For each c value from 4 to 14 with a step size of 2, λ_4,m,h and λ_1,m values were estimated from the source sequence with the parameter sets m and h, where the set change penalty was set to the value and the rest in m and h were unchanged. Since λ_3,m is very close to λ_1,m, λ_3,m is omitted here. The relationship between c and λ_4,m,h − λ_1,m is shown in the following data in the form of c∣(λ_4,m,h − λ_1,m): 4∣−0.009, 6∣−0.003, 8∣−0.002, 10∣0.003, 12∣0.004 and 14∣0.004. The data show that using a c value of 10 or higher kept λ_4,m,h above λ_1,m. Keeping λ_4,m,h above or close to λ_1,m is important in ensuring that an alignment of sufficiently higher score from GAP4 is more statistically significant than an alignment from SIM.

The statistical parameter values were used to assess the statistical significance of alignments from the three programs on the 100 families of homologous protein sequences. For each family, pairs of homologous protein sequences were formed by pairing each sequence with every other sequence in the family. For each pair of homologous sequences, if the percent identity of an alignment from SIM with m on the pair is <40%, then the pair was selected. A total of 257 716 pairs were selected. For each pair of selected sequences, GAP4 with the −g 0 option was run twice on the pair, first time with the parameter sets l, m and h, and second time with the parameter sets m and h, the P-value of the first alignment was computed by Equation 1 with the K_4,l,m,h and λ_4,l,m,h values, that of the second alignment was computed with the K_4,m,h and λ_4,m,h values, and the minimum of the two P-values was selected.

The GAP3 program with the −g 0 option was run three times on the pair, each with one of the three parameter sets, the P-value of each of the three alignments was computed with the corresponding pair of K and λ values, and the minimum of the three P-values was selected. Similarly, SIM with the one-alignment option was run three times on the pair, each with one of the three parameter sets, the P-value of each of the three alignments was computed with the corresponding pair of K and λ values, and the minimum of the three P-values was selected.

On 168 475 out of the 257 716 pairs (a rate of 65.4%), the P-value from GAP4 was smaller than the P-values from GAP3 and SIM. In 60 out of the 100 families, a rate of at least 59% in favor of GAP4 was observed for the family. The entire computation from taking as input a source sequence to reporting the P-values of alignments for all the pairs of sequences took three days on a processor. Most of the time was spent on computing alignments on a million pairs of random sequences, where GAP4 with the three parameter sets took twice as much time as SIM with the three parameter sets.

DISCUSSION

We have developed a dynamic programming algorithm for aligning two sequences with several parameter sets of different levels of stringency. The algorithm partitions the sequences into regions by similarity level and selects a proper set of parameter values for every pair of regions between the two sequences. The local alignment version of the algorithm and existing local alignment algorithms were evaluated on over 250 000 pairs of homologous sequences from 100 protein families. The experimental results show that the new algorithm with the dynamic use of two and three parameter sets produce more statistically significant alignments than the existing algorithms with the static use of each parameter set.

An unexpected observation from our evaluation of the statistical significance of alignments from the new and existing algorithms is that using multiple parameter sets that cover the entire stringency spectrum with the new algorithm leads to an alignment of the highest similarity score but not necessarily of the highest statistical significance. The reason is that the least stringent parameter set when used alone with the Smith–Waterman algorithm has the lowest λ value and that the λ value for the new algorithm with all the multiple parameter sets is close to the lowest λ value. Equation 1 says that the statistical significance of the alignment depends on the product of the alignment score and the λ value. The product of the highest alignment score and the lowest λ value is not necessarily larger than the product of a lower alignment score and a higher λ value.

This observation leads to two approaches to using multiple parameter sets with the new local alignment algorithm. Let s₁,s₂,…s_p be a list of parameter sets in order of increasing stringency. In approach one, for each j with 1 ≤ j < p, combination j consists of parameter sets s_j,s_j+1,…s_p. For each combination, the new algorithm is run with all parameter sets in the combination. From the p − 1 output alignments, a most statistically significant alignment is selected. In approach two, the Smith–Waterman algorithm is run for each of the p parameter sets, and a parameter set s_j that leads to a most statistically significant alignment is found. If j < p, then the new algorithm is run with parameter sets s_j,s_j+1,…s_p.

The global alignment examples show that the location of difference blocks and gaps in the output alignment is also affected by the algorithm with the dynamic use of multiple parameter sets. The alignment from the dynamic use of multiple parameter sets may be different in configuration from the alignments from the static use of each parameter set. In general, alignments from the algorithm with different parameter set combinations may be different in configuration.

It is important that the substitution matrices in the multiple parameter sets be scaled in the same way. For example, all the substitution matrices are in 1/3 bit units. If the substitution matrices were scaled differently, then the algorithm that makes the dynamic use of the multiple parameter sets with those matrices would produce sequence alignments of no biological significance. In addition, the change penalty for each parameter set has to be sufficiently large.

The algorithm is not efficient for comparing megabase genomic sequences or searching databases. However, an efficient version of the algorithm can be developed and incorporated into existing large-scale comparison programs (1–10).

There are existing algorithms that allow the user to use multiple parameter sets (21–24). The existing algorithms make the static use of each of the multiple parameter sets, whereas our new algorithm makes the dynamic use of the multiple parameter sets. Altschul (21) extends an alignment algorithm to use multiple parameter sets by computing an alignment with the algorithm for each of the multiple parameter sets and then selecting an alignment with the highest statistical significance. Webb et al. (24) develops a program named BALSA to use multiple parameter sets by computing alignments for each of the multiple parameter sets and then using the Bayes rule to see the effect of each parameter set. A natural way of integrating the dynamic use of multiple parameter sets with the BALSA program is to form a number of combinations of multiple parameter sets, make the dynamic use of the parameter sets in each combination, and use the Bayes rule to see the effect of each combination.

AVAILABILITY

The GAP4 program is freely available for academic use at http://deepc2.psi.iastate.edu/aat/align/align.html.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.