Response tuning in bacterial chemotaxis

Abstract

Chemotaxis of enteric bacteria in spatial gradients toward a source of chemoattractant is accomplished by increases in the length of swimming runs up the gradient. Biochemical components of the intracellular signal pathway have been identified, but mechanisms for achieving the high response sensitivity remain unknown. Binding of attractant ligand to its receptor inactivates a receptor-associated histidine kinase, CheA, which phosphorylates the signal protein CheY. The reduction in phospho-CheY, CheY-P, levels prolongs swimming runs. Here, the stimulus–response relation has been determined by measurement of excitation responses mediated by the Tar receptor to defined concentration jumps of the attractant, aspartate, administered within milliseconds by photolysis of a photolabile precursor. The bacteria responded to <1% changes in Tar occupancy when adapted to aspartate over concentrations spanning three orders of magnitude. Response amplitudes increased approximately logarithmically with stimulus strength, extending responsiveness over a greater stimulus range. The extent and form of this relation indicates that, in contrast to mechanisms for adaptive recovery, excitation signal generation involves amplification based on cooperative interactions. These interactions could entail inactivation of multiple receptor–CheA signaling complexes and/or simultaneous activation of CheY-P dephosphorylation.

Chemotaxis of the enteric bacteria, Escherichia coli and Salmonella typhimurium, provides a particularly well-understood example of a single-cell sensory response. The motility of these bacteria consists of a swimming pattern that alternates between runs and tumbles. Migration in spatial gradients is accomplished by increasing the length of runs up the gradient (1). In common with other sensory processes (2, 3), bacterial chemotaxis is exquisitely sensitive. The bacteria detect concentration differences over a background concentration that can vary over five orders of magnitude (4).

The components of the chemotaxis machinery have been identified. The attractant aspartate binds to Tar, one of a five-member family of transmembrane methyl accepting chemotaxis proteins (MCPs) in E. coli. The subsequent increase in Tar receptor occupancy (ΔR_occ) enhances counterclockwise (CCW) rotation. This lengthens swimming runs caused by increased stability of the flagellar bundle. The response is mediated by an intracellular phosphorelay that consists of the MCP-associated histidine kinase, CheA; the signal protein, CheY, which binds to the motor when phosphorylated; and the protein CheZ, which accelerates CheY-P dephosphorylation. This phosphorelay belongs to a super-family of histidyl-aspartyl “two-component” phosphorelays that mediate signal transduction processes in a wide range of species (5–7).

A temporal-gradient sensing mechanism is utilized to effect chemotaxis (8). Step increases in chemoattractant concentration result in sub-second motor responses. This excitation phase is followed by precise adaptation back to prestimulus behavior, even though the chemoeffector concentration remains elevated. Migration in chemotactic gradients is a complex function of adaptive and excitatory processes, as well as flagella bundle mechanics. Therefore, temporal assays are better suited for analysis of the biochemical determinants underlying response sensitivity.

Because the excitation phase has a rate constant of ≈10 s⁻¹, measurement of chemotactic response amplitudes requires an assay with <100-ms temporal resolution. This resolution was first achieved by iontophoretic stimulation of bacteria tethered by a single flagellum to Ab-coated glass coverslips (ref. 9 and references therein). These measurements showed that the response sensitivity was intrinsic to the intracellular signaling machinery; a net change in aspartate-Tar occupancy, ΔR_occ, of 0.4% resulted in a 22% increase in the CCW motor rotation bias. This result has been puzzling in the light of subsequent determination of chemotactic signal pathway phosphorylation reactions (10). Inhibition of CheA activity triggered by binding of attractant ligand has been the only mechanism for smooth swim signal generation (i.e., reduction of CheY-P levels) identified thus far (11, 12). For the experiment noted above, the applied ΔR_occ should result in an even smaller decrease (<0.4%) in CheY-P levels. Current knowledge of CheY–motor interactions (13, 14) cannot account for the increase in rotation bias observed. This difficulty has been highlighted by computer simulations of the intracellular signaling reactions (15).

We have investigated this issue with an alternative technique, a recently developed assay for chemotactic signaling based on computer-assisted motion-analysis (16). This assay allows rapid analysis in bacterial populations of responses triggered by photo-release of chemoeffectors from “caged” precursors with 33-ms video time-frame resolution. Subsaturation response amplitudes, defined by the fact that smooth swimming of the entire population is not obtained at peak response, were easily measured (17). This has allowed determination of the stimulus–response relation, as reported here.

METHODS

Caged Compounds.

Caged l-aspartate is the β-2,6-dinitrobenzyl ester of l-aspartic acid. Caged 8-hydroxypyrene-1-3-6-tris-sulfonic acid (HPTS) is the O-1-(2-nitrophenyl)ethyl ether of HPTS. It is nonfluorescent in contrast to HPTS. The product quantum yields of caged aspartate, Q_asp, and caged HPTS, Q_HPTS, are 0.21 and 0.13, respectively, with an error range of 20% in the Q_asp/Q_HPTS ratio (17). Rates of formation of HPTS and aspartate on photolysis of their caged precursors are 550 s⁻¹ and 630 s⁻¹, respectively, at pH 7.0, 0.1 M ionic strength, and 22°C, as inferred from decay of the aci-nitro intermediates (17).

The amount of aspartate released by photolysis in behavioral assays was determined as follows. Fluorescence caused by photo-release of the fluorophore HPTS from caged HPTS was related to amounts released from a calibration curve constructed by using HPTS solutions of known concentration, as described (17). The aspartate concentration, [Asp], present in the experimental sample containing bacteria, was determined from the equation [Asp] = [Asp]_caged⋅{(%cntmt) + [%HPTS⋅(number of flashes)⋅(Q_asp/Q_HPTS)]}, where [Asp]_caged is the concentration of caged aspartate, %cntmt is the percentile fraction of aspartate contamination in the caged aspartate sample (typically 1.4%), and %HPTS is the percentile fraction of caged HPTS photolyzed per flash.

Flash Photo-Release Assays.

Cultures of E. coli strain RP437 (16) or of S. typhimurium strain SJW1103 (18), both wild type for motility and chemotaxis, were inoculated and grown to late exponential phase in tryptone broth. They were washed thrice with, and resuspended in, motility buffer incubated with caged aspartate on ice and assayed, as described (17). Addition of l- or d-aspartate or l-serine, if any, was done before addition of caged aspartate. The bacteria were allowed to adapt to these changes at ambient temperature before being placed on ice.

The assays were carried out on samples observed on an Optiphot (Nikon) microscope. Photolysis of the entire sample was effected by a flash lamp directed onto the sample via a liquid light guide (Gert-Rapp Opto-Electronics, Hamburg, Germany) (19). Localized photo-release was accomplished by 30-ms shuttered epi-illumination from a 100-W continuous Hg arc lamp. For more details, see refs. 16 and 17. Responses of the bacteria were videotaped, digitized at 30 frames/s, and analyzed by using a centroid-based video-tracking algorithm (expertvision, version 4.1, Motion Analysis, Santa Rosa, CA). For any given condition, flashes were averaged to typically merge more than 1,000 bacterial paths for computation of the change in population rcd (Δrcd) triggered by aspartate photo-release (17).

Data Analysis.

Error analysis was as follows. The error in Δrcd (σ_Δrcd) = [(σ_rcdpre)² + (σ_rcdpeak)²]^1/2. The error in photo-released aspartate (σ_[Asp]) = σ_p/[(number of samples)⋅(number of flashes)]^1/2, where σ_p is cumulative error in amounts photo-released. Error in R_occ; σ_Rocc = σ_Asp⋅{K_D/([Asp]+K_D)²}. The error in ΔR_occ (σ_ΔR) = [(σ_Rpre)² + (σ_Rpost)²]^1/2. The fractional error in gain (σ_g/g) = [(σ_Δmb/Δmb)² + (σ_ΔR/ΔR_occ)²]^1/2.

RESULTS

Glossary of Terms.

The terms used in this paper are as follows: stimulus = ΔR_occ; response = Δmb; and chemotactic gain, g = Δmb/ΔR_occ.

Stimulus size, response amplitude, and g values are dimensionless because ΔR_occ and Δmb are ratios defined and estimated as specified below.

(i) ΔR_occ = Fractional change in Tar receptor occupancy = prestimulus receptor occupancy, R_post − poststimulus receptor occupancy, R_pre. l-aspartate occupancies of E. coli Tar were calculated by using weak and strong site K_D values of 1.2 and 70 μM respectively {e.g., R_pre = (0.5[Asp]_pre/([Asp]_pre + 1.2)) + (0.5[Asp]_pre/([Asp]_pre + 70)}. As reported previously (17), a low affinity site (K_D = 70 μM), in addition to the 1.2 μM site measured in vesicle preparations (20), was needed to fit adaptation time, t_r, versus l-aspartate concentration data (figure 4 of ref. 17). t_r was the time interval between stimulus application and recovery back to prestimulus swimming behavior as assessed by the population rcd (figure 6 of ref. 17). K_D values for calculation of d-aspartate occupancy of E. coli Tar [40 μM (21)] and l-aspartate occupancy of S. typhimurium Tar [0.2 and 1.0 μM (20)] were taken from the biochemical literature.

(ii) Δrcd = rcd_pre − rcd_peak. The rcd for a single cell path is the absolute angular rate of change of direction of the cell centroid in degrees⋅s⁻¹, determined for each digitized video frame-to-frame interval (ref. 16 and references therein). rcd_pre = mean rcd for a population of cell paths averaged over the prestimulus period; rcd_peak = minimum population rcd obtained at peak response, determined by averaging successive 10 frame (0.33-s time resolution) windows (17).

(iii) Δmb = Fractional increase in CCW motor rotation bias = (mb_pre − mb_peak)/mb_max. The population motor bias, mb = f_ccw/(f_ccw + f_cw), where f_ccw and f_cw are the respective CCW and CW spinning fraction of a tethered cell population in a given digitized video frame-to-frame interval (17). Maximum motor bias, mb_max = 1.0. Here, mb_pre and mb_peak were computed from the respective rcd_pre and rcd_peak values by using the empirical relation mb = 1 − [0.0012(rcd − 360)], valid for rcd values <950 degrees⋅s⁻¹ (figure 2 of ref. 16). Δmb values estimated in this way from Δrcd values obtained for swimming cell responses were indistinguishable from Δmb values determined directly from tethered cell responses to an equivalent stimulus (17).

Responses to Step Increments of Aspartate.

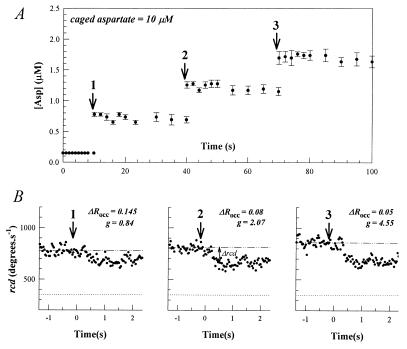
Evaluation of the stimulus-response relation required an assessment of its dependence on the prestimulus aspartate concentration, [Asp]_pre, and on the rate of stimulus application, d(ΔR_occ)/dt. The effect of [Asp]_pre was most clearly evident when sample-to-sample variations were eliminated, as in global photo-release experiments (Fig. 1). In these experiments, aspartate concentration jumps were effected by a xenon lamp flash onto the entire sample. Stimuli of defined magnitude were obtained by using a train of flashes to effect repetitive photolysis of the caged aspartate in the experimental samples. The concentration of the photo-released aspartate in the microscope field of view remained constant for 30 s, a time sufficient for complete adaptation to small (ΔR_occ < 0.2) stimuli (17). Thus, [Asp]_pre increased with successive flashes in these experiments, allowing evaluation of its effect on response strength. This increase was offset by the associated decrease in ΔR_occ. The increase in response amplitudes with successive flashes observed in Fig. 1 was not observed in localized photo-release experiments in which [Asp]_pre was constant from flash to flash. Localized photo-release was effected by arc lamp epi-illumination; the interval between photolyzing pulses being timed to allow the aspartate concentration to decay to its initial value between pulses (17). Therefore, the sequential increase in response sensitivity seen in Fig. 1 did not result from long-term changes in the chemotaxis circuitry triggered by transient exposure to aspartate, implying a direct dependence on [Asp]_pre. In accord with earlier work (9, 16), changes in response sensitivity were expressed as changes in gain, g. The g increased 5.4-fold from the first to the third flash in the experiment shown as [Asp]_pre increased from <0.2 to >1 μM.

Figure 1.

Chemotactic excitation responses of swimming bacteria to repetitive step stimuli of photo-released aspartate. Arrows denote photolyzing near-UV light flash from the xenon flash lamp. (A) Change in aspartate concentration over the video microscope observation area with time. Each point represents the mean (±SE) of values from three independent caged HPTS photolysis experiments. Changes in fluorescence intensity were converted to estimates of photo-released aspartate (Methods) (B) Motile responses of E. coli, as measured by changes in population rcd. The bacterial population was allowed to adapt back to rcd_pre (dashed dotted line) between flashes. Dotted lines indicate the rcd for complete smooth swimming, obtained after mixing with the potent attractant l-serine (1 mM) (16).

Stimulus Strength Does Not Depend on the Rate of Change of ΔR_occ.

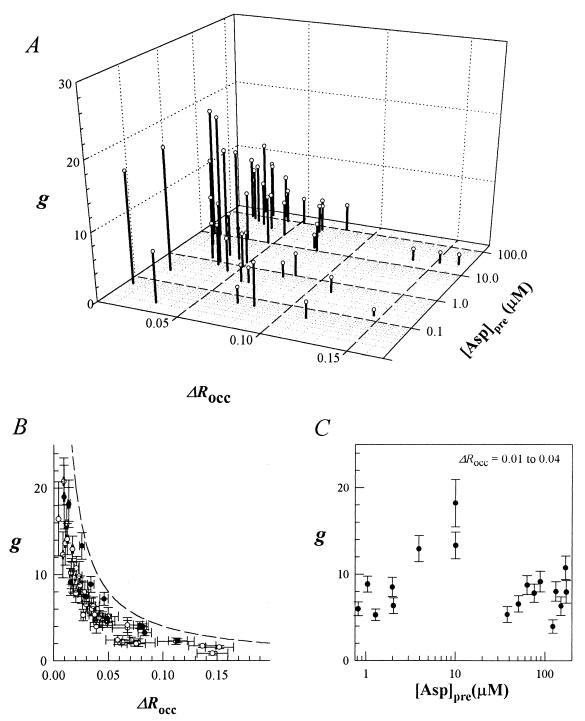
Data from both local and global photo-release experiments are shown in Fig. 2A. The aggregate data show that gain decreases as ΔR_occ increases and that this trend is not affected by [Asp]_pre. The gain increased by approximately an order of magnitude as stimulus strength was decreased from values typically required to produce a saturation smooth-swim population response (ΔR_occ = 0.18) to values that elicited responses at the detection limit of our technique (ΔR_occ = 0.004). Responses obtained in global and localized photo-release experiments for an equivalent ΔR_occ were superimposable, as best seen in a two-dimensional-plot of the data (Fig. 2B), even though d(ΔR_occ)/dt differed markedly in the two cases. Thus, when stimulus application was on time scales shorter than the chemotactic signal-processing time, response amplitudes did not depend on d(ΔR_occ)/dt.

Figure 2.

(A) Chemotactic gain, g, versus stimulus strength, ΔR_occ, and [Asp]_pre. Ligand concentrations were increased by addition of l-aspartate or d-aspartate. Computations using (Q_asp/Q_HPTS) ratios that were ±20% of the estimated ratio of 1.6 changed g by a similar fraction, but did not alter the form of its dependence on either ΔR_occ or [Asp]_prestim. (B) g versus ΔR_occ. The dashed line indicates g values required to produce the maximum possible Δmb of 1 − 0.6 = 0.4 (i.e., saturation smooth-swim response) as a function of ΔR_occ. ○, Responses of bacteria subjected to a train of flashes from a xenon flash lamp that photo-released aspartate in ≈1 ms (see Fig. 1). ●, Responses of bacteria to aspartate photo-released locally by arc-lamp epi-illumination over a 30-ms period. Bars denote standard errors. (C) g versus [Asp]_pre for a close-to-threshold (ΔR_occ = 0.01–0.04) stimulus range. Bars denote standard errors as in B.

High Sensitivity Is Maintained Over a Large Dynamic Range.

High response sensitivity was maintained for ΔR_occ values close to threshold (0.01–0.04) over a large (0.3–300 μM) [Asp]_pre range (Fig. 2C) when Tar occupancy was increased by adding aspartate or its nonmetabolizable analog, d-aspartate (21), to the medium. When [Asp]_pre was as low as 60 nM, a ΔR_occ of 0.004 corresponding to a 10 nM jump {17% (Δ[Asp]/[Asp]_pre) ratio} elicited detectable responses. There was a modest (3-fold) increase in g up to an [Asp]_pre of 10 μM. The significance of this increase was difficult to assess because there was a similar change in g over the 0.01–0.04 ΔR_occ range. Nevertheless, flash train experiments such as shown in Fig. 1 confirmed the validity of this increase over the 0.1- to 10-μM [Asp]_pre range. Although high sensitivity was maintained, g did not increase beyond [Asp]_pre values >10 μM.

The Stimulus Response Relation Is Logarithmic Rather Than Linear.

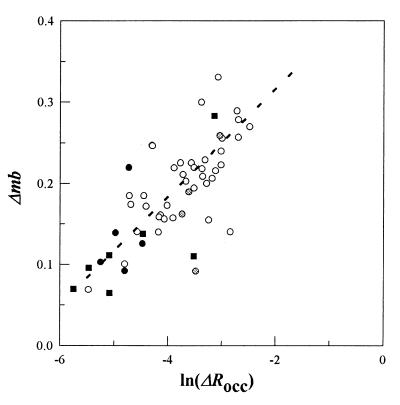
The single measurement of g = 55 obtained for a ΔR_occ of 0.004 (9) has been compared in theoretical simulations with estimates computed for other values; for example, g of 2.7 simulated for ΔR_occ = 0.11 (22). Such comparison assumes that g is invariant with ΔR_occ. This is not the case, as was realized most clearly by plotting Δmb against various ΔR_occ functions. A logarithmic rather than linear function provided a better fit for the stimulus response data (Fig. 3). The goodness of fit was estimated by using reduced χ² that was 1.26 (0.2 > P < 0.1) and 2.26 (P < 0.001) for a logarithmic and linear fit, respectively, with ±20% error for each datum. P is the probability that a greater χ² value would be obtained for the same sized sample (n = 40) obeying the function being fitted (23).

Figure 3.

The Δmb versus ln(ΔR_occ) over the 0–0.075 ΔR_occ range. About 80% of the total data fell within this range. Scarcity of data precluded an evaluation above the 0.075 ΔR_occ value. Culture-to-culture variability, as well as differences in [Asp]_pre, contribute to the scatter. The continuous line represents the best fit to the data for E. coli Tar (○). The form, but not the slope, of the fit was robust to a 10-fold variation in ΔR_occ values. ● and ■, Responses of S. typhimurium to aspartate photo-release for [Asp]_pre values of <0.1 (<25% occupancy) and 50 μM (>95% occupancy), respectively. , E. coli responses to photo-released aspartate in the presence of 250 μM serine (>90% Tsr occupancy).

Close-to-Saturation Occupancy of the Same or Another MCP Does Not Alter Response Sensitivity.

At high [Asp]_pre (>10 μM), interpretation of the response sensitivity depended on assumed, weak second site occupancy (70 μM), deduced from fitting adaptation time data (17). Responses of S. typhimurium bacteria to aspartate were therefore measured because these are not subject to this ambiguity. Biochemical studies have shown that both aspartate binding sites in S. typhimurium Tar are occupied with K_D values of 0.1 and 2.0 μM respectively; the different K_D values for the two initially equivalent binding sites being a consequence of the high negative co-operativity (20). At 50 μM [Asp]_pre, both sites would be >95% occupied. Nevertheless, responses to photo-released aspartate were unaltered (Fig. 3). However, estimates of ΔR_occ, and hence, of the sensitivity at high [Asp]_pre, depend on the assumption that the apparent K_D values obtained for the Tar receptor population do not change on incubation with aspartate. To circumvent this issue, responses of bacteria adapted to a saturating concentration of l-serine, an attractant sensed by the homologous MCP Tsr, were studied. Tsr has a single site K_D for l-serine of 5–25 μM as revealed by both behavioral (24) and binding (25) data. It should be >90% occupied in bacteria adapted to a 250 μM background concentration of l-serine. These bacteria had a response sensitivity comparable to control bacteria (Fig. 3).

DISCUSSION

Numerous studies have quantified the dependence of chemotactic response parameters on stimulus strength. In classic experiments, the response threshold, as measured by the accumulation of bacteria in capillaries containing aspartate scaled with concentration (4), in accord with Weber’s law (26). The duration of the adaptation response was proportional to ΔR_occ over a wide range when bacteria were subjected to large step changes in chemoeffector concentration (27, 28). These times matched with the kinetics of MCP methylation, which brings about adaptive recovery (29). When the chemoeffector concentration was changed slowly relative to the chemotactic excitation time in enzymatic digestion or ramp experiments (30, 31), the change in motile behavior was proportional to rate of change of receptor occupancy [d(ΔR_occ)/dt]. This dependence most likely reflects contributions from both excitatory and adaptive reactions to the response (22).

The quantification of the stimulus–response relation obtained on aspartate jumps reported here provides insights into the generation and amplification of the chemotactic signal, as discussed below.

Properties of the Stimulus–Response Relation.

First, response sensitivity near the detection limit was comparable to that obtained by using iontophoresis. In iontophoretic experiments g was 55 when ΔR_occ was 0.004 for a aspartate step stimulus administered at a prestimulus concentration of α-methylaspartate equal to its K_D for Tar (1.6 mM) (9). This value was 3-fold higher than the g value (≈18) obtained for an equivalent ΔR_occ in the present study (Fig. 2). Systematic calibration errors in estimation of iontophoretic and photo-released pulse magnitudes, as well as large random error in the iontophoresis experiments because of the small sample size, could contribute to this difference.

The present study documented responses to concentration increases as small as 10 nM aspartate. How might such small increases be sensed amidst thermal noise? A 60 nM solution of volume the size of E. coli (1 μm³) contains 36 molecules and will experience concentration fluctuations of rms amplitude (36)^1/2 (32) equivalent to the 10 nM or 17% increase sensed by the bacteria. However, correlation times for decay of fluctuations from peak values back to the mean will be short because these reflect times for diffusion of the ligand from the volume center to its periphery. The diffusion coefficient for aspartate, D = 0.9 × 10⁻⁵ cm²/s (33); therefore, the correlation time will be r²/6D < 0.1 ms, when r = 0.62 μm, the radius of a 1 μm³ sphere. The solution thus seems to be the relatively long chemotactic signal processing times, of the order of 0.1 s (17), which allow the bacteria to sample a volume [= (10³)^3/2 μm³] much larger than its size, thereby reducing the rms amplitude of spontaneous fluctuations by 10^2.25 to ≈0.1%. Thus E. coli utilizes temporal integration to average out thermal fluctuations (34) that could mask the detection of small but sustained concentration differences as it swims through shallow spatial gradients of chemoattractant.

Second, the rate of chemotactic migration in spatial gradients, the physiological response, depends on d(ΔR_occ)/dt (30). In contrast, the sensitivity does not depend on d(ΔR_occ)/dt in the concentration jump experiments analyzed here. This finding indicates that the bacteria can generate and process chemotactic signals in temporal isolation from attenuating adaptive reactions. This result is consistent with current understanding of chemotactic signaling; namely, that ligand binding and receptor conformational reactions involved in signal generation are rapid and processing is limited by CheY-P turnover (17).

Prior MCP occupancy may modulate response sensitivity through associated changes in methylation levels (35) or clustering (36). Consistent with the former idea, double mutant strains lacking the methyltransferase, CheR, and the methylesterase, CheB, have reduced sensitivity (9, 16). CheR and CheB, however, engage in multifaceted interactions with MCPs (37). Response sensitivity remained high from the lowest to the highest measurable [Asp]_pre, but was modulated over a limited range. It did not depend on occupancy of an alternate MCP. This result is similar to results obtained in sensitivity assays, which measured accumulation in capillaries (30).

Determination of the extremes of response range remains an important goal for placing limits on the validity of Weber’s law and elucidation of mechanism. For example, a recent formulation of cooperative sensing in receptor clusters predicts increased sensitivity at both extremes of the response range (38). If so, these extremes were not reached in the present study.

The Data Are Incompatible with Stoichiometric Inactivation.

The sensitivity of the bacterial chemotactic response has seemingly become controversial (39). Nevertheless, all available data indicate that bacteria sense small concentration differences. These data include capillary assays (4, 30), migration in layered spatial (40, 41), and temporal gradients generated by enzymatic digestion (1, 30), responses of tethered cells to ramp stimuli in a flow-cell (31) and to step and impulsive stimuli applied by iontophoresis (9). The parameters governing chemotactic migration are complex. Hence, the logical initial focus of biochemical modeling work has been prediction of excitation responses to small step stimuli (15).

In addition to “maximal” models designed to incorporate and simulate detailed features of the biochemical network, “minimal” models based on kinetic constraints are useful. Such a minimal model may be constructed given three simplifying assumptions supported by the biochemistry and behavioral data presented in this and earlier studies (17). These assumptions are: (i) modulation of motor rotation bias by chemotactic signals depends solely on the change in CheY-P levels; (ii) CheY-P turnover limits chemotactic signal processing; and (iii) adaptive reactions are too slow to influence excitation responses to concentration jumps of photo-released chemoeffectors.

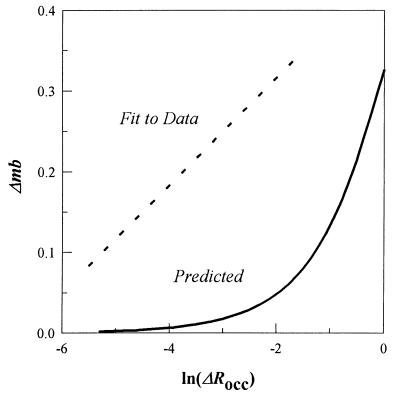
In such case, response amplitudes would be determined by the new steady-state level of CheY-P established on aspartate photo-release. This new CheY-P level, {[CheY-P]_post = [CheY]_total(k₁′/(k₂+ k₁′)}, where k₁′ and k₂ are poststimulus rate constants for CheY phosphorylation and CheY-P dephosphorylation, respectively. Prestimulus [CheY-P] is ≈30% of the total CheY ([CheY]_total) (14), so the prestimulus CheY phosphorylation rate constant is k₁ = (0.3/0.7)k₂. Given stoichiometric inactivation of the kinase CheA, k₂ would be unaffected and k₁′ = k₁(1 − 0.5ΔR_occ), where the ([Tar]/[MCP_total]) ratio is 0.5. The changes in CheY-P levels may be converted to corresponding motor rotation bias values by using the equation Δmb = {1.5[CheY-P]_pre/(1.5[CheY-P]^H_pre + [CheY-P]^H_post)} − 0.6, where prestimulus motor bias is 0.6 and H is the empirically determined apparent Hill coefficient of 3.5 (14). The predicted relation between Δmb and ΔR_occ (Fig. 4) has a different form from that observed. Further, Fig. 4 shows that over the entire measurable range, not only close to the response threshold, the observed amplitudes are greater than expected.

Figure 4.

Stimulus-response relation predicted for stoichiometric inactivation. The difference between the best fit to the observed data (dashed line) and prediction (continuous line) made on the basis of stoichiometric inactivation of MCP-associated CheA is shown.

Two general models for chemotactic signal amplification have been proposed. One class invokes conformational coupling within a MCP cluster (35) such that ligand binding inactivates CheA associated with adjacent, as well as target, receptors. There is a logarithmic relationship between stimulus (i.e., ΔR_occ) and response in such models because the probability of the ligand binding to Tar complexes already containing inactive CheA increases with stimulus size (42). Alternatively, excitation signal generation could involve simultaneous activation of CheZ, sequestered via CheAs with MCP complexes (43). This, too, would act to reduce CheY-P production nonstoichiometrically from a MCP cluster. Even so, these ideas need to be developed to account for the large response range over which high sensitivity is maintained close-to-threshold (Figs. 2 and 3). In addition, evidence for conformational coupling within a MCP cluster or ligand-induced CheZ activation is lacking thus far.

Excitation and Adaptation Pathways Diverge Before Signal Amplification.

In contrast to the dependence of response amplitudes on ΔR_occ, adaptation times vary linearly with ΔR_occ for large (27, 28) as well as small step stimuli (ref. 17, see also ref. 44). Thus, different relations characterize the dependence of chemotactic response parameters on stimulus strength, a fact not readily compatible with proportional control models in which adaptation rate is proportional to the amount of signal generated. Instead, this difference indicates that the excitatory and adaptive processes triggered by binding of attractant ligand diverge before amplification of the excitation signal.

Mechanisms where adaptive processes act only on ligand bound complexes, hence are proportional to ΔR_occ, whereas reduction of CheY-P levels is cooperative, hence nonlinear with ΔR_occ, may be envisaged (Fig. 5). Adaptation involves an increase in methylation level, in the final adapted state, of the target MCP alone (29). This is accomplished by two distinct ligand-induced conformational transitions in the MCP–CheA signaling complex (45). One involves changes in MCP configurational state that facilitate access to methylatable residues by CheR. The other inactivates receptor-associated CheA, which in turn lowers levels of phospho-CheB, CheB-P, the active form of the methylesterase (37). Only the latter, as noted earlier, is involved in excitation signal generation via concomitant reduction of CheY-P production. In conformational coupling models, adaptation kinetics would be stoichiometric with ΔR_occ, if the more open MCP conformation is not propagated, in contrast to the inactive CheA state, and CheB acts only on active complexes, as proposed to ensure robustness of precise adaptation (46). CheZ does not act on CheB-P (10), so reduction of CheB-P levels would remain stoichiometric with inactivation of the target MCP-associated CheA, hence ΔR_occ, in CheZ-activation based models for signal amplification. It remains to be seen whether any, one, or both types of mechanism are operative.

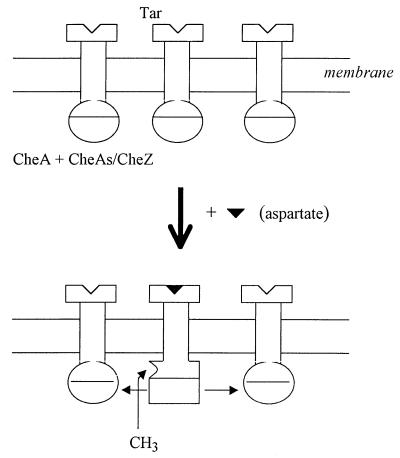
Figure 5.

Excitation and adaptation reactions triggered by increased Tar occupancy (ΔR_occ). Tar receptor complexes exist in at least two distinct states, corresponding to CheA-stimulating (hemispheres) and CheA-inhibiting (rectangles) forms respectively (48), which bind aspartate with comparable affinity (21, 35). Tar complexes with bound aspartate decrease formation of CheY-P by adjacent complexes within a MCP cluster. This lateral inhibition (horizontal arrows) effects signal amplification. This could occur by propagation of the inactive CheA conformation. Alternatively, aspartate binding could stimulate CheZ associated with the complexes via CheAs, in addition to inactivating CheA. The activated CheZ will dephosphorylate CheY-P, but not CheB-P, produced from complexes proximal to the aspartate-bound complex. Adaptation times will be proportional to ΔR_occ in the former case if these depend on CheR methylation at constant rate, as supposed (5), of the more open, nonpropagative Tar conformation favored by aspartate binding. A linear relation between adaptation time and ΔR_occ is expected in the latter case because CheB-P dephosphorylation is unaffected (see text).

Irrespective of mechanism, a logarithmic stimulus–response relation is advantageous for chemotaxis. It allows the bacteria to discriminate weak from strong chemotactic gradients, whereas retaining high sensitivity close to the detection threshold. Chemotactic gain would be constant for a linear relation and the bacteria would become completely smooth-swimming at stimulus strengths only 3-fold greater than those needed to evoke threshold responses (ΔR_occ = 0.004) (Fig. 2B). An exponentially decreasing dependence of response amplitudes on light intensity also characterizes processing of visual stimuli and presumably has similar utility for extending response range (47). However, distinct from the case of bacterial chemotaxis, the biochemical basis for signal amplification in vision or olfaction involves activation, rather than inhibition, of a phosphorylation cascade (2, 47).

ABBREVIATIONS

MCPs

methyl-accepting chemotaxis proteins

CCW

counterclockwise

CW

clockwise

[Asp]_pre

prestimulus aspartate concentration

ΔR_occ

net change in receptor occupancy

Δmb = change in motor rotation bias

g, gain

HPTS

8-hydroxypyrene-1-3-6-tris-sulfonic acid