Abstract
A model defining carbon isotope discrimination (Δ13C) for crassulacean acid metabolism (CAM) plants was experimentally validated using Kalanchoe daigremontiana. Simultaneous measurements of gas exchange and instantaneous CO2 discrimination (for 13C and 18O) were made from late photoperiod (phase IV of CAM), throughout the dark period (phase I), and into the light (phase II). Measurements of CO2 response curves throughout the dark period revealed changing phosphoenolpyruvate carboxylase (PEPC) capacity. These systematic changes in PEPC capacity were tracked by net CO2 uptake, stomatal conductance, and online Δ13C signal; all declined at the start of the dark period, then increased to a maximum 2 h before dawn. Measurements of Δ13C were higher than predicted from the ratio of intercellular to external CO2 (pi/pa) and fractionation associated with CO2 hydration and PEPC carboxylations alone, such that the dark period mesophyll conductance, gi, was 0.044 mol m−2 s−1 bar−1. A higher estimate of gi (0.085 mol m−2 s−1 bar−1) was needed to account for the modeled and measured Δ18O discrimination throughout the dark period. The differences in estimates of gi from the two isotope measurements, and an offset of −5.5‰ between the 18O content of source and transpired water, suggest spatial variations in either CO2 diffusion path length and/or carbonic anhydrase activity, either within individual cells or across a succulent leaf. Our measurements support the model predictions to show that internal CO2 diffusion limitations within CAM leaves increase Δ13C discrimination during nighttime CO2 fixation while reducing Δ13C during phase IV. When evaluating the phylogenetic distribution of CAM, carbon isotope composition will reflect these diffusive limitations as well as relative contributions from C3 and C4 biochemistry.
The metabolic and ecological plasticity associated with the crassulacean acid metabolism (CAM) cycle has allowed the use of stable isotopes both to define the occurrence of the CAM pathway (Bender et al., 1973; Osmond et al., 1973) and to investigate the interplay between activities of Rubisco (by day) and nocturnal phosphoenolpyruvate carboxylase (PEPC; O'Leary and Osmond, 1980; Griffiths et al., 1990; Dodd et al., 2003). The phases of CAM, as defined by Osmond (1978), include phase I, when nocturnal uptake of CO2 is mediated exclusively by PEPC, and phase III, when Rubisco operates with stomata closed in the light and CO2 is regenerated from malic acid. There are also two transient phases showing the switch between the major carboxylases, one early in the light period prior to stomatal closure (phase II) and the other in the late afternoon, when assimilation of atmospheric CO2 initially occurs directly via Rubisco (phase IV). The carbon isotope signal of organic material is traditionally thought to reflect the balance between the magnitude of these four phases (Osmond, 1978; Pierce et al., 2002a; Winter and Holtum, 2002).
During phase I of CAM, the fractionation of carbon isotopes during CO2 fixation was shown to reflect both photosynthetic biochemistry and fractionation during diffusion of CO2 through stomata, as shown by comparing the isotopic composition of the C4 carbon in malate with that of atmospheric CO2 (O'Leary and Osmond, 1980; Farquhar et al., 1982; Holtum et al., 1983; Deleens et al., 1985). Although PEPC operates without the company of Rubisco at night (in contrast to C4 plants by day), the isotopic composition of malate was more depleted in 13C than could be predicted from the model of discrimination proposed by O'Leary and Osmond (1980), which accounted for isotope fractionation by diffusion in air, CO2 hydration, and PEPC carboxylation. Holtum et al. (1983) also noted that carbon isotope discrimination (Δ13C) was higher than predicted from gas exchange ratios of internal to external CO2 partial pressure (pi/pa) and hypothesized that the differences might be due to a number of factors, including additional diffusion limitation in the liquid phase. Similar results have been observed during real-time measurements of Δ13C concurrently with gas exchange in phase I (O'Leary et al., 1986; Griffiths et al., 1990; Griffiths, 1992; Borland et al., 1993; Roberts et al., 1997, 1998).
The initial model of discrimination during CAM was also used to account for the activity of carbonic anhydrase (CA) in contrasting CAM plants (Holtum et al., 1984). The activity of CA was initially thought to limit certain CAM plants, such as Kalanchoe daigremontiana (Tsuzuki et al., 1982). However, Holtum et al. (1984) elegantly used the exchange of isotopically enriched 18O during the CA-catalyzed hydration of CO2 to show that K. daigremontiana has a 40-fold excess of CA activity relative to PEPC, inferring that there would be little influence of the CO2 hydration on Δ13C. Subsequently, the recognition that gas exchange measurements can be used to define the flux of 12CO2, while the 13C composition can be solved for specific fractionation effects, has allowed more detailed gas exchange and isotope discrimination models for C3 and C4 plants to be developed. These have been based on CO2 draw down and the sum of discrete fractionations across boundary layer, stomata, cell wall, and internal diffusion to carboxylation, as well as accounting for the effects of (photo) respiratory fractionations and bundle sheath leakage for C4 (Farquhar et al., 1982; Farquhar, 1983). For CAM plants, the integrated 13C isotope signal was suggested from a theoretical model (Farquhar et al., 1989) or derived directly from the proportional contribution of PEPC and Rubisco signals to isotope discrimination during gas exchange (Griffiths et al., 1990). To date, however, no systematic approach to modeling the changes in extent of discrimination during specific phases of CAM has been undertaken, to our knowledge.
The recent development of a direct, real-time mass spectrometric system allows concurrent measurements of CO2 uptake and Δ13C to be made at rapid time intervals (Cousins et al., 2006a). It has also been possible to measure, in parallel, the extent of 18O discrimination, which has been used to determine both the extent of CA equilibration and real-time evaporative fractionation during transpiration. The extent of 18O enrichment can be measured indirectly in CO2 exchanging with tissue water and retrodiffusing from the leaf and directly in the evaporated water vapor signal (Cousins et al., 2006b). In this study, we have used the constitutive CAM plant K. daigremontiana to measure online 13C and 18O discrimination throughout the dark period, as compared to the transitional phases II and IV. Our study was framed by the paucity of data on the extent of nighttime (phase I) Δ13C and concomitant measurements of pi/pa and the need to develop a comprehensive model to reconcile instantaneous and organic carbon isotope signals in CAM plants (Griffiths, 1992; Roberts et al., 1997). To do this, we have developed a quantitative model for Δ13C during the CAM cycle, which allows for a systematic analysis of the overall determinants of the integrated 13C signal seen in the tissues of CAM plants. By analogy with the C3 system (Evans et al., 1986), we show that fractionation factors during nighttime CO2 uptake for CAM reflect both biochemical and internal constraints of diffusion across cell walls and mesophyll cytosol, leading to Δ13C varying with photosynthetic rate in addition to pi/pa. Thus, changes in PEPC carboxylation capacity (perhaps mediated by changing activation by PEPC kinase; Dodd et al., 2003), which we demonstrate from a series of CO2 response curves, are important determinants of nocturnal Δ13C. We also show that the 13C and 18O signals in CO2 allow different components of the mesophyll conductance (gi) to be resolved, reflecting diffusive path lengths within cells and leaves.
Recently, there has been a resurgence of interest in using carbon isotopes to explore the potential contribution that CAM makes to organic material, as well as in determining the phylogenetic origins of CAM within an array of families (e.g. Pierce et al., 2002b; Holtum and Winter, 2003; Crayn et al., 2004). The agreement between modeled and measured Δ13C values suggests that leaf internal CO2 diffusion characteristics (influenced by leaf anatomy) determine the draw down of CO2 from intercellular airspace to sites of PEPC (or Rubisco) carboxylations. When used to survey populations for CAM, carbon isotope composition should be considered to reflect both the proportion of C3 and C4 carboxylation as well as the extent of internal diffusive limitations.
THEORY
Model of Δ13C during CAM Photosynthesis
The model was developed around the likely fractionations associated with the four phases of the CAM cycle described in the introduction and is designed to be used in the analysis of short-term measurements of Δ13C during CO2 uptake. The discrimination of the naturally occurring isotopes of carbon (12C and 13C) in the process of photosynthesis is influenced by environmental and biochemical factors (Vogel, 1980; O'Leary, 1981). Theory developed by Farquhar et al. (1982) and Farquhar (1983) showed that net fractionation by C3 and C4 photosynthesis can be described by an equation having diffusion and biochemistry-dependent terms.
The overall isotope effect during carbon fixation in leaves in general is:
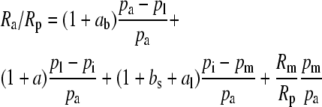 |
(1) |
where Ra, Rm, and Rp are the molar abundance ratios (13C to 12C) of the carbon in the atmosphere at the site of mesophyll carboxylation and of the carbon fixed. The symbols pl, pi, and pm denote leaf surface, intercellular, and mesophyll CO2 partial pressures (pCO2). The symbol ab is the fractionation occurring during diffusion in the boundary layer (2.9 × 10−3), a is the fractionation during diffusion in air (4.4 × 10−3), bs is the fractionation as CO2 enters solution (1.1 × 10−3), and al is the fractionation occurring during diffusion in water (0.7 × 10−3; Farquhar et al., 1982).
The magnitude of the isotope effects generally exceeds unity by a small amount only, so following (Farquhar and Richards, 1984), our results are generally expressed as the discrimination or fractionation, Δ, where
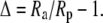 |
(2) |
The derivation of the isotope effect, Ra/Rp, for CAM is similar to the derivations of Ra/Rp for C3 and C4 species outlined by Farquhar et al. (1982) and Farquhar (1983), and the same arguments are followed using the Δ notation.
If the boundary layer conductance is large, it is convenient to contract 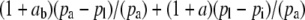 in Equation 1 to
in Equation 1 to 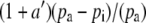 , where
, where
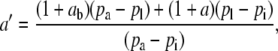 |
(3) |
such that
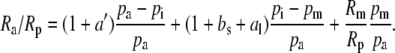 |
(4) |
Equation 4 can be rewritten in the Δ notation by subtracting 1 from both sides, such that
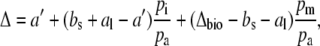 |
(5) |
where
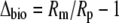 |
(6) |
and Δbio, the integrated net biochemical discrimination, depends on the biochemistry of net CO2 uptake, with expressions for the four phases of the CAM cycle given below.
The pm is dependent on the net CO2 assimilation rate, A, and the conductance to CO2 diffusion from the intercellular airspace to the site of carboxylation, gi, where
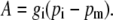 |
(7) |
It is useful to substitute 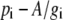 for pm in Equation 5, then
for pm in Equation 5, then
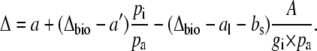 |
(8) |
The influence of the internal diffusion conductance on Δ13C can be calculated from the measured Δ as
 |
(9) |
where Δi is the carbon isotope predicted when gi is infinite.
Δ13C during CAM photosynthesis has been used as a diagnostic tool to estimate the biochemical fractionation. Equation 8 can also be solved for Δbio and
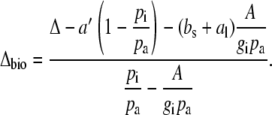 |
(10) |
The Biochemical Fractionation, Δbio, during CAM Photosynthesis
Assimilation rate during CAM photosynthesis can be written as a general equation
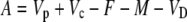 |
(11) |
where Vp and Vc are the rates of PEPC and Rubisco carboxylation, respectively, and F is the rate of photorespiration, M the rate of mitochondrial respiration, and VD is the rate of malate decarboxylation. Following the scheme of CAM photosynthesis outlined in Figure 1, we used Equation 11 to derive a general expression for Δbio of CAM photosynthesis (described in “Materials and Methods”):
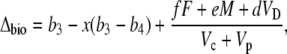 |
(12) |
where 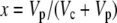 and b3 (29‰; Roeske and O'Leary, 1984) and b4 are the fractionations associated with Rubisco carboxylation and the combined fractionation of CO2 hydration and PEP carboxylation. The fractionation factor b4 is temperature dependent because of the temperature dependence of the hydration and dehydration reaction, which is given by
and b3 (29‰; Roeske and O'Leary, 1984) and b4 are the fractionations associated with Rubisco carboxylation and the combined fractionation of CO2 hydration and PEP carboxylation. The fractionation factor b4 is temperature dependent because of the temperature dependence of the hydration and dehydration reaction, which is given by
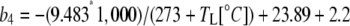 |
(13) |
if CA is in excess (Mook et al., 1974; Henderson et al., 1992; Cousins et al., 2006a).
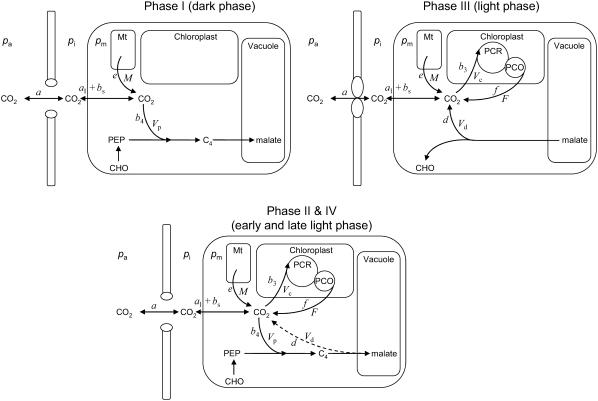
Figure 1.
A diagram showing the major factors that determine Δ13C during CO2 exchange in CAM species during the four phases of the CAM cycle according to Equations 5 and 12. The terms pa, pi, and pm are the partial pressures of CO2 in the atmosphere, the intercellular airspace, and in the mesophyll cells. PCR and PCO refer to the photosynthetic carbon reduction and oxygenation cycles, respectively. The associated fractionation factors are shown by lowercase letters and are described in the “Theory” section.
The fractionation factor f for photorespiration has been estimated to be about 8‰ (Ghashghaie et al., 2003). The fractionation factors e and d could be intrinsic fractionations occurring during respiration and decarboxylation but could also be variable describing the fact the substrate being respired or decarboxylated has a different isotope composition, Rp′ to the current photosynthate, Rp (i.e. 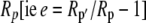 ). Such a change in internal source CO2 could be particularly important for malate decarboxylation, as the value of the fractionation factor d for malate decarboxylation is uncertain. The carbon being decarboxylated has the isotopic signature of the previous dark period photosynthetic discrimination with an added discrimination factor because of the fumarase randomization of the 13C signal in C1 and C4 of malate (Osmond et al., 1988). Deleens et al. (1985) noted that the decarboxylation of malate is known to show a large fractionation (near 30‰) but pointed out that if the release of malate from the vacuole is the limiting step, this large fractionation would not be expressed, which was supported by their experimental data.
). Such a change in internal source CO2 could be particularly important for malate decarboxylation, as the value of the fractionation factor d for malate decarboxylation is uncertain. The carbon being decarboxylated has the isotopic signature of the previous dark period photosynthetic discrimination with an added discrimination factor because of the fumarase randomization of the 13C signal in C1 and C4 of malate (Osmond et al., 1988). Deleens et al. (1985) noted that the decarboxylation of malate is known to show a large fractionation (near 30‰) but pointed out that if the release of malate from the vacuole is the limiting step, this large fractionation would not be expressed, which was supported by their experimental data.
Equation 12 will differ for the different phases of CAM as indicated in Figure 1. For example, during phase I, in the dark period, the fixation of inorganic carbon is mediated by cytosolic PEPC, with HCO3− substrate replenished by CA, and Vc, VD, and F will be 0 and x = 1, such that
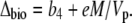 |
(14) |
Phase II and IV represent transitional stages. In phase II, after-dawn PEPC is usually rapidly down-regulated, and the activity of Rubisco progressively increases in the light (Griffiths et al., 1990; Dodd et al., 2002). The extent of phase IV depends on water and light availability and primarily represents the direct fixation of CO2 by Rubisco, although PEPC may contribute toward the end of the light period (Griffiths et al., 1990). In both these phases, A can be described by Equation 11 and Δbio by Equation 12 with the possibility that VD = 0. In the early part of phase IV, the equation is the one typical for C3 photosynthesis, when VD = 0 and PEPC carboxylation has not yet started (x = 0).
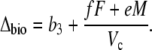 |
(15) |
In phase III, the decarboxylation phase, stomata close as high levels of internal CO2 are regenerated from malic acid and high Rubisco catalytic activities prevent excessive leakage of CO2 (Griffiths et al., 2002) and Vp = 0 (x = 0).
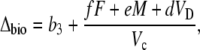 |
(16) |
although F will be close to zero if internal pCO2 is high. This equation is not particularly useful, because it is difficult, if not impossible, to make online measurements of Δ13C during this phase when stomata are closed.
Δ13C during Phase III from Malate to Fixed Carbon
The equations presented above are useful for the interpretation of measurements of online Δ13C. To help interpret the integrated signal of dry matter Δ13C, the discrimination occurring in the steps of malate decarboxylation and refixation by Rubisco need to be considered. In this case, we use an expression for the ratio Rp′/Rp, where Rp′ is the 13C/12C ratio of the malate fixed in the previous dark period and Rp that carbon fixed by Rubisco. Using the equation
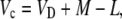 |
(17) |
where L = g pm is the leak rate of CO2 out of the leaf, it can be shown that
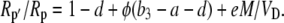 |
(18) |
Both photorespiration and CO2 diffusion into the leaf have been assumed to be negligible because of high internal pCO2. This equation is similar to the one derived by Farquhar et al. (1989), where d and e were assumed to be 0. Similar to the case of Rubisco in the bundle sheath of C4 species, Rubisco fractionation can only occur if there is some leakage of the decarboxylated CO2. If there is no CO2 leakage out of the leaf, the other potential influence on dry matter carbon isotope composition, other than secondary fractionations during remobilization and export, is the fractionation associated with malate decarboxylation, such as fumarase randomization of malate (as discussed above) or fractionation associated with respiration. If 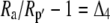 is the discrimination during the C4 fixation in phase I, then
is the discrimination during the C4 fixation in phase I, then 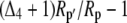 gives the overall discrimination occurring to carbon initially fixed by PEPC.
gives the overall discrimination occurring to carbon initially fixed by PEPC.
RESULTS
Dark Period PEPC and Stomatal Responses to CO2
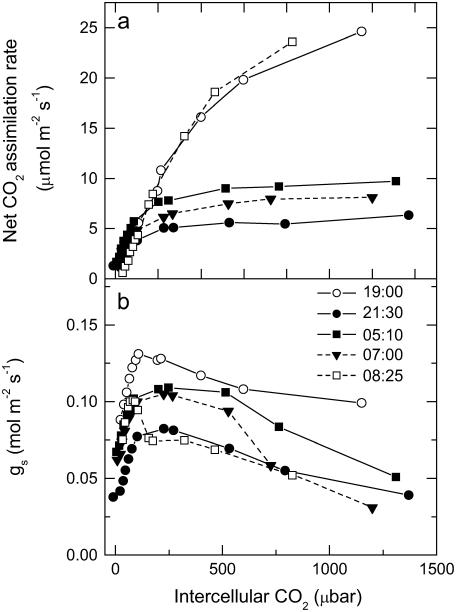
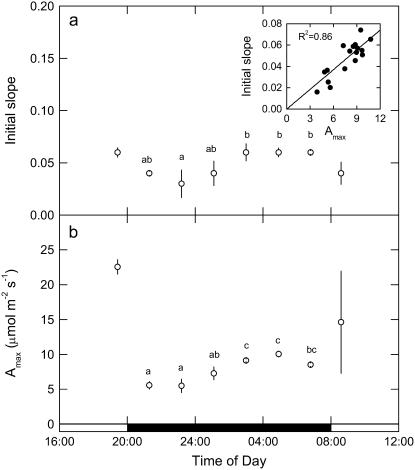
CO2 response curves of A to intercellular pCO2 (A/pi curves) were conducted from early evening (phase IV), throughout the dark period (phase I), and into the light (phase II) on different leaves for three successive nights, having programmed the gas exchange system to undertake a CO2 response curve every 2 h. Data are plotted as five representative, individual A/pi curves from a single leaf (Fig. 2A), with the associated stomatal conductance (gs) responses to pi shown in Figure 2B. First, we note that in the light periods, A/pi are typical for a C3 system, with a high CO2 compensation point and a photosynthetic rate of around 25 μmol m−2 s−1 at high pi (Fig. 2A; 19:00 h, 08:25 h). Second, the maximum assimilation capacity of PEPC, as well as the maximum gs, changed throughout the dark period (Fig. 2, A and B). The PEPC A/pi response (Fig. 2A) and gs (Fig. 2B) declined early in the dark period, then increased until 2 h before dawn before again decreasing. It is interesting to note that although the maximum conductance varies, stomata are responsive to CO2 concentration at all times in the light and the dark. To explore change in the kinetic parameters of PEPC in more detail for all of the leaves measured at each 2-h time interval, we plotted the initial slope of the A/pi responses and maximum assimilation rate (Amax) values (respectively, in Fig. 3, A and B) throughout the light-dark measurement cycle. The initial slope and Amax show a similar pattern, showing a statistically significant increase from the middle of the dark period. Most importantly, there was a linear relationship between the initial slope and Amax during the dark period (see inset to Fig. 3A), suggesting changes in maximal activity of PEPC (Vpmax) and a role for changing PEPC capacity in regulating net assimilation through the night.
Figure 2.
Net CO2 uptake (A) and gs responses as a function of changing pCO2 measured from late afternoon (phase IV) and throughout the dark period (phase I) and into the light (phase II; B). Representative data are plotted as individual response curves for one leaf at selected intervals during the dark period. Gas exchange measurements were made at an irradiance of 300 μmol quanta m−2 s−1 in the light period, with day/night temperatures of 25°C/20°C and a pCO2 varied against a background gas mixture of 909 mbar nitrogen and 48 mbar of O2.
Figure 3.
Initial slope of A/pi response (A) and variation in Amax measured every 2 h from late afternoon (phase IV) and throughout the dark period (phase I) and into the light (phase II; B). Data are plotted as mean ± SEM for three replicate leaves, with inset in A showing the relationship between initial slope and Amax, with experimental details in the Figure 1 legend. Different letters indicate significant differences between plants at P < 0.05.
Gas Exchange and Δ13C
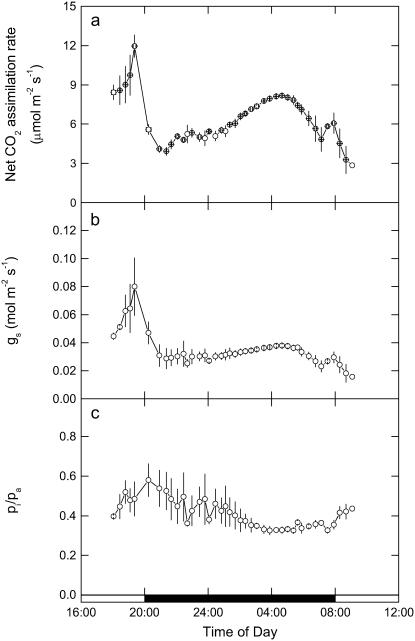
The continuous tracking of gas exchange characteristics was also undertaken for late phase IV, throughout the dark period, and into phase II in conjunction with the online mass spectrometric determinations (Fig. 4). The measurements, initially started in the light, show that A, gs, and pi/pa decline at the start of the dark period (Fig. 4, A–C), with A then gradually recovering over the next 6 h of the dark period. We note that pi/pa does not immediately decline during the early part of the dark period, although the large relative variation in this data set was due to one replicate leaf showing higher conductance early in the dark period (Fig. 4C). Toward the middle and end of the dark period, pi/pa was much more tightly coupled to gs and A, reaching a minimum 2 h before dawn, coincident with maximum A and gs. These continuous measurements reflect the changing activation state of PEPC, determined from the CO2 response data shown in Figure 2.
Figure 4.
A, Net A. B, gs. C, pi/pa measured from late afternoon (phase IV) and throughout the dark period (phase I) and into the light (phase II), with data (±SEM) for three replicate leaves from plants of K. daigremontiana maintained in a controlled-environment chamber on a reverse light/dark cycle. Gas exchange measurements were made at an irradiance of 300 μmol quanta m−2 s−1 in the light period, with day/night temperatures of 25°C/20°C and an inlet pCO2 of 531 μbar in 909 mbar of nitrogen and 48 mbar of O2 gas mixture.
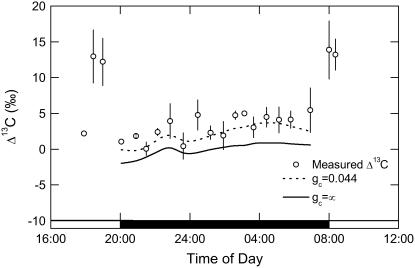
Δ13C, measured by the mass spectrometer simultaneously during gas exchange (Fig. 5), showed typically high values in the light when Rubisco is largely operating in the absence of PEPC (Griffiths et al., 1990; Dodd et al., 2002). There was a progressive increase in measured Δ13C throughout the dark period, with values lowest (around 0%) when gs was maximal at the start of the dark period (Figs. 4B and 5) and reaching a maximum of around 5.5‰ at the end of the dark period (Fig. 5). The data of A and pi/pa were used in Equation 9 to calculate a mean gi = 0.044 mol m−2 s−1 bar−1 (Fig. 5, dashed line). When using an infinite gi (effectively using pi/pa), predicted Δ13C values were consistently 2‰ to 3‰ lower than measured data (Fig. 5, continuous line).
Figure 5.
Δ13C measured in association with gas exchange from late afternoon (phase IV) and throughout the dark period (phase I) and into the light period (phase II), with data (white circles, ±SEM) for three replicate leaves from plants of K. daigremontiana maintained in a controlled-environment chamber on a reverse light/dark cycle. Predicted Δ13C for the dark period (phase I) determined from the model developed in this article (see “Theory” section for details); dashed line is modeled Δ13C including correction for the draw down from substomatal cavity to cytoplasm calculated with gi = 0.044 mol m−2 s−1 bar−1 with Equation 8 and 14 b4 = 6.27‰ at a leaf temperature of 20°C; continuous line is modeled Δ13C using infinite gi (effectively using pi/pa) to parameterize the model.
Transpiration, Evaporative Enrichment, and Determinants of ΔC18OO
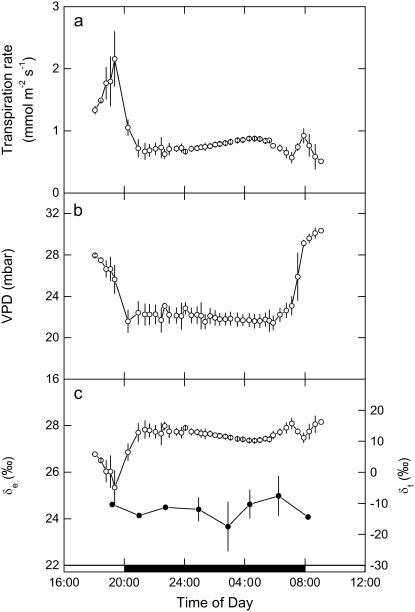
The constraints to PEPC activity in the dark (Figs. 2 and 3) will reflect the balance between the likely physical (wall and gi) and biochemical (PEPC and CA activities) determinants. To derive these components from the 18O signals in CO2 and transpired water, we first considered how transpiration rate and leaf-to-air vapor pressure difference (VPD) responded between light and dark cycles, as modified by stomatal responses during the dark period (Fig. 6, A and B; see also Fig. 4B). These factors contribute to the derivation of δe, the isotopic composition of water at the site of evaporation calculated from the Craig-Gordon (Eq. 20 in “Materials and Methods”) and are required for the interpretation of 18O in CO2. The higher transpiration rate and conductance in the light when leaf temperatures were higher are entirely consistent with the lower evaporative enrichment seen in δe during the late afternoon phase IV (Fig. 6C). Throughout most of the dark period, VPD was at steady state, and so the slight increase in conductance from the middle of the dark period (Fig. 4B) resulted in a slight but progressive decrease in δe. As maximum CO2 assimilation declined from 2 h before dawn (Fig. 4A), δe then increased, driven by the increase in VPD at that time (Fig. 6, B and C). During phase II, the relatively low gs and transpiration rates (Figs. 4B and 6B) resulted in a relatively constant δe (Fig. 6C). However, we note that the predicted δe is always higher than the 18O isotope composition measured directly in transpired water vapor (δt), which was trapped at 2-h intervals throughout the dark period (Fig. 6C).
Figure 6.
A, Transpiration rate. B, Leaf to air VPD. C, The 18O isotopic composition of δt and at the δe calculated from the Craig-Gordon model (Eq. 18), measured from late afternoon (phase IV) and throughout the dark period (phase I) and into the light (phase II) with data (±SEM) for three replicate leaves from plants of K. daigremontiana that had been maintained in a controlled-environment chamber on a reverse light/dark cycle. The source water used for irrigation of plants had an isotopic composition of δ18OVSMOW = −5.5‰.
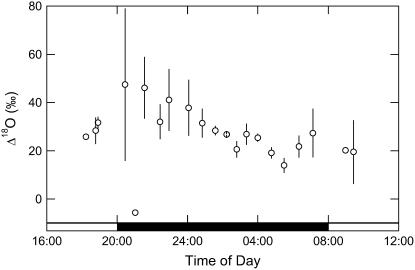
The predicted evaporative site enrichment, δe, is needed for the comparison with measured values of oxygen isotope discrimination (Δ18O; Fig. 7). The latter values are measured by the mass spectrometer in the air flow downstream of the leaf cuvette on CO2, which has retrodiffused from the leaf (Farquhar and Cernusak, 2005). The CO2 has first equilibrated with the cell-water 18O signal, catalyzed by the action of CA. It is interesting that Δ18O increases sharply at the start of the dark period (Fig. 7; around 50‰) when it is strongly regulated by gs; the wide variation in discrimination values is entirely consistent with the range of pi/pa calculated from gas exchange (Fig. 4, B and C). When PEPC activity reaches a maximum toward the end of the dark period (Figs. 2 and 3), Δ18O values are lower (around 20‰) and more tightly constrained (Fig. 7), consistent with gs and evaporation rate at this time (Figs. 4B and 6A).
Figure 7.
Δ18O measured in CO2 and in association with gas exchange, from late afternoon (phase IV) and throughout the dark period (phase I) and into the light period (phase II), with data (white circles, ± SEM) for three replicate leaves from plants of K. daigremontiana maintained in a controlled-environment chamber on a reverse light/dark cycle.
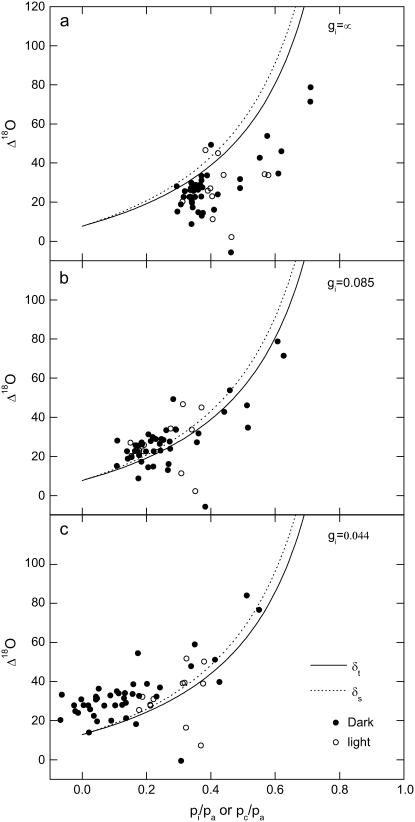
The values of Δ18O increased with pi/pa and pm/pa, as predicted from Equation 23 (“Materials and Methods”; Fig. 8). The two modeled curves in each part of Figure 8 relate the predicted isotopic discrimination when in equilibrium with either source water (δs, −5.5‰ ± 0.3‰ versus the Vienna Standard Mean Oceanic Water [VSMOW] standard, dotted line) or measured δt (mean measured value, −12.2‰ ± 1.1‰; see individual data in Fig. 6C), showing that the impact of changing between δs and δt on each plot is relatively minor. The measured values were always lower than predicted for full isotopic equilibrium, with an assumed constant Δea of 45‰ or 51‰ for either δt or δs values, respectively, when used in Equation 23 with an infinite wall and cytoplasmic conductance assumed (i.e. there is no draw down from pi to pm; Fig. 8A). The offset in Δ18O as a function of mesophyll pCO2 depended on the magnitude of the wall conductance and cytoplasmic gi used to calculate pm for Equation 23 (“Materials and Methods”; Fig. 8, A–C). Measurements made in both the light and the dark show a much better fit when the wall and cytoplasmic gi is estimated as 0.085 mol m−2 s−1 bar−1 (Fig. 8B), whereas the lower internal conductance, which provided a good predictor of Δ13C (0.044 mol m−2 s−1 bar−1), overestimated the Δ18O signal across the board (Fig. 8C).
Figure 8.
Δ18O as a function of pi/pa (A) and pm/pa (B and C). In A, no correction was made for gi, whereas in B and C, pm was derived by assuming a gi of 0.0.85 or 0.044 mol m−2 s−1 bar, respectively. The lines are not fitted to the data but represent the theoretical relationship of Δ18O and pi/pa or pm/pa at full isotopic equilibrium, where a = 7.7‰ and Δea = 45‰ or 51‰ using either the average δt or δs values, respectively, in Equation 24. The value of gi = 0.085 in B was estimated from minimizing the variance between measured and theoretical Δ18O calculated with the average δt. The CO2 supplied to the leaf had a Δ18O of 24‰ relative to VSMOW. Data points in each section represent the individual samples collected during light (white circles) and dark (black circles) from three replicate leaves of K. daigremontiana (for details, see Figs. 2 and 5, legends above).
DISCUSSION
Δ13C by the CAM pathway has traditionally been used to partition the extent of C3 and C4 carboxylation during the contrasting phases of CAM (Osmond, 1978; Griffiths et al., 1990; Griffiths, 1992; Roberts et al., 1997). A lack of consistency between theoretical and measured Δ13C suggested a need to reevaluate these approaches (Griffiths, 1992) and was highlighted by the difficulties of inferring the proportion of CAM species in various plant communities from carbon isotope composition (Pierce et al., 2002a; Holtum and Winter, 2003). In this study, we derived a model to evaluate instantaneous measurements of Δ13C in the contrasting CAM phases based on biochemical and diffusional constraints to carboxylation for both Rubisco and PEPC. Experimentally, we have focused on carbon uptake during the dark period to explore the actual variations in Δ13C in relation to the theoretical predictions from the model.
The interplay between gs and PEPC activity were previously shown to regulate inorganic carbon supply, CA activity, and metabolic partitioning in determining carbon isotope composition of malate synthesized in the dark period (O'Leary and Osmond, 1980; Holtum et al., 1984; Osmond et al., 1988; Kalt et al., 1990). The opportunity to couple a gas exchange system directly to a mass spectrometer allowed us to explore instantaneous discrimination against 13C during the dark period. Concomitant measurements of 18O discrimination in CO2 were used to highlight the internal diffusive constraints to Rubisco and PEPC carboxylation (in chloroplast and cytoplasm, respectively) and the potential interplay between CA activity, evaporation, and leaf water turnover (for the analogy with C4 pathway see Cousins et al., 2006a, 2006b). For online gas exchange and mass spectrometric measurements, partial pressures of CO2 and O2 were typical for those used to optimize the system in previous studies (Cousins et al., 2006a, 2006b).
Gas Exchange and PEPC Carboxylation Capacity during the Dark Period
The systematic changes in A during the dark period were associated with changes in PEPC carboxylation capacity (Figs. 2–5). Continuous measurements of gas exchange throughout the dark period, as well as the individual A/pi responses and the correlation between initial slope and Amax, confirm this observation. In particular, it seemed that PEPC activity was driving assimilation, because proportionally, there was a more modest stomatal response throughout the middle of the dark period, when pi/pa declined to a minimum (Fig. 4).
One question remains, however, as to the nature of the regulation underlying the shifts in PEPC capacity and Amax seen in our data. The low CO2 assimilation at the start of the dark period (Fig. 4), and subsequent recovery during the middle of the night, was tracked by catalytic capacity of PEPC (Figs. 2 and 3). This is consistent with the need to activate PEPC via PEPC kinase as malic acid accumulates, because high malic acid concentrations are likely to inhibit PEPC (Nimmo et al., 2001; Dodd et al., 2002), and PEPC kinase expression tends to occur rather late in the dark period in K. daigremontiana (Borland and Griffiths, 1997).
gi and Determinants of Instantaneous Δ13C at Night
Previously, estimates of carbon isotope composition have inferred the extent of daytime (Rubisco) and nighttime PEPC carboxylation, together with the varying contribution during phases II and IV, to overall organic material (Osmond, 1978; Griffiths, 1992; Roberts et al., 1997). Estimates of Δ13C for PEPC (without the company of Rubisco, as in C4 plants) have resulted in measured δ13C for newly fixed C in malate closer to theoretical predictions from pi/pa (Holtum et al., 1984; Deleens et al., 1985; Roberts et al., 1997). By including conductance for CO2 diffusion from intercellular airspace to the cytosol (gi), the model presented in this article provides a more effective representation of Δ13C during the CAM cycle, particularly across the dark period. Experimentally, by tracking gas exchange and real-time Δ13C throughout the dark period with measurable gs (Figs. 2 and 4), we could derive mesophyll limitations, which proved to dominate overall Δ13C.
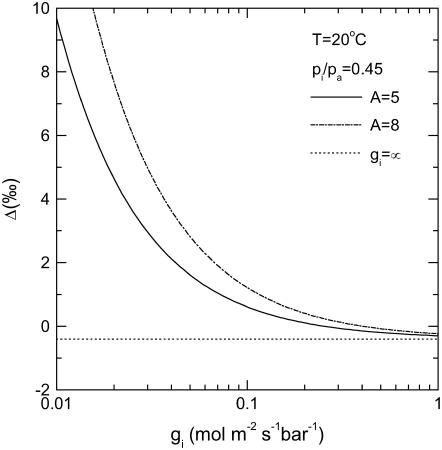
Diffusion limitation from intercellular airspace to the chloroplast stroma was shown to reduce Δ13C in C3 species (see Eq. 8; Evans et al., 1986) This is because the large value of Δbio, which is the result of a large Rubisco fractionation, is tempered by the diffusive draw down to carboxylation site. In C4 species, the internal CO2 diffusion limitation has very little influence on Δ13C, because the Δbio is close to 0 as the fractionation associated with Rubisco counter balances the fractionation associated with the hydration and PEPC carboxylation of CO2. Our theory shows that the internal diffusion limitation in CAM species can lead to a decrease in discrimination during phase II and IV, where Rubisco is active and stomata are open, but will increase discrimination during nighttime PEPC carboxylation. In our experiments, leaf temperatures were 20°C and Δbio = −6.27‰, and we could partition approximately 3.5‰ to the internal diffusion limitation at high assimilation rates. The mean value for the gi to PEPC derived from our measurements of Δ13C during the dark phase brought convergence between measured and modeled Δ13C throughout the night (Fig. 5; 0.044 mol m−2 s−1 bar−1). This value will be important for modeling the isotopic correlates of the C4 pathway. In Figure 9, we show that, depending on assimilation rate, as the value of the gi decreases, there is a predictable increase in Δ13C with values of 6‰ to 8‰ potentially associated with PEPC activity alone when constrained internally by CO2 diffusion. Accurate estimates of gi are also important if online measurements of Δ13C are to be used to partition CO2 uptake between Rubisco and PEPC carboxylations in phase II and IV. A low gi will decrease Δ13C during these phases, and if not taken into account, the contribution from PEPC is overestimated (see Eqs. 10 and 12).
Figure 9.
Modeled predictions (Eqs. 8 and 14) of Δ13C for two contrasting assimilation rates and a pi/pa = 0.45 using b4 = 6.27‰ at a leaf temperature of 20°C plotted as a function of varying gi during phase I.
The model provides a consistent explanation for the rather high values of Δ13C often found in many constitutive CAM plants, which have traditionally been used to infer the contribution from daytime Rubisco processes. One remaining question, however, relates to the effective path length through which CO2 diffuses to PEPC, which maybe distinguishable by the offset of cytoplasmic diffusion and effective wall conductance as determined by Δ13C and Δ18O seen in retrodiffusing CO2.
Evaporation, Isotopic Exchange, and CA Equilibrium at Night
The Δ18O data provided an additional insight into diffusional constraints to CO2 fixation during the dark period. The 18O in CO2 exchanging across the leaf surface, carrying the adopted evaporative signal, was primarily controlled by gs (compare Fig. 7 with Fig. 4, B and C) unlike Δ13C (Fig. 5). However, as well as providing the extent of evaporative enrichment in relation to the exchange of CO2, the 18O signal can be used to infer the extent of CA equilibration (Cousins et al., 2006b). It is intriguing that we needed to use a higher value of gm to model 18O exchange, and in general terms, the Δ18O signal clearly tracked pi/pa. While Δ13C was somewhat independent of pi/pa early in the dark period, a lower value gi was needed throughout, perhaps implying that PEPC is limited for CO2/HCO3 supply deep within cells or succulent tissues or perhaps that there is spatial variation in CA distribution and activity (Cousins et al., 2006a, 2006b). In contrast, the 18O signal of CO2 could reflect those sites closer to airspaces that are in evaporative equilibrium. Finally, the −5.5‰ offset between δs and δt (measured directly; Fig. 6) implied that evaporated water is not in equilibrium with source water, which occurs during isotopic steady state. This may be due to the large capacitance of succulent leaves (Smith et al., 1987) or the isotopic exchange of the water vapor signal that can occur at high humidities (Farquhar and Cernusak, 2005). While this is extremely important for CAM plants and their nocturnal stomatal opening under natural conditions (Helliker and Griffiths, 2007), it was precluded by our measurements at low ambient humidity.
Implications for Carbon Isotope Signals in Natural Vegetation
The model of Δ13C presented in this article can account for much higher values of discrimination than are normally associated with dark CO2 uptake and fixation by PEPC during the CAM cycle (Fig. 9). Previously, low values of Δ13C have been associated with CO2 uptake only at night or the C4 of malate accumulated during the dark period (Nalborczyk et al., 1975; Deleens et al., 1985). In the Clusiaceae, a rather unusual family of hemiepiphytic stranglers that show a range of CAM characteristics (Borland et al., 1993; Roberts et al., 1998), measured instantaneous values of online Δ13C were extremely low (−4‰ to −6‰) under high gs (with pi/pa of 0.7 and above; Roberts et al., 1997). Why, then, are measured Δ13C values in organic material so consistently higher than these measurements might predict? Holtum et al. (1984) invoked a number of responses, including the rate of dark respiration and refixation (accounted for in our model by Eq. 18). Rubisco operating in the light can lead to substantial fractionation being expressed, but on a small proportion of CO2 in phase III (Griffiths et al., 1990), or can contribute significantly to carbon gain and productivity during phase IV (Borland and Dodd, 2002; Dodd et al., 2002), which would lead to higher overall Δ13C in organic material. However, in this article, we have shown that the internal diffusion constraints from intercellular airspace to mesophyll cytosol increase Δ13C throughout the dark period in K. daigremontiana (Figs. 5 and 9) compared to the discrimination that would be predicted from the PEPC-mediated Δ13C alone. This will help the understanding of observed organic material signals.
Thus, the data presented in this article go some way to explaining two phenomena that arise when evaluating the distribution of CAM from Δ13C measurements of entire plant populations. First, even plants fully committed to dark CO2 fixation can show relatively high Δ13C values because of internal constraints to diffusion during the dark phase (Pierce et al., 2002a; Holtum and Winter, 2003). Second, variations in Δ13C have traditionally been thought to be dominated by the extent of direct Rubisco carboxylation during phases II and IV. We have now shown that internal constraints to diffusion can both decrease Rubisco-mediated discrimination in phases II and IV and increase PEPC-mediated discrimination in phase I, with both responses tending to stabilize organic material isotope signals and values tending to be intermediate between C3 and CAM ranges. This may be one of the reasons why organic Δ13C signals tend to be relatively constant across a wide range of habitats, as noted in a number of field studies and experimental manipulations (Griffiths et al., 1986; Griffiths, 1992).
MATERIALS AND METHODS
Growth Conditions
Kalanchoe daigremontiana plants were grown from vegetative plantlets, with material initially grown during the summer months in a glass house under natural light conditions (27°C day and 18°C night temperatures). Two weeks prior to experimentation, plants were acclimated within two controlled-environment, walk-in growth rooms under a photosynthetic photon flux density of 300 μmol quanta m−2 s−1 at plant height and air temperature of 25°C during the day and 18°C at night with a photoperiod of 12 h/d. One of the rooms was set to run under a reverse light/dark cycle to provide plant material for real-time isotope determinations for periods immediately before, during, and after the dark period. Plants were grown in 5-L pots in garden mix with 2.4 to 4.0 g Osmocote/L soil (15:4.8:10.8:1.2 N:P:K:Mg + trace elements: B, Cu, Fe, Mn, Mo, Zn; Scotts Australia) and watered daily.
Online Gas Exchange Measurements
The uppermost fully expanded leaves were placed into the leaf chamber of the LI-6400 2 h prior to the dark period and allowed to acclimate at 300 μmol photons m−2 s−1, 25°C leaf temperature, and a pCO2 of 531 μbar for 1 h. The pCO2 was elevated to reflect conditions in the growth facility. Subsequently, one to three online measurements (see below) were made prior to changing to the corresponding nighttime conditions (0 μmol photons m−2 s−1, 20°C leaf temperature, and pCO2 of 531 μbar). Throughout the night period, online measurements were made approximately every 20 min as described below. In coordination with the plants' day/night cycle, after the 12-h dark period, the leaf cuvette was returned to the corresponding daytime conditions, and several more measurements were made prior to stomatal closure.
Air entering the leaf chamber was prepared by using mass flow controllers (MKS Instruments) to obtain a gas mix of 909 mbar dry N2 and 48 mbar O2 (Cousins et al., 2006a, 2006b). A portion of the nitrogen/oxygen air was used to zero the mass spectrometer to correct for N2O and other contaminates contributing to the 44, 45, and 46 peaks. Pure CO2 (δ13CVPDB = −29‰, and δ18OVSMOW = 24‰) was added to the remaining air stream to obtain a pCO2 of approximately 531 μbar. Low oxygen (48 mbar) was used to minimize contamination of the 46 (mass-to-charge ratio [m/z]) signal caused by the interaction of O2 and N2 to produce NO2 with the mass spectrometer source and also to minimize the biological impact of secondary fractionations due to photorespiration during daytime gas exchange.
The gas mixtures were fed to the inlet of the LI-6400 console, and a flow rate of 200 μmol s−1 was maintained over the leaf. The remaining air stream was vented or used to determine the isotopic composition of air entering the leaf chamber (Cousins et al., 2006a, 2006b). The efflux from the leaf chamber was measured by replacing the match valve line with a line connected directly to the mass spectrometer. Gas exchange parameters were determined by the LI-6400, and pCO2 leaving the chamber was subsequently corrected for the dilution of CO2 by water vapor (von Caemmerer and Farquhar, 1981).
The efflux from the leaf chamber and the gas mix supplied to the LI-6400 system were linked to a mass spectrometer through an ethanol/dry ice water trap and a thin, gas-permeable silicone membrane that was housed in a temperature-controlled cuvette. Initially, the masses (m/z) 44 and 45 were monitored continuously, and the Δ13C during CO2 exchange was calculated from the ratio of mass 45 to 44 in the reference air, determined before and after each sample measurement, entering the chamber (Re) and the composition of the sample air leaving the leaf chamber (Ro), as described in (Evans et al., 1986):
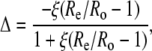 |
(19) |
where ξ = pe/(pe − po), and pe and po are the pCO2 of dry air entering and leaving the leaf chamber, respectively. At the end of the Δ13C measurements, the accelerating voltage of the mass spectrometer was adjusted to continuously monitor masses (m/z) 44 and 46 to determine the Δ18O, as described above. Zero values for the 44, 45, and 46 peaks were determined before and after the sample measurements were subtracted from both the sample and reference measurements prior to determining the mass ratios.
CO2 Response Curves
Using the same background air stream as above, the LI-6400 gas exchange system was programmed (using the 6400-01 CO2 injector) to run eight automated A/pi curves (measured as A and gs as a function of increasing pa, external pCO2) before (1×), during (6×), and after (1×) the dark period. The leaf was maintained at steady-state conditions (300 μmol photons m−2 s−1, 25°C leaf temperature, and a pCO2 of 383 μbar or 0 μmol quanta m−2 s−1, 20°C leaf temperature, and pCO2 of 383 μbar) for 1 h before the initiation of each A/pi curve. The A/pi curves were measured from low to high pCO2 at the leaf temperature and photon flux density corresponding to the appropriate times in relation to the growth conditions. Measurement of an A/pi curve took approximately 35 min.
Collection and 18O Isotopic Measurements of Water Vapor
A line connected directly to the exhaust port of the LI-6400 was used to cryogenically trap transpired water in a modified glass collection line submerged in an ethanol-dry ice bath, as described in detail by Cousins et al. (2006b). Water vapor was collected for 1 to 2 h before (1×), during (6×), and after (1×) the dark period. Because of the low volumes collected (usually less than 50 μL of water), the water was transferred from the collection tubes via a cryogenic trapping line in a stream of dry N2 gas and subsequently sealed with a gas torch under vacuum in 6-mm-o.d. silica glass vials attached via a Cajon ultra-torr fitting. The glass vials were subsequently scored, and where possible, 25 μL of liquid water was removed with a gas tight microsyringe (SGE) and injected into 10-mL head space vials with crimped tops containing butyl septa (Alltech), which had been previously flushed with 20 mbar CO2 (in a N2 background) at atmospheric pressure levels (Cousins et al., 2006b). Water and CO2 samples were left to equilibrate at room temperature for 48 h.
Prior to the isotopic measurements, the vials were placed for a minimum of 2.5 h on a temperature block set at 25°C. The CO2 samples were analyzed by injecting 200 μL of the headspace gas into a 500-μL N2 purged, gas tight, temperature-controlled cuvette containing a Teflon gas permeable membrane linked to the ISOPRIME mass spectrometer (Cousins et al., 2006b). Masses 44 and 46 were monitored continuously, and the zero values, determined before and after the sample measurements, were subtracted from the values prior to determining the mass ratios. The zero values were typically 3% to 4% of the 44 and 46 peak. Two standard laboratory waters were measured during each measurement to calibrate our measured values against known standards (Cousins et al., 2006b). Our standard waters (S1 = −6.44‰ and S2 = −22.83‰ as compared to the international VSMOW standard at 0‰) were calibrated by the Stable Isotope Facilities in the Earth Environment Group within the Research School of Earth Sciences at The Australian National University. The measured δ18O value was corrected for the contribution of oxygen from the CO2 used for equilibration and normalized against VSMOW, as described in Cousins et al. (2006b; see also Scrimgeour, 1995). The precision of analyses, based on the repeated measurements of gas samples sealed in vials, was 0.1‰ (1 sd, n = 8).
Water at the Site of Evaporation and Δ18O
The δ18O of water at the sites of evaporation within a leaf (δe) can be estimated from the Craig and Gordon model of evaporative enrichment (Craig and Gordon, 1965; Farquhar and Lloyd, 1993):
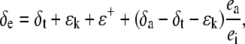 |
(20) |
where ea and ei are the vapor pressures in the atmosphere and the leaf intercellular spaces. δa is the isotopic composition of water vapor in the air. The kinetic fractionation during diffusion of water from leaf intercellular air spaces to the atmosphere (ɛk) can be calculated as in Cernusak et al. (2004):
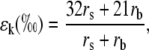 |
(21) |
where rs and rb are the stomatal and boundary layer resistance, and 32 and 21 are the fractionation factors in parts per mille. The equilibrium fractionation between liquid water and water vapor (ɛ+) is calculated as in Cernusak et al. (2004):
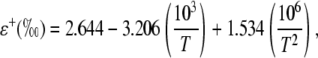 |
(22) |
where T is leaf temperature in degrees Kelvin. Under steady-state conditions, the value of δt is equal to the isotopic composition of δs, the water taken up by the plant (Harwood et al., 1998).
Discrimination against C18OO (Δ18O) when water at the site of exchange and CO2 are at full isotopic equilibrium (θ = 1) can be predicted (Farquhar and Lloyd, 1993) as:
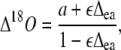 |
(23) |
where a is the diffusional discrimination (7.7‰) and ɛ is calculated as pm/(pa − pm). The 18O enrichment of CO2 compared to the atmosphere at the site of exchange in full oxygen isotope equilibrium with the water was calculated as in Cernusak et al. (2004):
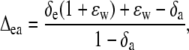 |
(24) |
where the equilibrium fractionation between water and CO2 (ɛw) can be calculated as in Cernusak et al. (2004):
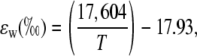 |
(25) |
where T is leaf temperature in degrees Kelvin.
Derivation of an Expression for the Biochemical Fractionation, Δbio, during CAM Photosynthesis
Assimilation rate during CAM photosynthesis can be written as a general equation
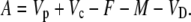 |
(26) |
In phase I:
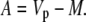 |
(27) |
In phase II and IV:
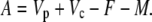 |
(28) |
In phase III:
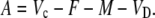 |
(29) |
Equation 26 can also be written for the assimilation of 13CO2
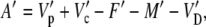 |
(30) |
and
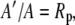 |
(31) |
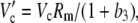 |
(32) |
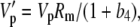 |
(33) |
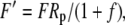 |
(34) |
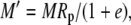 |
(35) |
and
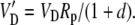 |
(36) |
The various fractionation factors have been defined in the theory section. Using Equations 26 and 30 to 36, it can be shown that:
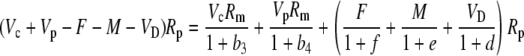 |
(37) |
and
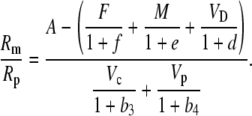 |
(38) |
Using the fact that 1/(1 + x) approximately (1 − x) when x < 1, Equation 38 can be rearranged such that
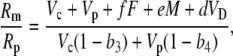 |
(39) |
if
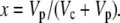 |
(40) |
Dividing numerator and denominator by Vc + Vp gives
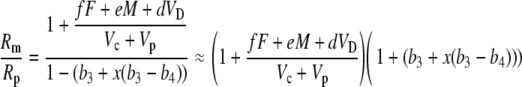 |
(41) |
Multiplying out and ignoring small terms, one can derive the general expression for Δbio:
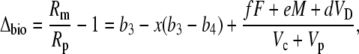 |
(42) |
and this is Equation 12 in the “Theory” section.
To derive the expression for the discrimination that occurs between malate decarboxylation and Rubisco refixation in phase III, one uses Equation 17 and
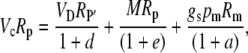 |
(43) |
substituting for Vc using Equation 17, dividing both sides of Equation 43 by Rp, and using the fact that Vc′ = VcRp and Rm/Rp = (1 + b3) and rearranging gives
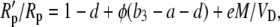 |
(44) |
where φ = L/VD = gspm/VD is the fraction of CO2 decarboxylated that leaks out of the leaf.
Statistical Analysis
ANOVA was conducted using repeated measures ANOVA in STATISTICA (version 6.0 StatSoft) on the measurements made during the dark period. Fisher lsd test was used for post hoc comparisons.
Acknowledgments
We thank Chin Wong for helpful advice on collecting transpired water, Hillary Stuart for analyzing the oxygen isotope composition of our CO2 tank, and Graham Farquhar for his support and helpful discussions.
This work was supported by the Molecular Plant Physiology and Environmental Biology Groups at the Research School of Biological Sciences, Australian National University (visiting fellowship to H.G.), and by the National Science Foundation (international postdoctoral fellowship to A.B.C.).
The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (www.plantphysiol.org) is: Howard Griffiths (hg230@cam.ac.uk).
References
- Bender MM, Rouhani I, Vines HM, Black CC (1973) C-13-C-12 ratio changes in crassulacean acid metabolism plants. Plant Physiol 52 427–430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borland AM, Dodd AN (2002) Carbohydrate partitioning in crassulacean acid metabolism plants: reconciling potential conflicts of interest. Funct Plant Biol 29 707–716 [DOI] [PubMed] [Google Scholar]
- Borland AM, Griffiths H (1997) A comparative study on the regulation of C-3 and C-4 carboxylation processes in the constitutive crassulacean acid metabolism (CAM) plant Kalanchoe daigremontiana and the C-3-CAM intermediate Clusia minor. Planta 201 368–378 [DOI] [PubMed] [Google Scholar]
- Borland AM, Griffiths H, Broadmeadow MSJ, Fordham MC, Maxwell C (1993) Short-term changes in carbon-isotope discrimination in the C3-CAM intermediate Clusia minor L growing in Trinidad. Oecologia 95 444–453 [DOI] [PubMed] [Google Scholar]
- Cernusak LA, Farquhar GD, Wong SC, Stuart-Williams H (2004) Measurement and interpretation of the oxygen isotope composition of carbon dioxide respired by leaves in the dark. Plant Physiol 136 3350–3363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cousins AB, Badger MR, von Caemmerer S (2006. a) Carbonic anhydrase and its influence on carbon isotope discrimination during C4 photosynthesis: insights from antisense RNA in Flaveria bidentis. Plant Physiol 141 232–242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cousins AB, Badger MR, von Caemmerer S (2006. b) A transgenic approach to understanding the influence of carbonic anhydrase on C18OO discrimination during C4 photosynthesis. Plant Physiol 142 662–672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig H, Gordon LI (1965) Deutrium and oxygen-18 variations in the ocean and the marine atmosphere. In E Tongiorgi, ed, Proceedings of a Conference on Stable Isotopes in Oceanographic Studies and Paleotemperatures. Consiglio Nazionale delle Ricerche, Laboratorie Geologia Nuclear, Pisa, Italy, pp 9–130
- Crayn DM, Winter K, Smith JAC (2004) Multiple origins of crassulacean acid metabolism and the epiphytic habit in the neotropical family Bromeliaceae. Proc Natl Acad Sci USA 101 3703–3708 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deleens E, Treichel I, O'Leary MH (1985) Temperature dependence of carbon isotope fractionation in CAM plants. Plant Physiol 79 202–206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodd AN, Borland AM, Haslam RP, Griffiths H, Maxwell K (2002) Crassulacean acid metabolism: plastic, fantastic. J Exp Bot 53 569–580 [DOI] [PubMed] [Google Scholar]
- Dodd AN, Griffiths H, Taybi T, Cushman JC, Borland AM (2003) Integrating diel starch metabolism with the circadian and environmental regulation of Crassulacean acid metabolism in Mesembryanthemum crystallinum. Planta 216 789–797 [DOI] [PubMed] [Google Scholar]
- Evans JR, Sharkey TD, Berry JA, Farquhar GD (1986) Carbon isotope discrimination measured concurrently with gas-exchange to investigate CO2 diffusion in leaves of higher-plants. Aust J Plant Physiol 13 281–292 [Google Scholar]
- Farquhar GD (1983) On the nature of carbon isotope discrimination in C4 species. Aust J Plant Physiol 10 205–226 [Google Scholar]
- Farquhar GD, Cernusak LA (2005) On the isotopic composition of leaf water in the non-steady state. Funct Plant Biol 32 293–303 [DOI] [PubMed] [Google Scholar]
- Farquhar GD, Ehleringer JR, Hubick KT (1989) Carbon isotope discrimination and photosynthesis. Annu Rev Plant Physiol Plant Mol Biol 40 503–537 [Google Scholar]
- Farquhar GD, Lloyd J (1993) Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere. In JR Ehleringer, AE Hall, GD Farquhar, eds, Stable Isotopes and Plant Carbon-Water Relations. Academic Press, New York, pp 47–70
- Farquhar GD, Oleary MH, Berry JA (1982) On the relationship between carbon isotope discrimination and the inter-cellular carbon-dioxide concentration in leaves. Aust J Plant Physiol 9 121–137 [Google Scholar]
- Farquhar GD, Richards RA (1984) Isotopic composition of plant carbon correlates with water-use efficiency of wheat genotypes. Aust J Plant Physiol 11 539–552 [Google Scholar]
- Ghashghaie J, Badeck F-W, Lanigan G, Nogues S, Tcherkez G, Deleens E, Cornic G, Griffiths H (2003) Carbon isotope fractionation during dark respiration and photorespiration in C3 plants. Phytochem Rev 2 145–161 [Google Scholar]
- Griffiths H (1992) Carbon isotope discrimination and the integration of carbon assimilation pathways in terrestrial cam plants. Plant Cell Environ 15 1051–1062 [Google Scholar]
- Griffiths H, Broadmeadow MSJ, Borland AM, Hetherington CS (1990) Short-term changes in carbon-isotope discrimination identify transitions between C-3 and C-4 carboxylation during crassulacean acid metabolism. Planta 181 604–610 [DOI] [PubMed] [Google Scholar]
- Griffiths H, Helliker B, Roberts A, Haslam RP, Girnus J, Robe WE, Borland AM, Maxwell K (2002) Regulation of Rubisco activity in crassulacean acid metabolism plants: better late than never. Funct Plant Biol 29 689–696 [DOI] [PubMed] [Google Scholar]
- Griffiths H, Luttge U, Stimmel KH, Crook CE, Griffiths NM, Smith JAC (1986) Comparative ecophysiology of CAM and C-3 bromeliads. 3. Environmental-influences on Co2 assimilation and transpiration. Plant Cell Environ 9 385–393 [Google Scholar]
- Harwood KG, Gillon JS, Griffiths H, Broadmeadow MSJ (1998) Diurnal variation of delta(CO2)-C-13, delta(COO)-O-18-O-16 and evaporative site enrichment of delta(H2O)-O-18 in Piper aduncum under field conditions in Trinidad. Plant Cell Environ 21 269–283 [Google Scholar]
- Helliker BR, Griffiths H (2007) Towards a plant-based proxy for the isotope ratio of atmospheric water vapor. Glob Change Biol (in press)
- Henderson SA, von Caemmerer S, Farquhar GD (1992) Short-term measurements of carbon isotope discrimination in several C4 species. Aust J Plant Physiol 19 263–285 [Google Scholar]
- Holtum JAM, O'Leary MH, Osmond CB (1983) Effect of varying CO2 partial pressure on photosynthesis and on carbon isotope composition of carbon-4 of malate from the crassulacean acid metabolism plant Kalanchoe daigremontiana Hamet et Perr. Plant Physiol 71 602–609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holtum JAM, Summons R, Roeske CA, Comins HN, Oleary MH (1984) O-18 incorporation into malic-acid during nocturnal carbon-dioxide fixation in crassulacean acid metabolism plants: a new approach to estimating in vivo carbonic-anhydrase activity. J Biol Chem 259 6870–6881 [PubMed] [Google Scholar]
- Holtum JAM, Winter K (2003) Photosynthetic CO2 uptake in seedlings of two tropical tree species exposed to oscillating elevated concentrations of CO2. Planta 218 152–158 [DOI] [PubMed] [Google Scholar]
- Kalt W, Osmond CB, Siedow JN (1990) Malate metabolism in the dark after (Co2)-C-13 fixation in the crassulacean plant Kalanchoe tubiflora. Plant Physiol 94 826–832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mook W, Bommerson J, Staverman W (1974) Carbon isotope fractionation between dissolved bicarbonate and gaseous carbon dioxide. Earth Planet Sci Lett 22 169–176 [Google Scholar]
- Nalborczyk E, Lacroix LJ, Hill RD (1975) Environmental influences on light and dark CO2 fixation by Kalanchoe daigremontiana. Can J Bot 53 1132–1138 [Google Scholar]
- Nimmo HG, Fontaine V, Hartwell J, Jenkins GI, Nimmo GA, Wilkins MB (2001) PEP carboxylase kinase is a novel protein kinase controlled at the level of expression. New Phytol 151 91–97 [DOI] [PubMed] [Google Scholar]
- O'Leary M (1981) Carbon isotope fractionation in plants. Phytochemistry 20 553–567 [Google Scholar]
- O'Leary MH, Osmond CB (1980) Diffusional contribution to carbon isotope fractionation during dark CO2 fixation in CAM plants. Plant Physiol 66 931–934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Leary MH, Treichel I, Rooney M (1986) Short-term measurement of carbon isotope fractionation in plants. Plant Physiol 80 578–582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osmond CB (1978) Crassulacean acid metabolism: curiosity in context. Annu Rev Plant Physiol Plant Mol Biol 29 379–414 [Google Scholar]
- Osmond CB, Allaway WG, Sutton BG, Troughto JH, Queiroz O, Luttge U, Winter K (1973) Carbon isotope discrimination in photosynthesis of cam plants. Nature 246 40–42 [Google Scholar]
- Osmond CB, Holtum JAM, Oleary MH, Roeske C, Wong OC, Summons RE, Avadhani PN (1988) Regulation of malic-acid metabolism in crassulacean-acid-metabolism plants in the dark and light: in vivo evidence from C-13-labeling patterns after (Co2)-C-13 fixation. Planta 175 184–192 [DOI] [PubMed] [Google Scholar]
- Pierce S, Winter K, Griffiths H (2002. a) Carbon isotope ratio and the extent of daily CAM use by Bromeliaceae. New Phytol 156 75–83 [Google Scholar]
- Pierce S, Winter K, Griffiths H (2002. b) The role of CAM in high rainfall cloud forests: an in situ comparison of photosynthetic pathways in Bromeliaceae. Plant Cell Environ 25 1181–1189 [Google Scholar]
- Roberts A, Borland AM, Griffiths H (1997) Discrimination processes and shifts in carboxylation during the phases of crassulacean acid metabolism. Plant Physiol 113 1283–1292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts A, Borland AM, Maxwell K, Griffiths H (1998) Ecophysiology of the C-3-CAM intermediate Clusia minor L. in Trinidad: seasonal and short-term photosynthetic characteristics of sun and shade leaves. J Exp Bot 49 1563–1573 [Google Scholar]
- Roeske CA, O'Leary MH (1984) Carbon isotope effects on the enzyme-catalyzed carboxylation of ribulose bisphosphate. Biochemistry 23 6275–6284 [DOI] [PubMed] [Google Scholar]
- Scrimgeour CM (1995) Measurement of plant and soil water isotope composition by direct equilibration methods. J Hydrol 172 261–274 [Google Scholar]
- Smith JAC, Schulte PJ, Nobel PS (1987) Water-flow and water storage in agave-deserti-osmotic implications of crassulacean acid metabolism. Plant Cell Environ 10 639–648 [Google Scholar]
- Tsuzuki M, Miyachi S, Winter K, Edwards GE (1982) Localization of carbonic-anhydrase in crassulacean acid metabolism plants. Plant Sci Lett 24 211–218 [Google Scholar]
- Vogel JC (1980) Fractionation of the carbon isotopes during photosynthesis. In Sitzungsberichte der Heidelberger Akademie der Wissenschaften Mathematisch-naturwissenschaftlicher Klasse Jahrgang. Springer Verlag, Berlin, pp 111–135
- von Caemmerer S, Farquhar GD (1981) Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves. Planta 153 376–387 [DOI] [PubMed] [Google Scholar]
- Winter K, Holtum JAM (2002) How closely do the delta C-13 values of crassulacean acid metabolism plants reflect the proportion of CO2 fixed during day and night? Plant Physiol 129 1843–1851 [DOI] [PMC free article] [PubMed] [Google Scholar]