Cellular scaling rules for primate brains

Abstract

Primates are usually found to have richer behavioral repertoires and better cognitive abilities than rodents of similar brain size. This finding raises the possibility that primate brains differ from rodent brains in their cellular composition. Here we examine the cellular scaling rules for primate brains and show that brain size increases approximately isometrically as a function of cell numbers, such that an 11× larger brain is built with 10× more neurons and ≈12× more nonneuronal cells of relatively constant average size. This isometric function is in contrast to rodent brains, which increase faster in size than in numbers of neurons. As a consequence of the linear cellular scaling rules, primate brains have a larger number of neurons than rodent brains of similar size, presumably endowing them with greater computational power and cognitive abilities.

Brain size varies by as much as 100,000× across mammalian species (1, 2), and a large number of comparative studies have concentrated on finding the shared regularities behind brain morphology and cellular composition across species of different brain sizes (1, 3, 4). Although any such regularities may reveal general principles underlying the development and evolution of the brain, one must keep in mind that major differences across orders may also exist. Because cellular composition of the brain is one of the major determinants of its computational capacities (5), species belonging to different orders, having different cognitive abilities, and possessing brains of similar sizes would be expected to differ in cellular composition.

We recently described the cellular scaling rules that apply to rodent brains from the mouse to the capybara (6). In that work, we showed that the rodent brain scales hypermetrically as a function of its numbers of neurons, and that the average neuronal size is larger in larger brains, whereas the average nonneuronal cell size remains comparatively stable. As in previous reports (1–3, 7–13), neuronal density decreases and the glia/neuron ratio increases with increasing brain size. We also showed that the ratio of total neuronal mass/total nonneuronal mass remains constant across rodent species, and we offered an explanation for how this ratio could be achieved during development (6).

These results prompted us to investigate whether the same scaling rules apply to other mammalian orders. Our aim was to establish what rules are shared among mammalian brains, and thus might reflect characteristics inherited from a common ancestor, and what rules differ across orders of mammals, and thus might account for phylogenetic variance across groups. We were particularly interested in cellular scaling differences that might have arisen in primates. If the same rules relating numbers of neurons to brain size in rodents (6) also applied to primates, a brain comparable to ours, with ≈100 billion neurons, would weigh >45 kg and belong to a body of 109 tons, about the mass of the heaviest living mammal, the blue whale. This simple calculation indicates quite dramatically that at least some cellular scaling rules must differ between rodents and primates, which is not surprising given the presumably different cognitive abilities of rodents and primates of similar brain size (e.g., between agoutis and owl monkeys or between capybaras and macaque monkeys).

To determine the cellular scaling rules for primate brains and to examine how they compare to the scaling rules for rodents, we used the isotropic fractionator (14), a nonstereological method, to estimate the total numbers of neuronal and nonneuronal cells in the cerebral cortex, cerebellum, and remaining structures of the brain and to examine how they scale across six species of the order Primata, from Callithrix to Macaca, and in the closely related tree shrew (order Scandentia).

Results

Across the six primate species examined, body mass (M_BO) varies 10.8-fold, from ≈360 g in Callithrix to ≈3,900 g in Macaca. Brain mass (M_BR) varies by a factor of 11.2, accompanied by a similar 10.0-fold increase in total number of neurons (N_N), from 636 million in Callithrix to 6.4 billion in Macaca, and a 12.1-fold increase in total number of nonneuronal cells (N_NN) (Table 1). The percentage of neurons in the brain does not vary significantly with brain size (Spearman correlation coefficient ρ = −0.321, P = 0.4311), and in all species but Macaca neurons comprise slightly more than 50% of all brain cells.

Table 1.

Comparative cellular composition of the brain of the tree shrew and six primate species

Species	Body mass, g	Brain mass, g	Total neurons, ×106	Total nonneurons, ×106
Tree shrew	172.5 ± 3.5	2.752 ± 0.011	261.40	199.65
Marmoset	361.0 ± 1.4	7.780 ± 0.654	635.80 ± 115.73	590.74 ± 70.81
Galago	946.7 ± 102.6	10.150 ± 0.060	936.00 ± 115.36	666.59 ± 63.50
Owl monkey	925.0 ± 35.4	15.730	1,468.41	1,195.13
Squirrel monkey	n.a.	30.216	3,246.43	2,075.03
Capuchin monkey	3,340.0	52.208	3,690.52	3,297.74
Macaque monkey	3,900.0	87.346	6,376.16	7,162.90
Variation, macaque/marmoset	10.8×	11.2×	10.0×	12.1×

Species ordered by increasing brain size. Values are mean ± SD. n.a., not available.

We find that M_BR in these primate species and the tree shrew is linearly proportional to 0.02 × M_BO (r² = 0.940) and also relates to M_BO according to the power function M_BR = 0.014 × M_BO^1.022 (P < 0.0001), which approaches linearity. Exclusion of the tree shrew from the calculation does not influence linearity (r² = 0.931; power exponent 1.017, P = 0.0097). Accordingly, the percentage of M_BR relative to M_BO varies between 1.14% in Otolemur and 2.25% in Callithrix, and this variation does not correlate with M_BO or M_BR (Spearman correlation coefficients ρ = 0.086 and 0.257, P = 0.8480 and P = 0.5653, respectively). These data indicate that, in contrast with previous observations in rodents (6) and other mammalian orders (15), brain size increases isometrically with body size across these primate species.

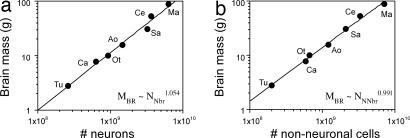
Total M_BR increases linearly as a function of the total N_N in the brains of these species (r² = 0.970) or as a power function of N_N with an exponent that does not differ significantly from unity [M_BR ∼ N_N^1.054; 95% confidence interval (C.I.), 0.910-1.197; Fig. 1a]. Total M_BR can also be expressed as a linear function of the total N_NN (r² = 0.981) or as a power function of N_NN with an exponent that also approaches unity (M_BR ∼ N_NN ^0.991; 95% C.I., 0.903-1.078; Fig. 1b). Strikingly, M_BR is also found to vary as a power function of N_N with an exponent of 1.0 (M_BO ∼ N_N^1.002, P = 0.0077) or as a linear function of N_N (r² = 0.915, P = 0.0109).

Fig. 1.

M_BR of different primate species and the tree shrew increases as a linear function of total number of neuronal (a) and nonneuronal cells (b). Each point represents the average for the species. (a) Variations in M_BR as a function of the number of neurons in the brain (N_Nbr) are equally well described by the linear equation M_BR = −3.127 + 1.372 × 10⁻⁸ × N_Nbr (r² = 0.970, P < 0.0001) and by the power function M_BR = 3.7 × 10⁻⁹ × N_Nbr^1.054 (shown in graph; P < 0.0001). (b) Variations in M_BR as a function of the number of nonneuronal cells in the brain (N_NNbr) are equally well described by the linear equation M_BR = 2.519 + 1.241 × 10⁻⁸ × N_NNbr (r² = 0.981, P < 0.0001) and by the power function M_BR = 1.688 × 10⁻⁸ × N_Nbr^0.991 (shown in graph; P < 0.0001). Tu, Tupaia glis; Ca, Callithrix jacchus; Ot, Otolemur garnettii; Ao, Aotus trivirgatus; Sa, Saimiri sciureus; Ce, Cebus apella; Ma, Macaca fascicularis.

Fractional Distribution of M_BR and Neurons.

As described in the literature (4), the mass of the cerebellum (M_CB) increases across the six primate species examined as a power function of cerebral cortex mass (M_CX), according to the equation M_CB = 0.229 × M_CX^0.849, whereas the mass of the remaining structures (M_RE) (M_BR − M_CB and M_CX) increases according to the equation M_RE = 0.638 × M_CX^0.656. The allometric exponents indicate that the M_CB and M_RE increase more slowly than the M_CX. Our data show that the N_N in these structures (N_Ncx, number of neurons in the cerebral cortex; N_Ncb, number of neurons in the cerebellum; N_Nre, number of neurons in the remaining areas) is also related by power functions, according to the equations N_Ncb = 21.118 × N_Ncx^0.887 and N_Nre = 2,908.62 × N_Ncx^0.483, indicating that the cerebellum and the remaining structures also gain neurons more slowly than the cerebral cortex.

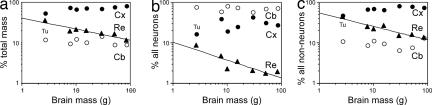
The cerebral cortex is the largest brain structure in the primates examined, comprising between 66.8% of total M_BR in Otolemur and 79.9% in Macaca [supporting information (SI) Table 2]. This cortical percentage of M_BR, however, fails to increase significantly with brain size in the primate species examined (Spearman correlation coefficient ρ = 0.600, P = 0.1797; Fig. 2a). Inclusion of the tree shrew (relative cortical size, 52.9%) improves the correlation coefficient between the percentage of the M_CX and total M_BR, but it still does not reach significance (ρ = 0.750, P = 0.0662). The percentage of M_CB varies little, as described in the literature (16, 17) (between 8.8% in Cebus and Macaca and 14.2% in Saimiri), whereas the percentage of the M_RE (brainstem, thalamus, and basal ganglia) decreases from 21.0% in Callithrix to 11.2% in Macaca as a power function of brain size regardless of whether the tree shrew is included in the correlation (P = 0.0020) or not (P = 0.0181; Fig. 2a).

Fig. 2.

Percentages of mass (a), number of neurons (b), and number of nonneuronal cells (c) contained in the cerebral cortex (filled circles), cerebellum (open circles), and remaining structures (filled triangles) relative to the whole brain in each species, plotted against M_BR. Values for Tupaia (Tu) are indicated. The power functions relating M_BR and the percentages of mass, neurons, and nonneuronal cells in the remaining areas in primates are shown in the respective graphs; all other comparisons were not significant (P > 0.05).

Although ≈70% of the M_BR is contained in the cerebral cortex, this structure only contains between 18.9% and 41.8% of all brain neurons (in Galago and Saimiri, respectively). The percentage of brain neurons located in the cerebral cortex does not significantly correlate with brain size regardless of whether the tree shrew is included in the analysis (P = 0.2938) or not (P = 0.8480; Fig. 2b). The cerebellum, in contrast, has the most of all brain neurons (from 56.2% in Saimiri to 79.0% in Galago) despite containing only ≈10% of the M_BR. As in the cortex, variations in the percentage of brain neurons located in the cerebellum do not correlate with brain size regardless of whether the tree shrew is included in the analysis (P = 0.3817) or not (P = 0.8480; Fig. 2b). In contrast, the percentage of brain neurons located in the remaining brain structures, which varies from 4.6% in Callithrix to 1.7% in Cebus, decreases significantly as a power function of brain size when the tree shrew is included in the analysis (P = 0.0086), although exclusion of the tree shrew yields a significant correlation (P = 0.0476) that fails to reach significance for a power law (P = 0.0756).

The percentage of all the nonneuronal cells in the cerebral cortex varies little among primates, between 64.3% in Aotus and 79.0% in Saimiri, is not significantly correlated with brain size regardless of whether the tree shrew is included in the analysis (P = 0.0662) or not (P = 0.1797; Fig. 2c). The cerebellum contains between 6.4% (in Saimiri) and 13.0% (in Macaca) of all nonneuronal cells in the brain, but this variation also does not correlate with brain size regardless of whether the tree shrew is included in the analysis (P = 0.9303) or not (P = 0.8480; Fig. 2c). In contrast, the percentage of all the nonneuronal cells in the remaining structures, which varies from 24.8% in Callithrix to 13.5% in Macaca, decreases significantly as a power function of brain size both when the tree shrew is included in the analysis (P = 0.0017) and when it is excluded from it (P = 0.0191).

Variations in the percentage of the M_CX are not significantly correlated with changes in the percentage of all neurons in the brain that are contained in the structure (P = 0.2207) or with variations in its percentage of all nonneuronal cells in the brain (P = 0.2938). Variations in the percentage of the M_CB are also not related to changes in the percentage of all brain neurons (P = 0.7930) or nonneuronal cells (P = 0.7930) in the structure. In contrast, the percentage of the M_RE decreases as a function of their decreasing percentage of all brain neurons and nonneuronal cells only when the tree shrew is included (P = 0.0442 and P = 0.0358, respectively; without the tree shrew, P = 0.1102 and P = 0.0845).

Structure Size Is a Linear Function of the Number of Neuronal and Nonneuronal Cells.

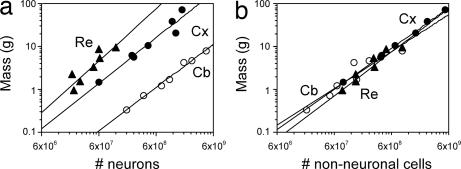
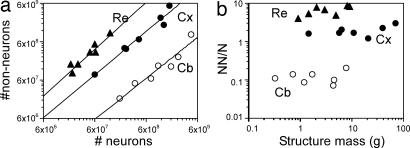
We find that the mass of the different brain structures (cerebral cortex, cerebellum, and remaining areas) varies among primate species as a function of total N_N and N_NN (Spearman correlation, ρ > 0.800 and P < 0.05 for all comparisons). The relationships between structure mass and N_N can be described by power functions of exponents close to unity for cerebral cortex (1.077), cerebellum (0.990), and remaining areas (1.040; Fig. 3a) and also by linear functions (all P < 0.01; data not shown). The power exponents relating structure mass to N_NN are slightly smaller, but also close to 1.000 for all structures (cerebral cortex, 0.963; cerebellum, 0.779; remaining areas, 0.950), approaching linearity, and this value is included in the 95% confidence range (Fig. 3b).

Fig. 3.

Cellular scaling rules for primate brains. (a) Structure mass as a function of the N_N in the structure. (b) Structure mass as a function of the N_NN in the structure. Each point represents the average values for one species. Plots are fitted with power functions with exponents described in the text (all P values <0.01). Filled circles, cerebral cortex (Cx); open circles, cerebellum (Cb); filled triangles, remaining structures (Re).

Cell Densities.

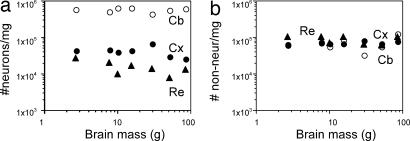
As expected from the linear relationship between the mass of brain structures and their number of neurons, neuronal density does not vary significantly with brain size across the six primate species analyzed included in this study (Fig. 4a). No significant correlation between nonneuronal density and M_BR is found either (Fig. 4b). Inclusion of the tree shrew in the analysis did not change the lack of any significant correlation between cell density in each structure and M_BR (data not shown). Neuronal and nonneuronal densities in each structure are also not significantly related to the mass of the individual structures (data not shown).

Fig. 4.

Variation in neuronal (a) and nonneuronal (b) cell density in cerebral cortex, cerebellum, and remaining areas plotted against M_BR. No correlation reaches significance (all P values >0.05). Filled circles, cerebral cortex (Cx); open circles, cerebellum (Cb); filled triangles, remaining structures (Re).

The cerebellum is distinct from the cerebral cortex and remaining brain areas in that it has larger neuronal densities than the other structures (Fig. 4a), but nonneuronal densities are comparable in the cerebellum, cerebral cortex, and remaining structures (Fig. 4b). These findings suggest that the addition of nonneuronal cells follows the same principle and contributes equally in all structures and species toward final structure size.

Linear Relationship Between N_N and N_NN.

In the cerebral cortex, cerebellum, and remaining areas, the N_NN varies as power functions of the N_N in each structure that approaches linearity (Fig. 5a), with exponents of 1.119, 1.064, and 1.217, respectively. All relations can also be fitted with linear equations (r² > 0.8, P < 0.01). The percentage of total cells in the cerebral cortex that are neurons varied between 24.5% in Macaca and 45.5% in Saimiri. The percentage of total cells in the cerebellum that are neurons varied between 83.0% in Macaca and 93.2% in Saimiri, and in the remaining structures the percentage varied between 10.9% in Cebus and 20.5% in Tupaia. These variations are not significantly correlated with structure mass. As a result, the ratio of nonneuronal/neuronal cells in each structure does not change significantly with structure mass (Fig. 5b) or N_N.

Fig. 5.

The N_NN varies linearly with the N_N in each structure. (a) N_NN in the cerebral cortex, cerebellum, and remaining areas plotted as a function of the total number of neurons in these structures. Power functions of exponents 1.119, 1.064, and 1.217 are plotted, but graphs are equally well fitted with linear functions. (b) Ratio of nonneuronal/neuronal cells in each structure plotted against structure mass. No significant correlation is found across primate species. Filled circles, cerebral cortex (Cx; P = 0.2774); open circles, cerebellum (Cb; P = 0.5653); filled triangles, remaining structures (Re; P = 0.2248).

Relative Contribution of Neuronal and Nonneuronal Cells to M_BR.

The constant neuronal and nonneuronal cell densities across species, the linear relationship between N_N and N_NN, and the increases in M_BR, N_N, and N_NN by similar factors across species indicate that neither the neuronal nor the nonneuronal average cell size increases significantly with brain size in primates.

If the mass of any given cell is considered to include all cellular processes and the surrounding extracellular space, then the mass of any brain division or the whole brain can be expressed as the sum of its total neuronal mass [the product of its N_N and the average mass of neuronal cells (M_N)] and its total nonneuronal mass [the product of its N_NN and the average mass of nonneuronal cells (M_NN)] according to the equation M_BR = (N_N × M_N) + (N_NN × M_NN). Because we observe that N_N and N_NN are related linearly in such a way that the N_NN/N_N ratio for each structure is constant across species (or N_NN = a × N_N) and because M_N and M_NN also appear to be constant among species, the ratio of total neuronal (N_N × M_N)/total nonneuronal (N_NN × M_NN) mass for each structure, and for the whole brain, is calculated to equal (N_N × M_N)/(a × N_N × M_NN), which is equivalent to the constant M_N/(a × M_NN). Thus, given the prior assumptions, the calculated ratio of total neuronal/total nonneuronal mass for each structure, and for the whole brain, remains constant across species regardless of brain size. This finding implies that increases in the size of primate brain structures are mainly due to an increased number of cells in those structures accompanied by an equivalent increase in the number of nonneuronal cells, such that the ratio of neurons/nonneurons remains constant.

Discussion

Our results indicate that the cellular scaling rules for primate brains differ from those for rodents. The main difference is that primate brains do not hyperscale as they gain neurons, as do rodent brains. Primate brains increase in size as a linear function of their numbers of neuronal cells, indicating that the average neuronal cell size remains constant, whereas rodent brains increase in size faster than they gain neurons, with increasing average neuronal cell size. As a consequence, neuronal densities remain stable in the primate brain, whereas they decrease in larger rodent brains and are higher in all primate brain structures than in rodent brains of equivalent size. Finally, in primate brains, the ratio of nonneuronal/neuronal cells does not correlate with M_BR as it does in rodents. Because the inclusion of tree shrews in the sample did not generally alter the conclusions of the study, tree shrews, as close relatives of primates, appear to largely conform to primate scaling rules.

Features of scaling that remain constant across these taxa are equally as important as the differences between primates and rodents. Most notably, in primates and rodents, the ratio of total neuronal/nonneuronal mass is held constant in the brain. Further, despite differences in neuronal density, nonneuronal cell densities are similar across all brain structures in both primates and rodents. In the following discussion, we consider the differences and similarities in cellular scaling rules in primates and other mammals, and we propose theories regarding the evolution of selection pressures that led to these phylogenetic differences. Finally, we discuss how these differences relate to processing capacity and the evolution of higher cognitive function in primate and nonprimate mammals.

Neuronal Cell Size and Neuronal Densities.

We find that the main difference in the cellular scaling rules for building rodent (6) and primate brains is that, in the latter, increased numbers of neurons are not accompanied by decreased neuronal densities, indicating that the average neuronal cell size remains stable across primate species. This finding is in line with a recent study of the sizes of the dendritic trees of pyramidal neurons of selected areas of cortex that found little variation across the same species considered here (18). Our findings, of course, do not rule out the possibility that cell size is more variable in larger brains, with larger pyramidal cells, for example, being compensated by smaller granular (stellate) cells.

The constant neuronal density in each brain structure across primate species is in contrast with the decreasing neuronal densities found in larger brains within the order Insectivora (1), within the order Rodentia (6), and across other mammalian orders (3, 7), but it is consistent with the results from one large comparative study (3) if only their primate data are considered. Primate brains have higher neuronal densities than rodent brains of equivalent size (6) (e.g., ≈40,000 neurons per mg in the cortex of Aotus, against 12,000 neurons per mg in the agouti), while maintaining similar nonneuronal cell densities, which indicates that the average neuronal size is smaller in primates than in rodents. Consequently, primate brains contain more neurons than rodent brains of equivalent size. The brain of the capuchin monkey, for instance, weighing 52 g, contains >3× more neurons in the cerebral cortex and ≈2× more neurons in the cerebellum than the larger brain of the capybara, weighing 76 g. The larger number of neurons per unit volume presumably endows primates with a larger computational capacity than rodent brains of equivalent size.

Primate Brains Scale Isometrically with Number of Neurons.

An important consequence of the unchanging neuronal cell size and density is that primate brains increase in size linearly as they gain neurons, instead of hyperscaling as do rodent brains, which increase rapidly in mass as a function of the N_N to the power of 1.587 (6). This result suggests that there has been a selective pressure against increases in average neuronal size with brain size, lest the brain becomes too large as it gains neurons (19). This type of increase allowed primate brains to accumulate large numbers of neurons without becoming prohibitively large. A macaque brain of 6.4 billion neurons built with the cellular scaling rules that apply to rodents would, for example, weigh 575 g, instead of its actual 87 g. These findings suggest that the divergence of primate evolution away from the common ancestor with rodents involved mechanisms that favored the concentration of larger numbers of neurons per unit volume of brain tissue. This discovery of course implies that the microcircuitry differs in primate and rodent brains.

Implications for Volume Comparisons Across Orders.

Volume and surface measurements of the cerebral cortex and cerebellum have been widely used in the literature as indicators of the computational capacity of these structures (16, 20, 21), with the tacit assumption that they vary directly according to the number of neurons in these modular structures (22, 23) (e.g., as more columns of the same total number of neurons are added) (24). Although absolute structure size is a function of its N_N, our failure to find a significant correlation between relative cortical mass and relative N_N questions the validity of previous conclusions based on relative mass (16). Moreover, our finding that primates have a much larger N_N than rodents within structures of the same size shows that brain volume cannot be used indiscriminately as a proxy for N_N or computational capacity across animal orders. As long as neurons are considered to be the functional integrative units of nervous tissue, inferences of computational power of brain structures should take their number into account. Consequently, cognitive and ecological significance of species differences in brain size across orders should be reevaluated by examining directly the numbers of neuronal and nonneuronal cells, and not only the volume or surface area of the brain.

Glia/Neuron Index.

Another difference found between the cellular scaling rules that apply to primates and rodents is that, in the primates we examined, the ratio of nonneuronal/neuronal cells, and thus presumably the glia/neuron index, does not correlate with M_BR. This result is in contrast with the view widely held in the literature that, as a whole, the glia/neuron index increases along with M_BR (1, 25). This view is based on comparisons of the index in the cerebral cortex across a few species of many different mammalian orders (3, 10–13) and has been confirmed in insectivores (1) and rodents (6), but so far has not been examined systematically in primates. In this regard, and in line with our observations, it is interesting that the documented glia/neuron ratio in the human cerebral cortex (10) is similar to the values found in the smaller primate species examined here. Although one recent study found that the glia/neuron ratio does increase with increasing brain weight in anthropoid primates (26), their analysis identified neurons in Nissl-stained brain sections, in which small neurons are difficult to distinguish from glia (27). In addition, the measures were restricted to two layers (II and III) of a particular cortical area (9L), rather than the whole cerebral cortex.

Our finding that the primate brain increases in size without any increasing numerical predominance of glial cells challenges the notion that an increased glia/neuron ratio would be necessary to cater to presumably larger metabolic needs associated with increasing brain size (13, 26), a view that has been disputed recently by the observation that the neuronal need for metabolic support is similar across species (25). Rather, the glia/neuron ratio may be regulated by mass factors in development, as discussed in the paragraph below.

Similarities Across Mammalian Orders.

In primates as well as rodents (6), the ratio of total neuronal/nonneuronal mass in the brain is kept constant across species. Given that N_N and N_NN in the primate brains are linearly related to each other and their average cell size does not seem to covary with M_BR, any increase in total neuronal mass is consequently matched by an equal increase in total nonneuronal mass. We have suggested previously (6) that this matching could be achieved in development if the increased neuronal proliferation that has been proposed to drive cortical growth across species (28, 29) is accompanied by a density-dependent glial precursor proliferation. This suggestion was based on the observations that gliogenesis only begins postnatally (30), once neurogenesis is over, and that glial precursor proliferation is density-dependent and ceases once a steady-state glial density has been achieved, most likely by cell–cell contact inhibition (31). Remarkably, we found that, although neuronal density is greater in primates than in rodents (6), nonneuronal cell densities are similar in all brain structures and across all rodent and primate species examined so far. This finding is consistent with the observation that, in both orders, nonneuronal cell size changes very little, if at all, with increasing brain size. This finding is also consistent with our suggestion that the N_NN in any brain tissue, and in any mammalian species, is regulated by the N_N by means of continued gliogenesis until confluency is reached in a formerly purely neuronal tissue (6). Thus, the glia/neuron ratio results from the mechanisms that maintain a constant neuronal/nonneuronal total ratio of mass. When brain size increases together with increased average neuronal size, as in rodents, the glia/neuron ratio increases (6). When brain size increases in the absence of significant changes in average neuronal size, the glia/neuron ratio remains constant, as in the primates examined here. The proposed developmental regulation of the neuronal/nonneuronal total mass ratio explains why the glia/neuron ratio varies with brain size in some but not all mammalian orders.

Implications for Humans.

The present data and those from rodents support the unexpected conclusion that larger brains do not have larger relative numbers of neurons in the cerebral cortex. In the primate species analyzed here, both the cerebral cortex and the cerebellum represent fractions of M_BR that do not covary significantly with increasing brain size. The same result is obtained for data found in the literature (4) for the species studied here. However, relative cortical size is seen to increase significantly with increasing brain size when larger species, such as great apes and humans, are considered (4). Once these primates are added to the comparison, it will be interesting to resolve whether the cellular scaling rules determined here apply to apes and humans. However, according to these rules, a primate brain containing 100 billion neurons (a number approximating the neurons in a human brain) would be expected to weigh ≈1,450 g and belong to a body of 72.7 kg, values that match the average mass of the human brain and body. The present study thus raises the intriguing possibility that humans and their brains are, after all, isometrically scaled-up versions of a common primate plan.

Methods

Animals.

Galagos (Otolemur garnettii, n = 3), marmosets (Callithrix jacchus, n = 3), owl monkeys (Aotus trivirgatus, n = 2), squirrel monkeys (Saimiri sciureus, n = 2), rhesus monkeys (Macaca mulatta, n = 2), and tree shrews (Tupaia glis, n = 2) were obtained from colonies in the Department of Psychology at Vanderbilt University and were young adults by the time of the experiments. One adult capuchin monkey (Cebus apella) was obtained from the colony at the Biophysics Institute at the Federal University of Rio de Janeiro.

Dissection.

All animals were killed by lethal injection of sodium pentobarbital, weighed and perfused transcardially with 0.9% PBS, followed by 4% phosphate-buffered paraformaldehyde. Brains were removed from the skull, weighed, and postfixed for 2 weeks to 18 months by immersion in 4% phosphate-buffered paraformaldehyde. The cerebellum was dissected by cutting the cerebellar peduncles at the surface of the brainstem. Cerebral cortex in all animals was defined as all cortical regions lateral to the olfactory tract, including hippocampus and piriform cortex, and was dissected from each hemisphere by peeling it away from striatum and other subcortical structures under a stereomicroscope. The olfactory bulb was not included in any brain. All other brain structures were pooled and processed together as “remaining areas.” These structures were not available for one galago, one owl monkey, one squirrel monkey, and one tree shrew. For all animals, only one of the two hemispheres was processed, and results were multiplied by 2 to estimate numbers for the whole brain.

Isotropic Fractionator.

Total numbers of cells, neurons, and nonneuronal cells were estimated as described previously by using the isotropic fractionator method (14). Briefly, each dissected brain division was turned into an isotropic suspension of isolated nuclei of known, defined volume and was kept homogeneous by agitation. The total number of nuclei in suspension, and therefore the total number of cells in the original tissue, was estimated by determining the density of nuclei in small aliquots stained with the fluorescent DNA marker DAPI under the microscope. Once the total cell number was known, the proportion of neurons was determined by immunocytochemical detection of neuronal nuclear antigen expressed in all nuclei of most neuronal cell types and not in nonneuronal cells (32). Estimates of the proportion of neuronal nuclear antigen-positive nuclei were considered reliable because the coefficient of variation among animals of the same species was typically <0.15 (see SI Table 2). The N_NN was derived by subtraction.

Data Analysis.

All statistical analyses and regressions were performed in Statview (SAS Institute, Cary, NC), with the average values obtained from the individuals of each species. Correlations between variables were calculated by using the Spearman correlation coefficient. If a significance criterion of P < 0.05 was reached, regressions of the data to linear and power functions were calculated.

Abbreviations

M_BR

brain mass

M_BO

body mass

M_CX

mass of cerebral cortex

M_CB

mass of the cerebellum

M_RE

mass of remaining structures

M_N

average mass of neuronal cells

M_NN

average mass of nonneuronal cells

N_N

number of neurons

N_NN

number of nonneuronal cells

N_Ncx

number of neurons in the cerebral cortex

N_Ncb

number of neurons in the cerebellum

N_Nre

number of neurons in the remaining areas.