Impact of spatiotemporally correlated images on the structure of memory

Abstract

How does experience modify what we store in long-term memory? Is it an effect of unattended experience or does it require supervision? What role is played by temporal correlations in the input stream? We present a plastic recurrent network in which memory of faces is initially embedded and then, in the absence of supervision, the presentation of temporally correlated faces drastically changes long-term memory. We model and interpret the results of recent experiments and provide predictions for future testing. The stimuli are frames of a morphing film, interpolating between two memorized faces: If the temporal order of presentation of the frame stimuli is random, then the structure of memory is basically unaffected by synaptic plasticity (memory preservation). If the temporal order is sequential, then all image frames are classified as the same memory (memory collapse). The empirical findings are reproduced in the simulated dynamics of the network, in which the evolution of neural activity is conditioned by the associated synaptic plasticity (learning). The results are captured by theoretical analysis, which leads to predictions concerning the critical parameters of the stimuli; a third phase is identified in which memory is erased (forgetting).

We study the effect of the unsupervised experience of a set of spatiotemporally correlated stimuli on memory structure. In particular, how well can classification memory fare in the presence of spatiotemporal correlations in a sequence of successive stimuli? How does classification memory depend on the presentation protocol? Temporal correlations affect significantly the structure of working memory and its neurophysiological correlate, i.e., delay activity (1–3). Temporal order of presentation of stimuli during training is reflected in correlations of their corresponding delay activity, as observed in anterior inferotemporal cortex (1). In the pair-associate task, temporal correlations and prospective delay activity are induced by presenting fixed pairs of stimuli in a given order (2, 3). Temporal associations between neural representations of memorized stimuli can be induced by Hebbian plasticity mediated by selective delay activity (4–7). Such delay activity carries the neural representations of stimuli across the delay interval separating successive stimulations. Patterns of activity of two successive stimuli can then overlap, and unsupervised Hebbian plasticity renders the two neural representations correlated. Motivated by psychophysical experiments, we propose another mechanism for the evolution of temporal associations between memorized stimuli on the basis of the spatiotemporal interpolation between them.

It has been found that the order of presentation of a sequence of spatially correlated visual images interpolating (morphing) between two human faces has a notable effect on classification performance (8, 9). In ref. 8, human subjects were trained with a set of morphing sequences with no supervision. In each sequence, one face was simultaneously rotated and morphed between two characters. Subjects were then asked to recognize whether a pair of faces, presented from different angles, belonged to the same person. It turns out that subjects confused the faces within the pairs of the morphing sequences. However, if during training the frames of each sequence were presented in random order (mixed), then subjects discriminated successfully.

In ref. 9, human subjects were trained to classify faces into two classes: F (friends) and NF (nonfriends). In each trial, one face was presented and, in the delay interval, was classified as F or NF. Feedback was provided to reinforce the correct classification. Upon reaching good performance, a morphing sequence was generated from one F to one NF, interpolating between the two familiar faces. Next, the images of the morphing sequence were presented for F–NF classification, interspersed with familiar faces. Two protocols were implemented: mixed, in which successive frames were selected at random, and sequential, in which frames followed the order of the morphing sequence. The statistics of F–NF classifications were monitored from session to session.

Subjects initially divided the morphing sequence equally: Frames of the first half were classified F, and those of the second half were classified NF. The separation threshold was near the middle of the sequence. As sessions proceeded, subjects exposed to the mixed protocol maintained the initial threshold for classification: Memory was preserved. In contrast, with the sequential protocol, the separation threshold moved toward NF: An increasing fraction of frames was classified F. Finally, all morphed frames were classified F: Memory collapsed. Hence, the unsupervised experience of spatially correlated stimuli affected strongly the memorized classification structure, depending on the temporal correlations of the presented stimuli.

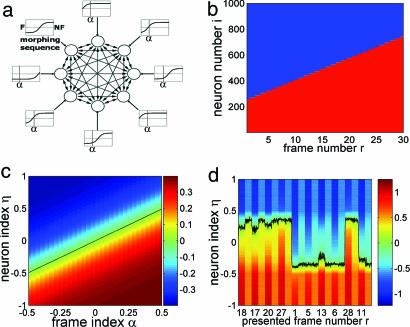
We present a simple realization of a plastic recurrent network, in which neural response interacts with synaptic plasticity, probing the interplay between memory and (unsupervised) learning. Input stimuli are represented by a distribution of external afferent currents to the neurons of the network. The current received by a given cell depends on the cell and on the presented frame. Hence, each cell has a “tuning curve.” Fig. 1a is a schematic illustration of the recurrent network (fully connected), neurons (circles), synaptic connections (arrows), and external input currents (rectangles “tuning curves”) (see Stimuli, Protocol, and Behavioral Interpretation).

Fig. 1.

The network, stimuli, and dynamics. (a) Scheme of the network. Circles, eight neurons (N = 1,000 neurons in simulations); two-headed arrows, recurrent synaptic connections connecting two neurons of the network; one-headed arrows, external connection (input stimulus); rectangles, tuning curves (sigmoidal) of the neurons along the morphing sequence, i.e., external current vs. frame stimulus index; vertical bar in each rectangle, index α of a sample frame stimulus. (b) The state of each neuron [+1, (red) or −1 (blue)] vs. frame number r along the morphing sequence. r = 1, network state F, has the highest number of neurons in −1 state (blue); r = 30: NF, has highest number of +1's (red). Neurons (features) are switched monotonically, proceeding from F to NF. (c) External current (color-coded) to all neurons vs. frame index α. Neurons are ordered vertically by increasing values of the neuron index η. The black line corresponds to zero current. (d) Sample network dynamics. The first 10 trials of a simulation (mixed protocol, c = 0.4, T = 0.5) are presented as the total current received by each neuron vs. time. For each presented frame r, the first column is the stimulation interval, and the second column is the corresponding delay interval. Values of the current are color-coded. The Black curve is at zero current (η = η*). Neurons above this curve are −1, and neurons below are +1. Two (delay) attractor states (η* = ±0.35) can be observed.

The results were observed in autonomous simulations, implementing the protocols of ref. 9 by using dynamical equations (see Neural Dynamics) driven by external stimuli with no external intervention. The model accounts for the findings and provides insights into the mechanism, and theoretical analysis captures the results of the simulations and predicts the role of different parameters.

Neural Dynamics.

A neuron i (i = 1, …, N) is modeled by a binary variable, S_i = ±1. The collection of all N neural states is a network “state” or “configuration.” The state of cell i at time t + 1 is +1 or −1, depending on whether the total afferent current at time t is higher or lower than the neural threshold (taken at 0) (10, 11), i.e.,

The current (square brackets) is the sum of the recurrent afferent h_i^rec (received from all other network cells); the external current h_i^ext, depending on the frame of the morphing sequence presented at time t (indexed α); and a Gaussian noise Γ_i (mean, 0; SD, σ = 0.05).

The recurrent part is as follows:

a sum over the activities of all N neurons of the network (j = 1, …, N), modulated by the synaptic weights J_ij (from j to i). In the simulations, N = 10³ neurons and ≈10⁶ synapses. At t = 0, the states of the neurons are initialized once at random (S_i = ±1 with equal probability) and are updated by Eq. 1 at each time step. Synaptic dynamics is described below in Synaptic Plasticity and Embedded Memory.

Stimuli, Protocol, and Behavioral Interpretation.

To model the set of morphed frames, we interpret each of the two extreme images, F and NF, as a collection of features; some are shared, and in others they differ. Morphing starts from F, taking off some features and adding others in a monotone, one-way process until NF. In the model with two-state neurons, a +1 neuron implies that a given feature is on; a −1 neuron implies that a another feature is on. When a neuron changes state (−1 → +1), one feature is taken off and another replaces it. In the model network, the state F has a certain number of neurons in the +1 state, and the rest are −1. Along the morphing sequence, from F to NF, neurons switch states always in the same direction, viz (−1 → +1). There are more −1's in the F state and more +1's in the NF state.

Because the morphing process is monotonic, we represent each network state in the sequence by a linear ordering of the neurons from −1 to +1 (Fig. 1b). Neurons are listed on the vertical axis (i = 1, …, 1,000); −1 and +1 neural states are depicted in blue and red, respectively. States corresponding to successive frames in the sequence (r = 1, …, 30) are in successive columns. The monotonically increasing height of the red part of the column, moving from left (r = 1 corresponds to F) to right (r = 30 corresponds to NF), are neurons that have switched state (feature) in the morphing process. Neurons maintaining their “color” along the sequence represent features that are common to F and NF. This representation does not imply a linear spatial structure of the network.

The transition of neurons from −1 to +1 is modeled by defining the external current afferent to neuron i upon presentation of a given frame stimulus r. We labeled neurons and frame stimuli by normalized indices, η instead of r and α instead of i. The n (= 30) interpolating frames of the morphing sequence labeled by (r = 1, …, n), are labeled by α = (r − 1)/(n − 1) − 0.5; with F by α = −0.5; and with NF by α = +0.5. With this notation, the first half of the morphing sequence has α < 0, and the second half has α > 0. Each neuron in the network (i = 1, …, N) is assigned a “neuron index,” η = 2(i − 1)/(N − 1) − 1 (−1 ≤ η ≤ 1). In F, 75% of the cells are −1 and 25% are +1; the opposite holds true for NF (Fig. 1 b and c).

We write the external current as the following:

This is an analog of the saturating, sigmoidal tuning curves for ocular disparity (12, 13). In Fig. 1c, each frame (labeled by α) is described by the variation, from neuron to neuron (labeled by η), of the external current (color-coded), starting from bright red up to deep blue. Each horizontal line is the “tuning curve” of a given neuron as the frame varies. Here, the black diagonal (α = η) in Fig. 1c is the index of the frame stimulus at which the external current to neuron η switches sign. In the absence of recurrents, S = sign(h^ext), and the corresponding neural state flips (Fig. 1b). Neurons about to flip in the next morphing step receive small currents, so that a small shift in α results in a sign change of the current. T is the width of the transition region, and c is the saturation amplitude.

In each simulation session, a sequence of values α is prepared according to one of the protocols: mixed, in which the values of α are picked in a random sequence, or sequential, in which the values of α follow the order of the morphing sequence. There are no repetitions in a single session. For each α, the corresponding external current h^ext(α) is injected (Eq. 3) for the duration of the stimulus presentation (50 steps of the network dynamics), followed by a delay interval (50 steps) in which there is no external current. A single session consists of 3,000 steps (50 + 50 steps × 30 stimuli), and a total of 10 successive sessions (30,000 steps) are simulated for each set of parameters (c, T), for each protocol.

Behavioral response takes place during delay periods after the offset of each stimulus. Correspondingly, in the model, classification is identified by the state reached by the network in the delay interval. If there is a majority of blue (−1) neurons, the response is F; if there are more red (+1) neurons, then the response is NF (Fig. 1b). If the difference in the numbers of the two types of neurons in the delay state is clear and stable, then so is the behavioral response. The delay state of the network is classified by an index η_d*, which is the index of the neuron that receives current closest to zero in that state and separates the +1's from the −1's. Hence, the delay state is classified by the index of the frame (α = η_d*) that would have produced the same bare stimulus state. If η_d* < 0, i.e., the blue majority in the delay state (nearer F), then there is an F response. If η_d* > 0, the red majority (nearer NF), then there is an NF response.

Synaptic Plasticity and Embedded Memory.

Plasticity is defined by a stochastic Hebbian dynamics of the synaptic efficacies J_ij (14–16). Each can assume one of two values: +J or −J (we set J = 1, i.e., external current and noise are in units of J). At each time step, after the states of all neurons are updated (Eq. 1), each synaptic efficacy evolves as follows: A synapse J_ij connecting two cells in the same activity state (S_i = S_j), becomes +J with probability p if it was −J, and it remains +J if it was +J. A synapse J_ij connecting two cells that are in opposite states (S_i = −S_j) becomes −J with probability p if it was +J, and it remains −J if it was −J.

When the network is in a given state, specifying all S_i (i = 1, …, N), the synapses vary stochastically, rendering that state more stable (17). Plasticity is assumed slow: P = 0.8 × 10⁻⁴ per available synaptic update; <0.4% of the synapses can change per stimulation interval. Synaptic dynamics takes place only during simulation: This emulates the physiological conditions for synaptic modifications, which relates plasticity to visual response, i.e., high- and low-spiking rates during presentation of stimuli.

In the experiment, the frames of the morphing sequence are presented after the memory of classes F and NF are well internalized (9). This is modeled by initializing the synaptic matrix to have two memories [see supporting information (SI) Text]. The network has two stable neural configurations (delay states) close to N and NF that can be read from a sample of the network dynamics in the first 10 trials of a simulation of the mixed protocol (Fig. 1d). The total afferent current to every neuron (color-coded) is presented vs. time. For each stimulation interval, the presented frame (r) is indicated along the time axis. The black curve indicates the neuron that receives a total current closest to threshold. This neuron separates +1 from −1 neurons in the network; its index η at time t is defined as η*(t) (= η_s* during stimulation and = η_d* during delay).

After a stimulus of the first half of the morphing sequence (r ≤ 15; α < 0), the network relaxes to a configuration close to the F state (majority −1's; η_d* < 0). A stimulus of the second half leads to a state near NF (majority +1's; η_d* > 0). The former case is interpreted as an F response, whereas the latter is interpreted as an NF response.

Note that the initial synaptic matrix represents the embedded classification memory of only two faces, one face from each of the two classes (used to generate the morphing sequence). Other F and NF faces are not considered (see Discussion).

Results

At each time step t (the entire network is updated^¶), the state of the network is recorded. A sample evolution is exhibited in Fig. 1d for the mixed protocol: The total afferent current to each neuron (labeled η) is plotted vs. time. As a preliminary result, to highlight the properties of the initial synaptic structure expressing the embedded memory of F and NF, we present the evolution of the network activity in the first 10 frame presentations (first session; see also Fig. 2a). The configuration of the network at each time step is characterized by the neuron at which the network flips from −1 (blue) to +1 (red), i.e., receiving threshold current. The black curve is the evolution of the index η*(t) of that neuron.

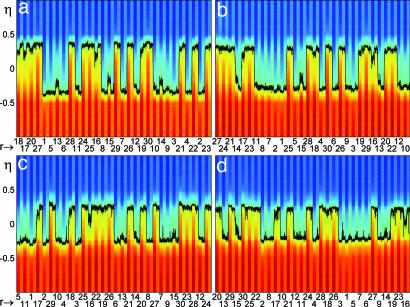
Fig. 2.

Network dynamics in the mixed protocol. Total current (color-coded) afferent to each neuron (labeled η) vs. time for 30 trials (one session). Each trial consists of stimulus + delay interval. Abscissa is the frame number (r) of each stimulus. The black curve is the label η* of the neuron receiving zero current. In each interval, stimulus or delay, η* fluctuates around a fixed value, respectively η_s* and η_d*. (a) Session 1. Two delay activity states are present at η_d* ≈ −0.35 (F response) and η_d* ≈ +0.35 (NF response). Visual responses vary from frame to frame. (b–d): Sessions 4 (η_d* ≈ ±0.29) (b), 7 (η_d* ≈ ±0.25) (c), and 10 (η_d* ≈ ±0.22). Stimuli from the first (second) half, i.e., r ≤ 15 (r > 15), result in F (NF) responses. (T = 0.5; c = 0.4).

Because the synapses evolve slowly over a single trial, each time a stimulus is presented or removed, the neural configuration converges rapidly to a stable state, corresponding either to a “visual”^‖ response or to a delay activity configuration. Within each interval, stimulus or delay, the instantaneous label η*(t) fluctuates around its time average for the corresponding interval, i.e., η_s* and η_d*, respectively. The visual response varies, depending on the presented frame r, but only two delay states are available, as can be observed by following the black curve in the figure. These two delay states correspond to the memory states.

For instance, the first frame presented (r = 18) leads to a visual response η_s* = +0.25 and to a delay activity η_d* = +0.35. For the fifth stimulus (r = 1; i.e., frame F), the visual response is η_s* = −0.375, and the delay activity is η_d* = −0.35. Each of the other stimuli leads to one of the two memory states, η_d* ≈ ±0.35, which correspond to the two behavioral choices, −0.35 to F and +0.35 to NF. The two memory states express the memory embedded in the synapses.

The first 10 input stimuli of the first session produce the following responses: 18 NF, 17 NF, 20 NF, 27 NF, 1 F, 5 F, 13 F, 6 F, 28 NF, and 11 F. Hence, stimuli of the first half of the morphing sequence (r ≤ 15) lead to delay states near F (with a blue majority) and consequently to an F response; stimuli of the second half (r > 15) lead to delay states near NF (red majority) and to an NF response. This behavior concords with behavior in the early stackes of the experiment.

Note that visual responses evoked by frames of the first half of the morphing sequence lead to negative values of η_s*, whereas frames of the second half lead to positive η_s* 's.

After the offset of a frame stimulus, the system relaxes to the memory state that is closer to the visual response: Stimuli from the first (second) half of the sequence are followed by delay states close to F (NF), resulting in a F (NF) response.

More specifically, the value of η_s* for any frame stimulus is in between the index α of the frame, i.e., the value of η_s* that would be obtained by the bare stimulus (no recurrents; see, e.g., Fig. 1 b and c), and the value of η_d* of the memory state (no external drive). This is a result of the tradeoff between the recurrent afferents modulated by the synaptic matrix of the memory states and the currents injected by the stimulus.

Mixed Protocol.

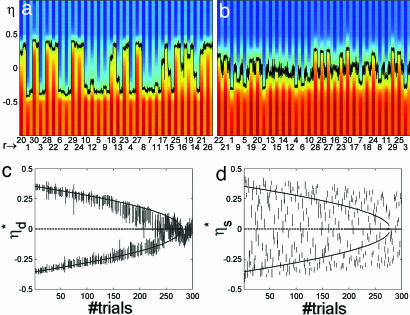
Fig. 2 presents the dynamics of the network along the full simulation for the mixed protocol. It displays the total current afferent to all neurons in 4 of the 10 sessions of the full protocol (sessions 1, 4, 7, and 10 in Fig. 2 a, b, c, and d, respectively). The current is color-coded, and is plotted for all neurons (labeled by η) vs. time (same format as in Fig. 1d). The indices of frames presented during stimulation intervals (r) are shown on the abscissa; each stimulus is followed by a delay interval. The black curve traces the instantaneous label η*(t) of the neuron receiving zero current, as in Fig. 1d. η* fluctuates within each interval, stimulus or delay, because of the built-in noise.

Along the simulation (10 sessions), the pattern of behavioral responses remains the same as in the first 10 trials (Fig. 1d): Stimuli from the first half of the sequence (r ≤ 15) determine an F response, and stimuli of the second half (r > 15) determine an NF response. This is in accordance with the experimental observations.

In a given session, the delay activity states after frame stimuli of the same half of the sequence are approximately independent of the frame. They vary from session to session as a consequence of synaptic plasticity: In session 1, the two delay states correspond to η_d* ≈ ±0.35; in session 4 they are at η_d* ≈ ±0.29; in session 7 η_d* ≈ ±0.25; and in the last session η_d* ≈ ±0.22. The two attractor states are gradually approaching each other along sessions, but theoretical analysis predicts that they remain distinctly separate as the number of sessions increases further. The prediction is that the difference between the two delay states (in terms of η_d*) converges asymptotically to a fixed value. This prediction is confirmed by the observation that, for both memory states, the variation of η_d* in successive sessions decreases.

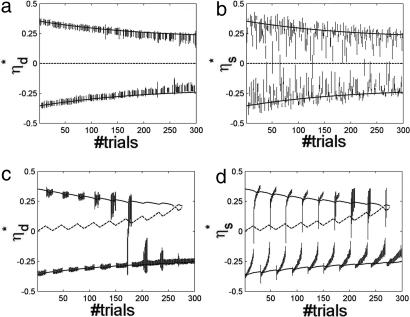
Fig. 3a presents the delay activity label η_d* (each with its respective SD) vs. trial number for all 300 trials of the 10 sessions. Curves are theoretical predictions at σ = 0 (solid lines for stable states; dashed line for the unstable state). The two lines characterizing the stable memory states are in good agreement with simulation results. The central line at 0 η_d* determines the unstable state, i.e., the watershed between the two memory states. As discussed above, the two memory states are seen to approach and remain separate.

Fig. 3.

Delay activity and visual response labels in 10 sessions (300 trials) of the simulations in each of the two protocols. (a) η_d*, label of delay activity states (average over fluctuations in the corresponding interval ± SD) vs. trial number in the mixed protocol. Curves, theoretical predictions; solid lines, labels of stable states; dashed line, label of unstable states. The two solid lines correspond to the two memory states, determining F and NF responses, in agreement with simulation results. The dashed line (η_d* = 0) represents the unstable state, the watershed between the two memory attractors. The two memory states are preserved. (b) η_s*, visual response label (average ± SD) vs. trial number in the mixed protocol. The format is the same as in a. Labels of visual response states cluster around the memory states. (c) Labels of delay activity states vs. trial number in the sequential protocol. The format is the same as in a. From session to session (30 trials each), the number of F responses increased, as is evidenced by the fact that the number of delay labels near the upper curve diminishes and that near the bottom curve they increase. Beyond trial 180, there are no NF responses. Next, the line of NF delay activity annihilates in a saddle node. (d) Labels of visual response states vs. trial number in the sequential protocol. Like memory states, visual responses tend to leave the NF line and move toward F until all stimuli evoke a state near F. (T = 0.5, c = 0.4).

Fig. 3b presents a scatter plot of the “visual” response label η_s* vs. the trial number, for the same 300 trials, accompanied by theoretical predictions of the delay activity labels η_d*, which are the same as in Fig. 3a. The labels group around the memory states, because beyond the effect of the afferent stimulus, they reflect in part the structure of memory (as observed above). In particular, the labels of most visual response states are in between the labels of the two memory states (see e.g., Fig. 3 b and d). Because synaptic plasticity tends to reinforce visual response states, the two memory states tend to converge toward each other.

The central result of this section is that the two classification memories are preserved along the 10 sessions, and synaptic plasticity does not change the initial macroscopic picture: The first half of the sequence remains associated with F responses and the second half with NF, in accordance with the experiment in ref. 9.

Sequential Protocol.

Fig. 4 presents the analog of Fig. 2 for the sequential protocol (same parameters). The total current afferent to every neuron vs. time is presented in four sessions (sessions 1, 4, 7, and 10 in Fig. 4 a, b, c, and d, respectively). The frame numbers (r) on the abscissa follow the sequential presentation order 1, …, 30.

Fig. 4.

Network dynamics in the sequential protocol (format is the same as in Fig. 3). Frame stimuli are presented sequentially (r = 1.,,30, abscissa). (a) Session 1. The transition of responses from NF (positive η_d*) to F (negative η_d*) at r = 18 is shown. (b) Session 4. Transition at r = 20 is shown. (c) Session 7. All frames are classified F, but η_s* > 0, for r approaching 30. (d) Session 10. All η_s* < 0, i.e., both visual responses and delay states close to the F state. (T = 0.5, c = 0.4).

In session 1, frames of approximately the first half of the sequence (r ≤ 17) determine negative values of η_s*_, a delay activity η_d* ≈ −0.35, and hence F responses. Frames of the second half (r > 17) evoke positive η_s* 's, the memory state η_d* ≈ +0.35, and NF responses. As a result, apart from the sequential ordering of presentations, there is little difference with respect to the mixed protocol. As the simulation proceeds, things change significantly: Session by session, more and more stimuli of the second half of the sequence evoke delay states with negative η_d*_, producing F responses. In session 4, the transition from F to NF responses occurs after frame 20. By session 7, all frame stimuli determine an F response (see also Fig. 3c). For the rest of the simulation (session 8, 9, and 10), all stimuli determine F responses.

Fig. 3c presents a scatter plot of η_d* (delay states) for all (300) trials of this protocol, together with theoretical predictions. The line representing the unstable state approaches the upper memory line (NF responses), until they annihilate in a saddle node. That memory state becomes unstable even before the saddle node because of the noise in the current (Eq. 1). In fact, in simulations, there are no NF responses after session 6, whereas the saddle node is at session 9. This can be seen noting that there are no delay activity labels near the upper curve in the figure. In between sessions 6 and 9, the memory state has a very small basin of attraction and is destabilized by the noise. Note that the gradual convergence of memory states, observed in the mixed protocol (Fig. 3a), is present in the sequential protocol as well, as long as the upper delay state exists.

Fig. 3d presents the η_s* of visual responses for all 300 trials of sequential protocol, together with theoretical prediction for the corresponding η_d*'s. One observes that as trials proceed, the labels of the visual response states move to negative values, i.e., toward the F state. However, even after the upper memory state (the one closer to NF) has disappeared (session 7, in simulations), frame stimuli can still evoke visual responses with η_s* > 0, i.e., close to the NF state.

Forgetting Phase.

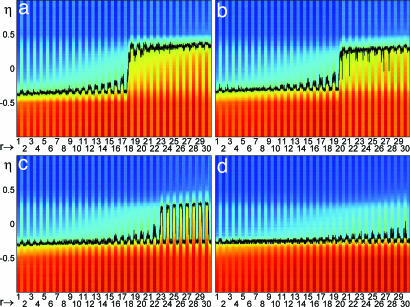
Theoretical analysis reveals that T/c (ratio of width to contrast of the tuning; see Eq. 3) is a critical parameter for the network dynamics. The critical point T/c = 1 separates two distinct phases: For T/c > 1, memory is preserved, whereas for T/c < 1, a long exposure to the morphing sequence provokes total memory erasure due to synaptic plasticity (SI Text). In the simulations shown in previous figures, T/c = 1.25. Instead, Fig. 5 shows the results of a simulation with the mixed protocol, at T/c = 0.6. Fig. 5 a and b present the network dynamics in sessions 1 and 10, respectively (as in Figs. 2 and 4 a and d). The first session is similar to Fig. 2a, except for a wider distribution of visual response labels (see also Fig. 5d). By session 10, the picture is very different: All delay states correspond to η_d* ≈ 0.

Fig. 5.

Forgetting regime. Network dynamics in the mixed protocol, for T/c = 0.6 is shown. (a and b) Total current (format is the same as in Fig. 2). (a) Session 1. This is very similar to Fig. 2a (T/c = 1.25), except for the more widely distributed visual responses. (b) Session 10. For all delay states, η_d* ≈ 0, i.e., equal numbers of blue and red neurons, hence random responses. (c) η_d* of delay activity states vs. trial number (format is the same as in Fig. 3). Lines are theoretical predictions for delay activity label. Solid lines, stable; dashed line, unstable. In contrast to the case T/c = 1.25 (Fig. 3a), the two memory states are not preserved; they collapse onto a single stable state after 275 trials. (d) Scatter plot of η_s* of visual response states vs. trial number. Visual responses are broadly distributed (compare with Fig. 3b for T/c = 1.25). (T = 0.3; c = 0.5).

Fig. 5 c and d show, respectively, the labels of delay activity states and visual responses in all 300 trials, as in Fig. 3. The stable delay states converge toward each other until they annihilate in a pitchfork after 275 trials (Fig. 5c). The visual response labels are not as clustered around the memory states as in Fig. 3b. They tend to spread more and more broadly as trials proceed (Fig. 5d). Given that in late trials η_d* ≈ 0, in the delay period after each stimulus, the network relaxes to a state in which the number of blue and red neurons are essentially equal, and excess in any direction is random. The behavioral responses are expected to be random and uncorrelated with the stimulus presented. This situation is identified with total forgetting.

The underlying reason for the appearance of this critical value of T/c is that for a frame stimulus of index α, neurons with η ≈ α are the ones that have their activity determined mostly by recurrent currents, because the external afferents they receive are near threshold (Eq. 3). These neurons are the ones sensitive to the structuring of long-term classification memory. Their fraction increases with T/c. If T/c is too small, the effect of memory in the process of plasticity is overcome by the external stimuli and is independent of previous memory structure. The result is that memory is lost.

Discussion

The model (for T/c > 1) captures, in a simple and complete way, the phenomenology described in ref. 9 and gives a rich picture of the interaction of memory with continued presentation of a sequence of spatiotemporally correlated stimuli. The resulting phenomenology is due to the interaction of neural activity and synaptic plasticity dynamics, which allows the interplay between memory and unsupervised exposure to the input stimuli. Neither neural nor synaptic dynamics are task-specific.

The underlying scenario is that, initially, each time a stimulus is presented, the corresponding visual response state is close to one of the two extreme frames, F or NF. Hebbian plasticity reinforces that state, increasing its stability, and the other state is correspondingly somewhat weakened. In the sequential protocol, in the middle of a session, i.e., in the middle of the morphing sequence, the recent past is characterized by a systematic presentation of stimuli from the first half of the sequence, all of which have enhanced the stability of the memory state near F, resulting in the expansion of the basin of attraction of that memory and a reduction of the basin of the other one. This is expressed by the drift of the unstable state toward the memory state near NF (Fig. 3c). As a result, some stimuli from the second half evoke a visual response near the F memory (frames16 and 17 in Fig. 4a). Beyond some position along the second half of the sequence, the states evoked are near NF, and synaptic plasticity allows some recovery of the lost basin, as seen by small back drifts of the unstable state toward the center near the end of every session. However, it does not recover fully: As sessions progress, this state eventually disappears (collapse). In contrast, in the mixed protocol, stimuli from both halves of the sequence alternate randomly, and the two memory basins remain balanced (Fig. 3 a and b). Consequently, the F and NF responses remain balanced, and classification memory is preserved. Note that the value of p, determining the speed of synaptic plasticity, is crucial: A very small p implies that plasticity is slow, and the two memories could be maintained even in the sequential protocol. For instance, at most 1.5% of synapses are expected to switch along 10 sessions if P = 10^−6. Conversely, if p is large, plasticity is fast, and memories are stored and/or lost instantly. If P = 10⁻², up to 40% of synapses are expected to switch during a single presentation. In that case, the collapse of memory would take place for every stimulus, even in the mixed protocol.

In the memory preservation regime, T/c > 1, neural configurations during and after stimulus presentation are related: Visual response states cluster around the delay activity states (Fig. 3 b and d). The presence of the two clusters of stimulated activity is due to the fact that the memory of F and NF is stored in the synaptic structure, and the visual response to an input stimulus reflects, in part, the embedded memory structure. However, the patterns of visual response can be separated from the patterns of delay activity. This appears in accordance with physiological observations (18).

The fact that in the mixed protocol (T/c > 1) two distinct delay activity states remain stable despite persistent synaptic plasticity (Fig. 3a) concords also with the physiological observation. In ref. 19, morphing sets of images were generated between two sets of visual stimuli. These images were presented for classification in random (mixed) order. The delay activity was found to maintain the coding for the class as trials went on, irrespective of the level of morphing of the input stimulus.

Also the memory collapse for the sequential protocol leads to a physiological prediction: The model predicts that the patterns of stable activity, where they exist, are only mildly affected by plasticity (Fig. 3c). But in well advanced sessions, the responses to frames in the second half of the sequence begin to be F (instead of NF). This implies, on the physiological level, that neurons should be observed that abruptly change their delay activity from F to NF selectivity more and more into the second half of the morphing sequence.

The model predicts also (for T/c < 1; Fig. 5) the total erasure (forgetting) of the classification memory (Fig. 5b), a phenomenon that could be observed experimentally. Unlike the previous cases, both delay activity states and visual response states are expected to be strongly affected by synaptic plasticity. This would lead to the broadening of the distribution of visual responses (Fig. 5d) and the drawing nearer of the two memory states (Fig. 5c). The delay activity patterns corresponding to the two distinct memories would become increasingly similar, until they merge. Subjects would then be expected to respond as if they did not remember the classification, i.e., by chance. Both extracellular recordings in vivo and psychophysical observations could detect this phenomenon. In particular, neurons should be found that switch their selectivity between NF and F shortly before total forgetting, i.e., before the subject starts responding by chance. The latter would correspond to neurons with η ≈ 0. To induce the “forgetting” effect, the stimuli should be designed by manipulating the smoothness of the transition of features along the morphing sequence. This can be effected, for example, by applying sigmoidal filters.

This study also suggests that, due to the convergence of the memory states, the perception of the “pure” F and NF faces should evolve from session to session. This could be checked in an experiment in which, at the end of each session, subjects are presented a line-up of several images for perusal and asked to identify the original F or NF. The responses may move toward the center of the morphing sequence.

The fact that each activity pattern is represented by the label of a single neuron (η*) should not be interpreted as a grandmother cell representation: It is not the activation of one neuron that accounts for one pattern, because the same neuron could be active (or inactive) both in F and in NF states. This type of label serves only for illustrative purposes and is not an intrinsic property of the network. Apart from the (innovative) treatment of external currents, the present model is set up with the ingredients of associative memory models (10, 11, 14, 15), with a large storage (20). In the context of our model, the capacity is not addressed, and only two memories are considered, a single F/NF pair. The present discussion regards the basin of attraction of these two memories. The question of more F and NF stored stimuli should be considered in the context of hierarchically structured attractor networks (21), where memories are considered parts of one large attractor.

Finally, a more realistic modeling of the network dynamics would employ spiking neurons and activity-driven synapses (22, 23), but the step seems rather innocuous. The simplifications of the present model render it aesthetically very attractive and make theoretical analysis accessible.

Abbreviations

F

friends

NF

nonfriends.