Intramolecular domain–domain association/dissociation and phosphoryl transfer in the mannitol transporter of Escherichia coli are not coupled

Abstract

The Escherichia coli mannitol transporter (II^Mtl) comprises three domains connected by flexible linkers: a transmembrane domain (C) and two cytoplasmic domains (A and B). II^Mtl catalyzes three successive phosphoryl-transfer reactions: one intermolecular (from histidine phosphocarrier protein to the A domain) and two intramolecular (from the A to the B domain and from the B domain to the incoming sugar bound to the C domain). A key functional requirement of II^Mtl is that the A and B cytoplasmic domains be able to rapidly associate and dissociate while maintaining reasonably high occupancy of an active stereospecific AB complex to ensure effective phosphoryl transfer along the pathway. We have investigated the rate of intramolecular domain–domain association and dissociation in IIBA^Mtl by using ¹H relaxation dispersion spectroscopy in the rotating frame. The open, dissociated state (comprising an ensemble of states) and the closed, associated state (comprising the stereospecific complex) are approximately equally populated. The first-order rate constants for intramolecular association and dissociation are 1.7 (±0.3) × 10⁴ and 1.8 (±0.4) × 10⁴ s⁻¹, respectively. These values compare to rate constants of ≈500 s⁻¹ for A → B and B → A phosphoryl transfer, derived from qualitative line-shape analysis of ¹H-¹⁵N correlation spectra taken during the course of active catalysis. Thus, on average, ≈80 association/dissociation events are required to effect a single phosphoryl-transfer reaction. We conclude that intramolecular phosphoryl transfer between the A and B domains of II^Mtl is rate-limited by chemistry and not by the rate of formation or dissociation of a stereospecific complex in which the active sites are optimally apposed.

The bacterial phosphoenolpyruvate (PEP):sugar phosphotransferase system (PTS) is a signaling pathway whereby sequential, reversible phosphoryl transfer via a series of transient bimolecular complexes is coupled to sugar uptake across the membrane (1). The transporter (enzyme II^Mtl) of the mannitol branch of the PTS consists of a single polypeptide chain organized into three domains, IIC^Mtl, IIB^Mtl, and IIA^Mtl (from the N to C terminus), connected by flexible linkers (1). The phosphoryl group is transferred from the histidine phosphocarrier protein (HPr) to IIA^Mtl via a bimolecular reaction and subsequently from IIA^Mtl to IIB^Mtl, and finally onto the incoming sugar bound to the cytoplasmic side of IIC^Mtl via unimolecular reactions. A key functional feature of II^Mtl is that intramolecular association and dissociation between the A and B domains must be fast to allow for effective phosphoryl transfer along the pathway.

Relaxation measurements, including relaxation dispersion, have been used to study dynamics of enzyme function and protein folding on milli- to microsecond time scales (2–10). Recent work has suggested that the dynamics of atomic motions observed by relaxation dispersion are directly linked to catalysis (5, 7, 8). For adenylate kinase, the rate of lid opening, which involves large-amplitude correlated motions, seems to represent the rate-limiting step in catalysis (5). This observation led to the suggestion that many enzymes have evolved such that the catalytic reaction itself is so fast that catalytic power is limited not by chemistry but by the rate at which conformational rearrangements can take place to optimally align the reactive atoms (5). However, this generalization has been called into question, because the correlation between conformational changes and kinetics observed for adenylate kinase does not necessarily imply a direct link between dynamics, correlated motions, and catalysis (11).

Previously, we determined the solution structure of an analog of the product complex of the phosphoryl-transfer reaction involving the isolated IIA^Mtl domain and a stably phosphorylated IIB^Mtl domain from Escherichia coli (12). IIB^Mtl was stably phosphorylated by mutating the active-site cysteine (Cys-384) to serine (13), whereas the active-site histidine (His-554) of IIA^Mtl was mutated to glutamine to prevent transfer of the phosphoryl group back to IIA^Mtl in the complex. The interaction between the isolated IIA^Mtl and phosphoIIB^Mtl domains is weak, with an equilibrium dissociation constant (K_d) of ≈3.7 mM. In the native enzyme, however, the two domains are connected by an ≈21-residue flexible linker (1). The linker renders the equilibrium between associated (closed) and dissociated (open) forms of intact IIBA^Mtl concentration independent and is expected to stabilize the associated state, because the reduction in configurational space that accompanies tethering is equivalent to raising the effective concentration of the domains (12, 14). In this article we investigate the dynamics of intramolecular domain–domain association and dissociation between the A and B domains of single-chain IIBA^Mtl of E. coli by using ¹H relaxation dispersion spectroscopy in the rotating frame and compare these rates with estimates of the reversible phosphoryl-transfer rates between the A and B domains derived from qualitative line-shape analysis of cross-peaks in ¹H-¹⁵N correlation spectra during the course of active catalysis. We show that the intramolecular domain–domain association and dissociation rates are not rate-limiting and that phosphoryl transfer occurs, on average, once for every ≈80 association and dissociation events.

Results

Chemical-Shift Perturbation.

For simplicity, phosphorylated IIBA^Mtl(C384S/H554Q/C571A) is denoted as phosphoIIBA^Mtl, phosphorylated IIB^Mtl(C384S) as phosphoIIB^Mtl, IIA^Mtl(H554Q/C571A) as IIA^Mtl, and the wild-type construct as IIBA^Mtl.

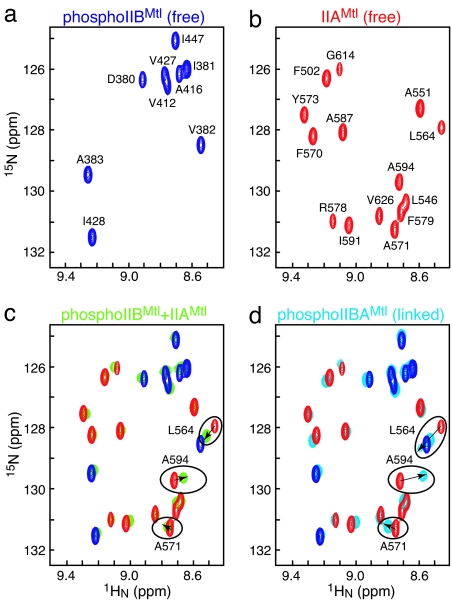
The profile of ¹H_N/¹⁵N chemical-shift perturbations relative to the free phosphoIIB^Mtl and free IIA^Mtl is essentially the same for the mixture of isolated IIA^Mtl and phosphoIIB^Ml (comprising ≈30% complex) and the intact phosphoIIBA^Mtl, indicating that the interaction of the two domains is the same in both systems (Fig. 1). The magnitudes of the perturbations, however, are larger for phosphoIIBA^Mtl than for the mixture, indicating that the fraction of closed (associated) form in the single-chain phosphoIIBA^Mtl is >30%. The ¹H_N/¹⁵N chemical shifts of phosphoIIBA^Mtl are not affected by concentration (over a range of 50–500 μM), indicating that the chemical-shift perturbation relative to the isolated IIA^Mtl and phosphoIIB^Mtl domains is solely caused by intramolecular association of the two domains.

Fig. 1.

Association of the A and B domains of II^Mtl in the context of phosphoIIBA^Mtl and the isolated phosphoIIB^Mtl and IIA^Mtl domains. Portion of the 2D ¹H-¹⁵N HSQC spectra of ¹⁵N-labeled phosphoIIB^Mtl (blue) (a); ¹⁵N-labeled IIA^Mtl (red) (b); a 1:1 mixture of 3 mM ¹⁵N-labeled IIA^Mtl and ¹⁵N-labeled phosphoIIB^Mtl (green) comprising ≈30% complex (c) superimposed on the spectra of the individual domains shown in a and b; and ²H,¹⁵N-labeled phosphoIIBA^Mtl (cyan) (d) superimposed on the spectra of the individual domains shown in a and b. Cross-peaks with large chemical-shift changes after association of the A and B domains are highlighted in c and d.

Large-Scale Interdomain Motion.

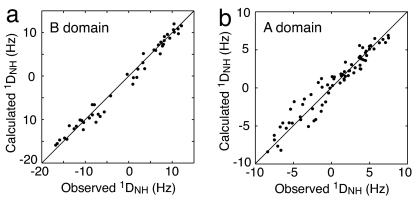
The values of the {¹H}-¹⁵N heteronuclear NOEs for the linker (residues 472–492) are all <0.6, indicating that the linker region is flexible. ¹D_NH residual dipolar couplings (RDCs) measured for phosphoIIBA^Mtl weakly aligned in a polyacrylamide gel reveal that the magnitude of the principal component of the alignment tensor for the B domain (−8.2 Hz) is approximately twice as large as that for the A domain (−4.2 Hz) (Fig. 2). Alignment in the neutral gel is dominated by steric effects and, hence, molecular shape (15). If the relative orientation of the two domains in phosphoIIBA^Mtl was fixed, both domains would have the same alignment tensor; the fact that the alignment tensors are significantly different indicates the presence of large-scale amplitude motions of the two domains relative to one another (16–18). Under these circumstances the observed alignment tensor for each domain is given by the weighted average of the alignment tensors in the open (associated) and closed (dissociated) states. In the closed state, the two domains share the same alignment tensor. In the open state, however, in which there is no interaction between the two domains and large-scale relative motion is present (because they are simply tethered by a long flexible linker), the A and B domains will effectively be aligned independently by the alignment medium; hence, their alignment tensors will be different, because the molecular shape and size of the two domains are distinct from one another.

Fig. 2.

Large-scale interdomain motion of the A and B domains in phosphoIIBA^Mtl ascertained from RDC measurements. Shown is a comparison of observed and calculated ¹D_NH RDCs measured in a 5% neutral polyacrylamide gel for the B (a) and A (b) domains of phosphoIIBA^Mtl. The magnitude of the axial component of the alignment tensor (D_a) and the rhombicity (η) are −8.2 Hz and 0.35 for the B domain but −4.2 Hz and 0.43 for the A domain, respectively. The RDC R factors and correlation coefficients are 12.4% and 0.99 for the B domain and 20.2% and 0.96 for the A domain, respectively. If the RDC data for the A and B domains are fit simultaneously to the coordinates of the IIA^Mtl–phosphoIIB^Mtl complex, the RDC R factor is increased to 58.4%. The coordinates of the A and B domains are taken from the coordinates of the IIA^Mtl–phosphoIIB^Mtl complex (ref. 12; PDB ID code 2FEW).

Kinetics of Intramolecular Association and Dissociation of the A and B Domains of IIBA^Mtl.

The intramolecular association/dissociation studied can be described by the scheme:

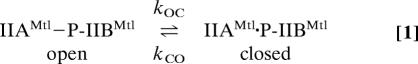where IIA^Mtl · P-IIB^Mtl is the closed state in which the A and B domains are associated to form a stereospecific complex, IIA^Mtl–P-IIB^Mtl is the open, dissociated, state (which, in reality, is an ensemble of states) in which there is no interaction between the A and B domains, and k_OC and k_CO are the unimolecular rate constants for the open-to-closed and closed-to-open transitions, respectively. For this two-state system, the overall relaxation rate in the rotating frame, R₁ρ, is given by the sum of the intrinsic relaxation rate, R_1ρ⁰, and the exchange of chemical-shifts contribution, R_ex (9):

Because exchange is fast on the relaxation time scale, (∣R_1ρ^closed − R_1ρ^open∣ ≪ k_ex), R_1ρ⁰ is given by

where R_1ρ^open and R_1ρ^closed are the intrinsic relaxation rates for the open and closed forms, respectively, and p_open and p_closed are the populations of the open and closed states, respectively, with p_open = (1 − p_closed). Note that the values of R₁ρ for the open and closed states in the absence of chemical exchange are not accessible experimentally because this is a unimolecular system in equilibrium.

In the fast-exchange limit, (Δω/k_ex)² ≪ 1, on the chemical-shift time scale, the R_ex contribution to R₁ρ is given by (10, 19, 20)

where Δω (= ω_closed − ω_open) is the frequency difference between the chemical shifts of the two states; k_ex is the sum of the two rate constants, k_OC and k_CO, for exchange between the two states; and ω_SL is the spin-lock frequency. In general, p_closed and (Δω)² cannot be determined independently of one another. In this instance, however, the chemical shifts of the open state, ω_open, are known, because they are the same as those for the two isolated domains (ω_free). The fraction of the closed state, therefore, is given by p_closed = (ω_obs − ω_free)/(ω_closed − ω_free), where ω_obs is the observed shift measured for phosphoIIBA^Mtl. Thus, R_ex can be expressed as

thereby enabling p_closed to be determined independently, because both ω_obs and ω_free are directly accessible experimentally.

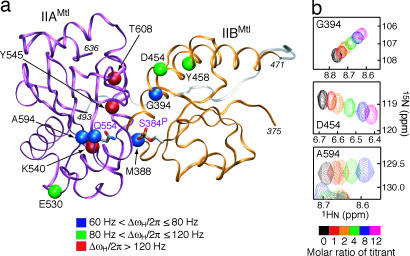
Mapping of the residues used for analysis of the relaxation dispersion data onto the structure of the previously determined IIA^Mtl–phosphoIIB^Mtl complex (12) is shown in Fig. 3. The titration spectra obtained with the isolated IIA^Mtl and IIB^Mtl domains were used to estimate the lower limit of k_ex and the range of Δω. Because the values of Δω were larger in the ¹H than ¹⁵N dimension and stronger spin-lock field strengths can be applied for ¹H than ¹⁵N to suppress the exchange contribution to R₁ρ, we made use of backbone amide proton (¹H_N) relaxation dispersion measurements in the rotating frame (20) by using perdeuterated phosphoIIBA^Mtl. Among the titrating residues of IIBA^Mtl, 10 residues with both well resolved cross-peaks in the 2D ¹H-¹⁵N correlation spectrum and large ¹H_N chemical-shift differences (Δω_H/2π > 60 Hz at a ¹H frequency of 750 MHz) relative to the free protein were selected for further analysis. Note that simulations of Eq. 4, varying the Δω_H, k_ex (for values larger than the estimated lower limit of k_ex), and ω_SL, indicate that a 60-Hz cutoff is required to ensure that R_ex values larger than the 3–4% experimental errors in R₁ρ can be detected.

Fig. 3.

Location of residues used for relaxation dispersion analysis on the structure of the IIA^Mtl–phosphoIIB^Mtl complex. (a) The differences in ¹H_N chemical shifts between intact phosphoIIBA^Mtl and the isolated domains are color-coded on the structure of the IIA^Mtl–phosphoIIB^Mtl complex (12) as follows: 60 Hz < Δω_H/2π ⩽ 80 Hz, blue balls (Met-388, Gly-394, Gln-554, and Ala-594); 80 Hz < Δω_H/2π ⩽ 120 Hz, green balls (Asp-454, Tyr-458, and Glu-530); and 120 Hz < Δω_H/2π, red balls (Tyr-545, Ala-595, and Thr-608) (at a ¹H frequency of 750 MHz). The backbone is displayed as a tube (IIA^Mtl, purple; IIB^Mtl, orange), and the active-site residues, phosphorylated Ser-384 of IIB^Mtl (C384S^P) and Gln-554 of IIA^Mtl (H554Q), are shown as a stick models colored according to atom type. The linker connecting the two domains is shown as a transparent tube (gray), and its conformation is modeled by simulated annealing (38), which indicates that it is long enough to bridge the C-terminal end of IIB^Mtl (residue 471) to the N-terminal end of IIA^Mtl (residue 493). (Note that although Glu-530 lies outside the interface, the perturbation in its ¹H_N chemical shift is caused by a secondary effect arising from close proximity to an aromatic residue, Tyr-531, which is itself in close proximity to His-600 at the interface.) (b) Chemical-shift perturbation of three residues (Gly-394, Asp-454, and Ala-594) after titration of the isolated IIA^Mtl and phosphoIIB^Mtl domains. In these spectra, the reference protein (0.6 mM) was titrated with varying molar ratios (color-coded) of the other protein in 20 mM Tris-d₁₁ (pH 7.4) at 30°C.

The relaxation dispersion data for the 10 selected residues were fit simultaneously by nonlinear least-squares minimization by using Eqs. 2 and 5, optimizing two global parameters, p_closed and k_ex, and one residue-specific parameter, R_1ρ⁰, by using the error function

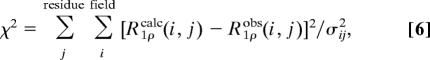where R_1ρ^calc(i, j) and R_1ρ^obs(i, j) are the calculated and observed R₁ρ values for the ith spin-lock field and jth residue, respectively, and σ_ij is the error obtained from Monte Carlo simulation for the single exponential fitting of R₁ρ.

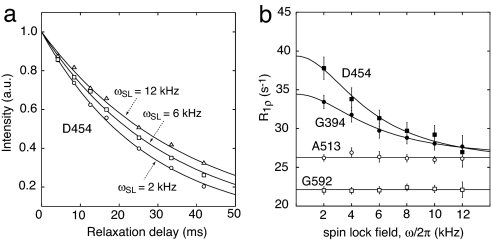
Fig. 4a shows typical R₁ρ data measured for the backbone amide proton of Asp-454 at three different field strengths, illustrating that the data follow single exponential decays. Selected relaxation dispersion profiles for residues with (Asp-454 and Gly-394) and without (Ala-513 and Gly-592) a chemical-exchange contribution to R₁ρ are displayed in Fig. 4b. Global fitting of the data for the 10 selected residues yielded values of k_ex = 3.5(±0.5) × 10⁴ s⁻¹ and p_closed = 0.48 ± 0.06 with χ²/N = 0.8 (where N is the number of degrees of freedom). The value of p_closed obtained from the relaxation dispersion data are in agreement with the approximate estimate derived from the observed chemical shifts of phospho-IIBA^Mtl, the chemical shifts of the isolated IIA^Mtl and phospho-IIB^Mtl domains free in solution, and the extrapolated chemical shifts of the fully saturated IIA^Mtl–phosphoIIB^Mtl complex derived from titration data with the isolated domains (note >90–95% saturation is difficult to achieve given the K_d of 3.7 mM). Because k_ex = k_OC + k_CO and p_closedk_CO = p_openk_OC at equilibrium, the unimolecular association (k_OC) and dissociation (k_CO) rate constants in Eq. 1 are given by p_closedk_ex and p_openk_ex, respectively, yielding values of k_OC = 1.7(±0.3) × 10⁴ and k_OC = 1.8(±0.4) × 10⁴ s⁻¹.

Fig. 4.

Backbone proton amide relaxation dispersion in the rotating frame measured on phosphoIIBA^Mtl. (a) ¹H_NR₁ρ data for Asp-454 at spin-lock field strengths of 2 (○), 6 (□), and 12 (▵) kHz with the single-exponential least-squares best-fit curves (solid lines). (b) R₁ρ dispersion with respect to spin-lock field strength for the backbone amide protons of Asp-454 (■), Gly-394 (●), Ala-513 (○), and Gly-592 (□). The solid lines for the R₁ρ dispersion curves of Asp-454 and Gly-394 represent nonlinear least-squares best fits using Eqs. 2 and 5 as described in the text. The data for Ala-513 and Gly-592 illustrate dispersion curves with no chemical-exchange contribution.

The pathway from the open to closed states probably involves the formation of an ensemble of very lowly populated, nonspecific encounter complexes, as has been demonstrated recently for several weak protein–protein complexes by using paramagnetic relaxation enhancement measurements (21). Because the relaxation dispersion data obtained for the 10 sites can be fit simultaneously within experimental error by using a simple two-site exchange model, the population of nonspecific encounter complexes must be very low (<5%). Consequently, the presence of such intermediates will not impact to any significant extent the values of the k_OC and k_CO rate constants obtained from the two-state fit. In addition, the average chemical shifts for the ensemble of nonspecific encounter complexes are anticipated to be virtually identical to those of the open state, thereby further reducing the impact of their presence on the estimated values of the rate constants to negligible levels. We note, however, that k_OC and k_CO can be expressed as k_OI · k_IC/(k_IO + k_IC) and k_IO · k_CI/(k_IO + k_IC), respectively, where k_OI and k_IO are the forward and backward rate constants, respectively, for the formation of nonspecific encounter complexes from the open state, and k_IC and k_CI are the forward and backward rate constants, respectively, for the formation of the closed state from nonspecific encounter complexes.

Kinetics of Reversible Intramolecular Phosphoryl Transfer Between the A and B Domains of IIAB^Mtl.

Under conditions of catalytic amounts of enzyme I and HPr and excess PEP, both the A and B domains of wild-type IIBA^Mtl are fully phosphorylated. Preliminary experiments indicated that the isolated phosphorylated IIA^Mtl domain is relatively unstable at neutral pH, and irreversible dephosphorylation by hydrolysis occurs with a half-life of ≈20 min. In contrast, the isolated phosphorylated IIB^Mtl domain is rather stable, and the phosphorylated form has a half-life of ≈17 h. Thus, PEP is continually consumed and inorganic phosphorus generated during the time course of the reaction. The ³¹P-NMR spectrum of fully phosphorylated IIBA^Mtl displays two resonances of equal intensity: one at 12.2 ppm corresponding to phospho-Cys-384 (B domain) and the other at −6.7 ppm corresponding to phospho-His-554 (A domain) (referenced relative to inorganic phosphate at 0 ppm), in perfect agreement with previous reports on full-length II^Mtl [ref. 22; see supporting information (SI) Fig. 6]. Once PEP is fully consumed, hydrolysis of phospho-His-554 occurs. The intensity of the resonances of phospho-His-554 and phospho-Cys-384 remain equal and decrease in concert to finally disappear after ≈4 h (SI Fig. 6). The two phosphorus resonances remain in slow exchange on the chemical-shift time scale throughout the reaction. Therefore, one can conclude that the overall phosphoryl-transfer reaction rate, k_ex^P (given by the sum of the Α → Β and B → A phosphoryl-transfer reaction rates), is at least 10-fold slower than Δω_P = 2.9 × 10⁴ s⁻¹ (calculated from the chemical-shift difference between the two signals, 18.9 ppm, and the ³¹P frequency of 242.94 MHz).

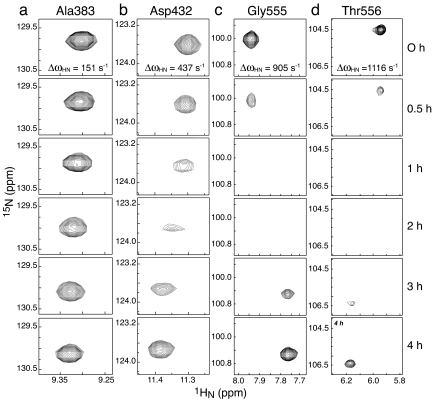
To further probe the rate of reversible phosphoryl transfer between the A and B domains we recorded a series of ¹H-¹⁵N heteronuclear single quantum coherence (HSQC) spectra (at a ¹H frequency of 800 MHz) during active phosphoryl transfer between the two domains subsequent to the depletion of PEP. The results are shown in Fig. 5. At time 0 h (the point at which PEP is fully depleted), the ¹H-¹⁵N HSQC spectrum reflects fully phosphorylated IIBA^Mtl, that is, the species in which both the B and A domains are phosphorylated. At 4 h subsequent to PEP depletion, the ¹H-¹⁵N HSQC spectrum corresponds to the fully unphosphorylated IIBA^Mtl species. The intermediate time points reflect a mixture of biphosphorylated, monophosphorylated, and unphosphorylated species, with the monophosphorylated species reaching a maximum between 1 and 2 h subsequent to PEP depletion. In some instances, the chemical shifts of the cross-peaks progressively shift during the course of the reaction from the fully phosphorylated to the unphosphorylated positions without any significant line broadening. This is the fast-exchange regime on the chemical-shift time scale and is exemplified by the cross-peak for Ala-383 (Fig. 5a). Δω_HN for Ala-383 is 151 s⁻¹, indicating that the overall phosphoryl-transfer reaction rate k_ex^P is in excess of ≈750 s⁻¹ (k_ex > 5Δω_HN). In the case of Asp-432 (Fig. 5b), a continual shift is also observed, but extensive line broadening is seen in the spectra taken at 1 and 2 h, characteristic of an exchange rate on the fast side of intermediate exchange: Δω_HN for Asp-432 is 437 s⁻¹, suggesting that k_ex^P ∼ 1,000 s⁻¹ (2Δω_HN < k_ex < 3Δω_HN). This estimate is fully confirmed by the behavior of the cross-peaks of Gly-555 (Δω_HN = 905 s⁻¹; Fig. 5c) and Thr-556 (Δω_HN = 1,116 s⁻¹; Fig. 5d) where the cross-peaks completely disappear in the ¹H-¹⁵N HSQC spectra taken at 1 and 2 h, which is indicative of the intermediate exchange regime where k_ex^P ∼ Δω_HN. Because the intensities of the ³¹P resonances of phospho-Cys-384 and phospho-His-554 decrease in concert and remain approximately equal to each other throughout the reaction, one can conclude that the forward and backward rate constants for phosphoryl transfer are approximately equal with a value of ≈500 s⁻¹.

Fig. 5.

Time course of selected ¹H_N/¹⁵N cross-peaks in ¹H-¹⁵N HSQC spectra of wild-type IIBA^Mtl during active intramolecular phosphoryl transfer subsequent to the depletion of PEP. (a) Ala-383; (b) Asp-432; (c) Gly-555; (d) Thr-556. The spectrum at 0 h, taken at the point of complete depletion of PEP, reflects the biphosphorylated state in which both the A and B domains are fully phosphorylated; the spectrum at 4 h represents fully dephosphorylated IIBA^Mtl. The effects of chemical exchange arising from reversible phosphoryl transfer between the A and B domains in species that are monophosphorylated are apparent in the spectra taken at intermediate times. The Δω_HN values were obtained from the chemical-shift differences between the spectra taken at 0 and 4 h (¹H frequency of 800 MHz).

Discussion

Impact of Flexible Linker Between the A and B Domains of IIBA^Mtl.

The K_d for the interaction of the isolated IIA^Mtl and phosphoIIB^Mtl domains is ≈3.7 mM (12). Because the occupancy of the closed (associated) state of phosphoIIBA^Mtl determined from the relaxation dispersion measurements is ≈48%, one can conclude that the 21-residue linker connecting the A and B domains in IIBA^Mtl results in an effective local concentration of ≈4 mM for each domain, a value that is in good accord with that predicted from polymer chain theory (12, 23) and configurational entropy calculations (14). Moreover, if the unimolecular association rate constant, k_OC (1.7 × 10⁴ s⁻¹), is divided by the effective local concentration, the value of ≈5 × 10⁶ M⁻¹·s⁻¹ for the apparent bimolecular rate constant is reasonably close to what one might expect for a diffusion-limited reaction between two proteins, particularly when factors such as the chain-diffusion coefficient of the linker are taken into account. Thus, intradomain association in the IIBA^Mtl system is tuned to function, which requires reasonably high occupancy coupled with rapid association and dissociation (≈2 × 10⁴ s⁻¹ in both directions) to efficiently carry out three sequential phosphoryl-transfer reactions, namely from HPr to IIA^Mtl, from IIA^Mtl to IIB^Mtl, and finally from IIB^Mtl onto the incoming sugar bound to the cytosolic side of IIC^Mtl.

Relationship Between Phosphoryl Transfer and Domain Dynamics.

The NMR data presented in this article clearly indicate that the rate constants for the forward (Α → Β) and backward (B → A) phosphoryl-transfer reactions are approximately equal with values of ≈500 s⁻¹, which is ≈40-fold lower than the rate constants for intramolecular domain–domain association and dissociation. Thus, on average, ≈80 association/dissociation events take place for every phosphoryl-transfer reaction. One can conclude, therefore, that the rate-limiting step for intramolecular phosphoryl transfer in IIBA^Mtl is governed by the chemistry of the phosphoryl-transfer reaction rather than the time it takes for the two domains to form a stereospecific complex in which the active sites of the A and B domains are optimally positioned for phosphoryl transfer. In this regard, it is worth noting that in the case of all of the bimolecular complexes of the PTS solved to date, including the N-terminal domain of enzyme I (EIN)–HPr (24), IIA^Glc–HPr (25), IIA^Mtl–HPr (26), IIA^Man–HPr (27), IIA^Glc–IIB^Glc (28), and IIA^Mtl–IIB^Mtl (12) complexes, either minimal or no backbone changes are required to form an optimal pentacoordinate phosphoryl-transition state.

Phosphoryl-Transfer Rates in the PTS.

There have been a number of kinetic studies on the glucose-branch PTS using rapid-quench techniques (29, 30). (Note that the kinetics of the intramolecular phosphoryl-transfer reaction studied here is not accessible to classical biochemical methodology.) The reported apparent second-order rate constants for reversible phosphoryl transfer along the enzyme I, HPr, IIA^Glc, and IICB^Glc pathway range from ≈4 × 10⁶ to 2 × 10⁸ M⁻¹·s⁻¹ (29). By using estimated intracellular protein concentrations of ≈5, 20–100, 20–60, and 10 μM for enzyme I (monomer), HPr, IIA^Glc, and IIBC^Glc, respectively (29), one can deduce that the upper limits of the pseudo-first-order rate constants for the forward and backward phosphoryl-transfer reactions in vivo are ≈1,000 and 160–800 s⁻¹, respectively, between enzyme I and HPr; 1,200–6,000 and 1,000–3,000 s⁻¹, respectively, between HPr and IIA^Glc, and 200–600 and 40 s⁻¹ between IIA^Glc and IICB^Glc, respectively. Thus, the intramolecular phosphoryl-transfer rates of ≈500 s⁻¹ observed here for IIBA^Mtl are quite comparable to those in the glucose branch of the PTS.

Comparison with Adenylate Kinase.

Adenylate kinase catalyzes the reversible transfer of phosphorus from two molecules of ADP to form ATP and AMP. Its structure comprises a core and two mobile domains (the lid and the AMP-binding domains) that close over the nucleotide-binding sites (31). The two mobile domains exist in either open or closed forms, and the transition between these two states involves large-scale correlated motions within the hinge regions connecting the two domains to the core (31). The opening rates for both a thermophilic and mesophilic adenylate kinase (≈40 and 290 s⁻¹, respectively) are essentially identical to the respective catalytic rates, whereas the closing rate (1,400–1,600 s⁻¹) is much faster (5). These data suggest that the conformational transition from closed to open states required for product release is rate-limiting in catalysis (5). In contrast, in the IIBA^Mtl system, the intramolecular domain–domain opening (dissociation/product release) and closing (association/substrate binding) rates are comparable (≈2 × 10⁴ s⁻¹), and it is the phosphoryl-transfer reaction that seems to be rate-limiting (≈500 s⁻¹).

The different behaviors observed for IIBA^Mtl and adenylate kinase may be rationalized in structural terms. In the case of IIBA^Mtl, the two domains are connected by a long 21-residue linker that behaves essentially as a random-coil polymer. Thus, concerted backbone motions within the linker are not required to bring the two domains together or move them apart; rather the function of the linker is to restrict diffusion of one domain relative to another to a volume limited by the average rms end-to-end distance of the linker. For adenylate kinase, however, motion of the lid and AMP-binding domains relative to the core domain is determined by concerted backbone conformational changes of a few residues at the hinge points between the domains. The concerted nature of these changes is presumably more complex and, therefore, energetically more costly and slower relative to the essentially random, largely uncorrelated nature of the motions within the IIBA^Mtl linker.

Biological Implications for the PTS.

In the absence of external sugar, the PTS is in the resting state with all signal transducers phosphorylated (32). When the bacterium encounters external sugar in the medium, the first event involves the transfer of the phosphoryl group from IIB to the incoming sugar located on IIC, thereby switching on the PTS signaling pathway. Dephosphorylated IIB and subsequently dephosphorylated upstream mediators (e.g., IIA and enzyme I) interact with several transcription factors to turn on or off a variety of proteins involved in sugar uptake. The fast intramolecular domain–domain association between the A and B domains of IIBA^Mtl and subsequent phosphoryl transfer represents an efficient means for rapid initiation and amplification of sugar-uptake signaling in bacteria.

Materials and Methods

Cloning, Expression, and Purification.

IIBA^Mtl was cloned to encompass the entire cytosolic AB component (residues 375–637) of the E. coli mannitol transporter (II^Mtl). The B domain extends from residues 375 to 471, the A domain from residues 493 to 637, and the linker from residues 472 to 492. From this construct, we mutated the active-site cysteine (Cys-384) of IIB^Mtl to Ser to permit stable phosphorylation, the active-site histidine (His-554) of IIA^Mtl to Gln to prevent reverse phosphoryl transfer from the B to the A domain, and Cys-571 to Ala to improve protein stability (12). The construct was verified by DNA sequencing and then subcloned into a modified pET-32a vector to form a thioredoxin fusion protein with a 6-His tag. After transformation with an expression vector, E. coli strain BL21star (DE3) (Novagen) was grown in minimal medium (either supplemented by ¹⁵NH₄Cl and ¹³C₆-glucose in H₂O or ¹⁵NH₄Cl and ²H₇-glucose in ²H₂O as the sole nitrogen or carbon sources, respectively), induced with 1 mM isopropyl-β-d-thiogalactopyranoside at an A₆₀₀ of ≈0.8 and harvested by centrifugation after 4 h of induction. Wild-type IIBA^Mtl and IIBA^Mtl(C384S/H554Q/C571A) were purified as described (12). Phosphorylation of the latter was carried out as described (12, 13). The isolated IIB^Mtl(C384S) and IIA^Mtl(H554QA/C571A) domains were expressed and purified as described (12).

NMR Spectroscopy.

NMR samples contained 0.5 mM ²H,¹⁵N- or ¹³C,¹⁵N-labeled phosphoIIBA^Mtl in 20 mM Tris-d₁₁ (pH 7.4), 0.01% (wt/vol) sodium azide, and 10% ²H₂O (vol/vol). ¹³C,¹⁵N-labeled phosphoIIBA^Mtl protein was used to assign the linker region and also to confirm assignments of each domain by using 3D HNCACB and CBCA(CO)NH experiments (33). The ¹H_N/¹⁵N assignments of the A and B domains of wild-type IIBA^Mtl in unphosphorylated and phosphorylated states were obtained directly by reference to those of the isolated IIA^Mtl (26) and IIB^Mtl (13, 34) domains in their respective unphosphorylated and phosphorylated states. ¹D_NH RDCs were obtained by taking the difference in the corresponding ¹J_NH couplings measured in aligned and isotropic (water) medium (15). The alignment medium comprised a neutral 5% polyacrylamide gel, prepared as described (13), and ¹J_NH couplings were measured from a 2D in-phase/antiphase ¹H-¹⁵N HSQC spectrum (15). Calculated ¹D_NH values were obtained by fitting the experimental RDC data to the coordinates of each domain (12) individually by using singular value decomposition (15). Agreement between observed and calculated RDCs is expressed as an RDC R factor that scales between 0% and 100% and is defined as the ratio of the rms deviation between observed and calculated values to the expected rms deviation if all of the N-H vectors were randomly distributed; the latter is given by [2D_a²(4 + η²)/5]^1/2, where D_a is the magnitude of the axial component of the alignment tensor, and η is the rhombicity (35).

R₁ρ-unlike spin relaxation rates in the rotating frame for backbone amide protons were measured on ²H,¹⁵N-labeled phospho-IIBA^Mt1 by using the pulse sequence described in ref. 20 with minor modifications. A 3-9-19 pulse train was used for water suppression in the WATERGATE scheme, and heat compensation was used during the relaxation delay (36). Proton R₁ρ measurements were carried out by using seven spin-lock times (4, 8, 13, 17, 25, 33, and 42 ms) on a Bruker DMX750 spectrometer at 30°C. The ¹H spin-lock field strengths (ω_H/2π) used for the relaxation dispersion measurements were 2, 4, 6, 8, 10, and 12 kHz, at three ¹H spin-lock frequencies of interest (7.03, 8.56, and 9.38 ppm) to ensure the on-resonance R₁ρ condition. With the offsets of amide proton frequencies from the spin-lock field frequency <300 Hz, the contribution of longitudinal relaxation to R₁ρ is <3% even for the lowest spin-lock field strength of 2 kHz, so that the on-resonance condition holds throughout the experiments (37). The relaxation dispersion curves were fit simultaneously as described in Results. Errors in optimized parameters were estimated by the jackknife method, in which one data set was removed in turn.

Time-course experiments during phosphoryl transfer between the A and B domains of wild-type IIBA^Mtl were carried out by using 2D ¹H-¹⁵N HSQC (¹H frequency = 800.13 MHz) and 1D ³¹P-NMR (³¹P frequency = 242.94 MHz) spectroscopy. ¹⁵N-labeled IIBA^Mtl (0.5 mM) was prepared in 20 mM Tris-d₁₁ buffer (pH 7.4) and phosphorylated by addition of 5 μM enzyme I/5 μM HPr/5 mM MgCl₂/1.5 mM PEP. The PEP stock solution was prepared in Trizma base, and the Trizma base buffer maintained the pH of the solution at 7.4 throughout the course of the reaction.

Abbreviations

PEP

phosphoenolpyruvate

PTS

PEP:sugar phosphotransferase system

HPr

histidine phosphocarrier protein

RDC

residual dipolar coupling

HSQC

heteronuclear single quantum coherence.