Interfacial plasticity governs strain rate sensitivity and ductility in nanostructured metals

Abstract

Nano-twinned copper exhibits an unusual combination of ultrahigh strength and high ductility, along with increased strain-rate sensitivity. We develop a mechanistic framework for predicting the rate sensitivity and elucidating the origin of ductility in terms of the interactions of dislocations with interfaces. Using atomistic reaction pathway calculations, we show that slip transfer reactions mediated by twin boundary are the rate-controlling mechanisms of plastic flow. We attribute the relatively high ductility of nano-twinned copper to the hardening of twin boundaries as they gradually lose coherency during plastic deformation. These findings provide insights into the possible means of optimizing strength and ductility through interfacial engineering.

Nanocrystalline metals with grain size finer than 100 nm routinely exhibit up to five times higher strength than their coarse-grained counterparts but suffer from greatly diminished ductility (1–3). Lu et al. (4–6) showed that introduction of coherent nano-twins, typically tens of nanometers in thickness, in ultrafine-grained copper (with grain size of several hundred nanometers) leads to an unusual combination of ultrahigh strength (≈1 GPa) and high ductility (14% elongation to failure). The plastic deformation characteristics of nanocrystalline metals have previously been rationalized on the basis of a number of mechanisms (7), including grain boundary (GB) sliding (8, 9), grain rotation (10), and diffusional creep (11). An effective experimental technique to probe the active deformation mechanism is to measure the sensitivity of flow stress to the rate of loading,^‖ because both the sensitivity index m and the associated activation volume v* can vary by orders of magnitude for different rate-limiting processes. For face-centered cubic metals such as copper, grain refinement into the nanocrystalline regime leads to an increase in m by up to an order of magnitude relative to microcrystalline metals with grain size in the micrometer range, and a concomitant decrease in the activation volume v* by two orders of magnitude (14, 15). Nano-twinned copper shows the same characteristics of increased rate sensitivity and reduced activation volume as nanocrystalline copper without twins (4, 5, 12, 13) even when the average grain size is several hundred nanometers. However, it achieves very high strength without severely compromising ductility (4, 5).

The commonly used strengthening model for nanocrystalline metals is the Hall–Petch relation (7, 16), which is a scaling function relating strength to grain size. The Hall–Petch relation is derived based on strengthening mechanisms (17) at internal interfaces, which proliferate in nanocrystals. However, it says nothing about ductility. To model ductility, it is necessary to revisit detailed physical processes at materials interfaces, in particular those involving dislocations, which are the carriers of plastic strain. Dislocation processes at internal interfaces usually involve slip transfer from one inelastic shear system to another (18–21). Various experimental observations, including high-resolution transmission electron microscopy, indicate that the involvement of bulk dislocations is indispensable for the plastic deformation of most nanocrystalline metals at low temperatures (13). The rationale is that, to sustain general plasticity at low temperature, five independent inelastic shear systems are necessary, which could be bulk slip, bulk twinning, GB sliding, GB migration, etc. Mechanisms such as GB sliding or migration, although locally favored [representable by the motion of GB dislocations (22, 23)], are usually geometrically insufficient to sustain general plasticity by themselves. Contributions of bulk dislocation are required in the absence of diffusion, through such processes as bulk dislocation transmission across GB, GB sliding accommodated by bulk dislocation emission at GB triple junctions, etc. These processes can be termed “slip transfer reactions,” because the Burgers vectors (amounts of geometric incompatibility) of bulk or GB dislocations must be conserved between the reactant(s) and product(s). For general discussion, at least one of the reactants or products should be a bulk dislocation. Consider a GB separating bulk crystals 1 and 2. The simplest slip transfer reactions are binary: the absorption of a bulk dislocation into GB to become a GB dislocation b_bulk1 → b_GB, or the reverse desorption reaction b_GB → b_bulk2; but also common are ternary reactions such as b_bulk1 → b_bulk2 + b_GB or b_GB1 → b_GB2 + b_bulk.

Here, we model several prototypical slip transfer reactions, both binary and ternary, near Σ3{111} twin boundary (TB) (a singular GB) (24, 25) by atomistic reaction path calculations (26, 27). The technique we use, the climbing image nudged elastic band (CINEB) method (28), is a chain-of-states atomistic approach (29) that does not suffer from the severe strain-rate limitations associated with molecular dynamics simulations. It has been shown to be extremely valuable for the quantification of thermally activated rate processes (26, 27), i.e., the atomistically calculated activation energy and activation volume can be directly compared with laboratory experiments performed at the time scale of seconds or hours. We have made an important improvement to the original CINEB method by allowing a movable end state as detailed in Methods. By this improvement the computational efficiency is significantly enhanced for an accurate characterization of the saddle points of nanomechanical processes.

Results and Discussion

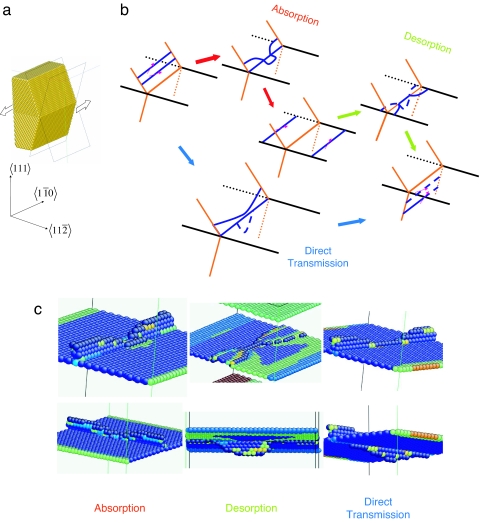
Consider a 〈11̄0〉 screw dislocation shown in Fig. 1 a and b, initially in the upper half of the pure copper bicrystal (bulk 1), subjected to an anti-plane shear stress that drives it toward the TB. Given a prescribed shear strain γ, we first obtain the relaxed atomic configuration using single-point energy minimization. With γ = 0.02, the leading Shockley partial dislocation is held up right at the TB, followed by the trailing Shockley partial ≈4b behind. The far-field resolved shear stress is τ = 252 MPa ≈ 0.006G, where G = 42 GPa is the {111}〈110〉 shear modulus. We also find from single-point calculations that when τ is greater than the athermal threshold stress for transmission τ_tms^ath = 340 MPa, the dislocation transmits across the TB into bulk 2 without the aid of thermal activation. This is in accord with experimentally measured yield strength σ ∼ 1 GPa of nano-twinned copper at room temperature, since the conversion ratio M ≈ 3.1 (Taylor factor) between the macroscopic tensile stress σ in a polycrystal and the resolved shear stress on a slip system (30). The calculated athermal threshold stress for absorption is very close to 340 MPa as well.

Fig. 1.

Atomistic modeling of interface-mediated slip transfer reactions. (a) A symmetric Cu bicrystal with a coherent TB in the middle, subjected to anti-plane shear. The bicrystal is cut to expose a pair of symmetric (111) slip planes inclined at θ = 70.5° with respect to the TB. (b) Schematic of two competing pathways of slip-transfer reaction discovered from CINEB calculations. The first pathway is a two-step process involving the absorption of an incoming screw into the TB, followed by desorption. The second involves direct transmission of the screw across the TB. (c) Atomic configurations of absorption, desorption and direct transmission; two views are shown for each state. Atoms are color coded by the central symmetry parameter, showing the stacking fault and TB.

We probe the kinetic pathways of slip transfer reaction using the CINEB method when the applied shear stress is below the athermal threshold. Two competing pathways are identified as illustrated in Fig. 1b, with the corresponding atomic configurations shown in Fig. 1c. The first path is a two-step process involving the absorption of the incoming screw dislocation into the TB, followed by desorption. Due to the special geometry, there is no residual Burgers vector content left in the TB after the two steps. We find that both absorption and desorption occur by the “Friedel–Escaig”-type cross-slip mechanism (31), where the two partials first constrict to a full screw dislocation, and then spread into TB (absorption) or bulk 2 (desorption). In contrast, the second pathway involves direct transmission of the incoming screw dislocation by the “Fleischer”-type cross-slip (32), where the leading partial penetrates into bulk 2 without waiting for the trailing partial still yet in bulk 1. This process temporarily leaves a sessile stair-rod dislocation on the TB, which is only freed when the trailing partial catches up. Thus, the TB acts as a sink or source of dislocations, as well as a barrier against direct transmission.

According to transition state theory, the rate of slip transfer reaction is given by vexp(−Q/k_BT), where v is the attempt frequency, Q is the activation energy, k_B is Boltzmann's constant, and T the temperature. We have computed the activation energy Q associated with each saddle point. At τ = 252 MPa, the CINEB calculation gives Q_abs = 0.49 eV (absorption) and Q_tms = 0.67 eV (direct transmission), respectively. In contrast, the desorption barrier Q_des is much higher, with a value of >5 eV. The large value of Q_des arises because clean TBs are very deep traps for screw dislocations. Specifically, unlike when they are in the bulk, these Shockley partials in TB are not bound by the stacking fault energy, because their Burgers vectors coincide with the displacement shift complete (DSC) lattice of the TB. With imposed periodic boundary conditions on the simulation supercell, the two TB Shockleys always separate to exactly one-half of the supercell width to minimize their elastic energy. In reality, however, they would separate to infinity on an infinite, clean TB (and simultaneously, the TB would migrate by one atomic spacing in 〈111〉). Thus, large activation energy is needed to constrict the two widely separated TB Shockley partials during desorption.

To demonstrate that TB-mediated slip transfer reactions are indeed the rate-controlling steps of plastic flow, we then compute the true activation volume, Ω ≡ −∂Q/∂τ, which can be taken as a kinetic signature of deformation mechanism (33, 34). We find Ω_abs ≈ 43b³ at τ = 252 MPa. Similarly, we calculate Ω_tms ≈ 79b³ for direct transmission. These true activation volumes from atomistic calculations compare favorably with the experimentally measured apparent activation volume $v*\equiv \sqrt{3}{k}_{B}T\partial \ln \mathrm{\epsilon ̇}/\partial \sigma$ of ≈10–20b³ for nano-twinned copper (13). Here, ε̇ denotes the tensile strain rate; there is a conversion factor $\sqrt{3}/M$ relating Ω to v*. To summarize, our atomistic calculation predicts the following macroscopic properties: σ = Mτ = 780 MPa, $v*=\Omega \sqrt{3}/M=24-44b^3$, $m=\sqrt{3}{k}_{B}T/v*\sigma =0.013-0.023$, at a laboratory strain rate corresponding to Q ≈ 0.49–0.67 eV. This parameter-free prediction is for an idealized situation where the TB is perfect without preexisting dislocations, ρ_int = 0, and the twin lamellae are thin enough (≈10 nm) that only a single bulk dislocation can be stopped at the TB at a given time (no pileup). To our knowledge, this is the first atomistic calculation that predicts reasonable strain-rate dependence of flow stress which can be directly compared with laboratory experiments (Table 1). Also shown for contrast in Table 1 are results from classical theories based on diffusion-controlled processes and bulk forest hardening. They are clearly excluded as possible mechanisms. The calculation result that Q_abs is lower than Q_tms by ≈0.2 eV suggests that absorption is more important than direct transmission near a clean TB (21). Finally, we note that although the quantitative predictions of the present simulations are in reasonable agreement with experimental results, these numbers should be taken as indicative of trends rather than as precise predictions.

Table 1.

Comparison of yield stress, activation volume, and strain-rate sensitivity between experimental measurements and atomistic calculation

		Yield stress	Activation volume v*	Strain-rate sensitivity m
Nano-twinned copper	Uniaxial tension [Lu04]	≈1 GPa
	Nanoindentation [Lu05]	>700 MPa†	12–22b3	0.025–0.036
	Atomistic calculation	780 MPa	24–44b3	0.013–0.023
Diffusion-controlled processes			≈0.1b3	≈1
Bulk forest hardening		$\approx \mu b\sqrt{{\rho }_{\text{bulk}}}$	100–1,000b3	0–0.005

^†Extracted from measured hardness H as H/3.

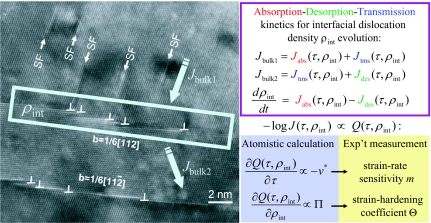
The kinetic rates of slip transfer reactions will dynamically evolve with dislocation accumulation in the TB. Specifically, assuming the same attempt frequency ν for different reactions, a lower Q_abs gives a higher kinetic rate of absorption compared with that of desorption. An imbalance in the rates of absorption and desorption will cause accumulation of interfacial dislocations (see Fig. 2). The accumulated TB dislocations will in turn affect the activation energies due to dislocation–dislocation interactions. According to Le Chatelier's principle, this should be expected to suppress subsequent absorption, enhance desorption, and change the direct transmission rates, such that a quasi-steady state of reactions is eventually reached at the TB.

Fig. 2.

Transmission electron microscopy image shows the accumulation of TB dislocations. Coarse-graining the discrete atomic-scale processes over time establishes an ADT kinetic equation. [Electron micrograph reproduced with permission from ref. 6 (Copyright 2006, Elsevier).]

We coarse-grain over time the above atomic-scale processes to establish an absorption–desorption–transmission (ADT) kinetic equation, shown in Fig. 2, where ρ_int denotes the density of TB dislocations, defined as the total length of TB dislocations per unit TB area. Generally speaking, Δρ_int quantifies the deformation-induced geometric incompatibilities trapped in the interface with reference to the predeformed state. J_tms is the dislocation flux of direct transmission from bulk 1 to 2, J_abs is the dislocation flux of direct transmission from bulk 1 to TB, and J_des is the dislocation flux of direct transmission from TB to bulk 2. The ADT equation should generally serve as the boundary condition for crystal plasticity models that are predicated on bulk dislocation density (ρ_bulk) (35). However, for nanocrystalline metals, the role played by bulk crystal plasticity would be greatly diminished because dislocations seldom stay inside the bulk but are either absorbed into or piled up near the GB. Correspondingly, the role of interfacial plasticity processes, as regulators of bulk dislocation fluxes and as carriers of plastic strain themselves (36), is markedly enhanced. In nano-twinned copper, the twin lamellae may be approximated as transparent (barrierless) to bulk dislocation flux if they are <10 nm thick (4, 13). The main resistance to plastic flow comes from the TBs, which as shown in this work appears to provide a satisfactory estimate of the macroscopic yield stress. Experimentally (24), it has been shown that coherent TBs in Cu can indeed offer GPa-level local resistance against the slip transmission of $\frac{1}{6}$〈112〉 type dislocations.

The rate of transmission J_tms(τ, ρ_int) is proportional to exp(−Q_tms(τ, ρ_int)/k_BT) and similar forms hold for J_abs(τ, ρ_int) and J_des(τ, ρ_int). The sensitivity of Q(τ, ρ_int) and thus J(τ, ρ_int) to their first argument of shear stress τ is given by the activation volume, which we have discussed above. The sensitivity of Q(τ, ρ_int) and J(τ, ρ_int) to the second argument ρ_int turns out to be a critical quantity as well and can be eventually related to ductility. Here we first highlight the physical consequence of this dependence and then present calculations of ρ_int dependence of activation energy Q. We define the interfacial hardening rate as Π ≡ −∂J/∂ρ_int|_τ that describes hardening of the TB as it becomes less coherent with more interfacial dislocations deposited in it. If it is assumed that the macroscopic yield stress of a nanocrystal is dominated by interfacial resistance to dislocation motion [the essence of the Hall–Petch relation (7, 9)], then it should be plausible that the macroscopic strain hardening rate Θ ≡ ∂σ/∂ε|_ε̇ [or the lack thereof (5)] reflects also, to a large degree, the interfacial hardening rate or the lack thereof. Thus, a linear relationship between Θ and Π would be expected.^‖ Θ is important because it directly governs the ductility of most nanocrystalline metals, which fail by severe plastic strain localization (5, 37). The higher the Π and therefore Θ, the better the ductility and the larger the range of uniform elongation, because according to Hart's criterion (38), Θ < (1 − m)σ for the initiation of plastic strain localization (5, 39).

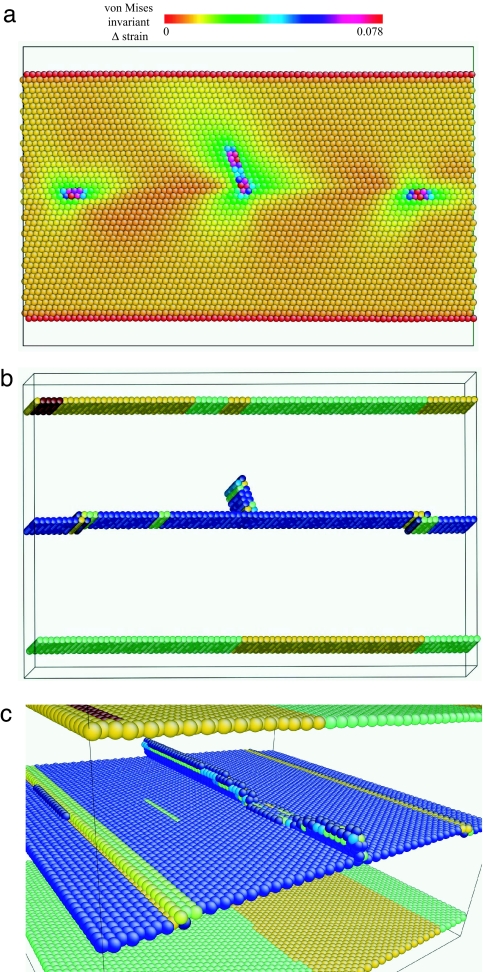
Our atomistic calculations show that the activation barriers Q(τ, ρ_int) of TB-meditated slip transfer reactions depend sensitively on ρ_int. Consider, as an example, the process of absorption. By introducing an extra pair of Shockley dislocations in the TB, we find that Q_abs increases from 0.49 to 1.01 eV, at identical far-field stress τ = 252 MPa (see Fig. 3). Similarly, the direct transmission barrier Q_tms increases from 0.67 to 1.3 eV. Thus, ρ_int dramatically influences Q(τ, ρ_int). Generally, we find that as ρ_int increases, both Q_abs(τ, ρ_int) and Q_tms(τ, ρ_int) increase, but Q_des(τ, ρ_int) decreases, such that eventually a dynamic steady state can be established in the ADT kinetics, and ρ̇_int → 0.

Fig. 3.

Screw dislocation absorption under the influence of preexisting TB dislocations. The preabsorption equilibrium state is shown in a and b; the transition state is shown in c. Atoms are color coded by Mises invariant of local strain (subtracting off the average strain) in a, showing elastic interaction of the incoming screw with two TB Shockley partials, and the central symmetry parameter (b and c). Note that the TB has migrated by one step after absorbing the two TB Shockley dislocations.

The real situation is much more complex, however. Instead of the present arrangement, where the Burgers vector lies in the TB plane, the incoming and outgoing dislocations may carry a net Burgers vector with out-of-plane components (18, 20, 21) and also leave behind residual dislocations on the TB after transmission. We therefore expect a 2D interfacial dislocation network to develop on the TB during general deformation, in which case both ρ_int and the J-fluxes should be tensorial quantities (35) instead of scalars. Furthermore, interfacial dislocations move and react on the interface, as well as “leak” at triple junctions, leading to additional terms in the ADT kinetic equations. Nonetheless, the following general points can be made. Work hardening (33) in the bulk obeys the ρ_bulk^1/2 law that can be rationalized based on the scaling argument of a governing lengthscale, the forest dislocation spacing L ∝ ρ_bulk^−1/2. The same scaling argument should be applicable to interfacial dislocation hardening (40). Note that the governing lengthscale L is ∝ ρ_int⁻¹ now because the interfacial dislocation networks are 2D because they are trapped inside the GBs and can only densify in-plane. Then we have an interfacial hardening law σ = σ₀(d) + h(d)μbρ_int, where h is dimensionless and depends only on the grain size, and μ denotes shear modulus of the polycrystal sample. Similar to bulk work hardening, as the governing lengthscale L (mesh spacing of interfacial dislocation network) refines, the material should harden, and the activation volume should decrease (for the same strain rate), compared with ρ_int = 0 values. Thus, our σ and v* predictions based on calculations at ρ_int = 0 seem to “err” on the right side compared with experiments.

The proposed hardening law σ = σ₀(d) + h(d)μbρ_int governing interfacial plasticity should work well for low-angle GBs, as well as GBs close to special boundaries, when ρ_int (∝ crystallographic ledge density on GB) is small. However, as ρ_int increases to a point where the interfacial dislocation cores start to overlap, saturation must set in, similar to plateauing of the GB energy at large misorientation angle (41). Then the GB hardening rate Π approaches zero. This may explain the generally poor ductility of common nanocrystals produced by powder consolidation or electrodeposition, because most of their GBs are high-angle (37). Consequently, Π is small, and therefore the grain assembly is susceptible to plastic strain localization. In contrast, nano-twinned copper has superior uniform elongation because TBs are singular interfaces^†† and are much more hardenable when they gradually lose coherency during deformation. This gives rise to an increased strain hardening rate and a consequent delay in the onset of necking (5) that leads to the improved tensile ductility.

In summary, the present modeling framework extends the time scale of atomistic simulations to provide mechanistic insights into the roles played by twin boundaries as nanostructural features that critically affect strength, rate sensitivity, and ductility. The reaction pathway calculation is critical for quantifying the realistic activation energy and activation volume of three-dimensional slip transfer reactions, so that a quantitative connection can be made between atomistic modeling and experimental measurements (Table 1). The atomistic approach presented here is general in that it is potentially capable of revealing the effects of interfacial structure, elastic anisotropy, stacking fault energy, and crystal structure, although the present results deal primarily with nano-twinned copper. Our study further highlights the essential fact that interfaces evolve in concert with the bulk during deformation: the ADT equation is a minimal description of the evolution dynamics of internal states ρ_int of the interfaces, which greatly influence the activation barriers of interfacial plasticity processes. The results reported in this work reveal the mechanistic underpinnings of the strength–ductility trade-offs in plastically deforming materials and point to possible routes for optimizing strength and ductility in nanostructured metals through controlled introduction of coherent internal interfaces.

Methods

The simulation cell consisted of a symmetric Cu bicrystal with a coherent Σ3{111} TB in the middle. The cell size was 8.9 nm × 11.8 nm × 7.7 nm (17.7 nm × 11.8 nm × 15.3 nm), with a total of N_a = 56,400 (225,600) atoms; all of the reported values were calculated by using the large cell, although the small cell provided satisfactory energetics in most cases. Periodic boundary conditions were imposed in both the 〈112〉 and 〈110〉 directions, with free space above the top and below the bottom (111) surfaces. As shown in Fig. 1a, in the adjoining bicrystal a pair of symmetric (111) slip planes were inclined at θ = 70.5° with respect to the twin plane, and they intersected along a common line in the TB. We probed slip transfer reactions between this particular pair of slip planes as well as between any one of them and the TB. We considered a straight dislocation that encounters the TB in screw orientation, i.e., the Burgers vector is parallel to the intersection of the slip plane and TB. This screw can cross-slip without leaving any residual content (e.g., stair-rod type dislocation) at the intersection of the slip plane in the TB. The interatomic interactions were modeled by using the embedded-atom method (EAM) potential for Cu by Mishin et al. (43), which has been validated against ab initio calculations (44). The stacking-fault energy given by the potential was 44.4 mJ/m², close to the experimental measurement of 45 mJ/m². The stress acting on the simulation cell was calculated by using the Virial formula (44).

We quantified the TB-mediated slip transfer reactions using atomistic reaction path calculations (26, 27, 45). Under a given shear stress, the CINEB method was used to determine the minimum energy path (MEP) of reaction. The activation energy was given by the maximum on the MEP, a saddle point on the potential energy surface of the system. In a CINEB calculation, two end states are first determined, then a discretized elastic band consisting of a finite number of replicas of the system (nodes) is constructed by linear interpolation to connect the two states. With appropriate relaxation, the band converges to the MEP. In our calculations of dislocation-TB reactions, e.g., direct transmission, we chose an initial state where a screw dislocation in the upper crystal was fully relaxed and held up at the TB, and a final state where the dislocation has cross-slipped into the lower crystal but before reaching the fully relaxed state where it exits the crystal.

The following describes the free-end CINEB method. To relax the elastic band, we improved the original CINEB method (28) by allowing a movable end state while keeping its energy unchanged. The end node (28) R_N now moved according to a force

where V(R_N) is the potential energy, and k_N is the “spring force” that node R_N−1 exerts on node R_N. The band was then able to “swing,” but the end node would be constrained on a potential energy contour (to enforce this constraint numerically, we also performed a quasi-Newton step after one relaxation step of Eq. 1). This way, one can keep the moving end state close to the saddle-point state. In our calculations, the final-state energy was fixed at 0.1 eV below the initial state, separated by the barrier. As a result, the number of replicas along the band could be significantly reduced while retaining a reasonable density of replicas near the saddle-point state, e.g., seven replicas are sufficient to obtain a converged saddle point. It can be proven that when the free-end algorithm converges, the band lies along a MEP even though the final state is not a local minimum.

The true activation volume Ω ≡ −∂Q/∂τ is related to the strain-rate sensitivity that one can measure experimentally. Physically, Ω is proportional to the number of atoms that undergo coherent inelastic displacements at the saddle point. We can compute Ω by calculating two saddle energies at slightly different stresses and then performing numerical differentiation, but there is also a second approximate estimate based on perturbation theory (45) that does not require two calculations, Ω ≈ Ω_xtal(τ_i − τ_s)/G, where Ω_xtal is the volume of bicrystal, G is the {111}〈110〉 shear modulus, and τ_i, τ_s are the Virial shear stress of the initial and saddle-point state, respectively, when the load is applied via displacement control identically on all MEP replicas.

Abbreviations

ADT

absorption–desorption–transmission

CINEB

climbing image nudged elastic band

GB

grain boundary

TB

twin boundary.