Cortical pooling algorithms for judging global motion direction

Abstract

Physiological studies suggest that decision networks read from the neural representation in the middle temporal area to determine the perceived direction of visual motion, whereas psychophysical studies tend to characterize motion perception in terms of the statistical properties of stimuli. To reconcile these different approaches, we examined whether estimating the central tendency of the physical direction of global motion was a better indicator of perceived direction than algorithms (e.g., maximum likelihood) that read from directionally tuned mechanisms near the end of the motion pathway. The task of human observers was to discriminate the global direction of random dot kinematograms composed of asymmetrical distributions of local directions with distinct measures of central tendency. None of the statistical measures of image direction central tendency provided consistently accurate predictions of perceived global motion direction. However, regardless of the local composition of motion directions, a maximum-likelihood decoder produced global motion estimates commensurate with the psychophysical data. Our results suggest that mechanism-based, read-out algorithms offer a more accurate and robust guide to human motion perception than any stimulus-based, statistical estimate of central tendency.

The brain depends on sensory information to make evolutionary stable decisions that guide the behavior of an organism. In transforming incoming sensory information into a perceptual decision, the brain must combine, or “pool,” neural signals from early sensory cortex into a representation that can be decoded by decision networks at later stages of processing. The fundamental psychophysical and neural mechanisms mediating early sensory processing are relatively well understood, but we are only beginning to elucidate how cortical decision networks collate their sensory input to form stable and reliable decisions.

Physiological studies have exploited the strict organization of the middle temporal (MT) visual area in extrastriate cortex to delineate the major neural steps in the transformation of visual information to a perceptual decision (1, 2). MT is central to visual motion perception: Neural activity is broadly tuned for retinal position as well as the direction and speed of stimuli (3–7). Moreover, activity is equally sensitive to and covaries with a monkey's direction discrimination performance (8–11). The representation of motion direction in MT is topographically organized and superimposed on a coarse retinotopic map: Columns of neurons oriented perpendicularly to the pial surface respond to similar directions of motion and retinal positions (12, 13). Cortical networks downstream from MT access its neural representation of visual motion to direct many forms of behavior, including saccadic and smooth pursuit eye movements (14) and perceptual judgements of motion direction (15, 16) and speed (17).

A key question that remains unanswered is exactly how cortical networks executing different forms of behavior decode the neural representation of visual motion in MT. Numerous physiological studies have attempted to distinguish between two population coding algorithms for reading out directionally tuned activity in MT: “vector average” (population vector of stimulus direction and magnitude calculated from average, direction-tuned neural responses weighted in proportion to their magnitude) and “winner-take-all” (most active directionally tuned column of MT neurons). In a series of pioneering studies combining visual stimulation with electrical microstimulation in monkeys, Newsome and colleagues (14, 18, 20) found that the algorithm deployed by cortical networks to decode the motion representation in MT depends on both task demands and the behavioral objective of the monkey. When discriminating very different visual motion directions, the perceptual system employs a winner-take-all algorithm (18), whereas the saccadic and smooth-pursuit eye movement systems read off the vector average of competing velocity signals in MT (14, 19). Moreover, monkeys' performance on a free report task that incorporated elements of both of these experiments was mediated by a vector average algorithm when the direction preferences of visually and microstimulated neurons differed by <140° and by a winner-take-all algorithm when they differed by more than this value (20).

However, winner-take-all and vector average algorithms are not optimal in every sensory situation. For example, a monkey's performance on a fine direction-discrimination task is better explained by an algorithm that selectively pools the most sensitive neurons (21). Furthermore, a growing body of work suggests that the likelihood function, representing the probability that a range of stimuli gave rise to the neural response, is an optimal estimator of performance on a wider range of perceptual tasks (22–27). Maximum-likelihood algorithms have been successfully applied to various sensory domains, including orientation perception (28), motion perception (29), and multisensory integration (30).

Surprisingly few human perceptual studies have investigated how the activity of directionally tuned mechanisms at late stages of motion processing is decoded to guide global motion perception. The few studies that have considered this question suggest that human observers exploit the statistical characteristics of stimuli to judge the direction and speed of global motion (31–35). Human perceptual judgments tend to coincide with the mean direction of a moving dot field when local dots directions are drawn from a uniform distribution with a restricted range (32). Having said this, when a small number of local directions dominate a moving dot field, observers' judgments are biased away from the mean toward the modal (31) direction of motion.

Thus, at present, it is unclear whether cortical decision networks simply exploit the statistical characteristics of moving stimuli or deploy one of a number of potential read-out algorithms to guide human perceptual judgements of global motion direction. Here we examine whether estimating the central tendency of the physical direction of global visual motion provides a better indication of perceived direction than an algorithm that reads from directionally tuned mechanisms at late stages of motion processing.

Results

Statistical Guides to the Perceived Direction of Global Motion.

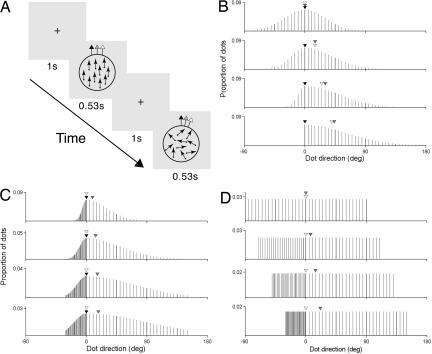
Our first objective was to determine the extent to which statistical characteristics of moving stimuli influence the perception of visual motion direction. In the first experiment, we sought to determine the relationship between the perceived and modal direction of global motion. The task in this and subsequent experiments was to judge whether a standard or comparison random dot kinematogram (RDK) had a more clockwise (CW) direction of motion (Fig. 1A). Dots of the standard RDK moved in a common direction (i.e., the vector average, median and modal direction were identical), randomly chosen on each trial from a range spanning 360°. Dot directions of the comparison RDK were sampled discretely from a Gaussian probability distribution. Across four conditions, we independently varied the half widths [standard deviations (SDs) counter-clockwise (CCW) and CW to the mode] of the distribution (see Fig. 1 B–D and Methods) to generate a modal direction for the comparison RDK that was increasingly distinct from the vector average and median directions.

Fig. 1.

Direction discrimination task and distributions of dot directions. (A) Direction discrimination task in which observers judged which of two sequentially presented RDKs had a more CW direction of motion. (B–D) Distributions of dot directions for the comparison RDK in each experiment, respectively. Arrows (A) and arrowheads (B and C) show the vector average (gray), median (white), and modal direction (black) of the comparison RDK.

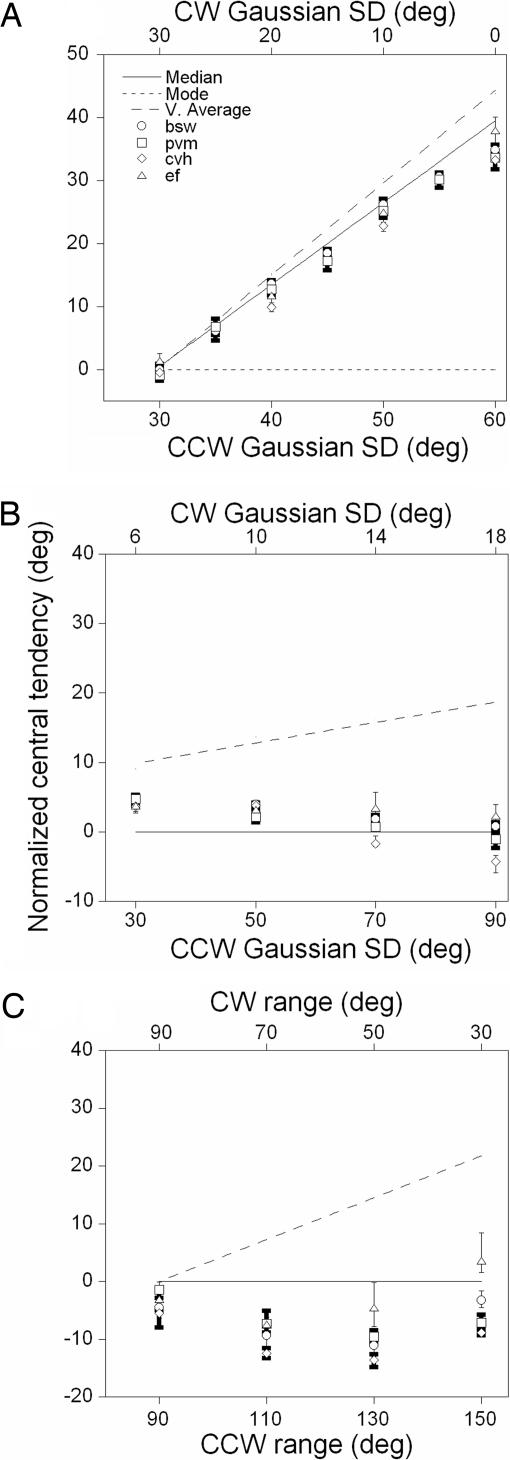
We expressed the data collected in each condition as the percentage of trials on which observers judged the modal direction of the comparison as more CW than the direction of the standard as a function of the angular difference between them. From logistic fits to these data, we estimated the modal direction of the comparison that had the same perceived direction as that of the standard (see Methods). Fig. 2A shows the results of this analysis for four observers as a function of the half-widths of the distribution of dot directions for the comparison RDK (symbols). Values on the ordinate are normalized to the modal direction of the comparison (dotted line). As the clockwise (CW) and counter-clockwise (CCW) half-widths of the distribution of dot directions narrow and broaden, respectively, the perceived direction of motion diverges from the modal direction toward the median (solid line) and vector average (dashed line). When dot directions for the comparison were drawn from a Gaussian with a CCW SD of 60° and a CW SD of 0°, the modal direction of the comparison had to be rotated, on average, by 35° to be indistinguishable from the standard. Clearly, the perceived direction does not match the modal direction [mean square error (MSE) between the perceived (average of four observers) and modal direction of physical motion, 494.46]. Rather, it appears to coincide relatively closely with the median direction (MSE, 1.7) and to a lesser extent with the vector average (MSE, 29.82).

Fig. 2.

Correspondence between perceived and statistical directions of global motion. (A) Symbols show for four observers the normalized modal direction of the comparison RDK with the same perceived direction as that of the standard as a function of the half-widths of the distribution of directions for the comparison RDK. Lines are the vector average (dashed), median (solid), and modal (dotted) direction of the comparison RDK. (B) Same as A for the second experiment. (C) Same as A with the exception that symbols show the normalized median direction of the comparison with the same perceived direction as that of the standard as a function of the half-widths of the distribution of directions for the comparison. Error bars: 95% CIs based on 5,000 bootstraps.

In a second experiment, we adopted the same approach used in the first with the following exception. In addition to varying the half-widths of the Gaussian distribution of directions for the comparison RDK, we sampled the CCW and CW halves of the distribution at 5° and 1° intervals, respectively. Using this method, we were able to generate distributions of dot directions for the comparison RDK with the same mode and median but an increasingly disparate vector average.

Fig. 2B shows the results of this experiment plotted and notated in the same fashion as in Fig. 2A. As the CCW and CW half-widths of the distribution of dot directions broaden, the perceived direction of motion diverges from the vector average and converges on the median (and modal) direction of motion. When the distribution of dot directions for the comparison had a CCW SD of 90° and a CW SD of 18°, the median direction of the comparison had to be rotated, on average, by only 0.5° to be indistinguishable from the standard. Once again, it is apparent that the perceived direction of motion does not match the vector average (MSE, 177.83) but does conform closely to the median direction of stimulus motion (MSE, 7.42).

Both experiments suggest that there is a close, but imperfect, correspondence between the perceived and median direction of global motion. One advantage of this strategy is that the median is a robust estimator of central tendency that minimizes the impact of outlying motion directions on the global percept. The aim of the third experiment was to determine whether we could produce the same pattern of results when the dot directions of the comparison RDK were chosen from a uniform (rectangular) distribution, which has no mode and equivalent energy at each local motion direction. To generate a median that was increasingly distinct from the vector average direction for the comparison RDK, we independently varied the ranges and used different sampling densities on the CCW and CW sides of the median of the distribution (see Fig. 1D and Methods).

To compare directly the perceived and median directions of motion, we estimated the median direction of the comparison that had the same perceived direction as that of the standard. Fig. 2C shows the results of this analysis as a function of the CCW and CW ranges of the distribution of dot directions for the comparison RDK. Values on the ordinate are normalized to the median direction of the comparison (solid line). When the distribution of dot directions for the comparison had a CCW range of 110° and a CW range of 70°, the median direction of the comparison had to be rotated, on average, by 9.14° to be indistinguishable from the standard. Therefore, when a moving stimulus consists of local directions with equivalent motion energy, there is a poor correspondence between the perceived and median global direction of motion (MSE, 51.58). Vector average (dashed line) is an even poorer estimator of perceived direction (MSE, 381.45), suggesting that computing the central tendency of the physical direction of global motion is not a particularly robust cue to the perceived direction of motion.

Neural Algorithms for Reading Out Global Motion Direction.

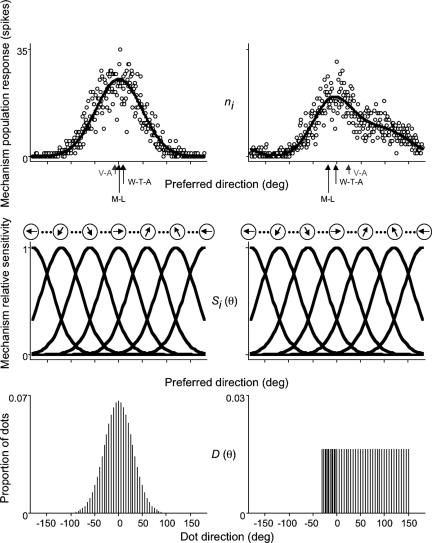
Our second objective was to determine whether an algorithm that reads from the activity of directionally tuned mechanisms near the end of the motion pathway offers a better estimate of the perceived direction of global motion. To tackle this question, we modeled the data collected in the three experiments on a trial-by-trial basis with three read-out algorithms: maximum likelihood, winner-take-all and vector average (see Fig. 4 and Methods). Briefly, each model consists of a bank of evenly (1°) spaced directionally tuned mechanisms that respond to a distribution of dot directions with a Gaussian sensitivity profile that is corrupted by Poisson noise. Chosen to be within the range obtained in previous psychophysical studies on the directional tuning of motion mechanisms (36–38) and physiological studies on the directional tuning of MT neurons (7, 39, 40), the bandwidth (half-width at half-height) of each mechanism was fixed at 45°. Maximum likelihood estimates the perceived direction of motion from the weighted sum of responses for the population of mechanisms, where the activity of each mechanism is multiplied by the log of its tuning function. Winner-take-all estimates perceived direction as the preferred direction of the most active mechanism from the population of responses; vector average arrives at a corresponding estimate by averaging the preferred directions of all mechanisms weighted in proportion to the magnitude of their responses. Vector average produced very similar estimates of the perceived direction of motion (data not shown) to that of the vector average direction of physical global motion. Because we have already shown that the vector average of local motions in the stimulus is a consistently poor predictor of perceived direction, we now concentrate on maximum likelihood and winner-take-all.

Fig. 4.

Estimating the perceived direction of global motion with different read-out algorithms. Schematic illustration of how we derived estimates of the perceived direction of motion with three read-out algorithms: maximum likelihood (M-L), winner-take-all (W-T-A), and vector average (V-A). On each trial, a bank of evenly spaced directionally tuned mechanisms (Middle) responds to a distribution of dot directions (Bottom). The number of spikes elicited in a response to a stimulus is Poisson distributed. We derive the average population response (solid line, Top) on a trial-by-trial basis (open circles, Top) to a given distribution of dot directions from the summed responses of the local directionally tuned mechanisms. The estimated perceived direction of motion of maximum-likelihood, winner-take-all, and vector-average algorithms are the same when dots are drawn from a symmetrical, in this example, Gaussian distribution (Left Bottom), but different when dots are drawn from an asymmetrical, in this case, uniform distribution (Right Bottom).

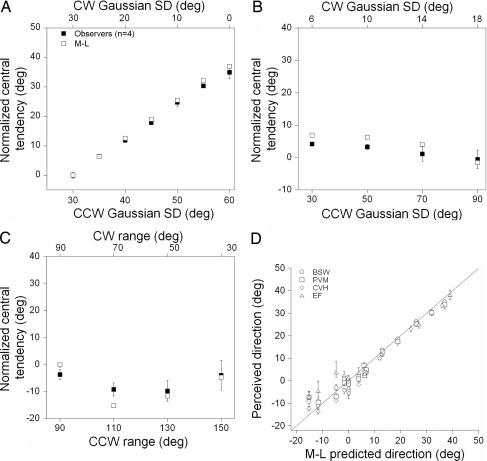
Both algorithms provided very accurate estimates of perceived direction in all stimulus conditions, but the variance of winner-take-all's estimate was consistently larger than that of maximum likelihood. Because maximum likelihood is an unbiased, optimal estimator of perceived direction with minimal variance over trials, we chose to present its estimate of perceived direction. Filled symbols in Fig. 3 A–C show the perceived direction of motion of the four observers (mean ± SD) plotted in the same fashion as Fig. 2 A–C. Open symbols show the estimated global motion direction of the maximum-likelihood algorithm. Unlike the median direction of physical global motion, maximum likelihood captures the variability in the perceived direction of different global patterns of motion in each experiment. [The MSE between the data of the four observers and the maximum likelihood algorithm was 1.32 (Fig. 3A), 6.56 (Fig. 3B), and 13.3 (Fig. 3C) for each experiment, respectively.] This point is reinforced in Fig. 3D, which shows the perceived direction of motion of each observer in each experiment as a function of the predictions of the maximum-likelihood algorithm. All data points cluster around the unity line, indicating that maximum likelihood provides a robust estimate of the perceived motion direction, explaining, on average, 96% of the variance in the performance of observers across all stimulus conditions.

Fig. 3.

Estimating the perceived direction of global motion with maximum likelihood. (A–C) Filled symbols show the perceived direction of motion of four observers (mean ± SD) in each experiment plotted as in Fig. 2. Open symbols show the estimated perceived direction of motion of the maximum-likelihood model. (D) Perceived direction of each observer in each experiment as a function of the predicted perceived direction of maximum likelihood.

Discussion

We investigated whether the central tendency of the physical direction of global visual motion was a better guide to the per-ceived direction of global motion than an algorithm that reads from directionally tuned mechanisms at late stages of motion processing. In global dot motion direction discrimination, there was a close correspondence between the median and perceived direction of motion if the pattern of motion consisted of a small number of dominant local directions, but much less so if it consisted of equivalent energy at each local motion direction. Regardless of the local composition of motion directions, both maximum-likelihood and winner-take-all read-out algorithms provided a much more robust guide to the perceived direction of global motion.

Previous psychophysical studies claim that estimates of the central tendency of the direction of global dot motion predicts the perceived direction of motion (31, 32). For example, Williams and Sekuler (32) found that a pattern appears to drift in a direction close to the mean of the dot directions when their range is constrained to be <180°. However, they used symmetrical distributions of dot directions and therefore could not distinguish the mean from other measures of central tendency. When a distribution of dot directions is skewed asymmetrically, the perceived direction can be biased away from the mean toward the modal direction of global motion (31). Zohary et al. (31) found that observers' judgements switched between the mean and modal direction, suggesting that the visual system has access to the entire distribution of local directions and adopts a flexible decision strategy. However, they did not consider the possibility that observers based their performance on the median direction of motion, which we have shown to be a better estimate of the global percept for patterns of motion dominated by small numbers of local directions. That said, in the present study the median failed to provide an accurate estimate across all conditions tested, suggesting that basing motion direction judgements on the statistical characteristics of a moving stimulus is not a reliable strategy for the visual system.

Zohary et al. (31) also assumed that the mode of an asymmetrically skewed distribution of dot directions corresponded to the most active directionally tuned mechanism. We have shown that this is not the case: The modal direction of patterns composed of asymmetrical distributions of directions is very different from that estimated by a winner-take-all, with the latter providing considerably more accurate estimates of the perceived direction. Indeed, both maximum likelihood and winner-take-all provided much more accurate and robust estimates of the perceived direction of global motion than any estimate of central tendency. This result demonstrates the benefit of designing stimuli that distinguish the statistical characteristics of physical stimulation from the underlying putative perceptual mechanism. Stochastic patterns composed of asymmetrical distributions of the parameter of interest are ideal for this purpose and as such may be a useful resource for future experimentation on motion perception. Such patterns could be used in physiological studies to distinguish between putative algorithms deployed by cortical networks to decode the velocity representation in MT. Similarly, psychophysical studies could use analogous stimulus distributions to study speed mechanisms. By way of example, Watamaniuk and Duchon (35) found that observers tend to base speed judgements on changes in the mean dot speed rather than the median or mode speeds. It follows from our results that an algorithm that reads from a bank of speed-tuned mechanisms may offer a better estimate of speed perception than the mean physical speed of motion.

Both physiological and computational studies have shown that winner-take-all and maximum likelihood are members of a group of algorithms deployed by cortical decision networks to read from the motion representation in MT (14, 18, 20–27, 41). This encourages the view that performance on our task is mediated by cortical decision networks that read from the motion representation in the human homologue of monkey MT (26, 41). Whether or not decision networks adopt a flexible strategy, deploying different population coding algorithms to meet the prevailing behavioral objective (14, 18, 20, 21), or use a singular probabilistic read-out strategy in MT (41), remains open to debate. The significance of our results is that read-out algorithms, such as maximum likelihood, offer a more accurate and robust guide to human motion perception than the statistical characteristics of physical stimulation.

Methods

Observers.

Four observers with normal or corrected-to-normal vision participated. Two were authors (B.S.W. and P.V.M.) and two (C.V.H. and E.F.) were naïve to the purpose of the experiments.

Stimuli.

RDKs (Fig. 1A) were generated on a Macintosh G5 (Apple, Cupertino, CA) by using software written in C. We displayed the RDKs on an Electron 22 Blue IV monitor (LaCie, Hillsboro, OR) with an update rate of 75 Hz at a viewing distance of 76 cm. Each RDK (generated anew before each trial) consisted of 10 frames, sequentially displayed at 18.75 Hz. Each frame consisted of 226 dots (luminance 0.05 cd/m²) on a uniform background (luminance 25 cd/m²) within a circular window (diameter 12°). The dot diameter was 0.1° and density was ≈2 dots/deg². On the first frame of a motion sequence, dots were randomly positioned inside the circular window; on subsequent frames, they drifted in a specified direction at 5°/sec. Dots that fell outside the circular window were redrawn inside at a random location.

Procedure.

Observers judged which of two sequentially presented RDKs had a more CW direction of motion. On each trial, we presented a standard and comparison RDK in a random temporal order, each presented for 0.53 sec and separated by a 1-sec interval containing a blank screen of mean luminance (Fig. 1A). The dots of the standard RDK were displaced in the same direction, randomly assigned on each trial from a range spanning 360°. For the comparison RDK, the direction of each dot displacement was drawn, with replacement, from a probability distribution and was independent of both its own direction on previous frames and the directions of other dots.

In the first experiment, dot directions of the comparison RDK were discretely sampled at 5° intervals from a Gaussian distribution spanning a total range of 180° (Fig. 1B). We assigned each half of the Gaussian (i.e., directions CW and CCW to the modal direction) a different SD, thus generating asymmetrically distributed directions of dot motion. The SD of the CCW half of the Gaussian was 30°, 40°, 50°, or 60°; the corresponding values for the CW half were 30°, 20°, 10°, or 0°.

In the second experiment, dot directions of the comparison RDK were discretely sampled from a Gaussian (Fig. 1C) with an SD of 30°, 50°, 70°, or 90° for the CCW half and 6°, 10°, 14°, or 18° for the CW half. We sampled the CCW and CW halves of the distribution at 5° and 1° intervals, respectively. This technique generated asymmetrical distributions of dot directions with the same mode and median but a different vector average. For both experiments, the modal direction of the comparison RDK was randomly chosen on each trial using the Method of Constant Stimuli.

In the final experiment, for the comparison RDK we generated a uniform (rectangular) distribution of dot directions with a total range of 180° (Fig. 1D). We assigned each half of the distribution (i.e., directions CW and CCW to the median direction) a different range and sampling density. Dot directions for the CCW half of the distribution were sampled at 5° intervals over a range of 90°, 110°, 130°, or 150°; the corresponding values for the CW half were 90°, 70°, 50°, or 30°. The median direction of the comparison RDK was randomly chosen on each trial by using the Method of Constant Stimuli.

Data Analysis.

For each condition, observers completed 3–7 runs of 180 trials. Data were expressed as the percentage of trials on which observers judged the modal (experiments 1 and 2) or median (experiment 3) direction of the comparison as more CW than the standard as a function of the angular difference between them and fitted with a logistic function:

where y is the percentage of CW judgements, μ is the stimulus level at which observers were unable to distinguish between the directions of the standard and comparison, and β is an estimate of direction discrimination threshold.

We modeled the pooling of local directional signals with three algorithms: maximum likelihood, winner-take-all, and vector average (Fig. 4). We simulated each model's performance on the direction discrimination task performed by the observers on a trial-by-trial basis using analogous methods. Each model consisted of a bank of evenly spaced directionally tuned mechanisms spanning 360°, each of which responded to a limited range of local directions with a Gaussian sensitivity profile that was corrupted by Poisson noise. The center-to-center separation between adjacent mechanisms was fixed at 1°. The sensitivity of the ith mechanism, centered at θ_i, to direction of motion θ is

where h is the bandwidth (half-height, half-width), fixed at 45°. The response profile of the ith mechanism to stimulus D with a distribution of dot directions, D(θ), is

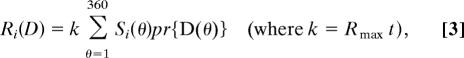where R_max is the maximum mean firing rate of the mechanism (to a stimulus in which all dots move in the preferred direction) in spikes per sec (60), t is stimulus duration, and pr{D(θ)} is the proportion of dot directions in the distribution. The number of spikes (n_i) elicited in response to a stimulus on a given presentation is Poisson distributed with a mean of R_i(D):

The log likelihood of any stimulus D is computed as a weighted sum of the responses of the population of mechanisms, where the activity of each mechanism is multiplied by the log of its tuning function (24):

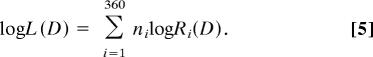The estimated direction is the value of θ_i for which log L(D) computed for all D is maximal. To obtain the estimated direction of the comparison from the winner-take-all model, we read off the preferred direction of the peak of the population response; to obtain the corresponding estimate from the vector average model, we calculated the average of the preferred directions of all mechanisms weighted in proportion to the magnitude of their responses.

Abbreviations

CW

clockwise

CCW

counter-clockwise

MSE

mean square error

MT

middle temporal

RDK

random dot kinematogram.