Color accuracy of commercial digital cameras for use in dentistry

Summary

Objectives

The use of calibrated, commercial digital cameras for dental applications is promising. The color accuracy of various calibration models were evaluated as applied to three commercial digital cameras for use in dental color matching.

Methods

CIE LAB values of 264 color patches and 65 shade tabs were measured with a spectroradiometer. Digital images of the samples were taken with the Nikon D100, Canon D60 and Sigma SD9 cameras. Four regression models were formulated from the color patch CIE LAB and the digital image values. Shade tab CIE LAB colors were predicted by applying the digital image values into the calibration models and were compared to the measured CIE LAB values. The Wilcoxon Rank-Sum test determined if the 12 camera/calibration models differed significantly from the color measurement setup.

Results

Every camera/calibration model (ΔE’s ranging from 1.79 to 5.25) showed a statistically significant difference from the color measurement setup.

Significance

Commercial SLR digital cameras when combined with the appropriate calibration protocols showed potential for use in the color replication process of clinical dentistry.

Introduction

The use of commercial digital cameras to capture accurate color in dentistry is advantageous in the color replication process [1] for any craniofacial prosthesis, given the potential to capture the polychromatic color of the structure, as well as form, texture and perceived translucency [2,3]. Use of commercial digital cameras in dental applications is also relevant to clinical research investigating color, and appealing, given the availability and relatively low cost of the cameras, as well as the ability to share calibration models easily.

When using instruments to capture color for clinical relevance, it is important to define the color difference parameters. The two parameters include the magnitude of color difference (ΔE) that is perceptible and acceptable by human observers. Perceptibility refers to the detection of color difference between a tooth and an adjacent colored restoration, while acceptability refers to the acceptance of the color of that restoration. The magnitude of perceptible and/or acceptable color difference for human observers is still not well-defined, nor ideally measured in dental color research. Perceptible color differences range from a ΔE of 1[4] and 2[5] in in-vitro studies to 3.7 in an in-vivo study [6]; while acceptable color differences can range from a ΔE of 2.72[7] and 3.3[8] for in-vitro studies to 6.8 in an in-vivo study [6].

Color information received from digital cameras is device-dependent, i.e. the actual color information (usually presented in red–green–blue or RGB color space) is different among different devices. Proper calibration and color adjustment among the digital devices is required for accurate color management [9,10]. In this study, the device-dependent color images of input devices (i.e. digital cameras) were converted to a standard device-independent color space (i.e. CIE LAB and XYZ).

Calibration of a very high-resolution studio camera based on line-scan capture technology has been carried out previously [10]. Least squares polynomial regression models were used to obtain a mapping of RGB values to XYZ color space. Six interpolation functions of orders 1 through 3 were evaluated. The average modeling accuracy obtained in the study was CMC (1:1) ΔE = 1. Given the lack of information in the literature, the purpose of this study was to evaluate the color accuracy of various calibration models on three conceptually different commercial digital single lens reflex (SLR) cameras for use in dentistry and to compare the calibration accuracy to the accuracy of the color measurement setup. Accuracy was defined as the CIE LAB color difference between the dentally relevant object (shade tab) and the image of that shade tab, as predicted by the calibration models for the digital cameras.

Materials and methods

Color measurement

A spectroradiometer (PR 705, Photo Research Inc., Chatsworth, CA, USA) and two D-65 desktop lamps (Sol-Source, GretagMacbeth, New Windsor, NY, USA) were fixed on an optical table (Mecom Inc., Risingsun, OH, USA), providing an optical setup of 0° observation and 45° illumination to the object (Fig. 1). For all color measurements in this study, spectral reflectance were obtained from 380 to 780 nm with a 2 nm interval and subsequently converted to CIE LAB values (D65 illumination and 2° observer).

Figure 1.

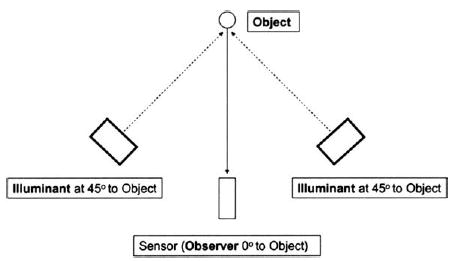
Schematic view of the experimental set-up.

The experimental measurement setup was evaluated for stability, accuracy and repeatability. To evaluate stability, spectral measurements of a smooth and homogenous white tile (SW) with known spectral reflectance were made 10 min after turning on the light source and the spectroradiometer. A total of 24 spectral measurements of SW were made every 10 min for 4 h. The initial incident light I_i(λ) was determined using Eq. (1) [11], because the spectral reflectance R_(λ) of SW was known and the reflected light I_o(λ) could be measured at time zero. All subsequent measurements of SW could be determined in this way. The reflectance data were then converted to CIE LAB values (D65 illumination and 2° observer) with respect to the initial incident light at time zero.

$$R_{(\lambda )}=\frac{I_{o(\lambda )}}{I_{i(\lambda )}}$$ (1)

To evaluate accuracy, color measurements were carried out on 24 color patches (Mini Color Checker, GretagMacbeth, New Windsor, NY, USA) and compared with the manufacturer data using linear regression. Mean color differences were calculated.

To evaluate repeatability, color measurements for 10% of the shade tabs (7 of 65) and 8.3% of the color patches on the Q60 card (22 of 264) were taken three times in a random order.

To optimize accuracy of the experimental setup, a model that incorporated SW measurements every five samples accounted for the average change of the reflected light source between two measurements of SW. If the average difference exceeded 0.2% and/or the RMS (root mean square) was larger than 0.003, then the spectral data of the samples in between those two SW measurements were discarded.

Color measurements were carried out for 264 color patches on the Q60 card and 65 dental shade tabs (Fig. 2), as follows: 16 tabs from the Vita Lumin Vacuum (Vident Inc., Brea, CA, USA), 26 tabs from 3D Master (Vident Inc., Brea, CA, USA), 3 bleaching shade tabs (Vident Inc., Brea, CA), and 20 tabs from Chromascop (Ivoclar, Vivadent, Amherst, NY, USA). For color measurements on all the shade tabs, the center 1/9th was measured, ensuring that the surface being measured was perpendicular to the color sensor’s line of observation in the spectroradiometer (Fig. 1).

Figure 2.

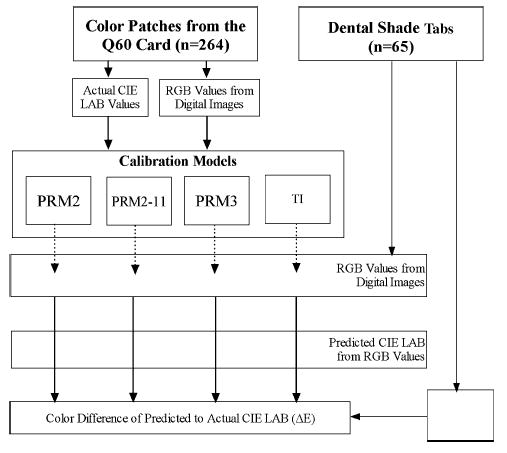
Overview of research model per digital camera.

Digital images of the samples

Digital images were taken with the following three commercial SLR cameras (Table 1) and their respective digital sensors: (1) Nikon D100 (Nikon Inc., Melville, NY, USA) with the charge couple device (CCD) sensor, (2) Canon EOS D60 (Canon USA Inc., Lake Success, NY, USA) with the complimentary metal oxide semi-micro conductor sensor (CMOS) and, (3) Sigma SD9 (Sigma Corporation of America, Ronkonkoma, NY, USA) with the Foveon x3 CMOS sensor (Foveon). The cameras were fixed on the optical table separately; with the foci positioned to measure the same sample area as the spectroradiometer. In the experimental setup, the digital camera replaced the spectroradiometer in the ‘Sensor’ position as shown in Fig. 1. The camera’s position to the sample was minimized so as to maximize the pixels of the samples. Each camera was used to take a total of 329 images (in raw format).

Table 1.

Individual camera settings for digital images of the samples.

	Nikon D100	Canon D60	Sigma SD9
Digital sensor	CCD	CMOS	Foveon
Lens used	105 mm Macro	100 mm Macro	50 mm Macro
Operation mode	Manual	Manual	Manual
ISO	200	200	200
F-stop	5	4.5	6.7
Shutter speed	1/400	1/125	1/125
Color space	Adobe RGB	sRGB	Adobe RGB
White balance	Direct sunlight	Sunlight	Sunlight
Image file format	Raw	Raw	Raw
Software	Nikon Capture 3	Raw Image Converter	Sigma Photo Pro

All raw format files were converted to ‘tiff’ format files via the converting software designed by the respective camera’s manufacturer (Table 1), with maximum image resolution (16 bits/channel) in the cameras’ respective color spaces. A 4 mm square of each image was then cropped using Adobe Photoshop 7.0 software (Adobe Systems Incorporated^®, San Jose, CA, USA) to standardize the sample areas measured by the spectroradiometer. The RGB values were obtained for each of the 987 cropped images.

Calibration models

Four calibration models were evaluated for each digital camera using the camera’s respective RGB values from the 264 color patches and the CIE LAB values (Fig. 2). For each camera, three regression models were established for each optical parameter (L*, a* and b*), including 2nd order (PRM2), 2nd order 11 terms (PRM2-11) and 3rd order (PRM3). Generic examples of each regression model Eqs. (2)–(4) are listed below for the L* parameter only, with R, G, and B representing the RGB values from the digital images, and l representing the parameter estimates.

2nd order polynomial regression (PRM2)

$$\begin{array}{c}L*=l_0+l_{1}R+l_{2}G+l_{3}B+l_{4}RG+l_{5}RB+l_{6}GB\\ +l_7{R}^2+l_8{G}^2+l_9{B}^2\end{array}$$ (2)

2nd order polynomial regression with 11 terms (PRM2-11)

$$\begin{array}{c}L*=l_0+l_{1}R+l_{2}G+l_{3}B+l_{4}RG+l_{5}RB+l_{6}GB\\ +l_7{R}^2+l_8{G}^2+l_9{B}^2+l_{10}RGB\end{array}$$ (3)

3rd order polynomial regression (PRM3)

$$\begin{array}{c}L*=l_0+l_{1}R+l_{2}G+l_{3}B+l_{4}RG+l_{5}RB+l_{6}GB\\ +l_7{R}^2+l_8{G}^2+l_9{B}^2+l_{10}RGB+l_{11}{R}^3\\ +l_{12}{G}^3+l_{13}{B}^3+l_{14}{R}^{2}G+l_{15}{R}^{2}B+l_{16}{G}^{2}R\\ +l_{17}{G}^{2}B+l_{18}{B}^{2}R+l_{19}{B}^{2}G\end{array}$$ (4)

A fourth model, based on tetrahedral interpolation (TI) technique [12], was also used. The measured RGB values for each color patch sample corresponded to points in the 3-dimensional RGB space and were triangulated, so that each RGB value for a particular sample was associated with its three nearest neighbors (color patches) in RGB space. Each point and its three nearest neighbors defined a tetrahedron. The RGB calibration space consisted of a lattice of non-intersecting tetrahedrons. The distances from the RGB point of the samples to the vertices of the enclosing tetrahedron were used to linearly weight the known CIE LAB values for vertices of the enclosing tetrahedron. This resulted in predicted CIE LAB values for the samples.

Accuracy of the calibration models

The shade tab RGB values were applied to the four calibration models, appropriate for the camera, to obtain four sets of predicted CIE LAB values for each camera. CIE LAB-based color differences between predicted and measured shade tab colors were then used as indices of accuracy for the camera/-calibration models.

The CIE LAB-based color difference formula, introduced in 1976 and recommended by the International Commission on Illumination [13], defines a color space (L*a*b*) in which L* represents lightness, a* represents the chromaticity coordinate for red–green (+a* = red direction; −a* = green direction), and b* represents the chromaticity coordinate for yellow–blue (+b* = yellow direction; −b* = blue direction). Color difference or ΔE (Eq. (5)) is defined by the following equation [13]:

$$\mathrm{\Delta }E=\sqrt{\mathrm{\Delta }{L}^{*2}+\mathrm{\Delta }{a}^{*2}+\mathrm{\Delta }{b}^{*2}}$$ (5)

where ΔL*, Δa* and Δb* are the respective difference between the measured and predicted CIE LAB values of the shade tabs.

Statistical analysis

CIE LAB-based color differences between the predicted and the measured shade tab colors were evaluated for normality. The Wilcoxon Rank–Sum test was used to determine if the ΔE obtained for each of the 12 camera/calibration models differed significantly from the accuracy (ΔE) of the experimental setup. Because there were 12 comparisons, a Bonferroni correction was performed to increase the confidence level from 95 to 99.58% (ultimate α = 0.05/12 = 0.0042).

Results

The stability of the color measurement setup was assessed by examining the color differences (ΔE) among the first measurements of SW to subsequent measurements. Irregular changes occurred in ΔE over time (Fig. 3). The maximum ΔE compared to the first measurement was 0.7, obtained nearly 2 h later. The maximum ΔE between two adjacent measurements was 0.4 ΔE. These results demonstrated the existence of mild system error and light source instability.

Figure 3.

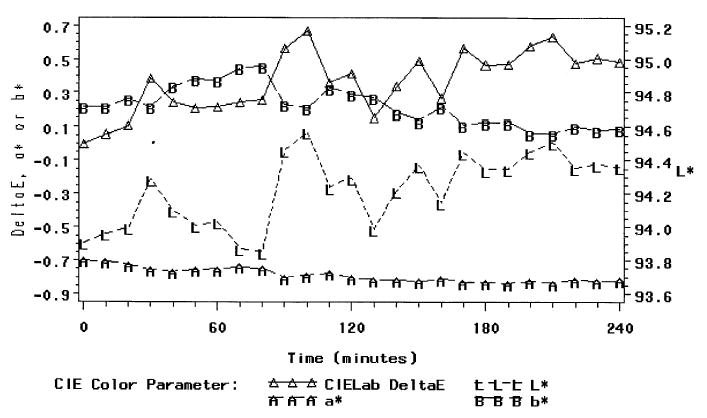
Stability of experimental setup.

The accuracy of the color measurement setup was verified by the high correlation (R-square = 0.977) between the measured and manufacturer-reported CIE LAB color data of the mini color checker. The intercept was not found to be statistically significantly different from zero (p = 0.3988). The color difference (ΔE) between the measured and manufacturer-reported data in this experiment was 1.32 (0.71).

Satisfactory repeatability was obtained for both the color patches and shade tabs. A pool SD of 0.31 for L*, 0.49 for a* and 1.0 for b* were obtained from the repeatability measurements of the color patches. The repeatability of the shade tabs obtained a pool SD of 0.42 for L*, 0.12 for a* and 0.36 for b*.

The average mean ΔE and standard error of the various camera/calibration models are presented in Table 2 under device-independent ‘LAB’ color space. The mean ΔE using the ‘XYZ’ color space to obtain the calibration models was also computed but not used for comparison in this study. Every camera/calibration model showed a statistically significant difference from the color accuracy of the color measurement setup. All of the p-values were <0.0001, except for the Nikon D100 (CCD sensor)/PRM3 model, which had a color accuracy of 1.79 ΔE (0.09) and a p-value of 0.0039.

Table 2.

Mean ΔE and standard error of each camera-calibration model.

	PRM3a		PRM2-11b		PRM2c		TId
	LABe	XYZf	LAB	XYZ	LAB	XYZ	LAB	XYZ
Canon D60/CMOS sensor	2.16 (0.08)	4.30 (1.63)	3.35 (0.20)	5.21 (3.40)	3.35 (0.20)	4.53 (2.88)	2.06 (0.11)	2.17 (0.94)
Nikon D100/CCD sensor	1.79 (0.09)	3.02 (1.50)	2.58 (0.30)	3.40 (1.96)	2.78 (0.13)	3.19 (1.54)	2.02 (0.08)	2.03 (0.80)
Sigma SD9/Foveon sensor	3.65 (0.16)	4.13 (1.57)	5.25 (0.18)	5.16 (1.98)	4.76 (0.19)	5.55 (1.97)	3.21 (0.16)	3.37 (1.3)

^aPRM3: 3rd order polynomial regression models.

^bPRM2-11: 2nd order polynomial regression model with 11 terms.

^cPRM2: 2nd order polynomial regression model.

^dTI: tetrahedral interpolation model.

^eLAB: Using the CIE LAB color space as the device-independent color space.

^fXYZ: Using the XYZ color as space as the device-independent color space.

Discussion

In this study, the CIE LAB color space was selected as the standard device-independent color space, i.e. the calibration models were computed with CIE LAB values (Fig. 2). Theoretically, the XYZ color space should be utilized because it is a uniform space [10], unlike the CIE LAB color space, which is perceptual. Overall, these results (Table 2) do not support the superiority of the XYZ color space [10] for use in these calibrations, given the lower ΔE’s (Table 2) found with the CIE LAB color space. It is postulated that error was minimized when a onestep regression predicted the CIE LAB values.

Increasing the terms and raising the order of the regression models improved the accuracy of a calibration model (Table 2). Using proper terms in the regression models has been found to be more important to the color accuracy of the calibration model than increasing the terms [10]. Such findings may explain why the Sigma SD9 (foveon sensor)/PRM2 resulted in better accuracy than with the PRM2-11. Generally, the use of TI produced better results than use of PRM2-11 for all cameras. The use of PRM3 was similar compared to TI, which has the advantage over polynomial regression models in that it is easy to implement in computer hardware [9].

The accuracy of the camera/calibration models (Table 2) were all above 1 ΔE, which can be perceived by 50% of human observers for opaque colors [4]. For tooth color replication, the acceptability limit of 2.1 ΔE [14] is more relevant. The accuracy of three camera/calibration models fell below that value: (1) the Nikon D100/CCD sensor with the PRM3 (1.79 ΔE), (2) the Nikon D100/CCD sensor with TI (2.02 ΔE), and (3) the Canon D60/CMOS sensor with TI (2.06 ΔE). Relatively inexpensive digital cameras, in combination with appropriate calibration protocols, do have the potential to be used clinically in the color replication process.

Given the interaction between cameras and calibration models (Table 2), no valid conclusions can be made of either of the cameras or the calibration models separately. Evaluating the individual sensors/cameras or calibration models requires examination of at least three randomly selected cameras for each digital sensor type to provide information regarding intra-camera variation.

In this experimental setup, each of the three sampled sensor/cameras was an experimental unit, in which four calibration models were used to convert the RGB to CIE LAB values. The variation within each sensor/camera experimental unit can contribute to the color accuracy. This variation includes the camera’s sensor, body, lenses, focal length, selected F-stop, white balance and software used to convert the raw format files. Unfortunately, the external validity of the study’s result only pertains to the three-sensor/camera experimental units selected and is not related to the individual variation within the experimental unit.

To the author’s knowledge, accuracy, stability and repeatability of this color measurement setup had not been evaluated previously, despite its use to collect color data of vital dentition [15,16]. Using colorimeters to measure dentition color is more repeatable than using this study’s experimental setup [17], given that actual contact is made with the teeth. Unfortunately, colorimeters are not ideal for the measurement of translucent objects [18]. The use of a movable contact probe to maintain a constant distance between the spectroradiometer and the measured object may improve repeatability and accuracy of this setup.

The stability of the optical setup was a limitation of this study, as shown in Fig. 3. Although every effort was made to minimize system error, light source instability may explain the high ΔE’s found between the predicted and measured CIE LAB values of the shade tabs, particularly in comparison to Hong et al.’s findings [10]. Proposed improvements include the use of a more stable light source, such as a xenon light source (300W Xe Arch Lamp, Oriel Instruments, Stratford, CT, USA).

Further research in the area of improved light source stability and practical alternatives for light sources would help translate studies such as this toward practical use in the clinical environment. The unanswered question remains regarding which camera–sensor/calibration model obtains the best color accuracy. The evaluation of a standard digital SLR camera with interchangeable digital sensors would help to answer this question.