Evaluation of a Two-Stage Neural Model of Glaucomatous Defect: An Approach to Reduce Test-Retest Variability

Abstract

Purpose.

The purpose of this study is to model perimetric defect and variability and identify stimulus conditions that can reduce variability while retaining good ability to detect glaucomatous defects.

Methods.

The two-stage neural model of Swanson et al.¹ was extended to explore relations among perimetric defect, response variability, and heterogeneous glaucomatous ganglion cell damage. Predictions of the model were evaluated by testing patients with glaucoma using a standard luminance increment 0.43° in diameter and two innovative stimuli designed to tap cortical mechanisms tuned to low spatial frequencies. The innovative stimuli were a luminance-modulated Gabor stimulus (0.5 c/deg) and circular equiluminant red-green chromatic stimuli whose sizes were close to normal Ricco’s areas for the chromatic mechanism. Seventeen patients with glaucoma were each tested twice within a 2-week period. Sensitivities were measured at eight locations at eccentricities from 10° to 21° selected in terms of the retinal nerve fiber bundle patterns. Defect depth and response (test-retest) variability were compared for the innovative stimuli and the standard stimulus.

Results.

The model predicted that response variability in defective areas would be lower for our innovative stimuli than for the conventional perimetric stimulus with similar defect depths if detection of the chromatic and Gabor stimuli was mediated by spatial mechanisms tuned to low spatial frequencies. Experimental data were consistent with these predictions. Depth of defect was similar for all three stimuli (F = 1.67, p > 0.19). Mean response variability was lower for the chromatic stimulus than for the other stimuli (F = 5.58, p < 0.005) and was lower for the Gabor stimulus than for the standard stimulus in areas with more severe defects (t = 2.68, p < 0.005). Variability increased with defect depth for the standard and Gabor stimuli (p < 0.005) but not for the chromatic stimulus (slope less than zero).

Conclusions.

Use of large perimetric stimuli detected by cortical mechanisms tuned to low spatial frequencies can make it possible to lower response variability without comprising the ability to detect glaucomatous defect.

Glaucoma is a heterogeneous group of disorders that manifests as progressive optic neuropathy and is estimated to be responsible for over 5 million cases of blindness worldwide.^2,3 Early diagnosis of glaucoma and early detection of progression of glaucoma are clinically important because progression can be slowed or halted with appropriate interventions.⁴ Diagnosis and treatment of glaucoma rely on perimetric assessments of the visual field as well as other clinical measures. There have been on-going efforts to improve perimetric techniques, many of which are aimed at specific visual functions that might be selectively impaired by glaucomatous damage. Relatively little effort has been made to decrease test-retest variability, which affects the ability to identify glaucomatous defect and progression. Standard automated perimetry, the most commonly used perimetry in modern clinics, exhibits high test-retest variability in areas of visual field damage.^5-7 This makes it inappropriate for detecting small changes in sensitivity. A minimum of 7 to 8 visual fields obtained over a 4- to 5-year time period can be required to accurately distinguish progressive glaucomatous visual field damage from test-retest variability.⁸

Among the perimetric techniques developed over the last 3 decades, test-retest variability in damaged locations of the visual field tends to be lower for methods that use large stimuli (e.g., high-pass resolution perimetry,^9,10 measurement of red-green chromatic sensitivity,¹¹ and frequency-doubling technology perimetry^12-14). For a given stimulus size, variability tends to be higher when ganglion cell density is low in normal eyes^15,16 and tends to be higher in glaucomatous defects.^5-7 Test-retest variability can be reduced by using a larger stimulus that stimulates more ganglion cells,^17,18 but depth of defect can be less severe for large stimuli.^19-21 Pearson et al.¹¹ suggested that the combination of low variability and good ability to detect glaucomatous defect could be obtained by using a large stimulus detected by cortical mechanisms with large spatial summation areas (i.e., tuned to low spatial frequencies).

The current study evaluated a quantitative implementation of Pearson’s hypothesis using the model of Swanson et al.¹ to relate perimetric defects with ganglion cell pathology. We extended the model by analyzing how normal fixational eye movements could interact with heterogeneous retinal ganglion cell damage to produce elevated variability of perimetric sensitivity for different types of stimuli. To evaluate predictions of the model, we measured test-retest variability (response variability) of patients with glaucoma using three different perimetric stimuli. Two innovative stimuli were designed based on model predictions of low variability with good sensitivity to defect, and a standard stimulus was used that had the same spatial properties as the Goldmann size III (0.43° diameter) stimulus used in conventional perimetry.²² A laboratory testing system was used to provide a perimetric algorithm providing more precise sensitivity estimates than possible with clinical algorithms, which use relatively few (6-7) stimulus presentations per location in the visual field. The laboratory algorithm tested a smaller number of visual locations with a larger number of trials to achieve more precise measurements of perimetric sensitivities without fatiguing the patients. We also assessed the first three reversals of the staircases to evaluate whether results of our precise measurements would hold with fewer trials as used in clinical perimetric tests. Results of the laboratory tests showed lower variability for the innovative stimuli, confirming the predictions of the model. This study provides insights into effects of perimetric stimuli on response variability and depth of defect based on standard models of spatial vision. The results lay the foundation for clinical studies aiming at reducing variability with newly designed perimetric stimuli.

PART I: MODEL METHODS

The two-stage neural model of Swanson et al.¹ for perimetric stimuli at eccentricities of 10° to 30° was implemented with Igor Pro (versions 4.01 through 5.01; Wavemetrics, Inc., Lake Oswego, OR) and extended to include additional stimuli. Two of the stimuli were circular with diameters of 0.43° and 1.72°, which are equivalent to the Goldmann size III and V diameters,²² respectively. The third stimulus was a Gabor sine with a peak spatial frequency of 0.5 c/deg and a 0.7 octave bandwidth, defined as

$$L(x,y)=L_{\text{mean}}\cdot (1+\sin \left(2\pi fx\right)\cdot e^{-\frac{{(x-x_0)}^2+{(y-y_0)}^2}{2\times {1.5}^2}})$$

where L is the luminance at location (x,y), (x₀, y₀) gives the center of the Gabor, f is the peak spatial frequency, and L_mean is the mean luminance of the background. Most of the energy of the Gabor stimulus was distributed within the central 4°. Sine phase was chosen rather than cosine phase to avoid a DC component.

In the first stage of the model, responses of hexagonal arrays of ganglion cells were computed for the different stimuli. Three types of ganglion cell arrays were used (Table 1): a denser array with smaller receptive fields, a sparser array with larger receptive fields, and an undersampled array with minimal receptive field overlap. The receptive field diameters spanned the range of values reported for macaque ganglion cells for eccentricities of 10° to 30°.^23-25 The cell spacing for the dense mosaic was based on human ganglion cell density at an eccentricity of 9°,²⁶ and for the sparse mosaic, it was assumed that only 5% of ganglion cells contributed to detection of the stimulus. Both mosaics had receptive field diameters large enough to provide a coverage factor of at least 3, because receptive field center sizes as estimated with single-unit electrophysiology yield coverage factors near 3 for both midget and parasol ganglion cell mosaics.^27,28 The undersampled mosaic had the same receptive field diameter as the sparse mosaic with fourfold lower density producing a coverage factor <1 (no overlap).

TABLE 1.

Parameters for the three ganglion cell mosaics used in the model

		Space constant
Mosaic	Cell spacing (°)	Center (°)	Surround (°)	Ratio of center/surround weights
Dense	0.036	0.07	0.54	129.7
Sparse	0.16	0.18	1.19	57.5
Undersampled	0.32	0.18	1.19	57.5

In the second stage of the model, the outputs of the ganglion cell arrays were pooled by spatial filters. A spatial filter represents processing of ganglion cell responses by a homogeneous population of cortical neurons, all neurons having similar excitatory and inhibitory weightings for responses from ganglion cells in that retinal area. Hexagonal arrays of spatial filters covered the region of visual space in which the stimulus was presented, with each filter centered on a ganglion cell; secondary calculations with variable density of spatial filters yielded similar results. A wide range of types of cortical receptive fields, described by Swanson et al.,¹ yielded similar results at any given peak spatial frequency. Therefore, we characterized the receptive fields in terms of the width of the central excitatory region, computed as one-half cycle of the peak spatial frequency, and varied the width from 1/8° to 2° (4.0-0.25 c/deg).

Psychophysical sensitivity of a spatial mechanism was computed by probability summation over the responses of spatial filters tuned to the same peak spatial frequency but with different orientations and locations. A vector sum with an exponent of 4.0 was used for the probability summation.^29-31

Effects of heterogeneous glaucomatous ganglion cell damage were simulated by removing cells in the first-stage ganglion cell arrays. Heterogeneous damage is consistent both with apoptosis as a mechanism of glaucomatous cell death³² and with heterogeneous dysfunction.¹ For a given initial cell density (dense, sparse, undersampled), cells were randomly removed to produce cell losses of 0%, 25%, 50%, 75%, 87.5%, 93.8%, 96.9%, 98.4%. By 75% loss, the coverage factor for the sparse mosaic dropped below 1.

Changes in stimulus location by as little as 0.5° have been shown to cause dramatic effects on perimetric sensitivity in glaucomatous defects,²⁰ so we evaluated the extent to which variability in sensitivity could be attributed to the microsaccades and drift typical of steady fixation. For perimetry, these eye movements usually keep the stimulus within ± 1° of putative location.³³ To simulate this, we used 13 different stimulus locations within a 2° circle with 0.5° hexagonal spacing. For a given ganglion cell array, stimulus configuration, and cortical population array, sensitivities were computed for the 13 stimulus locations. Response variability was computed as the standard deviation of the decibel (10-dB per log unit) sensitivities across these locations and the mean was computed as the perimetric sensitivity. Depth of defect was computed as the difference in mean decibel sensitivities for intact and degraded ganglion cell arrays.

For a given stimulus location, the model computes psychophysical sensitivity in the traditional sense: the reciprocal of the contrast for which a subject would be correct 75% of the time on a two-alternative forced-choice task if they were free from extraneous noise.³⁴ This definition of sensitivity is not affected by variations in intrinsic noise (slope of the psychometric function). By comparison, psychophysical tests produce estimates of sensitivity whose variability will be affected by intrinsic noise as well as by properties of the threshold algorithm. Our model evaluates a further source of variability, the interaction of inhomogeneous ganglion cell damage with normal fixational eye movements. To illustrate how these factors combine, we performed Monte Carlo simulations of the “full-threshold” perimetric algorithm. Sensitivity for an undamaged retinal mosaic was set to 32 dB for size III, 36 dB for size V, and 12 dB for the Gabor. For the damaged mosaics, 13 sensitivities were computed for the different stimulus locations. For each mosaic, 13 psychometric functions were constructed, which all had slopes of 4.0, false-positive and false-negative rates equal to zero, and which differed only in the sensitivity for each location. For each stimulus and mosaic, 1000 staircases were then simulated and the standard deviation was computed for the sensitivity estimates. For each simulated staircase, for each stimulus presentation, a random number between 0 and 1 was generated; if the number was higher than the value of the psychometric function at that stimulus contrast and location, then the trial was recorded as “seen”; otherwise, the trial was recorded as “not seen.” The staircases started with a step size of 4 dB, step size decreased to 2 dB after the first reversal, and the staircase terminated at the second reversal; threshold was set equal to the last stimulus, which generated a “seen” response.

These simulations were used to establish the conditions for which heterogeneous ganglion cell damage can yield low response variability while retaining good ability to detect glaucomatous defects.

RESULTS

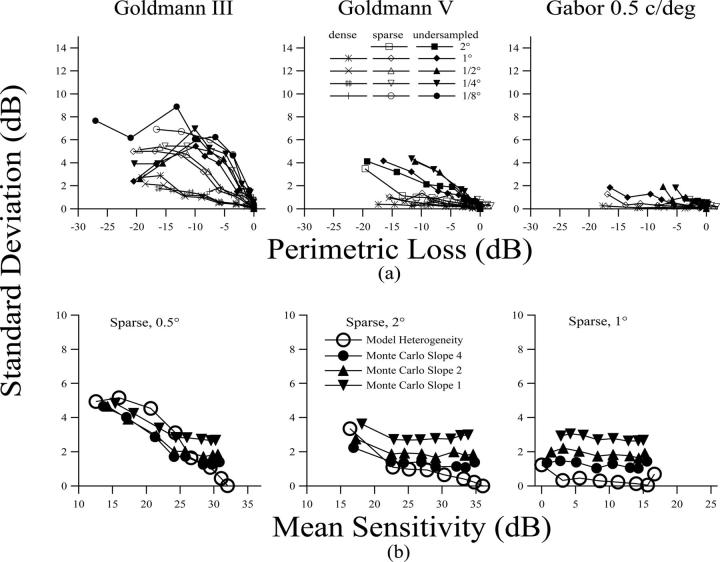
Figure 1 shows mean results of predictions for perimetric defect versus ganglion cell loss. When detection was mediated by cortical populations with receptive fields centers that were wide enough to cover the entire stimulus (cortical populations tuned to low spatial frequencies), the predicted defect depth was approximately equal to the amount of ganglion cell loss (thick gray line). With wide receptive fields, cortical populations centered at different parts of the stimulus will combine inputs from all ganglion cells responding to the stimulus. This means that all cortical populations will have similar losses in sensitivity to the stimulus and these losses will approximate the loss in ganglion cells in that region of the retina. For the 0.43° Goldmann size III stimulus, this required receptive field center widths of at least 0.25° to 0.5° (peak spatial frequencies 1-2 c/deg) depending on ganglion cell mosaic. For the 1.72° Goldmann size V stimulus, receptive field center widths needed to be at least 1° to 2° (peak spatial frequencies 0.25-0.5 c/deg). For the 0.5-c/deg Gabor stimulus (grating width 1°), equality was obtained when receptive field center width was close to grating width (peak spatial frequency 0.5 c/deg).

FIGURE 1.

Depth of defect computed as a function of ganglion cell loss for all three stimuli with a range of ganglion cell populations (dense, sparse, and undersampled) and cortical populations (receptive field center width from 2° to 1/8°, shown in figure captions; they correspond to peak spatial frequencies from 0.25 to 4.0 c/deg). The thick line shows equality, when perimetric defect equals ganglion cell loss. Points falling above the line of equality represent conditions of cortical redundancy (cortical populations sampling small portions of the stimulus).

For all stimuli, perimetric loss was milder than ganglion cell loss when cortical populations had narrow receptive field centers (i.e., tuned to high spatial frequencies). Because individual populations pooled responses of only a small portion of ganglion cells under the stimulus, if the stimulus fell on a small patch of surviving ganglion cells, then the cortical population pooling responses of that patch of cells could have near-normal sensitivity. We refer to this as cortical redundancy. Cortical redundancy was more prominent for the larger size V stimulus and the Gabor stimulus than for the size III stimulus, because these stimuli require larger receptive fields (lower spatial frequencies) to yield equality.

In general, Figure 1 shows that predicted perimetric defect depth tends to be milder when detection is mediated by cortical populations with narrow centers (higher peak spatial frequencies). The only exception was for the size III stimulus with the undersampled ganglion cell array, in which populations with a receptive field width of 1/8° gave the deepest defect. In this instance, when glaucomatous damage was severe, perimetric loss was even greater than ganglion cell loss. This aspect is discussed further in the “Discussion.”

Response variability was lower when detection was mediated by a large number of ganglion cells and tended to increase with depth of defect (Fig. 2). It was lower for the size V (0.1-4.3 dB) or the Gabor stimulus (0.1-2 dB) and was higher for the small Goldmann size III stimulus (5-9 dB). It was lower for the dense ganglion cell array than for the sparse or undersampled arrays and generally increased with peak spatial frequency of the cortical populations mediating detection.

FIGURE 2.

(a) Response variability as a function of mean defect for all three stimuli, with the ganglion cell and cortical cell parameters as in Figure. 1. Ganglion cell populations are characterized as dense, spare, and undersampled. Cortical populations cell populations are characterized by the width of the receptive field’s excitatory center (in degrees of visual angle). (b) Examples of effects of combined effects of heterogeneous damage and intrinsic noise. The open circles show heterogeneous damage for selected conditions replotted from the upper panels, and the solid symbols show results of Monte Carlo simulations of the full-threshold algorithm with increasing amounts of intrinsic noise (slopes from 4 to 1).

The lower panel of Figure 2 shows illustrative examples of results of Monte Carlo simulations of full-threshold perimetric staircases. Open circles show predicted effects of heterogeneous damage, and solid symbols show results of simulations of the combined effects of intrinsic noise, perimetric algorithm, and heterogeneous damage. When heterogeneous damage is minimal, simulated variability was determined by the amount of intrinsic noise. As intrinsic noise was increased (slope became shallower), the standard deviation increased from approximately 1.4 dB to 2.7 dB for locations with no ganglion cell loss. As long as the standard deviation for heterogeneous damage was less than the standard deviation for intrinsic noise, simulated variability showed little change with depth of defect. Once the standard deviation for heterogeneous damage grew larger than that for intrinsic noise, simulated variability began to increase with depth of defect. For the size V and Gabor stimuli, effects of heterogeneous damage generally remained low even in damaged areas, so simulated variability showed little change with depth of defect. For size III, in damaged areas, the effects of heterogeneous damage became large and simulated variability increased with depth of defect. The effects of perimetric algorithm tend to cause simulated variability in damaged areas to be slightly lower than model heterogeneity.

The most desirable perimetric stimulus should exhibit both low variability and high sensitivity to detect glaucomatous defect. Despite the advantage of lower response variability, the potential difficulty with large stimuli was that depth of defect might be milder than for the smaller size III stimulus^18-21 as shown in Figure 1. However, the model predicted that when mechanisms mediating detection were tuned to spatial frequencies that were low enough, then equality could be obtained and perimetric defect could approach ganglion cell loss no matter whether the stimulus was large or small. For the luminance increments used in standard perimetry, the cortical populations mediating detection may not have receptive field widths as large as the size V stimulus. However, innovative stimuli could be designed to use a large stimulus to isolate responses of cortical populations with large receptive fields (low spatial frequencies).

PART II: EVALUATION OF MODEL PREDICTIONS

Two innovative stimuli were designed to evaluate the predictions of the model. A low spatial frequency Gabor stimulus was designed to stimulate a large number of ganglion cells and to reduce contributions of mechanisms tuned to higher spatial frequencies. A circular chromatic stimulus was designed to tap the L-M mechanism (L, M represent Long-wavelength-sensitive and Middle-wavelength-sensitive cone photopigments, respectively), whose physiological substrate in the retina appears to be the parvocellular ganglion cells.³⁵ The size of the chromatic stimulus was chosen to be similar to the Ricco’s areas for the red-green chromatic mechanism. This was an attempt to approximate the widths of the receptive field centers of the spatial filters that mediate chromatic thresholds. Anderson³⁶ independently suggested that stimuli scaled to the size of Ricco’s area for each retinal pathway and eccentricity might have the potential for early detection of glaucoma. With a large Ricco’s area for the chromatic mechanism³⁷ and a high density for cells in the parvocellular pathway,^26,38 we expect responses of a large number of ganglion cells to be summed. For both the Gabor and chromatic stimuli, the model predicts that response variability in perimetric defects should be lower than for the size III stimulus, whereas depth of defect should be similar to that for the size III stimulus.

METHODS

Apparatus

Stimuli were displayed on a 21-inch SONY Trinitron F500 CRT monitor driven by a VSG2/5 video controller (Cambridge Research Systems, Cambridge, U.K.). The resolution of the monitor was 800 × 600 pixels and the frame rate was 150 Hz. Each phosphor was controlled with 15-bit precision. Gamma correction was obtained with the OptiCal photometer provided by Cambridge Research Systems. The spectral profile of each phosphor was measured with a Photo Research PR-704 spectroradiometer (Photo Research Inc., Chatsworth, CA), and was used to compute cone excitation based on the Smith and Pokorny cone fundamentals with macular pigment removed.^39,40

Stimuli

The Gabor Stimulus.

This stimulus was in sine phase and had a peak spatial frequency of 0.5 c/deg with a spatial bandwidth of 0.7 octave. Most of the energy of the stimulus was distributed within the central 4°. Sine phase was chosen rather than cosine phase to avoid a DC component.

The Circular Chromatic Stimuli.

These were circular stimuli modulated in an equiluminant color space⁴⁰ from an equal energy white (EEW) point along the L-M axis in a reddish direction. To estimate Ricco’s area, spatial summation functions for four normal subjects were measured at each of the eight locations (Fig. 3) in the main experiment with two to four locations each at three different eccentricities (9.5°, 15°, and 21°). For each eccentricity, sensitivities were then averaged across locations to derive mean sensitivity for each subject and stimulus size. The spatial summation data were fit with a two-parameter function¹⁹ to estimate the Ricco’s area. This resulted in diameters for the chromatic stimuli of 1.1°, 1.8°, and 2.4° at 9.5°, 15°, and 21° eccentricity, respectively.

FIGURE 3.

(a) Stimulus test locations indicated with the crosses. The ellipse represents the blind spot. (b) Standard stimulus. (c) Innovative stimuli.

Standard Stimulus.

A circular luminance increment 0.43° in diameter was used as a standard stimulus. The size of the stimulus was the same as the Goldmann size III stimulus used in perimetry.²¹

The background was an EEW field that subtended 54° by 42° at the 40-cm viewing distance. Subjects were corrected with full-diameter lenses for the test distance. The mean luminance of the background was 50 cd/m² for the chromatic and the Gabor stimuli. Background luminance for the size III stimulus was set to 10 cd/m² to expand the dynamic range. It has been shown that Weberian thresholds can be obtained at 10 cd/m² for standard perimetry.⁴¹ Higher adapting luminances are needed to reach the Weber region for the chromatic stimulus. A background luminance of 50 cd/m² should be sufficient for measuring Weberian thresholds for a subject with least a 3-mm pupil.⁴²

All stimuli were presented with a Gaussian temporal profile for contrast:

$$\text{Contrast}\left(t\right)=\frac{I_{\max }-I_{\text{mean}}}{I_{\text{mean}}}\cdot e^{-\frac{{(t-t_0)}^2}{2{\sigma }^2}}$$

where I represents luminance for the size III stimulus, luminance of the peak of the Gaussian envelope for the Gabor stimulus, and L-cone excitation for the chromatic pulses. Contrast was varied to find threshold. Contrast was represented in decibel units with 1 dB = 0.1 log unit.

The time constant of the temporal Gaussian (σ) was 100 ms. The temporal Gaussian was used to avoid high temporal frequencies, because the luminance required to reach the Weber region increases when temporal frequency is increased.⁴³ A low temporal frequency stimulus also helps to enhance contributions of the parvocellular pathway,⁴⁴ which has a high ganglion cell density.

Stimuli were presented at eight locations that were distributed at three eccentricities (9.5°, 15°, and 21°) in the visual field. The locations were chosen according to the retinal nerve fiber bundle layout and to sample both relatively severe and mild defects in the same eye. The stimulus locations and spatial profiles are shown in Figure 3.

Experimental Paradigm

Each threshold was determined by a one-down-one-up staircase⁴⁵ for a total of 12 reversals. Starting from the maximum contrast, contrast of the stimuli was varied in steps of 3 dB for the first two reversals and thereafter in steps of 1.5 dB. Contrast threshold was estimated as the mean of the last 10 reversals, and contrast sensitivity was defined as the reciprocal of contrast threshold. This paradigm was similar to the full-threshold strategy used in standard automated perimetry, with a larger number of trials per staircase, and had good patient acceptance. The subject’s task was to fixate on a cross at the center of the monitor and to press the mouse button whenever he or she saw a stimulus. Fixation stability was monitored with a video camera and the Heijl-Krakau blind spot monitoring technique.⁴⁶

Free trials and blank trials were intermixed with the staircases, and a maximum-likelihood technique³⁴ was used to evaluate the slope of the psychometric function and the false-negative (FN) and false-positive (FP) rates. The variable slope coefficient reduced the problem of high FN rates caused by shallow slopes.⁴⁷ The free trials, blank trials, and the blind spot trials each took approximately 3% (approximately 10 trials) of the total number of trials. Thresholds were rejected for fixation losses >33%, FN or FP rate >20%, or difference >1.5 dB between sensitivities estimated with the maximum-likelihood technique and with the mean of reversals (this is an indication that stimulus distribution was inadequate for accurate threshold estimation). Thresholds were considered non-measurable if the difference between the mean of reversals and the available maximum contrast was <1.5 dB.

Subjects

Seventeen patients with glaucoma (age, 56.5 ± 5.4 years) and 20 age-similar control subjects (age, 53.2 ± 7.3 years) were recruited from the University Optometric Center of SUNY State College of Optometry. The study protocol was approved by the SUNY State College of Optometry Institutional Review Board. Informed consent was obtained from all subjects after the procedures were explained and before testing, and the tenets of the Declaration of Helsinki were followed.

Inclusion criteria were: age range 40 to 70 years, spherical correction within ± 5.5 D, cylinder correction within ± 3.0 D, pupillary diameter >3 mm during test, no more than two errors made for the first 16 plates of the Ishihara plate test 24-plate series, and no other disease or medications known to affect contrast sensitivity, visual field, or color vision. Control subjects were also required to pass a comprehensive eye examination, to have no first-degree relative with glaucoma, and to have a best-corrected visual acuity of 20/20 or better.

Patients were recruited who had an established diagnosis of primary open-angle glaucoma (POAG) or combined mechanism glaucoma, with both open-angle and angle-closure components present (CMG) as defined by two or more of the following criteria: undergoing treatment for glaucoma at the SUNY Glaucoma Institute; glaucomatous optic nerve damage (cup-to-disk asymmetry between two eyes of 0.2 or more, rim-thinning, hemorrhage, notching, excavation, or nerve fiber layer defect); glaucomatous visual field damage defined by pattern standard deviation (PSD), Glaucoma Hemifield Test (GHT), or nasal step covering at least three contiguous points outside the 95% confidence limit. Patients with a diagnosis of CMG had undergone peripheral iridotomy at least 1 year before the experiment. Only one eye of each subject was tested with best-corrected visual acuity of 20/40 or better required. All subjects were tested twice within a 2-week period. Clinical characteristics of patients are summarized in Table 2.

TABLE 2.

Clinical characteristics for patients

Subject no.	Age	Acuity	Diagnosis	Refractive error	MD	PSD	Ishiharaa
1	61	20/25	POAG	+1.75-0.75 × 85	-6.96	5.53	0
2	43	20/20	POAG	Plano	-2.88	6.68	0
3	55	20/20	POAG	-0.75-0.75 × 70	-3.18	3.6	0
4	57	20/25	POAG	-3.00	-2.81	5.71	2
5	53	20/20-	POAG	+2.50-0.50 × 85	-2.01	2.23	0
6	67	20/30	CMG	-1.00 × 90	-1.67	2.43	0
7	51	20/20	POAG	-4.00-0.75 × 165	-6.96	6.94	0
8	61	20/30-	POAG	+0.75-0.50 × 120	-9.76	12.97	0
9	59	20/25	POAG	-1.00-0.75 × 90	-2.57	2.58	0
10	52	20/30	POAG	-5.00-0.5 × 75	-4.12	3.1	0
11	55	20/20	POAG	+1.75-0.25 × 80	-2.67	2.41	0
12	63	20/25	POAG	+0.50-0.75 × 125	-4.96	7.43	0
13	58	20/20	POAG	+1.00-1.00 × 90	-4.18	2.76	0
14	54	20/25+	POAG	+2.00-0.50 × 70	-3.61	2.87	0
15	60	20/20-	POAG	-3.25-0.75 × 170	-3.46	1.69	0
16	56	20/25+	POAG	+1.50	-4.23	5.19	2
17	55	20/20	CMG	+0.25-0.50 × 180	-7.95	4.83	0

^aNumber of errors made with the Ishihara plate tests based on the first 16 plates.

MD, PSD, mean deviation, pattern standard deviation (24-2); POAG, primary open-angle glaucoma; CMG, combined mechanism glaucoma.

Statistical Design

Control subjects were tested to estimate mean normal sensitivity and the one-tailed lower 95% confidence limit for normal for each stimulus at each test location. Between-subject standard deviations for the three stimuli were compared with F tests requiring p < 0.016 in order to avoid type II errors. The dynamic range was computed as the difference between mean normal threshold contrast and the maximum contrast available for the equipment.

For each stimulus condition and test location, sensitivities at the two visits were averaged for each patient, and the difference from mean normal was computed as depth of defect. An analysis of variance (ANOVA) was used to compare depth of defect for the three stimuli for the entire database. By pooling all data points, some patients contributed more data than other patients. To minimize this potential source of bias, so that each patient contributed equally to the statistical analysis, one test location was randomly selected from each patient and secondary analyses were performed on this subset.

To compare depth of defect for the new and the conventional stimuli on a pointwise basis, the method of Bland and Altman⁴⁸ was used: the difference between two defects was plotted versus their mean. Ability to detect glaucomatous defects was also evaluated in terms of the number of abnormal test locations that were identified using the stimulus, i.e., locations with sensitivities below the lower 95% confidence limit for normal. Two chi-squared tests were used to compare the fraction of abnormal data points for the standard and new stimuli requiring p < 0.025 to avoid type II errors.

The primary measure of response variability was test-retest variability, which was computed as the absolute value of the difference in log contrast sensitivity at the two visits computed separately for each stimulus condition, test location, and patient. The method of Bland and Altman was used to compare response variability with depth of defect, and linear regression was used to look for a relation between the two. Secondary analyses were used to assess validity of this definition for response variability. First, the learning effect was computed for each patient as the difference in mean contrast sensitivity between the second visit and the first visit; if learning effects are large, then they will influence the measure of response variability. Second, mean response variability was compared with the standard deviation of the unsigned difference between test and re-test for each location and patient; if our definition of response variability is valid, this estimate of response variability should be similar to the primary estimate.

RESULTS

The dynamic range varied across locations from 12 to 14 dB for the standard stimulus, from 11 to 13 dB for the Gabor stimulus, and from 4 to 7 dB for the chromatic stimuli. Normal interindividual variability, estimated as the standard deviation (SD) of sensitivities across subjects, averaged 1.9 dB for the size III, 1.6 dB for the Gabor, and 1.1 dB for the chromatic stimulus. F tests showed that the only significant difference across stimuli was that SD was lower for the chromatic stimuli than for the standard stimulus (F = 2.87, p < 0.012).

The number of excluded data points identified either as unreliable or nonmeasurable is summarized in Table 3. For all but nine test locations, when sensitivity to a stimulus was not measurable for one of the visits, it was also not measurable for the other visit. The smaller dynamic range for the chromatic stimuli resulted in a large number of nonmeasurable data.

TABLE 3.

Unreliable data and nonmeasurable data

Stimulus	Total number of nonmeasurable data points	Nonmeasurable data points for only one of the two tests	Number of unreliable data points
White	23/272	3/23	39/249
Gabor	5/272	1/5	22/267
Chromatic	103/272	5/103	21/169

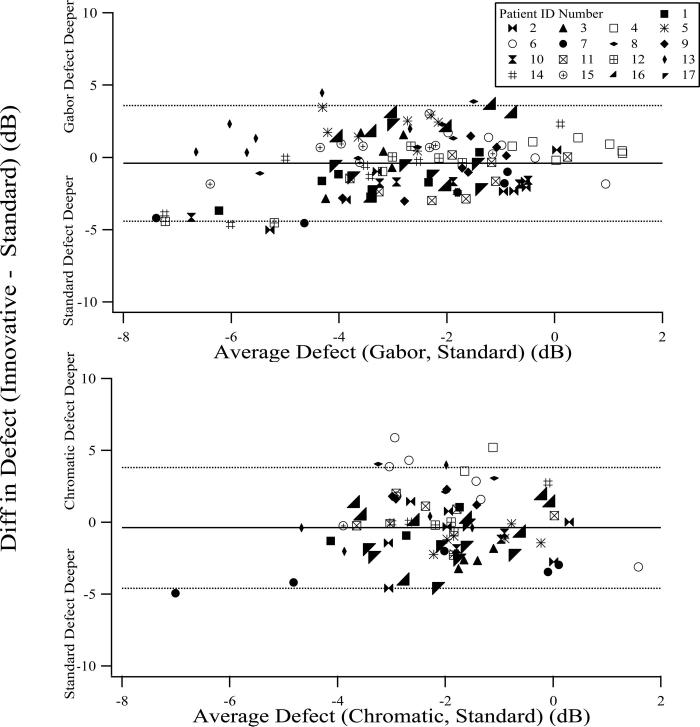
The difference in depth of defect between the innovative and standard stimuli is plotted against the mean of the defects for the two stimuli, in Figure 4, for each patient and location: data points falling below the zero line have deeper defect for the standard stimulus and data points falling above the zero line have lesser defect. The average defects for both the Gabor and the chromatic stimuli were within 0.4 dB of the defect for the standard stimulus with 95% confidence limits of ± 4 dB across subjects and locations.

FIGURE 4.

The difference in depth of defect between the innovative stimuli and the standard stimulus is plotted against their mean. Data from different subjects are shown with different symbols. Horizontal lines show the mean and the upper and lower 95% confidence limits for the difference in depth of defect. Upper panel: Gabor; lower panel: chromatic.

Mean depth of defect across all patients and test locations is shown in Figure 5A. A one-way within-subjects ANOVA did not find a significant difference across stimulus type (F = 1.67, p > 0.19). The within-subjects ANOVA matched data across stimulus type for patient and test location and reduced the sample size to 77 in each group. With this sample size and estimated variability, a difference as small as 0.8 dB would be detectable with 80% power at a significance level of 0.05. Secondary analyses with only one test location per patient obtained the same result (F = 0.63, p > 0.54); power analysis showed that a difference of 1.9 dB should be detectable for this sample size and estimated variability.

FIGURE 5.

(a) Mean depth of defect for the three stimuli is plotted both for the whole dataset (circles) and for a subset that contains one location randomly selected for each patient (squares). (b) Response variability, computed as the standard deviation of the difference in sensitivity between the two visits (asterisks) and computed on a point-by-point basis for the whole dataset (circles) and a subset (squares). Learning effect is shown with open triangles. Error bars show ± 1 standard error of mean.

As a result of the low dynamic range for the chromatic stimuli, many test locations were not included in the primary analysis. In secondary analyses, we examined the ability of each stimulus to identify abnormal test locations. We found that the SD for normal between-subject sensitivity was significantly lower for the chromatic stimuli than for the standard stimulus producing narrower confidence limits for normal than obtained for the standard stimulus. To make a conservative comparison of abnormality across test locations, in the primary calculations, we used the SD for the standard stimulus as a common standard to compute the normal confidence limit for all three stimuli. As shown in Figure 6A, for each stimulus, approximately 50% of test locations were identified as abnormal. Chi-squared tests for pairwise comparison found no difference between the innovative stimuli and the standard stimulus (chi-square <1.75, p > 0.18). Next, the confidence limit for normal sensitivity was recomputed for each stimulus by using the SD for normal between-subject variability for that stimulus to account for the effect of differences in normal between-subject variability. The lower normal SD for the chromatic stimulus resulted in more abnormal test locations for the chromatic stimulus than for the standard stimulus (chi-square = 69.1, p < 0.001). No difference was found between number of abnormal locations detected with the Gabor and the standard stimulus (chi-square = 0.73, p > 0.39).

FIGURE 6.

(a) Percentage of abnormal locations identified by each stimulus. (b) Concordance between the innovative stimuli and the standard stimulus as for whether a test location was normal or abnormal. See text for details.

Figure 6B shows the concordance across stimuli on whether a test location was normal or abnormal. When normal SD for the standard stimulus was used to compute the normal confidence limit, for each of the new stimuli, approximately 70% of locations had the same classification (e.g., either normal or abnormal) as for the standard stimulus. Approximately half of the remaining locations were abnormal for the innovative stimuli but not for the standard stimulus; the other half were abnormal only for the standard stimulus. When normal SD for each individual stimulus was used to compute the lower confidence limit for that stimulus, the concordance between the chromatic and the standard stimulus decreased to 53% as a result of the large number of test locations that were identified as abnormal for the chromatic but not for the standard stimulus.

As shown in Figure 5B, the three measures of response variability were quite similar. Mean learning effects were minimal, ranging from 0.2 to 0.3 dB for the three stimuli, and a one-way ANOVA did not find a significant effect of stimulus type (F = 0.07, p > 0.93). Any learning effect was small and similar across the three stimuli and could not substantially affect estimates of response variability.

Across all patients and locations, mean response variability was 1.2, 1.0, and 0.6 dB for the standard, Gabor, and the chromatic stimuli, respectively. A one-way within-subjects ANOVA revealed a significant effect of stimulus type on response variability (F = 5.58, p < 0.005); Tukey’s HSD post hoc test found significantly lower response variability for the chromatic stimulus than for the other two stimuli (p < 0.01). For reasons explained previously for depth of defect, the statistical analyses were also performed on a subset of data with one test location randomly selected from each patient. Results for the subset confirmed results for the whole dataset (ANOVA F = 3.78, p < 0.04; Tukey’s HSD found that chromatic stimuli had lower response variability, p < 0.05).

Figure 7 plots variability against depth of defect for the three stimuli. As expected from the literature,^5-7 for the standard stimulus, variability was greater in deeper defects (r² = 0.08, slope = 0.02, p < 0.009). A similar result was found for the Gabor stimulus (r² = 0.07, slope = 0.01, p < 0.005). For the chromatic stimulus, the slope was negative and the correlation was not significant (r² = 0.02, slope =-0.01, p > 0.20).

FIGURE 7.

Individual test-retest variability is plotted against depth of defect. Data from different subjects are shown with different symbols. Horizontal lines show the mean and the upper 95% confidence limits of test-retest variability. Test-retest variability was significantly correlated with depth of defect for the standard and the Gabor stimuli but not for the chromatic stimulus. Regression lines not shown on figure (r² <0.09).

Although overall response variability was similar for the Gabor and the standard stimulus, inspection of Figure 7 showed that in areas with more severe defect, the response variability appeared to be lower for the Gabor stimulus than for the standard stimulus. We therefore compared response variability in areas where defects were deeper than -4 dB (which is 1 to 2 dB below the lower confidence limit of normal sensitivity) and found that variability was significantly lower for the Gabor than for the standard stimulus (t = 2.68, p < 0.005). On a one-data-per-subject basis, the median response variability for defects deeper than -4 dB was identified for each subject. The median response variability was then compared for the Gabor and the standard stimuli with a paired t-test. With this small sample size, only borderline significance was found for lower response variability with the Gabor stimulus (t = 2.20, p < 0.03).

The smaller dynamic range for the chromatic stimulus limited our ability to measure severe defects, so the analysis of variability was performed over a smaller range of defects than for the standard stimulus. Because response variability for the standard stimulus increased in deeper defects, it is possible that the higher variability found for the standard stimulus was the result of including data from more severely damaged regions. To evaluate this possibility, response variability was computed for the standard and the chromatic stimuli restricted to points with defects no deeper than -4 dB. The analysis was performed using all available data (multiple data points per patient, t = 2.73, p < 0.005) and using one data point per patient (median variability was selected and paired for each subject, t = 2.92, p < 0.01). Both analyses found significantly lower response variability for the chromatic than for the standard stimulus. Therefore, differences in depth of defect can be excluded as the cause of lower variability for the chromatic stimulus.

To evaluate whether these findings would also be expected with clinical perimetric tests that use many fewer trials to estimate sensitivity, we next computed sensitivities by averaging the second and third reversals of the original staircases. Fixation loss >33% and false-positive rate >25% were used as criteria to reject unreliable data. The results were roughly consistent with those of the 12 reversal staircase, but with fewer trials, both depth of defect and response variability increased. A one-way ANOVA found no difference in depth of defect across stimuli (F = 2.87, p > 0.05); this sample had the power to detect a mean difference by 1 dB. Response variability was found to be different across stimuli (F = 3.91, p < 0.03); post hoc tests showed that variability was lower for the chromatic stimuli than for the other two types of stimuli (p < 0.05). Figure 8 plots variability against depth of defect. A significant correlation between variability and defect was found only for the standard stimulus (r² = 0.07, p < 0.02), not for the Gabor stimulus (r² = 0.03, p > 0.08) or the chromatic stimulus (r² = 0.03, p > 0.19).

FIGURE 8.

Individual test-retest variability is plotted against depth of defect for data obtained from the first three reversals of the original staircase. Horizontal lines show the mean and the upper 95% confidence limits of test-retest variability. Test-retest variability was significantly correlated with depth of defect for the standard stimulus (regression line shown) but not for the Gabor or the chromatic stimuli.

DISCUSSION

Our quantitative cortical pooling model of perimetry in glaucoma predicted that response variability resulting from heterogeneous ganglion cell damage should be lower when a larger stimulus is used or when a larger number of ganglion cells are stimulated. For all stimuli, depth of defect was predicted to be deepest when detection is mediated by spatial mechanisms tuned to low spatial frequencies. To test these predictions, we designed two large innovative stimuli (Gabor and chromatic) to tap mechanisms tuned to low spatial frequencies. The model predicts that perimetric defects measured with these stimuli should be equivalent to defects measured with luminance increments the size of the standard Goldmann size III stimulus and that the stimuli should yield reduced response variability in areas with glaucomatous defects. These predictions were confirmed in data from patients with glaucoma tested with these stimuli.

We provide an intuitive explanation for the predictions of the model. When small numbers of ganglion cells respond to perimetric stimuli, if there is heterogeneous ganglion cell damage, then minor changes in stimulus location can shift the stimulus from a patch of ganglion cells with extensive damage to a nearby patch of surviving ganglion cells. Therefore, minor changes in stimulus location have the potential to produce dramatic changes in sensitivity, producing high variability of perimetric responses. When a large number of ganglion cells contributes to detection, minor changes in stimulus location will have less effect on sensitivity and hence will produce less of an increase in response variability. This is why the model predicts that perimetric response variability can be lowered by using a large stimulus or a stimulus for which detection is mediated by a dense ganglion cell mosaic. On the other hand, if a stimulus is too large relative to the receptive fields of the cortical populations mediating detection, each population will respond to only a portion of the stimulus. If a small patch of intact ganglion cells respond to the stimulus, the cortical populations responding to this portion of the stimulus could have near-normal sensitivity. If the stimulus size is similar to or smaller than the central excitatory region of a receptive field, detection would to a large extent be mediated only by the cortical populations responding to the entire stimulus. Because these populations will have much greater sensitivity than populations that respond to only a portion of the stimulus, ability to detect glaucomatous damage can be preserved. One exception was that for the size III stimulus and the undersampled array, the 4-cpd filters yielded deeper defects when ganglion cell loss was extensive (Fig. 1). Ganglion cells in the undersampled array have minimal overlap of receptive field centers and a 0.32° center-to center spacing, so the small 4-cpd filters will each receive input primarily from only one ganglion cell and a 0.43° stimulus will fall on just a few cortical receptive field centers. When the stimulus is centered on a missing ganglion cell, the filters will be minimally responsive, giving an extremely low sensitivity, which dramatically affects both the mean and standard deviation of sensitivities across stimulus locations. Under this condition, the low sensitivity and high variability would make it difficult to evaluate progressive deterioration in advanced glaucoma.

The model assumes a heterogeneous pattern of ganglion cell loss, consistent with apoptotic cell death³² as well as with heterogeneous ganglion cell dysfunction.¹ The primary predictions of the model are based on interactions between minor changes in fixation, cortical pooling by spatial filters, and the heterogeneity of ganglion cell sensitivity. If perimetric sensitivity were also affected by homogeneous ganglion cell dysfunction (a uniform reduction in responsiveness of all ganglion cells), then the predictions concerning response variability would be similar except that variability would increase more slowly with depth of defect.

There was good agreement between defect depths measured with the innovative stimuli and the standard stimulus in that the mean was near zero and there was minimal correlation between stimulus effect and defect depth. However, agreement was weak in that the 95% confidence limits were ±4 dB for individual test locations within an eye (Fig. 4). This is consistent with results from previous studies^14,49: agreement between defect depths for different types of perimetric stimuli can be low for individual locations in individual eyes. For our data, the vector sum of test-retest confidence limits for two stimuli yields confidence limits for between-stimulus comparisons of ±2.5 dB for chromatic versus the standard and ±2.8 dB for Gabor versus the standard. This indicates that test-retest variability does not account for more than approximately half of the variance in between-stimulus comparisons (F > 1.9, p < 0.005). In damaged areas, some of the remaining variance can be explained in terms of the relative sizes of the stimuli. For the Gabor and chromatic stimuli, which tap mechanisms tuned to low spatial frequencies, the model predicts that the defect will approximate the loss in number of ganglion cells in the region covered by the stimuli so that loss of 50% of cells will yield a -3 dB defect and loss of 90% of cells will yield a -10 dB defect. Within the large regions of the retina covered by our large stimuli, there may be small patches with ganglion cell density that is much higher or lower than the mean across the entire region. When the smaller standard stimulus falls on a patch with high cell density, then defects will be milder than for the larger stimuli. Conversely, when the standard stimulus falls on a patch with low cell density, then defects will be deeper than for the larger stimuli. The same explanation can be applied to the finding by Artes et al.¹⁴ that some test locations in some eyes showed consistently large differences in depth of defect for standard perimetry and FDT perimetry.

Despite the low correspondence of depth of defect on a point-by-point basis, thresholds measured with the three types of stimuli agreed reasonably well in terms of whether a test location was normal or abnormal (Fig. 6). When sensitivities to two different stimuli are highly correlated on a point-by-point basis, it is unlikely that they yield different types of diagnostic information. In other words, we suggest that use of the two innovative stimuli might add new diagnostic information to what is obtained with the standard stimulus.

The overall response variability was similar for the Gabor stimulus and the standard stimulus and increased with defect depth. Nonetheless, the slope of the regression line was half as large for the Gabor stimulus, and in defective areas, response variability was lower for the Gabor stimulus than for the standard stimulus. This is consistent with the predictions of the model; although variability is expected to rise with glaucomatous defect for all types of stimuli, it is expected to rise at a slower rate when a large number of ganglion cells are stimulated. Therefore, an advantage of the Gabor stimulus is low variability in areas with glaucomatous defect.

Response variability was low for the chromatic stimulus in both normal and defective areas. Although the small dynamic range for the chromatic stimulus limited our ability to explore response variability in more severely damaged areas, the lower overall variability than for the standard and Gabor stimuli is a very desirable feature of the chromatic stimuli. Two factors make it unlikely that the lower variability for the chromatic stimuli is a result of the smaller dynamic range. First, the exclusion of unreliable data and nonmeasurable data (difference between threshold contrast and maximum available contrast <1.5 dB) helped to secure the accuracy of the measured thresholds. Second, of the test locations in which the chromatic stimulus did not yield measurable thresholds on one visit, identical results were obtained on the other visit for all but 5% (5 of 103) of locations (see Table 3). For these 5% of test locations, the mean difference between threshold contrast and the maximum contrast was 0.6 dB (range, 0-2 dB) for the chromatic stimulus compared with 2.8 dB (range, 0.5-6.6 dB) for the standard stimulus. In addition to low response variability, another advantage for the chromatic stimuli is low normal between-subject variability, which may be useful for early detection of glaucoma.

Despite the desirable features of the chromatic stimuli in terms of within-subject and between-subject variability, the small dynamic range and the high incidence of congenital red-green defects in the general population limits their potential for clinical use. However, for structure-function studies using linear measures of contrast sensitivity,⁵⁰ the dynamic range is suitable for detecting early abnormalities (-7 dB defect corresponds to 80% loss). The dynamic range for the chromatic stimuli was limited both by our apparatus and by the technique we used to isolate the parvocellular pathway. In the perimetric literature, much less attention has been paid to the parvocellular pathway than to the magnocellular or koniocellular pathways. Our results are in accord with studies which have addressed parvocellular pathways, and have found defects can be just as deep for stimuli designed for the parvocellular pathway as for stimuli designed for the magnocellular and koniocellular pathways.^11,51-53 Based on our initial findings of low within-subject and between-subject variability for normal red-green chromatic sensitivity, there is good potential for new perimetric stimuli to achieve both low variability and good ability to detect defect by assessing sensitivity of the parvocellular pathway.

The diameter of the chromatic stimuli was increased with eccentricity to approximate Ricco’s area for the chromatic mechanism, whereas the sizes of the standard and Gabor stimuli did not vary with eccentricity. A circular stimulus equal to Ricco’s area has approximately the same width as the central excitatory region of the cortical populations mediating detection.¹ By choosing chromatic stimuli based on Ricco’s area, we aimed to maximize the number of ganglion cell responses pooled by the receptive fields of the cortical populations mediating detection. Moreover, it is well-established that relative spatial scale varies with eccentricity,⁵⁴ and it has been suggested that, for a fixed size stimulus, changes in spatial scale can result in variation in the temporal properties of the mechanisms mediating detection.⁵⁵ By scaling the stimulus size to be similar to the Ricco’s area, we aimed to minimize effects of spatial scale. We did not try to scale the Gabor stimulus with eccentricity. Unlike a circular stimulus, which contains a wide range of spatial frequencies and could be detected by mechanisms with a range of peak spatial frequencies, the Gabor stimulus should be detected by those cortical populations with the peak spatial frequencies near 0.5 c/deg. There has been limited information on scaling perimetric stimuli with retinal eccentricity.^56,57 Our results support the suggestion that the clinical use of this approach should be explored³⁶ for both circular and grating stimuli.

In this study, we tried to improve the use of large stimuli for assessing glaucomatous defects by selecting the receptive field widths of cortical populations contributing to threshold (i.e., reducing the sensitivity of populations tuned to higher spatial frequencies). An analogy can be drawn between our approach and the “reduced redundancy” approach,⁵⁸ which proposed that glaucomatous defects may be deeper when assessed with stimuli for which a reduced number of ganglion cells are responsive. Rather than aiming to decrease the number of ganglion cells contributing to threshold, we aimed to decrease “redundancy” in the cortical populations by increasing the number of ganglion cells contributing to detection. Use of well-designed large stimuli could potentially allow the number of locations tested to be reduced in exchange for a greater number of trials at each location; a larger number of trials could allow more accurate and precise measures of perimetric sensitivity.

The cortical pooling model predicts, and experimental data confirm, that appropriately designed large stimuli can yield low response variability without compromising the ability to detect and quantify glaucomatous defects. The model predicts that this result should obtain for all large stimuli for which detection is mediated by cortical populations with appropriately wide receptive field centers. This study proposes a potential advancement for future perimetric stimuli that might help in early diagnosis of glaucoma and early detection of deterioration of glaucoma.