Monochromatic ocular wave aberrations in young monkeys

Abstract

High-order monochromatic aberrations could potentially influence vision-dependent refractive development in a variety of ways. As a first step in understanding the effects of wave aberration on refractive development, we characterized the maturational changes that take place in the high-order aberrations of infant rhesus monkey eyes. Specifically, we compared the monochromatic wave aberrations of infant and adolescent animals and measured the longitudinal changes in the high-order aberrations of infant monkeys during the early period when emmetropization takes place. Our main findings were that (1) adolescent monkey eyes have excellent optical quality, exhibiting total RMS errors that were slightly better than those for adult human eyes that have the same numerical aperture and (2) shortly after birth, infant rhesus monkeys exhibited relatively larger magnitudes of high-order aberrations predominately spherical aberration, coma, and trefoil, which decreased rapidly to assume adolescent values by about 200 days of age. The results demonstrate that rhesus monkey eyes are a good model for studying the contribution of individual ocular components to the eye’s overall aberration structure, the mechanisms responsible for the improvements in optical quality that occur during early ocular development, and the effects of high-order aberrations on ocular growth and emmetropization.

1. Introduction

In many animal species, optically altering visual experience early in life by imposing defocus with positive-or negative-powered lenses produces compensating changes in axial growth that eliminate the imposed refractive errors (Graham & Judge, 1999; Hung, Crawford, & Smith, 1995; Schaeffel, Glasser, & Howland, 1988; Shaikh, Siegwart, & Norton, 1999; Smith & Hung, 1999). Thus, emmetropization is a vision-dependent process and optical defocus can guide early ocular growth in a manner that eliminates refractive errors that are common in neonates (Norton & Siegwart, 1995; Smith, 1998; Wallman & Winawer, 2004; Wildsoet, 1997). It has also been established that chronic viewing conditions that degrade the spatial characteristics of the retinal image and prevent the formation of a clear retinal image disrupt emmetropization and typically result in a phenomenon called form deprivation myopia (FDM) (Smith, Harwerth, Crawford, & Von Noorden, 1987; Troilo & Judge, 1993; Wallman, 1993; Wiesel & Raviola, 1977). Even mild degrees of chronic image degradation that are equivalent to the reductions in image contrast produced by small amounts of defocus are capable of producing FDM (Bartmann & Schaeffel, 1994; Smith & Hung, 2000). These results emphasize that the potential for a clear retinal image is essential for normal refractive development.

In addition to the effects of spherical and astigmatic refractive errors, the optical quality of the retinal image is influenced by high-order aberrations that are caused by optical imperfections such as surface irregularities and tilts or misalignments in the eye’s optical components. All eyes suffer from such aberrations (Campbell & Gubisch, 1966; Howland & Howland, 1976; Jenkins, 1963; Liang, Grimm, Goelz, & Bille, 1994; Liang & Williams, 1997; Smirnov, 1961). Although the retinal image degradation due to high-order aberrations is usually modest, the degree of high-order aberrations (however, not necessarily the pattern of aberrations) (Cheng et al., 2004a; Thibos, 2002) is relatively constant over time, which is critical for a myopigenic stimulus to produce axial elongation (Kee et al., 2002b; Napper et al., 1997; Schmid & Wildsoet, 1996; Winawer & Wallman, 2002). Consequently, blur due to aberrations could potentially influence ocular growth and refractive development.

Early in life, during the rapid infantile phase of ocular growth, there are substantial changes in the eye’s optical and axial components that could influence the pattern and degree of high-order aberrations. In particular, changes in the curvature of the cornea and lens and in the refractive index and thickness of the lens not only influence the eye’s refractive status, but may also change the magnitude and the pattern of aberrations. In addition to being a potential stimulus for anomalous growth, such aberration changes may potentially alter the accuracy or the end point of the emmetropization process. Conversely, it is also possible that the optimum combination of certain types of aberrations may provide signals that guide emmetropization (Wallman & Winawer, 2004; Wilson, Decker, & Roorda, 2002). Thus, it is important to understand the developmental changes in high-order aberrations because they directly affect retinal image quality and may potentially influence the efficiency of the emmetropization process.

Recent population studies of both human children and adults have found large amounts of inter-individual variability both in the pattern and magnitude of high-order aberrations (Carkeet, Luo, Tong, Saw, & Tan, 2002; Castejon-Mochon, Lopez-Gil, Benito, & Artal, 2002; De Brabander et al., 2004; He, Burns, & Marcos, 2000; He et al., 2002; Porter, Guirao, Cox, & Williams, 2001; Thibos, Hong, Bradley, & Cheng, 2002c). Among the few studies that compared aberrations between adults and children, one study reported that the magnitude of high-order aberrations during childhood (5–20 years of age) was 40–50% higher in comparison to adults (Brunette, Bueno, Parent, Hamam, & Simonet, 2003) while a second study of 5-to 7-week-old infants found that infants had only 20% higher total RMS errors and that they exhibited similar patterns of aberrations as young adults (Wang & Candy, 2005). Although the differences in the results between these two studies can be explained partly by differences in the way aberrations were compared between infant and adult eyes (constant pupil size, Brunette et al., 2003, vs. constant numerical aperture, Wang & Candy, 2005), longitudinal data are needed to properly characterize the maturational changes in high-order aberrations, particularly the changes that take place during the early growth period when emmetropization normally takes place.

Animal models provide a unique opportunity to study normal longitudinal changes in high-order aberrations and the changes that occur during the development of abnormal refractive errors. Recent studies in both the chick and marmoset have shown that wavefront aberrations decrease with age (Campbell, Hunter, Kisilak, Irving, & Huang, 2003; Coletta, Triolo, Moskowitz, Nickla, & Marcos, 2004; Garcia de la Cera, Rodriguez, & Marcos, 2006; Thibos, Cheng, Phillips, & Collins, 2002b). However, the pattern and, in some studies, the magnitude of high-order aberrations in these species appear to be different from those found in humans. For example, infant marmosets exhibit negative spherical aberration whereas humans typically show positive spherical aberration (Coletta et al., 2004) and one study reported that the magnitude of high-order aberrations in chick eyes was about 6–10 times higher than that in human eyes (Thibos et al., 2002b). Consequently, qualitative differences in the shape, size, and organization between the eyes of humans and those of chicks and marmosets may confound direct comparison between these animals and humans.

The structural and developmental aspects of the rhesus monkey eye closely resemble those of human eyes thus making macaque monkeys good animal models for investigations of emmetropization and refractive development (Bradley, Fernandes, Lynn, Tigges, & Boothe, 1999; Smith, 1998). Studying wave aberrations in macaques could provide insights into the role of aberrations in emmetropization and refractive development. The goals of our study were to characterize the high-order aberrations and retinal image quality in infant rhesus monkeys and to compare them to those in adolescent monkeys. In addition, we determined the longitudinal changes in ocular monochromatic wavefront aberrations that took place during the course of emmetropization in a subgroup of infant monkeys. Some of the data from this study have been presented in abstract form elsewhere (Ramamirtham et al., 2002).

2. Methods

2.1. Subjects

Our subjects were 50 normal infant monkeys and 6 normal adolescent monkeys (Macaca mulatta). Cross-sectional biometric data on refractive state, monochromatic wavefront aberrations, and axial dimensions were obtained from both eyes of all 56 animals. Longitudinal biometric data were obtained from both eyes of five infants and four adolescent monkeys. All of the rearing and experimental procedures, many of which have been described previously (Hung et al., 1995; Smith & Hung, 1999), were approved by the University of Houston’s Institutional Animal Care and Use Committee and were in compliance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Cross-sectional data were collected in the infants at about 3 weeks of age (mean = 21 ± 3 days) and in the adolescents at 4–5 years of age (4.8 ± 0.6 years). Longitudinal data were obtained from five infants at 2-to 4-week intervals beginning at 3 weeks of age until the monkeys were about 200 days of age. This period encompasses the rapid infantile phase of ocular growth and the bulk of the emmetropization process, which in normal infant monkeys is largely complete by about 150 days of age (Bradley et al., 1999; Hung et al., 1995). The ocular growth in monkeys during the first 150 days of life is approximately equivalent to that which occurs during the first 2 years in human infants (Bradley et al., 1999). In order to determine the repeatability of the measured aberrations within and across sessions, longitudinal data were also obtained on 3–7 occasions over about a 1.5 year period in four adolescent monkeys.

2.2. Biometric measurements

To make the biometric measurements each animal was anesthetized with an intramuscular injection of ketamine hydrochloride (15–20 mg/kg) and acepromazine maleate (0.15–0.2 mg/kg). The cornea was topically anesthetized with 1–2 drops of 0.5% tetracaine hydrochloride. Cycloplegia was achieved by topically instilling two drops of 1% tropicamide, 20– 30 min before performing any measurement that would potentially be affected by the level of accommodation. While the measurements were being taken, the eyelids were gently held apart by a custom made speculum and the corneal tear film was maintained by frequent irrigation with a balanced saline solution. Care was taken to keep the eyes closed in between measurements.

Two investigators independently determined the spectacle-plane refractive correction for each eye along the pupillary axis using a streak retinoscope and hand-held lenses. The mean of these two measurements, specified in minus cylinder form, was taken as an eye’s refractive error (Harris, 1988).

The eyes’ axial dimensions were measured by A-scan ultrasonography implemented with a 7 MHz transducer (Image, 2000; Mentor, Norwell, MA). Ten separate measurements were averaged and the interocular distances were calculated using a weighted average velocity of 1550 m/s. A-scan ultrasonography was always performed at the end of session after the refractive and aberration measurements had been completed.

A custom-built Shack–Hartmann wavefront sensor (SHWS), which was based on the principles described by Liang and Williams (Liang et al., 1994; Liang & Williams, 1997), was used to measure each eye’s wave aberrations. We used a low intensity infrared superluminescent diode (10 μW, Hamamatsu Corp., USA) with a wavelength of 830 nm to produce a point source on the retina. A lenslet array (Thorlabs Inc., Newton, NJ) composed of a square grid of 0.4 mm-diameter lenslets each with 24 mm focal lengths was used to focus the light emerging from the eye onto a CCD camera. Wavefront sensing was done by reconstructing the emerging wavefront from the deviation of the individual spots captured on the CCD camera relative to the spots produced by an ideal planar wavefront (Liang et al., 1994; Wilson et al., 2002). The SHWS was calibrated based on lenslet geometry and focal length. This was validated by measuring different levels of defocus produced by placing a point source at distances varying from 33 to 6 m. Specifically, the focal distances between the optical components of the SHWS were adjusted until the instrument measured a given amount of defocus with an error of less than 0.05%.

The line of sight, which is the recommended reference axis for aberration measurements (Thibos, Applegate, Schwiegerling, & Webb, 2002a), passes through the eye’s entrance pupil center and connects the foveola and the fixation point. Based on photographs of the corneal light reflex of normal adult rhesus monkeys and from geometrical calculations, Quick and Boothe, (Quick & Boothe, 1989, 1992) determined that angle lambda (the angle between the pupillary axis and the line of sight) was approximately 2–4 degrees and the line of sight was nasal to the pupillary center. They also found that the Hirschberg ratio (the amount of rotation of the eye per millimeter displacement of the corneal light reflex from the center of the pupil) was constant at about 14 degrees for both infant and adult monkeys. Therefore, for distance fixation, we assumed that the monkey’s line of sight intersected the anterior corneal surface approximately 0.3 mm nasal to the center of the entrance pupil.

In order to obtain SHWS measurements along the presumed line of sight, the animal was placed on a stage with a head mount that allowed 5 degrees of movement (X–Y–Z + tip-tilt) to control the animal’s pupil location and direction of gaze. All our aberration measurements were performed by first centering the optical axis of the instrument on the eye’s pupillary axis. This was achieved by aligning a bull’s eye pattern arranged along the optical axis of the instrument with the center of the eye’s entrance pupil, which was viewed via a video camera. Without disrupting this alignment we next rotated the head of the monkey so that the corneal light reflex, generated by the coaxially aligned superluminescent diode source, was approximately 0.3 mm nasal to the center of the entrance pupil, thereby ensuring that measured aberrations were referenced to the presumed line of sight. During the course of the measurements, proper alignment was maintained by continuously monitoring the position of the corneal light reflex and the entrance pupil with a video camera. The corneal tear film was maintained by frequent irrigation (approximately every 10 s) with a balanced saline solution. The spot patterns stabilized approximately 5 s after each application of the saline solution. Aberration measurements were done only after the spot patterns were stable. The entire alignment and aberration measurement session lasted less than 5 min for both eyes of a given animal.

Five measurements in the form of Shack–Hartmann spot images were obtained for each eye during each session. The images were stored in a computer using a frame grabber. Each image was later analyzed individually using custom software (developed on Microsoft Visual C++ platform) to calculate the relative x–y displacement of each sampled point with respect to the reference center for a given lenslet. This provided the local slopes of the wavefront, which were fit with the derivative of Zernike’s circle polynomials (up to 10th order) by the method of least squares. The wave aberration function W(x,y) was represented by a weighted sum of the series of Zernike terms:

$$W(x,y)=\sum _{n,f}{C}_n^f{Z}_n^f,$$

where W(x,y) is defined over x–y coordinates of the pupil, C is the corresponding coefficient of the Zernike term, n and f are the degree of the polynomial and the meridional frequency, respectively. We used the double-index convention for naming and ordering the Zernike coefficients as recommended by the OSA/VSIA Standards Taskforce (Thibos et al., 2002a). Using the average Zernike coefficients obtained from the analysis of five such wavefront sensor images, the magnitude of an eye’s monochromatic high-order aberrations, excluding defocus and astigmatism, was expressed as the total root-mean-square error (RMS) between the measured and ideal wavefronts in units of microns. In addition, the best-corrected monochromatic point spread function (PSF), Strehl ratio, and radially averaged modulation transfer function (MTF) were calculated from each eye’s wavefront aberration function and employed to describe image quality (Charman, 1991; Howland & Howland, 1977; Mahajan, 1991; Walsh & Charman, 1985). All of the spot pattern images were analyzed with a fixed central 5 mm pupil size unless otherwise mentioned. Low-order aberrations refer to 2nd order Zernike terms (defocus and astigmatic terms) while high-order aberrations refer to Zernike terms from 3rd order and higher.

3. Results

3.1. Aberration measurements in adolescent monkeys

In order to determine the short-and long-term repeatability of our methods, we measured aberrations on four adolescent monkeys whose refractive status and axial dimensions remained stable over about a 1.5 year period. Fig. 1 shows the total RMS wavefront error as a function of age for the right and left eyes of the four adolescent monkeys. The average within session standard deviation of the total high-order RMS wavefront error for this group was 0.03 μm (range = 0.007 to 0.07 μm; λ/72 to λ/8), indicating that the total aberrations measured within a given session were highly repeatable. The average standard deviations for each Zernike term from 3rd to 10th order were also small (mean = 0.008 ± 0.009 μm; range = 0.0003 to 0.03 μm), indicating that in addition to the total RMS error, the coefficients of the individual Zernike terms were repeatable within a session.

Fig. 1.

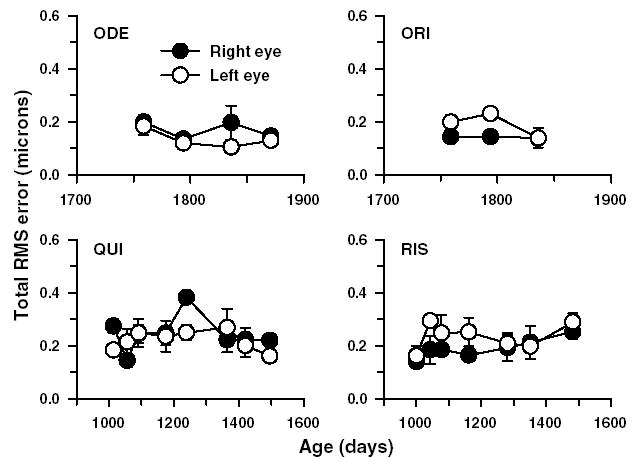
The total RMS error (3rd to 10th order) plotted as a function of age for four adolescent monkeys. Each data point represents the mean ± 1SD (n = 5). Data from both the right (●) and left eyes (○) are shown separately. Analyzed pupil diameter for all eyes was 5 mm.

In the same group of four adolescent monkeys, to test whether aberration measurements were repeatable from one session to the next, Bland–Altman plots were generated for 2nd to 5th order Zernike terms (Fig. 2). The interval between measurement sessions varied from 8 to 18 weeks. The magnitude of the upper and lower specification lines in Fig. 2, which were drawn at the mean ± 1.96SD, ranged from ±0.20 to ±0.70 μm for 2nd order terms and ±0.04 to ±0.16 μm for 3rd to 5th order terms, indicating that aberrations were relatively stable between two consecutive sessions. Also note that there were no systematic variations between measurements as a function of the absolute degree of the high-order aberrations.

Fig. 2.

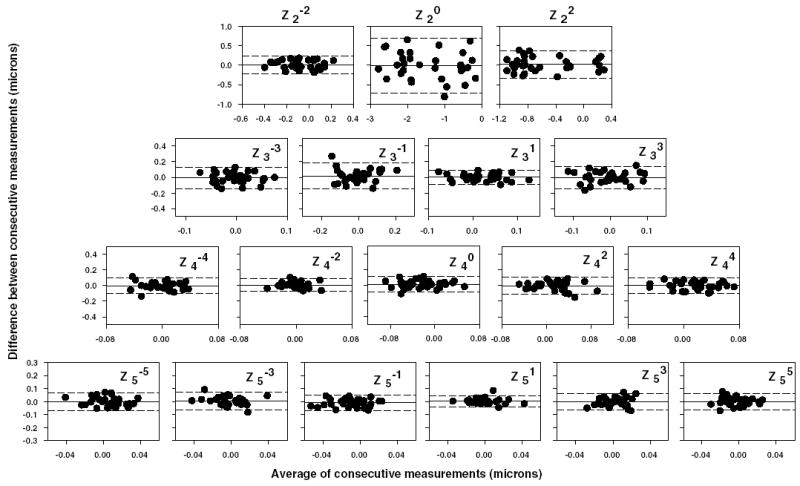
Bland–Altman plots for each of the Zernike terms from 2nd to 5th order. Each graph was obtained by plotting the difference between consecutive aberration measurements as a function of the average of the consecutive measurements for each eye of the four adolescent monkeys shown in Fig. 1. In each of the plots, the middle reference line indicates the mean difference. The upper and lower dotted lines were drawn at ±1.96SDs of the mean difference.

While the natural pupil diameter for both infant and the adolescent monkeys was about 3 mm, the dilated pupil diameters for infants were typically 5–6 mm and those for adolescents were about 6–7 mm. The aberration analyses in both infant and adolescents were restricted to a common pupil diameter of 5 mm to allow comparison across different age groups. Fig. 3 shows the average 2nd to 5th order Zernike coefficients for a 5 mm pupil diameter for the right (circles) and left eyes (squares) of the six adolescent monkeys. These cross-sectional aberration data were obtained from the last data points in each of the four plots in Fig. 1 and from two additional adolescent monkeys. The ages for these six monkeys were between 4 and 5 years. Since the number of subjects was small (n = 6), a sign-rank Wilcoxon test was used to determine whether any of the average coefficients were significantly different from zero and also to determine whether any average coefficient exceeded the Marechal criterion. According to the Marechal criterion if the total RMS wavefront error is less than or equal to wavelength/14 (equivalent to Strehl ratios ≥ 0.8), then the system is considered to be well corrected for aberrations and close to being diffraction limited (Cheng, Bradley, Hong, & Thibos, 2003; Marechal, 1947). Typically, the average amounts of high-order aberrations were small (mean total RMS error for the right eyes = 0.17 ± 0.05 μm; range = 0.13 to 0.25 μm), with only the defocus term being significantly greater than zero. Although Marechal criterion is generally applied to total RMS wavefront error, in order to determine the extent of image degradation due to any given Zernike term, the RMS error for each average coefficient was compared to Marechal criterion. None of the average coefficient values for terms from 3rd to 5th order (range = −0.03 to 0.02 μm) exceeded the Marechal criterion.

Fig. 3.

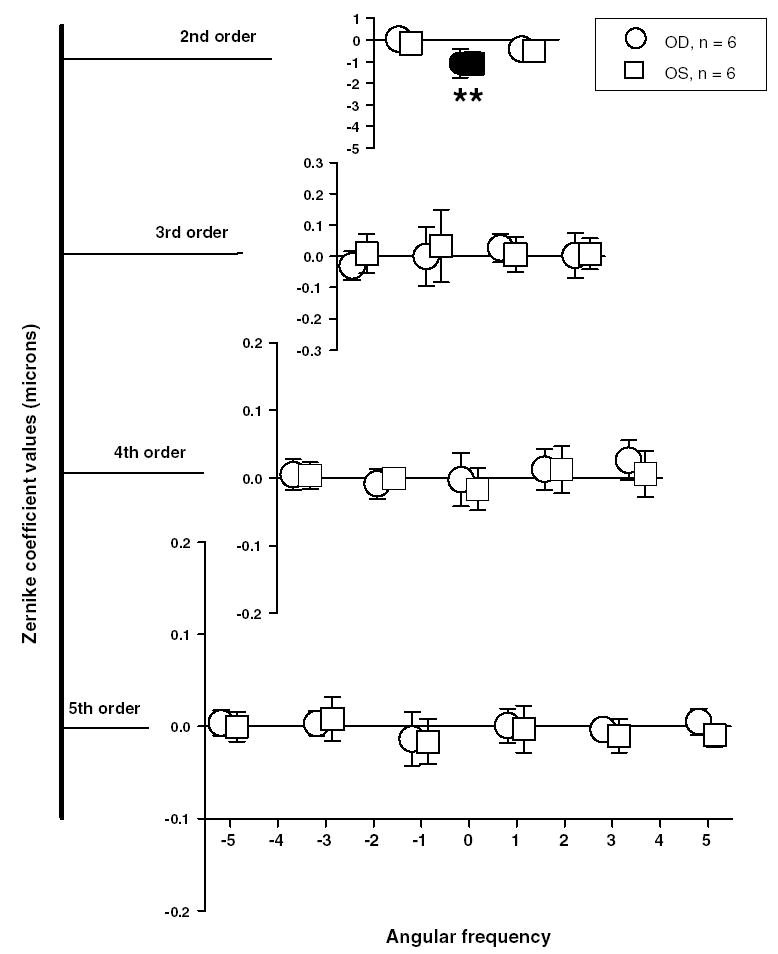
Mean ± 1SD of the Zernike coefficients (2nd to 5th order) for six adolescent monkeys at a mean age of 4.2 years. Each row from the top denotes increasing radial order and the corresponding angular frequency is shown on abscissa at the bottom. The circles and the squares denote the average magnitude of the Zernike coefficients for the right and left eyes, respectively. Filled symbols represent terms that are significantly different from zero (signrank Wilcoxon test). The magnitudes of the terms marked with asterisks (*) exceed the Marechal criterion (λ/14 > 0.039 μm; λ = 555 nm). Note that except for defocus no other term was statistically different from zero.

3.2. Optical quality of infant monkey eyes

Fig. 4 shows the typical spot pattern images obtained from the SHWS (left), wavefront contour plots (middle), and corresponding best corrected monochromatic point spread functions (right) derived from the wavefront aberration functions for one adolescent (top row) and three infant monkeys (bottom three rows). The three infant eyes were selected to illustrate the range of wave aberrations found in 3-week-old monkeys. The infants’ plots were arranged such that the eye with the least aberrations is represented in the second row while the eye with the most aberrations is represented in the bottom row. Qualitatively, the spot pattern images for the infants were similar to those obtained from adolescent monkeys. In the contour plots, which were obtained after the spot patterns were analyzed and fit with Zernike polynomials, the density of the contour lines reflects the rate of change in ocular aberrations (0.25 μm intervals for terms > 2nd order) with the higher densities indicating greater variations in the local slope of the wavefront and, therefore, higher magnitudes of aberrations. The corresponding best-corrected monochromatic PSFs, which describe the effect of aberrations in the spatial domain, show a great degree of variation in size illustrating that the aberrations and therefore, the retinal image quality was variable between the infant monkeys. The Strehl ratio, which is defined as the ratio of the central intensities of the aberrated PSF function and the diffraction-limited PSF, for these three infant eyes were 0.12, 0.026, and 0.013, with the lower Strehl ratios reflecting poorer image quality.

Fig. 4.

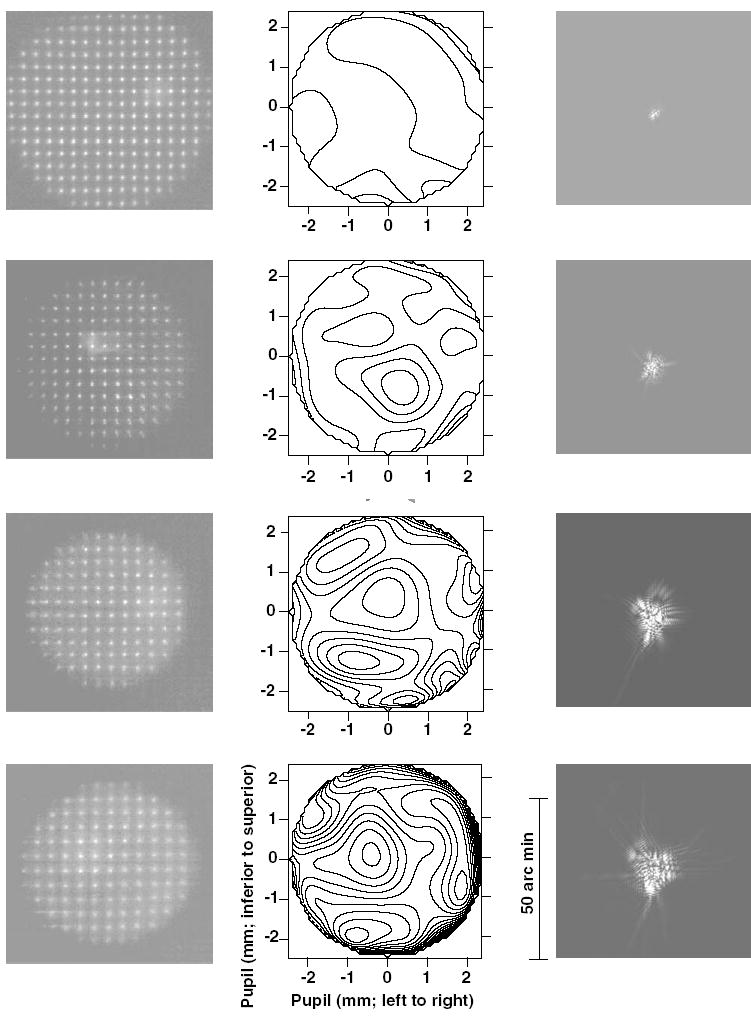
Spot patterns (left column), their corresponding wavefront contour maps (middle column), and the best corrected PSFs (right column) for one adolescent (top row) and three infant (2nd to bottom rows) monkey eyes arranged such that the image quality varies from best to worst. Contour plots showing the aberrated wavefront at the exit pupil plane (3rd to 10th order) were obtained after analyzing the spot patterns and fitting the resulting wavefront with Zernike polynomials. The contour intervals are 0.25 μm. The PSFs (3rd to 10th order) were obtained by inverse Fourier transformation of the fitted Zernike polynomials. The scale on the PSF is 50″ in length. All analyses are shown for a 5 mm pupil diameter.

Fig. 5 shows the average 2nd through 5th order Zernike coefficients for a 5 mm pupil diameter for the right (circles) and left eyes (squares) of the 50 infant monkeys. A 5 mm pupil diameter was chosen because in most infant monkeys the dilated pupil was consistently between 5 and 6 mm in diameter. In three of the 50 animals, one eye’s pupil was smaller than 5.0 mm. Hence, the data from those eyes were not included. On average the magnitude of the Zernike coefficients decreased as a function of the Zernike radial order. Although the average Zernike coefficients were close to zero for most of the terms, there were large between subject differences for some terms as indicated by the large standard errors. Also in Fig. 5, note that the average Zernike coefficients for the right and left eyes were typically similar in magnitude; however for some terms (e.g., 3rd order), the right and left eyes showed equal magnitudes but opposite signs, suggesting some degree of mirror symmetry between the two eyes.

Fig. 5.

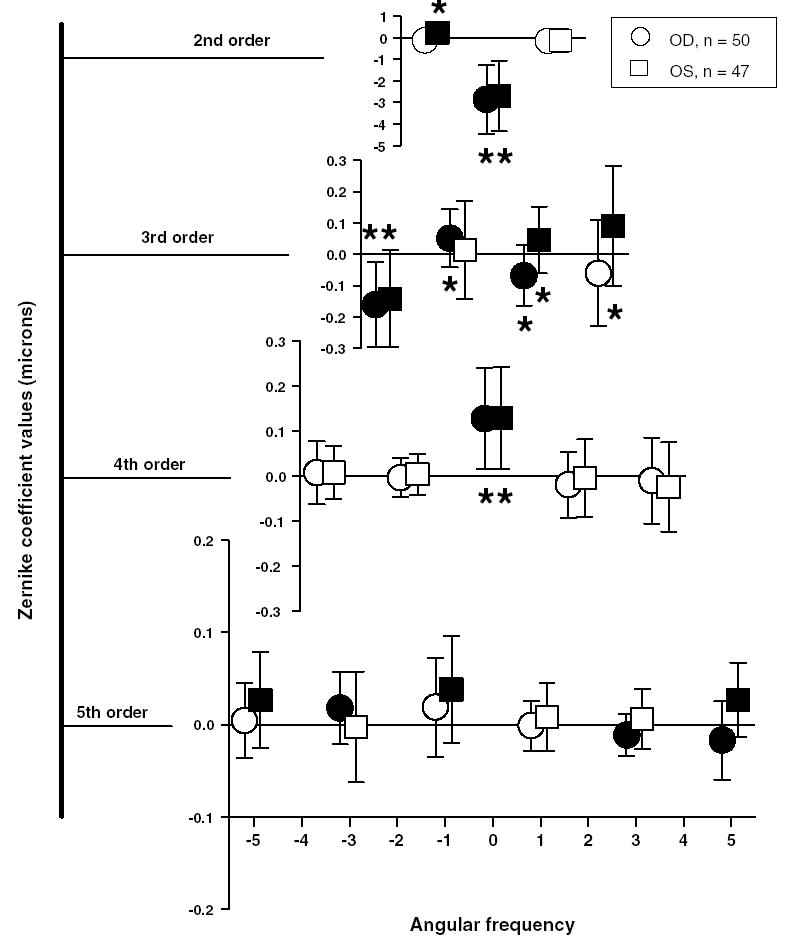
Average Zernike coefficients for 2nd to 5th order terms for 97 infant eyes (Mean ± 1 SD). Circles and squares represent the right and left eyes, respectively. Each row shows different radial orders. The abscissa denotes the corresponding angular frequency. Filled symbols are terms whose magnitudes were statistically significant (independent t-test, P ≤ 0.01). Asterisks indicate average coefficient values that exceeded the Marechal criterion (λ/14 = 0.039 μm; λ = 555 nm).

To test whether a given Zernike term was on average significantly different from zero, a one-sample, independent t-test was performed for each term for all right and left eyes, separately. The Zernike coefficients that are shown as filled symbols were found to be significantly different from zero with a P value ≤ 0.01. When we employed the Marechal criterion to test the visual consequence of the Zernike terms that were statistically significant (asterisk symbols in Fig. 5), many terms in the 2nd, 3rd, and 4th order significantly degraded the retinal image of the infant monkeys. Among the high-order aberrations coma, trefoil, and spherical aberration were the most dominant aberrations. None of the Zernike coefficients above 4th order exceeded the Marechal criterion, indicating that they do not significantly degrade retinal image quality. However, as noted by studies in humans (Applegate, Marcos, & Thibos, 2003), the Zernike coefficients greater than 4th order, although low in magnitude can have a beneficial or degrading effect on the overall optical quality of the eye when combined with other high-order aberrations such as coma or spherical aberration. Also, the sum of all of the aberrations that do not meet this criterion alone, could impact image quality. However, the contribution to overall wavefront aberrations from 5th order and higher is very low (see Fig. 6), indicating that they do not significantly degrade retinal image quality.

Fig. 6.

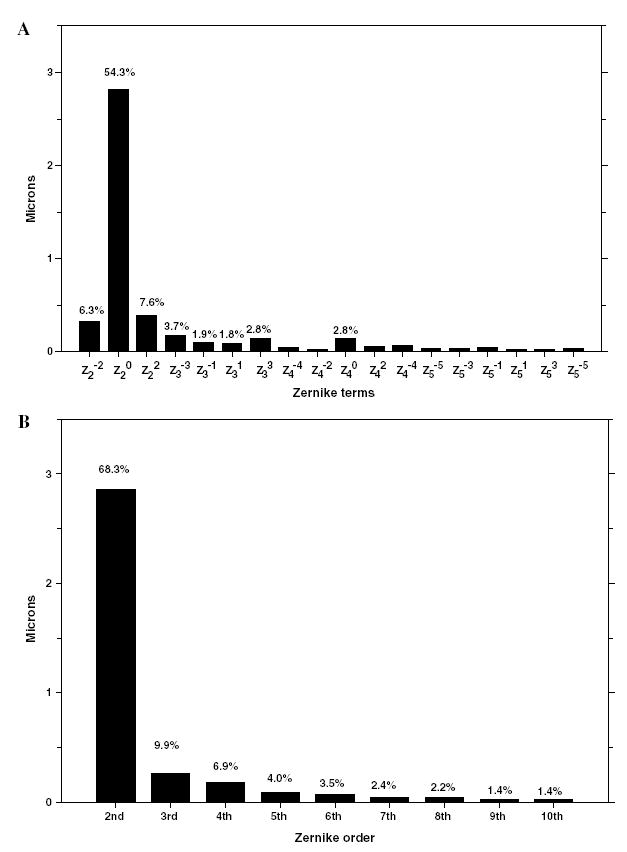
(A) Average absolute Zernike coefficients and percentage contributions of each of the Zernike terms from 2nd to 5th order to the overall wavefront aberrations for the 97 infant eyes. The percentage contributions were obtained from the average absolute values of the Zernike coefficients for each term. (B) Average absolute Zernike coefficients and percentage contribution of each Zernike order to the overall wavefront aberrations. The percentage contribution for each order was calculated as the RMS of the average absolute values of the Zernike coefficients in a given order.

Among the 2nd order terms, which contribute to astigmatism and defocus, only the defocus term ( $Z_2^0$) was statistically significant and exceeded the Marechal criterion. All the infant monkeys exhibited moderate amounts of hyperopia, which is expected at this age (Bradley et al., 1999; Smith & Hung, 1999). The defocus term ( $Z_2^0$) was on average −2.77 ± 1.62 μm (equivalent to +3.1 ± 1.8 D) for 97 eyes. Also, as previously reported (Kee, Hung, Qiao, Habib, & Smith, 2002a) we observed that the average astigmatism was minimal in all of the infants and both of the 2nd order astigmatic terms ( $Z_2^{-2}$ and $Z_2^2$) were below the Marechal criterion for the right eyes. Although the left eye $Z_2^{-2}$term exceeded the Marechal criterion, on average the magnitude of astigmatism when expressed in diopters was less than 0.25 D.

The spectacle plane refractive error derived from the measured 2nd order terms were similar to those measured by retinoscopy. Specifically, calculated values for the spherical component (r = 0.97) and the spherical equivalent refractive error (i.e., M, r = 0.95) correlated well with refractive values obtained by retinoscopy. However, since the infants exhibited very low amounts of astigmatism, the correlation for astigmatic terms was not high (J0, r = 0.28; J45, r = 0.48).

Among the 3rd order terms, which include coma and trefoil, several terms were significantly different from zero. For the right eyes, the average magnitude of coma (RMS of $Z_3^{-1}$ and $Z_3^1$) was 0.14 ± 0.08 μm and that of trefoil (RMS of $Z_3^{-3}$ and $Z_3^3$) was 0.23 ± 0.14 μm.

Spherical aberration ( $Z_4^0$) was the only aberration above 3rd order that was significantly different from zero. The infant monkeys exhibited on average positive spherical aberration (mean = +0.12 ± 0.11 μm; range = −0.14 to +0.40 μm). Out of the 97 eyes, 86 showed positive spherical aberration while only nine eyes exhibited negative spherical aberration. Fifty-seven eyes showed positive spherical aberration that was greater than +0.10 μm while only three monkeys showed amounts of negative spherical aberrations that were larger than −0.10 μm.

Fig. 6 shows the average absolute Zernike coefficients in microns for each term (Fig. 6A) and order (Fig. 6B) for the 97 eyes. Except for the spherical aberration term $Z_4^0$ the magnitude of average absolute Zernike coefficients were very small for terms greater than 3rd order. In addition, to determine the relative effect of each of the Zernike coefficients on the overall wavefront aberration, we calculated the percentage contribution of individual terms to the sum of the average absolute values of corresponding terms for the 97 eyes (Figs. 6A and B). The absolute values and the percentage contribution decreased with increasing order number. As expected, the 2nd order terms contributed most to the overall wavefront error (68%), with the defocus term accounting for 54% of the total wavefront error. Overall the high-order aberrations (orders > 2) accounted for 32% of the total wavefront error. The 3rd and 4th order terms accounted for 10 and 7%, respectively, which amounted to 52% of all high-order aberrations. The 5th order terms accounted for only 12% of all high-order aberrations. Thus, in infant monkeys, 3rd and 4th order aberrations dominate the high-order aberrations.

Studies of high-order aberrations in humans (Castejon-Mochon et al., 2002; Cheng et al., 2003; Porter et al., 2001) showed that wavefront aberrations are bilaterally mirror symmetric. We tested if this was the case in infant monkeys by determining Pearson’s correlation between individual Zernike terms for right and left eyes (no correction for multiple tests was applied). Since the magnitude of the aberrations above 5th order was very small, we restricted this analysis to 2nd through 5th order terms. The results are shown in Table 1. Zernike terms that are symmetric about the vertical axis (in the pupil plane) are called even-symmetric and those that are not are called odd-symmetric. An eye is said to be bilaterally mirror symmetric if the even-symmetric terms for the right and left eyes are equal in magnitude and positively correlated while the odd-symmetric terms are equal in magnitude but negatively correlated (opposite sign). In infant monkeys most of the even-and odd-symmetric terms for right and left eyes exhibit correlations in the correct direction (i.e., positive correlations for even-symmetric terms and negative correlations for odd-symmetric terms, see Table 1). Among the even-symmetric terms, $Z_2^0$ (defocus) showed the highest positive correlation, followed by $Z_4^0$ (spherical aberration), $Z_5^{-1}$ (secondary coma) and $Z_3^{-3}$ (trefoil). Among odd-symmetric terms, $Z_3^1$ (horizontal coma) showed the highest negative correlation, followed by $Z_2^{-2}$ (astigmatism) and $Z_5^5$ (pentafoil).

Table 1.

Pearson’s correlation coefficients between right and left eye Zernike terms for the 47 infant monkeys

Symmetry	Zernike term	r-value	P value
Odd sym	$Z_2^{-2}$	−0.403	0.005
Even sym	$Z_2^0$	0.965	0.000
Even sym	$Z_2^2$	0.301	0.040
Even sym	$Z_3^{-3}$	0.546	0.000
Even sym	$Z_3^{-1}$	0.226	0.127
Odd sym	$Z_3^1$	−0.465	0.001
Odd sym	$Z_3^3$	−0.259	0.078
Odd sym	$Z_4^{-4}$	−0.082	0.582
Odd sym	$Z_4^{-2}$	−0.076	0.613
Even sym	$Z_4^0$	0.705	0.000
Even sym	$Z_4^2$	0.146	0.327
Even sym	$Z_4^4$	0.047	0.752
Even sym	$Z_5^{-5}$	0.151	0.312
Even sym	$Z_5^{-3}$	0.237	0.108
Even sym	$Z_5^{-1}$	0.377	0.009
Odd sym	$Z_5^1$	0.081	0.590
Odd sym	$Z_5^3$	−0.021	0.888
Odd sym	$Z_5^5$	−0.292	0.047

The Zernike terms are classified as even or odd symmetric terms based on their symmetry about the vertical axis. The even symmetric terms show positive correlations while most of the odd symmetric terms show negative correlations. The strength of the correlations was tested for their statistical significance and resulting P values are shown in the right column.

The modulation transfer function (MTF) provides important information about the optical quality of the eye, specifically, the potential image contrast at each spatial frequency. Fig. 7A shows the radially averaged MTF for each of the 97 eyes calculated for the 3rd to 10th order Zernike coefficients for a 5 mm pupil size (thin black lines). The wide variation in the radial MTFs for these infant monkeys further indicates that optical quality varied between individual subjects. The dashed, single dotted, and thin lines in Fig. 7B represent the MTFs of the animals that had quartile Strehl ratios. The high spatial frequency cut-off for the median infant monkey at a modulation of 0.1 was approximately 15–16 cycles/degree. For reference, the radial MTFs for an aberration free eye and for a typical adolescent monkey eye are shown in Fig. 7B as the solid and dash–dot–dot lines, respectively. When compared to adolescent monkeys, most infants have poorer modulation transfer functions for the same pupil size

Fig. 7.

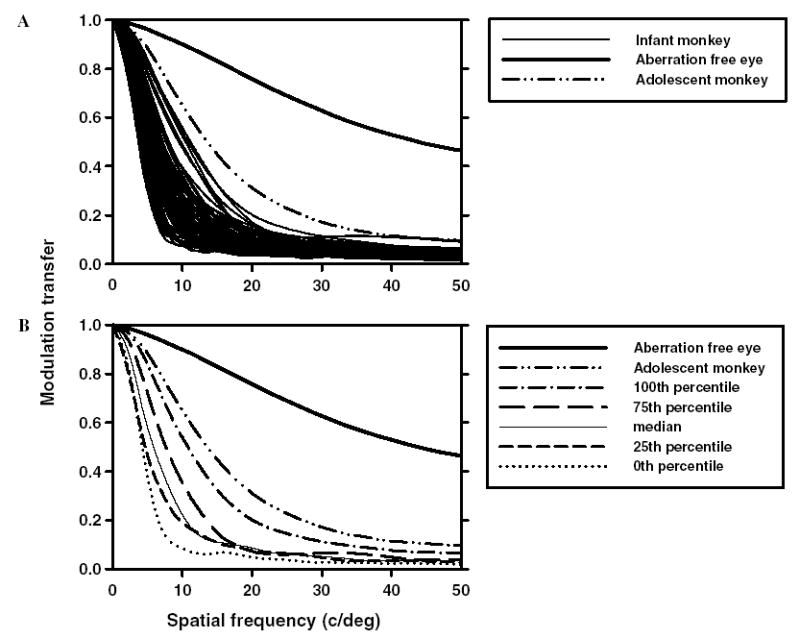
(A) Radially averaged MTFs for each of the 97 infant eyes (thin lines). (B) The thin, dotted and dashed lines are MTFs for the infant eyes that had quartile Strehl ratios. The dashed-double-dotted lines are the average MTFs for adolescent monkeys. The thick lines are the calculated MTFs for an aberration free eye, shown for reference.

3.3. High-order aberrations during emmetropization

All biometric measurements including wavefront measurements were made periodically on five infants during emmetropization. At the start of the observation period, the spherical-equivalent refractive errors were moderately hyperopic (mean for right eye = +4.3 ± 1.3 D; range = +3.0 to +5.2 D). For the next 3–4 months there was a systematic decrease in the degree of hyperopia and by 200 days the mean refractive error was +1.9 ± 0.9 D (range = +0.7 to +2.9 D). The changes in refractive error were associated with changes in the eyes’ axial dimensions, most significantly vitreous chamber depth, which increased from 8.73 ± 0.15 to 10.32 ± 0.04 mm during this same period.

During the first 100 days of rapid emmetropization, the total RMS wavefront error in all five infants decreased rapidly and then gradually until about 200 days of age (Fig. 8). The total RMS error represents the RMS error for high-order terms, calculated after excluding the defocus and astigmatic terms. At the first measurement, all five infants had total RMS errors greater than 0.40 μm, but by about 150 days of age, the total RMS error was consistently at about 0.20 μm. Also note that similar to refractive errors, the high-order total RMS errors for the two eyes of each animal were relatively well matched throughout the observation period.

Fig. 8.

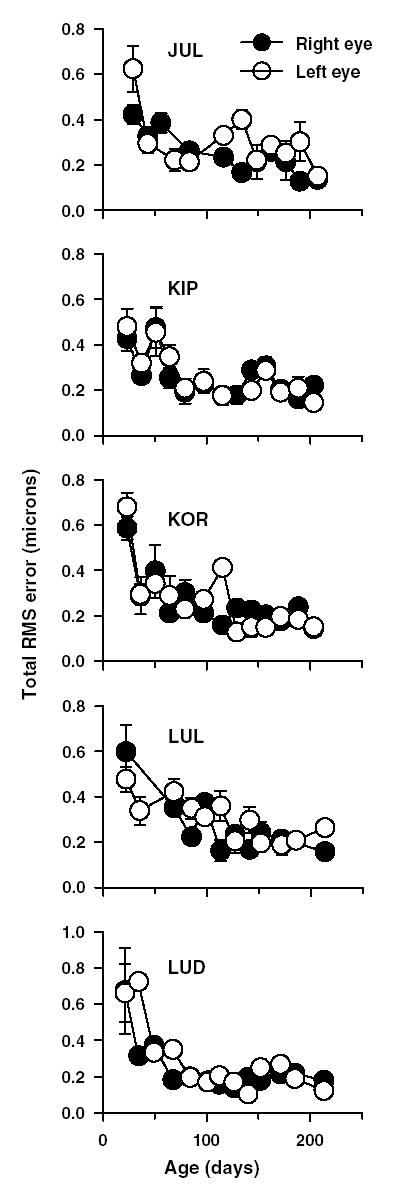
Magnitude of high-order aberrations (total RMS wavefront error in microns) plotted as a function of age for the right (•) and left eyes (○) of five infant monkeys. Each data point represents average of 5 measures ± 1 SD. A constant pupil size of 5 mmwas used for all these measurements. Note the decrease in high-order aberrations as a function of age in all five animals.

The left panel in Fig. 9 shows the average longitudinal decrease in total RMS error, spherical aberration and coma for right (filled circles) and left eyes (open circles). From this figure it is clear that the total RMS error, spherical aberration, and coma decreased with age, with spherical aberration showing a larger decrease than coma. Similarly, the aberrations from every order also decreased with age (figure not shown).

Fig. 9.

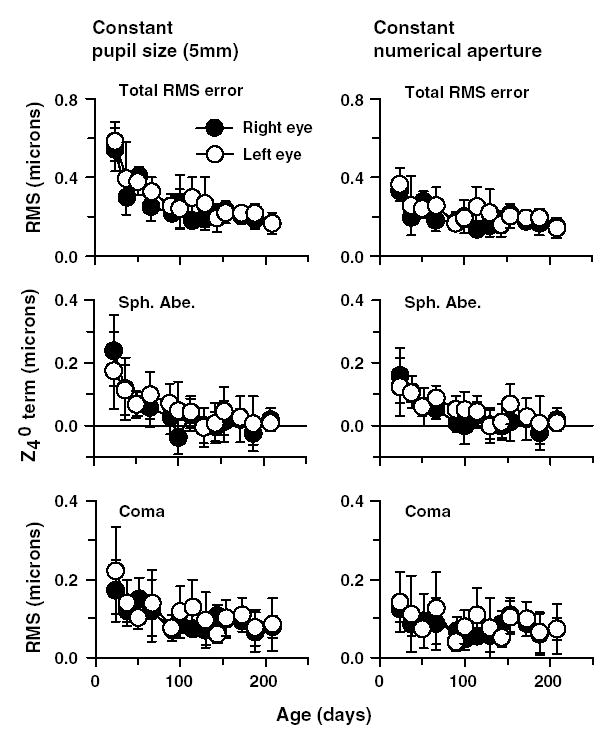
(Left panel) Average total RMS wavefront error, spherical aberration (Sph. Abe.) and coma (RMS of $Z_3^{-1}$ and $Z_3^1$) for a constant 5 mm pupil plotted as a function of age for the five infant monkeys. The filled and open symbols represent the averages for the right and left eyes, respectively. Note the decrease in aberrations as a function of age. (Right panel) Average wavefront errors plotted as a function of age using a constant numerical aperture. The appropriate apertures were calculated based on each monkey eye’s axial dimension, specifically, the anterior lens to retina distance. Thus, for smaller, younger eyes, the pupil size was comparatively small but increased in size as the eye grew. Specifically, the pupil size varied from 4.2 mm at the first measurement session to a maximum of 5 mm at the last measurement session. Note that the aberrations decreased with age even when constant numerical aperture was maintained.

In the above analyses, the pupil diameter was held constant at 5 mm. Such an analysis is expected to exaggerate the reduction in aberrations during maturation since, for the younger, smaller eye, a 5 mm pupil encompasses proportionally more of the eye’s optical zone, effectively including more marginal rays than in larger, older eyes. As the eye grows, the same 5 mm zone occupies a more paraxial region of the cornea and lens. These changes are large in the early stages of development where typically the axial length in an infant monkey eye increases from about 14 mm at 20 days of age to about 17 mm at 200 days of age (Bradley et al., 1999). Thus, the decrease in high-order aberrations that was observed was due in part to a passive reduction that is geometrically associated with eye elongation (Howland, 2005). To compensate for this passive improvement, we re-analyzed the aberrations employing a constant numerical aperture, which was achieved by scaling pupil size with respect to the size of the eye. Since eye growth is not equivalent to a simple uniform scaling of the eye along all dimensions (Howland, Merola, & Basarab, 2004), rather there are unequal increases in size along different dimensions, we established constant numerical apertures by scaling the eye in two different ways. First, we employed pupil to retina distance to scale for the increase in axial length. Second, we employed corneal diameter measured along the horizontal meridian as a scaling factor for the growth changes that occurred in the anterior segment of the eye (Howland, 2005).

Constant numerical apertures along the axial dimension were calculated using the formula, (a/b)*c, where a is the pupil to retina distance at a given age, b is the pupil to retina distance at the last measurement session (at 200 days of age) and c is a constant pupil size (5 mm diameter). The pupil to retina distance was determined from the A-scan ultrasound measurements of lens thickness and vitreous chamber depth. Using this scaling method, we used small pupil sizes for the youngest eyes and proportionately larger pupil sizes for the same eyes as they grew larger. We then used a custom Matlab program to re-calculate the wave aberrations for each eye for the scaled pupil sizes. Thus, for a constant numerical aperture, the analyzed pupil size progressively increased from 4.2 mm for small eyes at 23 days of age to 5 mm for larger eyes at 200 days of age. In the second scaling method, we used the same formula, however, a and b were the horizontal corneal diameters at the younger ages and at the last session, respectively. Corneal diameter measurements were performed only at ages 23 and 120 days. Pupil sizes for the corneal diameter scaling method varied from 4.6 mm at 23 days of age to 5 mm at 120 days of age.

Regardless of the scaling method used, with a constant numerical aperture, the total high-order aberrations decreased with age. However, this decrease was smaller than the decrease that was observed with a constant 5 mm pupil diameter. When a constant numerical aperture was maintained by scaling along the axial dimension, the average total RMS error for the right eyes decreased from 0.33 ± 0.03 μm at 23 days of age to 0.14 ± 0.03 μm at 200 days of age (right panel in Fig. 9). The magnitude of each Zernike order also decreased as a function of age with the spherical aberration term showing the most notable changes (+0.15 ± 0.08 to +0.01 ± 0.03 μm). Coma showed a smaller decrease from 0.12 ± 0.03 to 0.07 ± 0.02 m. Similarly, when corneal diameter was used as a scaling factor, the average total RMS error decreased from 0.41 ± 0.06 m at 23 days of age to 0.18 ± 0.03 m at 120 days of age (figure not shown). In addition, to improving image quality, these age-dependent changes in refractive error, in particular, the decrease in positive spherical aberration, contributed to the reduction in hyperopia associated with emmetropization (Cheng, Bradley, & Thibos, 2004b). Specifically, the decrease in spherical aberration altered the focal point that yielded the maximum Strehl ratio for an eye with the average amount of aberrations by 0.20 μm. Thus, a small aspect of emmetropization (equivalent defocus of about 0.17 D) could be attributed to changes in the eye’s high-order aberrations.

4. Discussion

Our main findings were that (1) adolescent rhesus monkey eyes have comparatively low amounts of high-order aberrations and excellent optical quality, (2) infant rhesus monkeys exhibited relatively larger magnitudes of high-order aberrations, particularly positive spherical aberration, coma, and trefoil, which all decreased rapidly during the normal period of emmetropization, and (3) high-order aberrations remained stable from about 4 months of age to late adolescence.

Even though all of our aberration measurements were performed on anesthetized animals, there were no qualitative differences in the clarity of the spot patterns obtained from the monkeys versus those obtained on awake, fixating humans with the same instrument and as in humans the aberration measurements in infant and adolescent monkey eyes were highly repeatable. Fig. 10 compares the total RMS wavefront error (3rd to 10th orders) as a function of pupil size for monkeys at 23 days of age, 200 days of age, and 4–5 years of age (filled symbols) with those obtained from adult humans (open symbols) in other laboratories (Calver, Cox, & Elliott, 1999; Carkeet et al., 2002; Cheng et al., 2003; Iglesias, Berrio, & Artal, 1998; Liang & Williams, 1997; Navarro, Moreno, & Dorronsoro, 1998; Paquin, Hamam, & Simonet, 2002; Porter et al., 2001; Walsh, Charman, & Howland, 1984). The pupil sizes for the monkeys were scaled based on their eyes’ axial dimensions so that a constant numerical aperture was maintained. When compared to human eyes that have the same absolute pupil size, adolescent rhesus monkeys have comparable magnitudes of high-order aberrations and when the pupils are scaled relative to eye size, adolescent monkeys exhibit better optical quality than the average human.

Fig. 10.

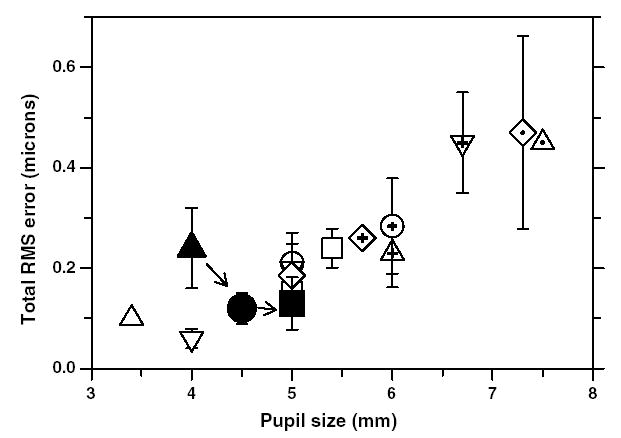
Comparison of total ocular wavefront aberrations between monkeys and humans. The data for monkeys in this study are shown as filled symbols. The filled triangle is the average RMS wavefront error for the 97 eyes at 23 days of age, the filled circle is the average RMS error at 200 days of age for five monkeys that were followed longitudinally and the filled square represent the average RMS error for six adolescent monkeys with mean age of 4.2 years. Error bars are ±1SD. Note that the aberrations are scaled to have a constant numerical aperture. Aberrations decrease with age in monkeys during emmetropization; however, they remain constant after about 200 days of age. The aberration data for humans are shown as open symbols (○, Iglesias et al., 1998; , Navarro et al., 1998; □, Liang et al., 1994; , ▵, Liang and Williams, 1997; ⬡, Walsh et al., 1984; ▽, , Calver et al., 1999; , Porter et al., 2001; , Cheng et al., 2003; , Paquin et al., 2002; ⋄, Carkeet et al., 2002; , Thibos et al., 2002a, 2002b, 2002c).

Similar to observations in young human adults, (Castejon-Mochon et al., 2002; Porter et al., 2001; Thibos et al., 2002c) infant monkey eyes showed inter-individual differences in both the pattern and magnitude of aberrations. Each Zernike coefficient showed a wide range of values, although on average most terms above 4th order were close to zero. The most dominant high-order aberration in adult humans is positive spherical aberration (Porter et al., 2001). However, in infant monkeys, in addition to positive spherical aberration, 3rd order aberrations such as coma and trefoil also contributed significantly to image degradation. Although some of the terms in the 5th order were, on average, significantly greater than zero, the magnitudes of these terms were so small (less than λ/14) that the image degradation due to these aberrations by themselves was negligible. However, as previously noted (Applegate et al., 2003), a combination of these 5th order aberrations with 3rd or 4th order aberrations can improve or degrade image quality.

None of the previous human studies (Castejon-Mochon et al., 2002; Porter et al., 2001; Thibos et al., 2002c) on adults or children have reported significant 3rd order aberrations. In contrast, our infant monkeys exhibited significant amounts of coma and trefoil. There are several possible explanations for this difference. First, our measurements were performed on the presumed line of sight. Thus, the relative nasal displacement of the line of sight with respect to the pupillary axis probably contributed to the amount of measured coma. However, when we aligned our SHWS on the pupillary axis, the measured aberrations were not very different from those obtained along the line of sight. Specifically, in adolescent monkeys, the magnitudes of horizontal coma along the pupillary axis and along the presumed line of sight differed by only about 0.04 μm and there were no significant differences in the magnitudes of the other Zernike terms. It is also important to note that angle lambda and the Hirschberg ratio do not change as a function of age in monkeys (Quick & Boothe, 1992). These results are in agreement with Kelly, Mihashi, and Howland (2004) and Artal, Benito, and Tabernero (2006), who have shown that ocular coma is independent of the line of sight position, since corneal coma aberration is reduced by internal aberrations of the opposite sign. Thus, the fact that we measured our aberrations along the presumed line of sight cannot, by itself, account for the higher magnitudes of coma found in our infant monkeys (mean coma for right eyes = 0.14 ± 0.08 μm). Coma can arise if the centers of the cornea or the lens are displaced relative to each other. This is possible in a rapidly growing eye. Compared to human infants, infant monkeys exhibit substantially higher corneal and lens powers; hence even a slight tilt or displacement of these optical elements can result in significant amounts of coma. The high magnitude of trefoil in infant monkeys could be an optical manifestation of the orientation of the crystalline lens sutures (Thibos et al., 2002a). Typically, infant primate eyes show prominent Y-shaped embryonic lens sutures (Kuszak, Zoltoski, & Tiedemann, 2004) and in vitro laser ray tracings through the lens sutures demonstrate poorer optical quality. Hence, it is possible that the prominent Y-shaped sutures in the infant monkey eye result in higher magnitudes of trefoil. On average, the even-symmetric trefoil term ( $Z_3^{-3}$, mean for right eyes, −0.16 ± 0.15 μm) was more negative than the odd-symmetric trefoil term ( $Z_3^3$, mean for right eyes, −0.06 ± 0.16 μm), which suggests that the Y sutures tend to orient in a similar way across infant monkeys (see Fig. 5).

We found higher amounts of positive spherical aberration in infant monkeys than in adolescent monkeys. In contrast, Wang and Candy (2005) found that human infants typically exhibited less positive spherical aberration than adults. Procedural differences could have contributed to the different maturational patterns observed in human and monkey infants. Whereas all of our measures in infant monkeys were obtained during cycloplegia, Wang and Candy did not control accommodation via a cycloplegic agent. Possibly Wang and Candy’s measures were confounded by positive accommodative, which in adult humans normally reduces the amount of positive spherical aberration (Cheng et al., 2004a). However, the position-dependent changes in refractive power that are responsible for spherical aberration are mainly due to asphericities of the cornea and lens surfaces, and the gradient refractive index of the lens. Consequently, differences in the magnitude of spherical aberration between infant humans and monkeys could reflect differences in corneal and/or lenticular shape. The mean corneal asphericity value (Q), obtained via corneal topography for the right eyes of 43 infant monkeys was −0.07 ± 0.24. In comparison, previous population studies in humans reported more negative corneal asphericity Q values of −0.40 ± 0.18 in young adults (Carney, Mainstone, & Henderson, 1997) and −0.35 ± 0.10 in 6-year-old children (Davis, Raasch, Mitchell, Mutti, & Zadnik, 2005). This means that the peripheral cornea is steeper in infant monkeys than in human adults and children. This could account, at least in part, for the more positive spherical aberration found in our infant monkeys.

Several studies on adult humans showed that the monochromatic aberrations were bilaterally symmetric. Specifically, one such study reported that ocular aberrations in human adults showed strong bilateral mirror symmetry for 75% of the Zernike terms from 2nd to 5th order (Porter et al., 2001). In the case of adolescent monkeys, the magnitudes of all high-order aberrations were so low that no meaningful conclusions could be drawn from correlational analysis between the right-and the left-eye coefficients. However, infant monkeys exhibited significant correlations for 33% of the terms from 2nd and 5th order. Specifically, strong interocular correlations were seen for defocus, spherical aberration, trefoil and coma terms (Table 1). Thus, although the magnitudes of these Zernike coefficients vary considerably between infant subjects, their magnitudes do not vary randomly within a given subject.

High-order aberrations have been measured in other animal models such as chicks and marmosets. However, the pattern of aberrations varies between species, presumably reflecting interspecies differences in eye shape and to some degree eye size. For example, whereas humans and infant monkeys typically exhibit positive spherical aberration, newly hatched chicks exhibit no spherical aberration and marmosets exhibit negative spherical aberration. With respect to the amount of aberrations, it has been reported that high-order aberrations in newly hatched chicks are 6–10 times greater than those found in humans (Thibos et al., 2002b). However, other studies done under similar experimental conditions reported much lower magnitudes of total RMS errors (Garcia de la Cera et al., 2006) and good optical quality (Coletta, Marcos, Wildsoet, & Troilo, 2003). The source of the difference in the results between these studies is not known. Nevertheless, when a constant numerical aperture was used to compare the results between chicks and monkeys, the magnitude of high-order aberrations of the chicks at hatching reported by Garcia de la Cera et al. (2006) compares well with the magnitude of aberrations found in our infant monkey eyes. Marmosets also appear to exhibit similar amounts of high order aberrations as rhesus monkeys. For example, Coletta et al. (2004) report that the total RMS error for 1-year-old marmosets for a 3 mm pupil was about 0.15 ± 0.06 μm. When a constant numerical aperture is used to compare the results between marmosets and macaque monkeys, the magnitudes of aberration reported in marmosets were similar to those found in young rhesus monkey eyes. With respect to maturational changes, there is general agreement that high-order wave aberrations decrease with age in chicks (Coletta et al., 2003; Garcia de la Cera et al., 2006; Kisilak, Campbell, Hunter, Huang, & Irving, 2004; Thibos et al., 2002a), marmosets (Coletta et al., 2004), and monkeys.

The decrease in high-order aberrations with age results in higher image contrasts at all spatial frequencies and thus, an improvement in retinal image quality. Figs. 11A and C show the modulation transfer with and without 2nd order terms for a constant numerical aperture for monkeys at 23 days, 200 days and 4–5 years of age. After scaling for eye size, the best-corrected modulation transfer for spatial frequencies near the peak of the contrast sensitivity function increased by a factor of about 1.5 from 23 to 200 days of age. This improvement in modulation transfer was observed even when MTFs were calculated for a natural pupil size (Figs. 11B and D). Based on the best corrected MTFs for a 3 mm pupil, the high spatial frequency cut off at 0.1 modulation increased from 30 cycles/degree at 23 days of age to 60 cycles/degree at 200 days of age. Based on behavioral measures of spatial contrast sensitivity in infant monkeys, Boothe, Kiorpes, Williams, and Teller (1988) and Boothe, Williams, Kiorpes, and Teller (1980) reported that the highest resolvable spatial frequency increased from about 3–4 cycles/degree at 5 weeks of age to about 20 cycles/degree at 28 weeks of age. At the same time, the peak in the behavioral contrast sensitivity function increased by a factor of about 10. Thus, only a small part of the maturational improvement in the monkey’s spatial contrast sensitivity can be attributed to a decrease in high-order aberrations and the concomitant improvement in the overall optical quality of the infant monkey eye. However, from an optical perspective low-order aberrations can potentially have a much greater impact on behavioral performance in infant monkeys. For example, when the defocus and the astigmatism terms were included in the MTF calculation, for a 23-day-old monkey for a 3 mm pupil, the high spatial frequency cut off was reduced from 30 cycles/degree to about 4.5 cycles/degree (Fig. 11B).

Fig. 11.

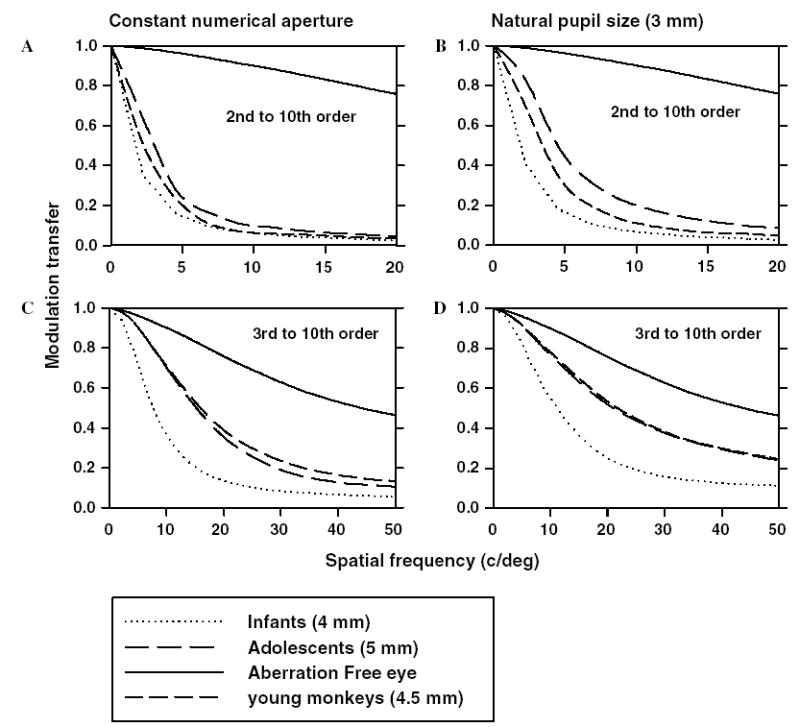
(A) Radially averaged MTFs calculated by including 2nd to 10th order terms for monkeys shown in Fig. 10, at ages 23 days (dotted lines), 200 days (medium dashed lines) and 4–5 years (long dashed lines). The MTFs were calculated by maintaining a constant numerical aperture with 4, 4.5 and 5 mm for monkeys at 23 days, 200 days and 4–5 years of age, respectively. (C) Best corrected, radially averaged MTFs calculated by including 3rd to 10th order terms for the same groups of monkeys shown in (A). (B and D) Radially averaged MTFs calculated for a pupil size of 3 mm with and without 2nd order terms, respectively.

The decrease in measured high-order aberrations in infant monkeys occurred during the rapid phase of emmetropization. The decrease was observed in all 10 orders and because they could not be attributed to simple scaling changes presumably occurred as a result of changes in the shape and organizational configuration of the cornea and lens. Although the overall effective refractive index of the crystalline lens does not change during early ocular growth (Qiao, Kee, Hung, & Smith, 2000), local or regional growth changes that occur in the gradient refractive index could also contribute to the decrease in high-order aberrations. Whether the shape and organizational changes in the eye’s optical components occur passively during early ocular growth or whether these changes are actively regulated by a vision-dependent mechanism is not known. Emmetropization is regulated by active, vision-dependent mechanisms; however, these mechanisms largely exert their influence on vitreous chamber growth. Alterations in corneal curvature, in particular in corneal toricity, can be produced by altered visual experience that impacts the course of emmetropization (Kee, Hung, Qiao-Grider, Roorda, & Smith, 2004). However, these anterior segment changes appear to be side effects of altered ocular growth rather than the consequence of an active mechanism that regulates anterior segment growth to optimize image quality. Hence, the decrease in aberrations may be due to passive maturation of the anterior segment of the eye and may not be regulated by vision-dependent mechanisms similar to those that regulate emmetropization. This, however, does not preclude the argument that aberrations can influence the efficiency of emmetropization because they directly affect the retinal image quality.

It has been shown that, in the absence of other polychromatic clues, humans can discriminate hyperopic defocus from myopic defocus based on monochromatic aberrations and the ability to discriminate sign of defocus increases with the magnitude of aberrations, specifically, with even-symmetric aberrations such as spherical aberration (Wilson et al., 2002). Therefore, the high amounts of positive spherical aberrations found in infant monkey eyes, in combination with defocus could provide a cue to guide eye growth toward the optimal refractive state. Hence, one could argue that the presence of high magnitudes of spherical aberration in the infant monkey eye may facilitate emmetropization.

In conclusion, the eyes of young and adolescent rhesus monkeys have excellent optical quality. In infant rhesus monkeys, the high-order aberrations are larger than those in mature animals; however due to maturation of the anterior segment of the eye, aberrations rapidly decrease within the first 4 months of life, resulting in a relative improvement in retinal image quality. Thus, infant monkey eyes are a good model to study not only emmetropization and refractive error development, but also the effects of high-order aberrations on retinal image quality during normal and abnormal ocular growth.