Central representation of time during motor learning

Abstract

This study stemmed from the observation that the brain of human as well as nonhuman primates is capable of forming and memorizing remarkably accurate internal representations of the dynamics of the arm. These dynamics establish a functional relation between applied force and ensuing arm motion, a relation that generally is quite complex and nonlinear. Current evidence shows that the motor control system is capable of adapting to perturbing forces that depend on motion variables such as position, velocity, and acceleration. The experiments we report here were aimed at establishing whether or not the motor system also may adapt to forces that depend explicitly on time rather than on motion variables. Surprisingly, the experiments suggest a negative answer. When asked to compensate for a predictable and repeated time-varying pattern of disturbing forces, subjects learned to counteract the disturbance by producing forces that did not depend on time but on the velocity and the position of the arm. We conclude from this evidence that time and time-dependent dynamics are not explicitly represented within the neural structures that are responsible for motor adaptation. Although our findings are not sufficient to rule out the presence of a timing structure within the central nervous system, they are consistent with other investigations that conspicuously failed to find evidence for such a central clock.

Recent studies of motor adaptation in humans have taken advantage of robot technology to alter the dynamics of a subject’s arm and to study the ensuing adaptive process (1–5). In these studies subjects made reaching movements with their hands, while holding the end-point of a robotic arm, which was programmed to behave either as a passive manipulandum with low inertia or to generate a field of disturbing forces. In some of these experiments, the robot acted as a passive device with low impedance and the subject’s hand moved along approximately straight paths, joining the initial and final positions. In addition, the instantaneous velocity of the hand followed a unimodal, bell-shaped temporal profile. These characteristics express a property of smoothness typical of unperturbed reaching movements of the hand (6, 7). The unexpected application of a disturbing force field altered quite significantly these kinematic features. With velocity-dependent disturbing fields (1–3, 5) the trajectories became markedly curvilinear. After repeating several movements in the field requiring 40 min to 1 hr, all subjects recovered the initial movement characteristics. At that point, if the disturbing field were suddenly removed, significant aftereffects have been observed in the form of curvilinear motions opposite and symmetrical to those caused by the initial application of the field.

Aftereffects generally have been considered as evidence for the formation of an internal model of the disturbing field within the central nervous system (2, 3, 8–10). Shadmehr and Mussa-Ivaldi (1) interpreted the aftereffects induced by adaptation to a force field as evidence for the existence within the central nervous system of a variable mapping between limb dynamics and motor commands. This mapping governs the transformation of movement plans into the driving forces that the neuromuscular apparatus must generate to implement these plans.

Additional evidence for the existence of internal models within the motor control system came from similar experiments in which hand movements were persistently disturbed by a velocity-dependent force field. After adaptation of rectilinear reaching movements, subjects were asked to execute circular movements in the same force field (3). It was found that learning generalized to the circular trajectories. These circular trajectories passed through the same region of space as the rectilinear reaching movements used for training. In addition, the amplitude and direction of the instantaneous velocity of the hand during the circular movements were always similar to the amplitude and direction of hand velocity for some of the reaching movements. Then, as the disturbing force field depended on the instantaneous velocity of the hand, it followed that the forces experienced during the execution of circular movements were similar in amplitude and direction to the forces experienced earlier, during the execution of reaching movements. However, the temporal sequences of positions and velocities as well as the overall movement duration were significantly different for circular and reaching movements. And yet, after subjects adapted to the field by executing reaching movements, they could compensate for the same field while executing circular movements. Thus, it was concluded that the internal model developed by the subjects generated a force output, which, like the disturbing field, depended on position and velocity but not on time.

What would subjects learn if they experience forces that depend explicitly on time and not on the state of motion of the hand? Would they develop the appropriate representation in this case? The distinction between time and state dependency is subtle but quite significant. State and time information are intertwined during movements. When we say that a force field depends on the state of the arm, we mean that the force is determined by the position and velocity of the arm. During a movement of the arm, a state-dependent force varies with time because the arm’s position and velocity change with time. A similar ambiguity arises when a force depends on time. During a movement of the arm, a time-dependent force varies with the arm’s state because the arm changes position and velocity with the passing of time.

To avoid ambiguities, it is necessary to distinguish between what one means by “depending on time” and by “varying with time.” We say that a force depends on time when each instant after the onset of movement corresponds to a unique value of the force, which is an explicit functional dependence. On the other hand, we say that the force varies with time when we merely observe a change of the force at different instants. Uniqueness is not implied in this second case, as the temporal variation may be inherited from the time dependence of a state variable. For example, consider a force proportional to the velocity of the hand. A rapid movement and a slow movement both result in a time-varying force. However, the force experienced 100 ms from the onset of the slow movement is smaller than the force experienced at the same time during the rapid movement. In this case, the force perturbation varies with time but does not depend on time. Conversely, we say that force depends on time and not on the state of the arm if there is a unique association between time and force. In such case, the force experienced 100 ms from the onset of a movement is the same for both the slow and the fast movements. Following this argument, we conclude that to determine whether the motor system develops a correct representation of a perturbing time-dependent force, one may test if learning to compensate this force over a specific group of trajectories generalizes to novel trajectories over the same region of state space. The ability of a subject to compensate for a time-dependent force when the arm moves through a new sequence of positions and velocities would be a clear indication that the subject’s motor system has captured the true nature of this force. Conversely, the inability to generalize could not be attributed to some deficiency in the force production. The new trajectories lie in a region of state space where, during training, the subject has demonstrated an ability to produce the appropriate forces. The inability to generalize would reflect an incorrect representation of the force dependency on time.

We have adopted the above rationale for determining whether human subjects are capable of developing internal models for time-dependent force fields. We have addressed this question in three experiments. In the first experiment, we tested the ability of subjects to compensate for a perturbing force with a predictable time course. We found that after training in this time-dependent field, all subjects recovered the original unperturbed trajectories of the hand. In addition, when the field was removed, we observed typical aftereffects.

In the second experiment, we trained subjects to execute reaching movements in the same time-dependent field of the first experiment. At the end of training, as the compensation of the time-dependent forces was complete, we asked them to execute circular movements in the same region where they had practiced reaching movements. We found that adaptation did not generalize to these new movements: the circular trajectories displayed significant distortions induced by the disturbing field. To cancel these distortions, subjects had to practice the circular movements within the time-dependent field.

Finally, the third experiment provided us with evidence that when exposed to a time-dependent field, subjects developed an erroneous internal model. In this internal model, the disturbing forces were interpreted as being a function of the hand velocity rather than of time. As the subject’s hand moved along the training trajectories, this internal model generated a time-varying force that accurately compensated for the disturbing forces.

These experiments have revealed a defining feature of motor adaptation: while the central nervous system was capable of representing the dependence of the environmental forces on position and velocity (1–4) the same system was not capable of developing a similar representation of time dependence. When the environmental forces depended on time, they were compensated as if they were instead a function of the state of motion of the controlled limb. To create an internal model of a state-dependent field, the motor system must have access to position and velocity information. These could be carried both by sensory feedback and by the outflow of motor commands. In contrast, to generate an internal model of a time-dependent field, the motor system must have access to time-coding information equivalent to the ticking of a clock. Our results suggests that while a representation of the limb position and velocity is continuously available to construct internal models of the controlled dynamics, the same cannot be concluded for a consistent representation of time.

METHODS

Experimental Setup.

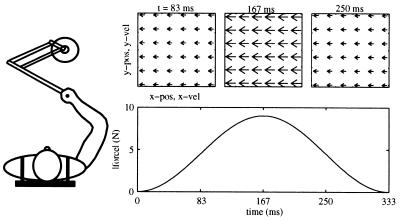
Subjects executed arm movements while holding the handle of a two-degree-of-freedom robot manipulandum (Fig. 1 Left). Both hand position and velocity were determined from digital encoders mounted on each axis of the manipulandum. Two torque motors operating independently on each joint were programmed to apply controlled force perturbations to the hand of the subject. The torque motors were either left inactive (null field condition) or they were programmed to generate forces at the handle that depended on time (Fig. 1 Right) or on the velocity of the manipulandum (see Fig. 4e). The mathematical structure of the time-dependent field was F_x = 4.5⋅(1 − cos(2π(3Hz)t)), F_y = 0, (0 ≤ t ≤ 0.333 sec), and F_X = F_Y = 0 for t > 0.333 sec. This waveform generates a field of forces directed from right to left and with an amplitude that starts from zero, reaches a maximum value and returns to zero in a time comparable to an average movement duration. The velocity-dependent field, F_x = 13 Ns/m ·(|ẋ|+|ẏ| − (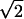 − 2)·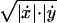|) and F_y = 0, where ẋand ẏ are the hand velocities in meters per sec.

Figure 1.

Experimental setup and structure of the time-dependent force field. (Left) Top view of the subject and the manipulandum (Right) time-dependent field. (Lower) The temporal evolution of the force vector magnitude. (Upper) The forces at three latencies from the onset of movement, plotted in either the position or the velocity workspace. At any instant of time, the force experienced is the same regardless of the hand position or velocity, exemplifying the independence of the force field from the motion variables.

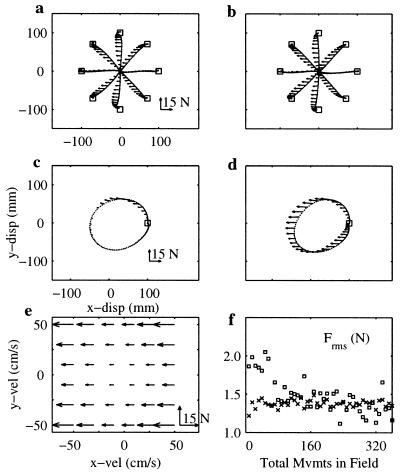
Figure 4.

Comparison of the time-dependent and velocity-dependent force fields. (a) Average hand trajectories and forces experienced because of the time-dependent force field while making reaching movements in eight directions. (b) Average hand trajectories and forces experienced because of the velocity-dependent force field while making reaching movements. The forces experienced because of the two fields are virtually identical when making these movements. (c) Average hand trajectories and forces experienced because of the time-dependent field while making circles. (d) Average hand trajectories and forces experienced because of the velocity-dependent field while making circles. The forces experienced because of the two fields are extremely different while making circles. (e) Plot of the nonlinear viscous force field in the hand velocity workspace. (f) Plot of the rms of the force experienced while making reaching movements during adaptation to the two different fields for one subject (□, velocity-dependent force field; x, time-dependent force field). Subjects experience different forces during the initial stages of adaptation, but the forces generated by the two different fields as the subjects regained the desired straight-line trajectories.

Procedures and Data Analysis.

The experimental paradigms for adaptation were similar to the ones described in greater detail elsewhere (1, 3). We followed three protocols.

Adaptation to a time-dependent field.

The goal of this experiment was to test adaptation of goal-directed reaching movements to a time-dependent, state-independent force. Nine subjects with no known neuromotor disorders, ranging in age from 24 to 31 years, executed reaching movements of the hand while holding the handle of a planar two-joint robot. The position of the robot handle was displayed as a small cursor on a monitor above the manipulandum. A square target was presented on the monitor and the subject was asked to move the cursor inside the target square, a distance of 10 cm. Reaching movements were oriented in eight different directions and presented randomly. Subjects were instructed to make the movement duration 333 ± 50 ms and given categorical feedback of the actual movement time (too fast/too slow/correct) after termination of the movement. As a result, the actual duration of the baseline reaching movements across all subjects averaged 334 ± 99 ms. Subjects first completed a set (192 movements, 24 in each direction) in the null field, during which the motors compensated for the inertia of the robot arm and the motor rotors, but did not apply any other forces to the hand of the subject. Subjects then completed three sets in the adaptive stage during which the motors consistently applied a time-dependent endpoint force field described above. The time course of the perturbation was synchronized with the requested movement duration, which all subjects successfully complied with, and was triggered by the onset of movement. The force amplitude started to rise when the tangential velocity of the hand exceeded 1 cm/s, reached a maximum midway through the movement and fell back to zero after 333 ms. In a small number of random trials in the null-field stage (24 movements, three in each direction) the time-dependent force field unexpectedly was applied to assess the initial response of the subject to time-dependent forces before adaptation might take place. In the same number of trials per set during the adaptive stage, the applied endpoint field suddenly was removed to assess the aftereffects of adaptation.

Test for generalization.

To test the ability to generalize compensation for a time-dependent field, nine subjects completed a second experiment consisting of two tests. In the first test (T1), subjects executed reaching movements in the time-dependent field until adaptation occurred. After adaptation, they were required to execute circular movements either in the same time-dependent force field (transferred adaptation) or in the null field (transferred aftereffects). The movement length for the reaching movements was limited to 10 cm to limit the total length of the circular movements to about 60 cm. A large square (19 × 19 cm) was presented on the monitor and subjects were asked to make circles within the square, with a movement time of 1,000 ± 50 ms. The actual duration of the baseline circular movements across all subjects averaged 1,060 ± 110 ms. The circular movements passed through positions and velocities experienced during the execution of reaching movements in the training phase, but in a different temporal order. In a control experiment (T2), the same subjects executed several circular movements in the time-varying force field until adaptation occurred. After training, subjects performed the same circular movements either in the same time-dependent force field (direct adaptation) or in the null field (direct aftereffects). The difference in the two tests, T1 and T2, is the type of movement made during training. Performance was quantified by an error measure that captures the difference in shape between two trajectories (3). A one-way ANOVA first was performed to reject the null hypothesis that all sets of trajectories were the same. Then a Tukey’s posthoc paired comparison test was performed to determine which sets differed from which (P < 0.05) (11).

A velocity-dependent model for the time-dependent force.

The third paradigm was aimed at testing the hypothesis that while learning to move in a time-dependent field, subjects developed an internal representation of a velocity-dependent field. The time-dependent field and the velocity-dependent field were specifically designed to generate the same forces along the trajectories executed during training (see Fig. 4 a and b). However, these fields generate sharply different forces along circular trajectories in the same region of the state space (see Fig. 4 d and e). Eight subjects participated in two tests. In the first test, reaching movements first were made in the time-dependent field. After adaptation, the field was switched to the velocity-dependent field and circular movements were made to determine whether subjects were able to compensate for the viscous field after adapting to the time-dependent field. For comparison, the same subjects executed reaching movements in the velocity-dependent field. After adaptation, circular movements were made either in the same field or in the null field. The difference in the two tests is the type of force field experienced during the training reaching movements. Trajectories were compared by calculating the figural distance between a template trajectory and all other observed trajectories (3). As template trajectories, we used each subject’s average baseline reaching movements in the eight directions and the average baseline circular movement. The figural distance is a normalized distance metric that captures the difference in the shapes of trajectories. A one-way ANOVA and Tukey’s posthoc multiple comparison test was performed on these figural distances to determine performance differences (P < 0.05).

RESULTS

Compensation of Time-Varying Field.

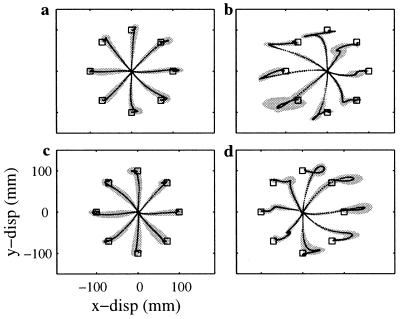
In the first experiment, nine subjects executed reaching movements of the hand in eight directions while holding the handle of a planar two-joint robot. The robot was programmed to generate a force that depended only on time (Fig. 1 Right). The force direction remained constant and its amplitude followed a sinusoidal time course independent of movement direction and speed. The time course of the perturbation was synchronized with the requested movement duration and was triggered by the onset of movement. Initial exposure to the perturbation (Fig. 2b) produced trajectories with significant deviations from the unperturbed trajectories (Fig. 2a). However after approximately 100 movements, all subjects recovered the original unperturbed kinematics (Fig. 2c). On sudden removal of the perturbation, subjects produced clear aftereffects (Fig. 2d). Although subjects were able to compensate for the time-dependent perturbation, this observation alone is not sufficient to conclude that they developed a correct internal representation of the force field (3). As we already stressed, a defining property of a correct internal representation of the disturbing field—that is of the dependence of the force on time or state—is the ability of this representation to produce appropriate responses beyond the particular movements in which the field has been experienced. Lack of such generalization would disprove the existence of an internal model of the time-dependent perturbation.

Figure 2.

Compensation of time-dependent forces. (a) Average (±SD) baseline hand trajectories before exposure to the time-dependent field (n = 21). (b) Average hand trajectories during the unexpected first exposure to the force field (n = 3). (c) Average hand trajectories in the time-dependent force field after three training sets (n = 21). (d) Average (±SD) aftereffects during the unexpected removal of the force field after three training sets (n = 3). The aftereffects shown in d are mirror images of the initial exposure trajectories shown in b. These results are consistent across all subjects.

Lack of Generalization.

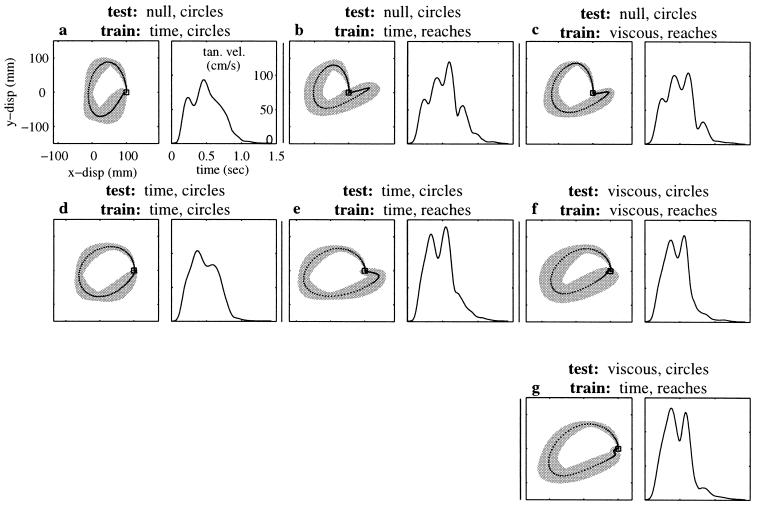
To test the ability to generalize compensation for a time-dependent field nine subjects completed a second experiment consisting of two tests. In the first test (T1), they were trained to execute reaching movements in the time-dependent field until adaptation occurred. Then, after training, they were asked to execute circular movements in the same time-dependent force field (Fig. 3e) and in the null field (Fig. 3b). The circular movements passed through positions and velocities experienced during the execution of reaching movements in the training phase, but in a different temporal order. In the second test (T2), the same subjects executed circular movements in the time-varying force field until adaptation occurred. After training, subjects performed the same circular movements in the force field (Fig. 3d) and in the null field (Fig. 3a). The difference in the two protocols, T1 and T2, is the movement made during training. The comparison of the performance in the two tests shows a significant difference in the circles made after adaptation depending on whether adaptation occurred while making reaches or circles (P < 0.05, all subjects). We conclude that repeated exposure to the time-varying field during the execution of reaching movements did not lead to a correct representation of the field. Had the adaptive system achieved such a representation, the performance at the end of the training period would generalize to different trajectories passing through the same positions and velocities experienced during training.

Figure 3.

Results of test for generalization of learning time-dependent forces. (a) Average (±SD) aftereffect circle (trajectory and tangential velocity profile) made in the null field after training in the time-dependent field with circles (n = 16). (b) Average aftereffect circle made in the null field after training in the time-dependent field with reaching movements (n = 16). (c) Average aftereffect circle made in the null field after training in the velocity-dependent field with reaching movements (n = 17). (d) Average circle made in the time-dependent field after training in the same field with the same movements (n = 26). (e) Average circle made in the time-dependent field after training in the same field with reaching movements (n = 30). If the actual time series of forces was learned during the adaptation shown in Fig. 2, the trajectories comprising the averages in d and e should be the same as should the circles in a and b, but in fact both are significantly different (P < 0.05, all subjects). (f) Average circle made in the velocity-dependent field after training in the same field with reaching movements (n = 31). (g) Average circle made in the velocity-dependent field after training in the time-dependent field with reaching movements (n = 28). There is no statistical difference between either the trajectories comprising the averages in f and g or between the aftereffect circles in b and c (P > 0.05, all subjects). These results are consistent across all subjects.

The Time-Dependent Field Is Misrepresented as a State-Dependent Field.

What did the subjects learn when exposed to a time-varying field? A third set of experiments addressed this question based on the observation that a time-dependent field and a state-dependent field may be designed to generate the same forces over a set of reaching movements. In particular, the forces generated by the time-dependent field used in the previous experiment can be matched by the forces of the velocity-dependent field shown in Fig. 4e. However this matching applies only to the eight target reaching movements (Fig. 4 a and b). When circles are made, the forces generated by the time-dependent field (Fig. 4c) are significantly different from the forces generated by the velocity-dependent field (Fig. 4d), allowing us to test a specific hypothesis: the adaptive system has a strong bias toward learning state-dependent fields, fields that depend on position and velocity but not on time. Accordingly, if a time-varying force pattern were experienced, the adaptive system would approximate these forces with an erroneous internal representation of a state-dependent field. In the end, subjects eventually would learn to compensate a time-varying disturbance along a set of reaching movements. But when asked, after training, to execute a new movement, they would compensate for the state-dependent forces. This hypothesis is supported by our experimental evidence.

Eight subjects performed two tests. In the first test, we trained subjects to execute reaching movements in the time-dependent field (Fig. 1 Right). Immediately after adaptation, we switched to the velocity-dependent field (Fig. 4e) and asked the subjects to then execute circular movements (Fig. 3g). In the second test, we trained the same subjects to execute reaching movements in the velocity-dependent field. After adaptation, circular movements were made either in the same field (Fig. 3f) or in the null field (Fig. 3c). The difference in the two protocols is the type of force field experienced during the training movements. By comparing the outcomes of these tests, we found that (a) circles executed in the velocity-dependent field after training in the time-varying field (Fig. 3g) were not significantly different from the circles executed in the velocity-dependent field after training in the same field (Fig. 3f) (P > 0.05, all subjects), and (b) aftereffects following the two training procedures (Fig. 3 b and c) were not significantly different (P > 0.05, all subjects). It should be noted that the training information was not equivalent for the state- and time-dependent fields (Fig. 4e). The two fields were designed to coincide only along the adapted and the unperturbed trajectories. However, during the initial trials in either field, the perturbation displaced the arm away from these trajectories. As a consequence, the forces initially experienced by the subjects with time- and state-dependent fields were dramatically different. As shown in Fig. 4e, during the first 50 initial trials in the field, the rms amplitude of the force perturbation (across each trial) was more than 50% larger when the subjects moved in the velocity-dependent field than when they moved in the time-dependent field. As the trajectories performed in both fields converged toward the unperturbed kinematics, the forces experienced also converged. Despite training differences in the two fields, the subjects converged toward what appears to be a single-state-dependent representation. These observations all are consistent with the hypothesis that subjects misinterpreted the time-dependent forces (Fig. 1 Right) as a velocity-dependent perturbation (Fig. 4c).

DISCUSSION

In summary, while the available evidence indicates that the adaptive system has access to a representation of the state of motion of the limb, its position, and velocity, the same cannot be concluded for temporal information. Our results indicate that the dynamics of the limb coupled with its environment tend to be represented as a time-invariant relation between the state of motion of the limb and the ensuing forces, even when these forces are a function of time. Mathematically, the dynamics of the arm are captured by a nonlinear differential equation that relates the joint angles, angular velocities, and accelerations to the joint torque generated by the neuromuscular system. In very general terms, this differential equation may be written as

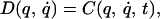1

where, q is a vector of joint angles that describes the instantaneous configuration of the arm, q̇ is the instantaneous angular velocity, and q̈ is the instantaneous angular acceleration of the two joints. D represents the passive dynamics of the limb. These dynamics are determined by the inertia of the limb segments and by the passive viscoelastic and friction properties of muscles, skin and connective tissues. C represents the torque generated by neuromuscular activation. In general, this latter torque may be assumed to depend on time and on the system’s state (position and velocity). The behavior resulting from Eq. 1 for any setting of the initial conditions is the corresponding solution q̂(t). In constructing the command for a particular limb movement, the brain must effectively solve for C(q, q̇, t) from the intended movement trajectory q̂(t). In previous experiments, the dynamics of the arm was modified by robot-generated forces that depended on the velocity of the hand, that is on the joint angles and their first time derivatives. The equation of the arm coupled with the external field,

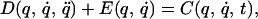2

has a solution, q*(t), that is generally different from the unperturbed trajectory, q̈(t). Current evidence from adaptation studies is consistent with the hypothesis that after prolonged exposure to the disturbing field, subjects develop an internal model of the disturbance. This internal model may be represented as a field, ℰ(q, q̇), that approximates the disturbing field. Adding this internal model, Eq. 2 becomes

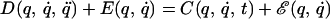3

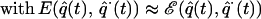Under sufficient smoothness conditions, the solution to Eq. 3 admits a solution that approximates the original movement, q̂(t). In the experiment described here, we have used a perturbing force, E(t), that depended solely on time. Our result indicate that this disturbing force is matched by an internal model that still depends on the state of motion of the limb. That is, after adaptation, the dynamics are

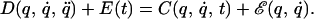4

For this equation to be consistent with the initial movement, q̈(t), it is sufficient for the internal model to satisfy the condition E(t) ≈ ℰ(q̂(t), q̂^⋅(t)). This condition is satisfied along the reaching movements if E(t) is the field of Fig. 1 Right and ℰ(q, q̇) is the field of Fig. 4e.

There is little doubt that we are capable of learning accurately timed movements. In the above equations, the ability to generate accurately timed movements corresponds to the ability to form accurately timed control functions, C(q, q̇, t). In this regard, the process of adaptive learning must be distinguished from the process of learning new movements. Adaptive learning leads to the formation of internal models, represented as ℰ(q, q̇, q̈) in Eqs. 3 and 4. The purpose of these models is to allow for the invariance of the control functions, C(q, q̇, q̈, t), so that it is not necessary to relearn previously acquired motor patterns after the mechanical environment has undergone some change. The experiments reported here indicate that the adaptive system may not be endowed with the computational primitives that would be necessary for representing time-varying dynamics. One such primitive would be a neural clock. The presence of a neural clock within the sensory motor system is a hotly debated topic. Some investigators (12) have proposed that the inferior olive generates a clock-like signal for the cerebellum. Others (13) have suggested that there is no evidence for such a signal. Although our findings do not rule out the general hypothesis that neural clocks may indeed exist, they suggest that the brain structures specifically involved in motor adaptation may operate independently of any such device by compensating repeated time-dependent forces as state-dependent perturbations. Aside from suggesting the presence of a clock, a correct representation of a time-varying force could be acquired by a proper combination of sensory and outflow information. In this regard, our experiments suggest that while both sources of information are available to different neural structures, the system that is responsible for adapting the movement seems to be unable to combine afferent and efferent signals in a model of the perturbed dynamics when these dynamics do not depend only on the state of the controlled limb.