Abstract
We present herein a topological invariant of oriented alternating knots and links that predicts the three-dimensional (3D) writhe of the ideal geometrical configuration of the considered knot/link. The fact that we can correlate a geometrical property of a given configuration with a topological invariant supports the notion that the ideal configuration contains important information about knots and links. The importance of the concept of ideal configuration was already suggested by the good correlation between the 3D writhe of ideal knot configurations and the ensemble average of the 3D writhe of random configurations of the considered knots. The values of the new invariant are quantized: multiples of 4/7 for links with an odd number of components (including knots) and 2/7 plus multiples of 4/7 for links with an even number of components.
Ideal Configurations of Knots and Links
A knot type (or simply “knot”) is a class of non-self- intersecting closed curves in three-dimensional (3D) space that are “equivalent,” i.e., that can be continuously deformed into each other without passing through themselves. Many efforts have been made to find for each knot type a “canonical” configuration by minimizing a configuration-dependent energy function (e.g., see various energy functions in ref. 1). One of the simplest and best-behaved energy functions is the thickness energy of the knot (2, 3). By representing the knot by a closed impenetrable cylindrical tube of uniform diameter whose axis is the knot, the associated thickness energy is the ratio of the length of the tube axis (L) over the diameter of the tube (D). The knot configuration at which the L/D ratio reaches its global minimum has been termed “ideal” (3). Generalization to a link type, i.e., (a class of) several closed nonintersecting curves called components, can be done by imposing that the diameters of all component tubes be identical (4). Up to now, ideal configurations for knots and links have been obtained by computer simulations.
The ideal configuration is believed to constitute an essential characteristic of knots and links. For example, the 3D writhe of ideal knot configurations (which will be defined in the next paragraph) correlates very well with the ensemble average of the 3D writhe of random configurations of the considered knots (3, 5, 6).
2D Writhe, 3D Writhe, and Topological Writhe
Different notions of writhe are associated with oriented links (from now on, knots will be considered as special cases of links with one component, and orientation will always be assumed). Projecting a particular configuration of a link in a particular direction, each right-handed crossing is scored as +1 and each left-handed crossing is scored as −1 (e.g., see Fig. 1; ref. 7). The total of these is called the 2D writhe of the given projection of the given link configuration. The average of the 2D writhe over all possible directions of projection constitutes the 3D writhe of the given link configuration and is denoted by Wr (8). Both the 2D writhe and the 3D writhe are geometrical notions, because they depend on the configuration.
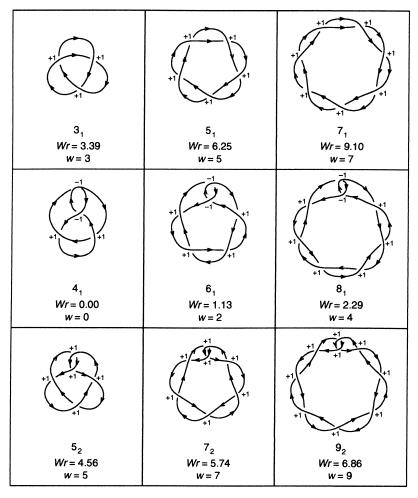
Figure 1.
Families of knots, with crossing sign assignment. (Top) Family of torus knots. (Middle) Family of twist knots with even crossing number. (Bottom) Family of twist knots with odd crossing number. Wr is the 3D writhe of the ideal configuration obtained by simulation. (Note that for each chiral knot, we chose the enantiomorph having a positive topological writhe. For all the knots represented in this figure, this enantiomorph corresponds to the mirror image of the enantiomorph usually presented in reference tables; ref. 7.)
Let us now consider the minimum of the 2D writhe over all possible projections of all possible configurations of a link. The obtained number depends on the link type only and is thus a topological invariant of the link. It is the topological writhe, denoted by w, which is also called Tait number, because the notion first appeared in the work of P. G. Tait (9). The topological writhe is very simple to compute for alternating links (links where the overcrossings and undercrossings alternate along each component): it is the 2D writhe of any projection of the link without nugatory crossing (a nugatory crossing is a crossing that can be removed from the projection just by rotating a part of the link). Let us call such a projection a standard projection. The notions of writhe are crucial in knot theory and in its applications to molecules like DNA, which can be knotted and catenated, because a nonzero writhe detects chirality (geometrical chirality or topological chirality depending on whether w or Wr is considered; ref. 10).
Prediction of the 3D Writhe from a Standard Projection
From its definition, it is easy to see that the topological writhe of a link is an integer. We can describe it as a quantity that is quantized by steps of 1. On the contrary, the 3D writhe is a real number, because it results from an averaging. It has been observed, however, that the 3D writhe of ideal configurations of knots obtained by computer simulations is quantized too but not by steps of 1 (3, 11). For example (3), in the family of torus knots (31, 51, 71, … ), each time two crossings are added, w changes by steps of 2, whereas Wr of the corresponding ideal configurations changes by steps of about 2.86; in the families of twist knots with even (41, 61, 81, … ) or odd (52, 72, 92, … ) crossing number, each time two crossings are added, w changes by steps of 2, whereas Wr of the corresponding ideal configurations changes by steps of about 1.14 (see Fig. 1). It was suggested in ref. 12 that the steps in Wr could actually be rational numbers (i.e., 20/7 and 8/7, respectively), such that the addition of each crossing contributes 10/7 in the first case and 4/7 in the second case. By inspecting standard projections of many links, we could extend this idea and arrive at the following formula for alternating links:
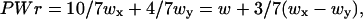 |
1 |
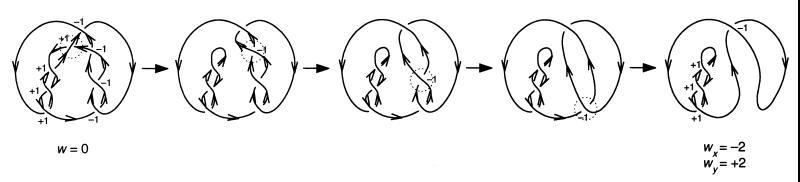
where PWr stands for predicted 3D writhe of the ideal configuration of the link and w, wx, and wy are the topological writhe, the nullification writhe, and the remaining writhe of the link, respectively. The nullification writhe and the remaining writhe are defined as follows (13): transform a standard projection by nullifying (or smoothing) successive crossings until the unknot is reached, while, at each step, preventing the diagram from becoming disconnected. Notice that, on each elimination of a crossing, the open ends are spliced in such a way that the directionality of the knot contour is maintained (14). Then, wx is the sum of the signs of the nullified crossings, and wy is the sum of the signs of the remaining crossings, with wx + wy = w. An example is shown in Fig. 2.
Figure 2.
Example of calculation of the nullification writhe (wx) and the remaining writhe (wy) of a knot. Successive crossings are nullified until the unknot is reached, while, at each step, the diagram is prevented from becoming disconnected. The open ends arising after elimination of crossings are spliced in such a way that directionality along the knot contour is maintained. Then, wx is the sum of the signs of the nullified crossings, and wy is the sum of the signs of the remaining crossings, with wx + wy = w, the topological writhe.
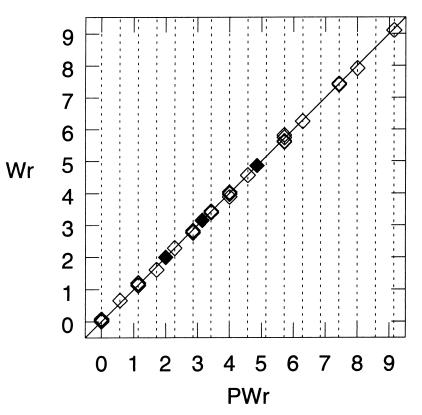
PWr is an invariant of oriented alternating links, because w, wx, and wy are invariants of oriented alternating links (13). Moreover, its correlation with the actual Wr of the ideal configuration of alternating links obtained by simulations is remarkably good (see Fig. 3). The fact that we can accurately predict a geometrical property of a given link configuration starting from topological invariants of the link supports the notion that the ideal configuration contains essential information about alternating links. The reader might be interested to compare this way of predicting Wr with the one presented in ref. 12. Dylan Thurston (personal communication) pointed out to us that PWr can also be expressed as w + 3/7 (no. white − no. black), where no. white and no. black are the numbers of white and black regions in a checkerboard coloring of the link.
Figure 3.
Correlation between the computed 3D writhe of the ideal configuration of alternating knots and links (Wr) and the predicted value (PWr). Alternating knots up to eight crossings are indicated by an open diamond (Wr data from ref. 5), and alternating two-component links up to four crossings are indicated by a filled diamond (Wr data provided by Ben Laurie, personal communication). It is to be observed that the PWr of knots are multiples of 4/7 (vertical dotted lines) and that the PWr of two-component links are equal to 2/7 plus multiples of 4/7 (between two vertical dotted lines).
About the 3/7 Factor
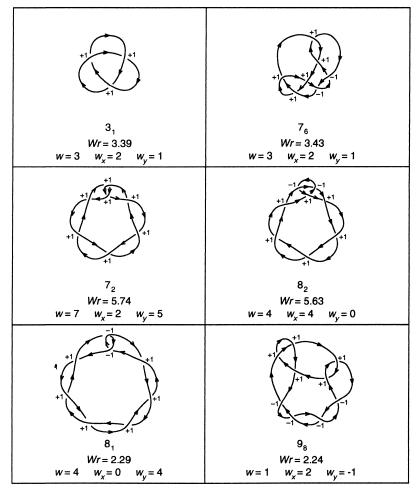
A natural question to ask about the formula of PWr is whether the 3/7 factor is just an ad hoc adjustment that could as well be replaced with 0.42 or 0.43 or whether it has some deeper justification. A partial answer to this question is the following. Some observed values of 3D writhe for the ideal configuration of different links are very close to each other (5, 11), and we are tempted to make the hypothesis that the discrepancies arise from the intrinsic limitations of the simulations. For example, it is an open problem whether the configuration obtained by minimizing the thickness energy of a link corresponds to a global minimum. Another example of limitation is the necessity to represent the curves by a succession of straight segments. Making the hypothesis that a “perfect” simulation would yield exactly the same 3D writhe for the links whose observed 3D writhes are close to each other, we would like that the corresponding predicted 3D writhes PWr be equal. Imposing this condition gives rise to a series of equations in which the factor 3/7 is replaced with a variable x. Most of these equations lead to an indeterminacy, the left- and right-hand sides being identical. As an example, imposing that the PWr of knots 31 and 76 are equal (see Fig. 4) gives rise to the equation:
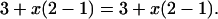 |
2 |
[Note that for each chiral link, we choose the enantiomorph that has a positive w. The equation would be the same (each term would be multiplied by −1) had we chosen the other enantiomorph.]
Figure 4.
Some pairs of knots have observed values of Wr close to each other. Wr is the 3D writhe of the ideal configuration obtained by simulation. (Note that, for each chiral knot, we chose the enantiomorph having a positive topological writhe. For some knots, this enantiomorph corresponds to the mirror image of the enantiomorph usually presented in reference tables; ref. 7).
However, some equations do lead to the solution x = 3/7. Actually, all equations that we tried that do not lead to an indeterminacy lead to that solution. Two examples are given hereafter, when identifying the PWr of knots 72 and 82 and the PWr of knots 81 and 98 (see Fig. 4):
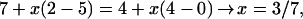 |
3 |
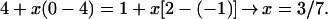 |
4 |
In conclusion, if one admits a perfect quantization of the 3D writhe of ideal configurations of alternating links, the factor in the formula of PWr has to be exactly 3/7.
Quantization of the 3D Writhe
Observing and trying to understand the quantization of the 3D writhe of ideal knot configurations has been a hot subject during recent years (3, 5, 6, 11, 12). Let us analyze the consequences of the formula PWr = 10/7 wx + 4/7 wy on the quantization of the Wr of ideal configurations of alternating links. The largest common divider of 10/7 and 4/7 is 2/7; thus, PWr must be quantized by steps of 2/7. Actually, it is possible to make a stronger statement, by invoking the fact that wx is even for an alternating link with an odd number of components and odd for an alternating link with an even number of components (13). It follows that PWr of alternating links with an odd number of components (including knots) is a multiple of 4/7, whereas PWr of alternating links with an even number of components is equal to 2/7 plus a multiple of 4/7. All observed values of Wr are in accordance with these predictions (see Fig. 3).
Discussion
The topological invariant of alternating knots and links described in this paper, PWr, is altogether very easy to calculate from a standard projection, and it provides a testing ground for the powerful conjecture that it correlates with geometrical and physical properties of knots and links. This conjecture predicts with great accuracy the 3D writhe of an ideal knot configuration or, equivalently, the 3D writhe averaged over an ensemble of random knot configurations.
Until now, most simulations of 3D writhe have been done on knots, and some have been done on two-component links. We suggest herein to extend the simulations to three- and four-component alternating links, which would allow our predictions to be checked experimentally relative to the 3D writhe of their ideal configuration and the confirmation of their fascinating property of quantization.
As we already mentioned, PWr is invariant for alternating knots and links only. More work is still needed to try to find an invariant of nonalternating as well as alternating knots and links that would correlate with the 3D writhe of ideal knots and links configurations.
Let us finally express the wish that this work might help and motivate the effort to find an analytical solution to the ideal configuration of knots and links.
Acknowledgments
We thank Piotr Pieranski for numerous discussions on the quantization of writhe, Dylan Thurston for sharing his ideas about PWr, Ben Laurie for providing us with his unpublished Wr data on two-component links, and Jacques Dubochet and Claude Weber for their interest in the project. This work was supported in part by Swiss National Foundation Grant 31-42158.94 to J. Dubochet and A.S.
Abbreviations
- 2D and 3D
two- and three-dimensional
References
- 1.Diao Y, Ernst C, Janse Van Rensburg E J. In: Topology and Geometry in Polymer Science. Whittington S G, Sumners D W, Lodge T, editors. New York: Springer; 1998. pp. 37–47. [Google Scholar]
- 2.Buck G, Orloff J. Topol Appl. 1993;51:246–253. [Google Scholar]
- 3.Katritch V, Bednar J, Michoud D, Scharein R G, Dubochet J, Stasiak A. Nature (London) 1996;384:142–145. doi: 10.1038/384122a0. [DOI] [PubMed] [Google Scholar]
- 4.Laurie B, Katritch V, Sogo J, Koller T, Dubochet J, Stasiak A. Biophys J. 1998;74:2815–2822. doi: 10.1016/S0006-3495(98)77988-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stasiak A, Dubochet J, Katritch V, Pieranski P. In: Ideal Knots. Stasiak A, Katritch V, Kauffman L H, editors. Singapore: World Scientific; 1998. pp. 1–19. [Google Scholar]
- 6.Janse van Rensburg E J, Sumners D W, Whittington S G. In: Ideal Knots. Stasiak A, Katritch V, Kauffman L H, editors. Singapore: World Scientific; 1998. pp. 70–87. [Google Scholar]
- 7.Adams C. The Knot Book. New York: Freeman; 1994. [Google Scholar]
- 8.Fuller F B. Proc Natl Acad Sci USA. 1971;68:815–819. doi: 10.1073/pnas.68.4.815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tait P G. Scientific Papers. I. London: Cambridge Univ. Press; 1898. pp. 273–347. [Google Scholar]
- 10.Cerf C. In: Chemical Topology: Applications and Techniques. Bonchev D, Rouvray D H, editors. Amsterdam: Gordon and Breach; 1999. pp. 1–33. [Google Scholar]
- 11.Pieranski P. In: Ideal Knots. Stasiak A, Katritch V, Kauffman L H, editors. Singapore: World Scientific; 1998. pp. 20–41. [Google Scholar]
- 12.Stasiak A. In: Proceedings of the Delphi Conference on Knots. Gordon C, Jones V F R, Kauffman L, Lambropoulou S, Przytycki J H, editors. Singapore: World Scientific; 2000. , in press. [Google Scholar]
- 13.Cerf C. J Knot Theory Ramifications. 1997;6:621–632. [Google Scholar]
- 14.Murasugi K. Knot Theory and Its Applications. Boston: Birkhäuser; 1996. [Google Scholar]