The metabolic signature related to high plant growth rate in Arabidopsis thaliana

Abstract

The decline of available fossil fuel reserves has triggered world-wide efforts to develop alternative energy sources based on plant biomass. Detailed knowledge of the relations of metabolism and biomass accumulation can be expected to yield powerful novel tools to accelerate and enhance energy plant breeding programs. We used metabolic profiling in the model Arabidopsis to study the relation between biomass and metabolic composition using a recombinant inbred line (RIL) population. A highly significant canonical correlation (0.73) was observed, revealing a close link between biomass and a specific combination of metabolites. Dividing the entire data set into training and test sets resulted in a median correlation between predicted and true biomass of 0.58. The demonstrated high predictive power of metabolic composition for biomass features this composite measure as an excellent biomarker and opens new opportunities to enhance plant breeding specifically in the context of renewable resources.

Multicellular organisms have to optimize the use of available resources to fit their needs in terms of energy, biosynthetic building blocks, and reserves. Green plants unlike animals produce their own organic compounds. Their ability to grow thus solely depends on their own photosynthetic and metabolic capacity. Biomass accumulation in the vegetative growth phase of a plant can therefore be regarded as the ultimate expression of its metabolic performance. Plants function as integrated systems, in which metabolic and developmental pathways draw on common resource pools and respond to changes in environmental energy and resource supplies (1). The distribution of metabolites between growth, production of defense compounds and storage compounds therefore has to be very tightly regulated. Growth and the concomitant drain of metabolites into cellular components has to be adjusted to the metabolic capacity of the system, i.e., the ability to supply sufficient amounts of organic compounds. This regulation is demonstrated by several observations of growth depression upon reduction of primary metabolism such as sucrose synthesis (2, 3). Growth ceases upon severe starvation caused by an extended dark period and is reinitiated only after a lag period of several hours after relief from the starvation by reillumination (4). Recent observations of the roles of the DELLA proteins in plants indicate that plant growth is limited to a submaximum level to enable plants to cope with unfavorable conditions (5). Thus, growth rate has to be adjusted to the metabolic status of a plant that needs to be translated into an appropriate response. This interaction between metabolism and the growth regulatory mechanisms may operate in two ways: either a high supply of metabolites triggers growth, or growth drains metabolites to a minimum tolerable level upon which growth is restricted. Metabolites may exert control on growth either by acting as substrates for the synthesis of cellular components, that become limiting under conditions of maximum tolerable growth, or by acting as signals that are sensed leading to subsequent changes in growth. Sugars such as glucose and sucrose have been shown to act as metabolic signals and to be involved in the control of plant growth and development (6). Trehalose-6-phosphate has recently been shown to be involved in signaling of the plant sugar status and in control of growth and development (7, 8).

Metabolic profiling is a mass-spectrometry (MS)- or NMR-based technology for an unbiased analysis of the metabolome of a given biological system with a high diagnostic power (9). Thus, in case of e.g., yeast or plants metabolic analysis allows to distinguish between different genotypes, developmental status or environmental conditions (10–12). In the case of humans, metabolomic approaches allow us to predict the response of individuals to drugs opening aspects of personalized drug treatments (13). In addition, single or a small number of metabolites can be extracted from metabolic profiling studies that have the potential to be developed into rapidly accessible biomarkers (14).

Based on the above considerations between the metabolic status of a plant system and growth and the proven high diagnostic power of metabolic profiling approaches, we decided to test whether biomass of a plant is correlated with and can thus be predicted by its metabolic composition. To this end we took advantage of a recombinant inbred line (RIL) population of Arabidopsis thaliana derived from a cross between the Arabidopsis lines Col-0 and C24 (15), which in previous studies showed strong transgressive segregation for biomass (16). RILs represent permanent segregating populations of homozygous lines, which allow to reduce the environmental variance in replicated experiments (17). The extensive biochemical variation in Arabidopsis is largely under genetic control (11). Therefore, the use of such a population for an exploratory analysis of relations between growth and metabolite levels is particularly advantageous (over e.g., using environmental perturbations to modulate growth and metabolism) as it offers the opportunity to identify the genetic determinants of all studied traits in addition to the determination of correlations.

As shown below, when applying multivariate analysis to the combined data sets of biomasses and metabolic profiles, a statistically highly significant correlation between metabolic composition and biomass was obtained. We believe this result to be of high relevance for our basic understanding of plant growth and metabolism and to have obvious implications for breeding of high plant biomass producers, an aspect which in recent years has become of increasing importance regarding renewable resources as energy supply (18, 19). It furthermore provides precedence for the utility of molecular profiling data to extract biomarkers with high predictive power for a complex trait.

Results

Biomass and Metabolite Profile Determination of Col-0/C24 RILs.

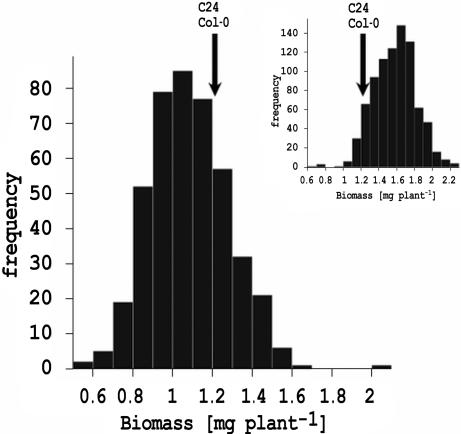
The combined analysis of biomass and metabolic profile was performed on a total of 1,144 genotypes. Of these lines, 429 genotypes were derived from a RIL population from the reciprocal crosses Col-0 × C24 (228 lines) and C24 × Col-0 (201 lines) and 715 lines were derived from crosses of the RILs to parents Col-0 and C24. All plants were grown under controlled conditions in six replicated experiments. Plants were harvested 15 days after sowing and used for shoot biomass determination or were pooled and frozen for metabolite profiling by gas-chromatography/mass-spectrometry (GC/MS). The distribution of mean biomass within the population clearly shows transgressive segregation (Fig. 1). We detected no significant differences in biomass (t test, P = 0.238) between the two subpopulations, and therefore treated the RILs as one population in subsequent analyses.

Fig. 1.

Distribution of shoot biomass in the recombinant inbred line (RIL) population. Shown is the mean biomass (milligrams per plant) estimated by REML. The arrow indicates the biomass determined for the parental lines C24 (1.265 mg per plant) and Col-0 (1.254 mg per plant). The histogram of the shoot biomass of the RIL crosses to the parents is shown in Inset.

From the metabolic profiling data we took only those metabolites into account, which were detected reproducibly in at least 85% of the samples analyzed. Major groups among these metabolites are organic acids, sugars, sugar phosphates, polyols, amines and amino acids. Concentrations could be determined for a set of 181 compounds, 84 of which were assigned a chemical structure by comparison with a library (20, 21). The remaining compounds were classified into chemical groups by using representative masses.

Canonical Correlation Reveals a Close Link Between Biomass and a Specific Combination of Metabolites.

In a first approach distributions of single metabolites were queried for their predictive power with respect to the biomass distribution by calculating pairwise correlations between all 181 measured metabolite levels and biomass [supporting information (SI) Table 2]. Because a normal distribution cannot be assumed for all variables rank correlation was used as a robust estimation of the correlation coefficient. The highest absolute correlation found was for a carbohydrate, which yielded a value of 0.266. Although the correlation is statistically highly significant (P value of 5.17 × 10⁻²⁰), it can only explain 7.07% of the variance. Other significantly correlated compounds are ethanolamine (0.238; P = 3.87 × 10⁻¹⁶), fructose-6-phosphate (−0.177; P = 1.65 × 10⁻⁹, glutamine (−0.177, P = 1.81 × 10⁻⁹), glucose-6-phosphate (−0.175; P = 2.44 × 10⁻⁹ and citric acid (−0.175; P = 2.80 × 10⁻⁹). Their individual contribution to the explained variance is smaller than 5.64%.

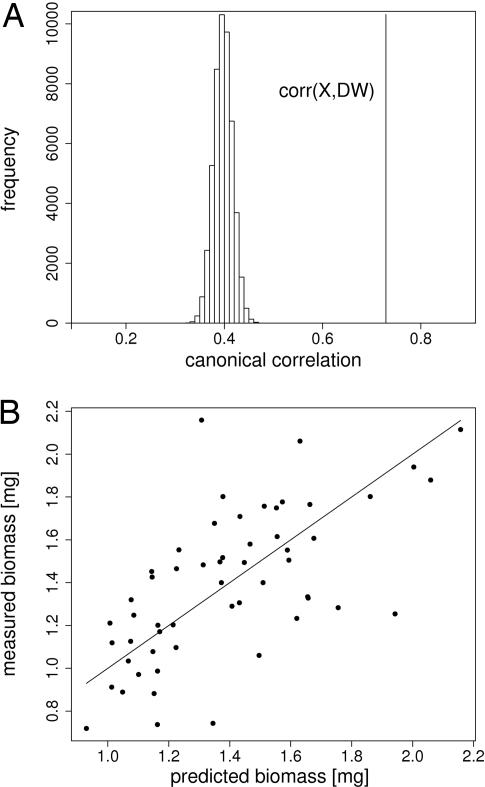
In the second approach we applied multivariate tools to analyze the relationships between the two large groups of metabolite and biomass variables. Canonical correlation analysis (CCA) is a multivariate technique often used in psychological, climate and ecological studies to quantify the associations between two separate data sets measured on the same experimental units (22–25). In contrast to the aforementioned pairwise correlation analysis, CCA yielded a much stronger correlation of 0.73. This value corresponds to 53.29% of variance explained by the linear combination of metabolites, almost 10 times more than explained by any individual metabolite. To test the significance of this result, the biomass vector was permutated 50,000 times. At this point the maximum correlation did not increase significantly with additional permutations. This maximum value is 0.46. The distance between the median of the random correlations and the estimated value amounts to 17 standard deviations (Fig. 2A), which for normal distributions corresponds to a P value of 4.1 × 10⁻⁶⁵ strongly suggesting that the model is statistically highly significant.

Fig. 2.

Significance (A) and predictive power (B) of the multiplicative model. (A) Histogram of canonical correlations between the metabolite matrix and random permutations of the biomass vector. The vertical line on the right corresponds to the canonical correlation between the actual biomass vector (DW) and the metabolite matrix (X)R. The distance to the median of the random correlations amounts to 17 standard deviations. (B) Prediction of the biomass by the metabolite matrix. Shown is one representative example of 20 repeats in the cross-validation. Size of the training set was 1,086, the 58 data points of the test set are displayed. The straight line represents the exact prediction.

Predictive Power of Metabolic Composition for Biomass.

In a final step we wanted to test the predictive power of metabolite composition for biomass. To this end, we decided to apply the partial least square (PLS) approach, because CCA yields the maximum correlation and thus an upper limit for the true correlation, but is notoriously inferior to other methods, especially PLS, for cross-validation (26). (compare also SI Text). Thus, the metabolite matrix and biomass vector were divided into training and test sets. The PLS coefficients estimated in the training set explaining 90% of the variance of the training data were used to predict the biomass in the test set. This procedure was repeated 20 times. For a size of the training set of 1086 genotypes we obtained a median correlation between predicted and true biomass of 0.58 in the remaining 58 genotypes (representing the test set) confirming a strong predictive power of metabolic composition for biomass (Fig. 2B). To evaluate the significance the same permutation as for CCA was applied. For each of the 500 permutations a cross-validation was performed. The median of the corresponding correlations was −0.001 ± 0.052, thus, using the same assumption as above, we estimate a P value of 3.4 × 10⁻²⁹.

Metabolites Most Relevant for Biomass Accumulation.

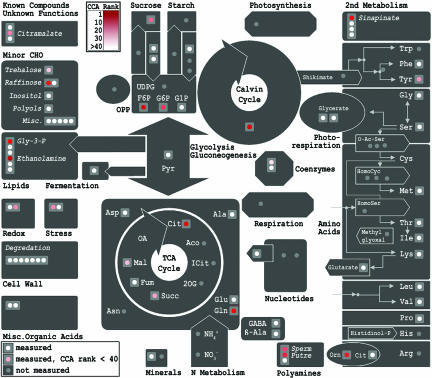
As a next step in our analysis we extracted the metabolites most relevant for biomass accumulation by their correlation to the canonical variate (27). The first 44 metabolites with significant correlations are listed in Table 1 and displayed on biochemical pathways (28) in Fig. 3. Strongly represented are central metabolism derived compounds such as glucose-6-phosphate and fructose-6-phosphate, members of the tricarboxylic acid (TCA) cycle such as succinate, citrate and malate, members of the membrane/phospholipid biosynthesis such as glycerol-3-phosphate, ethanolamine and sinapine, or sucrose. A list of all relevant metabolites is given in SI Table 3.

Table 1.

List of top 44 signature metabolites ranked according to the strength of the canonical correlation.

Metabolite	COR	PV
Unknown_038*	0.37833	0.00E + 00
Unknown_035*	0.31038	0.00E + 00
Ethanolamine	0.30515	0.00E + 00
Unknown_086*	−0.27201	7.45E−21
Fructose 6-phosphate	−0.24840	1.51E−17
Citric acid	−0.24195	1.06E−16
Unknown_078*	0.23882	2.22E−16
Unknown_061*	0.22967	3.77E−15
Glutamine	−0.22258	2.62E−14
Glycerol-3-phosphate	−0.22088	4.16E−14
Sinapic acid (cis)	−0.21462	2.19E−13
Raffinose	−0.20030	8.09E−12
Ornithine	0.19723	1.70E−11
Putrescine	0.19409	3.57E−11
Unknown_051	0.19398	3.68E−11
Glucose 6-phosphate	−0.18921	1.11E−10
Spermidine (major)	0.18798	1.47E−10
Unknown_048	−0.18557	2.54E−10
Sinapic acid (trans)	−0.17943	9.84E−10
Sucrose	−0.17937	9.98E−10
Unknown_074	0.17879	1.13E−09
Citramalic acid	−0.17388	3.22E−09
Ascorbic acid	−0.16929	8.34E−09
Tyrosine	−0.15838	7.25E−08
Unknown_062	−0.15359	1.79E−07
Succinic acid	−0.15190	2.44E−07
Unknown_071*	−0.14931	3.92E−07
Malic acid	−0.14215	1.39E−06
Trehalose	0.13961	2.14E−06
Unknown_033	0.13924	2.28E−06
Unknown_091	0.13649	3.60E−06
Unknown_060	0.12791	1.43E−05
Nicotinic acid	0.12497	2.25E−05
Unknown_043	0.12443	2.44E−05
Unknown_054	−0.12395	2.62E−05
Unknown_063	0.12240	3.31E−05
Unknown_088	−0.11951	5.07E−05
Unknown_011	0.11505	9.62E−05
Unknown_084	0.11208	1.46E−04
Maleic acid	−0.11167	1.54E−04
Phenylalanine	−0.11090	1.71E−04
Salicylic acid	−0.11060	1.78E−04
Unknown_005	−0.10851	2.36E−04
Unknown_056	0.10746	2.71E−04

Given are correlation (COR) and corresponding P value (PV).

*MassSpectrum indicates following chemical classes for these unknown compounds: 038, sugar; 035, glucopyranoside; 086, lactobionic acid; 078, pyranoside; 061, polyol; 071, sugar phosphate.

Fig. 3.

Representation of the most important metabolites known by structure according to CCA on biochemical pathways. This representation of metabolism indicates all known metabolites we analyzed by using GC/MS that could be annotated in MapMan (28). Red color visualizes metabolites which are high ranked in CCA (positions 1–44), with ranking according to the color-coded scale bar.

Discussion

We took advantage of an Arabidopsis thaliana RIL population for a parallel and integrative analysis of vegetative biomass accumulation and metabolic composition to answer the question whether or not biomass can be described as a function of metabolic composition.

As outlined in the Results section, pairwise correlation analysis of biomass and single metabolites could explain a maximum of 7% of the total variance observed in biomass. These data strongly suggest that there is no single “magic” compound detectable, which could explain the biomass variance in a satisfying way. In contrast, canonical correlation analysis yielded a highly significant (the estimated P value based on permutations is lower than 10⁻⁶⁴) canonical correlation of 0.73 (compare Fig. 2A). Furthermore, in cross-validations a median correlation of 0.58 between the predicted and the observed biomass was observed (compare Fig. 2B).

This result demonstrates that a combination of the levels of a large number of metabolites rather than few individual metabolites show a close correlation with growth. It indicates that variation in growth coincides with characteristic combinatorial changes of metabolite levels, whereas individual metabolites may fluctuate largely independently of alterations in growth. To exclude the possibility that the strong correlation between biomass and metabolic composition is simply due to coincidental overlap of quantitative trait loci (QTL) for biomass and metabolites, we performed a QTL analysis on the RIL data set (429 lines) and detected a total of 157 QTL for 84 metabolites and six QTL for biomass (data not shown). Of the latter only two colocate with significantly more metabolite QTL than expected by random, thus making this explanation highly unlikely.

Inspection of the metabolites highly ranked in CCA and thus representing the main drivers of the correlation shows that central metabolism derived metabolites are strongly represented. Of high relevance are the three metabolic intermediates of the hexose phosphate pool, fructose-6-phosphate, glucose-6-phosphate, and glucose-1-phosphate, which link carbon flow from photosynthesis and starch and sucrose metabolism with cell wall formation, the oxidative pentose phosphate pathway (it provides substrates for nucleic acid synthesis and for lignin, polyphenol and amino acid synthesis) and glycolysis. Members of the TCA cycle such as succinate, citrate, and malate are highly ranked. This finding underpins the central importance of this pathway which together with reactions of the glycolysis pathway and the oxidative phosphorylation constitutes a key process delivering carbon skeletons, reduction equivalents, and energy for the vast majority of biochemical pathways. Also highly ranked is sucrose, the major transport form of carbon from source to sink tissue and which is central to the export from the sources and the import to the sinks. It thus represents the interface between carbohydrate production and utilization at the whole plant level Other metabolites such as glycerol-3-phosphate or ethanolamine play a major role in membrane/phospholipid biosynthesis. The anti-oxidant ascorbic acid (vitamin C) has been implicated in cell division (29) and plant growth regulation by means of its role as enzyme cofactor (30). Glutamine as a central metabolite in nitrogen assimilation and the major primary donor of reduced nitrogen is also found amongst the most important metabolites. This observation is contrasted by the fact that nearly all other amino acids analyzed are of rather low contribution based on the CCA. Further highly ranking metabolites can be assigned to general stress metabolites such as sinapine as the major phenylpropanoid in Brassicaceae, ornithine, the polyamines putrescine and spermidine, and trehalose. Thus, a link between the metabolites ranked high in the CCA and biomass accumulation is plausible because central metabolism and stress response are of utmost importance to plant growth, and thus biomass.

Another noteworthy observation is that the canonical variate determined by means of a multiplicative model resulted in closer correlations between the predicted and the observed biomass values than by means of an additive model (data not shown). It indicates that the involved metabolites act synergistically rather than additively which is very plausible as the aforementioned closely interlinked pathways of carbon metabolism are required for different cellular components that all are crucial for growth/biomass formation. The strong reciprocal interrelation between nitrogen and carbon assimilation would also strongly argue for synergistic and not additive effects between key metabolites representing these classes of biochemical compounds as observed in our case. Similar arguments can be made for e.g., ethanolamine synthesized via serine as a major constituent of membranes or sinapic acid as the major phenylpropanoid component in Arabidopsis.

A surprising observation from our data are the occurrence of both positive and negative correlations between metabolites and biomass. The large majority of known metabolites displaying a negative correlation to the biomass vector are the aforementioned intermediates of central metabolic pathways including sucrose, glucose- and fructose-6-phosphate, the TCA cycle members citric acid, succinate or malic acid, as well as the amino acids glutamine and phenylalanine. On the other hand, amongst the positively correlated metabolites are a large fraction of unknown chemical structure as well as some metabolites discussed in stress response such as nicotinic acid (31) or putrescine (32), or the stress metabolite trehalose discussed in connection with drought resistance (33). A negative correlation suggests that pool sizes of these metabolites are reduced to low levels when strong growth occurs. It is conceivable that this process involves mostly metabolites providing the major building blocks for growth such as the central metabolites mentioned. In conclusion, this observation would suggest that growth drives metabolism and not vice versa. This finding would indicate that high growth rates cause a depletion of central metabolite pools rather than growth being enhanced through increased supply of substrates for the synthesis of cellular components. A similar conclusion of metabolism driven by growth has been derived from a study of the relationship between tomato fruit size and metabolites (34). In this scenario, the positively correlated metabolites could play a role in plant defense against abiotic and biotic stress and it is comprehensible that higher concentrations of these metabolites would coincide with better armed plants. For both groups of substances, however, the relation with growth may be nonlinear. On the one hand, the reduction of central metabolite levels below a certain minimum necessary to sustain high flux rates may result in growth limitation and thus a breakdown of a linear negative relationship. Similarly, a positive effect on growth because of elevated stress tolerance may be achieved in a certain range of stress metabolite levels above which no further beneficial or even detrimental effects may occur. As the procedures applied here determine linear correlations, it is not unexpected that no tighter relationships (stronger correlations) were detected. A complementary hypothesis regards metabolites not primarily as chemicals for growth and defense but rather as signals. Under this assumption positively correlated metabolites are positive signals regulating plant growth and the contrary would be true for negatively correlated metabolites. In the context of signal molecules the large number of positively correlated compounds of as yet unknown structure is worth noting and stresses the need for identification of their chemical nature. They might constitute unusual products of metabolic side reactions that are derived from primary metabolites generated for signaling purposes and which can move to sites of perception without further conversion along the major metabolic reactions or transport pathways. Further studies querying some testable predictions from such models (e.g., the presence of receptors/sensors or the elicitation of specific responses in case of signaling metabolites) are needed to validate these models.

Conclusion

Using an Arabidopsis thaliana RIL population and conducting a combined analysis of biomass and metabolite profiles allowed the prediction of biomass as a function of metabolic composition providing a direct proof for the hypothesis that metabolic composition is related to biomass and thus growth. The observations made here further extend this hypothesis toward the notion that major global changes in metabolism are the result of variation in growth rather than vice versa. In addition to fostering our basic understanding, these data are of immediate potential for a number of applied purposes. The possibility to predict biomass on the basis of the metabolic signature of a plant presents a first precedence for the use of metabolite profiles as biomarkers with high predictive power and could potentially revolutionize the selection and thus breeding process for biomass producers such as trees that are cultivated for decades before harvest. Identification of highly productive genotypes already at an early growth stage would result in enormous time and cost-savings. In the light of reduced availability of fossil fuels and increasing reliance on bio-derived energy, the importance of such an opportunity can hardly be overestimated.

Materials and Methods

Creation of Recombinant Inbred Line (RIL) Population.

Two reciprocal sets of RILs were developed from a cross between the two Arabidopsis thaliana accessions C24 and Col-0 as described elsewhere (15). The population consisted of 228 Col-0 × C24 F₈ and 201 C24 × Col-0 F₈ individual lines.

Plant Cultivation.

The RILs were planted in a split plot design with 54 incomplete blocks and four replicates, repeated six times. Plants were grown in 1:1 mixture of GS 90 soil and vermiculite in 96-well-trays. Six plants of the same line were grown per well. Seeds were germinated in a growth chamber at 6°C for 2 days before transfer to a long-day regime (16 h fluorescent light [120 μmol·m⁻²·s⁻¹] at 20°C and 60% relative humidity/8 h dark at 18°C and 75% relative humidity). To avoid position effects, trays were rotated around the growth chamber every 2 days.

Shoot Dry Biomass.

Shoot dry biomass was determined 15 days after sowing. Plants from the same well were harvested together and placed in a vacuum oven at 80°C for 48 h. Dry biomass was recorded by using an analysis balance. Mean shoot dry biomass in mg/plant per plant was estimated by using the linear mixed model (35) G + E:E·G + E·GC + E·GC·T where E is experiment, G is genotype, GC is growth chamber, T is tray (REML procedure in Genstat). Biomass in the two subpopulations was compared with a two-sided t test. We detected no significant differences in biomass (P = 0.238) between the two subpopulations, and treated the RILs as one population in subsequent analyses.

Metabolite Data.

Sample Preparation, Measurement, and Data Processing.

Samples for the analysis of metabolic composition were collected together with the material for dry biomass analysis at 15 days after sowing. Harvested material (shoot and leaf) was cooled below −80°C immediately and kept at this temperature until further processing. Derivatization, GC/MS analysis, and data processing were done as described elsewhere (36). All 181 metabolic signatures that have been evaluated within this experiment are listed in SI Table 4. The GC/MS spectra of evaluated metabolites that are unknown with respect to their actual chemical formula but can be repeatedly found in Arabidopsis are available in SI Table 4.

The extracted metabolite data consist of unique mass intensity values for each referenced compound and measurement respectively. These raw data were normalized and otherwise directly used for analysis. This method allows between sample comparisons but no quantitative statements about single metabolites.

Normalization.

Metabolite data were normalized by dividing each raw value by the median of all measurements of a day for one metabolite.

Missing Value Estimation.

For the canonical correlation analysis (CCA) missing value replacement is necessary. The 6% missing values in the metabolite matrix were imputed with a self-organizing map (SOM) algorithm (37). The mean square error was estimated by the comparison of known values with those calculated from the SOM algorithm. The coefficient of variation (root mean square error divided by the mean) was 0.3.

Integrated Analysis of Phenotypic and Metabolite Data.

Linear models for the relation between metabolite profile and biomass.

The relation between biomass and metabolite profile was measured by simple Spearman correlation between the dry biomass and relative abundances of all metabolites, and by a more complex multiplicative model. The first corresponds to the following model, referred to as model 1:

The second model can be described by:

B denotes the biomass, x the relative metabolite abundance and c the corresponding constants for all i metabolites.

Multivariate linear analysis.

Canonical correlation analysis (CCA) calculates the highest possible correlation between linear combinations of the columns from two matrices with the same number of rows. If the second matrix has only one column, this procedure corresponds to a ordinary least square (OLS) regression. The correlation thus found is called canonical correlation, the corresponding linear combination canonical variate. The mathematical foundation is described in the literature (23, 37). The R function cancor was used to calculate the canonical correlation between metabolites and biomass. For cross-validation a partial least square (PLS) regression was performed. This method (38) seeks to maximize the covariance instead of the correlation between the matrices. To carry out the procedure the R function plsr was used. These functions are publicly available (www.r-project.org). All procedures were applied after missing value estimation followed by normalization of the metabolic matrix. To test the robustness of the selection of the signature metabolites, we applied the following procedure: with 90% of the 1,144 genotypes chosen at random the canonical variate was calculated and the important metabolites selected as described above. Selected metabolites, which were not in the original list of 44 metabolites, were regarded as false. This procedure was repeated 100 times. We obtained a median “false positive rate” of 0.048 (±0.034).

Abbreviations

RIL

recombinant inbred line

CCA

canonical correlation analysis

PLS

partial least square

TCA

tricarboxylic acid

QTL

quantitative trait loci.