Abstract
Despite the insights obtained from click responses, the effects of medial-olivocochlear (MOC) efferents on click responses from single-auditory-nerve (AN) fibers have not been reported. We recorded responses of cat single AN fibers to randomized click level series with and without electrical stimulation of MOC efferents. MOC stimulation inhibited (1) the whole response at low sound levels, (2) the decaying part of the response at all sound levels, and (3) the first peak of the response at moderate to high sound levels. The first two effects were expected from previous reports using tones and are consistent with a MOC-induced reduction of cochlear amplification. The inhibition of the AN first peak, which was strongest in the apex and middle of the cochlea, was unexpected because the first peak of the classic basilar-membrane (BM) traveling wave receives little or no amplification. In the cochlear base, the click data were ambiguous, but tone data showed particularly short group delays in the tail-frequency region that is strongly inhibited by MOC efferents. Overall, the data support the hypothesis that there is a motion that bends inner-hair-cell stereocilia and can be inhibited by MOC efferents, a motion that is present through most, or all, of the cochlea and for which there is no counterpart in the classic BM traveling wave.
I. INTRODUCTION
For many decades, excitation of auditory-nerve (AN) fi-bers in the mammalian cochlea has been thought to be due solely to motion produced by the basilar membrane (BM) traveling wave (Békésy, 1960). In the classic view, the traveling wave drives the motion throughout the organ of Corti, including bending inner hair cell (IHC) stereocilia, thereby exciting AN fibers (Patuzzi, 1996). The traveling wave is thought to be amplified by outer hair cells (OHCs), mecha-noreceptor cells endowed with sound-frequency somatic motility produced by the motor protein prestin (Brownell et al., 1985; Zheng et al., 2002; Liberman et al., 2002), and/or with stereocilia motility, as suggested by stereocilia negative stiffness (Kennedy et al., 2005).
Conceptions of the classic traveling wave are based primarily on BM measurements from the basal turn of the cochlea but are typically assumed to hold throughout the cochlea, or at least in regions where AN click-response “glides” go upward [characteristic frequencies (CFs) >1 kHz]. The classic BM traveling wave is frequency dispersive such that at each place, low-frequency energy arrives before high-frequency energy (Shera, 2001). Consistent with this, in BM responses to clicks in the basal turn of the cochlea, the frequency content starts below the local CF and increases to CF, i.e., it shows an upward “glide” (de Boer and Nuttall, 1997; Shera 2001). In contrast, in the apex, glides go in the opposite, nonclassic direction (Carney et al., 1999; Lin and Guinan 2000; 2004). In the classic traveling wave, an important consequence of the low-frequency energy arriving first is that the click-response first peak is from energy that is below the local CF and receives little or no amplification. This aspect of the classic traveling wave is consistent with basal-turn BM motion, which shows a click-response first peak that has almost linear growth and that changes little after death (Robles et al., 1976; Ruggero et al., 1992; Recio et al., 1998; Recio and Rhode, 2000).
BM motion is modulated by medial olivocochlear (MOC) efferents, nerve fibers that originate in the brainstem and synapse on OHCs (Guinan, 1996). Activation of MOC fibers decreases BM motion in response to low-level tones, presumably by decreasing the gain of the cochlear amplifier (Murugasu and Russell 1996; Russell and Murugasu 1997; Dolan et al., 1997; Cooper and Guinan, 2003). The role of MOC efferents in hearing is not fully understood, but it is thought that MOC efferents reduce damage due to intense sounds and reduce the masking of transient sounds by background sounds, among other things (Guinan, 1996).
Since MOC efferents synapse directly on OHCs, they provide a way to reversibly change OHC properties without opening or damaging the cochlea. Extending previous work on AN responses to clicks (Lin and Guinan, 2000, 2004), we studied the effects of MOC efferents on click responses of single AN fibers. We report here the unexpected finding that MOC efferents inhibit the click-response first peak of AN fibers throughout much of the cochlea. This first-peak inhibition cannot be explained with the common view that motion throughout the cochlea is produced solely by a traveling wave that mimics BM motion in the cochlear base, because the first peak of BM motion receives little or no amplification and is little changed by MOC stimulation (Guinan and Cooper, 2005). Thus, MOC inhibition of the AN first peak indicates that this peak is due to motion separate from the classic traveling wave, and that this motion is strongly influenced, perhaps produced, by OHCs.
Our analysis of MOC effects on the first peak of the AN click response did not produce a clear result for fibers with CFs>10 kHz so we pursued this issue in a second set of experiments using low-frequency tones. The rational for these additional experiments is developed in a second Introduction (Sec. IV), and the results are presented in (Sec. V). Methods for both experiments are presented in Sec. II (Methods).
II. METHODS
We stimulated MOC efferents electrically in the brainstems of anesthetized cats, and monitored cochlear output by recording spikes from single AN fibers, as schematized in Fig. 1. Treatment of experimental animals was in accordance with protocols approved by the Committee on Animal Care at the Massachusetts Eye and Ear Infirmary.
FIG. 1.
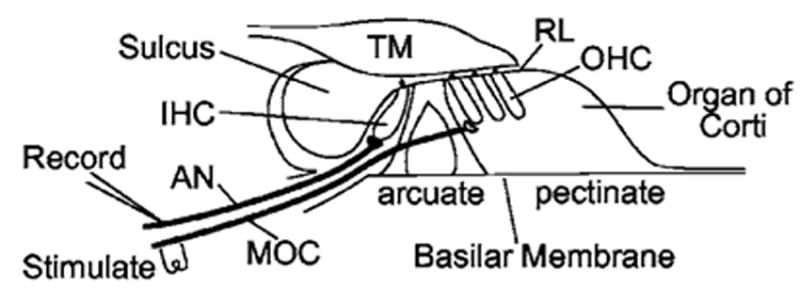
A diagram of the experimental setup. AN: auditory nerve; IHC: inner hair cell; MOC: medial olivocochlear efferent nerve; OHC: outer hair cell; RL: reticular lamina; TM: tectorial membrane.
A. Animal preparation and MOC stimulation
The surgical preparation, methods for single-fiber recording and the paradigms for MOC stimulation and click presentation were based on previously published methods (Guinan and Stankovic, 1996; Lin and Guinan, 2000). Adult cats were anesthetized with diallyl barbiturate in urethane. The floor of the fourth ventricle and the AN were exposed dorsally. AN fibers were monitored with pipette electrodes and only recordings with an accurate spike timing were used. AN compound action potentials (CAPs) were monitored with an electrode near the round window, and an automated tone-pip audiogram determined the sound levels for CAP thresholds (10 μV) at frequencies 1–32 kHz. Data were used only when CAP thresholds were in the normal range.
MOC fibers were stimulated with a bipolar electrode along the midline of the floor of the fourth ventricle using trains of shocks lasting 0.6–1.1 s, with 200 shocks/s at levels that evoked little or no visible animal movement. Shock pulses were monophasic or diphasic (~300 μs per phase) and were shaped to reduce high frequencies that could produce electrical artifacts on the microelectrode. Such shocks excite medial but not lateral efferent (LOC) fibers (Gifford and Guinan, 1987; Stankovic and Guinan, 1999). In some cats middle-ear-muscle (MEM) tendons were cut to prevent the shocks from affecting middle-ear transmission. In other cats, we avoided exciting MEMs by adjusting electrode configuration, placement, and shock level. We determined when there were MEM contractions from measurements of ear-canal sound pressure using a low-frequency probe tone (typically 500 Hz, 50 dB SPL). This test was made selective for middle-ear impedance changes by suppressing the stimulus-frequency otoacoustic emission (SFOAE) from the probe tone with a second tone that was ~100 Hz lower in frequency and 20 dB more intense.
B. Clicks
Clicks were generated by rectangular electrical pulses to a condenser earphone (Bruel & Kjaer 4145) in a closed acoustic assembly (Lin and Guinan, 2000). Although condenser earphones are nonlinear, they have the important advantage of producing less ringing than most earphone types. To compensate for the nonlinear, square-law characteristic of the earphone, the electrical output was adjusted in amplitude so that rarefaction and condensation clicks were equivalent in peak acoustic level and had almost identical spectra (they were within 1 dB at all frequencies of interest). For fibers with CFs<7 kHz and some fibers with higher CFs, we used 90 or 100 μs pulses. These relatively long-duration click pulses were chosen to provide as much low-frequency energy as possible without causing acoustic trauma (Lin and Guinan, 2000) but have the disadvantage of nulls in their acoustic spectra at multiples of 11.1 or 10 kHz. For animals in which high-CF fibers were targeted, spectral nulls near fiber CF were avoided by using 50 μs clicks for CFs 7–15 kHz, 24 μs clicks for CFs 15–30 kHz, and 14 μs clicks for CFs>30 kHz. Trains of clicks were presented with the interval between clicks typically 15–30 ms for CFs<7 kHz, 8 ms for CFs 7–15 kHz, and 5 ms for CFs>15 kHz. These rates were chosen to be as high as possible while providing enough time for each response to finish before the next click. The use of high-rate clicks produced strong adaptation, which was necessary to lower the overall probability of spikes. Without adaptation, high-level clicks evoke spikes with near unity probability early in each click response, which makes it impossible to calculate recovered probability histograms (Lin and Guinan, 2000). In early experiments, each click level series had a constant polarity (condensation or rarefaction) and a run with one polarity was followed by a run with the other polarity. In later experiments alternating polarity clicks were used in each run. Similar results were found with both methods. The click level is expressed as peak-equivalent sound pressure (pSPL) computed as in Lin and Guinan (2000) from calibrations done on each animal and each click duration. A click level series had 6–18 levels (typically 11) ranging downward from the highest level the acoustic system produced (typically 110 dB for 50–100 μs clicks; less for shorter clicks). In each level series, the level steps were normally 6 dB at high levels where click responses often changed rapidly with level, and 10–12 dB at lower sound levels.
C. Stimulus paradigm
On each AN fiber, we obtained a tuning curve (from which CF was determined) and one or more click-level-series runs with and without MOC stimulation. A click-level-series run consisted of a series of same-duration trials that were long enough (3–4 s) for a fixed burst of MOC shocks to produce an MOC effect, and for the MOC effect to recover before the next trial. On each trial, clicks were presented at a fixed sound level and fixed repetition rate, but the sound level was randomized across trials. Two basic paradigms were used. In the first [Fig. 2(a)], both the click level and the presence/absence of shocks were randomized across levels, and “with MOC stimulation,” versus “without MOC stimulation,” comparisons were done using data from the same time period in each trial. In the second paradigm [Fig. 2(b)], MOC stimulation was presented on every trial, and “with MOC stimulation” versus “without MOC stimulation” comparisons were done using data from a time window during the shocks versus a time window more than 1 s after any shocks. No differences were noted between results from these two methods.
FIG. 2.
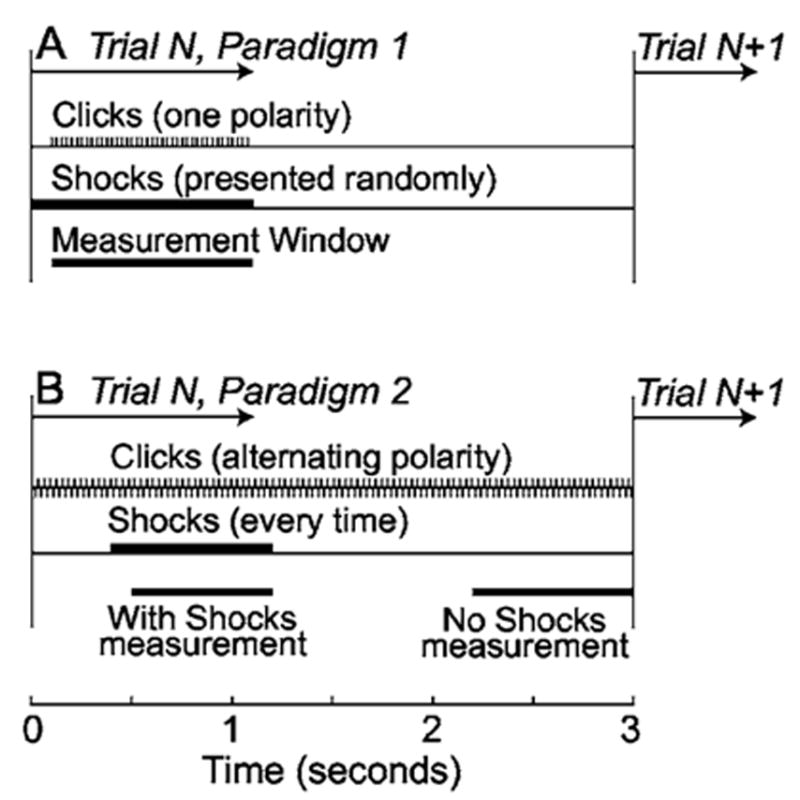
The timing of clicks, shocks, and response windows for a single trial of paradigms 1 and 2. A: Across the trials of a paradigm 1 run, both click level and the presence/absence of the shock train were randomized; the response was always measured in the same time window which was either “with shocks” or “without shocks” depending on the shock randomization of the trial. B, across the trials of a paradigm 2 run, click level was randomized and shocks were always present; “with shocks” and “no shocks” measurements were obtained each trial from separate windows, as indicated. In both paradigms, response histograms for a trial were formed from all of the same-polarity click responses within the measurement window. With paradigm 1, a run with one click polarity was always followed by a run with the other click polarity, whereas paradigm 2 used alternating polarity clicks so one run provided responses from clicks of both polarities.
On a fiber that was contacted sufficiently long, multiple runs were obtained, each with a different randomization of click levels, and (when applicable) shock presence. The results from runs with identical parameters were combined.
D. Data analysis
From the spike and click times at each level, we calculated peristimulus-time (PST) histograms, recovered-probability PST (rpPST) histograms, and compound rpPST histograms. A rpPST histogram shows the probability that a spike will occur in a time bin at a given latency, using only time bins (and spikes) at least P seconds after a previous spike. This computation reduces the distortion of the PSTs caused by fiber refractoriness and fast adaptation (Gray, 1967). We used a P of 3 ms that appeared to maximize the number of spikes while preserving the rpPST shapes shown by recovered histograms with longer P’s. For Fig. 3, we formed compound rpPST histograms from the rpPSTs by combining rarefaction-click rpPSTs plotted upward with condensation-click rpPSTs plotted downward. Since individual rpPSTs resemble rectified versions of stereocilia motion and IHC receptor potentials, compound rpPST histograms, which combine data from both odd and even half cycles of the response, provide a better estimate of the overall waveform of these variables (Pfeiffer and Kim, 1972; Lin and Guinan, 2000).
FIG. 3.
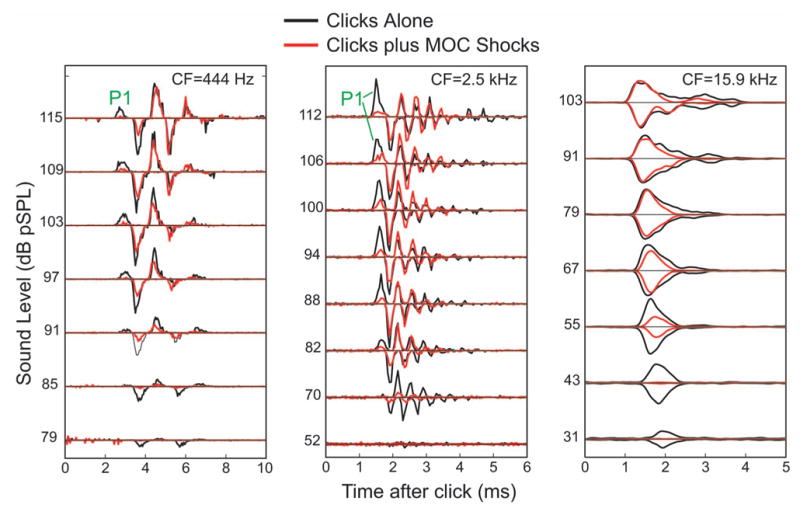
Examples of the effects of MOC stimulation on AN responses to clicks from fibers with low, medium, and high CFs. Compound rpPST histograms from three AN fibers showing responses to clicks at selected sound levels, with (red) and without (black) MOC stimulation. “P1” indicates the first peak.
To quantify MOC effects, we segmented the click responses into first and second peaks. For each fiber, boundaries were chosen by hand with rarefaction and condensation click responses done separately, and each boundary applying to responses at all levels. For fibers of all CFs, a boundary was chosen just before the onset of the first peak (at any level). For fibers in which separate peaks could be distinguished (CFs<4 kHz, sometimes up to 6 kHz), boundaries were chosen at the valleys between peaks 1–3. Normally the boundary line at one click polarity was at the response peak of the other click polarity. For CFs>4–6 kHz, where separate peaks at 1/CF intervals could not be distinguished, we tried two methods for setting boundaries. In high-CF fibers, a distinguishable initial peak can often be seen that corresponds to the “offset-peaks” response (Lin and Guinan, 2000) in which high-level clicks elicit early peaks with different latencies for rarefaction and condensation clicks. The first method attempted to use this peak, with the second peak assumed to be equal in duration to the first. However, this first peak could be clearly distinguished only on a minority of fibers, and we saw no consistent pattern of MOC effects using this method. The second method, which was used in making Fig. 6, placed the boundaries that marked the supposed end of the first and second “peaks” so that each peak lasted a fixed time and there was no gap between the peaks. The fixed time (which was the same for all fibers) was varied from 0.1–1 ms in trial analyses of the data. After determining the peak boundaries, the amplitude of each peak was taken to be the average spike rate within its time window. Finally, data were used only from fibers for which the recovered-probability firing rate exceeded 1.5 spikes/ms at least at one click level. This criterion mainly removed fibers with low spontaneous rates and some with medium spontaneous rates, and was done because these fibers showed few, if any, short-latency spikes so that the time of the first peak was uncertain.
FIG. 6.
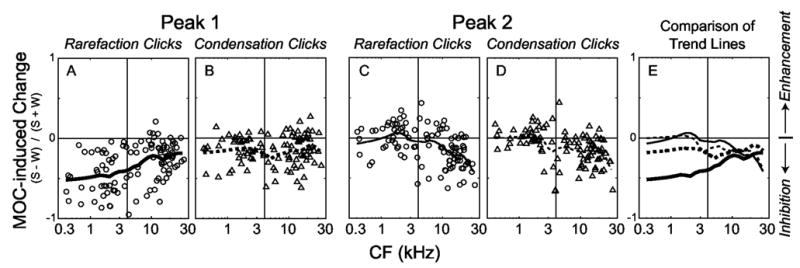
MOC-induced changes in the first and second click-response peaks. Panels A–D: Each symbol shows the change from an individual fiber; panel E: Comparison of MOC-induced changes on different peaks using the Loess-fit curves from A–D. “MOC-induced change” is the rpPST peak amplitude with MOC shocks, S, minus the rpPST peak amplitude without shocks, W, normalized by their sum, S+W. For each fiber, rarefaction and condensation responses were considered separately, the response was segmented into peaks, responses from levels 75–100 dB pSPL were averaged, the average number of spikes in each peak was computed, and the MOC-induced change was calculated from these averages. Points from 104 fibers from 10 cats. The lines are Loess-fit (Cleveland, 1993) curves to the data that show trends across frequency. The vertical lines mark 4 kHz, below which individual peaks were readily discernable.
E. Group delays
Group delays at frequencies in the low-frequency “tail” of high-CF tuning curves were obtained from measurements of tone-response phase versus frequency functions on AN fibers in two cats. These measurements used tone bursts that were swept in frequency at a fixed level (80–85 dB SPL) with tone-burst parameters and phase measuring techniques as in Stankovic and Guinan (2000). Briefly, the phase was determined from period histograms of the spikes relative to the zero crossings of the tone waveform, and data were only used if the standard error of the phase, ΦSE, was |ΦSE| < =30°. Group delays were calculated from the phase gradient across two to four points (two to three at the edges and four in the center of the frequency functions).
III. RESULTS A: MOC EFFECTS ON CLICK RESPONSES
The stimulation of MOC efferents produced effects on auditory-nerve responses to clicks that depended on the click level and time after the start of the response. Typical MOC effects for AN fibers with low, medium, and high CFs are shown in Fig. 3. This figure shows compound rpPST histograms of responses with and without MOC stimulation from selected levels of the click-level series. The pattern of MOC effects can be seen in Fig. 3 but requires detailed comparisons across peaks and sound levels, so we developed an easier way to visualize such data, as illustrated in Fig. 4. This figure shows rpPST histograms of all of the click responses that were obtained as a function of level without and with MOC stimulation (columns A and B), and the difference, the MOC-induced change in the response, in column C. Data from rarefaction clicks (top) and condensation clicks (bottom) are shown separately in Figs. 4(a)–4(c). The MOC-induced changes, with rarefaction and condensation changes added together, are shown in D, in rpPST format at left, and as a color-coded plot of the same data at right. The color plot provides a presentation of the MOC-induced changes that is both easy to see and much more compact. Color plots from 9 fibers with CFs from 0.44 to 19.6 kHz are shown in Fig. 5, which illustrates the patterns of MOC effects found across a wide range of CFs.
FIG. 4.
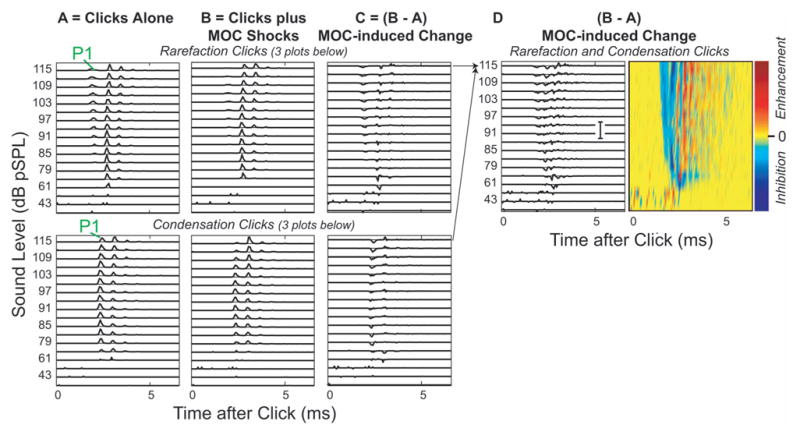
MOC effects on click responses from a single AN fiber showing the formation of color-coded response plots. A,B: rpPST histograms from 18 levels of rarefaction clicks (top) and condensation clicks (bottom), with (B) and without (A) MOC shocks. “P1” indicates the first peak. C: the MOC-induced change, which is B-A. D: MOC-induced changes from rarefaction and condensation responses added together at each level, in rpPST format (D—left, scale bar =10 spikes/ms also applies to A–C) and as a color-coded plot of the same data (D—right). Fiber #39-12, CF=1.52 kHz.
FIG. 5.
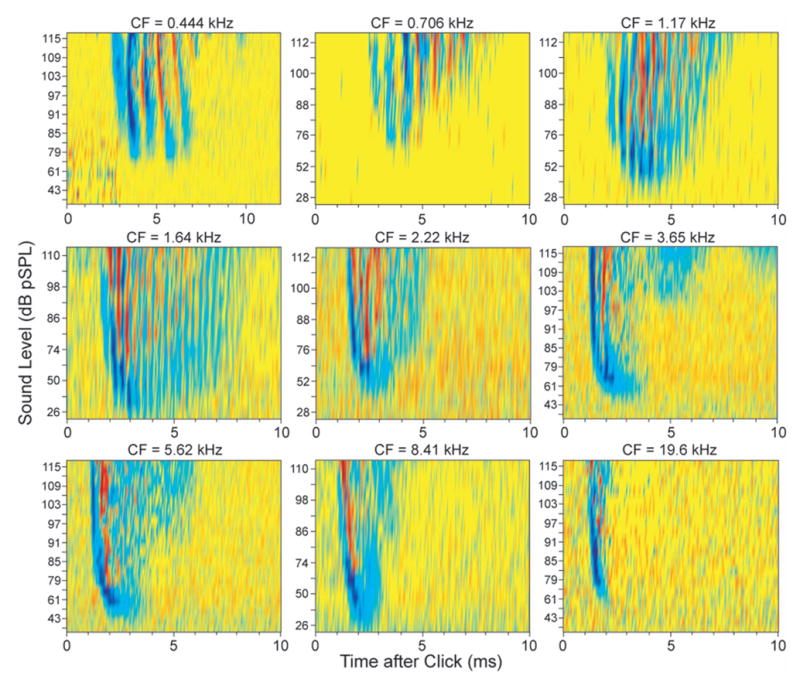
MOC effects on click responses from nine AN fibers spanning a wide range of CFs. Color-coded response plots as in Fig. 4 with purple-blue showing inhibition and red-orange showing enhancement.
Figures 3–5 show that in the responses of auditory-nerve fibers to clicks, activation of MOC efferents produced (1) the inhibition of all peaks at low sound levels, (2) the inhibition in the decaying part of the response at all sound levels, and (3) the inhibition of the first peak of the response at moderate to high sound levels. MOC inhibition of AN click responses at low levels and at the end of the ringing is what is expected from previous reports that MOC stimulation inhibits tone responses at low sound levels and broadens most tuning curves (Guinan and Gifford, 1988; reviewed by Guinan, 1996). Broadening of tuning curves corresponds, in click responses, to a reduction in the duration of ringing, which is seen in Figs. 3–5 as an inhibition in the decaying parts of the responses.
A. First-peak inhibition
The new finding is that the first peaks of AN click responses were strongly inhibited by MOC stimulation, at least for fibers with CFs(4 kHz. For fibers with CFs)4 kHz, individual peaks can be readily discerned in the rpPST histograms. Presumably, these peaks are due to the click-response half-cycles that are excitatory at IHC stereocilia. Inhibition of the first peak can be seen in Figs. 3, 4(a)–4(b) (the peak labeled P1) and in the color plots of Figs. 4(d) and 5 (the initial blue/purple at moderate to high sound levels). Note that by “first peak” we mean the peak with the shortest latency across all sound levels; the earliest peak that can be seen at low sound levels is not the “first peak.” This definition of the “first peak” was chosen so that the AN first peak would be as comparable as possible to the first peak of BM click responses (also defined as the first peak seen at any sound level). Presumably the “first peak” is not seen in AN responses at low sound levels because the corresponding mechanical motion is below threshold for evoking an AN response. Above 100 dB pSPL, some responses showed a reversal of the polarity that produced the first peak (Lin and Guinan, 2000). In these cases, there was inhibition of the first peak at levels below the reversal, but little MOC effect at levels above the reversal.1
We quantified the inhibition of the AN first peak by counting spikes in the click-response peaks with and without MOC stimulation for sound levels 75–100 dB pSPL. Quantification was straightforward for fibers with CFs<4 kHz, where individual peaks could be discerned easily. The results (Fig. 6, left half of each panel) show that for CFs<4 kHz, the rarefaction first peak is consistently inhibited and the condensation first peak is often inhibited, whereas the second peaks from both condensation and rarefaction, on average, show little change from MOC stimulation. The MOC-induced change for the rarefaction first peak was significantly stronger than the MOC-induced change for the rarefaction second peak (T test, P < 0.0001). In almost all AN fibers, the rarefaction first peak preceded the condensation first peak, which indicates that the rarefaction-click first peak corresponds to the first half-cycle of the mechanical response that drives IHC stereocilia and the condensation-click first peak corresponds to the second half-cycle of the mechanical drive. Thus, Fig. 6 shows that, for CFs<4 kHz, the strength of the inhibition is related to the sequence in which the peaks appear, i.e., inhibition is strongest on the first half-cycle, moderate on the second half-cycle, and negligible on the next cycle.
For fibers with CFs 4–6 kHz, individual peaks separated by 1/CF are no longer separate. However, for many fibers, clear, although overlapping, peaks could still be seen and similar counts were made on the first and second peaks. These showed trends similar to fibers with CFs<4 kHz.
For fibers with CFs<4–6 kHz, where individual peaks were no longer visible, the determination of whether there was MOC inhibition of the first peak could not be done in the way used for low-CF fibers. Instead, we compared responses with and without MOC stimulation in two sequential, equal-duration windows, starting at the onset of the click response. MOC-induced changes measured with a window duration of 0.2 ms are shown in Fig. 6 (the right half of each panel). Loess-fit (Cleveland, 1993) trend lines for the data are shown in Figs. 6(a)–6(d), and are superimposed in Fig. 6(e). Window durations from 0.1 to 1 ms were tried. When a short window of 0.1 ms was used, the rarefaction-peak-1 trend line was lower than the others at almost all CFs, but the scatter in the points increased greatly. As the window was made longer than 0.2 ms, the scatter changed little, but all four trend lines became similar at CFs greater than ~8 kHz.
The data in Fig. 6 show that for fibers with CFs below about 10 kHz, MOC stimulation inhibited rarefaction peak 1 more than rarefaction or condensation peak 2. For fibers 4–10 kHz, taken together, the MOC-induced change for the rarefaction first peak was significantly stronger than the MOC-induced change for the rarefaction second peak (t test, P < 0.01). For fibers with CFs above 10 kHz, the difference between rarefaction first and second peaks was small and not statistically significant. Condensation peak 1 was inhibited about the same, on average, at all CFs. Overall, the data in Fig. 6 show that at moderate-to-high sound levels and for CFs<4 kHz, there is strong first peak inhibition and little second peak inhibition, and that as CF increases, the difference between these peaks decreases, at least with the methods used to detect these peaks. Considering the dependence of the trend lines on the window duration for CFs >8–10 kHz, the data in this CF range are consistent with there being first peak inhibition, but are not at all conclusive.
IV. INTRODUCTION B: RATIONALE FOR STUDYING TAIL-FREQUENCY INHIBITION
As an alternate method for gaining insight into possible first-peak inhibition in high-CF fibers, we looked at AN responses to tones at frequencies far below CF (“tail” frequencies). There are several reasons for thinking that tail-frequency tone responses correspond to the earliest peak of click responses. First, in the classic traveling wave the low-frequency energy arrives first so the low-frequency tail response would be expected to have the shortest latency (Shera, 2001). Second, click- and tone-evoked AN responses from normal guinea pigs are fit well by a model with two drives that mimic tuning-curve tips and tails, and this model shows that the excitation drive that produces tuning-curve tails also produces short-latency peaks in click responses, whereas the drive that produces tuning-curve tips also produces long-latency peaks in click responses (Schoonhoven et al. 1994). Furthermore, the patterns of both click and tone responses in noise-damaged guinea pigs fit this model (Versnel et al., 1997). Thus, all of these data are consistent with the hypothesis that tail-frequency responses correspond to the first peak of click responses, at least for high-CF fibers.
In previous work, we found that MOC stimulation inhibited AN responses to tones at frequencies in the tuning-curve tails of fibers with high-CFs (CFs>10 kHz) (Stankovic and Guinan, 1999). The inhibition was weak (a few dB) at low frequencies (0.5–1.3 kHz) and strong (up to 10 dB) in a narrow frequency range of approximately 2–4 kHz [Fig. 7(b)]. It has long been known that MOC stimulation produces a small decrease in endocochlear potential (EP) (Fex, 1967; Gifford and Guinan, 1987). This decrease in EP reduces the voltage drive to IHC mechanoelectric transduction and thereby reduces responses at all frequencies by a few dB (Sewell, 1984) and can account for the MOC inhibition of high-CF-fiber responses to 0.5–1.3 kHz tones (Stankovic and Guinan, 1999). The “strong tail inhibition” in the 2–4 kHz range is too large to be accounted for by the decrease in EP and was attributed by Stankovic and Guinan (1999; 2000) to MOC-induced changes in cochlear micromechanics. We hypothesize that, in high-CF fibers, the tone “strong tail inhibition” corresponds to a click “first peak inhibition” similar to the first peak inhibition seen in low-CF fibers. If true, the frequency region with “strong tail inhibition” should have the shortest latency. As a test of this, we measured group delays at different tail frequencies.
FIG. 7.
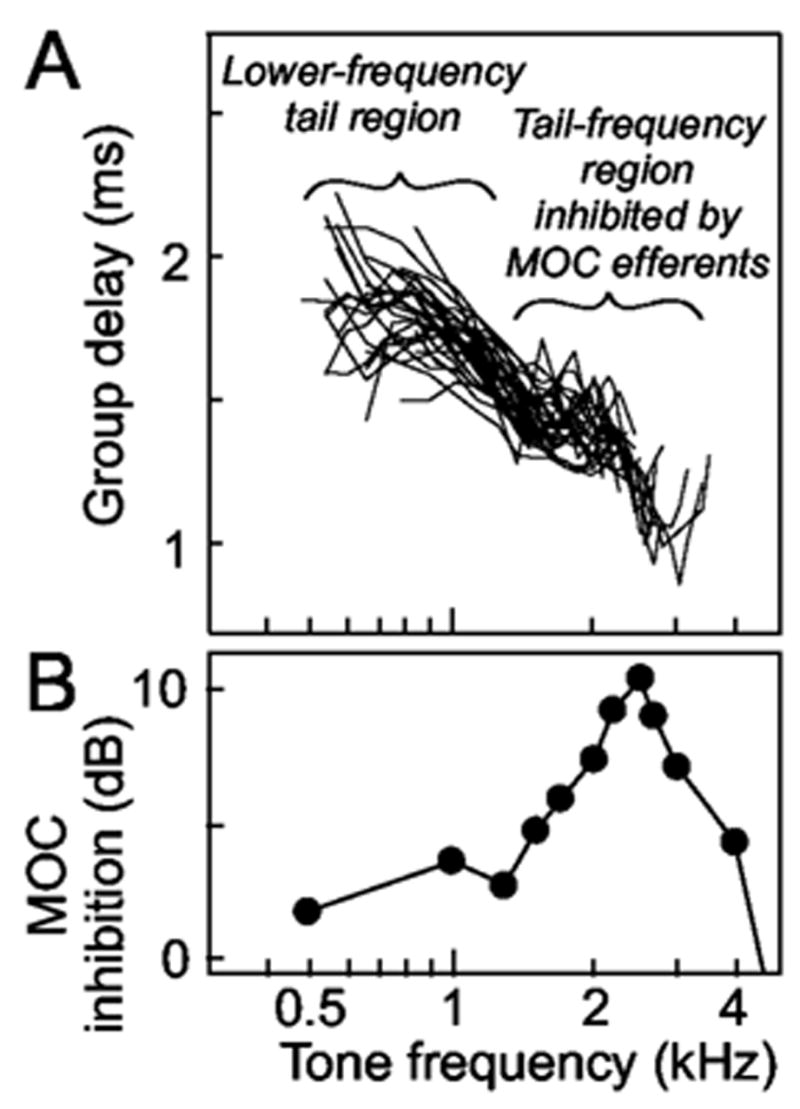
Group delays from the slopes of tone-response phase-versus-frequency plots from 32 AN fibers (CFs>5 kHz) from 2 cats (A), and MOC inhibition at tail frequencies (data from Fig. 8(b) of Stankovic and Guinan, 1999) (B). To obtain the “MOC inhibition” shown in B, normalized level shifts from single AN fibers were averaged at each measurement frequency. The level shift is the amount (in dB) that the sound level must be increased with MOC stimulation to produce the same firing rate that is produced without efferent stimulation. For each unit at each stimulus frequency, all level shifts at sound levels <=85 dB SPL were averaged, and to make measurements across animals comparable, they were normalized by the level shift of the AN compound action potential in that animal. For further details see Stankovic and Guinan (1999).
V. RESULTS B: LATENCIES AT FREQUENCIES WITH TAIL-FREQUENCY INHIBITION
Group delays determined from the slopes of tone-response phase-versus-frequency plots from AN fibers with CFs>5 kHz revealed a tail-frequency region with particularly short group delays [Fig. 7(a)]. The frequencies with short group delays correspond to the frequencies with “strong tail inhibition” found by Stankovic and Guinan (1999) [Fig. 7(b)]. Furthermore, group delays at “strong tail inhibition” frequencies were similar to the average first-peak click latency of 1.2 ms for AN fibers with CFs>5 kHz [from Fig 6(a) of Lin and Guinan, 2000].
VI. DISCUSSION
It is well known that MOC stimulation reduces the amplitude of AN compound action potential responses to clicks (Galambos, 1956; Wiederhold and Peake, 1966; Gifford and Guinan, 1987), but no previous study has reported MOC effects on click responses in single AN fibers. As already noted, the MOC inhibition of click responses at low levels and in the decaying part of the response was expected based on MOC effects on AN responses to tones. The surprising new finding is the MOC inhibition of the first peak of the single-fiber AN click response, a finding that is clear for fibers with CFs< ~ 6 kHz. This inhibition is strongest on the first half-cycle of the response, is less on the second half cycle, and is negligible on the next cycle (Fig. 6).
A factor to consider when using shocks to evoke MOC activity is whether LOC efferents are also activated and whether they might account for the effects seen. With the midline electrical stimulation of the olivocochlear bundle used in these experiments, the efferent effects are almost certainly due to MOC efferents that terminate on OHCs, rather than LOC efferents that terminate on the dendrites of AN fibers, because (1) we use high-rate shocks (>=200/s). LOC fibers are thin and unmyelinated (Guinan et al., 1983), and such unmyelinated fibers do not give sustained responses to shock rates greater than 20–50/s (Hallin and Torebjork, 1973; Fitzgerald and Woolf, 1981). (2) There are few LOC fibers that cross the midline (Guinan et al., 1984). (3) In experiments in which LOC efferents were activated, the responses attributable to LOC efferents had time courses on the scale of minutes, much slower than the durations of the effects studied here (Groff and Liberman, 2003). Finally, (4) it is difficult to imagine how any LOC effect on the dendrites of AN fibers could selectively inhibit the first peak of the response (which is present at moderate-to-high click levels in only a fraction of the responses) without also inhibiting the other peaks.
Another issue in interpreting AN responses is that neural adaptation limits the extent to which AN responses show the mechanical drive to IHCs, but not so much that adaptation invalidates the comparison of MOC inhibition of the first versus the second click-response peaks. In order to get valid rpPST histograms, which show the overall shape of the AN response while minimizing the effects of refractoriness and ms-time-scale adaptation, we used high-rate clicks, rates that can cause substantial long-term adaptation from high-level clicks. Thus, the overall firing rates in the AN click responses are partially determined by AN adaptation so that inhibition of the first peak and/or the decaying part of the response can have the effect of slightly increasing the spike probability in the rest of the response. We think that this effect is responsible for the apparent increase in the firing rate during MOC shocks in the middle of the click response (e.g., the red/orange areas in Fig. 5). However, this effect cannot account for the inhibition of the first peak being more than the inhibition of the second peak (Figs. 3–6) because in all the cases considered here, the second peak was within 3 ms (the recovered-probability exclusion time) of the first peak, so that the probability of the second peak was always determined from responses in which there was no first-peak response, and any long-term adaptation would have affected the two peaks equally.
In summary, we conclude that the observed pattern of MOC inhibition, in particular the strong inhibition of the first response peak relative to the second response peak, cannot be explained by experimental artifacts and represents the actual pattern of MOC inhibition of AN-fiber click responses. This pattern of MOC inhibition contrasts sharply with the MOC inhibition of BM motion in response to clicks that is zero or very small in the first half-cycle of the response and grows over many cycles (Guinan and Cooper, 2005).
A. First peak inhibition in high-CF fibers
Since current conceptions of mammalian cochlear mechanics are based largely on measurements of BM motion from the high-CF basal turn (Robles and Ruggero, 2001), it is important to determine the extent to which our results apply to high-CF fibers. Our attempts to use click data to determine whether the first peak of AN click responses is inhibited in high-CF fibers were not conclusive. The most telling data on this issue are our tone-response results that the frequencies with strong tail inhibition have particularly short group delays (Fig. 7). A similar pattern of group delays, i.e., that the shortest below-CF delay was not at the lowest frequency, has been reported previously for fibers with CFs >1 kHz (Geisler et al., 1974; Gummer and Johnstone, 1982; Allen, 1983; van der Heijden and Joris, 2003). The presence of a region of particularly short group delays just below the tip of the tuning curve is interesting because it is not expected from excitation by the classic traveling wave. In the classic traveling wave, for frequencies below CF, lower-frequency energy arrives before higher-frequency energy, and the lowest-frequency would be expected to excite fibers with the earliest latency (Shera, 2001).
Group delays must be interpreted with caution. The short group delays at ~1.5–4 kHz (Fig. 7) do not necessarily mean that a click response from energy in this frequency region would start before a click response from the lower-frequency region because a group delay includes both a wave-front latency and a filter buildup time. However, the “strong tail inhibition” component appears to be narrower in bandwidth than the rest of the tail (Fig. 7; also see Stankovic and Guinan, 1999), which would indicate that it has a longer buildup time. Thus, to account for its shorter overall group delay, the “strong tail inhibition” component would have to have a very short wave-front latency which suggests that in a click response, this component would correspond to the first peak. Finally, group delays at “strong tail inhibition” frequencies [Fig. 7(a)] were similar to the average first-peak click latency of 1.2 ms for AN fibers with CFs>5 kHz (Lin and Guinan, 2000), which also supports the correspondence of tone “strong tail inhibition” responses and click first-peak responses.
In summary, the data show that the tone-frequency region with short group delays [Fig. 7(a)] corresponds to the tone “strong tail inhibition” region of Stankovic and Guinan (1999) [Fig. 7(b)], which, in turn, provides strong support for the hypothesis that this tone inhibition corresponds, in click responses, to an inhibition of the first peak similar to that seen in low-CF fibers. Thus, the data in Fig. 7 are consistent with the hypothesis that for fibers with CFs>5 kHz, there is MOC inhibition of the first peak of the click response.
Since Fig. 7 provides evidence of MOC inhibition at short latencies in high-CF fibers, one might ask “Why is similar inhibition not seen more clearly in the click-response data of Fig. 6?” In high-CF fibers, the “strong tail inhibition” frequency range appears to be quite narrow (~1.5–4 kHz) so that possibly our clicks did not go to high enough levels to provide the energy necessary to excite this region. Another possibility is that an inhibited first-peak response is present in the data of Fig. 6 for CFs>10 kHz, but is so merged with other response peaks that it cannot be separated. Whatever the reasons for not seeing clear first peak inhibition for CFs>10 kHz, the tone data provide evidence that MOC efferents inhibit an aspect of the cochlear response that starts very early, with a latency comparable to the first click-response peak. Finally, judging from the latencies in Fig. 7, the response inhibited by MOC efferents has a shorter latency than the earliest response produced by low-frequency energy in the tail, which is presumably the earliest energy to arrive from the classic traveling wave.
B. Relationship of first peak inhibition to the classic traveling wave
The MOC inhibition of the first peak of AN responses to clicks does not fit with current conceptions of mammalian cochlear mechanics. The usual view (e.g., Patuzzi, 1996; Geisler, 1998) is that all motion of the organ of Corti is produced by the BM traveling wave that mimics BM motion in the basal turn and extends throughout the cochlea [although it is recognized that the classic traveling wave does not explain many phenomena in the apical turn, e.g. downward glides (Carney et al., 1999; Shera, 2001; Lin and Guinan, 2004)]. However, MOC inhibition of the AN click-response first peak cannot be explained by inhibition of the classic traveling wave first peak because, as shown by basal BM responses, the first peak of the classic traveling wave receives little or no cochlear amplification, and is little changed by MOC stimulation or by death (Robles et al., 1976; Ruggero et al., 1992; Recio, et al., 1998; Recio and Rhode, 2000; Robles and Ruggero, 2001; Guinan and Cooper, 2005). Thus, the strong MOC inhibition of the AN first peak must be due to inhibition of something other than the classic traveling wave.
We hypothesize that MOC inhibition of the AN first peak is due to an OHC-dependent motion of structures or fluid that bends IHC stereocilia and is separate from motion of the classic traveling wave. Electrical coupling from OHCs to IHCs via local extracellular fields is unlikely to account for the AN first peak inhibition because MOC efferents increase OHC extracellular current, the opposite direction to the effect seen, and any electrical effect in the first peak should be bigger on later peaks. To account for strong AN first-peak inhibition, there must normally be an OHC-dependent motion of structures and/or fluid that bends IHC stereocilia and produces the AN initial peak (ANIP), and this ANIP motion must be reduced by MOC activation. The ANIP motion could come from OHC somatic motility or the hypothesized OHC stereocilia motility as long as MOC efferents can inhibit the motion. Presumably, the ANIP motion is the first part of a vibrational response mode that continues past the first peak. However, the lack of MOC inhibition of the second cycle of the AN click-response (Fig. 6) suggests that the ANIP motion decays quickly so that by the second cycle it is less than the little-inhibited motion that evokes the second AN peak, presumably motion due to the classic traveling wave.
A variety of previous data provide evidence for cochlear motion that is separate from, or in addition to, the motion of the classic traveling wave. First, in the apex, two group delays in AN responses and cochlear motion have been reported many times (Pfeiffer and Molnar, 1970; Kiang and Moxon, 1972; Geisler et al., 1974; Kiang, 1984; Gummer et al., 1996; Cooper and Rhode, 1997; Khanna and Hao, 1999; Zinn et al., 2000; van der Heijden and Joris, 2003, 2005). Although an artifactual “fast wave” from opening the cochlea can contaminate apical mechanical measurements (Cooper and Rhode, 1996), Zinn and co-workers (2000) found that computationally removing the fast wave still left response dips and multiple group delays. Furthermore, in intact cochleae, AN responses show tuning curves with multilobed shapes (Liberman and Kiang 1978) and different group delays in each lobe (Kiang et al., 1977; Kiang, 1984). These data provide evidence from intact cochleae that two interacting drives with different group delays excite apical AN fibers. Second, the previously anomalous phenomenon of downward glides in the apex may be explained by the interaction of two motions: a first-arriving, above-CF wave and a later-arriving CF wave (Lin and Guinan, 2004). Finally, interference of two motions may explain many observations of apparent cancellations and phase reversals in AN and BM responses (reviewed by Ruggero et al., 2000). Although all of the phenomena just cited indicate the presence of two cochlear motions, it cannot be said whether the two motions in each example correspond to the ANIP motion and the motion produced by the classic traveling wave. However, all of these examples indicate that motion of the classic traveling wave does not provide the only excitation of AN fibers.
The ANIP motion appears to extend through most the cochlea. MOC inhibition of the ANIP motion is evident, for CFs up to ~8 kHz, as inhibition of the AN click-response first peak (Figs. 3–6); and for fibers with CFs>5 kHz, perhaps by the inhibition of short-latency, tail-frequency tone responses (Fig. 7). The dividing line between the supposed basal and apical patterns of BM motion is often thought to be ~1 kHz, the region where click-response glides change from upward to downward (Carney et al., 1999; Lin and Guinan, 2004) and tuning-curve “tails” change from below CF to above CF (Kiang et al., 1977; Kiang 1984). There are, however, almost no motion measurements in living cochleae with good thresholds between the basal turn and the apex on which to base a judgment of the dividing line. It seems plausible that the classic traveling wave and the ANIP motion are both present throughout the cochlea, perhaps with their relative strengths changing from base to apex. In this view, the classic traveling wave is dominant in the base and the ANIP motion gains in prominence going toward the apex.
C. What is the origin of the ANIP motion?
Since the ANIP motion appears to be separate from the classic traveling wave and is inhibited by MOC efferents that synapse on OHCs, it appears to be due to OHCs, or at least is strongly influenced by OHCs. It seems possible that the ANIP motion is due to an active, energy-consuming process and may be, in some sense, an amplified motion. Even though we have quantified the AN first-peak inhibition only at moderate to high sound levels, it may be present at low sound levels, especially in the apex. Which mechanisms in OHCs produce and/or modify the ANIP motion are unknown.
Nonetheless, it is useful to elaborate on some hypothetical mechanisms by which the ANIP motion might be produced and to consider the consequences of these hypotheses. To fit all of the data, the mechanism should excite AN fibers early enough to produce the first peak of the click response in the middle and apex of the cochlea and to produce the short-group-delay tone response in the base, and should be inhibited by MOC efferents without changing the first peak of the BM response in the base.
1. Possible ANIP source: OHC fluid pumping
One hypothesis for the origin of the ANIP motion is OHC “fluid pumping.” Sound-frequency electrical stimulation in an excised gerbil cochlea produces OHC contractions and expansions that squeeze and extend the cochlear partition producing sound-frequency fluid motion along the tunnel of Corti, i.e., OHCs act as fluid pumps (Karavitaki and Mountain, 2003). OHC squeezing and extension of the organ of Corti has also been reported in guinea pigs2 (Mammano and Ashmore, 1993) and may be the origin of the phase differences between BM motion in the arcuate and pectinate zones (Xue et al., 1993; Nilsen and Russell, 1999; Nuttall et al., 1999; Cooper 1999). With this hypothesis, pressure differences across the cochlear partition produce the classic traveling wave that is a transverse motion of the basilar membrane, and pressure differences inside to outside the organ of Corti produce the ANIP motion which, presumably, is an encircling wave in which the walls of the organ of Corti expand and contract. Presumably, the pressure difference inside to outside the organ of Corti produces a large ANIP motion at the reticular lamina, but not at the BM, because the first peak is primarily from below-CF energy (where stiffness dominates) and the effective stiffness of the reticular lamina is much less than that of the BM (Mammano and Ashmore, 1993; Scherer and Gummer, 2004). Thus, the ANIP motion should be much greater at the reticular lamina (and presumably, at IHC stereocilia and in AN firing) than at the BM. Finally, the ANIP motion might have a shorter delay than the classic traveling wave because tunnel fluid motion extends ahead of OHC contractions (Karavitaki and Mountain, 2003).
2. Possible ANIP source: Stereocilia motility
Another possible source of the ANIP motion is calcium-mediated stereocilia motility, a motility suggested to be present in the mammalian cochlea by recent experiments (Kennedy et al., 2003, 2005; Chan and Hudspeth, 2005). One appeal of this mechanism is that an OHC stereocilia twitch could be readily coupled from OHC stereocilia to IHC stereocilia by the tectorial membrane without requiring intervening BM motion. In this hypothesis, the ANIP motion is the motion of the tectorial membrane and/or the fluid in the space between the reticular lamina and the tectorial membrane that bends IHC stereocilia. A drawback of this hypothesis is the lack of a clear mechanism by which MOC synapses would affect this motion. Although stereocilia motility is influenced by membrane voltage, MOC synapses hyperpolarize OHCs, which would be expected to increase the OHC stereocilia motility, not inhibit it.
3. Possible ANIP source: Direct acoustic coupling to OHCs
Yet another mechanism that might produce the ANIP motion is direct acoustic coupling from the forward cochlear pressure wave. Ren (2004) and Ruggero (2004) have provided data that suggests that mammalian OAEs may be generated by organ-of-Corti motion that is coupled back to stapes motion by fast fluid-pressure waves. Any cochlear process that couples organ-of-Corti motion to fluid pressure waves is likely to be reciprocal, which would imply that normal (forward) cochlear pressure waves may directly produce motion of the organ of Corti. To account for the ANIP motion, such motion, or the amplification of this motion, must be affected by OHCs. This mechanism has the advantage that it readily explains how the ANIP motion can produce a response peak that starts before the lowest-frequency part of the traveling wave. However, it is difficult to account for the long delays of the ANIP motion in the apex of the cochlea if the classic traveling wave is bypassed completely.
As can be noted from the above, a question related to the origin of the ANIP motion is how the ANIP motion travels along the cochlea. Is the ANIP motion a second wave along the cochlea, a separate vibrational mode excited by the classic traveling wave, or a vibrational mode excited directly by the fast cochlear pressure wave (e.g., due to OHC pressure sensitivity)? An important constraint is that the latency of the click-response first peak changes over ~2.5 ms from the base to the apex (Lin and Guinan, 2000), but this does not separate the hypotheses. Since the ANIP response is clearly first in the apex (Figs. 3–6) and appears to arise before the lowest-frequency tone response (which we earlier argued is due to the classic traveling wave) in the base (Fig. 7), it seems unlikely that the ANIP response is a separate vibrational mode excited by the classic traveling wave. However, definitive data are needed to settle this issue.
In the context of considering mechanisms that might account for the AN first peak inhibition, it might be thought that the OHC hyperpolarization produced by MOC synapses would cause a lengthening of OHCs, and thereby change the coupling of BM motion to IHC stereocilia. Whether this is true, or not, it cannot explain how MOC excitation inhibits the first peak of the click response without producing a similar change in the second and later peaks.
As the above hypotheses point out, there are many possible ways by which the ANIP motion may be produced and determining which one, or if more than one, is correct requires additional data. Whatever mechanisms are involved, the presence of the OHC-generated ANIP motion early in the response puts it at a time that could influence, shape, or be a first step in cochlear amplification.
D. Effects of the ANIP motion on signal coding and hearing function
Excitation of AN fibers by the ANIP motion seems likely to have a different frequency filter than the classic traveling wave, but does not appear to sharpen the response and produce an old-style “second filter” (Evans and Wilson, 1975). Our click results suggest that the ANIP motion has an important influence on neural responses at moderate-to-high sound levels (Figs. 3–5). For tones, a component of the AN response due to ANIP motion was not evident at the threshold at the base of the cochlea (Narayan et al., 1998), but an ANIP response may be evident at higher sound levels in the base, and perhaps at low sound levels in the apex.
Since the first peak is part of the neural response to clicks at moderate to high sound levels (Figs. 3–5), neural inhibition of the first peak can be expected to have behavioral consequences. Medial efferents improve the detection of transient sounds in background noise (May and McQuone, 1995; Micheyl and Collet, 1996; Zeng et al., 2000) and MOC inhibition of the ANIP response may be partly responsible for this. MOC fibers are also functionally significant in providing protection from sound trauma (Rajan, 1988; Maison et al., 2002). Again, MOC inhibition of the ANIP response may be involved. In short, any MOC effect at moderate to high sound levels may have a component, or be entirely, due to MOC inhibition of the ANIP response.
VII. CONCLUSIONS
In click responses of single AN fibers with CFs< ~ 8 kHz, stimulation of MOC efferents unexpectedly inhibits the first peak of the response, in addition to inhibiting at low sound levels and in the decaying part of the response, as expected from tone data.
For AN fibers with CFs>5 kHz, tones at tail frequencies produce responses with the shortest group delays at frequencies with “strong tail inhibition,” which shows that there is short-latency MOC inhibition in the cochlear base.
The MOC inhibition of the first peak of the AN click response cannot be attributed to a corresponding inhibition of the first peak of the click response in the classic traveling wave. This implies that there is a motion, the ANIP motion, which bends IHC stereocilia, is produced (or strongly influenced) by OHCs, and is separate from (and perhaps comes before) the first peak of the classic traveling wave.
Although the origin of the ANIP motion is unknown, its presence highlights the need for a new conceptual paradigm for cochlear mechanics in which the classic BM traveling wave is not the only motion that excites AN fibers.
Acknowledgments
We thank Dr. M. C. Brown, Dr. M. C. Liberman, and Dr. C. A. Shera for comments on a previous version of the manuscript. This study was supported by NIDCD Grant No. RO1-DC-00235.
Footnotes
Lin and Guinan (2000) interpreted the first-peak reversal to the entry at high click levels of an excitation drive (presumably a motion that bends IHC stereocilia) that is opposite in direction, and more than cancels the low-level drive. If true, the lack of inhibition above a first-peak reversal implies that this high-level drive is not inhibited by MOC efferents.
Using electrical stimulation across an isolated guinea-pig organ-of-Corti, Nowotny et al. 2004 found a squeezing and extension of the subtectorial space. This implies a radial fluid motion in the subtectorial space that could drive IHC stereocilia. The motion seen by Nowotny et al. 2004 was presumably produced by OHC motility, and might be inhibited by MOC efferents. How OHCs produce the squeezing and extension of the subtec-torial space is not clear, but it is possible that in the intact cochlea, this motion might be produced without a corresponding motion of the basilar membrane, at least in the basal turn. If so, such a motion is a candidate for the ANIP motion.
Contributor Information
John J. Guinan, Jr, Eaton-Peabody Laboratory of Auditory Physiology, Department of Otolaryngology, Massachusetts Eye and Ear Infirmary, 243 Charles St., Boston, Massachusetts 02114-3002, Department of Otology and Laryngology, Harvard Medical School, Boston, Massachusetts 02115, and Speech and Hearing Biosciences and Technology Program, Harvard–MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139.
Tai Lin, Eaton-Peabody Laboratory of Auditory Physiology, Department of Otolaryngology, Massachusetts Eye and Ear Infirmary, 243 Charles St., Boston, Massachusetts 02114-3002.
Holden Cheng, Eaton-Peabody Laboratory of Auditory Physiology, Department of Otolaryngology, Massachusetts Eye and Ear Infirmary, 243 Charles St., Boston, Massachusetts 02114-3002, and Speech and Hearing Biosciences and Technology Program, Harvard–MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139.
References
- Allen JB. Magnitude and phase-frequency response to single tones in the auditory nerve. J Acoust Soc Am. 1983;73:2071–2092. doi: 10.1121/1.389575. [DOI] [PubMed] [Google Scholar]
- Békésy Gv. Experiments in Hearing. McGraw Hill; New York: 1960. [Google Scholar]
- Brownell WE, Bader CR, Bertrand D, de Ribaupierre Y. Evoked mechanical response of isolated cochlear outer hair cells. Science. 1985;277:194–196. doi: 10.1126/science.3966153. [DOI] [PubMed] [Google Scholar]
- Carney LH, McDuffy MJ, Shekhter I. Frequency glides in the impulse responses of auditory-nerve fibers. J Acoust Soc Am. 1999;105:2384–2391. doi: 10.1121/1.426843. [DOI] [PubMed] [Google Scholar]
- Chan DK, Hudspeth AJ. Ca(2+) current-driven nonlinear amplification by the mammalian cochlea in vitro. Nat Neurosci. 2005;8:149–155. doi: 10.1038/nn1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleveland WS. Visualizing Data. AT&T Bell Laboratories; Murray Hill, NJ: 1993. [Google Scholar]
- Cooper NP. Radial variation in the vibrations of the cochlear partition. In: Wada H, et al., editors. Recent Developments in Auditory Mechanics. World Scientific; Singapore: 1999. [Google Scholar]
- Cooper NP, Guinan JJ., Jr Separate mechanical processes underlie fast and slow effects of medial olivocochlear efferent activity. J Appl Physiol. 2003;548:307–312. doi: 10.1113/jphysiol.2003.039081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Fast travelling waves, slow travelling waves and their interactions in experimental studies of apical co-chlear mechanics. Aud Neurosci. 1996;2:289–299. [Google Scholar]
- Cooper NP, Rhode WS. Apical cochlear mechanics: A review of recent observations. In: Palmer AR, et al., editors. Phychophysical and Physiological Advances in Hearing, Proceedings of the 11th International Symposium on Hearing. Whurr; London: 1997. pp. 11–17. [Google Scholar]
- de Boer E, Nuttall AL. The mechanical waveform of the basilar membrane. I Frequency modulations (”glides”) in impulse responses and cross-corelation functions. J Acoust Soc Am. 1997;101:3583–3592. doi: 10.1121/1.418319. [DOI] [PubMed] [Google Scholar]
- Dolan DF, Guo MH, Nuttall AL. Frequency-dependent enhancement of basilar membrane velocity during olivocochlear bundle stimulation. J Acoust Soc Am. 1997;102:3587–3596. doi: 10.1121/1.421008. [DOI] [PubMed] [Google Scholar]
- Evans EF, Wilson JP. Cochlear tuning properties: concurrent basilar membrane and single nerve fiber measurements. Science. 1975;190:1218–1221. doi: 10.1126/science.1198110. [DOI] [PubMed] [Google Scholar]
- Fex J. Efferent inhibition in the cochlea related to hair-cell dc activity: Study of postsynaptic activity of the crossed olivo-cochlear fibers in the cat. J Acoust Soc Am. 1967;41:666–675. doi: 10.1121/1.1910395. [DOI] [PubMed] [Google Scholar]
- Fitzgerald M, Woolf CJ. Effects of cutaneous nerve and intraspinal conditioning on C-fibre efferent terminal excitability in decerebrate spinal rats. J Physiol (London) 1981;318:25–39. doi: 10.1113/jphysiol.1981.sp013848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galambos R. Suppression of auditory activity by stimulation of efferent fibers to the cochlea. J Neurophysiol. 1956;19:424–437. doi: 10.1152/jn.1956.19.5.424. [DOI] [PubMed] [Google Scholar]
- Geisler CD. From Sound to Synapse. Physiology of the Mammalian Ear. Oxford University Press; New York: 1998. [Google Scholar]
- Geisler CD, Rhode WS, Kennedy DT. Responses to tonal stimuli of single auditory nerve fibers and their relationship to basilar membrane motion in the squirrel monkey. J Neurophysiol. 1974;37:1156–1172. doi: 10.1152/jn.1974.37.6.1156. [DOI] [PubMed] [Google Scholar]
- Gifford ML, Guinan JJ., Jr Effects of electrical stimulation of medial olivocochlear neurons on ipsilateral and contralateral cochlear responses. Hear Res. 1987;29:179–194. doi: 10.1016/0378-5955(87)90166-3. [DOI] [PubMed] [Google Scholar]
- Gray PR. Conditional probability analyses of the spike activity of single neurons. Biophys J. 1967;7:759–777. doi: 10.1016/S0006-3495(67)86621-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groff JA, Liberman MC. Modulation of cochlear afferent response by the lateral olivocochlear system: activation via electrical stimulation of the inferior colliculus. J Neurophysiol. 2003;90:3178–3200. doi: 10.1152/jn.00537.2003. [DOI] [PubMed] [Google Scholar]
- Guinan JJ., Jr . The physiology of olivocochlear efferents. In: Dallos PJ, editor. The Cochlea. Springer-Verlag; New York: 1996. pp. 435–502. [Google Scholar]
- Guinan JJ, Jr, Cooper NP. Medial olivocochlear efferent inhibition of basilar-membrane click responsesAssoc. Res Otolaryngol Abstr. 2005;28:340. [Google Scholar]
- Guinan JJ, Jr, Gifford ML. Effects of electrical stimulation of efferent olivocochlear neurons on cat auditory-nerve fibers.III Tuning curves and thresholds at CF. Hear Res. 1988;37:29–46. doi: 10.1016/0378-5955(88)90075-5. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Stankovic KM. Medial efferent inhibition produces the largest equivalent attenuations at moderate to high sound levels in cat auditory-nerve fibers. J Acoust Soc Am. 1996;100:1680–1690. doi: 10.1121/1.416066. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Warr WB, Norris BE. Differential olivo-cochlear projections from lateral vs. medial zones of the superior olivary complex. J Comp Neurol. 1983;221:358–370. doi: 10.1002/cne.902210310. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Warr WB, Norris BE. Topographic organization of the olivocochlear projections from the lateral and medial zones of the superior olivary complex. J Comp Neurol. 1984;226:21–27. doi: 10.1002/cne.902260103. [DOI] [PubMed] [Google Scholar]
- Gummer AW, Johnstone BM. Group delay measurements from spiral ganglion cells in the guinea pig cochlea. Arch Oto-Rhino-Laryngol. 1982;234:189–190. doi: 10.1007/BF00453629. [DOI] [PubMed] [Google Scholar]
- Gummer AW, Hemmert W, Zenner HP. Resonant tectorial membrane motion in the inner ear: its crucial role in frequency tuning. Proc Natl Acad Sci USA. 1996;93:8727–8732. doi: 10.1073/pnas.93.16.8727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallin RG, Torebjork HE. Electrically induced A and C fibre responses in intact human skin nerves. Exp Brain Res. 1973;16:309–320. doi: 10.1007/BF00233333. [DOI] [PubMed] [Google Scholar]
- Karavitaki KD, Mountain DC. Is the cochlear amplifier a fluid pump? In: Gummer AW, et al., editors. The Biophysics of the Cochlea: Molecules to Models. World Scientific; Singapore: 2003. pp. 310–311. [Google Scholar]
- Kennedy HJ, Evans MG, Crawford AC, Fettiplace R. Fast adaptation of mechanoelectrical transducer channels in mammalian cochlear hair cells. Nat Neurosci. 2003;6:832–836. doi: 10.1038/nn1089. [DOI] [PubMed] [Google Scholar]
- Kennedy HJ, Crawford AC, Fettiplace R. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 2005;433:880–883. doi: 10.1038/nature03367. [DOI] [PubMed] [Google Scholar]
- Khanna SM, Hao LF. Reticular lamina vibrations in the apical turn of a living guinea pig cochlea. Hear Res. 1999;132:15–33. doi: 10.1016/s0378-5955(99)00027-1. [DOI] [PubMed] [Google Scholar]
- Kiang NYS. Handbook of Physiology, Section 1: The Nervous System. Vol. 3. Am Physiological Soc; Bethesda, MD: 1984. Peripheral neural processing of auditory information; pp. 639–674. Sensory Processes. [Google Scholar]
- Kiang NYS, Liberman MC, Baer T. Tuning curves of auditory-nerve fibers. J Acoust Soc Am. 1977;61:S27 (A). [Google Scholar]
- Kiang NYS, Moxon EC. Physiological considerations in artificial stimulation of the inner ear. Ann Otol Rhinol Laryngol. 1972;81:714–731. doi: 10.1177/000348947208100513. [DOI] [PubMed] [Google Scholar]
- Liberman MC, Gao J, He DZ, Wu X, Jai S, Zuo J. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 2002;419:300–304. doi: 10.1038/nature01059. [DOI] [PubMed] [Google Scholar]
- Liberman MC, Kiang NYS. Acoustic trauma in cats. Cochlear pathology and auditory-nerve activity. Acta Oto-Laryngol. 1978;Supplement 358(Suppl):1–63. [PubMed] [Google Scholar]
- Lin T, Guinan JJ., Jr Auditory-nerve-fiber responses to high-level clicks: interference patterns indicate that excitation is due to the combination of multiple drives. J Acoust Soc Am. 2000;107:2615–2630. doi: 10.1121/1.428648. [DOI] [PubMed] [Google Scholar]
- Lin T, Guinan JJ., Jr Time-frequency analysis of auditory-nerve-fiber and basilar-membrane click responses reveal glide irregularities and non-characteristic-frequency skirts. J Acoust Soc Am. 2004;116:405–416. doi: 10.1121/1.1753294. [DOI] [PubMed] [Google Scholar]
- Maison SF, Luebke AE, Liberman MC, Zuo J. Efferent protection from acoustic injury is mediated via alpha9 nicotinic acetylcholine receptors on outer hair cells. J Neurosci. 2002;22:10838–10846. doi: 10.1523/JNEUROSCI.22-24-10838.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mammano F, Ashmore JF. Reverse transduction measured in the isolated cochlea by laser Michelson interferometry. Nature. 1993;365:838–841. doi: 10.1038/365838a0. [DOI] [PubMed] [Google Scholar]
- May BJ, McQuone SJ. Effects of bilateral olivocochlear lesions on pure-tone discrimination in cats. Aud Neurosci. 1995;1:385–400. [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Collet L. Involvement of the olivocochlear bundle in the detection of tones in noise. J Acoust Soc Am. 1996;99:1064–1610. doi: 10.1121/1.414734. [DOI] [PubMed] [Google Scholar]
- Murugasu E, Russell IJ. The effect of efferent stimulation on basilar membrane displacement in the basal turn of the guinea pig cochlea. J Neurosci. 1996;16:325–332. doi: 10.1523/JNEUROSCI.16-01-00325.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayan SS, Temchin AN, Recio A, Ruggero MA. Frequency tuning of basilar membrane and auditory nerve fibers in the same cochleae. Science. 1998;282:1882–1884. doi: 10.1126/science.282.5395.1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsen KE, Russell IJ. Timing of cochlear feedback: spatial and temporal representation of a tone across the basilar membrane [published erratum appears in Nat Neurosci 1999 Sep;2(9):848] Nat Neurosci. 1999;2:642–648. doi: 10.1038/12230. 2, 848 (1999) [DOI] [PubMed] [Google Scholar]
- Nowotny M, Zenner HP, Gummer AW. Impact of outer hair cell electromotility on organ of Corti vibration - Results from an In-Situ preparation. Assoc Res Otolaryngol Abstr. 2004;27:Abs 1002. [Google Scholar]
- Nuttall AL, Guo M, Ren T. The radial pattern of basilar membrane motion evoked by electric stimulation of the cochlea. Hear Res. 1999;131:39–46. doi: 10.1016/s0378-5955(99)00009-x. [DOI] [PubMed] [Google Scholar]
- Patuzzi R. Cochlear micomechanics and macromechanics. In: Dallos PJ, et al., editors. The Cochlea. Springer-Verlag; New York: 1996. pp. 186–257. [Google Scholar]
- Pfeiffer RR, Kim DO. Response patterns of single cochlear nerve fibers to click stimuli: descriptions for cat. J Acoust Soc Am. 1972;52:1669–1677. doi: 10.1121/1.1913301. [DOI] [PubMed] [Google Scholar]
- Pfeiffer RR, Molnar CE. Cochlear nerve fiber discharge patterns: Relationship to the cochlear microphonic. Science. 1970;167:1614–1616. doi: 10.1126/science.167.3925.1614. [DOI] [PubMed] [Google Scholar]
- Rajan R. Effect of electrical stimulation of the crossed olivoco-chlear bundle on temporary threshold shifts in auditory sensitivity. I Dependence on electrical stimulation parameters. J Neurophysiol. 1988;60:549–568. doi: 10.1152/jn.1988.60.2.549. [DOI] [PubMed] [Google Scholar]
- Recio A, Rhode WS. Basilar membrane responses to broadband stimuli. J Acoust Soc Am. 2000;108:2281–2298. doi: 10.1121/1.1318898. [DOI] [PubMed] [Google Scholar]
- Recio A, Rich NC, Narayan SS, Ruggero MA. Basilar-membrane responses to clicks at the base of the chinchilla cochlea. J Acoust Soc Am. 1998;103:1972–1989. doi: 10.1121/1.421377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren T. Reverse propagation of sound in the gerbil cochlea. Nat Neurosci. 2004;7:333–334. doi: 10.1038/nn1216. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robles L, Rhode WS, Geisler CD. Transient response of the basilar membrane measured in squirrel monkeys using the Mössbauer effect. J Acoust Soc Am. 1976;59:926–939. doi: 10.1121/1.380953. [DOI] [PubMed] [Google Scholar]
- Ruggero M. Comparison of group delays of 2f1-f2 distortion product otoacoustic emissions and cochlear travel times. ARLO. 2004;5:143–147. doi: 10.1121/1.1771711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Recio A. Basilar membrane responses to clicks. In: Cazals Y, et al., editors. Cazals, Auditory Physiology and Perception. Pergamon; Oxford: 1992. pp. 85–91. [Google Scholar]
- Ruggero MA, Narayan SS, Temchin AN, Recio A. Mechanical bases of frequency tuning and neural excitation at the base of the cochlea: comparison of basilar-membrane vibrations and auditory-nerve-fiber responses in chinchilla. Proc Natl Acad Sci USA. 2000;97:11 744–11 750. doi: 10.1073/pnas.97.22.11744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell IJ, Murugasu E. Medial efferent inhibition suppresses basilar membrane responses to near characteristic frequency tones of moderate to high intensities. J Acoust Soc Am. 1997;102:1734–1738. doi: 10.1121/1.420083. [DOI] [PubMed] [Google Scholar]
- Scherer MP, Gummer AW. Impedance analysis of the organ of Corti with magnetically actuated probes. Biophys J. 2004;87:1378–1391. doi: 10.1529/biophysj.103.037184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoonhoven R, Keijzer J, Versnel H, Prijs VF. A dual filter model describing single-fiber responses to clicks in the normal and noise-damaged cochlea. J Acoust Soc Am. 1994;95:2104–2121. doi: 10.1121/1.408672. [DOI] [PubMed] [Google Scholar]
- Sewell WF. The effects of furosemide on the endocochlear potential and auditory-nerve fiber tuning curves in cats. Hear Res. 1984;14:305–314. doi: 10.1016/0378-5955(84)90057-1. [DOI] [PubMed] [Google Scholar]
- Shera CA. Frequency glides in click responses of the basilar membrane and auditory nerve: Their scaling behavior and origin in traveling-wave dispersion. J Acoust Soc Am. 2001;109:2023–2034. doi: 10.1121/1.1366372. [DOI] [PubMed] [Google Scholar]
- Stankovic KM, Guinan JJ., Jr Medial efferent effects on auditory-nerve responses to tail-frequency tones I: Rate reduction. J Acoust Soc Am. 1999;106:857–869. doi: 10.1121/1.427102. [DOI] [PubMed] [Google Scholar]
- Stankovic KM, Guinan JJ., Jr Medial efferent effects on auditory-nerve responses to tail-frequency tones II: Alteration of Phase. J Acoust Soc Am. 2000;108:664–678. doi: 10.1121/1.429599. [DOI] [PubMed] [Google Scholar]
- van der Heijden M, Joris PX. Cochlear phase and amplitude retrieved from the auditory nerve at arbitrary frequencies. J Neurosci. 2003;23:9194–9198. doi: 10.1523/JNEUROSCI.23-27-09194.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Heijden M, Joris PX. Group delays in the auditory nerve of the cat. Assoc Res Otolaryngol Abstr. 2005;28:349. [Google Scholar]
- Versnel H, Prijs VF, Schoonhoven R. Auditory-nerve fiber responses to clicks in guinea pigs with a damaged cochlea. J Acoust Soc Am. 1997;101:993–1009. doi: 10.1121/1.418057. [DOI] [PubMed] [Google Scholar]
- Wiederhold ML, Peake WT. Efferent inhibition of auditory nerve responses: dependence on acoustic stimulus parameters. J Acoust Soc Am. 1966;40:1427–1430. doi: 10.1121/1.1910243. [DOI] [PubMed] [Google Scholar]
- Xue S, Mountain DC, Hubbard AE. Direct measurement of electrically-evoked basilar membrane motion. In: Duifhuis H, et al., editors. Biophysics of Hair Cell Sensory Systems. World Scientific; Singapore: 1993. pp. 361–368. [Google Scholar]
- Zeng F, Martino KM, Linthicum FH, Soli SD. Auditory perception in vestibular neurectomy subjects. Hear Res. 2000;142:102–112. doi: 10.1016/s0378-5955(00)00011-3. [DOI] [PubMed] [Google Scholar]
- Zheng J, Madison LD, Oliver D, Fakler B, Dallos P. Prestin, the motor protein of outer hair cells. Audiol Neuro-Otol. 2002;7:9–12. doi: 10.1159/000046855. [DOI] [PubMed] [Google Scholar]
- Zinn C, Maier H, Zenner H, Gummer AW. Evidence for active, nonlinear, negative feedback in the vibration response of the apical region of the in-vivo guinea-pig cochlea. Hear Res. 2000;142:159–183. doi: 10.1016/s0378-5955(00)00012-5. [DOI] [PubMed] [Google Scholar]


