Abstract
An increasing number of structural studies of large macromolecular complexes, both in X-ray crystallography and electron cryomicroscopy, have resulted in intermediate resolution (5–10 Å) structures. Despite being limited in resolution, significant structural and functional information may be extractable from these maps. To aid in the analysis and annotation of these complexes, we have developed SSEhunter, a tool for the quantitative detection of α-helices and β-sheets. Based on density skeletonization, local geometry calculations and a template-based search, SSEhunter has been tested and validated on a variety of simulated and authentic subnanometer resolution density maps. The result is a robust, user-friendly approach that allows users to quickly visualize, assess and annotate intermediate resolution density maps. Beyond secondary structure element identification, the skeletonization algorithm in SSEhunter provides secondary structure topology, potentially useful in leading to structural models of individual molecular components directly from the density.
Introduction
Individual gene products rarely function independently; large multi-component protein assemblies are typically responsible for complex cellular functions. Thus, a major challenge in the post genomics era is the quantitative description of the organization and function of these complex biological assemblies (Sali, 1998; Sali, 2003). Structural studies are crucial in understanding the mechanisms of action in these large macromolecular complexes, which can either be made up of one molecule repeated several times (e.g. GroEL (Braig et al., 1994)) or up to tens of non-equivalent molecules (e.g. ribosome (Ban et al., 2000)). Traditionally, such understanding has been acquired by determining the 3D structures of individual proteins or small complexes using X-ray crystallography and NMR spectroscopy. In recent years, electron cryomicroscopy (cryoEM) has become increasingly used in determining intermediate resolution structures of macromolecular complexes, such as ribosomes, chaperonins, large viruses and ion channels (reviewed in (Chiu et al., 2006; Chiu et al., 2005)). Currently, the Protein Data Bank (PDB) archives over 1100 structures of macromolecules greater than 250kDa, while there are nearly 250 macromolecular structures in the EMDB, EBI’s electron microscopy structure database (http://www.ebi.ac.uk/msd-srv/emsearch). Interestingly, many of the structures in both the EMDB and PDB have reported resolutions lower than 4Å.
While the size, complexity and dynamic nature of macromolecular complexes may limit structure determination by X-ray crystallography or cryoEM to intermediate resolutions (5–10Å), a wealth of structural information may still be extracted from these structures. It is often possible to detect long α-helices and large β-sheets in this resolution range (Baker et al., 2003; Baker et al., 2005; Kong et al., 2004; Zhou et al., 2001). At this resolution, α-helices distinguish themselves as relatively straight rods of densities approximately 5–6Å in diameter with variable lengths, while β-sheets appear as continuous plates with varying shapes and sizes. These observations have led to the use of graphics tools for manual identification of secondary structures (Zhou et al., 2000), as well as automated methods for α-helix (Jiang et al., 2001) and β-sheet (Kong and Ma, 2003; Kong et al., 2004) detection in individual subunits within a cryoEM density map.
As α-helices have a fairly regular shape, simple pattern recognition methods are adequate for detecting α-helices. HELIXHUNTER, a semi-automated pattern recognition tool (Jiang et al., 2001), is based on an exhaustive cross-correlation with a prototypical helix with a density map. Several examples of successful application of this procedure have resulted in structural models for individual proteins, including the capsid proteins in the 6.8Å resolution cryoEM structure of rice dwarf virus (RDV) (Zhou et al., 2001) . The identification of nine α-helices in the lower domain of the outer capsid shell protein, P8, was confirmed by subsequent crystal structure determination (Nakagawa et al., 2003; Zhou et al., 2001).
Contrary to α-helices, which are relatively rigid, β-sheets adopt a variety of planar shapes and varying considerably in size. Sheetminer, which uses an ad hoc morphological analysis to identify “kernel voxels” that have a single dimension and are nearly flat (Kong and Ma, 2003). This is followed by a process of kernel condensation and disk sampling. β-sheets are then identified, filtered, clustered and extended to provide a final β-sheet description through Sheetracer (Kong et al., 2004).
Despite being able to visualize secondary structure elements, the aforementioned methods share a common drawback in that they lack robust statistical, quantitative and simultaneous estimation for α-helix and β-sheet assignment. In contrast, sequence-based structure prediction algorithms generally evaluate α-helix and β-sheet propensity simultaneously, providing both a prediction of structure and a measure of confidence for each amino acid. No such measures are available in either HELIXHUNTER or Sheetminer/Sheetracer. Furthermore, neither method can be used to identify the other type of secondary structure elements, thus making simultaneous evaluation of secondary structure impossible.
In this work, we discuss a quantitative framework for simultaneous identification of both α-helices and β-sheets in intermediate resolution (10–5 Å) density maps. In addition to the detection of secondary structure elements, both confidence measures and topology are addressed, resulting in a simple yet comprehensive tool for analyzing, visualizing and annotating density maps. The resulting tools for feature detection have been incorporated into a software package called AIRS (Analysis of Intermediate Resolution Structures), which is a part of the EMAN image processing suite (Ludtke et al., 1999).
Approach
Due to the unique characteristics of α-helices and β-sheets in intermediate resolution density maps, a series of integrated feature detection steps are needed for complete and comprehensive secondary structure element identification. The core procedure can be divided into five steps (described below): density reduction, skeletonization, cross-correlation, local shape analysis, and visualization/annotation (Figure 1). These techniques have been implemented in SSEhunter (Secondary Structure Element hunter) and its companion program, SSEbuilder.
Figure 1.
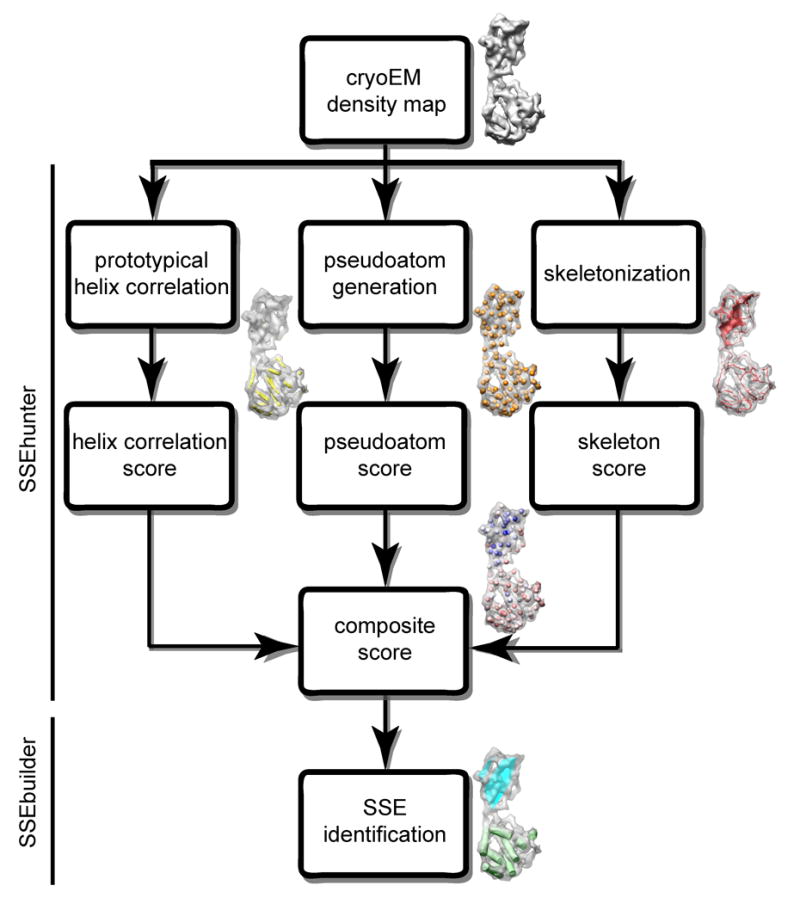
Flowchart for identification of secondary structure elements in SSEhunter. Three independent scoring algorithms, correlation with a prototypical α-helix (yellow density), pseudoatom geometry (orange spheres) and density skeletonization (red density), are combined to form a composite SSEhunter score which can be mapped back to individual pseudoatoms (blue to red spheres). Based on this score, a user can then annotate the secondary structure elements using SSEbuilder (cyan and green polygons).
Data Reduction Using Pseudoatoms
Intermediate resolution density maps are often very difficult to visualize and interpret; though it is often possible to visualize some local structural features. However, there is no natural or direct method for associating meta-data to the density map or the observed structural features. A small set of points (pseudoatoms), each centered in a region of locally high density values, can reduce the complexity of the map and provide a standard mechanism for mapping external data to the density maps while still maintaining the basic shape and density distribution of a density map. Examples of such algorithms and their use in cryoEM structure analysis have already been established and can be found in both EMAN (Ludtke et al., 1999) and Situs (Wriggers et al., 1999).
For this work, a data reduction step was chosen for two purposes; combining/mapping the individual scoring procedures and computing local geometry predicates, described later. A simple threshold-based approach for data reduction was implemented, where a pseudoatom is assigned to the highest value voxel in the density map (Figure 2A). In this approach, each pseudoatom correlates with a region of density proportional to the approximate resolution of the density map. In terms of implementation, the value of the current highest value voxel in the density map is then set to zero and neighboring voxels are down-weighted based on a Gaussian falloff proportional to the resolution of the map. This process is iterated until a user-defined threshold is reached. In general, this threshold is set to the isosurface value that approximates the mass or size of the protein component in question. As implemented, the data reduction step only requires the density map, a threshold, resolution and sampling size to produce a set of pseudoatoms, recorded as a standard PDB file (see http://www.pdb.org for format specifications). Initially, these pseudoatoms represent density markers which serve as a mechanism for aggregating and visualizing local secondary structure propensity assigned by the individual algorithms (described below).
Figure 2.
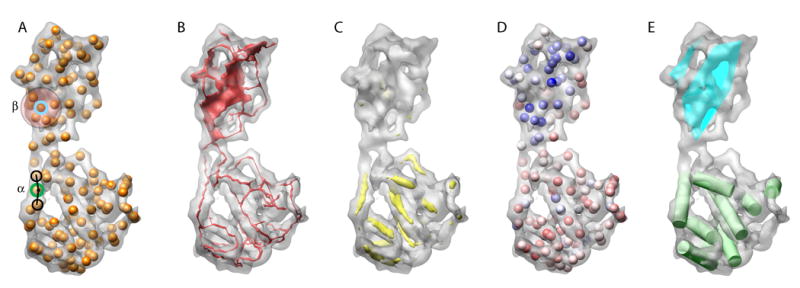
Data representation in SSEhunter. During the identification of secondary structure elements, pseudoatoms are first generated to approximate the density distribution of the density map. The pseudoatom representation for the 8Å resolution simulated density map of 2BTV VP7 is shown in (A). These pseudoatoms are subsequently scored using several metrics based on their local environment. As examples, a pseudoatom in an α-helix (green, α) and its two closest neighboring pseudoatoms form nearly a straight line, while β-sheets contains multiple pseudoatoms with similar distances to each other (cyan, β). Skeletonization of the density then occurs and is shown in (B). The results of cross-correlation with a prototypical α-helix are shown in (C). Finally, the scores from skeletonization, cross-correlation and local geometry predicates are mapped back to individual pseudoatoms and colored based on their propensity to be α-helical (red) or β-sheet (blue) (D). The final annotation of VP7 is shown in (E), where α-helices are represented as green cylinders and β-sheets are shown as cyan planes.
Density Skeletonization
In order to extract descriptive structural information from an intermediate resolution density map, we have implemented a new skeletonization algorithm (Ju et al., 2006) (Figure 2B). In general terms, a skeleton refers to a medial, geometric representation that approximates the overall shape and topology of a volumetric object (Borgefors et al., 1999; Lee et al., 1994). More specifically, the skeleton of a three-dimensional object, in this case a density map, consists of one-dimensional (e.g., curves) and two-dimensional (e.g., surfaces) geometrical elements. Such skeleton curves and surfaces are centered on cylindrical or plate-like shape components of the original object, respectively. Skeletons of volumetric objects are traditionally derived using a morphological thinning operation, which is an iterative process that repeatedly removes voxels from the outer layer of a volumetric object in a topology-preserving manner. In the new skeletonization algorithm [17], a skeleton pruning operation is introduced that, when combined with thinning, results in more stable and descriptive skeleton geometry from irregularly shaped objects. In particular, when applied to intermediate resolution density maps of biological macromolecules, the skeleton curves and surfaces correspond well to tubular or plate-like density distributions, thus preserving the features and topology of the density map. As such, the skeleton is useful as a simplified, geometric representation of the target density map with the same size, sampling and origin (Supplementary Figure 1). In this representation, β-sheets are described by the surfaces of the skeleton, while other features, namely loops and α-helices, can be simply described as curves. However, further distinction among the curve-associated secondary structure elements can be gained when considering the total curvature of a curve. For instance, a helix generally has relatively minimal total curvature.
With these considerations, the individual pseudoatoms can be scored such that each pseudoatom is associated with a corresponding point on the skeleton reflective of the local density geometry/feature. The skeleton itself is scored such that the skeletal features, curves and surfaces, are assigned values of (+1) and (−1), respectively. As such, pseudoatoms which lie on or near skeletal surfaces are assigned scores close to (−1) while pseudoatoms more proximal to curves are assigned values close (+1). More specifically, the individual pseudoatoms are projected onto the skeleton and a distance weighted average score based on the skeletal map features is calculated at each pseudoatom. Due to the construction of the skeletal map and pseudoatoms, each pseudoatom will encompass a skeletal element, however not every skeletal element will be assigned to a unique pseudoatom. The score for each pseudoatom is equivalent to the moment-of-inertia in the skeletal map defined over a sub-volume with a specific radius centered about each pseudoatom.
α-Helix Correlation
As mentioned previously, HELIXHUNTER (Jiang et al., 2001), which relies on an exhaustive cross-correlation search with a prototypical α-helix followed by segmentation and feature extraction steps, has been successful in identifying long α-helices (Baker et al., 2003; Booth et al., 2004; Jiang et al., 2003). This type of search is conducive for identifying α-helices, as they have a relatively fixed cylindrical shape. Furthermore, feature extraction assumes the α-helices have a uniform radius which is much smaller than the total α-helix length, resulting in one large principal axis (length) and two smaller, nearly equal axes (radii). Practically, this is not always the case for real data and may result in partial α-helix identification or misidentification.
A cross-correlation routine, nearly identical to the original HELIXHUNTER routine for identifying regions of cylindrical-line density, was implemented (Figure 2C). The result of this routine is a cross-correlation map, identical in size to the original map, where each voxel in the correlation map contains the best helix cross-correlation value (from 0 to 1) from the exhaustive five-dimensional search. In this representation, α-helices typically have correlation values closer to 1, while β-sheets and other structural features, which are not explicitly detected with this algorithm, have values near zero. Again, individual pseudoatoms can be assigned a score based on their corresponding value in the helix correlation map. As with skeletal map, the pseudoatoms can be projected onto the correlation map. When the voxel corresponding to a given pseudoatom exceeds the mean correlation value (ranging from 0 to 1), that pseudoatom is scored based on the positive mean difference. Conversely, a pseudoatom corresponding to a voxel below the mean correlation value would be scored with the negative mean difference. The final scores for all pseudoatoms are then normalized such that the scores would range from (+1) to (−1) and the mean correlation value is zero.
Local Geometry Predicates
The distribution of the aforementioned pseudoatoms provides a small, discrete set of points that describe the global and local features of the intermediate resolution density map. As such, these points can be used to calculate the local geometry that describes the density features. At each point, the following shape descriptors are calculated (Figure 2A):
Number of neighbors. Pseudoatoms are considered neighbors of another pseudoatom if their Euclidian distance is less than the stated resolution of the density map. A point in an α-helix is typically bordered by no more than three neighboring points, while points within β-sheets typically have greater than four neighbors. As such pseudoatoms were assigned a (−1) value if there were four or more neighbors and (+1) if there were less than four neighbors.
Geometry of neighboring points. In an α-helix point, the closest neighbors are nearly co-linear with each other, while the distribution of neighboring points in β-sheets vary considerably. If the angle between the two vectors formed by itself and each of its two closest neighbors, calculated from the dot product of the two vectors, are within 40 degrees, the point was considered as α-helix. Conversely, neighbor points that were separated by more than 50 degrees, were considered β-sheet like. Additionally, a normal at the pseudoatom, calculated from any two of its neighbors, is similar in direction and magnitude to that of a normal of its neighboring pseudoatoms in an α-helix. Pseudoatoms in β-sheets typically have normals with different directions from each other. Pseudoatom points were considered α-helix like if the angular distance of neighboring normals was below 45 degrees and β-sheet like if the curvature was greater than 45 degrees. The composite of these two measurements were again assigned a (−1) value for β-sheet propensity and (+1) for α-helix propensity.
Aspect ratio. A localized aspect ratio of the density is calculated at each pseudoatom by excising a region of density, centered about the pseudoatom, and then examining the principal axes at this region. In an α-helix the magnitude of the first principal axis is much larger than the magnitude of the second and third principal axes, while the magnitudes of the second and third principal axis are nearly identical. Pseudoatoms were scored (+1) if the aspect ratio of the two smallest principal axes was less than 2. For a sheet, the magnitudes of the first and second principal axes are similar, while the magnitude of the third axis is much smaller than the other two. Points were assigned a value of (−1) the aspect ratio of the second and third principal axes was greater than 3.
Each of these individual scores were summed and normalized from (−1) to (+1), reflecting the local propensity for sheet-like and α-helix-like features, respectively. As this local geometry score is already mapped to the pseudoatoms, no further mapping of the score to the pseudoatoms is required.
Visualization of Secondary Structure Elements
Each pseudoatom is assigned a composite score based on the aforementioned skeletonization, correlation and local geometry indices. All three of these scores are summed equally; however, individual weights can be applied to the three scores independently. The final score, ranging from (−3) to (+3), is then encoded in the pseudoatom file in the “B-factor column” according to PDB standards. Individual pseudoatom scores can then be visualized (Figure 2D) using UCSF’s Chimera (Pettersen et al., 2004) or other visualization software.
To annotate the secondary structure elements individual pseudoatoms must be grouped into linear distributions (α-helices) and planar patches (β-sheets). The scoring of pseudoatoms gives both global and local metrics for assessing structure propensity, and as such represents a quantitative assessment of the putative secondary structure elements.
The grouping of secondary structure elements can then be accomplished by either a fully automated approach or a manual clustering of pseudoatoms. In the automated clustering routine, individual scored pseudoatoms are projected onto the α-helix correlation map and the skeleton map. Pseudoatoms common to a skeleton surface are assigned to a sheet, while pseudoatoms that occupy a common density segment in the correlation map (thresholded at the mean map value) are grouped together and assigned to be an α-helix. Alternatively the user can interactively annotate individual secondary structure elements through manual selection of clusters of pseudoatoms for each element. Not as constraining as the automated procedure, this allows the user to examine the scored pseudoatoms and cluster in an intuitive and dynamic manner.
Data representation is accomplished through VRML planes for β-sheets and VRML cylinders for α-helices (Figure 2E). Alternatively, α-helices may be represented as PDB-style poly-alanine α-helices. In addition to the visual representation of secondary structure elements, individual elements are also saved as a collection of pseudoatoms in a text file. α-helices are also saved in the DejaVu format (Kleywegt and Jones, 1997).
Results
The ability of SSEhunter to resolve both α-helices and β-sheets was first tested on a set of unrelated proteins, representative of the four SCOP families, available from the Protein Data Bank. Previously, these structures (PDB ids: 1C3W (Luecke et al., 1999), 1IRK (Hubbard et al., 1994), 1TIM (Banner et al., 1976) and 2BTV (Grimes et al., 1998)) were used in the assessment of α-helices in HELIXHUNTER (Jiang et al., 2001), and as such were again used to test the α-helix and β-sheet recognition of SSEhunter. In addition to these four structures, the representative structures from the top ten most commonly occurring folds (Gerstein, 1997) were analyzed using SSEhunter. Finally, a set of four proteins from three authentic cryoEM density maps for which high resolution X-ray crystal structures are available were also tested.
Simulated Data
In each of the four representative structures, SSEhunter was able to correctly identify the majority of α-helices and β-sheets in the 8Å resolution structures (Figure 3, Table 1). SSEhunter identified a total of 36 out of a possible 40 α-helices and 7 of 9 β-sheets in the four proteins without any false positives. Each of the α-helices was identified within one turn of the actual α-helix length and the helix centroid RMSD’s for each structure was less than 2.5Å based on the corresponding the X-ray crystallography structures. All α-helices greater than eight amino acids and all β-sheets larger than two strands were correctly identified. All four missed α-helices were less than two turns (~7 amino acids). Similarly, the two missed β-sheets were small. In 1IRK, the β-sheet contained only two strands constituting four amino acids. In 2BTV, a small strand was missed that forms a β-sheet with a neighboring subunit. As only one subunit was simulated, the detection of this β-sheet was not possible.
Figure 3.
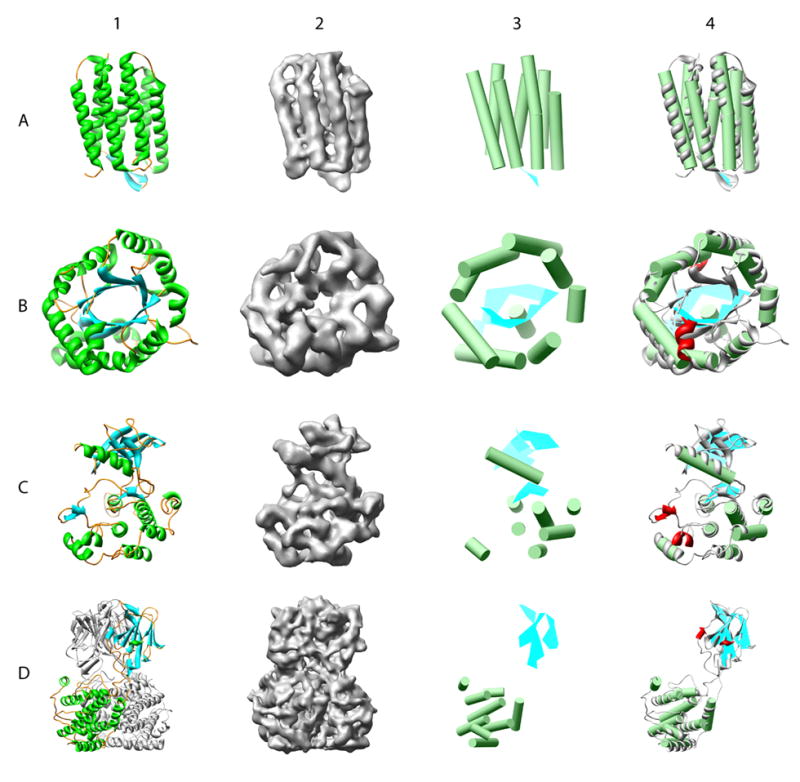
Secondary structure element identification on simulated density maps at 8 Å resolution. Four model structures, bacteriorhodopsin (A, pdb id: 1C3W), triose phosphate isomerase (B, pdb id: 1TIM), insulin receptor tyrosine kinase domain (C, 1IRK) and a trimer of bluetongue virus capsid protein VP7 (D, 2BTV), were used for validation. Column 1 shows a ribbon diagram for each of the structures, while column 2 shows the 8Å resolution simulated density maps. In column 3, the results of secondary structure identification are shown, represented by green α-helices and cyan β-sheets. Comparison of the X-ray structure and identified secondary structure elements are shown in column 4. Deviations from the real structure are colored in red. Only one monomer of the 2BTV trimer was analyzed.
Table 1.
Assessment of SSEHunter Secondary Structure Prediction. A summary of the comparison of SSEhunter identified and actual secondary structure elements from the corresponding X-ray structures are shown for the tested data sets. For P22, the HK97 X-ray structure was used to assess SSEhunter.
| Structure | helix ≤ 4aa | 5–8aa helix | helix > 8aa | sheet ≤ 2 strands | sheet > 2 strands |
|---|---|---|---|---|---|
| 1C3W, 8Å | 0/0 | 0/0 | 8/8 | 1/1 | 0/0 |
| 1TIM, 8Å | 0/0 | 3/5 | 8/8 | 0/0 | 1/1 |
| 1IRK, 8Å | 1/1 | 2/3 | 5/5 | 1/2 | 1/1 |
| 2BTV, 8Å | 0/1 | 2/2 | 7/7 | 1/2 | 2/2 |
| RDV P3, 6.8Å | 0/6 | 10/18 | 26/26 | 1/9 | 5/5 |
| RDV P8, 6.8Å | 0/2 | 3/4 | 8/8 | 0/1 | 2/2 |
| HSV VP5, 8.5Å | 0/0 | 6/8 | 11/12 | 0/1 | 1/1 |
| P22, 9.5Å | 0/0 | 1/2 | 2/2 | 2/2 | 2/2 |
| 10 most common folds* | 6/14 | 12/16 | 58/58 | 1/6 | 11/11 |
| Totals | 7/24 (29.2%) | 39/58 (67.2%) | 133/134 | 7/24 (29.2%) | 25/25 (100%) |
results for the ten most common folds can be seen in the Supplementary Table and online at http://ncmi.bcm.tmc.edu/software/AIRS/ssehunter/)
Like the aforementioned representative structures, SSEhunter demonstrated the reliability and accuracy of secondary structure element identification with the representative structures from the top ten most common folds simulated at 8Å resolution (Supplementary Table, http://ncmi.bcm.tmc.edu/software/AIRS/ssehunter/). For both α-helices greater than eight amino acids and β-sheets larger than two strands, SSEhunter correctly identified the location and orientation of all these secondary structure elements. In addition, SSEhunter was also able to identify three-fourths of all helices between five and eight amino acids in length. However, α-helices less then five amino acids in length and β-sheets of less than three strands could not be reliably predicted.
Resolution
In addition to the 8Å resolution simulated density maps, SSEhunter was assessed on 6Å and 10Å resolution simulated data sets. At all of these resolutions, SSEhunter had similar accuracy in identifying α-helices and β-sheets in the simulated density maps (Figures 4). However, β-sheets in the 10Å resolution datasets were not as well resolved as those in the 6 and 8Å resolution datasets. Conversely, three of the missed α-helices in the 8Å resolution density maps of 1IRK and 1TIM were resolved in the 6Å datasets. As with the previous tests, no false positives were identified.
Figure 4.
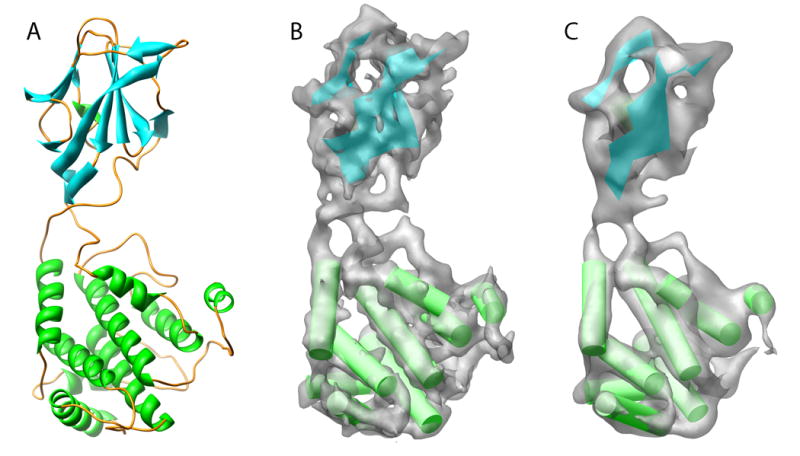
Resolution assessment of simulated data. Structural analysis of the four simulated test structures was carried out at 6, 8 and 10Å resolution. Shown in (A) is a monomer from 2BTV; (B) and (C) show simulated density at 6 and 10Å resolution with their resulting secondary structures determined by SSEhunter, respectively. Figure 2 contains the 8Å resolution data. Similar results were obtained with the other three structures at the equivalent resolutions.
Rice Dwarf Virus
In addition to the simulated data sets, the two capsid proteins, P3 and P8, from the 6.8Å resolution cryoEM density map of RDV (EMDB id: 1060) (Zhou et al., 2001) were analyzed using SSEhunter. As with the simulated data, SSEhunter was able to identify the majority of β-sheets and α-helices in both P3 and P8 (Figure 5A, B). Helix assignment by SSEhunter was within one turn of the actual helix length in all but one helix and within 2.4Å centroid RMSD of the α-helix positions in both P3 and P8 X-ray structure. Like the simulated data, all α-helices greater than eight amino acids and all β-sheets larger than two strands were correctly identified (Table 1). Additionally, 13 of the 22 helices between five and eight amino acids were also correctly identified. However, no smaller α-helices and only one of ten β-sheets smaller than three strands could be identified.
Figure 5.
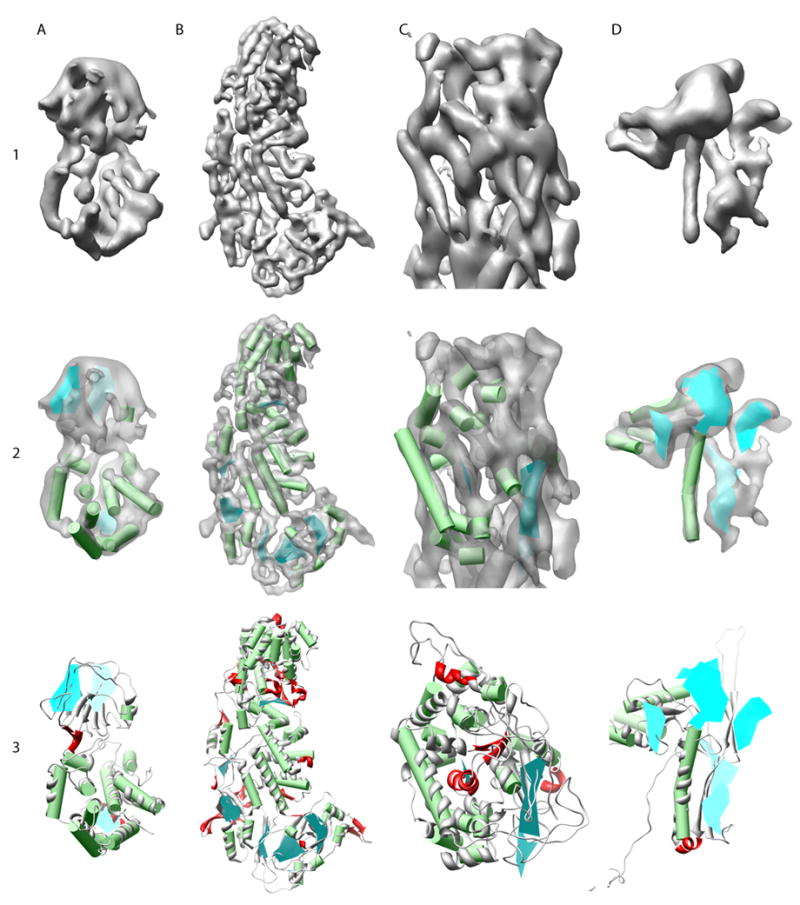
Secondary structure element identification on authentic cryoEM density maps. The 6.8Å resolution RDV (EMDB ID: 1060) capsid proteins, P8 and P3, are shown in columns (A) and (B). The upper domain of a hexon subunit, containing both VP5 and VP26, from the 8Å resolution HSV-1 cryoEM density map is shown in column (C). A Gp5 monomer from the 9.5Å resolution structure of the P22 phage (EMDB ID: 1101) is shown in column (D). The results of SSEhunter (row 2) on the corresponding density maps (row 1) are shown where α-helices are represented as green cylinders and β-sheets as cyan polygons. The X-ray structures, fit to the cryoEM density using FOLDHUNTER, are shown superimposed on the SSEhunter results in row 3 (PDB IDs: 1UF2, 1NO7 and 1OHG). Discrepancies in identification are colored in red. In HSV-1 VP5, only the upper domain is shown as only this region has a corresponding high-resolution structure. No x-ray structure for GP5 of P22 is known, however the structural homolog, Gp5 from HK97, is shown in row 3, column (D).
Two small regions, one in P3 and one in P8, were incorrectly identified as a sheet. Both of these regions in the density map appear to have sheet-like character. In P3, the false positive occurs near another two-stranded β-sheet. Based on the X-ray structure of P3, this region is composed of two loops with amino acid geometry similar to that of a β-sheet. In P8, the false positive occurs in a region of density that appears to be less well resolved. Again based on the X-ray structure of P8, this region contains two small, poorly organized α-helices and a relatively large loop producing an appearance similar to a sheet. In a related reovirus capsid structure (1QHD (Mathieu et al., 2001)), this region is in fact a β-sheet. In both of the false positives, the local structure appears to be more similar to a β-sheet than any other possible secondary structure.
In comparison to the original analysis of the RDV structure using HELIXHUNTER (Jiang et al., 2001), SSEhunter was able to correctly resolve two additional α-helices in P8, one in the upper domain and one in the lower domain, not previously identified using HELIXHUNTER. Both of these helices were approximately two turns in length, below the threshold for identification. Like P8, SSEhunter was able to identify several smaller helices that were previously missed in the prior analysis.
HSV-1 VP5
Unlike rice dwarf virus, the entire crystal structure of the Herpes Simplex Virus-1 (HSV-1) capsid is not known. However, in addition to the 8.5Å resolution cryoEM map of HSV-1 capsid (Zhou et al., 2000), a portion of the major capsid protein, VP5 (149kDa), has been solved by X-ray crystallography (PDB id: 1NO7) (Bowman et al., 2003). The entire hexon subunit, containing both VP5 and VP26 (12kDa), was analyzed using SSEhunter and then compare to the partial X-ray structure of VP5, which constitutes the majority of the upper third of the hexon subunit (Figure 5 C). SSEhunter correctly detected all β-sheets larger than two strands and all but one of the α-helices (Table 1) greater than eight amino acids in length (2.37Å alpha α-helix centroids RMSD). SSEhunter also identified correctly six of eight α-helices smaller than nine amino acids, and one of the two small β-sheets (two-strand) at the lower boundary of the VP5 X-ray structure.
SSEhunter did misidentify one α-helix as a β-sheet, however in the previous structural analysis of VP5, this α-helix, along with two other α-helices were not identified using Helixhunter on the same VP5 density map (Baker et al., 2003). In contrast to the mis-identified α-helix, the other two α-helices not previously identified, in addition to all of the other identified α-helices, are now clearly resolved by SSEhunter. It should be also be noted that SSEhunter, and the earlier HELIXHUNTER, could not accurately identify a second large helix. This helix, however is a 310 helix and has a different geometry and density profile than other α-helices.
Bacteriophage P22
While no high-resolution structure for the bacteriophage P22 capsid protein GP5 (Jiang et al., 2003) is known, a structural homolog has been previously identified, that of the HK97 capsid protein (Helgstrand et al., 2003). Analysis of the GP5 subunit, segmented from the 9.5Å resolution cryoEM map of P22 (EMDB id: 1101), by SSEhunter (Figure 5D) not only reveals the three previously HELIXHUNTER detected α-helices and visually assigned β-sheet, but also the presence of four newly detected β-sheets (Table 1). Three of these β-sheets are consistent with the HK97 capsid protein structure, while the largest one is unique to P22 GP5. This large β-sheet appears to occupy nearly the entire protrusion domain, a knob-like region protruding outward from the capsid and capsid protein.
Topology of Secondary Structure Elements
As demonstrated, SSEhunter is capable of identifying α-helices greater than eight amino acids and β-sheets larger than two strands with relatively high fidelity. However, the description of the secondary structure elements provides only spatial information. As described, the skeletonization routine in SSEhunter provides a compact geometrical representation which preserves structural features and topology (Ju et al., 2006). As this skeleton should preserve structural topology, or more generally the ordering and connectivity of secondary structure elements, it may provide a mechanism for assigning topology to the observed secondary structure elements.
As such, the skeletons generated from SSEhunter were superimposed on the density and predicted secondary structure elements from SSEhunter and compared to the corresponding X-ray structures (Grimes et al., 1998; Nakagawa et al., 2003). In both the simulated density maps (Supplementary Figure 2) and authentic cryoEM data (Figure 6), the skeletons approximate the backbone of the structure. Although strands are not resolvable in this resolution range (5–10 Å), the overall disposition of the secondary structure elements and their connectivity is resolved using the skeletonization routine in SSEhunter.
Figure 6.
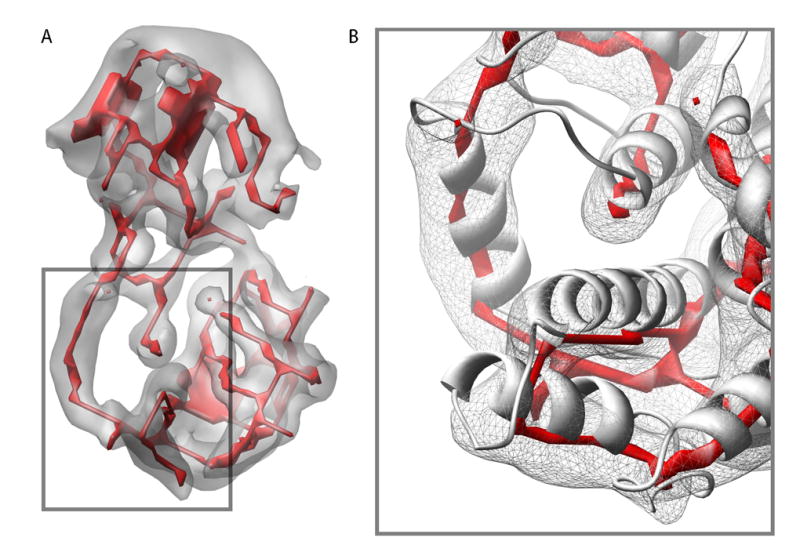
SSEhunter skeleton from segmented cryoEM density of RDV P8. The segmented cryoEM density is shown in grey with the skeleton in red (A). In (B), a zoomed in view of portion of the lower domain of P8 is shown with the X-ray structure (1UF2, ribbon) superimposed on the density map and skeleton, illustrating the ability of the skeleton to approximate the polypeptide chain. While the skeleton does approximate the overall path of the polypeptide chain, the exact path in the skeleton is ambiguous in certain regions containing branches and breaks corresponding to the density features.
Discussion
While previous techniques have already established the utility of secondary structure identification (Jiang et al., 2001; Kong and Ma, 2003; Kong et al., 2004), none has been capable of simultaneous identification of both α-helices and β-sheets. SSEhunter and its companion program, SSEbuilder, provide end-users a unique and easy way to simultaneously assess, visualize and annotate both α-helices and β-sheets in intermediate resolution density maps from both cryoEM and X-ray crystallography. Furthermore, the underlying methodology provides a new framework for determining structural topology and ultimately a platform for direct structural modeling.
Algorithm
The intrinsic properties of α-helices and β-sheets are such that it is difficult for a single algorithm to properly identify these elements. As such, the aforementioned methodology leverages the best techniques to describe these secondary structure elements. As α-helices are rigid bodies, best described as cylinders, correlation techniques and curvature descriptors make for the best detection methodologies. However, these techniques are grossly inadequate to properly describe the various sizes and shapes of β-sheets. Thus, the incorporation of a shape detection algorithm, in this case skeletonization, is necessary to uniquely describe β-sheets. In addition to these techniques, local geometrical features, such as density distribution, can help augment the localization of structural features in ambiguous areas, particularly at the edges of secondary structure elements. These ideas form the core concepts of SSEhunter and are integrated in such a manner that their independent natures are transparent to the end-user, although each individual metric can be visualized and assessed independently. This architecture also allows for the development and integration of future feature detection algorithms into SSEhunter.
Representation
Common in sequence-based secondary structure prediction is the assignment of a reliability score to every amino acid and its cognate secondary structure assignment. While the reliability metrics vary in how they are calculated and reported, the score still provides users a convenient way to assess the results. As such, SSEhunter has adopted such an approach to aid the visualization and analysis of the secondary structure identification. In the density reduction step, which is used to define the local geometrical features, the density is represented as a set of representative pseudoatoms, which are represented as Cα atoms in the PDB file. The pseudoatoms themselves represent a region of density that is proportional to the approximate resolution of the density map itself. In this regard, the pseudoatoms do not correspond to any physical characteristic, i.e. amino acid, structural feature, except for the density itself and merely function as points for scoring, integrating and visualizing SSEhunter results. Moreover, as the pseudoatoms are merely an abstract representation of the density, different algorithms for density reduction may give slightly different results. In practice however, other data reduction techniques, such as K-means and vector quantization with approximately the same number of pseudoatoms, resulted in almost identical placement and scoring of the pseudoatoms (data not shown). While these differences may slightly affect the scoring of the pseudoatoms, it is unlikely that these differences would account for a significant difference in the assignment of secondary structure elements and therefore provide a relatively robust mechanism for the quantitative and visual assessment of the SSEhunter results. However, one significant caveat should be noted. The data reduction step does not seek to improve/enhance the features within a density map. If a density artifact is present in the map at the threshold selected by the user, it will be represented as a pseudoatom and scored appropriately. Therefore, the robustness of both the data reduction and scoring is an issue of map quality and not algorithm design.
Interface
Much of the novelty and advantages in SSEhunter focus on the interface to the software and resulting data. In all previous secondary structure identification programs, the primary interface is through the command line, thereby separating the user from the data. In SSEhunter, as well as all other AIRS programs, the user is provided with a convenient graphical interface through the freely available Chimera molecular visualization software from UCSF (Pettersen et al., 2004) (Supplementary Figure 3). This integration allows the user to remain connected with the data and help to set parameters, i.e. voxel size and threshold, and evaluate the results more effectively. As such, this provides the user with a more effective means for structural discovery.
More than just providing an interface, the integration of these tools with Chimera provides the end-user with the most flexibility in visualizing and annotating the structural analysis of the density. Specifically, SSEhunter provides a per-point scoring system for secondary structure identification, while SSEbuilder provides a separate interface for annotating and rendering the secondary structure elements. In this regard, SSEhunter provides the user with the “best-guess” of secondary structure from which the user can be guided to independently build the individual secondary structure elements using SSEbuilder. In decoupling the assessment of the density and the annotation of the secondary structure elements, the user has the flexibility in discovering and annotating secondary structure elements. This allows the user to incorporate additional information, such as mutagenesis or cross-linking data that may help to describe the secondary structure elements. However, the same flexibility may result in the over interpretation of the data. Therefore, an initial evaluation of the secondary structure elements using the automatic annotation routine in SSEhunter followed by user evaluation and final annotation may result in the most accurate and reliable secondary structure elements.
Assessment
The biggest factor in detecting features in the density map is the map itself as it may not have uniform resolution or quality throughout the entire map. SSEhunter essentially discerns the characteristic patterns of secondary structure elements in subnanometer resolution density maps using feature recognition. In simulated and real intermediate resolution density maps, SSEhunter was able to correctly identify and annotate nearly all of the individual secondary structure elements, where the predicted α-helix accuracy was better than 2.5 Å centroids RMSD (Table 1). Prediction of small secondary structure elements (α-helices <2 turns and 2-stranded β-sheets) were less reliable in authentic maps, although α-helices five to eight amino acids in length were identified correctly nearly two-thirds (20/32) of the time.
Conversely, false positives are a potential problem and may indeed alter the interpretation of the structure. In the authentic cryoEM maps, false positives are present, although infrequent, while no false positives were detected in the simulated density maps. These mis-identifications, both missed and false identification, usually occurred in regions of the density maps that were poorly resolved. It is imperative to realize that these errors are not necessarily due to the algorithm for feature detection rather they are related to issues concerning the quality and resolvability of the density map in the local region. Moreover, these types of errors will become more noticeable as the resolution worsens and the resolvability of the map decreases as SSEhunter itself is not ‘aware’ of the quality or resolvability of the density map. Hence, the reliability of SSEhunter is dependant primarily on the quality of map in relation to the structural features in question and helps to explain the relative differences in the accuracy of the SSEhunter results between the simulated and real data sets.
In terms of resolution, SSEhunter appears to work successfully regardless of the tested resolution (6–10Å) on both real and simulated data sets. As with other structural analysis programs, the feature detection routines are limited to the resolvability of the secondary structure elements. As demonstrated previously, α-helix identification can be reliably achieved even at 12Å resolution on simulated data (Jiang et al., 2001). Practically, feature detection is constrained to subnanometer resolutions, where the cylindrical and planar features of α-helices and β-sheets, respectively, can be discerned. However, it may be possible to visualize α-helices before β-sheets in these structures. Therefore, resolution boundaries for secondary structure identification are ambiguous at best. Again, it is important to realize that feature recognition techniques such as SSEhunter are mainly constrained by the resolvability of the features in question.
Beyond Secondary Structure
While the identification of secondary structure is critical in the development of structural models from density maps, it also offers a wealth of additional information. Previous work has utilized secondary structure elements to assign sequence elements to a density map and develop structural model. In preliminary implementations of SSEhunter, the identified structural features have been used to establish virus evolutionary relationships (Baker et al., 2005) and compare ion channel structures (Ludtke et al., 2005). However, the use of secondary structure in these examples provides only general spatial information and does not establish topology.
Interestingly, the skeletonization routine used in the analysis of secondary structure begins to address issue of topology (connectivity of secondary structure elements). Mathematically, the derived skeleton is topologically equivalent to the given volumetric object. In our context, this implies that the connectivity of the protein object, bounded by iso-surfaces extracted from the cryoEM at a specific density threshold, is preserved by the connectivity of the skeleton curves and surfaces. As such, the skeleton not only compactly represents the geometric features of the density map, such as the tubular and plate-like distributions, but also approximates the topology of the distribution (and thus of the protein itself) with the exception of a possibly small number of branch or break points due to the insufficient resolution and noise in the cryoEM data. The result is essentially a “density trace”, and assuming the density is of good quality, reflective of the actual topological linkages between secondary structure elements. At high enough resolution (~4–5Å resolution), this “density trace” approximates the actual protein backbone trace. As exemplified in both simulated and real data, the skeleton is a very good approximation of the actual protein backbone. It should be noted that this backbone is not perfect. Individual strands within the β-sheets are not visible. As such, the “density trace” near β-sheets is not well resolved and will not be discernable until the individual strands in a β-sheet can be observed (~4.5 Å resolution or better). Furthermore, branching of the skeleton may result in alternative topological assessments. In these cases, the skeleton may provide multiple topologies that require the end user to assess potential pathways. Regardless, the use of the skeleton as a tool for topological assessment of secondary structure elements is promising. The development of this combined with sequence analysis offers a new opportunity for building models directly from density.
Conclusion
As the number of intermediate resolution structures of macromolecules increases, the development of tools for visualization and annotation of the individual components of macromolecular complexes will become increasingly important. The accurate, simultaneous identification of α-helices and β-sheets in this work represents a significant advancement in the ability to quantitatively analyze and understand macromolecular assemblies. Moreover, the skeletonization method adopted in this work provides not only feature recognition, but also topological information. As such, SSEhunter, coupled with SSEbuilder, represents the first step in direct structural model building from intermediate resolution density maps.
Experimental Procedure
SSEhunter and SSEbuilder were implemented as described above (Approach). Both programs and their graphical interfaces were written in Python and bind the EMAN image processing libraries (Ludtke et al., 1999). SSEhunter is available through the command line, while both SSEhunter and SSEbuilder are available through a graphical interface in UCSF’s Chimera (Pettersen et al., 2004) (Supplementary Figure 3). SSEbuilder and SSEhunter are distributed as part of the Analysis of Intermediate Resolution Structures (AIRS) toolkit, which itself is distributed with the EMAN image processing software.
Benchmark
A benchmark set of proteins were simulated at 6, 8, and 10Å resolution with the EMAN program pdb2mrc with a sampling of 1Å/pixel. Initial testing was done on four representative structures (1C3W, 1IRK, 1TIM and 2BTV) that had been used in previous secondary structure assessment (Jiang et al., 2001). To provide a larger and more complete sampling, the representative structures from the top ten most commonly occurring folds (Gerstein, 1997) were analyzed using SSEhunter. Additional testing of the algorithm was done on the 6.8Å resolution map of the rice dwarf virus (RDV) P3 and P8 capsid proteins (1.6358 Å/pixel)(Zhou et al., 2001) and the major capsid proteins from the 8.5Å resolution map of HSV-1 capsid (VP5, 1.4 Å/pixel) (Ludtke et al., 2004) and the 9.5Å resolution map of bacteriophage P22 (GP5, 1.815 Å/pixel) (Jiang et al., 2003). In all cases, only the resolution, sampling and a threshold corresponding to the approximate molecular weight of the subunit was provided to SSEhunter. In these examples, typical runtimes for SSEhunter were on the 2.5–5 minutes on a modern desktop PC, depending on the size of the density maps, which ranged from 643 to 1283. Secondary structure element assignment was done using the automated assignment in the simulated data, requiring less than 5 seconds of computational time. In the authentic data, a combination of automatic assignment and SSEbuilder was used. Assignment of secondary structures using SSEbuilder for these data sets required 5–10 minutes for an experienced user. Validation of the identified secondary structure elements was made possible through the fitting of the corresponding X-ray structures (Braig et al., 1995; Helgstrand et al., 2003; Nakagawa et al., 2003) (RDV: 1UF2, HSV-1 VP5: 1NO7, P22/HK97 Gp5: 1OHG) into the density using FOLDHUNTER (Jiang et al., 2001), also found in the AIRS toolkit.
The overall accuracy of secondary structure prediction was assessed by visually comparing the SSEhunter predicted secondary structure to the real secondary structure features defined in the corresponding PDB files. Additionally, the quality of α-helix assignment was assessed by comparing the α-helix lengths and centroids positions using the “bones search” option in DejaVu (Nakagawa et al., 2003). Assessment of β-sheets was done manually as individual strand assignment is not made in SSEhunter or SSEbuilder.
Display
By rendering the pseudoatoms based on their secondary structure propensity, encoded in the B-factor column of the pseudoatom PDB file, the secondary structure features can immediately be visualized. For the purpose of this work, individual pseudoatoms were rendered as spheres and colored where the most likely β-sheets pseudoatoms (negative score) are set to blue, while the most likely α-helix pseudoatoms (positive score) are set to red; pseudoatoms with values near zero are set to white. As such, a continuous scoring of secondary structure propensity can be accomplished where the intensity of color represents the likelihood of the assignment.
All images were created using UCSF’s Chimera molecular visualization software (Pettersen et al., 2004). Thresholds for visualization corresponded roughly to the correct molecular mass of the proteins; this threshold was also used in the SSEhunter calculations. Unless otherwise noted, all figures were created with the 8Å resolution models for illustration purposes.
Supplementary Material
Acknowledgments
We would like to thank Dr. Steve Ludtke, Dr. Michael Schmid, Dr. Wen Jiang and Dr. Christopher Booth for their helpful discussions. This research was supported by NSF (EIA-0325004) and NCRR (P41RR02250 and P20RR020647).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Baker ML, Jiang W, Bowman BR, Zhou ZH, Quiocho FA, Rixon FJ, Chiu W. Architecture of the herpes simplex virus major capsid protein derived from structural bioinformatics. J Mol Biol. 2003;331:447–456. doi: 10.1016/s0022-2836(03)00696-x. [DOI] [PubMed] [Google Scholar]
- Baker ML, Jiang W, Rixon FJ, Chiu W. Common ancestry of herpesviruses and tailed DNA bacteriophages. J Virol. 2005;79:14967–14970. doi: 10.1128/JVI.79.23.14967-14970.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ban N, Nissen P, Hansen J, Moore PB, Steitz TA. The complete atomic structure of the large ribosomal subunit at 2.4 Å resolution. Science. 2000;289:905–920. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- Banner DW, Bloomer A, Petsko GA, Phillips DC, Wilson IA. Atomic coordinates for triose phosphate isomerase from chicken muscle. Biochem Biophys Res Commun. 1976;72:146–155. doi: 10.1016/0006-291x(76)90972-4. [DOI] [PubMed] [Google Scholar]
- Booth CR, Jiang W, Baker ML, Zhou ZH, Ludtke SJ, Chiu W. A 9 angstroms single particle reconstruction from CCD captured images on a 200 kV electron cryomicroscope. J Struct Biol. 2004;147:116–127. doi: 10.1016/j.jsb.2004.02.004. [DOI] [PubMed] [Google Scholar]
- Borgefors G, Nystrom I, Baja GSd. Computing skeletons in three dimensions. Pattern Recognition. 1999;32:1225–1236. [Google Scholar]
- Bowman BR, Baker ML, Rixon FJ, Chiu W, Quiocho FA. Structure of the herpesvirus major capsid protein. Embo J. 2003;22:757–765. doi: 10.1093/emboj/cdg086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braig K, Adams PD, Brunger AT. Conformational variability in the refined structure of the chaperonin GroEL at 2.8 Å resolution. Nat Struct Biol. 1995;2:1083–1094. doi: 10.1038/nsb1295-1083. [DOI] [PubMed] [Google Scholar]
- Braig K, Otwinowski Z, Hegde R, Boisvert DC, Joachimiak A, Horwich AL, Sigler PB. The crystal structure of the bacterial chaperonin GroEL at 2.8 Å. Nature. 1994;371:578–586. doi: 10.1038/371578a0. [DOI] [PubMed] [Google Scholar]
- Chiu W, Baker ML, Almo SC. Structural biology of cellular machines. Trends Cell Biol. 2006;16:144–150. doi: 10.1016/j.tcb.2006.01.002. [DOI] [PubMed] [Google Scholar]
- Chiu W, Baker ML, Jiang W, Dougherty M, Schmid MF. Electron cryomicroscopy of biological machines at subnanometer resolution. Structure (Camb) 2005;13:363–372. doi: 10.1016/j.str.2004.12.016. [DOI] [PubMed] [Google Scholar]
- Gerstein M. A structural census of genomes: comparing bacterial, eukaryotic, and archaeal genomes in terms of protein structure. J Mol Biol. 1997;274:562–576. doi: 10.1006/jmbi.1997.1412. [DOI] [PubMed] [Google Scholar]
- Grimes JM, Burroughs JN, Gouet P, Diprose JM, Malby R, Zientara S, Mertens PPC, Stuart DI. The atomic structure of the bluetongue virus core. Nature. 1998;395:470–477. doi: 10.1038/26694. [DOI] [PubMed] [Google Scholar]
- Helgstrand C, Wikoff WR, Duda RL, Hendrix RW, Johnson JE, Liljas L. The refined structure of a protein catenane: the HK97 bacteriophage capsid at 3.44 A resolution. J Mol Biol. 2003;334:885–899. doi: 10.1016/j.jmb.2003.09.035. [DOI] [PubMed] [Google Scholar]
- Hubbard SR, Wei L, Ellis L, Hendrickson WA. Crystal structure of the tyrosine kinase domain of the human insulin receptor. Nature. 1994;372:746–754. doi: 10.1038/372746a0. [DOI] [PubMed] [Google Scholar]
- Jiang W, Baker ML, Ludtke SJ, Chiu W. Bridging the information gap: computational tools for intermediate resolution structure interpretation. J Mol Biol. 2001;308:1033–1044. doi: 10.1006/jmbi.2001.4633. [DOI] [PubMed] [Google Scholar]
- Jiang W, Li Z, Zhang Z, Baker ML, Prevelige PE, Jr, Chiu W. Coat protein fold and maturation transition of bacteriophage P22 seen at subnanometer resolutions. Nat Struct Biol. 2003;10:131–135. doi: 10.1038/nsb891. [DOI] [PubMed] [Google Scholar]
- Ju T, Baker ML, Chiu W. Computing a family of skeletons of volumetric models for shape description; Paper presented at: Geometric Modeling and Processing 2006 (accepted); 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleywegt GJ, Jones TA. Detecting folding motifs and similarities in protein structures. Methods Enzymol. 1997;277:525–545. doi: 10.1016/s0076-6879(97)77029-0. [DOI] [PubMed] [Google Scholar]
- Kong Y, Ma J. A structural-informatics approach for mining beta-sheets: locating sheets in intermediate-resolution density maps. J Mol Biol. 2003;332:399–413. doi: 10.1016/s0022-2836(03)00859-3. [DOI] [PubMed] [Google Scholar]
- Kong Y, Zhang X, Baker TS, Ma J. A Structural-informatics approach for tracing beta-sheets: building pseudo-C(alpha) traces for beta-strands in intermediate-resolution density maps. J Mol Biol. 2004;339:117–130. doi: 10.1016/j.jmb.2004.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TC, Kashyap RL, Chu CN. Building skeleton models via 3-D medial surface/axis thinning algorithms. CVGIP: Graph Models Image Process. 1994;56:462–478. [Google Scholar]
- Ludtke SJ, Baldwin PR, Chiu W. EMAN: Semi-automated software for high resolution single particle reconstructions. J Struct Biol. 1999;128:82–97. doi: 10.1006/jsbi.1999.4174. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Chen DH, Song JL, Chuang DT, Chiu W. Seeing GroEL at 6 Å Resolution by Single Particle Electron Cryomicroscopy. Structure (Camb) 2004;12:1129–1136. doi: 10.1016/j.str.2004.05.006. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Serysheva II, Hamilton SL, Chiu W. The pore structure of the closed RyR1 channel. Structure (Camb) 2005;13:1203–1211. doi: 10.1016/j.str.2005.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luecke H, Schobert B, Richter HT, Cartailler JP, Lanyi JK. Structure of bacteriorhodopsin at 1.55 A resolution. J Mol Biol. 1999;291:899–911. doi: 10.1006/jmbi.1999.3027. [DOI] [PubMed] [Google Scholar]
- Mathieu M, Petitpas I, Navaza J, Lepault J, Kohli E, Pothier P, Prasad BV, Cohen J, Rey FA. Atomic structure of the major capsid protein of rotavirus: implications for the architecture of the virion. Embo J. 2001;20:1485–1497. doi: 10.1093/emboj/20.7.1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakagawa A, Miyazaki N, Taka J, Naitow H, Ogawa A, Fujimoto Z, Mizuno H, Higashi T, Watanabe Y, Omura T, et al. The atomic structure of rice dwarf virus reveals the self-assembly mechanism of component proteins. Structure (Camb) 2003;11:1227–1238. doi: 10.1016/j.str.2003.08.012. [DOI] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera--a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Sali A. 100,000 protein structures for the biologist. Nat Struct Biol. 1998;5:1029–1032. doi: 10.1038/4136. [DOI] [PubMed] [Google Scholar]
- Sali A. NIH workshop on structural proteomics of biological complexes. Structure (Camb) 2003;11:1043–1047. doi: 10.1016/s0969-2126(03)00163-1. [DOI] [PubMed] [Google Scholar]
- Wriggers W, Milligan RA, McCammon JA. Situs: A package for docking crystal structures into low-resolution maps from electron microscopy. J Struct Biol. 1999;125:185–195. doi: 10.1006/jsbi.1998.4080. [DOI] [PubMed] [Google Scholar]
- Zhou ZH, Baker ML, Jiang W, Dougherty M, Jakana J, Dong G, Lu G, Chiu W. Electron cryomicroscopy and bioinformatics suggest protein fold models for rice dwarf virus. Nat Struct Biol. 2001;8:868–873. doi: 10.1038/nsb1001-868. [DOI] [PubMed] [Google Scholar]
- Zhou ZH, Dougherty M, Jakana J, Chiu W, Jing H, Rixon FJ. Seeing the herpesvirus capsid at 8.5 Å. Science. 2000;288:877–880. doi: 10.1126/science.288.5467.877. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


