Osmotic stress, crowding, preferential hydration, and binding: A comparison of perspectives

Abstract

There has been much confusion recently about the relative merits of different approaches, osmotic stress, preferential interaction, and crowding, to describe the indirect effect of solutes on macromolecular conformations and reactions. To strengthen all interpretations of measurements and to forestall further unnecessary conceptual or linguistic confusion, we show here how the different perspectives all can be reconciled. Our approach is through the Gibbs-Duhem relation, the universal constraint on the number of ways it is possible to change the temperature, pressure, and chemical potentials of the several components in any thermodynamically defined system. From this general Gibbs-Duhem equation, it is possible to see the equivalence of the different perspectives and even to show the precise identity of the more specialized equations that the different approaches use.

The popular and instructive application of osmotic stress (1) has been used to measure the changes in macromolecular hydration for several reactions. In its transit from fully deoxy to fully oxygenated forms, hemoglobin loads some 60 water molecules (2). Going from closed to successive open states, the ionic channels of alamethicin take up 100 waters (3). Biting down on glucose, hexokinase expels 320 water molecules (4). The nonspecific DNA complex of the restriction nuclease EcoRI sequesters some 110 more waters than the specific complex (5). These are waters that are preferentially associated with, or dissociated from, a protein or macromolecule, waters taken away or released to the solutes in the bathing medium. Such quantitative measurements of water as ligand are possible when it can be demonstrated that the work to create different macromolecular states changes in proportion to the chemical potential of water rather than the chemical potentials of agents used to change water activity.

At the same time, there is growing realization that molecules in the cell sterically “crowd” each other in their cohabited aqueous space (6) and that this steric interaction can be enhanced by the preferential hydration of molecules (7). The powerful perspectives of osmotic stress, preferential hydration, and crowding grow out of a common origin in solution theory (8). In particular, solution theory can be specialized to recognize the indirect effects of solutes on macromolecules that occur in addition to direct action of specific solutes through binding to macromolecules.

The prescient work of Asakura and Oosawa (9) as well as the early work of Tanford (10) and Timasheff (7) directed us all to see the multiple ways that molecules can act on each other. In principle (10) and in practice (11), a solute can have a double effect. The same molecule that directly binds to a protein also can indirectly affect protein conformation through changes in the activity of water. Modern quantitative work on specific systems has shown that it is possible to choose knowingly among different perspectives depending on the way macromolecules are seen to respond to added solutes. In practice, these different views each can be instructive depending on the macromolecular system, the experimental design, and the properties being observed.

Both the crowding and preferential hydration pictures focus on the properties of solutes that are excluded from macromolecules. Osmotic stress emphasizes the role of the water that is necessarily included if solutes are excluded. Specifically, crowding formulations use the size and geometry of solutes or polymers in solution to calculate the contribution of hard-core repulsion to the free energy of a macromolecule immediately through, for example, scaled particle theory. Preferential hydration and osmotic stress both are based on the Gibbs-Duhem equation.

These different views of molecular action are complementary and not mutually exclusive. Recently, Timasheff (12) has questioned the application of osmotic stress to single molecules. He asserts that the osmotic stress approach “involves a conflict with the laws of thermodynamics” but then, in the same sentence, absolves osmotic stress by saying that it “is simply a restricted case of preferential interactions, as practiced for three decades.” His criticism is further confounded by the acknowledgment that the osmotic stress approach gives the right numbers:

“The paradox is that, even though the theoretical basis as presented in osmotic stress is incorrect, the experiments have produced correct numerical values of changes in preferential hydration, δ(∂m₁/∂m₂), because the plots used [equations such as Eqs. 3 and 6 and their variants] are correct.”

There is no paradox. Had Timasheff converted his symbols to those used in osmotic stress analysis, he would have reassured himself that the osmotic stress and the preferential hydration analyses use equations that are equivalent. The alleged conflict of osmotic stress with thermodynamic laws arises from a particular interpretation of “inert” imposed by Timasheff, an interpretation that itself contradicts the explicit thermodynamic use of the Gibbs-Duhem equation. His particular usage leads him to think that the energetic consequences of solute or cosolvent exclusion have been ignored and that conservation of energy is violated. This is not the case.

Rather than being “a restricted case of preferential interactions” (12), osmotic stress analysis can in fact give not only a sharpened picture of what is going on between the macromolecule and all solution components but also a direct thermodynamic measure of hydration achieved after doing osmotic stress measurements with several kinds of solutes. While “thermodynamics is a wonderful structure with no content” (attributed to Aharon Katchalsky), that structure is a scaffold on which we can organize our thoughts about the factors that govern macromolecular stability and function.

Thermodynamic Constraints Link the Different Perspectives

The Gibbs-Duhem equation

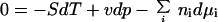1

defines the constraints between changes in temperature T, in hydrostatic pressure p, and in the chemical potentials μ_i of the component species that make up a preparation. Any violation of this constraint violates the conservation of energy. Weighted by entropy S, volume v, and numbers of molecules n_i, at least one of these variables (T, p, μ_i) must change to accommodate any change in another.

A macromolecule will exert its influence on the surrounding solutions, attracting and accumulating some species, repelling others. The traditional starting point for analyzing the interactions of solution components with macromolecules is to consider an equilibrium dialysis experiment. We consider for simplicity a combination of only three species: water solvent w, macromolecule M, and small solute s. (w, M, and s are sometimes designated 1, 2, and 3, respectively, see Table 1). A solution of macromolecules containing N_w and N_s molecules of water and solute per macromolecule is on one side of a semipermeable membrane. This solution is in equilibrium with a reference solution containing n_w and n_s molecules of water and solutes.

Table 1.

Symbol translations

Timasheff (12)	Parsegian, Rand, & Rau (1)
1 or w, water	w, water
2, macromolecule	M, macromolecule
3, cosolvent	s, solute
mx/mw, with x = 3	ns/nw
v̄x, B3	Ns
v̄w, B1	Nw
v̄x − (mx/mw) v̄w or B3 − (m3/m1) B1	Ns − Nw (ns/nw)
[cf. equations 2 and 3b of Timasheff (2)]	(cf., Eqs. 5a and 6a, this paper)
δB3	Nsb − Nsa = ΔNsab
δB1	Nwb − Nwa = ΔNwab

Then for preparations kept at constant pressure p and constant temperature T, the Gibbs-Duhem constraint links the change in macromolecular chemical potential or free energy to changes in solute and water chemical potentials,

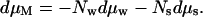2

The reference solution has its own Gibbs-Duhem constraint,

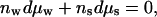3

which requires that changes in the chemical potential of water and of solute are necessarily coupled:

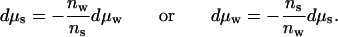4

Because of this μ_s ↔ μ_w coupling, it is possible to look at the direct and indirect influence of solute and of water on the macromolecule.

The artifice of a dialysis membrane is often not necessary as long as measurements are made on preparations sufficiently dilute in the macromolecule that the observed behavior does not include contributions from interactions between macromolecules. Then with complete rigor we can think of each macromolecule as bathed by a solution that effectively has no other macromolecules. In this limit, the water and solute are in such excess that the presence of a semipermeable membrane is superfluous (Fig. 1). Each macromolecule can be treated as being in equilibrium with regions of the solution that are far enough away from the macromolecule that these regions have the same properties as the macromolecule-free reference solution. In these regions, the solute/water concentration ratio is the same as that of the constructed reference solution. One can think of each hydrated molecule as surrounded by its own effective membrane discriminating between bathing species (Fig. 2).

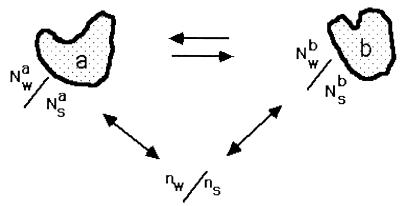
Figure 1.

Dilute macromolecules are equilibrated with a bulk solution that contains a ratio n_s/n_w of solute to water. In a region around the macromolecule, the ratio of solute to water, N_s/N_w, can be different from the bulk for various reasons. If this ratio is different between two conformations of the macromolecule, here labeled a and b, then the effect of solute or water chemical potential on the equilibrium can be described by Eq. 5. N_s and N_w are to be considered in the nature of an integrated Gibbs excess or deficit (Appendix), i.e., how N_s/N_w differs from n_s/n_w.

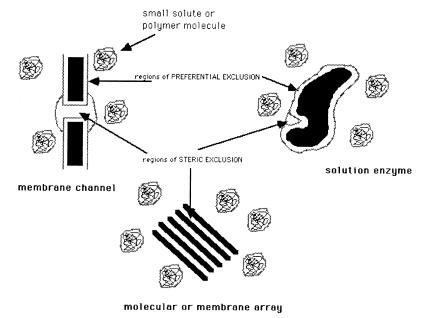
Figure 2.

A schematic representation of how solutes can produce osmotic stress on a variety of systems as a result of their exclusion. Solute can be sterically excluded from water-filled cavities, grooves, channels, or other such enclosed volumes. The crowding and preferential hydration viewpoints are specifically concerned with the exclusion of solutes from exposed macromolecular surfaces.

It is possible to shift the coordinates, to put an individual macromolecule at the center of our thinking. We will now write Gs from the idea of a Gibbs free energy rather than μs for the part of the chemical potential that is independent of the concentration of macromolecules. At constant, dilute macromolecular concentration, the change in the free energy is still described by Eq. 2, dμ_M = −N_wdμ_w − N_sdμ_s, but this relation is experimentally impractical without the constraint of Eq. 4 so that

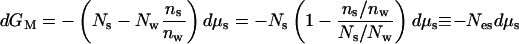5a

or

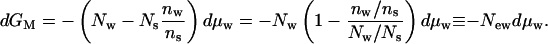5b

N_ew is the excess (or deficit) number of waters in the environs of the macromolecule; N_es is the excess (or deficit) number of solutes. These numbers are completely analogous to the Gibbs surface excess (or deficit) that describes the change in free energy of a surface with the addition of attracted or repelled solutes (see Appendix).

The change in solute chemical potential dμ_s equals d[kT ln(a_s)], where a_s is the solute activity, or dμ_s = d[kT ln(γC_s)], where γ is the solute activity coefficient and C_s its concentration. Similarly, the change in water chemical potential dμ_w equals −V̄_w dΠ, where V̄_w is the molecular volume of water and dΠ is the incremental contribution to the osmotic pressure of the solution from added solute. Osmotic pressure is, of course, a colligative property of the solution; it depends on the activities of all components. In our equations and in the equivalent equations of Timasheff, however, the activities of all components other than one solute and water are held constant.

It should be obvious that if the large molecule has no effect on the distribution of solute or water, then added solute has no effect on the free energy of the macromolecule. Only to the extent that the ratio N_s/N_w of solute to water in the vicinity of the macromolecule differs from their number ratio n_s/n_w in the bathing solution will there be a change in the free energy of the macromolecule. Direct binding of solutes to the macromolecule means that N_s/N_w > n_s/n_w; alternately, if a macromolecule attracts water more strongly than it attracts solute, then N_s/N_w < n_s/n_w. It is at this point that Timasheff alleges a conflict with the laws of thermodynamics because of his use of the word inert. For us, an inert solute is one that does not act directly on the macromolecule; there is no reaction nor binding that causes a change the conformation of the macromolecule. One wide class of such inert molecules is that of the naturally occurring osmoprotectants such as betaine and glycerol (13, 14). This particular use of inert is intrinsic to the thermodynamic use of the Gibbs-Duhem relation.§ At the same time, the particularities of the agents used make the procedure less than purely thermodynamic.

Whether a semipermeable membrane is necessary or not is dictated by the nature of the experiment. Measurement of N_ew (or, equivalently, N_es) for the individual a or b states by densitometry, equilibrium centrifugation, or light scattering (7, 15), for example, requires the use of a semipermeable membrane because the ratios of solute and water in the reference and macromolecular solutions are determined separately. The hydrostatic pressure arising from the impermeant macromolecule will affect the distribution of solute and water between the two compartments. This effect is negligible in the dilute solution limit. Measurement of the difference ΔN_ew (or ΔN_es) between two macromolecular states does not require a semipermeable membrane, but only a technique to determine the concentration or probability ratio between the two states. The redistribution of solute and water surrounding the macromolecule will affect the bulk solute concentration far from the macromolecule. This effect is also negligible in the dilute solution limit.

Instructive experiments are those that involve switching between allosteric states, that let us look at the differences in probabilities in states of a molecule (as with ionic channel opening/closing) or differences in concentration (as with hemoglobin oxygenation) when we change solution conditions. If there are two forms of a macromolecule a and b, the ratio of their concentrations (or their probabilities) goes as an exponential in the work or free energy difference ΔG_ab = G_b − G_a necessary for an individual molecule to go between the two forms, [b]/[a] = K_eq = e^(−ΔG_ab/kT).

From Eq. 5, we have

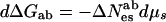6a

or

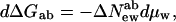6b

with ΔN_ew^ab = N_ew^b − N_ew^a and ΔN_es^ab = N_es^b − N_es^a. The observed change in the ratio [b]/[a] therefore measures the difference in the numbers N_ew or N_es for the two states.

These two equations and Eqs. 5a and 5b are strictly equivalent to the “fundamental equations” 2, 3a, and 3b of Timasheff (12) because his m₃/m₁ = n_s/n_w, δv̄₃ = (N_s^b − N_s^a) = ΔN_s^ab, and δv̄₁ = (N_w^b − N_w^a) = ΔN_w^ab (see Table 1 for a complete symbol translation between the two sets of equations).

Eq. 6a is equivalent to the standard Gibbs adsorption isotherm commonly used to compute the energetic consequences of direct solute binding. In cases where there is no significant difference in the number of associated waters, i.e., N_w^a = N_w^b, then because ΔN_es^ab = ΔN_s^ab, Eq. 6b becomes,

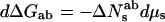7a

or

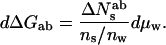7b

For solute concentrations large compared with their constant of dissociation from the macromolecule, ΔN_es^ab is constant. Plots of ΔG_ab vs. Δμ_s, as prescribed by Eq. 7a, are then linear with slopes that directly give ΔN_s^ab = N_s^b − N_s^a. Application of Eq. 7b would give nonlinear plots of ΔG_ab vs. Δμ_w that are not as instructive. In these cases of a difference in direct solute binding to the two states of the macromolecule, it makes better sense to use Eq. 7a that relates differences in macromolecular chemical potentials to changes in the chemical potential of the included solute.

In cases where solutes are net excluded (N_s/N_w < n_s/n_w), the factor N_ew in Eq. 5b is literally the net excess number of water molecules associated or included with the macromolecule. For a macromolecular reaction or conformational change from state a to state b, the difference term in Eq. 6b, ΔN_ew^ab, is just the difference between states a and b in this excess number of waters included with the macromolecule.

In the language of osmotic stress, Eq. 6b can now be simply written as the change in the difference of chemical potentials between states a and b, ΔG_ab, vs. the change in water chemical potential or the osmotic pressure, Π, and the molecular volume of water, V̄_w,

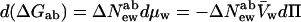8

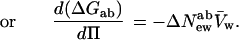In the several examples mentioned by Timasheff (12), the opening/closing reaction of membrane channels (3), the oxygenation of hemoglobin (2), the binding of glucose by hexokinase (4), the B-Z transition of poly(dG-m5dC) (16), the operator binding of gal operon repressor (17), the specific/nonspecific binding equilibrium of EcoRI (5), ΔG_ab was found within experimental accuracy to vary linearly with the osmotic pressure Π over a wide range of solute concentrations. Typically this linearity included the important limit of [solute] → 0. This linearity cannot be expected, however, to extend to arbitrarily high stresses. At sufficiently high concentrations, excluded solute can be expected to exchange with preferentially included water on exposed macromolecular surfaces (18, 19). Additionally, osmotic stress will eventually deform the macromolecule and distort states a and b; their individual N_s and N_w would change with Π to give a distorted estimate of ΔN_ew^ab.

The linearity of ΔG_ab vs. Π in these several cases means that the difference in the excess number of waters included or associated with the two macromolecular states is well defined and remains constant as solute concentration is increased. Constant ΔN_ew^ab does not mean there is no binding of solutes to the macromolecules in the examples listed above, only that there is no or very little difference in solute binding to the two states. Any significant difference in the direct binding of solute to specific sites on the two macromolecular states in addition to exclusion will have the practical effect that the apparent ΔN_ew^ab will not be constant and will depend on solute activity or, equivalently, on osmotic pressure. A double role for solute has been seen most clearly in the effect of chloride ion that has both direct-binding and osmotic-stressing modes of action on hemoglobin oxygenation. These modes were individually measured by independently varying water activity and chloride ion activity by using a second solute (11).

Effects and Causes

The perspective of osmotic stress provides an instructively sharpened picture of causal effects in solutions. Fig. 2 illustrates two possibilities that can cause an exclusion of solutes from a macromolecular state. The macromolecule may have pockets or channels of water with openings to the bulk solution that are simply too small for solutes to enter. Additionally, solutes can be excluded from exposed macromolecular surfaces. The crowding and preferential hydration perspectives have been developed specifically to account for this latter kind of exclusion. Osmotic stress measurements with several solutes of different sizes and chemical natures, all of whose effects track linearly with their contribution to water chemical potential, can discriminate between the various mechanisms. Fig. 3 illustrates the differences that can be observed. In Fig. 3a, the osmotic stress dependence of the binding free energy of Escherichia coli gal repressor to a DNA fragment containing its operator sequence is shown for two solutes, the zwitterion betaine glycine and the comparatively nonpolar triethylene glycol. A burial of exposed surface area accompanies the binding of free protein to DNA. Fig. 3b shows the osmotic pressure dependence of the free energy change for transferring the restriction nuclease EcoRI from a complex with nonspecific DNA to its recognition sequence shown for the same two solutes. A change in surface area caused by binding of free protein is avoided in this scheme. In both systems, the plots are linear, indicating that the difference in the number of included waters between the two sides of the reaction is constant over the range of solute concentrations examined. The significant dependence of ΔN_ew^ab (Eq. 6a) on the solute identity for binding of free protein in Fig. 3a is characteristic of reactions accompanied by significant changes in exposed surface area. The corresponding insensitivity to solute identity seen for the transfer of protein from one DNA sequence to another in Fig. 3b is characteristic of reactions accompanied by dominating changes in numbers of water molecules sterically sequestered in pockets or channels.

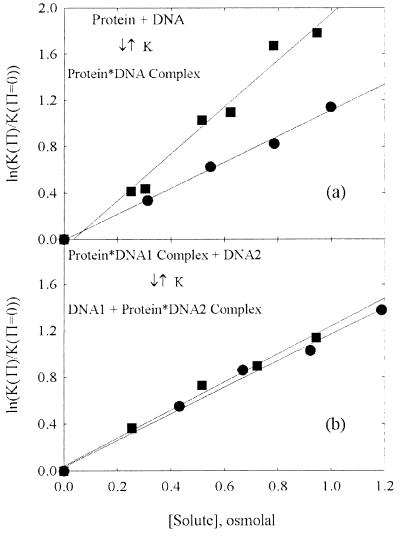
Figure 3.

The observed dependence of an osmotic stress effect on the solute nature gives insight into the basis of the exclusion. (a) The change in the binding energy of E. coli gal repressor to a DNA containing its operator sequence with increasing solute concentration is shown as a function of the osmotic pressure of the solute, in osmolal units (data taken from ref. 17). Both betaine glycine (●) and triethylene glycol (■) are apparently acting on the reaction through a difference in N_ew between the free protein and DNA in solution and in the complex. The difference in waters, however, depends on the solute; ΔN_ew = 180 waters per complex for triethylene glycol and 100 for betaine glycine. This difference is characteristic of reactions that bury exposed surface area. (b) The osmotic stress dependence of the energy difference between the specific binding of the restriction nuclease EcoRI to a DNA fragment (DNA2) that contains its recognition sequence vs. the nonspecific binding of the enzyme to a DNA oligonucleotide (DNA1) that does not carry the recognition sequence. This is shown for the same two solutes, betaine glycine (●) and triethylene glycol (■) (data taken from ref. 8). In this case the effect of the two solutes is identical, within experimental error, with ΔN_ew = 110 waters. This result is characteristic of reactions with changes in the numbers of waters that are sequestered in sterically inaccessible pockets or cavities.

Steric Exclusion from Water-Filled Volumes

Much osmotic stress work has used inert solutes to probe changes in the size of water-filled cavities, grooves, channels, or pockets that are simply not solute accessible. This exclusion can be enforced by a dialysis membrane as was done for the gelation reaction of sickle hemoglobin (20). The distinguishing characteristic of these systems—e.g., the opening/closing reaction of several channels (3), the oxygenation of hemoglobin (2), and the specific/nonspecific binding equilibrium of EcoRI (5)—is that ΔN_ew^ab varies negligibly or at worst very weakly with the identity of the solute used to change the chemical potential of water. These systems are the most straightforward for visualizing osmotic stress. Once again, there may be direct solute binding and there most probably is exclusion from exposed surfaces, but there is little or no difference in this binding or exclusion from exposed surfaces between the two states. The difference in the number of waters between the two states represents a real physical volume that gives direct information about structure.

Crowding

Solutes often are unable to occupy a region near a wall or near a large macromolecular surface. The effect of this exclusion is to create depletion forces that push together the solute-excluding regions (9). There is a release into the solute-containing solution of some number of water molecules, ΔN_ew. This classical crowding formulation assumes that exclusion of solute is strictly a steric effect. Excluded volumes are calculated from the interaction of hard spheres. The characteristic feature of a crowding exclusion is a predictable dependence of the excluded volume on solute size, but not on chemical nature. Because there is no solute binding considered within this theoretical framework, the underlying thermodynamics within the Gibbs-Duhem approach can be treated strictly from the viewpoint of the included water. Indeed, to the first-order approximation often used in crowding analysis (e.g., ref. 21) in which solute-solute interactions are neglected, the treatment transparently gives a change in macromolecular free energy that is the product of the calculated excluded volume, V̄_wΔN_ew, and the first-order approximation to the osmotic pressure of the solute (linear in solute concentration in accord with the van't Hoff law of ideal solutions). The estimated excluded volume may depend on osmotic pressure once higher-order terms are included. Such higher-order computations are difficult because inclusion of these terms must for self-consistency also predict solute osmotic pressures. To avoid such tangles, only measured osmotic pressures are used in the osmotic stress approach.

Hard particle equations of state that are used to estimate crowding might give geometric insight into the space wars between molecules. For larger particles, on the colloidal scale, depletion forces can be rigorously quantified (22). However, for polymers acting on proteins there are assumptions that render a hard-sphere picture only qualitative. Can a random coiled polymer be modeled as an effective hard sphere of fixed diameter? The measured exclusion of polyethylene glycol of different molecular weights from proteins is arguably (23, 24) consistent with crowding by hard spheres (whose radii are approximated by the radii of gyration of the polyethylene glycol polymers). Molecular Coulter Counter measurements (25, 26), however, show that polyethylene glycol polymers of different sizes are not always excluded from well-defined cavities, as a hard-sphere model would require [e.g., figure 4 of Bezrukov et al. (25)]. Rather, there is a wide range of partial exclusion as a function of molecular size.

Preferential Hydration

The chemical nature of the solute, as well as its size, can determine exclusion from macromolecular surfaces. The interaction energy of a DNA phosphate group, for example, with a methylene group of triethylene glycol is very different from that with water. Timasheff (7, 27) has likened this mechanism for the exclusion of solute from exposed macromolecular surfaces to the increase in surface tension at air-water interfaces caused by polar solutes and salts that also must reflect an exclusion from that particular interface. The analogy can be further extended by constructing a Gibbs dividing surface for the exclusion of solutes from exposed protein surfaces as has been insightfully done for the effect of solutes on air-water surface tensions (see Appendix). Arakawa and Timasheff (28) measured a dependence of lactose exclusion free energies on protein surface area. The observed value of 1.5 cal/mole protein per mole lactose per Ų surface area translates into an equivalent Gibbs dividing surface that is located ∼ 4 Å from the protein surface. It is as though within this distance (about one water layer), no lactose would be found; the outside would have the bulk lactose concentration. The energy needed to create this equivalent zone free of solute is the work of the solute osmotic pressure times the cleared volume.

The macromolecular reactions we have studied that clearly involve a change in exposed surface area, as, for example, the BZ transition of poly(dG-m⁵dC) (16) and the binding of free E. coli gal repressor to its operator sequence (17), showed that the exclusion of each individual solute could be well described by a constant number of included waters, ΔN_ew^ab, (over the range of solute concentrations used), but this difference in the excess number of waters between two states is very sensitive to both the size and chemical nature of the solute probing the reaction.

Prospectives

Our interest in measuring waters displaced in macromolecular reactions is rooted in the direct measurement of forces between macromolecules. In this case, macroscopic, condensed arrays of ordered macromolecules are equilibrated against a solution of a polymer that is excluded from the macromolecular phase (typically polyethylene glycol) and the spacings between the macromolecules are measured (typically by x-ray scattering) as a function of the polymer osmotic pressure. Thermodynamic force vs. distance curves have been measured now for all classes of biological macromolecules, lipid bilayers, DNA, several polysaccharides, and proteins. The striking feature of these forces is their similarity for all the very different systems, charged, net neutral, or totally uncharged. We have interpreted these measurements as indicating that macromolecular interactions in the last 10–15 Å of separation are dominated by the structuring of water between surfaces (29). These hydration forces are much stronger at close spacings than van der Waals or electrostatic interactions that are conventionally considered important. From this perspective, the key to understanding the strength and specificity that characterizes most all biologically important recognition reactions is in the water that is released when two complementary surfaces mate.

Regardless of which perspective one prefers in thinking about the consequences of solute or polymer exclusion on reactions between macromolecular states or conformations, the energies induced can suffice to change conformations of individual states. Not only can one measure a change in solute exclusion caused by the closure of the active site cleft of hexokinase with glucose binding, but one can also apparently use the strong exclusion of solute to close the cleft even in the absence of glucose (4). One can now begin to separate the mechanics of cleft opening and closing from the energetics of glucose binding. Not only can a difference in sequestered water between the deoxy and liganded conformations of Scapharca dimeric hemoglobin be measured by the osmotic stress approach, but also high osmotic pressures seem capable of changing the conformation of the deoxy form to the liganded structure even in the absence of ligand (30). Not only can there be a difference in sequestered water between complexes of the restriction nuclease EcoRI that are specifically and nonspecifically bound to DNA, but high osmotic pressures can remove this sequestered water from nonspecific complexes with particular DNA sequences that are closely related to the specific binding sequence, but not others (31).

These are only a few encouraging examples of what can be learned about macromolecules from looking explicitly at their response to the activity of water.

Counting the Number of Molecules Adsorbed to or Repelled from a Macromolecule

Among the more difficult concepts in physical biochemistry is how to estimate the number of molecules bound/attracted to or repelled from a macromolecule. Confusion is especially severe when there is an accumulation or repulsion of small molecules near the macromolecule rather than clean, fixed binding.

As in many thermodynamic problems, the issue was confronted and solved conceptually by Gibbs. Consider the change in the energy of a surface caused by solute added to the solution bathing it. The Gibbs adsorption isotherm says that the free energy of the surface will decrease with the solute chemical potential in direct proportion to the number density Γ of solutes associated with the surface, dG = −Γ dμ_solute. Associated means the excess number of solute molecules, N_es, on or about the surface compared to the number of solutes that would be in the same volume of bulk solution.

Similarly repulsion from the surface, negative N_es, means that solution near the macromolecules must be cleared of solute, costing energy. Increased chemical potential of the solute in the bath pushes solute toward the surface and increases this cost of clearing.

One way to visualize the energetic cost of solute exclusion is to recognize that there is variation in number density N(x) near a surface, a deviation from the bulk density, N_solute(∞). If we consider an infinite planar surface in contact with an aqueous solute solution, the connection between changes in the free energy of the surface and changes in the solute and water chemical potentials is through this solute concentration variation,

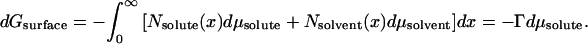A1

Once again, the Gibbs-Duhem relation for species far from the surface, N_solute(∞)dμ_solute + N_solvent(∞)dμ_solvent = 0, makes this equation practical. The integral over the region away from the surface becomes

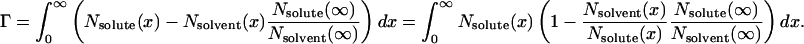A2

There is a change in the free energy of the surface only to the extent that the ratio of solute to solvent differs from that in the bulk.

A macromolecule and the attracted/repelled components of its bathing solution act together in the same way. For solutions dilute in macromolecules, the properties of this solution are proportional to macromolecule concentration. It is possible to integrate the excess number [N_i − N_i(∞)] of all species in all the space around each macromolecule, in the spirit of the Gibbs adsorption isotherm.

Two-zone models of single-solute exclusion (32) and Eq. A2 can be connected by a Gibbs dividing surface construction that replaces the actual solute profile N_solute(x) with a step function in concentration from 0 to N_solute(∞). The location of the dividing surface, X_Gibbs, is fixed to give the same surface deficit of solute as the actual gradient or ∫₀^∞[N(x) − N_solute(x)]dx = −N_solute(∞)X_Gibbs. In this way, the energy associated with creating this clear zone can be seen as the work needed to push a semipermeable membrane (permeable for water, but not solute) from the surface at x = 0 to X_Gibbs. This displacement incurs an osmotic work per unit area Π_osmotic X_Gibbs = kT N_solute(∞) X_Gibbs, in the van't Hoff limit. An elegant application of this reasoning is in the Onsager-Samaras theory of increasing surface tension when strong electrolyte is added to a solution (33). To the extent that salt is repelled from the surface there is an increase in work needed to create that surface.