Limit, logic, and computation

Abstract

We introduce “ultrafilter limits” into the classical Turing model of computation and develop a paradigm for interpreting the problem of distinguishing the class P from NP as a logical problem of decidability. We use P(NP) to denote decision problems which can be solved on a (nondeterministic) Turing machine in polynomial time. The concept is that in an appropriate limit it may be possible to prove that problems in P are still decidable, so a problem whose limit is undecidable would be established as lying outside of P.

The Turing machine T represents an abstraction of the principles of mechanical computation. The machine consists of a head and a tape. The head is capable of being in one of a finite number of “internal states” {q_i} and can read and overwrite a symbol ∈ {S_j} from a finite set of symbols and then shift one block left or right along the tape. It contains a finite internal program which directs its operations. At any time the complete state of T is the record on the tape together with the internal state. Consider a problem Q, with a yes/no answer, for which infinitely many instances exist, for example, the satisfiability of Boolean formulae. The decision problem Q is said to lie in class P if there is an internal program which will correctly answer all instances I of Q “yes” (“no”) by halting on symbol (0) after a number of operations which is some fixed polynomial function in the number of bits of the input. One says Q lies in NP (nondeterministic polynomial time) if there is an “existential” program operating on I plus a number of “guess bits” which correctly answers all instances I in polynomial time. The existential program is deemed to answer “yes” if for some setting of the guess bits the machine halts on 1.

Since the P/NP problem has at its core the distinction between polynomial and exponential growth, it is natural to look for perspective to other models within mathematics where this dichotomy is manifest. In complex analysis an exponential function, e.g., 2^z, has an essential singularity at infinity, in contrast to the continuous branched structure at infinity exhibited by a polynomial. This dichotomy is mirrored in cardinal arithmetic (1) where the function 2^x is discontinuous at every limit cardinal α, for which no smaller cardinal β has a power set P(β) equinumerous with P(α), that is,

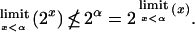This last fact, for α = ℵ₀, influenced Sipser (2) in his thinking that the distinction between analytic (projections of Borel) sets and coanalytic sets (the complement of an analytic set) in analysis might provide a tool for distinguishing NP sets (sets accepted by NP-time Turing machines) from co-NP sets (the complement of NP sets).

The theory of group presentations may be taken as an analog of computation. Milnor (3) and Schwarzc (4) introduced the notion of the growth of a finitely generated group G. The group G has polynomial growth (exponential growth), if it has a presentation in which the number of distinct elements of G which can be written as words of length = ℓ in the generators and their inverses is ≤P(ℓ) for some polynomial P (≥b^ℓ for some base b > 1). It is easy to show that both these properties are in fact independent of the presentation and depend only on the group G.

Within this theory we will explain how taking the appropriate limit transforms a distinction in growth rates into a dimensional dichotomy. A celebrated theorem of Gromov’s (5) states that G has polynomial growth iff it contains a nilpotent subgroup of finite index. The proof considers a sequence of base-pointed metric spaces {(G_ɛ, id)}, ɛ → 0, where G_ɛ has metric dist(g₁, g₂) = ɛ (minimum word length (g₁g₂⁻¹)). This sequence has a convergent subsequence, in the Gromov-Hausdorff sense, if and only if G has polynomial growth, in which case the limiting metric space (Y, y₀) is finite-dimensional.* The proof proceeds by representing G into isometries (Y), which is a Lie group by the Montgomery-Zippen theorem. Ultimately, the limit Y is seen to be a nilpotent Lie group endowed with a Carno-metric. For example, if G = integers Z, then Y is the real line R. If G = Zⁿ, then Y = Rⁿ. If G is the discrete Heisenberg group

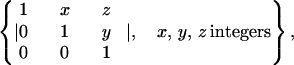then Y is the continuous Heisenberg group with x, y, and z real.

If G has faster than polynomial growth, {G_ɛ, id} will not approach a limit in the Gromov-Hausdorff sense, but an ultrafilter limit can be forcibly extracted. Let (X_i, ∗_i) be any sequence of pointed metric spaces i = 1, 2, 3, . . . . Consider admissible sequences {x_i ∈ X|, there exists a constant c so that dist(∗_i, x_i) < ic. Let ω be any non-principle ultrafilter in Ž⁺, i.e., ω belongs to the growth Ž⁺∖Z⁺ in the Stone-Cěch compactification Ž⁺ of Z⁺. Using the universal property

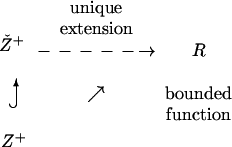Gromov (6) defines a unique real number

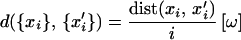which induces a pseudo-metric on the admissible sequences. Dividing by the equivalence relation—points with distance = 0 are equivalent—yields a metric space X, which we call the ω-limit of (X_i). It has been conjectured that the homeomorphism type of the ω-limit is independent of the choice of non-principle ultrafilter ω.

If the sequence ((X_i, 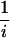dist_i), ∗_i) is convergent in the Gromov-Hausdorff sense, then this limit is also the ω-limit; however, the ω-limit exists in complete generality. For example, when applied to the constant sequence {G, id}, G a word-hyperbolic group (the generic case for groups of nonpolynomial growth; ref. 6), then the ω-limit is an ℝ-tree (a space in which there is a unique imbedded interval joining every two points). Although of covering dimension one, this ℝ-tree is enormously large, in the sense that there is no countable basis for its topology and its Hausdorff dimension is infinite.

The paradigm: “polynomial growth implies a well-behaved limit,” if applied to the P/NP problem, would take the schematic following form:

A polynomial time algorithm T solving a finite-decision problem Q should “converge” to some “continuous procedure” for solving an infinitary version of Q, whereas an exponential-time algorithm should not be expected to have any sensible limit.

Applications of Paradigm

There is a toy model of computation, the search of a database, in which this paradigm applies. Consider the databases consisting of the positive orthant of Zⁿ and W, where Zⁿ is the integer lattice in Euclidean n-space and W is the universal unrooted 3-valent tree with edges of length = 1. (W could also be taken to be a co-compact lattice in any hyperbolic space Hⁿ, n ≥ 2, and all the following assertions would remain true but be slightly more technical to check.) Writing each integer r ∈ Z in base 2, the kth component f_k(r) of a map f : Z⁺ ∪ 0 → Zⁿ is defined by reading only the digits congruent to k mod n. Now fix any non-principle ultrafilter ω ∈ Ž⁺. Regarding Z⁺ ∪ 0 as a sequence of spaces where the jth copy has its standard metric multiplied by (j)⁻⁽ⁿ⁻¹⁾, and regarding Zⁿ as the constant sequence of spaces, a Hölder-1/n continuous ω-limit f̄ : R⁺ ∪ 0 → Rⁿ is obtained from applying the limit construction to domain and range simultaneously. The map f may be interpreted as a particularly efficient† search of the positive orthant of Zⁿ; the rescaling of Z amounts to a speed-up of the search, so that the ball of radius j in the jth Zⁿ is searched in time proportional to j. Finally, f̄ is the limiting solution to the infinitary version of the search problem in which all points in the positive orthant of Rⁿ must be visited. The map f̄ is the Peano-Hilbert curve.

Turn now to ω-limit (W, w₀) where some vertex of W has been chosen as basepoint. There are 2^ℵ₀ edge paths leaving w₀ and heading toward infinity. These define an uncountable set of sequences {w_i,j}, i ∈ Z⁺, j ∈ 2^ℵ₀, whose mutual ω-distances d({w_i,j}, j, {w_i,j′}) = 2 are all two. This implies that the ω-limit W = W̄ has no countable basis for its topology. Consequently, W̄ is not equal to the image under any continuous map of any second countable space, e.g., R⁺ ∪ 0. Thus no discrete search of W can be constructed so that a rescaled limit leads to a continuous search (i.e., epimorphism) of W̄. In these models we see “polynomial time” converging to continuous and “exponential time,” failing to define an appropriate limit, echoing the observations in complex analysis and cardinal arithmetic.

Let N_k be the set of Boolean formulae which are conjuctions of k-fold disjuncts of a finite alphabet of literals; k-sat denotes the satisfaction problem for fomuli in N_k. It is well known (7) that 2-sat lies in P, whereas 3-sat is NP-complete. In “k-sat on Groups and Undecidability” (unpublished work), an infinitary version of k-sat is introduced which depends on a fixed infinite group. Truth assignments for group elements are sought subject to a family of disjunctive clauses closed under right multiplication by a finite index subgroup H ⊂ G. It is shown that for this extension of the satisfaction problem for G ≅ Z ⊕ Z, 2-sat remains decidable while 3-sat becomes undecidable in ZFC. While supporting the paradigm, the proof does not argue on the basis of the inclusion 2-sat ⊂ P and therefore does not immediately generalize. In view of the first two examples, w-limits seem to be a promising general approach to constructing decidable‡ limits of problems in P.

What follows are two speculations on how the introduction of ω-limits could have a role in distinguishing P from NP. The sketched arguments should be read as design criteria for limits that we do not know how to construct. The first is based on the preservation of connectivity under a continuous map. The second searches for a bridge to Gödel’s incompleteness theorem. Fix a non-principal ultrafilter ω ∈ Ž⁺ and let 𝔽 be the set of finite Boolean formulae on an infinite alphabet organized into a pointed metric space, or perhaps some weaker structure, in some manner which we do not yet know how to specify. Let 𝔽̄ be an ω-limit or some similar limit of 𝔽. For the argument-plan we propose, the definition of the structure and the details of the limit taken must be such that 𝔽̄ is connected. However, it is necessary that if we restrict to 𝔽′ ⊂ 𝔽, a class of formulae which can be checked for satisfiability in poly-time, the limit yields a disconnected space 𝔽̄′. We suppose that the ω-satisfiability (1) or unsatisfiability (0) of f̄ = {f_i} ∈ 𝔽̄ can be defined by applying ω to the satisfiability of each f_i in a sequence defining f̄. One can imagine that a polynomial time algorithm T could be rewritten “efficiently”—as in our choice of scanning function f into the positive orthant of Zⁿ—so that it would converge to a “continuous decision procedure” T : 𝔽̄ → {0, 1}, contradicting the connectivity of 𝔽̄. The picture is that T would evolve f̄ ∈ 𝔽̄ through a succession (variable t) of complete state sequences (variable i) {S_i,t} defining a path with parameter t ∈ [0, 1] in S, the ω-limit of the discrete space of sequences of complete states {S_i}. Thus T would define a homotopy T̄ : 𝔽̄ × I → S whose end T̄(F × 1) must be disconnected according to yes/no on ω-satisfiability. This would contradict the topological connectivity of 𝔽̄.

The first-order theory A of arithmetic is known to contain weak fragments A⁻ for which there exists a decision procedure (carried out within first-order arithmetic, say by a Turing machine) for the provability in A of statements in A⁻. The best known example (and a high tide mark of Hilbert’s program to axiomatize mathematics) is Presberger Arithmetic PrA (8), which is essentially Peano arithmetic§ absent multiplication. Without multiplication, indexing of formulae cannot be achieved, so Presberger Arithmetic escapes Gödel’s incompleteness theorem. It seems plausible that a suitable ultrafilter limit could resurrect multiplication, since multiplication by any fixed integer is explicitly expressible as a repeated addition. Thus one might have a schematic formula on the level of ω-limits:

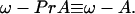In A, the Gödel sentence “there exists an integer x₀ which codes for a proof of 0 = 1” requires only a single unbounded existential quantifier. Suppose that we can construct a fragment of arithmetic A⁻ in which (i) the problem Q, of deciding (in A) the validity of sentences of A⁻ with only one unbound existential quantifier, lies in NP and (ii) ω − A⁻ ≡ ω − A. With regard to (i) we note that ref. 9 proves that PA is a bit too strong a fragment; a nondeterministic Turing machine must run at least ≥2^ℓc, for some c > 0, to decide such sentences of length = ℓ. One may have to look to systems as weak as A⁻ = quantified Boolean formulae to achieve this condition. Note that a Boolean formula can be written to specify the ith bit of multiplication so some aspect of arithmetic is retained even at this level. The paradigm that things polynomial have well behaved limits would then suggest that a polynomial-time algorithm for Q would yield a decision procedure (suitably interpreted) for “ω-sentences” in ω − A⁻ with a single unbounded quantifier. By (ii) such ω-sentences would include Gödel-like ω-sentences and hence be undecidable. Such a contradiction would show P to be strictly smaller than NP. The philosophy is that within an appropriate limit, quick should become decidable, whereas slow may become undecidable.