A stochastic, cantilever approach to the evaluation of solution phase thermodynamic quantities

Abstract

A cantilever device based on competitive binding of an immobilized receptor to immobilized and soluble ligand and capable of measuring solution-phase thermodynamic quantities is described. Through multiple binary queries, the device stochastically measures the probability of the formation of a bound complex between immobilized protein and immobilized ligand as a function of soluble ligand concentration. The resulting binding isotherm is described by a binding polynomial consisting of the activities of soluble and immobilized ligand and binding constants for the association of immobilized protein with free and immobilized ligand. Evaluation of the polynomial reveals an association constant for the formation of a complex between immobilized ligand and immobilized protein close to that for the formation of complex between soluble protein and soluble ligand. The methodology lays the foundation for construction of practical portable sensing devices.

Technologies that permit the rapid quantitative determination of analytes have myriad applications in point-of-care diagnostics and environmental and food safety monitoring. Most rely on the formation of specific complexes between an analyte and a receptor and require an experimentally observable measure of binding. By far, the most commonly used signal is a change in optical properties, either absorptive or emissive. However, many systems of interest lack useable optical properties, either because of the inherent optical properties of the analytes themselves or because of the characteristics of the sample milieu, and in recent years a number of general approaches have emerged for the measurement of intermolecular binding. During the past several years, titration microcalorimeters have become commercially available (1, 2). These instruments measure the heat evolved during ligand binding as a function of ligand concentration; this information can be fit to a simple binding isotherm to reveal binding free energies and enthalpies. Another group of techniques, typified by surface plasmon resonance and quartz crystal microbalance, use changes in the electro-optical properties of a surface as a small- or macromolecular species is deposited (3–5). This signal is used to determine kinetic values for binding and unbinding, and the ratio of these parameters furnishes a binding constant. Although broadly applicable, both techniques require long sampling times (hours) and have material and operational characteristics that preclude their utility in field applications.

Dynamic force spectroscopy, typified by the atomic force microscope (AFM) and the optical trap, measures the force required to unbind individual molecular complexes (6–20). Unbinding forces are not simply related to free energies or to association rates, because the application of force necessarily removes the bound complex from an equilibrium condition (21). The study of unbinding kinetics by dynamic force spectroscopy is further complicated by the application of force along a single vector: this limitation precludes the evaluation of microstates leading to an unbinding transition state (22). Even at an equilibrium condition, the relationship between unbinding force and free energy is tenuous (23). Although forced unfolding has been used to calculate the free energy of denaturation of RNA by application of the Jarzynski equality, the experimental approach is controversial and, in any event, incompatible with ligand binding (24–26). Other cantilever-based approaches have been used to characterize both the thermodynamics and kinetics of binding. For example, functionalized oscillating cantilevers have been used to register the deposition of recognition elements by observing changes in resonant frequency (27–32). Still, force spectroscopy in its present state provides only a limited biophysical characterization of the bound complex. New strategies are required for the application of AFM to the study of binding thermodynamics.

Here, we describe a cantilever-based method for the evaluation of solution-phase thermodynamic quantities. The approach uses threshold sensing, or the evaluation of the binary probability of binding by stochastic measurement. In this approach, ligand immobilized on a cantilever tip is used to probe the binding of soluble ligand to receptors tethered to an apposing surface. By measuring the probability of the formation of a complex between immobilized ligand and immobilized protein over a range of soluble ligand concentrations a binding isotherm is generated. The binding isotherm is described by a polynomial that contains information about the binding constants for complexation of immobilized protein to free and immobilized ligand and about the activities of free and immobilized ligand. We demonstrate the methodology by using a model system of immobilized and soluble lactose binding to an immobilized carbohydrate-binding protein, galectin 3.

Results

Preparation of Surfaces and Tips.

Our proof-of-concept device is based on the mammalian lactose/N-acetyl lactosamine binding protein galectin 3. We have used the murine protein; although the structure of this lectin has not been reported, a crystal structure of the highly homologous human analogue (84% identity overall; 95% identity in the carbohydrate recognition domain) in complex with lactose is available. The carbohydrate recognition domain (CRD) resides at the C terminus of the protein. Therefore, we chose to immobilize the protein through an His₆-tag at the distal N terminus, a disordered collagen-like repeat of 120 aa: this immobilization should expose the CRD in an orientation free to interact with ligand (33). Lactose interacts with the CRD primarily through the nonreducing terminal galactose moiety, making relatively few contacts with the glucosidic residue. Thus, we immobilized lactose through the glucose anomeric carbon, an orientation that should not influence protein–carbohydrate contacts in either a positive or negative fashion.

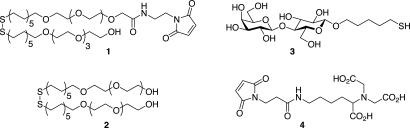
The binding system was constructed by using self-assembled monolayers of dialkyl disulfides on gold-coated cantilevers (Fig. 1). The disulfides consisted of a mixture of undecanyl-oligoethylene glycol 2 and maleimide-terminated undecanyl-oligoethylene glycol 1 at a predetermined mole fraction of maleimide (34). The embedded maleimide serves as an anchor point for the attachment of mercaptopentyl lactoside (3), the immobilized ligand for galectin 3. Although many common immobilization strategies employ the gold–thiol interaction for the formation of self-assembled monolayer, the use of thiol is not appropriate in this context because of thiol-maleimide cross-reactivity. For the cognate surface, we used quartz slides functionalized with the metal chelate nitrilotriacetic acid (4), providing oriented surface immobilization of His₆-tagged galectin 3 (35). Functionalization was achieved by treating oxidized quartz surfaces with mercaptopropyl trimethoxy silane and exposing the resulting surface to a solution of 4. Finally, functionalized slides were exposed to a solution of His₆-tagged protein in the presence of Ni²⁺.

Fig. 1.

Molecules used for immobilization of lactose and galectin 3.

Competitive Binding and Signal Processing.

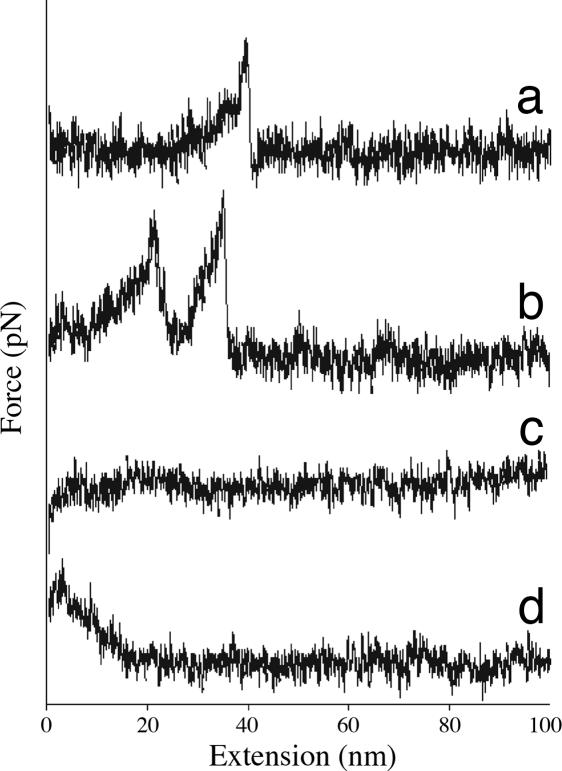
Fig. 2 shows typical force-extension plots for the dissociation of immobilized lactose galectin-3 complex during tip retraction. Implantation of the tip into the receptor-coated surface led to a variety of undesirable events, including denaturation and nonspecific adsorption of receptor onto the tip, or complex interactions that were impossible to deconvolute. To minimize implantation, computer-controlled approach was conducted in single nanometer increments. At each position a small voltage ramp was applied to drive the substrate 1 nm closer to the tip and then a retract–approach cycle was initiated. Proximity or gentle contact was judged by the resulting force-extension curve: the observation of binding events (Fig. 2 a and b), contact forces (Fig. 2c), or nonspecific adhesion forces (Fig. 2d) indicated proximity.

Fig. 2.

Typical force-extension plots for binding of lactose and galectin 3.

The process was repeated until no fewer than 350 proximity-related events were recorded. Each event was scored as nonbinding, i.e., contact without specific binding or nonspecific adhesion at extensions of <10 nm, or binding, i.e., ruptures between 25 and 300 pN at extensions of 10–50 nm. The extensions observed presumably reflect unfolding of the disordered N-terminal collagen-like domain. Under these criteria, the instrument observed binding events in 91% of the approaches achieving proximity.

Because the chemistry used for immobilization of protein relies on zinc chelation, unbinding could represent rupture of either the metal–histidine or lactose–galectin 3 interaction. Measurement of the force required to rupture the metal–histidine complex has been accomplished by several groups, although not at the loading rate used here (36–39). Iron(III) complexes require a significantly larger rupture force than those based on Ni²⁺. To determine the point of rupture, substrates were prepared by using Fe³⁺ as the immobilizing ion and ≈350 binding events were collected.^§ The average rupture forces observed by using Fe³⁺ and Ni²⁺ were 71 and 72 pN, respectively, consistent with rupture of the galectin 3–lactose complex.

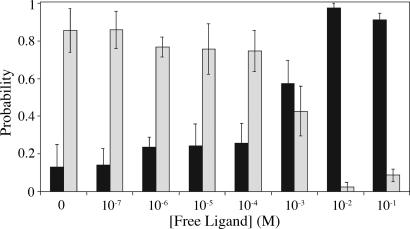
With boundaries established for differentiating binding and nonbinding events we turned to the competition experiments that will both sense soluble ligand concentration and provide binding constants characterizing complexation of immobilized species. Multiple binding events lead to a range of interaction forces with magnitudes ranging from 25–300 pN and at extensions between 10 and 50 nm: the impact of multivalency is considered below. For the competitive assay we use these limits to discern between binding (10 < l_rupture < 50 nm, 25 < F_rupture < 300 pN) and nonbinding (l_rupture < 10 nm, F_contact or F_adhesion). Using this rule, we measured the binary probability of binding vs. nonbinding as a function of soluble ligand concentration (Fig. 3).

Fig. 3.

Effect of soluble ligand on binding probability. Dark bars represent the probability of nonbinding and light bars represent binding. Errors were evaluated at each concentration by binning groups of 100 pulls for binding/nonbinding and determining the standard deviation between groups. Error bars represent one standard deviation from the mean.

Between 350 and 800 proximity-related events (contact, nonspecific adhesion, binding events) were collected at concentrations spanning six orders of magnitude in soluble ligand concentration (10⁻⁷ to 10⁻¹ M). Each approach–retract cycle was evaluated as binding or nonbinding, providing a probability of binding at each concentration. As expected, the probability of binding varies with the concentration of soluble ligand. At low concentrations, binding between the ligand and tip occurs with the greatest frequency. As soluble ligand concentration rises, there is a diminution of the likelihood of binding concomitant with an increase in the probability of nonbinding: this observation is consistent with a model of competition between soluble and immobilized ligand. When plotted as a function of soluble ligand concentration, the fraction of immobilized protein bound by free ligand (ν_Lf) gives a Langmuir isotherm. (The fractional occupancy of soluble ligand is defined as the number of occupied sites divided by the total number of surface sites.). The concentration of free ligand at the inflection point, ≈1 mM, provides information about the equilibrium processes probed by this experiment.

Discussion

Assuming the experimental design presents no insurmountable kinetic barriers to binding, the competing equilibria probed during binding in the presence of free and immobilized ligand are depicted in Eq. 1.

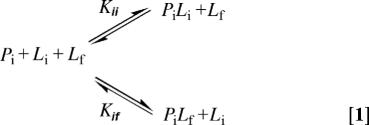Thus, protein binding sites on the surface (P_i) are bound by free ligand (L_f) in an equilibrium described by K_if. Upon approach, P_i may also bind immobilized ligand (L_i) in an equilibrium described by K_ii. When brought into proximity, the immobilized protein (P_i) and immobilized ligand (L_i) are in equilibrium with the tip-surface complex (P_iL_i); the immobilized binding constant K_ii describes this equilibrium. The free ligand (L_f) competes for surface binding sites through formation of a P_iL_f complex, a process governed by the free association constant K_if. The binding polynomial for competing equilibria is

where a_Li and a_Lf are the activities of immobilized and soluble ligand, respectively (40). The fraction of binding sites occupied by free ligand, ν_Lf, is given by the partial derivative of the natural logarithm of the binding polynomial (ln Q) with respect to the natural logarithm of the free ligand activity, i.e.,

This expression provides a relationship between fractional occupancy and the equilibrium constants K_ii and K_if. We equate K_if to the association constant measured calorimetrically in solution [6,400 ± 100 M⁻¹, see supporting information (SI) Text and SI Fig. 6]: a large body of binding data evaluated by surface plasmon resonance techniques supports this assumption.^¶ The experimental design developed here facilitates evaluation of K_ii, a value that, to our knowledge, has not been characterized.

Nonlinear curve fitting of the data to Eq. 4 provides numerical solutions, although the resulting values of K_ii show a strong dependence on the initial fitting value of a_Li. The nominal concentration of ligand tethered to a polymer anchor is simply 1/N_A divided by the swept volume of the head group: these values provide a “concentration” of ≈30 mM.^‖ Equating this value of with the activity of immobilized ligand and fitting the uncorrected data of Fig. 3 provides a value of K_ii of 150 M⁻¹, ≈40-fold less than the solution-phase value. This value, however, counts only bound and unbound retractions, regardless of the number of discrete protein-carbohydrate complexes formed. The observed value, then, must be corrected for multivalency effects.

The Effect of Multivalency.

Our immobilization protocol produces tips and surfaces functionalized at a density that results in multiple protein–ligand complexes on each approach; simple calculation predicts ≈13 interactions are feasible, given the cantilever design and the nature of our surface functionalization. Multivalency has a significant effect on the derivation of K_ii, and evaluation of this term requires knowledge of the total number of protein–carbohydrate interactions ruptured on each pull. Deconvolution of this value requires knowledge of the force required to rupture a single interaction.

The autocorrelation function is a convenient tool for identifying periodicity (41) and Florin and coworkers reported the use of such functions to observe the periodic nature in force-bin count histograms (8). Briefly, the histogram of bin counts as a function of rupture force was fit to a polynomial function and an autocorrelation function based upon the difference between the polynomial fit of the histogram evaluated at the center of the bin was subtracted from the actual histogram data (8, 42). The periods observed in the autocorrelation function were then averaged to determine the fundamental period, which was equated with the fundamental rupture force of a single binding event at a fixed loading rate, an equality that assumes a linear relationship between valency and unbinding force. As described by Williams (43), this approach yields an underestimate of the fundamental binding force, because the rupture force for individual complexes in a multiply bound complex vary as the loading rate, a value not necessarily equivalent for multiple sequential unbindings. This correction, however, will be negligible for low (2–3) valent bindings, and small even at higher values and, for the purpose of this study, the approach yields a reasonable approximation.

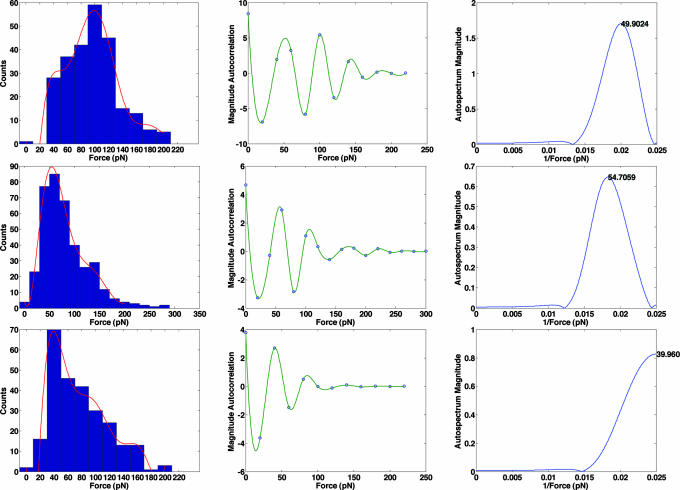
We have extended this approach, calculating the monomeric rupture force through the use of power spectra. The histogram bin spacing, ΔF, is analogous to time in discrete-time signal processing, where the sample rate is computed from 1/Δt and the Nyquist frequency (1/(2Δt)) sets an upper limit to the frequency that can be resolved. The Fourier transform of the autocorrelation function produces an autospectrum, which is in turn used to determine the frequency of a periodic signal in the time domain. By analogy, 1/(2ΔF) defines the upper bound for the “frequency” that can be resolved for the periodic signal from the force data. The microcantilevers used here afford a resolution of ≈20 pN: this value sets a lower bound on the bin size, and the smallest force that can be resolved, 2ΔF, or 40 pN. A polynomial fit was applied to the histogram compiled at each soluble ligand concentration: the order of the polynomial was selected so as to capture the best fit of the dominant peak and the remainder of the bins in the histogram. From this fit, an autocorrelation function was derived and a Fourier transform was computed to identify the fundamental force present in the data. The clear advantage of this approach is that derivation of the fundamental force is based on integration over all data in the autocorrelation function, as opposed to an average of the period observed from a limited number of data points.

Fig. 4 Upper Left shows the force histogram in the absence of soluble ligand, fit to a ninth-order polynomial. The resulting autocorrelation function (Fig. 4 Upper Center) shows obvious periodicity of ≈50 pN. The corresponding autospectrum, obtained from the Fourier transform of the autocorrelation function (Fig. 4 Upper Right) is consistent with this observation, showing a peak at 0.02 pN⁻¹, suggesting a monovalent rupture force of 50 ± 10 pN, or any integer factor of this value. The process was repeated in the presence of 10⁻⁷ (Fig. 4 Middle) and 10⁻⁵ (Fig. 4 Lower) M lactose. As expected, the addition of soluble ligand diminishes the probability of multiple binding events. Comparison of the histograms at 0 (Fig. 4 Upper Left), 10⁻⁷ (Fig. 4 Upper Center), and 10⁻⁵ (Fig. 4 Upper Right) M soluble ligand shows a shift in the maximum bin count from 100 to 60 to 40 pN, respectively. At 10⁻⁷ M soluble lactose, a fundamental period of 50 pN is again observed: at 10⁻⁵ M the fundamental period appears at 40 pN, the smallest period that can be resolved based on the Nyquist criterion for the sampled data set.

Fig. 4.

Histograms (Left), autocorrelation functions (Center), and power spectra (Right) for the rupture of immobilized lactose-galectin 3 complexes in the presence of 0 (Top), 10⁻⁷ (Middle), and 10⁻⁵ (Bottom) M soluble lactose.

The histogram continued to shift toward lower rupture forces as the concentration of soluble ligand increased. At 10⁻³ M, 242 of the 380 data points correspond to rupture forces at bins centered at 20 and 40 pN (SI Fig. 7): these values fix the fundamental monovalent unbinding force. The 40 and 50 pN periods identified at lower soluble ligand concentrations are integer multiples of 20 and 25 pN, suggesting a fundamental unbinding force for a monovalent protein-ligand interaction of between 20 and 25 pN. This value is comparable to AFM values reported for the rupture of other lectin-carbohydrate interactions (44), although a direct comparison of rupture forces is not straightforward because such values depend critically on loading rate (39). A monomeric unbinding force of 20–25 pN suggests that tip–surface encounter in the absence of soluble ligand most commonly results in the formation of five or six bound complexes; accepting nonidealities of the system this value is in good agreement with the predicted maximum number of interactions.

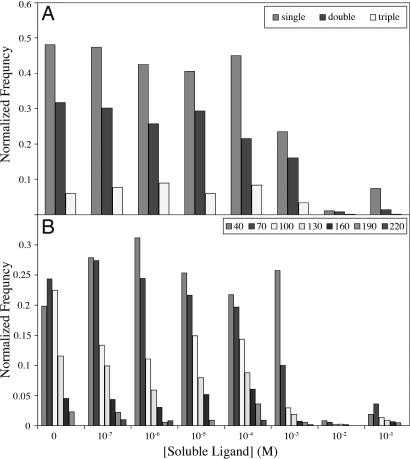
Fig. 5 shows the effect of correction for multiple binding interactions between the tip and substrate on the binding isotherm. Although beyond 1 mM too few binding events are collected to make meaningful observations, the correction for multivalent attachment shifts the binding isotherm to the right by roughly one order of magnitude. Reconsideration of Eqs. 2–4 in light of this shift increases K_ii by roughly one order of magnitude, bringing it significantly closer to the solution phase value (K_ff) of 6,400 M⁻¹.

Fig. 5.

Effect of soluble ligand on multivalency. (A) Bin breadths correspond to single multiples of complex formation. (B) Bar colors relate the frequency of each type of attachment observed, only binding events are tallied, and bin counts are normalized to the total number of pulls collected at the concentration (binding + nonbinding).

Accounting for multivalency, the numerical value of K_ii is in remarkable agreement with K_ff, differing by no more than a factor of five. A value of K_ii in close agreement to K_ff has significant implications for the range of values possible for both the translational and rotational entropy of dissolved species and for the conformational entropy associated with rotation about a single bond. Because association of two species tethered to surfaces proceeds with no loss of translational or rotational mobility, the association of immobilized species should be more favorable than association of the corresponding unconstrained partners by a term related to the exponent of the translational and rotational entropy lost during binding, a value variously estimated between 2 and 15 kcal mol⁻¹ (45). On the other hand, the binding of tethered partners results in a loss of conformational entropy, as the flexible torsions in the linker domains are frozen. This value too has been the source of considerable controversy, with estimates ranging from 0.5 to 1.5 kcal mol⁻¹ per rotor (46–48). Here, the difference in free energy for formation of a complex between two immobilized species and two soluble species is no more than 1 kcal mol⁻¹: either the translational and rotational entropic savings are nearly exactly offset by the conformational entropy penalty of restricting rotors in the tethers upon association of the two immobilized species, or the entropic consequences of both events are significantly smaller the values typically assigned to them.

Conclusions

We have described a device that uses stochastic determination of the probability of the formation of a bound complex between an immobilized ligand and an immobilized receptor to evaluate solution-phase thermodynamic quantities, including association constants and concentrations. The approach facilitates the biophysical study of immobilized species, a process of great relevance to biological processes and inaccessible by other biophysical techniques. Understanding the fundamental biophysics of the underlying phenomenology and the development of practical application of the methodology require further study.

Materials and Methods

Synthesis of Dialkyl Disulfides and Mercaptopentyl Lactose.

Dialkyl disulfides bearing either cross-reactive maleimide-linked oligoethylene glycol 1 (maleimido disulfide) or underivatized oligoethylene glycol 2 (blank disulfide) were synthesized following the general approach of Houseman et al. (34) Mercaptopentyl lactoside 3 was synthesized from acetobromolactose by glycosylation of pent-5-en-1-ol (49, 50). The resulting pentenyl glycoside was subjected to radical addition of thiol acetic acid; global deprotection in basic methanol provided the desired lactose derivative (51). Full experimental details as well as spectral data are presented in SI Text.

Preparation of AFM Tips.

Triangular silicon nitride cantelivers (Model NP, Veeco, Woodbury, NY) were coated sequentially with a 70-Å chromium adhesion layer followed by 230 Å gold layer using an electron-beam metal evaporator (CHA Industries, Fremont, CA). Formation of self-assembled monolayers (SAMs) on gold using disulfide mixtures has been described previously (34). Briefly, a disulfide mixture with a 0.10 mole fraction of maleimido disulfide in blank disulfide was dissolved in ethanol. Gold-coated cantilevers were submerged in this solution for 12 h at room temperature then rinsed with ethanol. The cantilevers were submerged for 4 h at 37°C in an aqueous solution containing 2.25 mM mercaptopentyl glycoside 3. The ligand-derivatized cantilevers were rinsed with water and ethanol and dried under a stream of N₂.

Protein Purification.

The gene for wild-type galectin-3 was obtained by PCR amplification from the plasmid prCBP35s (obtained from J. L. Wang, Michigan State University, East Lansing) and digested with EcoRI and BamHI. The digested PCR product was ligated into a similarly prepared pET28b plasmid and transformed into XL10-Gold Cells. Resultant colonies were isolated, analyzed for insert by PCR, and sequenced to validate the coding frame. The validated plasmid was transformed into BL21(DE3) cells via heat shock. Single colonies from this transformation were grown to an OD₆₀₀ = 0.6–0.8, induced for 4 h at 37°C with 125 mg liter⁻¹ isopropyl thiogalactopyranoside and harvested by centrifugation. The construct yields ≈20 mg of protein per liter of cell growth. Protein was purified in the standard fashion over nickel-affinity resin (Novagen, San Diego, CA).

Preparation of Surfaces.

The method of Vogel and coworkers was used to immobilize His₆-tagged proteins to quartz surfaces bearing the metal chelate nitrilotriacetic acid (35). Quartz coverslips were oxidized in a boiling solution of peroxide and hydrochloric acid, rinsed thoroughly and dried at 150°C. The surface was silanized with mercaptopropyl trimethoxysilane under vacuum at room temperature for 24 h. The resulting free thiols were capped with N^α-bis-carboxymethyl-N^ε-3-maleimidopropionyl lysine 4 (35) in 10 mM sodium carbonate buffer (pH 7.00) and charged with 50 mM nickel(II) chloride during 5-min immersion. After rinsing, the slide was incubated with a solution of His₆-tagged galectin 3 (≈50 μM) in 50 mM sodium phosphate (pH 7.50) at 4°C for 1 h. The protein-bearing slides were rinsed with 5 mM imidazole buffer (Tris, pH 7.90) and adhered to a metal disk.

Competition Experiments.

Metal discs with adherent protein slides were placed on the magnetic holder of a one-dimensional piezoelectric actuator. Cantilevers were fixed in the liquid chamber of a commercially available atomic force microscope head (Veeco/Digital Instruments) and positioned above the slide. The spring constant of each AFM cantilever was calibrated in solution using the thermal noise method (52). The liquid chamber was filled with buffer containing varying concentrations of β-methyl lactoside (0–100 mM) and the cell was allowed to reach thermal equilibrium at 21°C. Force measurements were obtained during a retract/approach cycle by manually bringing the surface proximal to or in gentle (<100 pN) contact with the tip and then retracting at a rate of 0.205 nm ms⁻¹. Minimal contact was essential to minimize intractable nonspecific interactions between tip and substrate. At each position, a small voltage ramp was used to drive the sample closer to the tip. This process was stopped after the retracting trace revealed an adhesion force, and little indentation was made on approach. The photodiode signal was filtered during acquisition at 500 Hz. Force-extension curves were collected and analyzed in LabView. Although not every approach resulted in interaction between the surface and tip, we recorded all forces (exceeding the 20 pN noise background) in the range of 0–300 pN at extensions of 0–100 nm. The typical experiment constituted 800–1,000 individual retractions, resulting in 350–800 measured forces. The position of the tip on the horizontal plane of the substrate was varied after 10 pulls resulting in recorded forces.

Abbreviation

AFM

atomic force microscopy.