Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics

Abstract

In 1988, Felsenstein described a framework for assessing the likelihood of a genetic data set in which all of the possible genealogical histories of the data are considered, each in proportion to their probability. Although not analytically solvable, several approaches, including Markov chain Monte Carlo methods, have been developed to find approximate solutions. Here, we describe an approach in which Markov chain Monte Carlo simulations are used to integrate over the space of genealogies, whereas other parameters are integrated out analytically. The result is an approximation to the full joint posterior density of the model parameters. For many purposes, this function can be treated as a likelihood, thereby permitting likelihood-based analyses, including likelihood ratio tests of nested models. Several examples, including an application to the divergence of chimpanzee subspecies, are provided.

Population genetic and phylogenetic models that take a genealogical (i.e., gene tree) approach suffer two nested levels of ambiguity. First, the uncertainty of an estimate of a genealogy can be large and difficult to quantify, and second, it can be difficult to interpret a genealogy estimate explicitly in terms of an evolutionary or population genetics model. In his 1988 review, Felsenstein (1) conceptualized a way thru these uncertainties by positioning the genealogy as a nuisance variable in the definition of the likelihood of the parameters given the data (proportional to the sampling probability of the data):

where X is the data, G is a genealogy, ψ is the set of all possible genealogies, and Θ is the vector of model parameters to be estimated. The basic idea of considering all of the possible genealogies in proportion to their probability is also contained explicitly in the recursion approach of Griffiths (2) and is suggested in much other work on genealogical models. Although Felsenstein used the notation for summation, integral forms have often since been used, reflecting the fact that genealogies are complex entities with both discrete components (branching topology) and continuous components (branch lengths).

Felsenstein's equation does not have a general closed-form solution, and numerical evaluation is difficult because of the very large number of possible tree topologies for even small data sets. It is possible to approximate Eq. 1 by simulating k independent genealogies from p(G|Θ), G₁, …, G_k, in which case, a simulation-consistent estimator of the likelihood can be obtained as

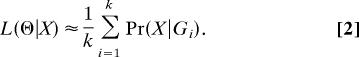However, this is usually far too inefficient, because the variance in Pr(X|G) will be very large for randomly generated genealogies. Efficient stochastic evaluation of Eq. 1 requires the availability of methods for sampling G with some consideration of the data. For a given parameter value, Θ, the distribution of G that minimizes the simulation variance is

However, direct sampling from this distribution is not possible because it requires that the likelihood function can be calculated analytically (3).

Kuhner, Yamato, and Felsenstein (1995).

A solution to the question of how to sample genealogies was described by Kuhner et al. (4), who devised a Markov chain Monte Carlo (MCMC) simulation approach. In the simulation, updates of G are accepted with probability given by the Metropolis–Hastings (5, 6) criterion

where q(G → G*) is the probability that G* is proposed as an update from G. At stationarity, the residence time in the Markov chain will be proportional to the posterior density of that genealogy (i.e., as given by Eq. 3), and trees sampled successively from the Markov chain are correlated draws from the posterior density of genealogies.

The approach devised by Kuhner et al. and used thereafter for a variety of models (7–10) is to use the genealogies that have been sampled by using one parameter value, Θ₀, to estimate the relative likelihood for other values. The likelihood surface for Θ is obtained by running a Markov chain at a fixed value Θ₀ close to the mode of the likelihood function while evaluating the likelihood for multiple values of Θ by using importance sampling (11). Let p(G|Θ₀) be p(G|Θ) evaluated at the point Θ = Θ₀, and assume p(G|Θ₀) > 0 if p(G|Θ) > 0 for all Θ and G. Then from Eqs. 1 and 3, we see that

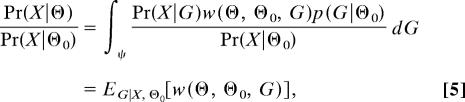where w(Θ, Θ₀, G) = p(G|Θ)/p(G|Θ₀). A single set of values of G are drawn from p(G|X, Θ₀) (i.e., by sampling from the Markov chain) and used to estimate the relative likelihoods for other values of Θ:

where w_i(Θ, Θ₀, G) and G⁽ⁱ⁾ are the value of w_i(Θ, Θ₀, G) and G, respectively, in the ith sampled step of the chain.

The method of Kuhner et al. (4) was the first true MCMC method in population genetics, and it showed that likelihood inference of population genetics parameters is possible for complex mutational models. It lead to the development of related methods (12–14), and it preceded the use of closely related MCMC methods for phylogenetic inference (15–17). However, it suffers the significant shortcoming that the distribution of w_i(Θ, Θ₀, G) will be very skewed when Θ differs from Θ₀, causing the variance of the estimate of the likelihood to be very large and difficult to estimate when |Θ − Θ₀| is large (14, 18). Because of the skewed distribution of w_i(Θ, Θ₀, G), the method will tend to underestimate the likelihood when Θ differs from Θ₀ and thus bias the estimator toward values close to Θ₀. Kuhner et al. (4) address the problem of large variance when |Θ − Θ₀| is large by running multiple chains and updating Θ₀ each time the chain is restarted (19).

An alternative to MCMC sampling of genealogies is the sequential importance sampling method of Griffiths and Tavaré (20, 21). Stephens and Donnelly (22) suggested a modification of the approach of Griffiths and Tavaré that samples more efficiently from an approximation to Eq. 3.

Bayesian MCMC.

One way to extend the MCMC approach to generating likelihood surfaces is to explicitly consider a prior distribution of Θ, p(Θ), and to simulate a Markov chain with stationary measure given by the joint posterior density of G and Θ,

(12, 14, 23). This approach, of running a Markov chain over a state space of genealogies and model parameters, has been extended to multilocus applications for a variety of models (24–27). Apart from having a large state space and associated MCMC mixing challenges, the main shortcomings stem from the essential form of the result, which is not a function estimate but merely a record of parameter values. Density estimates can be obtained by binning or by kernel estimators, but the nature of the results effectively precludes estimates of the joint posterior density for models with more than a small number of parameters. In such cases the volume of the parameter space is so large that the number of recorded values that will fall in any portion of it may be low, even for very long runs and even for portions of the parameter space associated with high posterior densities. Because of this “curse of dimensionality,” the number of samples needed increases exponentially with the dimension (28). This means that applications have mostly been limited to the generation of estimates of the marginal posterior densities for each of the model parameters. It also means that it has been difficult to estimate likelihood ratios for models involving several parameters. Here, we propose a method that eliminates the need for a driving value (Θ₀) and that generates estimates of the entire posterior probability density function, suitable for optimization and likelihood-ratio tests of nested models.

Theory.

This approach relies on the analytical calculation of the prior probability of G by integration of p(G|Θ) over the prior distribution of Θ. This makes it possible to draw samples by MCMC directly from the marginal posterior probability of genealogies, p(G|X). Then, using a sample of these genealogies, one can construct an estimate of the posterior density function, p(Θ|X).

As we will show, the calculation of the marginal prior density of genealogies,

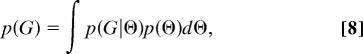can be done analytically and easily when p(Θ) has a uniform distribution. Access to the prior for G permits an MCMC simulation that has a marginal posterior density for G given by

(contrast with Eq. 7). Then, the posterior density for Θ is given by

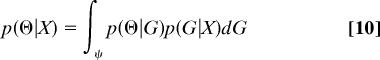(contrast with Eq. 1). This can be proved by noting that under the proper scaling, p(X|G, Θ) = Pr(X|G) (4). Then p(Θ|G, X) = Pr(X|G, Θ)p(Θ|G)/Pr(X|G) = p(Θ|G), and Eq. 10 follows by the law of total probability.

The posterior density of Θ can then be consistently estimated as

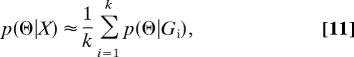where G_i, i = 1, 2, …, k, are the samples from p(G|X) that are generated by the MCMC simulation. Inferences can then be based on p(Θ|X) or on the likelihood function deduced as L(Θ) ∝ p(Θ|X)/p(Θ). If p(Θ) is a constant, then the posterior probability is directly proportional to the likelihood over the prior range of Θ. In effect, a Bayesian sampling strategy is being used to generate an estimate of the relative likelihood, which can be used in turn to find a maximum likelihood estimate of Θ and to conduct other likelihood-based analyses. It is also useful to note that Pr(X|G) is not part of the final calculation in Eq. 11. As in the method of Kuhner et al., (4) the data are used to determine the probability density from which the genealogies are sampled and thereafter are not required (29).

A Single-Population Model.

Consider a model in which Θ includes just one parameter, θ = 4Nu, and a sample of n gene copies, for a locus with neutral mutation rate u, drawn from a population with effective chromosomal population size 2N and evolving according to Kingman's coalescent (30). Letting the coalescent times in the genealogy be τ = {τ₂, …, τ_n}, where τ_i is the time interval in G in which there are i ancestors of the sample, then

where

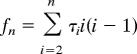is the total coalescent rate measured over the genealogy (30, 31). If we consider a uniform prior distribution for θ over the interval {0, θ_max}, then placing Eq. 12 into Eq. 8 yields

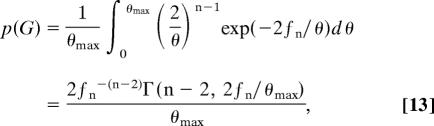where Γ(a, b) is the incomplete Gamma function with parameters a and b. Similarly, we find

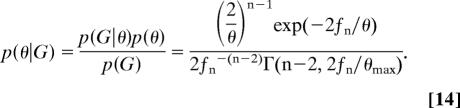Generation of the estimate of the posterior density function, which is a sum of functions in the form of Eq. 14 (see ref. 11) requires only that f_n be recorded at intervals from the Markov chain simulation.

Multipopulation Models.

Now consider a family of models (so-called “island models”) in which multiple populations, each of constant size, have been exchanging genes at constant rates for sufficiently long that the probability of a genealogy is solely a function of population sizes and migration rates (32, 33). Here, we develop the case for two populations with a pair of population size parameters (θ₁, θ₂) and two scaled migration rate parameters (m₁ and m₂) (8), but the approach can be extended to any number of populations.

For a sample of n₁ and n₂ gene copies, from each population respectively, G will include n₁ + n₂ − 1 coalescent events as well as a variable number of migration events. Let c₁ and c₂ be the number of coalescents in populations 1 and 2, respectively; and let w₁ and w₂ be the number of migration events out of population 1 and 2, respectively. When the coalescent and migration events are ordered in time, there are a total of a = n₁ + n₂ + w₁ + w₂ − 1 time intervals. The probability density of the genealogy, as a function of the parameter set Θ = {θ₁, θ₂, m₁, m₂}, is

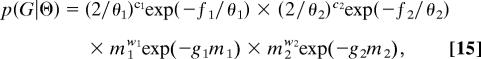where the f and g terms refer to the total coalescent and migration rates, respectively, over the corresponding portions of G, such that

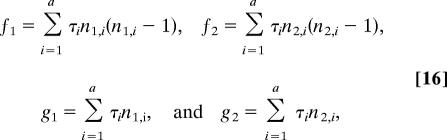where n_1,i and n_2,i are the number of gene copies in populations 1 and 2 during interval i. Then integration over each of the four elements in Θ yields the prior probability

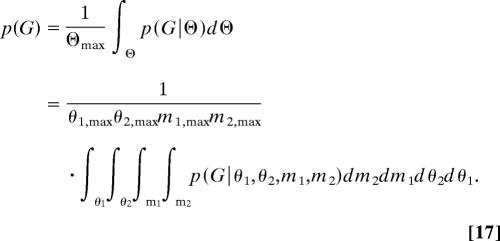The result of this integration is a product of four terms, including two that take the same form as Eq. 12 for the scaled population size parameters, as well as two migration terms, each of which takes the form

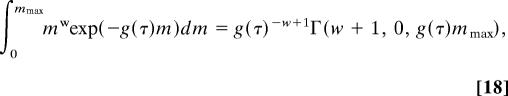where Γ(a, 0, b) is the lower incomplete Gamma function.

Finally, recall that

where, for this model, the numerator is the product of Eq. 15 and the prior distribution, and the denominator is given by Eq. 17. Then, as with the case of a single-parameter model, p(Θ|G) can be used in Eq. 11 for each of a set of sampled genealogies.

The estimate of p(Θ|X) obtained by using Eq. 11 has some desirable properties. First, the integration over Θ will necessarily equal 1, because it is equivalent to integrating each of the k components of the sum, the result of each of which will necessarily equal 1 (see Eq. 19). Second, because each of the component functions that are summed in Eq. 11 are calculable and differentiable over the prior of Θ, so is the overall function. This means that the function can, in principal, be maximized for all, or any subset, of the parameters in Θ.

Models with Population Splitting and Multiple Loci.

Conventional island models assume an equilibrium between migration and genetic drift and cannot well represent histories that include recent population-splitting events. Such splitting events are a typical component of the speciation process, and they underlie the hierarchical structure of the phylogenetic history of life on earth. By incorporating population-splitting events into multipopulation genetic models it becomes possible to conjoin phylogenetic models with population genetics ones.

Described in supporting information (SI) Text is the two-population “isolation with migration model,” in which there are six parameters including three for population sizes (θ₁, θ₂, and θ_a, where θ_a is the value of θ in the ancestral population); the scaled time at which the ancestral population gave rise to the two descendant populations, t; and the two scaled migration rates, m₁ and m₂ (23, 25). In this context, G is partly a function of the splitting time (23) and so it is not clearly feasible to develop a prior for G by analytically integrating over t (unlike the case with only population size and migration parameters). However, we can calculate analytically the joint prior, p(G, t), and we can sample pairs of values of G and t, from a Markov chain simulation. The result is an estimate of the posterior density function for all of the parameters apart from t,

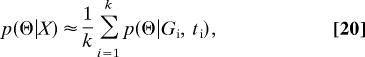where Θ includes all parameters except t. Although t is not integrated over analytically, the simulations do reveal an estimate of the marginal posterior density for t. Also described in SI Text is a method for considering data from multiple loci that vary in their neutral mutation rates.

Implementation and Examples.

A computer program was written that implements a Markov chain simulation for generating samples from p(G|X) for models with one or two populations, as well as for a two-population isolation with migration model (i.e., with a population-splitting time parameter, t). The state space of the Markov chain includes the prior distribution of G (and t if population splitting is in the model), with a general Metropolis–Hastings update criterion

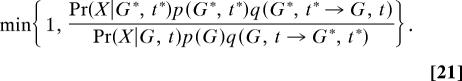The update of G to G* is done by using branch sliding (14) in which a randomly selected branch is moved a random distance in the tree. The migration events originally on the branch are removed, and a random number of new migration events is drawn from a Poisson distribution, conditioned on there being an even or odd number of migration events (depending on whether the starting and ending populations of the branch are the same). The Poisson parameter is taken to be the expected number of migrations over the span of the new branch length, given the current number of migration events that occur over the total length of the tree.

If the model includes t, then it is also necessary to do joint updates of G and t. For these updates, we follow the method of Rannala and Yang (34), in which the new value, t*, is drawn from a uniform distribution over the interval {0, t_max}, and the times of all migration and coalescent events in G before t are multiplied by t*/t, and the times of events after t are summed with (t* − t). At evenly spaced intervals, records are made of t, p(G, t), and of those quantities from G that are needed to calculate p(G|Θ, t). For the case of multiple loci, the updates of the mutation rate scalars are done as in Hey and Nielsen (25).

In general, it is expected that each genealogy will make its greatest contribution to the overall probability over some limited range of Θ. By including a large number of genealogies, sampled from a long-running, well-mixing Markov chain that has reached stationarity, it should be possible to obtain good estimates of p(Θ|X) for any value of Θ. Optimization of the estimate function, under full or nested models, requires some care because the surface may be multimodal over broad and fine scales, either because of the data or because of the particular genealogies that happened to end up in the sample. After trying a number of approaches, we settled on the simulated annealing algorithm that is implemented in the AMEBSA code of Press et al. (35).

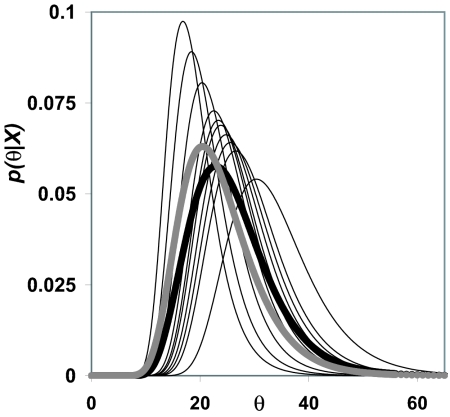
Fig. 1 shows an example for the simple case of a data set simulated under a single population model (one parameter, θ = 4Nu). Ten likelihood functions, each based on a single genealogy, are shown together with their average as well as the average for 100 samples drawn from the same simulation.

Fig. 1.

A single population model was simulated with a sample of 20 gene copies drawn from a population with a true population mutation rate of θ = 20. Functions based on 10 individual sampled genealogies are shown along with their mean (gray line) as well as the mean for 100 sampled genealogies (black line).

Nested models and likelihood-ratio tests.

In addition to an estimate of the posterior density, p′(Θ|X), the method can also be used to study nested submodels, e.g., a model with parameter space Θ_r, where Θ_r contains a subset of the parameters in Θ, and the remaining parameters take on fixed values. By using Eq. 11, the functions p′(Θ|X) and p′(Θ_r|X) can be maximized to find the highest probabilities and the associated parameter values, Θ and Θ_r. Because the posterior probability density of Θ is uniformly proportional to the likelihood, p(Θ|X) = cL(Θ|X) and p(Θ_r|X) = cL(Θ_r|X), where c = p(Θ)/p(X) Thus, the posterior density ratio equals the likelihood ratio. If Λ is the log of the ratio of the highest likelihoods found under each model, then this can be estimated from the ratios of the two functions, each at its maximal value, Λ̂ = 1n(p′(Θ̂_r|X)/p′(Θ̂|X)). If the two density functions are good estimates of the true densities, and if the data set X consists of a large number of independent observations, then this ratio can be used in a conventional likelihood-ratio test. If Θ_r is the true model, then, for unbounded parameters and under certain regularity conditions, we expect that −2Λ̂ asymptotically will follow a χ² distribution with k degrees of freedom, where k is the difference in the number of dimensions (parameters) between Θ_r and Θ.

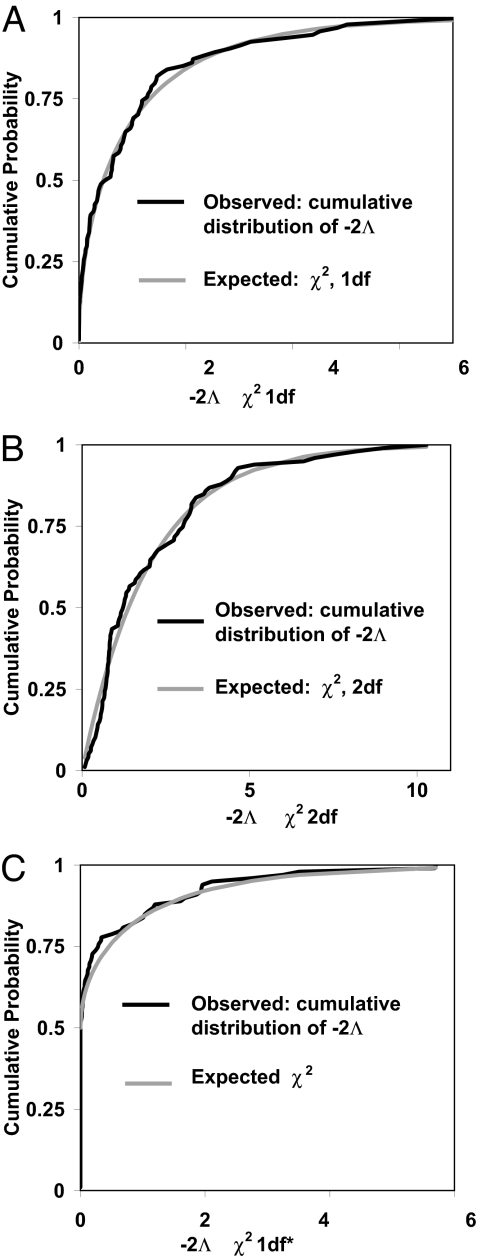
To examine the actual distribution of −2Λ̂, data sets were simulated under a particular model, Θ_r. For each data set, a Markov chain simulation was run to generate an estimate of the posterior density function under the full model, p′(Θ|X). This function was maximized over all parameters to generate p′(Θ̂|X) and then maximized over just those parameters that were free to vary in Θ_r to generate p′(Θ̂_r X), and −2Λ̂ was calculated. Fig. 2 shows the resulting cumulative distributions for three different models, each of which is consistent with the corresponding χ² distribution, showing that the asymptotic result holds approximately for these moderately sized simulated data sets and that the added simulation variance introduced by the method does not invalidate the use of the classical likelihood-ratio tests. Additionally, the good fit of the χ² distribution suggests that the estimation and optimization of the likelihood surface is reasonable accurate. Other simulations with small data sets do show that, as expected with less data, that the distribution of −2Λ̂ will have a variance larger than that for the corresponding χ² distribution.

Fig. 2.

Cumulative distributions of −2Λ̂ calculated from Markov chain simulations run on 100 simulated data sets. (A) The true model has two populations of identical size, with simulated data sets sampled following: θ₁ = θ₂ = 10, m₁ = 0.5, m₂ = 0.01, six loci, and 15 gene copies sampled for each population per locus. The MCMC simulation generated 5,000 genealogies with prior maxima: θ₁ = θ₂ = 100, m₁ = m₂ = 5. The observed cumulative distribution of −2Λ̂ is shown with that expected from a χ² distribution with 1 degree of freedom. The Kolmogorov–Smirnov test statistic (the greatest departure between two cumulative distributions), is 0.0851, which does not approach statistical significance. (B) The true model has two populations with identical migration rates and population sizes with simulated data sets sampled following: θ₁ = θ₂ = 20, m₁ = m₂ = 0.1, 25 loci, and six gene copies sampled for each population per locus. The Markov chain simulations generated samples of 8,000 genealogies with prior maximum values as follows: θ₁ = θ₂ = 500, m₁ = m₂ = 1. The Kolmogorov–Smirnov test statistic is 0.0791, which does not approach statistical significance. (C) The true model is an isolation with migration model with unidirectional gene flow. Simulated data sets were sampled following: θ₁ = 20; θ₂ = 40, θ_A = 30, m₁ = 0.15, m₂ = 0, t = 10, 25 loci, and six gene copies sampled for each population per locus. The estimated posterior density has four dimensions [for θ₁, θ₂,θ_A, and m₁ (note that m₂ = 0)]. Given one parameter fixed at the boundary of the parameter space, the likelihood ratio statistic, contrasting the true model and the full five-parameter model, should be asymptotically distributed as a random variable that takes the value 0 with probability 0.5 and takes on a value from a χ₁² distribution with probability 0.5 (23, 37). The Kolmogorov–Smirnov test statistic is 0.0590, which does not approach statistical significance.

Chimpanzee case study.

To demonstrate the approach for a model in which an ancestral populations splits into two, we considered the case of two chimpanzee subspecies, Pan troglodytes troglodytes (the Central African Chimpanzee) and Pan troglodytes verus (the Western African Chimpanzee). This divergence has previously been studied by using a Markov chain simulation in which the state space includes both genealogies and model parameters for a data set of 48 genes drawn from the literature (36).

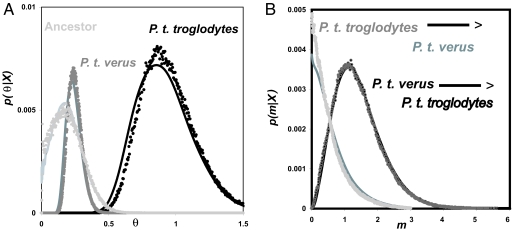
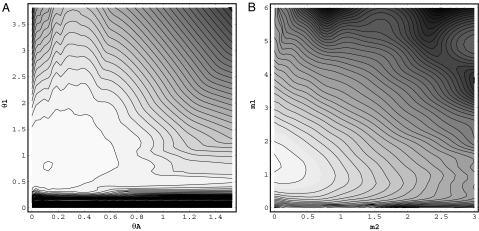
Fig. 3 shows the marginal posterior density estimates from the original method (36), which generates histogram-based estimates, and the new method. As expected, both sets of marginal density estimates are very similar. Fig. 4 shows examples of contour plots of marginal posterior density estimates for pairs of parameters.

Fig. 3.

Posterior probability estimates for population size and migration parameters for P. t. troglodytes and P. t. verus. Histograms generated by a Markov chain with state space that includes genealogies and parameters (36) are shown as dots (one for each of 1,000 bins between 0 and the maximum of the prior) together with curves plotted by using estimated marginal functions (solid lines). See Won and Hey (36) for details on the data set and the histogram plots. Marginal functions were generated by using 15,000 genealogies sampled from a Markov chain simulation. (A) Population size parameters for each sampled population and their ancestor. (B) Migration parameters in each direction between the sampled populations.

Fig. 4.

Two dimensional contour plots of marginal posterior density estimates for P. t. troglodytes and P. t. verus. (A) θ₁ (for P. t. troglodytes) and θ_A. (B) m₁ and m₂.

Table 1 shows the likelihood ratio statistic for a series of nested models applied to the chimpanzee data. All of the ratio statistics were calculated as the difference between the highest posterior probability for the full model and the highest posterior probability for the nested model. Only two models were not rejected: the model in which the two migration rates are equal to each other and the one in which m₂ is equal to 0. If we were to correct for multiple tests, then other models would also not be rejected.

Table 1.

Tests of nested models for P. t. troglodytes and P. t. verus

Model (Θ)	log(p′(Θ̂|X))	−2Λ̂	P	df
θ1 θ2 θAm1m2	7.734	−		−
θ1 θ2 θAm1 = 0m2	5.976	3.516	0.03039*	1†
θ1 θ2 θAm1m2 = 0	7.131	1.206	0.13606	1†
θ1 θ2 θAm1 = m2	6.403	2.663	0.10271	1
θ1 = θ2 θAm1m2	−24.925	65.319	6.4 × 10−16*	1
θ1 = θ2 = θAm1m2	−38.951	93.37	5.3 × 10−21*	2
θ1 = θ2 θAm1 = m2	−31.34	78.148	1.1 × 10−17*	2
θ1 = θ2 = θAm1 = m2	−60.058	135.584	3.4 × 10−29*	3
θ2 θ1 = θAm1m2	1.548	12.374	0.00043*	1
θ2 θ1 = θAm1 = m2	0.097	15.274	0.00048*	2
θ1 θ2 = θAm1m2	4.73	6.01	0.01423*	1
θ1 θ2 = θAm1 = m2	3.131	9.207	0.01002*	2

*The probability of achieving the test statistic by chance under the null model is <0.05.

^†When the null model is true and has a parameter fixed at the boundary of the parameter space, the expected distribution is a mixture. In the case of a single fixed parameter, −2Λ̂ should be asymptotically distributed as a random variable that takes the value 0 with probability 0.5 and takes on a value from a χ ₁² distribution with probability 0.5 (23, 37).

Discussion

Felsenstein's equation has become a centerpiece of modern population genetics and phylogenetic analysis as computational approaches have been developed for faster and improved approximate solutions. Here, we describe an approach that provides greatly improved access to a broad family of population genetics models, i.e., those that can be described with one or more population size and migration parameters. Relying on a Markov chain simulation, the state space is limited to just the posterior density of genealogies, thereby avoiding those MCMC mixing problems that arise because of correlations between G and Θ, when both are part of the state space (25). In addition, the method provides a convenient approach for estimating likelihood ratios.

The finding that the estimate of the likelihood ratio, from nested models, closely approximates the χ² distribution that is expected under asymptotic assumptions is strong affirmation of the validity of the approach, and it means that the method can be used for many questions that involve a contrast of different demographic models. Model selection and testing of demographic hypotheses based on the full-likelihood function have often been neglected in the fields of molecular ecology and population genetics because appropriate tools for calculating likelihood ratios have not be available. The methods described here should greatly alleviate this problem by providing a powerful computational framework for estimating likelihood functions and likelihood ratios.

Abbreviation

MCMC

Markov chain Monte Carlo.