Ictal Source Analysis: Localization and Imaging of Causal Interactions in Humans

Abstract

We propose a new integrative approach to characterize the structure of seizures in the space, time, and frequency domains. Such characterization leads to a new technical development for ictal source analysis for the presurgical evaluation of epilepsy patients. The present new ictal source analysis method consists of three parts. First, a three-dimensional source scanning procedure is performed by a spatio-temporal FINE source localization method to locate the multiple sources responsible for the time evolving ictal rhythms at their onsets. Next, the dynamic behavior of the sources is modeled by a multivariate autoregressive process (MVAR). Lastly, the causal interaction patterns among the sources as a function of frequency are estimated from the MVAR modeling of the source temporal dynamics. The causal interaction patterns indicate the dynamic communications between sources, which are useful to distinguish the primary sources responsible for the ictal onset from the secondary sources caused by the ictal propagation. The present ictal analysis strategy has been applied to a number of seizures from five epilepsy patients, and their results are consistent with observations from either MRI lesions or SPECT scans, which indicate its effectiveness. Each step of the ictal source analysis is statistically evaluated in order to guarantee the confidence in the results.

Introduction

In clinical research and practice, understanding the internal generators responsible for seizures is important in determining the epileptogenic zone in patients being considered for surgical resection (Engel et al., 1990; Alarcon et al., 1994). In line with clinical and research needs, an essential task of increasing interest is to characterize the structure of seizures in the space, time, and frequency domains. Techniques such as non-invasive EEG and MEG have been demonstrated useful in many studies. Observations from both techniques can provide rich clues, reflecting locations and dynamics of seizures, as to epileptogenic zones (Risinger et al., 1989; Wieser et al., 1993). The diagnostic procedure is usually performed by experienced epileptologists who manually screen out suspect seizures in continuous EEG traces from multiple channels using morphology, amplitude, and frequency information. The development of spectral analysis techniques furthermore allows for quantitative characterization of rhythmic discharges in seizures by computers (Lantz et al., 1999; Michel et al., 1999), which aids the noninvasive seizure lateralization and localization. However, they are unable to accurately characterize information regarding source locations due to the relatively large distances of the electrodes from the cortex and also owing to the smearing caused by the volume conductor effect of a series of barriers (scalp, skull, dura mater) (He & Lian, 2002; He, 2004; Nunez & Srinivasan, 2005).

Seizure localization has been advanced by source localization and imaging techniques using both EEG (Assaf & Ebersole, 1997; Lantz et al., 1999; Michel et al., 1999; Worrell et al., 2000) and MEG (Ebersole, 1997; Assaf et al., 2003) to characterize seizures in the source space instead of the sensor space. Such techniques handle the volume conductor effect and, thus, are able to identify the internal sources behind the seizures by solving the so-called inverse problem (von Helmholtz, 1853). In the above mentioned methods, Assaf & Ebersole (1997) used few discrete spatio-temporal dipoles to characterize ictal generators. Lantz et al. (1999) combined the frequency analysis and dipole source localization together which led to the “FFT dipole approximation”. The distributed source model (Hamalainen & Ilmoniemi, 1984) was adopted to model more distributed seizure sources. Michel et al. (1999) proposed the temporal segmentation of ictal rhythms which divided activities in the time domain into a series of “functional microstates” (Lehmann, 1987) with each microstate stable within its time window. The source localization can thus be achieved using a mean potential map from a microstate. Worrell et al. (2000) extended “FFT dipole approximation” concept for the dipole sources to the distributed sources in which a well-known source imaging technique, i.e. LORETA (Pascual-Marqui et al., 1994) was applied to seizure analysis on a frequency component.

These methods integrate information from the space, time, and frequency domains which lead to possible seizure source characterization. The idea behind these approaches is based upon a two-steps procedure: (i) multi-channel time-frequency parameterization of EEG/MEG time series; (ii) source localization or imaging on the parameterized EEG/MEG components. The first step narrows down the information from the scalp recordings into certain spatial patterns within a time domain or specific frequency bin. The hypothesis behind them assumes that the parameterization only rejects signals which are not of interest. Unfortunately, this may not always be true. While the parameterized components often lose useful signals, it is also difficult to delineate the signals of interest. In terms of seizure source localization, the major difficulty is distinguishing the sources which initiate the seizure activity (the primary sources) from the sources which are generated by propagation of pathological activity (the secondary sources). Such propagation can be rapid in time and within similar bands in frequency (Quesney et al. 1992; Williamson et al. 1992), and can be distant from the primary focus such as in cortical areas contralateral to pathological structures (Pacia & Ebersole, 1997). It often complicates the seizure onset activity and leads to false localization or even false lateralization of ictal events (Sammaritano et al. 1987). Considering these difficulties, we propose a new ictal source analysis approach which reverses the sequence of two steps in the above mentioned procedure. The two steps are: (i) spatio-temporal source localization or imaging followed by (ii) time-frequency parameterization of time series from multiple sources. The new strategy is not going to compress the signals in time domain or narrow them down into specific frequency bins. More specifically, we adopt the directed transfer function (DTF) technique (Kaminski and Blinowska, 1991) in the second step to estimate dynamic causal interaction patterns among the sources obtained from the first step, which can be used to distinguish primary sources from secondary sources.

The DTF techniques as applied to EEG or MEG signals were developed based on the Granger (1969) theory. While Granger causality could only be applied to determine the directional causal interaction between two signals at a time (Freiwald et al., 1999), the DTF technique can be used to determine the directional causal interaction for an arbitrary number of signals. The DTF technique estimates the causal interaction through multivariate autoregressive (MVAR) modeling (Franaszczuk et al., 1985). While the Granger causality has been successfully applied to data from intracranial recordings recently (Brovelli et al., 2004), the DTF technique has also been used to decide the onset and propagation of seizure activities with ECoG signals (Franaszczuk et al., 1994; Franaszczuk & Bergey, 1998). An advantage of performing DTF on intracranial recordings is that such signals are measured at near field locations close to the sources whereas EEG and MEG are measured at relatively far fields, which complicates the estimation of causal interactions with the volume conductor effect. However, ECoG is invasive and, due to the difficulties in obtaining broad cortical coverage, electrodes may not practically be placed over the entire area of interest, i.e. epileptogenic zone. Thus, it is anticipated that the development of a causal interaction estimate on the source space, obtained by solving the inverse problem, could avoid invasive measurements and provide information about a greater portion of the cortex.

In the present study, we have developed a new integrative technique to characterize the structure of seizures in the space, time, and frequency domains. Its direct benefit is to help the ictal source analysis by distinguishing the primary sources from secondary sources. The method proposed here is based upon a combination of the subspace source localization technique (Xu et al., 2004; Ding & He, 2006) and the spectrum-based causal interaction estimation technique employing the directed transfer function (DTF) (Kaminski and Blinowska, 1991; Kaminski et al., 2001). The subspace source localization technique, FINE (Xu et al., 2004; Ding & He, 2006), performed as the first step, is able to locate multiple dipole sources by means of a scanning procedure (Mosher et al., 1992). MVAR modeling was used to model the time series of these identified sources. DTF was then able to characterize the causal interactions in the spectral domain among multiple sources obtained from FINE based on the MVAR modeling. The causal relationships were then used to test the hypothesis that the responsible sources for seizure onset were those sources at the start points of the topographical links of directional causal interactions (primary sources). The proposed technique was evaluated in a group of adult patients with medically intractable partial epilepsy who had clear symptomatic MRI lesions or SPECT scans.

Methods

Spatio-temporal source localization: FINE

The source model used in subspace source localization is the equivalent current dipole, which represents an idealized point source. According to the linearity of Maxwell’s equations, an arbitrary source configuration can be written as a linear superposition of these point sources. A set of measurements along the time axis can be further written in matrix format as:

$$\mathrm{\Phi }(\overline{t})=A(R,Q)S(\overline{t})$$ (1)

Here, Φ is the spatio-temporal measurement on multiple EEG electrodes and S is the source temporal behavior matrix. A is the lead field matrix where R is a set of location vectors, $\overline{r}$, for multiple arbitrary source configrations and Q is a set of their associated orientation vectors, $\overline{q}$.

The concept of subspace source localization is based on calculating the subspace correlation (SC) between dipolar topographies, i.e. $A(\overline{r},\overline{q})$ corresponding to a particular dipole and an estimated signal subspace or noise-only subspace. By performing singular value decomposition (SVD) to the data matrix, Φ = UΛV^T, the measurement space can be partitioned into the signal subspace Us and the noise-only subspace Un (Schmidt, 1979). The p-dimensional signal subspace consists of the columns from U whose corresponding singular values 1… p lie above the noise level. The noise-only subspace consists of the rest columns with dimension of N-p, where N is the number of electrodes. In the FINE method (Xu et al., 2004; Ding & He, 2006), for each scanned point, a region Θ (which surrounds the scanned point) can be found and a small set of vectors in the noise-only subspace (denoted by FINE vector set F_Θ) can be identified as an intersection set between the noise-only subspace and the array manifold spanned by the specific region Θ , based on the concept of principal angles (Golub and Van Loan, 1983; Buckley and Xu, 1990). The SC metric for FINE can thus be expressed as

$$S{C}_{\text{FINE}}^2(\overline{r})={min}_{\overline{q}}\left(\frac{A{(\overline{r},\overline{q})}^T{F}_{\mathrm{\Theta }}{F}_{\mathrm{\Theta }}^{T}A(\overline{r},\overline{q})}{A{(\overline{r},\overline{q})}^{T}A(\overline{r},\overline{q})}\right)$$ (2)

Sources can be found as those for which the scanning metric $S{C}_{\text{FINE}}^2(\overline{r})\hspace{0.17em}$ is sufficiently close to zero. The orientation of each source is defined by the $\overline{q}$ value which minimizes the scanning metric at possible source location $\overline{r}$. It can be obtained by transforming equation (2) into a generalized eigen-decomposition problem (see details in Mosher et al., 1992). With the known multiple locations, R , and the corresponding orientations, Q , of the multiple estimated dipole sources from equation (2), the lead field matrix A can be constructed for these dipoles. The source waveforms can be calculated by S = A⁺Φ, where A⁺ is the pseudo-inverse solution of A obtained by truncated SVD (Golub & van Loan; 1983).

MultiVariate Autoregressive Modeling (MVAR)

Let $S={[\overline{s_1}(t),\overline{s_2}(t),\cdots ,\overline{s_k}(t)]}^T$ be a set of source waveforms from the output of FINE. Here t refers to the time index and k is the number of estimated sources. Supposing that the following MVAR process is an adequate description of the data set S :

$$S(t)=\sum _{i=1}^h\mathrm{\Lambda }(i)S(t-i)+E(t)$$ (3)

where S(t) is the data vector in time; Λ(i) are matrices of model coefficients; E(t) is a vector of multivariate zero-mean uncorrelated white noise; and h is the model order. The optimum order, h, of a MVAR model is generally chosen as the optimizer of an order selection criterion (Lutkepoh, 1993). We used Schwarz’s Bayesian Criterion (Schwarz 1978) in the present study, which has been shown to possess a high degree of accuracy (Lutkepoh, 1985). Model coefficients Λ(i) are computed by a stepwise least squares algorithm for high-dimensional data set (Neumaier & Schneider, 2001).

Directed Transfer Function (DTF)

After the model order and coefficients for a MVAR model are adequately estimated, equation (3) can then be transformed into the frequency domain:

$$\mathrm{\Lambda }(f)S(f)=E(f)$$ (4)

where $\mathrm{\Lambda }(f)=\sum _{i=0}^h\mathrm{\Lambda }(i)e^{-j2\pi fi\mathrm{\Delta }t}$ with Λ(0)= −I . Equation (4) can be rewritten as:

$$S(f)={\mathrm{\Lambda }}^{-1}(f)E(f)=H(f)E(f)$$ (5)

where H (f) is the matrix transfer function of the system, f is frequency and Δt is the sampling interval. The DTF function, ${\gamma }_{ij}^2(f)$, (Kaminski & Blinoswka, 1991) is defined by the elements of the transfer matrix in the spectrum domain which describes the directional causality from source j to source i:

$${\gamma }_{ij}^2(f)=\frac{|H_{ij}(f){|}^2}{\sum _{m=1}^k|H_{im}(f){|}^2}$$ (6)

The DTF values are in the interval of [0, 1] and the normalization condition $\sum _{m=1}^k{\gamma }_{im}^2(f)=1$ is applied. Note that the DTF value is a function of frequency and its statistical significance test is performed over a selected frequency band which covers the major ictal rhythms.

Statistical assessment of causality: Surrogate test

The DTF function has a highly nonlinear relation to the time series data from which it is derived. As a result, the distribution of its estimator under the null hypothesis case is not well established and a proper priori distribution can not be accurately assigned and computed for parametric statistical analysis. In the present study we used a nonparametric statistical test technique using surrogate data (Theiler et al., 1992; Palus & Hoyer, 1998). Specifically, we computed the Fourier transform (FT) of the time series, kept the magnitudes of the Fourier coefficients unchanged, but randomly and independently shuffled the phases of the Fourier coefficients and performed the inverse FT into the time domain to create a surrogate data set. Then a new MVAR model was created and fitted to this surrogate data set and, similarly, the DTF values were estimated from the model. The procedure reserved the spectral structure of surrogate data as the original time series, which is critical to the test of frequency-specific causal interactions estimated by DTF. We repeated the shuffling procedure 5,000 times for each set of source time series and created an empirical distribution for the DTF values under the condition that null hypothesis of no causality is true. Using this distribution, we then assessed the statistical significance of the DTF value evaluated from the actual source time series.

Patients and data acquisition

Five patients with medically intractable partial epilepsy were studied using a protocol approved by the Institutional Review Boards of the University of Minnesota and Mayo Clinic. Each patient was admitted to the Mayo Clinic epilepsy monitoring unit for presurgical evaluation. The patients’ EEGs were recorded using 31 electrodes in the modified 10/20 system and were collected continuously using a C_z reference montage at a sampling rate of 200 Hz with a bandpass filter of 1.0 to 35 Hz, which covers the EEG frequency of the most seizures (3 – 29 Hz) (Gotman, 1982). The positions of electrodes as well as the positions of 3 fiducial points on the head (nasion and left and right preauricular points) were digitized by using a handheld magnetic digitizer (Polhemus, Inc., Colchester, VT). Each patient had a standardized seizure protocol MRI (Jack 1995), which demonstrated a potentially epileptogenic structural abnormality. The MRI was acquired on a 1.5-Tesla GE Signa using a SPGR sequence (TR = 24 ms, TE = 5.4 ms) with a 220 mm field of view. The 120-coronal-slice protocol produces a voxel dimension of 0.9375×0.9375×1.6 mm. A trained EEG technician performed the ictal injection of 99Tcm-ECD during the patients’ habitual seizures. The injection was performed as soon as possible after seizure onset. The interictal injection was performed when the patient had been seizure-free for at least 24 hours. The single photon emission computerized tomography (SPECT) images were acquired between 2 to 3 hours after isotope injection using a Helix systems (Elscint Inc.) gamma camera. The interictal and ictal images were subtracted using a brain surface matching algorithm (Brinkmann et al., 1999) and regions exceeding two standard deviations were co-registered onto the patients’ MRIs.

Ictal source analysis protocol

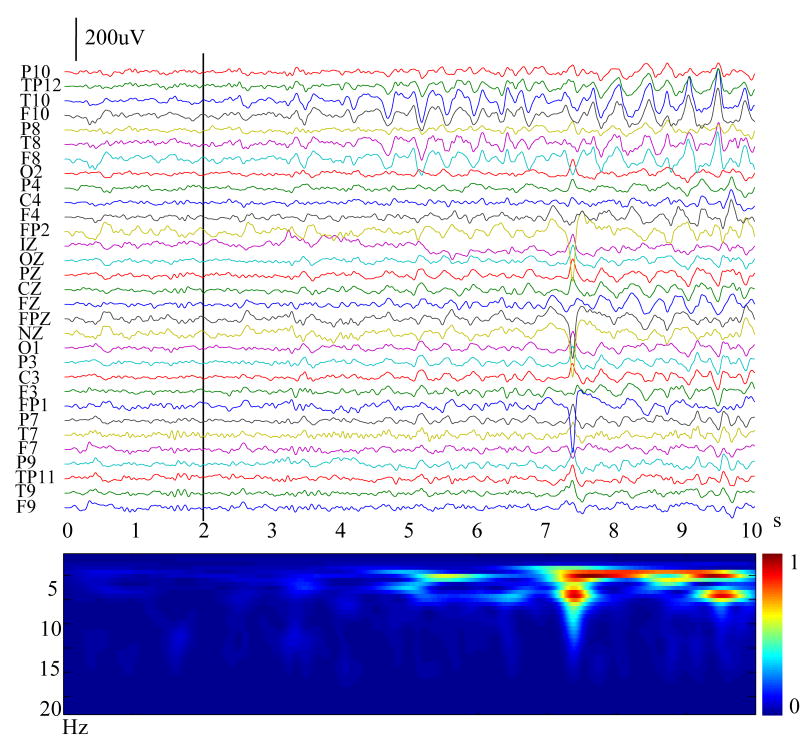
The scalp EEG and video monitoring was reviewed for the occurrence of ictal rhythms via visual inspection, and the time points of ictal onset were determined by two experienced epileptologists. All together, 23 seizures (2–8 per patient) were identified and 3 of them were rejected for ictal source analysis because of too many artifacts during the ictal onset period. Ultimately, 20 seizures were analyzed (2–7 per patient) as summarized in Table 1. Fig. 1 (top) shows an example of the 31-channel scalp waveforms from Patient #1. The temporal evolution of ictal rhythms was examined using time-frequency representation (TFR), which convolutes signal by complex Morlet’s wavelets (Qin et al., 2004) and provides a time-varying energy of signal in each frequency band (Fig. 1, bottom). The vertical black bar on the channels indicates the ictal onset time point for this patient. The build-up process of the seizure occurrence can be observed after the ictal onset. In order for MVAR to sufficiently model ictal sources, the selected ictal onset segment must be quasi-stationary (Franaszczuk et al., 1994). The channel waveforms and TFR drawn in Fig. 1 were used to segment the appropriate ictal onset period for subsequent ictal source analysis. For instance, in Fig. 1 any of the first 3 seconds provided suitably quasi-stationary data because it had no obvious abrupt transition. Generally, longer data will provide more accurate subspace source localization and dynamic causality estimates. We then used the entire 3-second (Fig. 3(a)) data subject for the ictal source analysis.

Table 1.

Summary of the ictal source identification results in 5 patients, with comparison of the estimated primary sources to visible MRI lesions (or pathological sites for Patient #5). ++: within or on the edge of the visible lesion; +: within the vicinity of the visible lesion (< 1.5 cm); −: far away from the visible lesion; ×: rejected trials; Total: number of seizures recorded.

	Patient #1	Patient #2	Patient #3	Patient #4	Patient #5
++	2	1	5	5	4
+	0	1	2	0	0
−	0	0	0	0	0
×	0	0	1	2	0
Total	2	2	8	7	4

Figure 1.

Example of a set of 10-seconds-long 31-channel scalp waveforms (top) for an ictal rhythm (Patient #1). The time-varying energy of the ictal rhythm in each frequency band (bottom) examined by time-frequency representation. The vertical black bar on the channels indicates the ictal onset determined by experienced epileptologists.

Figure 3.

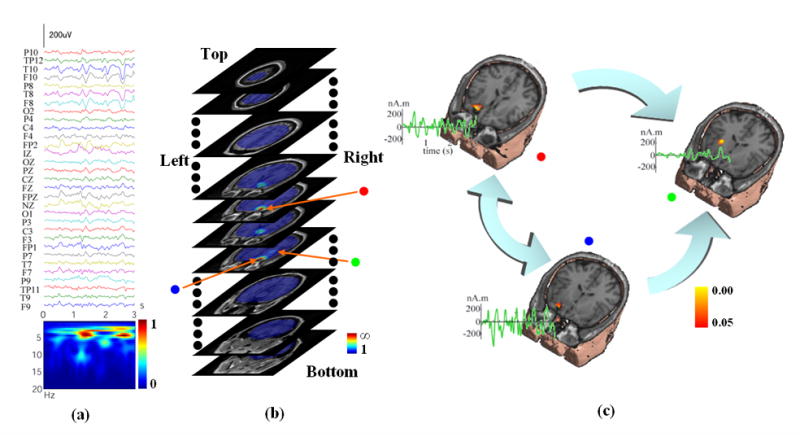
(a) 3-seconds-long 31-channel scalp waveforms from Fig. 1 for subspace source localization analysis. (b) Example of a 3D scanning result by FINE for an ictal activity (Fig. 1, Patient #1) displayed with gray MRI slices. The pseudo-colors show the reciprocal of subspace correlation (SC). Red: low SC; Blue: high SC. The extent of pseudo-colors indicates the coverage of the possible solution space. Three identified sources in the 3D scanning are marked with red, blue, and green dots, respectively. (c) Locations (pseudo-colors on MRI images), waveforms (green curves), and causality patterns (big arrows) for identified sources from Fig. 3(b).

The layered realistic geometry inhomogeneous head model, which consists of three major conductivity boundaries, including the interfaces between the air and scalp, the scalp and skull, and the skull and brain, was used. The segmentations of the scalp and skull were performed on the MRI images using Curry software (NeuroScan Labs, TX) for each subject. The subject-specific head models were then constructed based on the segmentation results. Co-registration of the recording electrodes was achieved by matching the location of 3 fiducial points (nasion and left and right preauricular points) on the MRI to the digitized coordinates of these points. The conductivities for the scalp and brain tissue are 0.33/Ω.m, and the conductivity ratio between the brain and skull is 1:1/20 (Lai et al., 2005).

Results

Illustration of signal subspace

Fig. 2 shows the curve for the singular values from the SVD of ictal data for Patient #1 (Fig. 3(a)) along with the scalp potential patterns for the four largest singular values (up-down sequence), which belong to the signal subspace. Although the noise-only subspace is used in equation (2), for illustration purposes, the complementary signal subspace will be more informative. These images show that the signal subspace from this ictal data consists of the activities in the right temporal and frontal lobes, which are consistent with the results from the ictal source analysis shown in Fig. 3. The curve for the singular value could be used to decide the order of signal subspace (the p value). The p value in this case was chosen as 4. However, a more conservative choice, e.g. 5 or 6, will not change the source localization results significantly, which are also discussed by Mosher et al. (1992).

Figure 2.

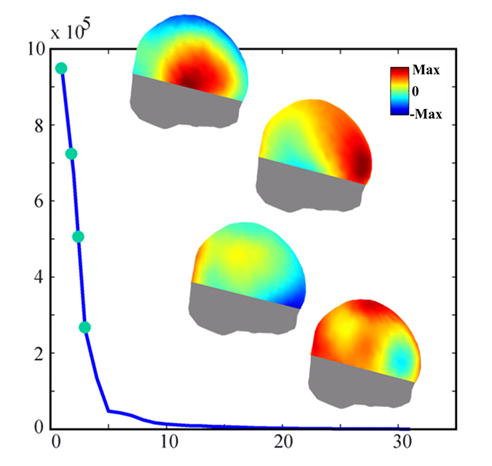
Example of a curve for singular values from the SVD analysis of an ictal rhythm (Fig. 1, Patient #1). The four scalp potential patterns (up-down sequence) are the corresponding singular vectors for the four largest singular values.

Ictal source distributions and dynamics

The FINE method was used to scan the possible solution space in a three-dimensional (3D) brain volume. Fig. 3(b) shows an example of the 3D scanning for the seizure activity (Fig. 3(a)) from Patient #1. The pseudo-colors displayed with gray MRI slices show the reciprocal of subspace correlations against the FINE vectors at each scanned point within the solution space. The red color indicates the low subspace correlations while the blue color indicates the high subspace correlations. The extent of pseudo-colors also indicates the coverage of the solution space. We used 5% as the threshold of subspace correlation for FINE, which means any value below this threshold can be regarded as a possible source. Due to the fact that the present method is based on the discrete dipole source model, another criterion for a source at a scanned point is that the subspace correlation of the point is a local minimum in the 3D tomography of subspace correlations. A procedure was thus developed to search such source points in the 3D tomography, and three sources were identified in this example (Fig. 3(b)), which are marked with red, blue, and green dots.

In Fig. 3(c), we show these three sources together with the structural MRI to indicate their locations. In 20 analyzed seizures from all five patients, single or multiple source(s) were identified by FINE, which exist in areas either near to or far from the MRI lesions. For Patients #2–5, the examples are shown similarly in Fig. 5(a–d), respectively. Those cases with multiple sources (Fig. 3(c) and Fig. 5) were subject to causal interaction estimation. The reconstructed source waveforms in the time domain are also shown in Fig. 3(c) and Fig. 5 with green curves. The MVAR models were used to model these reconstructed source waveforms and the model orders from total 20 ictal activities ranged from 5 to 22, which were sufficiently small as compared with the time points for each waveform (around 600) to achieve accurate MVAR modeling.

Figure 5.

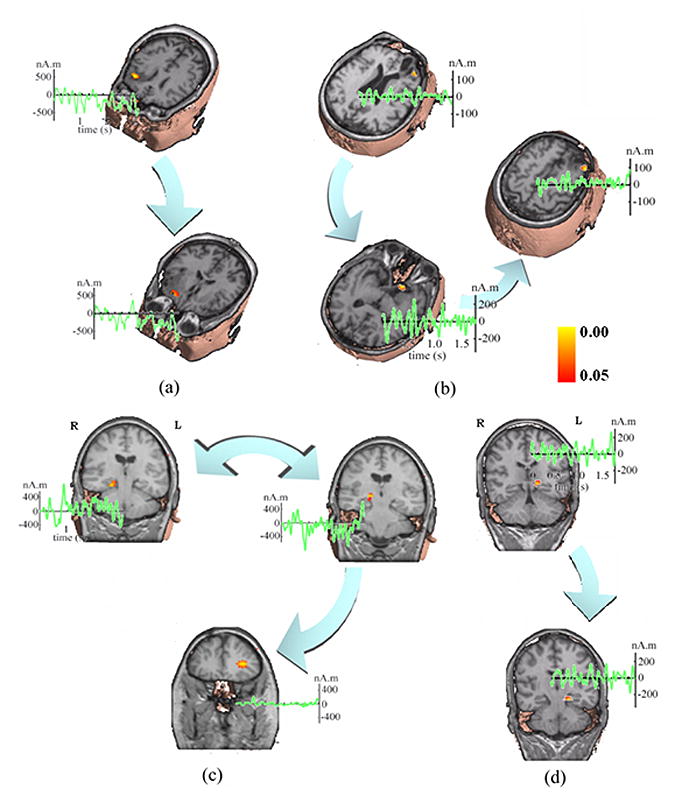
Locations (pseudo-colors on MRI images), waveforms (green curves), and causality patterns (big arrows) from the ictal source analysis of (a) Patient #2; (b) Patient #3; (c) Patient #4; and (d) Patient #5.

Ictal source causal interaction patterns

Fig. 4(b) shows the log plots of the statistical significances of the DTF causality values as a function of frequency for the three sources as shown in Fig. 3 for Patient #1. To examine the statistical significance of these causality values we adopted the surrogate data strategy discussed above. Fig. 4(a) shows an example of the empirical distribution of the surrogate DTF function values between two waveforms as a function of frequency (note that the plot does not cover the entire DTF function value interval [0, 1], because of its less informative contents at the tails of the distribution). From the distribution of surrogate DTF function values, we can find significant levels of the DTF values from the original source waveforms. The black curve in each small box of Fig. 4(b) depicts the significance of directional DTF causalities, e.g. from the red-dotted source to the other two sources for the first row and similarly for the other two rows. The red curves indicates the significance level of p = 0.05. We set the achievable highest significance is 1/5000 (i.e. p = 0.0002) since the DTF distribution was reconstructed by 5,000 repeats. And the lowest significance is 1. We can observe for Patient #1 that significant (p < 0.05) bidirectional information flows between the red-dotted source and blue-dotted source. However, only unidirectional information flows from either the red-dotted source or the blue-dotted source to the green-dotted source. This flow of directional information forms a causal interaction topography, and each link within the topography is shown with large arrows, as in Fig. 3(c) for Patient #1. The two-tail arrow means bidirectional information flow, while the one-tail arrow indicates unidirectional information flow. The starting nodes of the topography are regarded as the primary sources in the causal interaction pattern, and other nodes in the topography are considered as the secondary sources. In this example, the red- and blue-dotted sources are the primary sources and the green-dotted source is the secondary source. The source causal interaction topographies are also shown in Fig. 5 for other patients. In these examples, Patient #2 has two sources in the right frontal lobe with unidirectional information flow. Patient #3 has three sources in the right frontal lobe, with directional causal interactions from the first source within the lesion (left top) to the second source (left bottom) and then to the third source (right), both of which are in the vicinity of the lesion. Patient #4 has three sources (two in the right mesial temporal lobe and one in the left frontal lobe), and the bidirectional causal interaction was estimated between the two sources within same lobe. The unidirectional causal interaction was found from one source in the mesial temporal lobe (top right) to the source in the left frontal lobe. Patient #5 has two sources in left mesial temporal lobe with unidirectional causal interaction.

Figure 4.

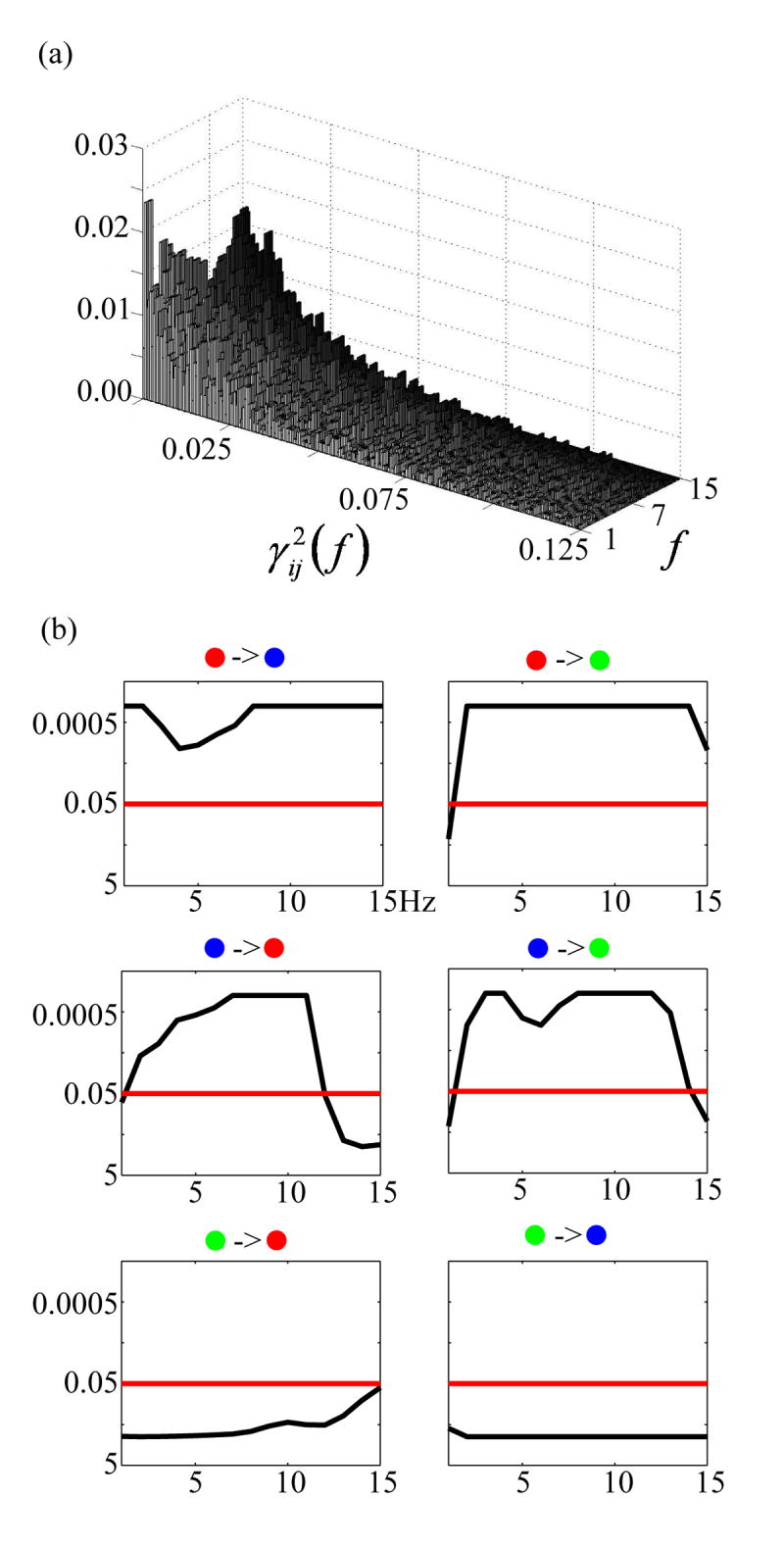
(a) Example of a histogram of the surrogate DTF function values as a function of frequency. (b) The statistical significances of the DFT function values (the thin curve in each small box) as a function of frequency inspected upon the sources from the example shown in Fig. 3. First row: from the red dotted source to other two sources; second row: from blue dotted source to other two sources; third row: from green dotted source to other two sources. The black curve in each small box indicates the statistical significance of the directional DTF values between two sources as a function of frequency. The red straight line indicates the significant level of p = 0.05.

Comparison between ictal source analysis, MRI, and SPECT

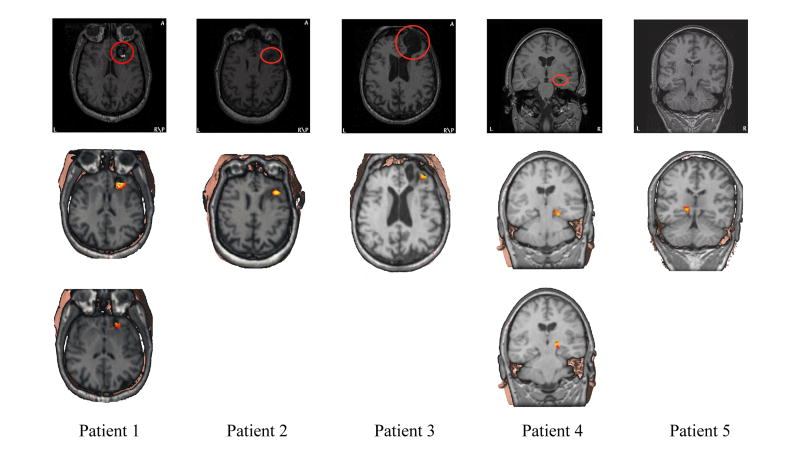
The primary sources identified from Fig. 3(c) and Fig. 5, after ictal source localization and causal interaction estimation, are shown together with MRI images in Fig. 6 for all five patients. The first row shows MRI slices with clear lesions in the first four patients (marked with red circles) and a coronal MRI slice for Patient #5 to show the mesial temporal lobe and hippocampus, which are considered to be the pathological sites for this patient. The second and third rows, if more than one primary source is available, show the locations of the primary sources for ictal activities from all five patients. The consistency between the primary ictal source and MRI lesion is indicated for the first four patients. For the last patient, the locations of the estimated primary sources are consistent with the presurgical evaluation. Furthermore, the SPECT scan performed on this patient also indicates left mesial temporal epilepsy. The positions of the primary sources identified from the entire 20 seizures relative to the MRI visible lesions (or pathological sites for Patient #5) are summarized in Table 1, which is classified into the following three categories: sources within or on the edge of the MRI visible lesions (++), sources in the vicinity (< 1.5 cm) of the MRI visible lesions (+), and sources far away from the lesion (−). The primary sources in 20 seizures appeared either within or on the edge of the lesions or very close to the lesions. There is no single seizure with primary sources completely outside of the lesions.

Figure 6.

MRI images (first row) and illustrations of the primary source locations from the ictal source analysis (second and third rows) for all five patients. The MRI lesions are marked with red circles.

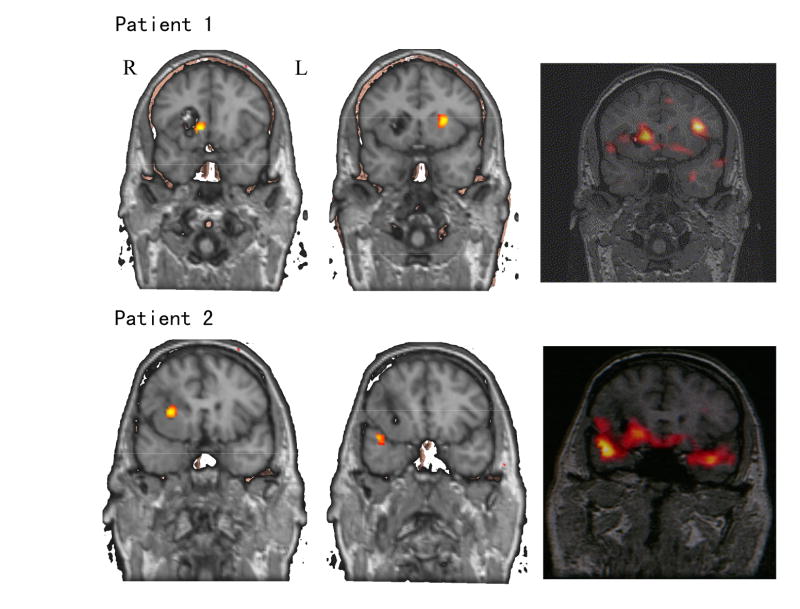
Fig. 7 shows the epilepsy source localization comparison between the ictal source analysis and SPECT imaging for Patients #1 and #2. Because the isotope injections during the SPECT imaging were performed approximately 30 seconds after the ictal onset, we selected the ictal data around injection time to perform ictal source localization analysis for the purpose of comparison. In Patient #1, bilateral sources in both hemispheres were identified by SPECT scan. Two ictal sources were close to the two SPECT image sources. However, the source in the left hemisphere, which is far away from the MRI lesion, was not present in the ictal onset source analysis (Fig. 3), which suggested that it was generated by the propagation of seizure activities due to the injection delay. Similarly for Patient #2, most of the activities in the SPECT images could be identified in ictal source localization analysis. Some of the primary sources were found in ictal onset source analysis, e.g. the source in the right frontal lobe, and the rest are considered to be caused by propagation, e.g. the sources in the right or left temporal lobes.

Figure 7.

Examples of SPECT scans (right column) from Patients #1 (first row) and #2 (second row) together with the ictal source localization analysis results (left two columns) around the isotope injection times.

Discussion

Ictal source analysis

The EEG and MEG source localization and imaging techniques (Assaf & Ebersole, 1997; Ebersole, 1997; Lantz et al., 1999; Michel et al., 1999; Worrell et al., 2000; Assaf et al., 2003) have advanced our knowledge about seizures from the sensor space to the source space. However, the additional requirement for ictal source analysis in epilepsy patients is the distinction between the primary sources which initiate the ictal activity and the secondary sources which are due to propagation. The traditional methods judge ictal onset and propagation by the inspection of EEG traces and then do source analysis to find their responsible underlying generators. The disentanglement of ictal onset and propagation involves preprocessing in either time domain or frequency domain (Lantz et al., 1999; Michel et al., 1999; Worrell et al., 2000). However, the sources at ictal onset and after ictal propagation may already be entangled when they appear in the scalp EEG measurements, (Sammaritano et al. 1987; Quesney et al. 1992; Williamson et al. 1992) and their frequency components normally occupy similar bands. The ictal source analysis performed in the present study integrates all possible available information in the space, time, and frequency domains in a unique way. We first performed a spatio-temporal multiple source localization task to locate the multiple sources responsible for the broad-frequency band, time-evolving ictal rhythms. After that, we characterized their temporal dynamics using the MVAR modeling and, most importantly, we estimated the causal interaction topography among the multiple identified sources. It is believed that sources identified by source localization and imaging techniques should include all sources responsible for both seizure onset and propagation. Among them, only those sources at the starting points of the directional causal interaction topography (Fig. 3(c), Fig. 5) should be considered as primary sources. We tested our hypothesis in twenty seizures (2–7 per person) from five epilepsy patients undergoing presurgical evaluations. The results obtained from the ictal source analysis were compared with MRI lesions (Fig. 6) and SPECT scans (Fig. 7). The results indicate that all primary sources identified by ictal source analysis are consistent with MRI lesions or presurgical evaluation for a nonlesional patient (Patient #5). The secondary sources obtained from ictal source analysis could either appear close to the lesional areas (examples shown from Patient #2 & #3) due to local propagation or far away from the lesions (examples shown from Patient #1 & #4) due to inter-lobe propagation. Based on the present results, the causal interaction patterns are thus especially useful for understanding the ictal onset and ictal propagation. The present promising results indicate that the proposed integrative technique is a promising method for understanding the structure of seizures.

Source modeling and subspace source localization

The equivalent current dipole model used in the present study is considered to be a powerful tool for modeling focal sources (Mosher et al., 1999), as in focal partial epilepsy. The dipole source model is limited to only providing the source location for the gravity point instead of the entire activated area (He et al., 1987). However, the proposed integrative source analysis technique has the potential to overcome this limitation. Other source localization and imaging techniques based on distributed source models (Hamalainen & Ilmoniemi, 1984; Pascual-Marqui et al., 1994; Michel et al., 1999; He et al., 2001, 2002a, 2002b) can be incorporated in this framework. Other related information flow estimate studies on source space (e.g. cortical current density estimated from the evoked potential (EP) instead of spontaneous EEG) are actually using the distributed source model (Astolfi et al., 2005; Babiloni et al., 2005). On the other hand, it is also proposed that the tomography obtained in subspace source scanning can be used to gain information on source extent using thresholding techniques (Darvas et al., 2004). However, the advantage of equivalent current dipole sources is the ease with which one can estimate their dynamic waveforms, which makes the subsequent causal interaction estimation straightforward. One possible way to describe the waveforms for a source with extent is to average the waveforms for a region of interest (ROI) (Astolfi et al., 2005; Babiloni et al., 2005). The advantage of subspace source localization is its ability to treat spatio-temporal measurements efficiently without data preprocessing and modeling to obtain a single map for subsequent source analysis (Lantz et al., 1999; Michel et al., 1999; Worrell et al., 2000). Of course, as is the case for the source models described above, many other source localization and imaging methods can also be adopted, as suggested in cortical connectivity analysis (Babiloni et al., 2005).

MVAR modeling

The MVAR modeling is a powerful tool for spectrum based analysis, including spectrum power, coherence, and causality, for stationary stochastic processes. It parameterizes the multiple time series system into a series of coefficient matrices, (equation (3)) and these parameters can easily be used to characterize the dynamics of multiple time series and their spectral features (Lutkepohl, 1993). In order to accurately model multiple time series, it is important to keep the temporal dynamics stationary. While it is difficult to keep all signals stationary during the evolvement of spontaneous EEGs, we select an ictal onset data segment by avoiding rapid activity pattern transitions in scalp EEG waveforms in order to maintain quasi-stationarity. A similar concept has been used effectively in ECoG studies by other researchers (Franaszczuk et al., 1994; Franaszczuk & Bergey, 1998). The present results also indicate that the system formed by epileptic sources can be efficiently and accurately modeled by MVAR. The only difference is that we use autoregressive processes to model the source system, and other researchers have used it to model the system formed by a group of field measurements at different recording sites. The advantages of MVAR modeling are for multiple signals (> 2) in the computation of causal interactions as compared with other pair-wise estimates (Gotman, 2003), which have recently been demonstrated, for example, with respect to the pair-wise DTF estimates (Kus et al., 2004).

Statistical assessment

The accuracy for the experimental and clinical data analysis is difficult to evaluate and assess because there is no “ground truth” available during each step of the analysis. In the present study, the ictal source analysis involves many intermediate steps to achieve the final analysis goal. This makes the accuracy assessment more important considering that any error in a previous step may propagate to and accumulate in latter steps. We thus propose using various statistical tests to assess the statistical significance of the results obtained in the each step of ictal source analysis, as has been suggested by others (Darvas et al., 2004) for validation of EEG and MEG mapping techniques. The square of the subspace correlation could be interpreted as the “R-squared” statistic (Mosher & Leahy, 1998), which indicates the variance of the topography generated by a dipole source identified in the measurement data. The subspace correlation threshold of 0.05, is a conservative choice which explains, from the signal subspace, approximately 90% of the variance in the topography generated by a dipole source. More importantly, we examined the values of the DTF causality from the viewpoint of statistical significance, which was tested using surrogate data strategy (Palus & Hoyer, 1998), instead of real DTF values since the DTF values from different sets of time series and at different frequency component may obey different distributions. Furthermore, the DTF functions themselves are with statistical means since the equivalence between the Granger causality and DTF causality has been studied (Kaminski et al., 2001) and the statistical properties of the various measures of the Granger causality have been extensively discussed (Caines & Chan, 1975; Geweke, 1982; Brovelli et al., 2004). The series of statistical assessments ensures us with the confidence about the results obtained during the ictal source analysis.

Different imaging modalities in epilepsy patient evaluation

The non-invasive epilepsy patient evaluation used to develop a clinical hypothesis about the location(s) of the epileptogenic zone most commonly includes MRI, SPECT, PET, video scalp EEG, and seizure semiology. Recently, different imaging modalities in clinical epilepsy evaluation have come to be viewed as complementary rather than competing modalities. It is believed that the consistent results from different evaluation means should have the highest localization accuracy in presurgical evaluation of epileptogenic foci (Rosenow & Luders, 2001).

The outcomes from ictal source analysis, MRI, and SPECT for all five epilepsy patients are summarized in Table 2. Compared with the results presented in Fig. 6 and Table 1 with MRI and the results in Fig. 7 with SPECT, the consistency between them indicate not only the accuracy of the ictal source analysis method, but also demonstrates the accurate localization of epileptogenic zone in the group of patients studied. On the other hand, the ictal source analysis is more useful when no explicit structural abnormalities exist in MRI. Its temporal resolution is thought to be able to distinguish the primary source from the secondary source as compared with SPECT which involves a delay of seizure acquisition due to the amount of time consumed during isotope injection and delivery. The ictal source analysis presented in the present study could also be extended to the interictal analysis (Scherg et al., 1999; Huiskamp et al., 2004).

Table 2.

Summary of MRI, SPECT, and Ictal source analysis for all five patients

	MRI lesions	SPECT	Ictal source analysis
Patient 1	Right frontal cavernous hemangioma	Right and left frontal	Right frontal
Patient 2	Right frontal tumor	Mainly right frontal and right anterior temporal tip	Right frontal
Patient 3	Right frontal abscess with residual encephalomalacia	Mainly right frontal	Right frontal
Patient 4	Right mesial temporal sclerosis	Right temporal	Right medial temporal
Patient 5	Normal MRI	Left temporal	Left medial temporal

Conclusions

In the present study, we have developed a novel integrative approach to characterize the structure of seizures in the space, time, and frequency domains. The direct benefit for such multi-domain feature characterization is a new ictal source analysis technique. This technique combines source localization together with the estimation of causal interaction among sources. The source localization technique finds the source locations and the causal interaction estimation technique indicates the dynamic information flow patterns existing among the sources. These dynamic patterns can then be used to distinguish the primary source, which initiates the ictal activity, from the secondary source, which is generated due to the ictal activity propagation. The noninvasive ictal source localization and causality analysis results have been evaluated by comparing with other imaging modalities notably MRI and SPECT, suggesting good consistency between the EEG-based ictal source analysis results with MRI/SPECT results. The present promising results suggest the possibility of distinguishing the primary sources from the secondary sources non-invasively, and that the proposed approach may become an important alternative for seizure source analysis aiding presurgical planning in epilepsy patients.