Mapping the MRI Voxel Volume in Which Thermal Noise Matches Physiological Noise-Implications for fMRI.

Abstract

This work addresses the choice of the imaging voxel volume in blood oxygen level dependent (BOLD) functional magnetic resonance imaging (fMRI). Noise of physiological origin that is present in the voxel time course is a prohibitive factor in the detection of small activation-induced BOLD signal changes. If the physiological noise contribution dominates over the temporal fluctuation contribution in the imaging voxel, further increases in the voxel signal-to-noise ratio (SNR) will have diminished corresponding increases in temporal signal-to-noise (TSNR), resulting in reduced corresponding increases in the ability to detect activation induced signal changes.. On the other hand, if the thermal and system noise dominate(suggesting a relatively low SNR) further decreases in SNR can prohibit detection of activation-induced signal changes. Here we have proposed and called the “suggested” voxel volume for fMRI the volume where thermal plus system-related and physiological noise variances are equal. Based on this condition we have created maps of fMRI suggested voxel volume from our experimental data at 3T, since this value will spatially vary depending on the contribution of physiologic noise in each voxel. Based on our fast EPI segmentation technique we have found that for gray matter (GM), white matter (WM), and cerebral spinal fluid (CSF) brain compartments the mean suggested cubical voxel volume is: (1.8mm)³, (2.1mm)³ and (1.4mm)³, respectively. Serendipitously, (1.8mm)³ cubical voxel volume for GMapproximately matches the cortical thickness, thus optimizing BOLD contrast by minimizing partial volume averaging. The introduced suggested fMRI voxel volume can be a useful parameter for choice of imaging volume for functional studies.

Introduction.

Since its inception, functional magnetic resonance imaging (fMRI) has become an important tool for studying human brain function and organization. Blood oxygenation level dependent (BOLD) contrast is the most commonly used in fMRI. To improve BOLD specificity it is desirable to obtain high spatial resolution functional maps (Cheng et al., 2001; Beauchamp et al., 2004). However, minimum voxel size in fMRI is limited by the MRI signal-to-noise ratio (SNR) (Edelstein et al., 1986). It is not advantageous to choose a voxel size that is too large either. Not only does this reduce specificity because of partial volume effects (PVE), but also more significantly, while increases in SNR are achieved, diminishing gains in temporal signal to noise ration (TSNR) result because of increasing contribution of physiologic noise (Yo et al., 2001; Parish et al., 2000; Krüger et al., 2001). TSNR is defined as a ratio of the average voxel time course signal over time course standard deviation. TSNR is the primary measure of the ability to detect BOLD signal changes (Parish et al., 2000; Bellgowan et al., 2006). The nonlinear relationship between TSNR and SNR in gradient-echo BOLD imaging has been characterized at 3 Tesla, and has recently been verified and confirmed at 7 Tesla (Triantafyllou et al., 2005). At 3 Tesla we take advantage of the recent advances in multichannel MRI receiver and multi-element array coil technology (Bodurka et al., 2004; de Zwart et al., 2004) to map the relationship between TSNR and SNR. From this relationship, on a voxel-wise basis, we introduce the “suggested” voxel volume (SVV) for fMRI and construct voxel-wise SVV maps illustrating its spatial non-uniformity. We define the SVV as the imaging volume in which the physiological noise contribution (σ_P) equals the non-physiological (σ₀ =thermal+MRI scanner) system noise. Starting from this “suggested” point, if one tries to increase signal to noise by reducing resolution, the gains are increasingly diminishing. On the other hand if one tries to increase resolution, the losses in SNR are relatively rapid. This is essentially the point at which one can get the highest SNR for the least loss in resolution.

The choice of a somewhat arbitrary assignment and definition of “suggested point” helps to characterize the entire curve relating TSNR and SNR. The primary problem with providing a more quantitative “cost function” (based on SNR) is that it varies depending on the parameters of each investigator’s study. For some studies, it might be unacceptable to have a signal to noise below a certain level. For other studies, there might be more time in which to average, thus allowing a lower “suggested” value.

At the SVV, shown schematically on Figure 1, as the voxel volume increases further, increases in SNR translate into diminishing increases in TSNR. Therefore, larger voxels and/or improved MRI signal reception do not necessarily translate to improved BOLD detection. On the other hand, if the voxel volume is reduced relative to the SVV, the SNR and TSNR are reduced in increasingly direct proportion, potentially prohibiting detection of small BOLD signal changes.

Figure 1.

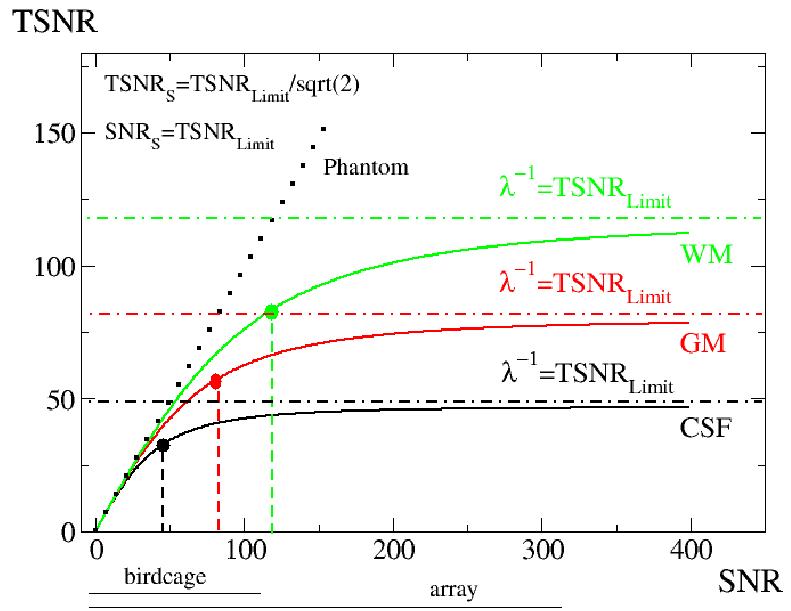
A simulation of the TSNR versus SNR relationship (Equation 1) for three different brain tissue components and a phantom is shown. The lines represent the human brain white matter (green), gray matter (red), and cerbro-spinal fluid (black). The dark dotted line represents the expected result for a phantom (no physiological noise present). The locations of the suggested voxels for specific brain compartments where Equation 2 holds are marked using large color dots. The dashed vertical lines indicate TSNR and SNR coordinates for OVV and the horizontal dotted/dashed lines limit for TSNR. The black horizontal lines below the horizontal axis show the SNR range available with the system standard transmit/receive birdcage coil and the 16 channel receive-only surface coil brain array are used.

In summary, in this work we: a) determine the theoretical expressions for the suggested fMRI voxel volume and the image SNR necessary to reach this volume; b) introduce a fast and simple EPI T₁ mapping technique for brain segmentation; c) experimentally map and determine the suggested volumes for different brain tissue compartments; and d) discuss implications for fMRI.

Theory.

A) Suggested fMRI voxel volume.

It is assumed that the noise variance in the imaging voxel is a superposition of thermal plus MRI scanner-related noise (σ²₀) and physiological noise contributions (σ²_p). Krüger et al., (2001) introduced the model describing the physiological noise in gradient-echo EPI BOLD resting state brain data that depends on the MRI signal strength (σ_p=λS, where S is MRI time course average signal strength after reaching steady state). This physiological noise is shown to be significantly greater in cortical gray matter (GM) than in white matter (WM). The proportionality constantλ that characterizes physiological noise is therefore tissue specific.

From this model, the relationship between TSNR and SNR is schematically shown on Figure 1 and is given as:

$$\mathit{TSNR}=\frac{S}{\sqrt{{\sigma }_0^2+{\sigma }_P^2}}=\frac{\mathit{SNR}}{\sqrt{1+{\lambda }^2{\mathit{SNR}}^2}}$$ [1]

This model also predicts that as image SNR increases or when ratio of σ_P/σ₀ is larger then one it causes the temporal signal-to-noise ratio in the oxygenation-sensitive MRI BOLD signal to saturate, also as shown in Figure 1. In such case equation [1] shows that the proportionality constant λ is equal to the reciprocal of the TSNR limit: λ=1/TSNR_L. In the low SNR situation or when ratio of σ_P/σ₀ is smaller than one TSNR equals SNR as expected for systems without physiological noise (phantoms). Situation where the ratio of σ_P/σ₀ equals one or the thermal noise equals physiological noise we described as “suggested”. The “suggested” equality condition for thermal noise and physiological noise can be written as:

$${\sigma }_0^2={\sigma }_P^2$$ [2]

From Equation [1] one can find the TSNR and SNR values where “suggested” condition [2] holds as

$${\mathit{TSNR}}_S({\sigma }_0^2={\sigma }_P^2)=\frac{{\mathit{TSNR}}_L}{\sqrt{2}}$$ [3-1]

$${\mathit{SNR}}_S({\sigma }_0^2={\sigma }_P^2)={\mathit{TSNR}}_L$$ [3-2]

MRI signal strength is proportional to imaging voxel volume (Edelstein et al., 1986). The proportionality constant, denoted as C, can be estimated on a voxel-wise basis from the first EPI time course image (C=M₁/V₀, where M₁ is MRI signal intensity for the first time course image). Therefore, the image signal-to-noise ratio (SNR) for the imaging volume V can be written as:

$$\mathit{SNR}={\mathit{SNR}}_0\frac{V}{V_0}$$ [4]

where SNR₀ is signal to noise at imaging volume V₀.

Assuming that [2] holds and combining Equations [1,3,4] one can obtain the Equation for the suggested voxel volume (V≡V_S) as:

$$V_S=\frac{V_0}{{\mathit{SNR}}_0}\frac{{\mathit{TSNR}}_S}{\sqrt{1-{\lambda }^2{\mathit{TSNR}}_S^2}}=\frac{V_0}{{\mathit{SNR}}_0}\frac{1}{\lambda }$$ [5]

From Equation [5] one may estimate the SNR₀ to obtain the suggested fMRI voxel as:

$${\mathit{SNR}}_0=\frac{V_0}{V_S}{\mathit{TSNR}}_L$$ [6]

Therefore, if the imaging volume V₀ is set to be equal to the suggested volume V_S, then the signal-to-noise ratio needed (SNR₀=SNR_S) is simply equal to TSNR_L, which is in agreement with Equation 3.2. Because of the TSNR_L =1/λ limit values for different tissue compartments are known (Krüger et al., 2000; Bodurka et. al., 2005) or can be measured. Equation 6 can serve as a simple estimate for the required SNR₀ needed to reach the suggested fMRI volume or the volume at which thermal plus system noise equals physiological noise.

B) Fast EPI T₁ mapping for image segmentation.

Voxel-wise fast T₁ EPI mapping allows efficient tissue segmentation, relying on T₁ differences between gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). In a spoiled serial gradient echo EPI acquisition, or if TR⪢T₂, a Steady State Incoherent Signal develops, and there will be no signal present during an RF excitation resulting from previous excitations (Zur et al., 1991; Zhao et al., 2000). In that case, steady state signal for a 90° degree flip angle and neglecting flip angle non-uniformity is given by:

$$M_{\mathit{SIIS}}=M_0(1-e^{-TR∕T_1})e^{-TE∕T_2^{\ast }}$$ [7]

The signal for the first EPI volume is:

$$M_1=M_0{e}^{-TE∕T_2^{\ast }}$$ [8]

From Equations [7] and [8] a T₁ map can be calculated from the ratio (R=M₁/M_SSIS) of the first time course and steady state images as:

$$T_1=\frac{TR}{\mathit{ln}\left(\frac{R}{R-1}\right)}$$ [9]

Equation [9] shows the necessity for R>1. Therefore, the repetition time must obey the relation: TR<5T₁.

Material and Methods.

Imaging hardware included: 3 Tesla General Electric Signa VH/3 MRI scanner (3T/90cm, whole body gradient inset 40mT/m, slew rate 150 T/m/s, whole body RF coil) equipped with home-built 16 channel MRI digital receiver (Bodurka et al., 2004); standard T/R head coil, and 16-channel receive-only brain array (Nova Medical Inc) (de Zwart et al., 2004). For functional runs, a single shot full k-space gradient echo EPI with matrix size 128x96 was used. Time series data were collected during which the subject was lying in the scanner with closed eyes. Experiments were performed on three human subjects. The experimental protocol was NIH IRB approved and all subjects were monetarily compensated. Imaging parameters: Axial plane, 8 slices, FOV: 220mm×165mm, slice 4mm, TR=3sec, TE=45ms, flip angles (90,70,45,20,1,0 degrees), number of volumes 70. The combination of the multi-channel digital MRI receiver and the 16-element array offered substantial SNR improvements (on average, 3-fold compared to a GE birdcage coil, Bodurka et al., 2004). This guaranteed that at this resolution and with a flip angle of 90 degrees, a sufficient SNR range for Equation [1] is covered (Bodurka et al., 2005). In order to fully assess the physiological noise contributions to the imaging data no physiological noise correction schemes were applied (Hu et al, 1995; Glover et al., 2000). For all computations, image processing and visualization, Scilab and AFNI were used (INRIA; Cox, 1996).

For each subject and for segmentation purposes, the T₁ maps were computed from the ratio of the first image in the EPI time course (infinite TR, FA=90 degrees) over an average steady state image (Equation 9). Specific binary masks were obtained from the segmented tissue. Since the same EPI images were used for the segmentation and for the time series collection, a direct registration was achieved.

We determined image SNR as the ratio of the image signal over the standard deviation of the image background noise from a region-of-interest in the image background with no visible MRI signal, and we accounted for non-Gaussian noise distribution (Gudbjartsson and Patz, 1995). Additionally, to verify our SNR estimates, we used the NEMA method (NEMA, 1988) which yields very similar results. To compute the suggested voxel volume (SVV) maps for each subject we collected high-resolution (voxel volume 12mm³) single-shot EPI resting state fMRI runs varying the flip angles with each run. TSNR maps were calculated for each flip angle. Next, on a voxel-wise basis, we fitted the TSNR versus the SNR data to physiological model Equation [1] in order to find the suggested TSNR/SNR (Equation [3]). Based on the suggested SNR value and the assumption that the MRI signal is proportional to a voxel volume, we computed the map for the suggested fMRI voxel volume based on Equation [5]. To obtain tissue-specific information for each subject, binary segmentation masks were applied onto SVV maps. Within the tissue mask the mean and the standard deviation of SVV voxel values were computed. Finally, individual subject data were pooled together based on different brain tissue compartments and mean +/- standard deviation SVV values for GM, WM, and CSF were reported.

Results.

Figure 1 shows the relationship between the TSNR and SNR ratios (Equation [1] simulation) for three different brain compartments and a phantom. The suggested voxel volumes, where system (thermal and scanner related) noise equals physiological noise, are marked as large green, red, and black points for white, gray matter, and CSF, respectively. Brain tissue specific upper limits of TSNR are also shown. The TSNR_L limits for GM, WM, and CSF of 78, 117, and 47, respectively, were used (Bodurka et al., 2005). The TSNR and SNR values for the suggested conditions are shown as well (Equations [3.1] and [3.2]).

Figure 2 shows the results of the Equation [5] simulation for three different brain compartments, namely the relationship between an suggested cubical voxel size “a” and image signal-to-noise ratio SNR₀. An experimental imaging value for imaging volume V₀, as well as TSNR_L, was used. The suggested cubical voxel volumes in brain gray matter for two different coils are shown, marked as a red oval (2.5 mm³) and a red square (1.8 mm³), respectively. Coil 1 is the GE transmit receive birdcage head coil. Coil 2, a receive-only array, has 2.8 times higher SNR over the whole brain as compared to Coil 1 (de Zwart et al., 2004).

Figure 2.

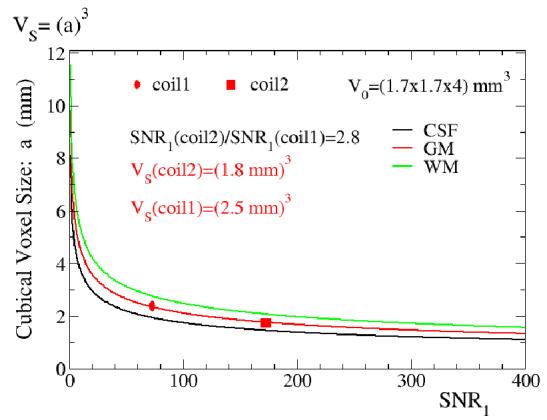
A plot of the suggested cubical voxel size versus SNR₀ for three different brain tissues (Equation [5] simulation) is shown. The imaging voxel volume V₀ matches the volume used in experiments, and the TSNR_L or 1/λ values obtained in experiments were used (GM: 80, WM 130, CSF 45). The suggested voxel volumes for two different coils: a standard system provided birdcage head coil- coil1 (birdcage) and a 16 channel receive-only surface coil brain array- coil2 (array) are shown in gray matter (coil1 marked as a red oval, coil2 marked as a red square). Coil2 (array) has 2.8 times better SNR over the whole brain than coil1 (birdcage).

Figure 3a shows the T₁ histogram plot of 111726 voxels from all subjects (n=3). For the segmentation we define T₁ ranges for predominantly WM, GM, and CSF compartments as (0.5s-1.05s), (1.1s-1.49s), and (>1.5s), respectively. Representative single subject and single slice T₁ maps and the resulting masks for WM, GM, and CSF are shown on Figures 3b, 3c, 3d, and 3e, respectively. The mean T₁ values within each brain compartment, GM, WM, and CSF, pooled across all subjects were were: T_1GM=1.25s, T_1WM=0.85s, and T_1CSF=3.35s. These values were expected to match the literature (Wansapura et al., 1999, Zhao et al., 2000) since the ranges were chosen based on the literature values. Most importantly, the maps of CSF, GM, and WM matched the expected distribution of these components..

Figure 3.

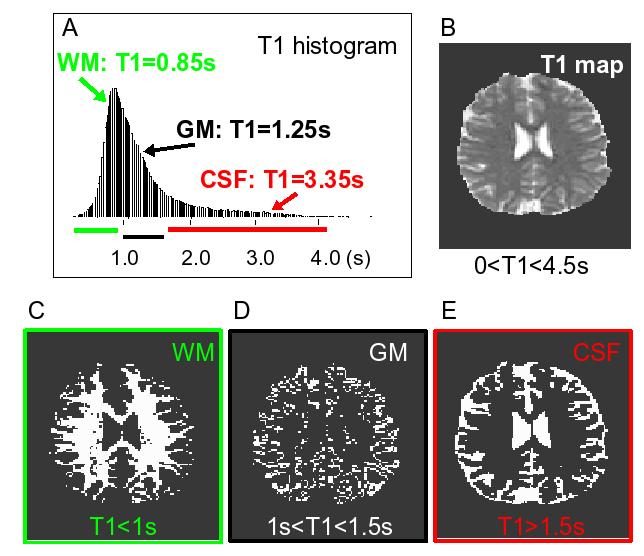
An example of the echo planar image segmentation is shown. a) A histogram of the T₁ values from all voxels in all subjects (n=111726) is shown. The colored horizontal lines represent the T₁ ranges used for segmentation; b) An example of single slice T₁ map is shown. Grey scale display range: 0s (black) to 4.5s (white). Examples of the resulting binary segmentation masks are also shown: c) white matter (WM); d) gray matter (GM); e) cerebrospinal fluid (CSF).

Figure 4 shows the suggested fMRI cubical voxel volume maps for all slices from a single subject. Large black blotches are from susceptibility-related signal dropouts and result from an applied automatic masking operation to extract only the brain tissue area. Figure 5 shows a comparison of a single slice: SNR (a) and TSNR (b) maps, both acquired with a 90 degree flip angle, with SNR_S =TSNR_Limit, (c) computed from a corresponding cubical SVV map (Figure 4, yellow box).

Figure 4.

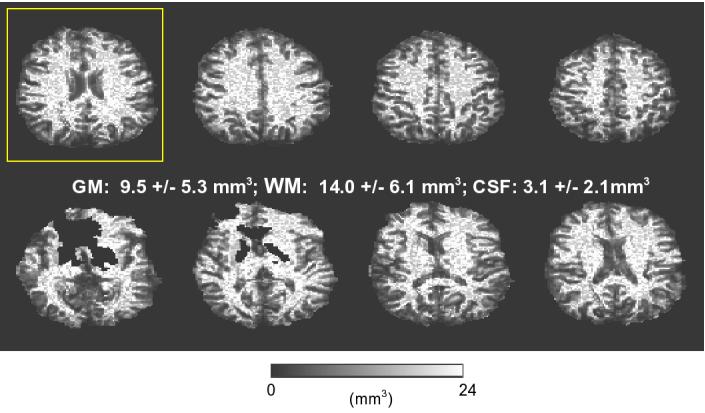
An example of single subject suggested fMRI cubical voxel maps is shown (display range: 0 mm³ (black) to 24 mm³ (white)). SVV mean value plus standard deviation for different tissue compartments are displayed.

Figure 5.

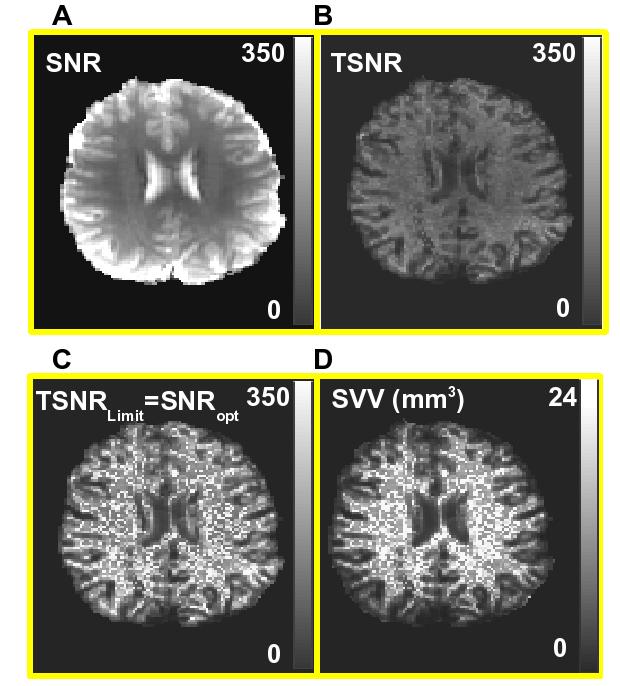
Computed from the first image in Figure 4 (marked by a yellow box) maps of: a) SNR, b) TSNR, c) SNR_S=TSNR_Limit and, d) SVV map (display range: 0 mm³ (black) -24 mm³ (white)) are shown.

Group data from all 3 subjects are shown in Table 1. Based on a large number of voxels within tissue masks, we have obtained the following suggested cubical voxel sizes (mean +/-standard deviation) for different brain compartments: GM 1.78+/-0.4 mm; WM 2.1+/-0.4 mm, and CSF 1.36+/-0.31 mm. Of course, the only region of relevance for most BOLD based brain mapping is GM. Reporting of the “suggested” voxel volume for WM and CSF is simply to illustrate the relative influence of physiologic noise on this voxel volume measure.

Discussion.

The imaging voxel volume for BOLD fMRI studies is one of the most important variables affecting activation detection and specificity in functional brain imaging. Based on the physiological noise model in BOLD imaging (Krüger and Glover, 2001; Krüger et al., 2001), we have derived a novel formula to compute the “suggested” fMRI voxel volume (Equations [3-5]), taking into consideration the relationship between SNR and TSNR. At the “suggested” fMRI voxel volume (SVV) the magnitude of physiologic fluctuations is equal to thermal and system noise magnitudes (Equation [2]). As one increases SNR, physiologic noise will dominate and the rate of improvement in TNSR will diminish. From a starting point of the SVV, if one were to increase SNR by either lowering resolution or using more sensitive RF coils for example, the gains in TSNR would diminish relative to gains in SNR. On the other hand, one were to decrease SNR by increasing resolution, the loss in SNR and TSNR would be matched. If one has more time than the typical one hour or so to average and is interested in even higher resolution imaging, then this condition of imaging below the “suggested” resolution is of course acceptable and perhaps “optimal” for that particular study. Nevertheless, an important point that is brought out in this manuscript is that TSNR drops very rapidly once TSNR and SNR are linearly related (at low enough SNR such that system and thermal noise begin to dominate). Therefore, this suggested imaging volume (SVV) is expected to provide helpful guidance for designing fMRI studies.

Temporal signal-to-noise ratio limit values (TSNR_L) for different brain compartments determine the suggested voxel volume and the best achievable time course stability -a key parameter to detect small BOLD signal changes. Those experimental constants were determined in this study on a voxel-wise basis and they are in general agreement with earlier measurements with a 16-element brain array and using only birdcage coil (GM: 78-90, WM: 117-167, CSF 47-53) (Krüger et al., 2000, Bodurka et al., 2005). Specific values for TSNR_L may depend on spatial resolution used in the experiment because partial volume effect, data post-processing with physiological noise correction, definition and size of used region-of-interest to define specific tissue, and most importantly, on available SNR in the experiment, which may or may not allow for proper sampling of the TSNR versus the SNR curve. Insufficient SNR available at 1.5T and 3T with a standard transmit/receive head birdcage coil was the reason the physiological noise model proposed by Krüger et al., (2000) was only recently verified at 7T and also at 3T with the use of a highly sensitive MRI receiver/reception system (Triantafyllou et al., 2005; Bodurka et al., 2005).

In order to find out the suggested voxel volumes on the basis of different brain tissues we have introduced a simple fast EPI-based T₁ mapping technique. This technique neglects possible flip angle non-uniformities, and therefore, is not recommended for quantitative voxel-wise T₁ mapping. Depending on the imaging resolution, partial volume effects can affect computed T₁ values in some voxels and result in those voxels in apparent T₁ values rather than “true” tissue specific values. Nevertheless, this technique allow for robust EPI image segmentation since obtained T₁ maps experienced clear contrast (T₁ difference) between different brain tissue compartments (Figure 3). Resulting individual brain tissue masks, in addition to the proper anatomical location, feature a very large number of voxels instead of small hand-drawn ROIs. The histogram of measured T₁ values (Figure 3a) and the mean T₁ values obtained with GM,WM and CSF compartments matches literature data (Lu et al., 2000, Wansapura et al., 1999, Zhao et al., 2000). However, mean T₁ values can be somewhat biased since we used predefined T₁ ranges to define GM,WM and CSF compartments (Results). T₁ mapping results suggests that flip angle non-uniformity is not prohibitive factor or, in other words, the spatial variations in flip angle using our coil configuration and at 3T cause miss-estimations of T₁ that are still within the normal ranges of T₁ for each tissue type. Also the maps appear to correspond to those expected from each tissue component. An important advantage of this approach besides its simplicity and computational efficiency is that segmentation mask and fMRI images both have identical image distortions and are exactly registered in space. We have obtained a mask for each slice location for GM, WM, and CSF brain compartments. This allowed us to compute the mean values of the suggested voxel volumes within individual masks composed of a very large number of voxels and easy-to-pool data from different subjects. Performing these calculations on a voxel-wise basis allowed us to map the suggested cubical fMRI voxel volume. For gradient-echo BOLD imaging at 3 Tesla with a sensitive 16 channel brain array, we have found that for GM, WM, and CSF brain compartments the suggested cubical voxel volume is: (1.8mm)³ , (2.1mm)³, _and (1.4mm)³ , respectively. Serendipitously, (1.8mm)³ cubical voxel for GM matches restraints from cerebral cortex anatomy (Duvernoy et al., 1981), and appears to correspond well with an experimental observation of Hyde et al., (2001).

It should be noted that a recently published paper by Mazaheri et al. (2006) similarly exploits a transient part of the time course EPI acquisition, with the goal to discriminate veins. The primary difference in techniques is that our T₁ mapping technique does not require a short TR since it only uses the first (TR = infinity) and stead state images for the calculations. In addition, no nonlinear fitting is required either. Although the issue of scan duration for a given TSNR was not addressed in this study, it is expected that at 3 Tesla the GM TSNR at this volume (TSNR_L/√2 ∼ (55-64) or normalized time course stability of 1.8 %-1.6 %) should allow detection of small (1-2%) BOLD signal changes in typical scan time of approximately 5 minutes (Parrish et al., 2000).

Another an important observation is significant differences in TSNR_L values between different brain compartments, which in turn affects suggested voxel volumes for GM, WM, and CSF. TSNR_L limits reflect tissue specific physiological noise contribution, and variations within GM may reflect different vessel densities different “resting state” brain activity, or simply variations in partial volume averaging with CSF or WM. Differences between GM and WM may be understood as reflecting differences in cerebral vasculature density. Consequently, for WM, the imaging volume where thermal noise matches physiological noise is larger as compared to GM. In CSF regions, because of the proximity to major arteries and vessels and/or cerebro-spinal fluid pulsation and motion, the physiological noise level is the highest. Therefore, the suggested voxel volume condition is met at the lowest SNR₀, as compared to GM and WM, resulting in the smallest imaging volume.

We have also derived the relationship between the required image SNR₀ needed to reach the suggested voxel volume (V₀=V_S) for a given TSNR_L value (Equation [6]). This equation provides a simple estimate for the SNR₀ required to reach the suggested voxel volume condition. If SNR₀ for a given imaging volume V₀ is less than TSNR_L the suggested fMRI voxel conditions cannot be met. In this case, noise in the fMRI voxel will be dominated by thermal noise (linear part of TSNR versus SNR plot, Figure 1). As such, spatial smoothing commonly used in fMRI data analysis would certainly improve BOLD detection since the spatial averaging would effectively suppress thermal noise contribution (which would not be the case where spatially coherent physiological noise dominates). Spatial smoothing can improve BOLD contrast and is important for the averaging of spatially-normalized multi-subject data. However, it comes at a significant cost of specificity to activation sites. Due to recent sensitivity advances in MRI technology (Bodurka et al., 2004), high field MRI advances (above 3 Tesla) (Kim, 2005), and recent trends in fMRI data analysis techniques that characterize high spatial frequency “patterns” (Haxby et al., 2001; Kamitani and Tong, 2005; Haynes and Rees, 2005; Kriegeskorte et al., 2006), the use of high resolution data can provide unique information about the functional organization of individual brains (Beauchamp et al., 2004; Cheng et al., 2001).

An important experimental parameter is the image SNR₀ available in the experiment. In addition to the general imaging parameters (TR,TE,flip angle etc.) and sequence used in the experiment, the available SNR₀ depends mostly on field strength and imaging hardware. As it is shown on Figure 2, if available SNR₀ in experiments increases with a better reception antenna (ie, coil2 array), the suggested fMRI volume decreases as compared to coil1 (birdcage). Also, for example, in gray matter a 2-fold SNR₀ increase from 200 to 400 results in a cubical voxel volume size change from a=1.68 mm to a=1.33mm. In the low SNR₀ situation, a further reduction in SNR₀ results in increases in cubical voxel sizes (for example, the SNR₀ change from 20 to 10 results in about a≅3.61mm to about a≅4.59 mm). This clearly shows that an increase in SNR₀ decreases suggested voxel volumes and therefore can allow detection of fMRI signal changes at higher spatial resolution (as low as cubical voxels with 1.5mm-2mm size), which matches anatomical constraints of human cerebral cortex grey matter (Duvernoy et al., 1981; Hyde et al., 2001). This also shows that in order to perform fMRI with an suggested cubical voxel volume below 1 mm³, more improvement in MRI signal sensitivity would be needed. Such sensitivity improvement can be achieved by going to higher than 3T field strength and/or with even more sensitive MRI signal receivers and RF coils combination, or by reducing the contribution of physiologic noise.

If available SNR₀ is high enough, it is expected that setting up the imaging voxel volume to be equal or close to the suggested volume for gray matter will be beneficial and potentially “optimal” for gradientecho EPI fMRI experiments. We describe “optimal” as achieving the highest resolution possible with the least sacrifice in TSNR. In other words, this “suggested” point is “optimal” if one has enough TSNR and averaging time (practically, a typical scanning session of about an hour) to achieve significant activation. If one has more time to average, and is focused on achieving higher resolution, then the “optimal” resolution may be even higher than the “suggested” resolution. Nevertheless, even the “suggested” volume offers higher spatial resolution relative to the typical 3×3×5 mm³ volumes used-therefore minimizing partial volume averaging and increasing spatial localization while still maintaining sufficient BOLD sensitivity (Beauchamp et al., 2004).

Conclusions:

We propose the “suggested” voxel volume for gradient-echo EPI BOLD imaging, which we define as the voxel volume where the physiological noise contribution is equal to system and thermal noise contribution. We have provided a simple criteria for a necessary SNR in order to reach the SVV condition. At the suggested voxel volume the image SNR is equal to the temporal SNR limit for a given brain tissue compartment. The temporal SNR limits for different brain compartments in fMRI are known and/or can be easily measured. From our experimental data at 3 Tesla with a 16 channel detector array head coil, we have computed and mapped the suggested voxel volume on a voxel-wise basis. We have found that for GM, WM, and CSF brain compartments the mean suggested cubical voxel volume is:(1.8mm)³, (2.1mm)³, and (1.4mm)³, respectively. The introduced SVV can be a useful parameter for choice of imaging volume for fMRI studies.

Table 1.

Cubical voxel volume sizes for different brain tissues computed from the condition where the thermal plus system noise is equal to physiological noise. Group data from all subjects (n=3).

	Gray Matter (GM)	White Matter (WM)	Cerebrospinal fluid (CSF)
Number of voxels	33789	55262	26296
V=(a) 3 Mean +/- st. dev.	a=(1.78 +/- 0.4) mm	a=(2.1 +/- 0.4) mm	a=(1.36 +/- 0.31) mm