Magnetoacoustic Tomography with Magnetic Induction (MAT-MI)

Abstract

We report our theoretical and experimental investigations on a new imaging modality, magnetoacoustic tomography with magnetic induction (MAT-MI). In MAT-MI, the sample is located in a static magnetic field and a time-varying (μs ) magnetic field. The time-varying magnetic field induces eddy current in the sample. Consequently, the sample will emit ultrasonic waves by the Lorentz force. The ultrasonic signals are collected around the object to reconstruct images related with the electrical impedance distribution in the sample. MAT-MI combines the good contrast of electrical impedance tomography with the good spatial resolution of sonography. In principle, MAT-MI mainly has two unique features due to the solenoid nature of the induced electrical field. Firstly, MAT-MI could provide explicit or simple quantitative reconstruction algorithm for the electrical impedance distribution. Secondly, it promises to eliminate the shielding effects of other imaging modalities in which the current is applied directly with electrodes. In the theoretical part, we provide the formulas for both the forward and inverse problems of MAT-MI and estimate the signal amplitude in biological tissues. In the experimental part, the experiment setup and methods are introduced and the signals and the image of a metal object by means of MAT-MI are presented. The promising pilot experimental results suggest the feasibility of the proposed MAT-MI approach.

INTRODUCTION

Electrical impedance tomography (EIT) (Krestel 1990, Webb 1992, Paulson et al 1993, Morucci and Rigaud 1996) has been used in various clinical applications and continues to attract substantial research interest because of its functional information. However, the spatial resolution of EIT is low. In order to provide high spatial resolution of impedance information, we have developed a new approach called magnetoacoustic tomography with magnetic induction (MAT-MI) by combining ultrasound and magnetism. In this method, the sample is put in a static magnetic field and a time-varying (μs ) magnetic field (Fig. 1). The time-varying magnetic field induces eddy current in the sample. Consequently, the sample will emit ultrasonic waves through the Lorentz force produced by the combination of the eddy current and the static magnetic field. The ultrasonic waves are then collected by the detectors located around the sample for image reconstruction. MAT-MI combines the good contrast of EIT with the good spatial resolution of ultrasound.

Fig. 1.

Illustration of MAT-MI.

The MAT-MI is similar to magnetoacoustic tomography (MAT) (Towe and Islam 1988, Islam and Towe 1988, Roth et al 1994, Roth et al 1998) or the reverse mode of Hall effect imaging (HEI) (Wen et al 1998, Wen 1999, Wen 2000) where electric stimulation instead of magnetic stimulation is employed. In MAT and HEI/MAT the current is either spontaneous or injected into a sample by applying electrodes on the surface of the sample. As a contrast, in MAT-MI a magnetic inductor is used to generate a time-varying magnetic field, which in turn induces a pulsed electrical field and eddy current. The magnetic inductor used in MAT-MI is similar to the magnetic stimulator (MS) widely used in the research and clinical environment, especially for the intracranial delivery of magnetic energy into the brain (Irwin et al 1970, Barker et al 1990, Roth and Basser 1990 , Malmivuo and Plonsey 1995, Davey and Epstein 2000, Wagner et al 2004). But the induced electric pulse width (in the μs scale ) in the MAT-MI is much shorter than that of commercial magnetic stimulators (in the ms scale) in order to obtain the spatial resolution of mm scale. This is because the resolution in MAT-MI is approximately the electric pulse width times the acoustic speed in soft tissues (about 1.5 km/s).

Compared with the other similar imaging modalities aimed at obtaining the electrical impedance distribution such as EIT, magnetic induction tomography (MIT) (Al-Zeibak et al 1995, Griffiths et al 1996, Merwa et al 2005), HEI/MAT, and magnetic resonance electrical impedance tomography (MREIT) (Woo et al 1994, Kwon et al 2002, Gao et al 2005), MAT-MI has several unique features. Firstly, it will not be affected by the low-conductivity layer of tissue at/near the surface of human body, such as the skull of the head and the fat layer of the breast. This is because the magnetic fields, unlike electrical currents, can go into the low-conductivity layer easily. For example, assume we have a two-layered object in a conductive medium (Fig. 2). The outer layer has a low conductivity like the skull or fat, while the inner layer has a high conductivity like the muscle or brain tissue. If we inject currents into the medium with electrodes, as used in EIT, HEI/MAT, and MREIT (Woo et al 1994, Kwon et al 2002, Gao et al 2005) the outer layer will reduce the amount of current entering into the inner layer. This will decrease the sensitivity to the changes of conductivity in the inner layer. As an extreme example, there will be no current in the inner layer if the outer layer is insulating. Under such extreme case, the conductivity distribution within the inner layer can not be reconstructed no matter what kind of reconstruction algorithm is used in the imaging modalities. We call this shielding effect (Wen 1999, Tidswell et al 2001). As a contrast, there is still current in the inner layer in MAT-MI even the outer layer is insulating. There is also no shielding effect in MIT due to the use of magnetic induction. But no high-spatial-resolution MIT has been reported. The second unique feature of MAT-MI is that the electrical field induced by a time-varying magnetic field in MAT-MI is a solenoid field, while irrotational fields are used in most other tomography related with the electrical properties, such as EIT, HEI/MAT, and MREIT. We find that there are explicit formulas to reconstruct conductivity from acoustic signals in MAT-MI due to this unique feature of solenoid field, as will be shown in the reconstruction methods. At last, MAT-MI is compatible with MRI setup. In both imaging modalities, the sample is located in a static magnetic field and a time-varying magnetic field. However, MAT-MI is much less demanding in the field homogeneity and stability than MRI.

Fig. 2.

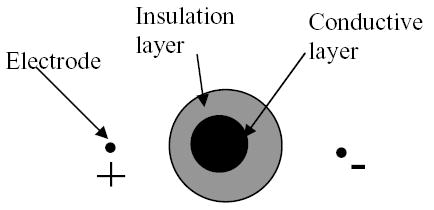
Shielding effect when injecting current with electrodes.

In the Theory section, we present the formulas for both the forward and inverse problem in MAT-MI and estimate the pressure induced in biological tissues. In the Experiments section, the experimental setup and methods are introduced. The MAT-MI signals and an image from metal samples are also shown.

THEORY

In this section, we first derive the formulas for the forward problem, which express the acoustic pressure in terms of the eddy current and the static magnetic field. Then, we estimate the pressure induced in biological tissue by computing the acoustic waves from a sphere in a uniform electrical and magnetic field. At last, we will provide the formulas for the inverse problem in MAT-MI.

Forward problem

In a medium with a current distribution $\stackrel{\sim }{\mathbf{J}}$ (in this paper, the tilt over a variable means that the variable is a function of time; otherwise, the variable is not a function of time if not denoted explicitly) in a static magnetic field B₀, we have the following wave equation for the induced pressure $\stackrel{\sim }{p}(\mathbf{r},t)$ (Roth et al 1994),

$${\nabla }^2\stackrel{\sim }{p}-\frac{1}{c_s^2}\frac{{\partial }^2\stackrel{\sim }{p}}{\partial t^2}=\nabla \cdot (\stackrel{\sim }{\mathbf{J}}\times {\mathbf{B}}_0),$$ (1)

where $c_s=\sqrt{\frac{1}{{\rho }_0{\beta }_s}}$ is the acoustic speed, ρ₀ is the density of the medium at rest, and β_s is the adiabatic compressibility of the medium. We have assumed that ${\stackrel{\sim }{\mathbf{B}}}_1(\mathbf{r},t)\ll {\mathbf{B}}_0(\mathbf{r})$ in the above equation, where ${\stackrel{\sim }{\mathbf{B}}}_1(\mathbf{r},t)={\mathbf{B}}_1(\mathbf{r})step(t)$ is the time-varying magnetic field in our experiments and step(t) is the step function (it equals 1 when t is larger than zero and equals zero otherwise). This is because the time-varying magnetic field is generated by discharging a capacitor for only about 1 microsecond and the current in the coil is approximately proportional to the discharging time. Therefore the current in the coil should not be large enough to produce a magnetic field that is comparable with the static magnetic field. The estimate from our experiments also supports this assumption, as will be shown in the experimental setup section. $\stackrel{\sim }{\mathbf{J}}$ in the source term can further be written as the product of a purely spatial and a purely temporal component i.e., $\stackrel{\sim }{\mathbf{J}}(\mathbf{r},t)=\mathbf{J}(\mathbf{r})\eta (t),$ where J(r) describes the spatial distribution of the induced eddy current density, and η(t) describes the shape of the stimulating pulse. Note that J(r) has the unit of As/m². Here we consider J(r) to be the induced eddy current since the current generated by excitable membranes within a biological system is in the frequency of several KHz while the induced current in MAT-MI used for image reconstruction is in a much higher frequency range. We consider only the case that the stimulating pulse is very short η(t) ≈ δ(t). In experiments, the temporal profile of the induced current includes a strong short positive peak (μs) and a small long negative tail (ms). The net area under the profile is zero. But if we measure only the part of the signal that is within a short time after the positive peak (for example 100 μs ), the net area under this portion of profile is positive and we can approximate this profile as a delta function. In the following estimate on the pressure, we have $\mathbf{J}(\mathbf{r})\approx {\stackrel{\sim }{\mathbf{J}}}_{ave}(\mathbf{r})\tau$ by using $\mathbf{J}(\mathbf{r})={\int }_0^{+\infty }\stackrel{\sim }{\mathbf{J}}(\mathbf{r},t)dt,$ where τ is the excitation pulse length and J_ave (r) is the average current density during the excitation.

After using Green’s function, the solution of Eq. 1 can be written as (Morse and Feshbach 1953)

$$\stackrel{\sim }{p}(\mathbf{r},t)=-\frac{1}{4\pi }\underset{V}{\oint }d{\mathbf{r}}^{\prime }{\nabla }_{{\mathbf{r}}^{\prime }}\cdot [\mathbf{J}({\mathbf{r}}^{\prime })\times {\mathbf{B}}_0({\mathbf{r}}^{\prime })]\frac{\delta (t-R/c_s)}{R},$$ (2)

where $R=\hspace{0.17em}|\mathbf{r}-{\mathbf{r}}^{\prime }|$ and the integration is over the sample volume. The physical meaning of this equation is that, in an acoustically homogenous medium, the pressure p, at a spatial point r and time t, is proportional to the integration of ∇ · (J × B₀) over a spherical surface [a circle in the two-dimensional (2-D) case]. The spherical surface is centered at r and has a radius of tc_s. Applying integration by parts to Eq. 2, we have

$$\stackrel{\sim }{p}(\mathbf{r},t)=-\frac{1}{4\pi }\underset{V}{\oint }d{\mathbf{r}}^{\prime }\mathbf{J}({\mathbf{r}}^{\prime })\times {\mathbf{B}}_0({\mathbf{r}}^{\prime })\cdot {\nabla }_{{\mathbf{r}}^{\prime }}\frac{\delta (t-R/c_s)}{R}.$$ (3)

Using ∇_r′, = −∇_r, we have

$$\stackrel{\sim }{p}(\mathbf{r},t)=-\frac{-1}{4\pi }\underset{V}{\oint }d{\mathbf{r}}^{\prime }\mathbf{J}({\mathbf{r}}^{\prime })\times {\mathbf{B}}_0({\mathbf{r}}^{\prime })\cdot {\nabla }_{\mathbf{r}}\frac{\delta (t-R/c_s)}{R}.$$ (4)

Now the differentiation over r can be moved out of the integration and we have

$$\stackrel{\sim }{p}(\mathbf{r},t)=-\frac{1}{4\pi }\nabla \cdot \underset{V}{\oint }d{\mathbf{r}}^{\prime }\mathbf{J}({\mathbf{r}}^{\prime })\times {\mathbf{B}}_0({\mathbf{r}}^{\prime })\frac{\delta (t-R/c_s)}{R}.$$ (5)

This equation is easier to compute in the theoretical analysis and numerical simulations.

Estimation of the pressure

We use a spherical sample to estimate the amplitude of the MAT-MI signal from biological tissues. Assume a sphere with a radius a in a static magnetic field B₀ and a time-varying magnetic field. For simplicity, we assume that ${\mathbf{B}}_0=B_0\widehat{\mathbf{y}}$ and the electric field induced by the time-varying magnetic field ${\mathbf{E}}_{ext}=E_0\widehat{\mathbf{x}}$ are homogeneous. Although the total electric field in the sphere is different from E_ext (see Eq. 9), we will use E_ext to approximate the total electric field for simplicity because we only want to estimate the order of the induced pressure. The sphere and background is acoustically homogeneous and has the same acoustic properties. Take the center of the sphere as the origin, the electrical conductivity of the system is

$$\begin{array}{l}\sigma (\mathbf{r})={\sigma }_0{s}_a(\mathbf{r}),\\ s_a(\mathbf{r})=\{\begin{array}{c}1,\hspace{0.17em}\text{if\hspace{0.17em}}r<a\\ 0,\hspace{0.17em}\text{if\hspace{0.17em}}r\hspace{0.17em}>\hspace{0.17em}a\end{array}.\end{array}$$

In the estimation, we use $\stackrel{\sim }{\mathbf{J}}=\sigma \stackrel{\sim }{\mathbf{E}}$, where we have ignored the displacement current $-\partial \stackrel{\sim }{\mathbf{D}}/\partial t$, because the ratio of displacement to conduction current is on the scale of ωɛ/σ (Wang and Eisenberg 1994), where ɛ is the permittivity of the sample (~10⁻⁹ F/m in biological tissue) and ω is the frequency, and the ratio is on the scale of 0.001 at the MHz range in the biological tissues. The pressure can be computed through Eq. 5 as

$$\stackrel{\sim }{p}(\mathbf{r},t)=\frac{a{c}_s\tau {\sigma }_0{E}_0{B}_0}{2r}\widehat{\mathbf{z}}\cdot \widehat{\mathbf{r}}(h(\widehat{t})+\frac{h_1(\widehat{t})a}{r}).$$ (6)

where $\widehat{\mathbf{r}}$ is a unit vector along r , $\widehat{t}=(t{c}_s-r)/a,$

$$h(\widehat{t})=\{\begin{array}{c}-\widehat{t},\hspace{0.17em}\text{if\hspace{0.17em}}|\widehat{t}|<1\\ 0,\hspace{0.17em}\text{if\hspace{0.17em}}|\widehat{t}|>1\end{array},$$ (7)

and $h_1(t)={\int }_{-\infty }^{t}dth(t)$

$$h_1(t)=\{\begin{array}{c}(1-t^2)/2,\hspace{0.17em}\text{if\hspace{0.17em}}|t|<1\\ 0,\hspace{0.17em}if\hspace{0.17em}|t|>\hspace{0.17em}1\end{array}.$$ (8)

From Eq. 6, the amplitude of the pressure can be estimated as $\stackrel{\sim }{p}(\mathbf{r},t)=\frac{a{c}_s\tau {\sigma }_0{E}_0{B}_0}{2r}\hspace{0.17em}\widehat{\mathbf{z}}\cdot \widehat{\mathbf{r}}.$

We use the following parameters for estimation. a = 10mm, r = 50mm, c_s = 1500m / s , τ = 0.5μs . B₀ = 1T is in the same scale of commercial MRI scanners. σ = 0.2Sm⁻¹ is typical for soft biological tissues. E_o = 1000Vm⁻¹ is in the same scale of commercial magnetic stimulators. According to Eq. 6, we have $p(r,t)=0.015\cdot \widehat{\mathbf{z}}\cdot \widehat{\mathbf{r}}$ Pascal, which means that the pressure is anisotropic in the spatial distribution. When measuring from along z axis (which is the direction of J × B₀), the amplitude is maximal, 0.015 Pa. This level of pressure should be measurable for current acoustic detectors.

Inverse problem

The inverse problem can be divided into two steps. In the first step, we will reconstruct ∇ · (J × B₀) from pressure. In the second step, we will reconstruct the conductivity distribution from ∇ · (J × B₀). The first step can be accomplished with back-projection algorithm. The reconstruction step from ∇ · (J × B₀) to σ is more challenging. The total electrical field in the sample can be divided into two parts

$$\mathbf{E}={\mathbf{E}}_{ext}+{\mathbf{E}}_{rsp},$$ (9)

where the first part E_ext represents the solenoid electrical field induced directly by the changing magnetic field, and E_rsp represents the electrical field caused by the conductivity heterogeneity of the sample (Malmivuo and Plonsey 1995). It is of electrostatic nature, so it can be expressed as the gradient of a scalar potential

$${\mathbf{E}}_{rsp}=-\nabla \phi .$$ (10)

E_ext can be computed easily when the coil configuration is known. However, E_rsp can not be measured from experiments. The challenge in the reconstruction step from ∇ · (J × B₀) to σ lie in how to derive σ without using E_rsp .

From $\stackrel{\sim }{p}$ to ∇ · (J × B₀)

Assume we can measure the acoustic signals across a surface ∑ around the to-be-imaged object. Let’s consider Eq. 1 for the case of $\widehat{\mathbf{J}}(\mathbf{r},t)=\mathbf{J}(\mathbf{r})\delta (t)$. After integrating both sides of Eq. 1 over the time range (−∞,0⁺) , where 0⁺ is an infinitely small real, we have

$${-\frac{1}{c_s^2}\frac{\partial \stackrel{\sim }{p}}{\partial t}|}_{t=0^{+}}=\nabla \cdot (\mathbf{J}\times {\mathbf{B}}_0).$$ (11)

The spatial derivative term disappears in the integration because the pressure is zero before time zero. In the appendix, we show that Eq. 11 is still valid in an acoustically heterogeneous medium. Eq. 11 means that we can obtain ∇ · (J × B₀) if we can derive ${-\frac{1}{c_s^2}\frac{\partial \stackrel{\sim }{p}}{\partial t}|}_{t=0^{+}}$from the pressure measured over ∑. In an acoustically homogeneous medium, this step can be accomplished by time reversing the acoustic waves using Eq. 15 in (Xu and Wang 2004a) as

$${\stackrel{\sim }{p}}^{\prime }(r,0^{+})\approx \frac{1}{2\pi c_s}\underset{\mathrm{\Sigma }}{\int }\int d{S}_d\frac{\mathbf{n}\cdot ({\mathbf{r}}_d-\mathbf{r})}{|\mathbf{r}-{\mathbf{r}}_d{|}^2}{\stackrel{\sim }{p}}^{″}({\mathbf{r}}_d,|\mathbf{r}-{\mathbf{r}}_d|/c_s),$$ (12)

where r_d is a point on the detection surface ∑, r is a point in the object space, and the single and double prime represent the first and second derivative over time, respectively. In deriving Eq. 12, we have ignored the first term in the integrand on the right hand side of Eq. 15 in (Xu and Wang 2004a), because it is much smaller than the second term in the MHz range. Combining Eq. 11 and Eq. 12, we have

$$\nabla \cdot (\mathbf{J}\times {\mathbf{B}}_0)\approx \frac{-1}{2\pi c_s^3}\underset{\mathrm{\Sigma }}{\int }\int d{S}_d\frac{\mathbf{n}\cdot ({\mathbf{r}}_d-\mathbf{r})}{|\mathbf{r}-{\mathbf{r}}_d{|}^2}{\stackrel{\sim }{p}}^{″}({\mathbf{r}}_d,|\mathbf{r}-{\mathbf{r}}_d|/c_s)$$ (13)

This is a back-projection algorithm, in which the pressure at each time point is projected (assigned) to each point on the sphere over which the integration of the object value yields the pressure, as shown in Fig. 3.

Fig. 3.

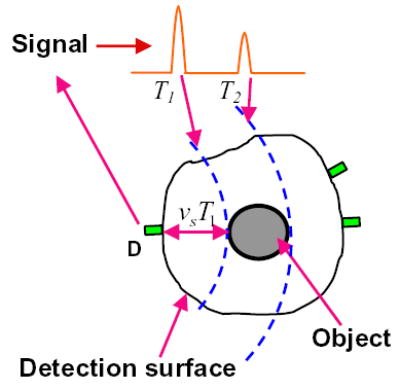
Illustration of backprojection.

From ∇ · (J × B₀) to σ

Here we propose two methods for the second step in the reconstruction.

Method 1 Piecewise distribution

In this method, we don’t need to change the direction of the static magnetic field B₀ because only one set of measurement is needed. This is a major advantage of this method over the other methods.

First, according to Faraday’s law,

$$\nabla \times \stackrel{\sim }{\mathbf{E}}=-\frac{\partial {\stackrel{\sim }{\mathbf{B}}}_1}{\partial t}.$$ (14)

Using ${\stackrel{\sim }{\mathbf{B}}}_1(\mathbf{r},t)={\mathbf{B}}_1(\mathbf{r})step(t),$ we have $\stackrel{\sim }{\mathbf{E}}(\mathbf{r},t)=\mathbf{E}(\mathbf{r})\delta (t),$ where E is the spatial component of the electrical field and obeys

$$\nabla \times \mathbf{E}=-{\mathbf{B}}_1.$$ (15)

Combing Eq. 15 with J = σE , we have

$$\nabla \times (\mathbf{J}/\sigma )=-{\mathbf{B}}_1.$$ (16)

After expanding the cross product, we have

$$(\nabla \times \mathbf{J})/\sigma +\nabla (\frac{1}{\sigma })\times \mathbf{J}=-{\mathbf{B}}_1.$$ (17)

If we assume the sample is piecewise smooth, then we have |∇σ|/σ << |∇ × J| / |J| except at the boundary points, therefore the second term in Eq. 17 can be ignored and we take an inner product of both sides of Eq. 17 with B₀ , we have

$$\sigma \approx -\frac{(\nabla \times \mathbf{J})\cdot {\mathbf{B}}_0}{{\mathbf{B}}_1\cdot {\mathbf{B}}_0}=-\frac{\nabla \cdot (\mathbf{J}\times {\mathbf{B}}_0)}{{\mathbf{B}}_1\cdot {\mathbf{B}}_0}$$ (18)

for the points inside a smooth piece, where we replace (∇ × J) · B₀ with ∇ · (J × B₀ ) after using ∇ × B₀ = 0 for the point in the sample due to the fact that the magnetic field is generated by the sources outside the sample. ∇ (J × B₀ ) can be obtained from pressure according to Eq. 13. Eq. 18 does not hold on the boundary between regions with different conductivity. Therefore we have to distinguish the internal smooth point from the boundary point, where |∇σ|/σ > |∇ × J| / |J|. The result given by Eq. 18 can be improved iteratively by the following algorithm:

$${\sigma }_n=\frac{-(\nabla \times \mathbf{J})\cdot {\mathbf{B}}_0}{[{\mathbf{B}}_1+\nabla (1/{\sigma }_{n-1})\times {\mathbf{J}}_{n-1}]\cdot {\mathbf{B}}_0},$$ (19)

where (∇ × J) · B₀ , B₀ , and B₁ are measured or derived from measurement in the experiments, σ_n−1 and σ_n are the conductivity distribution obtained after the (n−1)-th and n-th iteration, respectively, and J_n−1 is the computed current distribution corresponding to σ_n−1 . To start the iteration, σ₀ is given by Eq. 18. Then for the given σ_n−1 and boundary conditions, J_n−1 can be computed by solving the forward linear system of equations using the conjugate gradient method for sparse matrix. After that, the conductivity will be updated according to Eq. 19 in each iteration until a stopping condition is met.

Method 2: Solve J

In the second method, we need to change the direction of the static magnetic field B₀. According to ωɛ/σ << 1 and Ampere’s law, we have

$$\nabla \cdot \mathbf{J}=0.$$ (20)

B₀ · (∇ × J) can be reconstructed from the pressure measured around the objects. Therefore if we make three sets of measurements, where B₀ is along three perpendicular directions, we can determine ∇ × J. After combining the boundary condition J · n|_∑ = 0 and Eq. 20, J can be determined. Then we take an inner product of both sides of Eq. 17 with J , we have

$$\sigma =-\frac{(\nabla \times \mathbf{J})\cdot \mathbf{J}}{{\mathbf{B}}_1\cdot \mathbf{J}}.$$ (21)

Compared with the first method, this method is more accurate. But it is obviously more challenging, because there are more intermediate steps, which makes the problem complex. At last, it should be pointed out that the above two methods are unique to MAT-MI, because both of them require B₁ = −∇ × E ≠ 0. Magnetic induction can satisfy this requirement, but electrical stimulation cannot.

EXPERIMENTS

MAT-MI is intrinsically a 3-D imaging modality, in which the acoustic signals should be detected across a surface surrounding the to-be-imaged object. The reconstruction algorithms for the quantitative distribution of conductivity proposed in the theory section are based on the data collected in a 3-D configuration. However, in the present experimental study, we focus on the demonstration of the proposed idea in a 2-D system, in which the detector scans around the object in a circle, because of the huge cost and effort necessary to build a 3-D system. Nevertheless, the 2-D system can correctly image the boundaries of the object that is approximately positioned within a plane, such as the wire loop used in our experiments.

In the image reconstruction, we use only the first step described in the inverse problem subsection of the theoretical studies. This is because the second step is significant only for quantitative imaging and our current 2-D system is not sufficient for quantitative imaging as discussed above. The reconstruction formula is modified from Eq. 13 as

$$I(\mathbf{r})=\sum _{i=1}^n\frac{\mathbf{n}\cdot ({\mathbf{r}}_i-\mathbf{r})}{|\mathbf{r}-{\mathbf{r}}_i{|}^2}\stackrel{\sim }{p}({\mathbf{r}}_i,|\mathbf{r}-{\mathbf{r}}_i|/v_s),$$ (22)

where r_i is the position of the detector at the i-th scanning point, and the summation is over all the scanning points. Therefore, the reconstructed image represents the boundary of ∇ · (J × B₀ ) induced by the magnetic induction in the sample. The acoustic signals are processed by a high-pass filter to eliminate the low-frequency disturbance.

Experimental setup

Fig. 4 shows a diagram of the experiment setup. The unfocused transducer (V303, Panametrics) has a central frequency of 1 MHz and a diameter of 13 mm. It points horizontally to the sample. For good coupling of acoustic waves, both the transducer and the sample were immersed in water. The transducer scanned around the object in a circular orbit with a radius of 130 mm. The step size of the scanning is 2.5 degrees. We can only scan 340 degrees of the circular orbit because the rack used to hold the magnetic inductor blocks part of the scanning orbit. Nevertheless, a partial view data is sufficient to reconstruct the boundary of the sample (Xu and Wang 2004b).

Fig. 4.

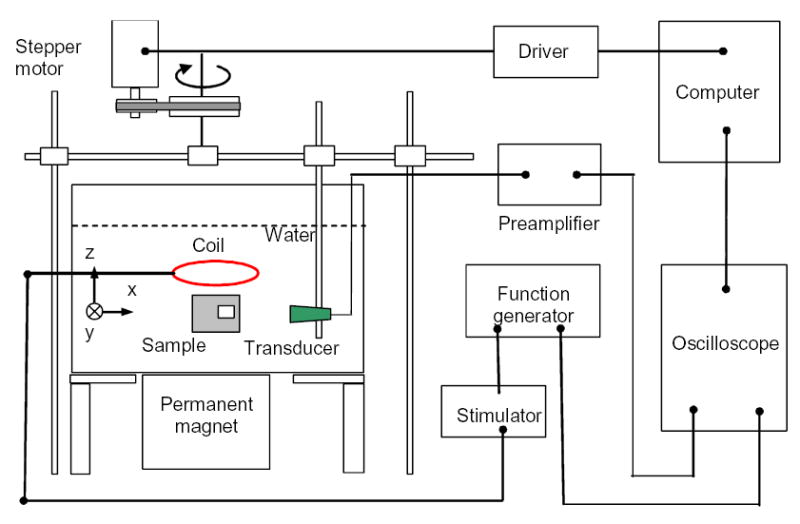
Experimental setup

A home-made magnetic inductor induces electric pulses with a width of 1.2 μs at the rate of 4 Hz. The circular coil of the magnetic inductor has a radius of 40 mm. We used a single-turn coil with a radius of r_c = 4 cm to estimate the induced electrical field in the space, E_ind . In our experiments, the electrical field induced by the circular coil of the magnetic inductor is symmetrical and oriented in circular loops around the axis of the inductor coil, while the probe coil is located concentrically with the stimulator coil. Therefore, the probe coil approximately fits into one of the electrical field lines (loops). Consequently, we have E_ind = V/(2πr_c ) , where V is the voltage measured over the probe coil. The induced electrical field right around the coil of the inductor is measured to be about 250 Vm⁻¹ while the induced electrical field at the position of the samples in our experiments (about 5 cm away from the coil of the inductor) is measured to be around 25 Vm⁻¹ . According to the measured electrical field, we can estimate the final magnitude of the time-varying magnetic field at the sample’s position as B₁ = 2τE_ind/r_c = 0.00125 T after considering $\frac{d(B_1\cdot \pi r_c^2)}{dt}=-E_{ind}\cdot 2\pi r_c$ and E_ind is almost constant during the excitation period.

A permanent magnet (50 mm by 50 mm by 25 mm) was put around 2 cm under the sample. The permanent magnet can create a magnetic field along the z-axis with a flux density of about 0.1 T at 2 cm from its surface. A function generator was used to trigger the magnetic inductor, control its pulse length, and synchronize the oscilloscope sampling. The signal from the transducer was first amplified, then recorded and averaged 100 times by a software oscilloscope (National Instruments, Austin). A personal computer was used to control the step motor for scanning the detector and transferring the data. A multifunctional card in the computer acted as the function generator, oscilloscope, and part of the driver for the stepper motor.

Experiment results

Firstly, we used a copper stripe with a section of 1 mm by 4 mm as the sample for observing the MAT-MI signals. The long dimension of the strip is perpendicular to the scanning plane. A major peak was observed in the signals after high-pass filtering (Fig. 5). When we moved the copper back and forth, the peak also moved accordingly, as shown by comparing the two figures in Fig. 5. We also moved the detector around the copper. In most positions, we can detect the signal from the copper although the amplitude of the signal varies. Basically, the amplitude of the signal increased when the detector moved closer to the object.

Fig. 5.

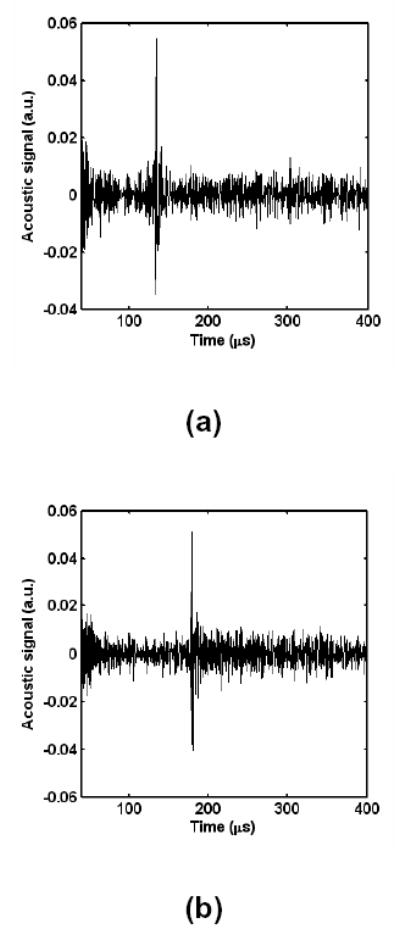
The signals from the point object at different locations.

Then we imaged a close metal loop, which is made from a 0.5 mm diameter metal wire. We did not observed any signal due to the scattering by the wire. Fig. 6 shows the signal. There are two major peaks with a time delay of about 30 μs , which matches with the distance between the front and rear boundary of the loop when looking from the position of the transducer. This shows that the two major peaks correspond to the two boundaries. When we moved the detector around the object, the signal looks similar except that the time delay between the two peaks is different.

Fig. 6.

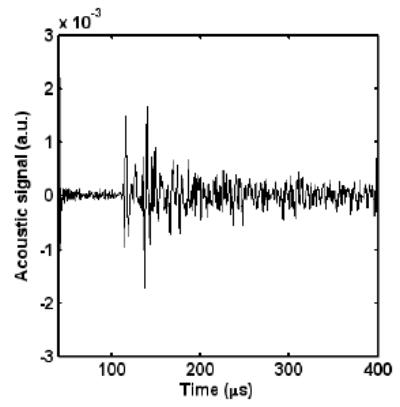
The signals from a metal wire loop.

Fig. 7 shows the MAT-MI and the photo of a metal wire loop. The center of the image is the origin of the circular scanning orbit of the transducer. The reconstructed image represents the boundary of ∇ · (J × B₀ ) induced by the magnetic induction in the sample. Therefore we compare only the size and shape of the loop in the MAT-MI image and the corresponding photo and we find they are in good agreement.

Fig. 7.

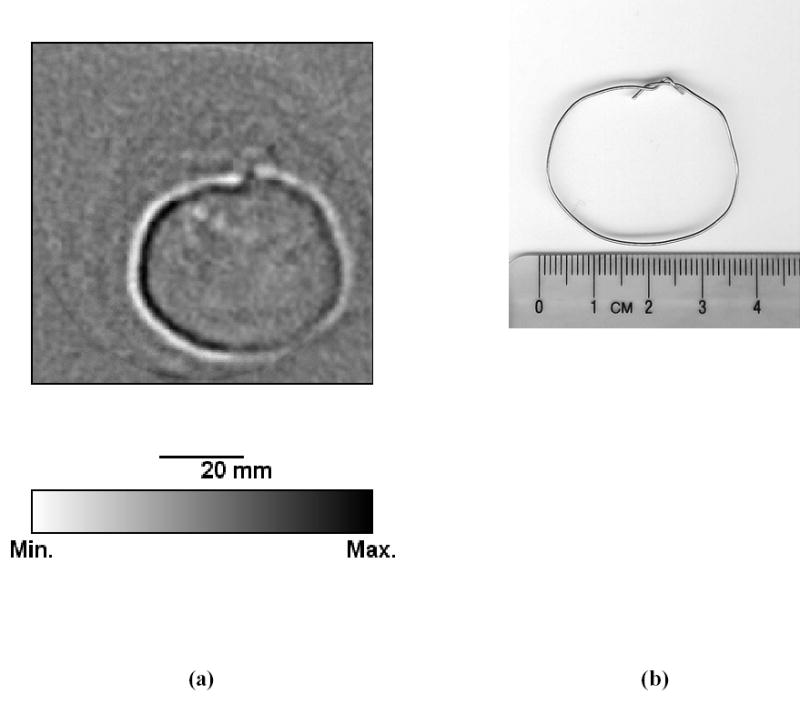
(a) The image representing the boundary of ∇ · (J × B₀) induced by the magnetic induction after the first step of the reconstruction and (b) the photo of a metal wire loop.

DISCUSSION

Imaging electrical impedance with noninvasive measurements is important to various biomedical applications. A number of efforts have been made to probe the physiological or pathological status of biological systems from the information on the electrical impedance of tissues. Such impedance information on the biological tissues may also be useful to other biomedical research such as electric source imaging, in which electromagnetic measurements are made over the body surface or out of the body while the tissue impedance information is necessary to solve the forward problem (He 2004; He and Lian, 2005).

Under the acoustic homogeneity assumption, we have derived explicit theoretical formulas governing MAT-MI. This theoretical development is important because it offers a well-posed problem to solve the electrical-impedance imaging problem. In many other impedance imaging approaches such as EIT or MIT, the inverse problem is ill-posed which limits the spatial resolution of the methods.

The conductivity of copper is substantially larger that the conductivity of biological tissues. Therefore, the signals measured in the present experiments might be much larger than the signals from biological tissues of the same size. Therefore, considerable improvement of the sensitivity of the detection system is necessary to apply this method to imaging biological tissues. Nonetheless, the present experimental results suggest the feasibility of the proposed MAT-MI in detecting electrical impedance.

Most of the theoretical studies in this paper are about the acoustically homogeneous medium. Therefore the application of this method is mainly limited to soft-tissue imaging. We expect that the acoustic heterogeneity in the soft tissues will only bring minor distortion. Because firstly, the acoustic heterogeneity is within 10% in soft tissues, and the wave reflection at the tissue interfaces will be small. Secondly, the acoustic signals are mostly below 1 MHz in our experiments. Therefore, the corresponding wave scattering is negligible. The effect of acoustic heterogeneity in MAT-MI is similar to that of another imaging modality, photoacoustic tomography (PAT) (Wang et al 2003). In PAT, when electromagnetic radiation is absorbed in biological tissues, the heating and the subsequent expansion will cause emission of acoustic signals, called the thermoacoustic effect. The thermoacoustic signals from a tissue sample are collected to map the distribution of the radiative absorption within the sample. MIT-MI differs from PAT only in the mechanism of generating acoustic waves. In PAT, it has been demonstrated both theoretically (Xu and Wang 2003) and experimentally (Wang et al 2003) that the effect of the acoustic heterogeneity in soft tissues is negligible. It is therefore anticipated that the effect of the acoustic heterogeneity on MIT-MI in soft tissues should also be negligible.

In summary, we have developed a new imaging technique – magnetoacoustic tomography with magnetic induction (MAT-MI) for high-resolution imaging of electrical impedance distribution. We present the results of our theoretical and experimental investigations on the new imaging modality. In the theoretical part, we provide the formulas for both the forward and inverse problems of MAT-MI. In the experimental study, we show the signals from point metal objects and a metal wire loop. The MAT-MI image of the metal wire loop is in good agreement with the shape of the object, which demonstrates the feasibility of the proposed MAT-MI approach. Using more sensitive detecting system would allow us to obtain images from biological tissues.

APPENDIX DERIVATION OF EQ. 11 IN AN ACOUSTICALLY HETEROGENEOUS MEDIUM

According to Newton’s second law of motion we have

$$\frac{\partial ({\rho }_0\stackrel{\sim }{\mathbf{v}}(\mathbf{r},t))}{\partial t}=\stackrel{\sim }{\mathbf{J}}\times {\mathbf{B}}_0-\nabla \stackrel{\sim }{p},$$ (23)

where v(r,t) is the velocity at point r and time t ; ρ₀ is the density of the medium at rest; $\stackrel{\sim }{p}$ is the pressure. In the case of $\stackrel{\sim }{\mathbf{J}}(\mathbf{r},t)=\mathbf{J}(\mathbf{r})\delta (t)$, after integrating both sides of Eq. 1 over the time range (−∞,0⁺) , where 0⁺ is an infinitely small real, we have

$${\rho }_0\stackrel{\sim }{\mathbf{v}}(\mathbf{r},0^{+})=\mathbf{J}\times {\mathbf{B}}_0.$$ (24)

Now using the conservation of mass we have

$$-\nabla \cdot ({\rho }_0\stackrel{\sim }{\mathbf{v}})=\frac{\partial \rho }{\partial t},$$ (25)

where ρ is the density variation. At last, using the following equation

$$\frac{\rho }{{\rho }_0}={\beta }_{s}p,$$ (26)

where β_s is the adiabatic compressibility of the medium, taking a divergence of both sides of Eq. 24, and using $c_s=\sqrt{\frac{1}{{\rho }_0{\beta }_s}},$ we have Eq.11.