Chromatic Properties of Horizontal and Ganglion Cell Responses Follow a Dual Gradient in Cone Opsin Expression

Abstract

In guinea pig retina, immunostaining reveals a dual gradient of opsins: cones expressing opsin sensitive to medium wavelengths (M) predominate in the upper retina, whereas cones expressing opsin sensitive to shorter wavelengths (S) predominate in the lower retina. Whether these gradients correspond to functional gradients in postreceptoral neurons is essentially unknown. Using monochromatic flashes, we measured the relative weights with which M, S, and rod signals contribute to horizontal cell responses. For a background that produced 4.76 log₁₀ photoisomerizations per rod per second (Rh*/rod/s), mean weights in superior retina were 52% (M), 2% (S), and 46% (rod). Mean weights in inferior retina were 9% (M), 50% (S), and 41% (rod). In superior retina, cone opsin weights agreed quantitatively with relative pigment density estimates from immunostaining. In inferior retina, cone opsin weights agreed qualitatively with relative pigment density estimates, but quantitative comparison was impossible because individual cones coexpress both opsins to varying and unquantifiable degrees. We further characterized the functional gradients in horizontal and brisk-transient ganglion cells using flickering stimuli produced by various mixtures of blue and green primary lights. Cone weights for both cell types resembled those obtained for horizontal cells using monochromatic flashes. Because the brisk-transient ganglion cell is thought to mediate behavioral detection of luminance contrast, our results are consistent with the hypothesis that the dual gradient of cone opsins assists achromatic contrast detection against different spectral backgrounds. In our preparation, rod responses did not completely saturate, even at background light levels typical of outdoor sunlight (5.14 log₁₀ Rh*/rod/s).

Introduction

Most mammals are dichromatic, encoding spectral information with one cone opsin sensitive to medium wavelengths (M) and another sensitive to shorter wavelengths (S) (Jacobs, 1993; Peichl, 2005). Generally, S cones comprise ∼10% of the total and distribute evenly over the retina (Ahnelt and Kolb, 2000). However, in certain rodents, such as guinea pig, rabbit, and mouse, immunostaining shows a dual gradient: cones expressing M opsin peak in superior retina and decline inferiorly; whereas cones expressing S opsin peak in inferior retina and decline superiorly (Röhlich et al., 1994; Applebury et al., 2000; Haverkamp et al., 2005; Nikonov et al., 2005). This dual gradient in animals that scurry along the ground might be an evolutionary adaptation to detect objects against different spectral backgrounds, such as ground vegetation (seen by superior retina) and sky (seen by inferior retina) (Szél et al., 2000; Osorio and Vorobyev, 2005).

If this idea is correct, the gradients revealed by immunostaining should also be present in the responses of postreceptoral neurons. The existing data are suggestive but qualitative (Calderone and Jacobs, 1995; Ekesten and Gouras, 2005). Here we study the chromatic properties of horizontal and brisk-transient ganglion cells in superior and inferior retina of guinea pig. The horizontal cell is directly postsynaptic to cones and in dichromats generally collects from most cones within its dendritic field (Peichl and Gonzalez-Soriano, 1994; Hack and Peichl, 1999). However, in some species, the type A horizontal cell is selective for S cones (Sandmann et al., 1996).

The brisk-transient ganglion cell is postsynaptic to bipolar cells, some of which are known to be cone selective (Calkins and Sterling, 1999; Haverkamp et al., 2005). Thus, horizontal and ganglion cells might simply propagate signals from all of the overlying cones and reflect the predictions from immunostaining (Diller et al., 2004; Jusuf et al., 2006) or they might collect selectively from one cone type, for example, to smooth out the gradients. Another possible mechanism for smoothing the gradient would be if synaptic gains on signals from M and S cones varied with retinal location. The brisk-transient ganglion cell was chosen from among the many known ganglion cell types because it is thought to mediate detection and processing of achromatic contrast (Merigan and Maunsell, 1993; Dhingra et al., 2003; Silveira et al., 2004).

Because ∼90% of guinea pig photoreceptors are rods (Peichl and Gonzalez-Soriano, 1994) and under steady bright light they recover from saturation (Demontis et al., 1993), rods might contribute to vision at intensities normally considered photopic. Accordingly, we measured the rod contribution to horizontal cell responses across a wide range of intensities and incorporated these measurements into our estimates of cone weights in horizontal and ganglion cells. The cone weights matched the immunostaining pattern, showing that the dual gradient is preserved in the centrally projecting neurons that mediate achromatic contrast detection. This fits the broad hypothesis that the dual opsin gradient is an adaptation to optimize contrast detection.

Materials and Methods

Tissue preparation.

We used albino guinea pigs weighing ∼300–500 g.Vingrys and Bui (2001) showed that albino guinea pigs give large but otherwise normal ERG responses and that the ERG components develop with age in the same way as with the pigmented animal. Although albino animals such as mouse and rat have a lower rod density compared with pigmented ones (Jeffery et al., 1997; Ilia and Jeffery, 2000), the transverse absorbance of rat rod outer segments has been shown to be the same (Grant et al., 2001).

An animal was overdosed with anesthetic (ketamine, 100 mg/kg; xylazine, 20 mg/kg; and pentobarbital, 50 mg/kg), and both eyes were removed. The eyecup was flattened on a membrane filter with ganglion cells up. This preparation was placed into a chamber on a microscope stage (BX50WI; Olympus Optical, Melville, NY) and superfused with oxygenated (95% O₂ and 5% CO₂) Ames' medium (Sigma, St. Louis, MO) containing sodium bicarbonate (1.9 g/L) and glucose (0.8 g/L) at ∼5–7 ml/min. The chamber temperature was maintained between 34 and 37°C. The retina was dark adapted for 0.5 h before measurements were made.

To help find particular retinal regions during the experiment, three circular holes were cut in the membrane filter. When the tissue was flattened onto the filter, the middle hole (1 mm diameter) was positioned over the optic disk and the filter was oriented so that the other two holes were located above or below the optic disk along the superior–inferior axis of the tissue. Recordings were made from within the locations defined by these two holes (2 mm diameter, 3 mm superior or inferior to the optic disk) (see Fig. 1B).

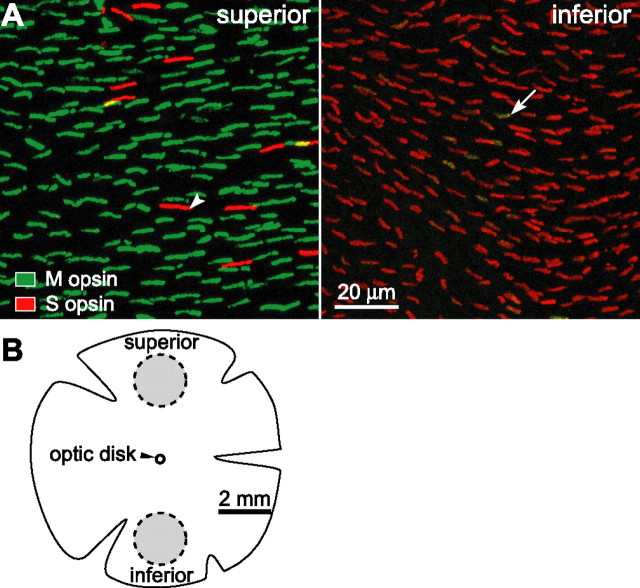
Figure 1.

M opsin is expressed predominately in superior retina, and S opsin is expressed predominately in inferior retina.A, Cone outer segments labeled by antibodies against M and S opsins. M opsin labeling is shown in green, and S opsin labeling is shown in red. In superior retina (left), each cone expressed only one type of cone opsin and there were fewer S cones (arrowhead; ∼6% of all cones). Small regions in yellow were attributable to the overlay of M- and S-cone outer segments but not the coexpression of both cone opsins in the same cone outer segment. In inferior retina (right), all cones expressed S opsin and a few cones (arrow) coexpressed M opsin. Brightness and contrast of the images were enhanced in Photoshop (Adobe Systems, San Jose, CA).B, Schematic diagram of the retina. Images in A were taken from locations within the two circular areas (gray; 2 mm in diameter and 3 mm from their centers to optic disk). These are the same regions from which horizontal and ganglion cell responses were recorded.

Electrical recording.

Horizontal cells were recorded intracellularly with sharp electrodes (tip impedance, 70–200 MΩ). Responses were amplified (NeuroData IR-283; Cygnus Technology, Delaware Water Gap, PA), digitized at a 5 kHz sampling rate with 12-bit precision (DigiData 1200; Molecular Devices, Sunnyvale, CA), and stored for later analysis (AxoScope; Molecular Devices). Voltage traces were smoothed by averaging the sampled data within 1 ms bins.

Horizontal cells were targeted by advancing electrodes in the presence of full-field flicker and observing whether the recorded potential was modulated. A cell was selected for recording if it responded strongly to full-field luminance flicker, sinusoidally modulated at ∼40% contrast. The mean resting membrane potential in light (at the main background) of cells selected for recording was −36 mV, with large variation across cells (±17 mV, SD). For many cells, the resting potential drifted gradually toward more positive values during recording.

Brisk-transient ganglion cells were recorded extracellularly with loose patch electrodes (tip impedance, 2–4 MΩ). Responses were recorded using the same equipment as for the horizontal cells. Spikes were identified using a threshold detection method. Spike rates were calculated for ∼15 ms bins. Some cells were repatched after the seal between pipette and cell membrane weakened. With this preparation, stable recording from a single cell was possible for up to 2 h.

Brisk-transient ganglion cells were identified for recording by observing the tissue through the infrared differential interference contrast optics of the microscope and locating cells with large somas (18–23 μm diameter). A ganglion cell was selected for recording if it gave clear and stable responses to a 10% contrast flickering spot and if the recorded spike was biphasic with amplitude of at least 2 mV. Cell identity was confirmed by the large size of the receptive field center (400–600 μm diameter) and the “brisk-transient” response (Cleland et al., 1975; Demb et al., 2001; Dhingra et al., 2003). In pilot experiments, cells were sometimes penetrated with a sharp electrode after recording and stained with Lucifer yellow (3%, in 0.1 m LiCl solution) for visualization. This method provided morphological validation of the cell identification procedures used. It was not used during the main experiments to avoid excessive exposure of the tissue to light.

Measuring photoreceptor inputs to horizontal and ganglion cells. Cone and rod inputs were characterized by recording responses to spots of different spectral composition. “Flash experiments” measured the action spectra to flashed monochromatic spots on a spatially uniform background. This was slow but rather completely characterized the spectral properties of a cell.“Flicker experiments” measured responses to spots on a spatially uniform background produced by modulating mixtures of two primary lights. This was more efficient, but analyzing the data to estimate cone weights required assumptions about the photopigment action spectra and the strength of rod input.

We used two optical systems: (1) In the “LCD system,” light from a liquid crystal display (LCD) projector (PowerLite 730c; Epson America, Long Beach, CA) was used. The relative spectra and input–output relationships (gamma functions) of the independent color primaries (red, green, and blue) of this projector were measured at the tissue plane using a CVI SM-240 (CVI Spectral Products, Albuquerque, NM) spectrometer. The total irradiance (integrated over wavelength) arriving at the tissue was also characterized (IL1400A; International Light, Peabody, MA). In the plane of the tissue, the full image subtended ∼2.4 × 3.2 mm, with each pixel corresponding to ∼3.1 × 3.1 μm. The refresh rate of the display was 70 Hz. (2) In the “lamp system,” light from a xenon lamp (HLX 64642; Osram, Munich, Germany), collimated and fed through a narrowband, tunable filter (VariSpec; Cambridge Research and Instrumentation, Woburn, MA) and an adjustable aperture to produce a uniform spot of monochromatic light (∼10 nm bandwidth) on the tissue was used. The temporal profile of the spot was controlled by a mechanical shutter (VS25S2T1 shutter and 122-BP controller; Uniblitz, Rochester, NY). Lamp voltage, wavelength, and shutter timing were all computer controlled. To deliver lights of desired intensities during the experiment, the relationship between lamp voltage and irradiance across wavelengths at the tissue was coarsely characterized beforehand. The exact irradiances of the stimuli presented were measured after each experiment. The outputs of the two optical systems were combined through a beam splitter and delivered to the tissue through the camera port on the microscope and the objective.

The flash experiments used monochromatic spots from the lamp system on a background produced by the LCD system. The main background produced nearly equal isomerization rates in M and S cones [4.17 and 4.12 log₁₀ photoisomerizations per cone per second (Rh*/photoreceptor/s)] and a somewhat higher rate in rods (4.76 log₁₀ Rh*/photoreceptor/s). In some measurements, neutral density filters were inserted into (or removed from) the light path to vary the overall light level. The spectral transmittance of these filters was individually measured, and the measurements were included in the stimulus characterization. A ∼2000-μm-diameter spot was generally flashed for 300 ms, and the flash was repeated at least 10 times per trial at 1 s intervals. The exception was for some of the measurements using the dimmest backgrounds, at which the duration was 400 ms with 1.25 s intervals.

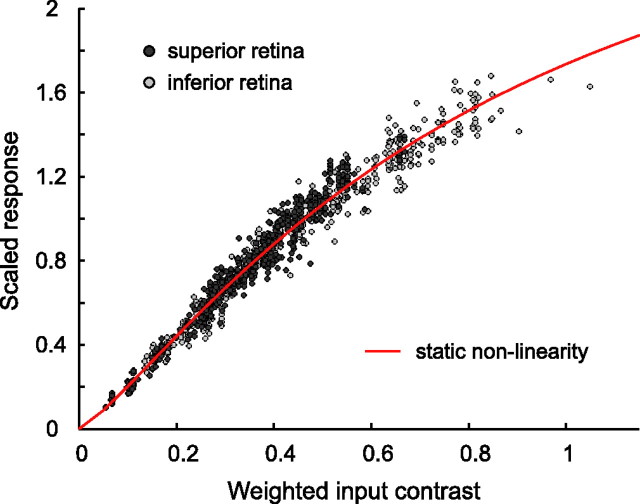
Horizontal cell responses were characterized by the peak response (maximum hyperpolarization), in which response amplitude was measured from the peak to resting level (see Figs. 2A,D, 4A). Horizontal cell action spectra were measured with monochromatic flashes (425–620 nm). For most cells (43 of 48), we corrected for nonstationarities in the response. To do so, a 520 nm reference flash was interspersed approximately every five flashes, and the responses to it were used to compute a multiplicative drift-correction factor (see Appendix B). A few cells (n = 5) were recorded without interposed 520 nm flashes, but these recordings were stable over time. Where shown in the plots, SEs of responses at each wavelength were computed from the responses across multiple trials. Appendix B describes how we analyzed the flash data to account for a horizontal cell response nonlinearity in our estimation of action spectra.

Figure 2.

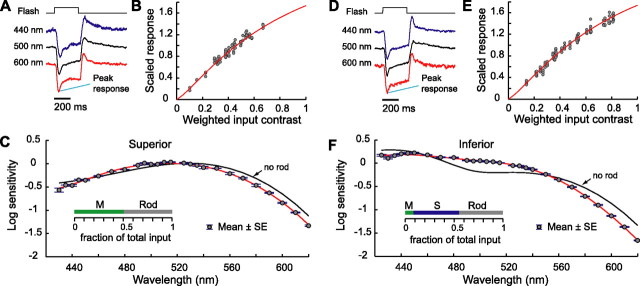
At high light levels, horizontal cells from superior and inferior retina had different action spectra.A, Response waveforms of horizontal cell from superior retina to monochromatic flashes at wavelengths of 440, 500, and 600 nm. Each waveform is shown normalized to its peak response amplitude, which was measured as the difference between the resting level and maximum hyperpolarization after flash onset. The peak response amplitudes and flash intensities were 1.7 mV and 3.36e+4 quanta/μm²/s (440 nm), 4.1 mV and 3.10e+4 quanta/μm²/s (500 nm), and 2.6 mV and 1.23e+5 quanta/μm²/s (600 nm). The background produced 4.17 (M), 4.12 (S), and 4.76 (rod) log₁₀ Rh*/photoreceptor/s. Responses from the same cell at the same background are also reported in B and C. B, Flash contrast–response function. The scaled monochromatic flash responses (see Materials and Methods and Appendix B) are plotted against weighted input contrast C_input, which is computed from the flash intensity using the photoreceptor weights of the cell estimated in C. The average gain of the cell was 4.5 mV/100% weighted input contrast. The red line shows the static nonlinearity that describes the horizontal cell contrast–response function at the background intensity used. Its shape was derived from flash data of all cells studied at the same background (see Appendix B and Fig. 7).C, Action spectrum of a horizontal cell from superior retina. The cell was presented with monochromatic flashes of varying wavelengths from 420 to 620 nm. The action spectrum was computed and plotted according to the procedure described in Appendix B. Data (gray circles) are means ± 1 SE. The red line shown is a weighted sum of M, S, and rod contrast sensitivities. The relative weights are as follows: M, 0.51; S, 0.0; and rod, 0.49. These weights are shown in the inset. The second fit shown by the black line is the result of refitting the data with the same static nonlinearity but without the rod contribution. This fit deviates from the data.D, Response waveforms of horizontal cell from inferior retina to monochromatic flashes at wavelengths of 440, 500, and 600 nm. Same format as A. The peak response amplitudes and flash intensities were 2.3 mV and 2.58e+4 quanta/μm²/s (440 nm), 3.9 mV and 7.58e+4 quanta/μm²/s (500 nm), and 1.5 mV and 3.66e+5 quanta/μm²/s (600 nm). The background produced 4.17 (M), 4.12 (S), and 4.76 (rod) log₁₀ Rh*/photoreceptor/s. Responses from the same cell at the same background are also reported in E and F. E, Flash contrast–response function. Same format and same nonlinearity as B. The average gain of the cell was 3.5 mV/100% contrast.F, Action spectrum of a horizontal cell from inferior retina. Same format as C. Here the relative weights of the best fit (red line) are as follows: M, 0.09; S, 0.47; and rod, 0.45. The second fit (black line), obtained using the same static nonlinearity but without rod contribution, deviates from the data.

Figure 4.

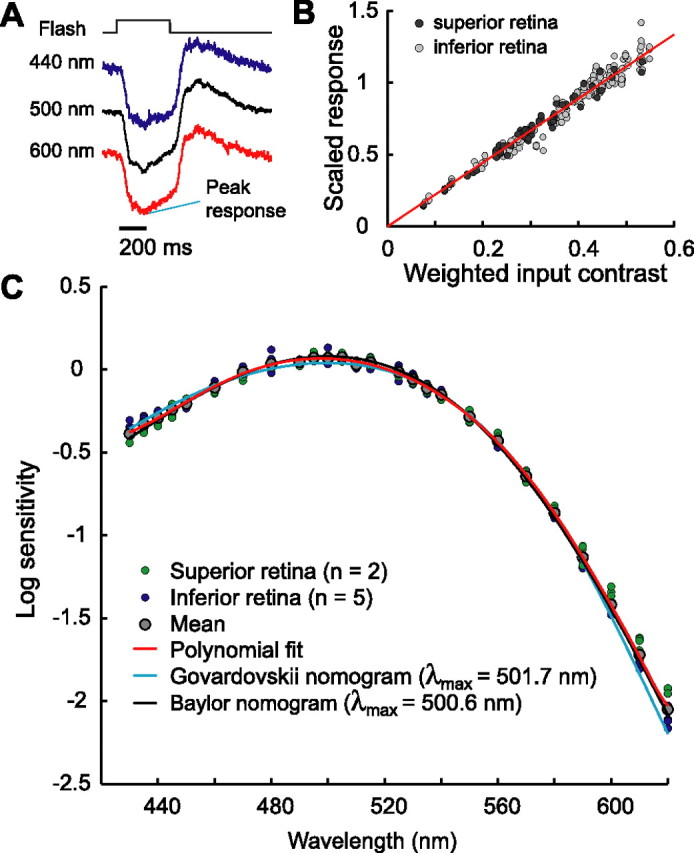
At low light levels, action spectra of horizontal cells matched rod spectral sensitivity.A, Response waveforms of horizontal cell from inferior retina to monochromatic flashes at wavelengths of 440, 500, and 600 nm. Same format as Figure 2, A and D. The responses lacked a clear transient phase and reached maximum hyperpolarization slowly, in contrast with the time course of responses observed at high light levels (Fig. 2A,D). The peak response amplitudes and flash intensities were 1.0 mV and 50 quanta/μm²/s (440 nm), 2.2 mV and 52 quanta/μm²/s (500 nm), and 1.3 mV and 938 quanta/μm²/s (600 nm). The background produced 1.50 (M), 1.39 (S), and 2.08 (rod) log₁₀ Rh*/photoreceptor/s. All panels used the same background.B, Flash contrast–response function. Same format as Figure 2, B and E. The monochromatic flash responses of all cells shown in C (superior retina, dark gray dots; inferior retina, light gray dots) were scaled and plotted against corresponding input contrasts (see Appendix B). Input contrasts were computed by fitting action spectra determined under the assumption that the contrast–response functions of the cells were linear for the range of stimuli presented. This linearity assumption is supported by the plot, which shows that the data cluster near a straight line. The average gain of all cells (n = 7) was 4.3 mV/100% contrast.C, Action spectra of all horizontal cells measured against the dimmest background. Action spectra were computed as described in Appendix B under the assumption that the contrast–response functions of the cells were linear for the range of stimuli presented. Rod spectral sensitivities derived from two photopigment nomograms (Baylor et al., 1987; Govardovskii et al., 2000), with values of λ_max as 500.6 or 501.7 nm, respectively, describe the data well. Action spectra of individual cells are shown as green dots (from superior retina) and blue dots (from inferior retina), with the mean data shown as gray dots. Data from the two retinal regions did not differ substantially. The red curve shows a polynomial fit to the mean data, which we used as our estimate of rod spectral sensitivity for other calculations reported in this study.

The flicker experiments used the LCD system alone to modulate a spot (horizontal cells, ∼2000 μm diameter; ganglion cells, ∼400–600 μm diameter) around the background at 2 Hz with a temporal sinusoid. The background was the same as the main background used for the flash experiments, and the cell was adapted continuously throughout the recording. The flickering stimulus was repeated for at least 16 cycles. The response was taken as the signed fundamental response amplitude (F1), with the sign indicating whether the response was best described as in-phase or out-of-phase with the stimulus modulation (after accounting for a small response delay.) Responses during the first and last stimulus cycles were excluded from the analysis.

For the flashed monochromatic spots produced using the lamp system, stimulus strength at each wavelength was characterized in terms of irradiance (quanta per square micrometer per second). For the flickering spots produced using the LCD system, when the stimulus was a mixture of two primaries, the most natural units are those of cone and rod contrast (C_M, C_S, and C_Rod) at the time of maximum excursion from the background (Brainard, 1996). Stimuli from the flash experiments were also converted to contrast units for some of the analyses.

To convert physical light spectra to contrast units, spectral sensitivities for guinea pig cone photopigments were generated using the nomogram developed by Govardovskii et al. (2000), with λ_max values obtained using ERG (Jacobs and Deegan, 1994); rod spectral sensitivities were estimated directly from our spectral measurements (see Fig. 4C). From these spectral sensitivities, we computed isomerization rates and contrasts for each opsin type (M, S, and rod), using estimates of receptor properties described in Appendix A. Matlab (MathWorks, Natick, MA) code for performing conversions between physical spectra and pigment isomerization rates is available as part of the Psychophysics Toolbox (http://psychtoolbox.org) (Brainard, 1997; Pelli, 1997).

Immunostaining.

We stained the retina with antibodies to M and S opsin to confirm previous measurements (Röhlich et al., 1994) of opsin gradients in guinea pig. An eyecup was kept in dark for 0.5 h in oxygenated Ames' medium, then fixed in 4% paraformaldehyde in 0.1 m phosphate buffer (PB) for 1 h, and washed briefly in PB. The retina was peeled from the pigment epithelium and incubated in blocking buffer (10% normal goat serum and 5% Triton X-100 in PB with 5% sucrose) for 1 h to reduce nonspecific binding. To stain M and S opsins, the tissue was reacted with primary antibodies (in blocking buffer). For M opsin, we used mouse anti-COS1 (kindly provided by Prof. Á. Szél, Department of Human Morphology and Developmental Biology, Semmelweis University, Budapest, Hungary) (Röhlich et al., 1994) at a dilution of 1:40, and, for S opsin, we used rabbit anti-S opsin (Chemicon, Temecula, CA) at a dilution of 1:600 for 35 h at 4°C. After several washes in PB with 5% sucrose (SPB), the tissue was reacted with secondary antibodies (4 h, room temperature) to visualize the opsin staining. M opsin was tagged with FITC (Invitrogen, Carlsbad, CA), and S opsin was tagged with cyanine 5 (Invitrogen). Finally, after several washes in SPB, the tissue was mounted on a glass slide with the photoreceptor side up and then covered with mounting medium (Vectashield; Vector Laboratories, Burlingame, CA) and a coverslip.

The tissue was examined using a confocal microscope (Leica TCSNT; Leica, Nussloch, Germany) with 40× objective (1.25 numerical aperture) and 100× objective (1.4 numerical aperture). A preliminary scan was performed to optimize the photomultiplier tube settings. Image stacks of the photoreceptor layer from both superior and inferior retina were then obtained, with a total z-depth covering the cone outer segments. Within each image stack, cone outer segments were outlined in Volocity (Improvision; Lexington, MA) and counted manually.

Outdoor spectra of skylight and ground cover.

Using a spectraradiometer (PR-650; Photo Research, Chatsworth, CA), we measured the spectra of skylight and light reflected from ground cover (e.g., grass, leaves, fruits, tree barks, and earth) in direct sunlight or under shade of trees in a local botanic garden (Philadelphia, PA; early afternoon in July, clear sky with clouds). To convert the spectra into retinal irradiance, we used a posterior nodal distance of 5.05 mm for guinea pig eye (Do-Nascimento et al., 1991) and adjusted the pupil size used in the calculation according to the light intensity. Photopigment isomerization rates for each opsin type (M, S, and rod) were calculated from retinal irradiance as described above.

Results

Immunostaining

We confirmed the observations of Röhlich et al. (1994). Superior retina contained ∼20,000 cones/mm². Individual cones stained for either M opsin (94%) or S opsin (6%) but not both (Fig. 1A, left). Inferior retina contained ∼24,000 cones/mm². All cones stained for S opsin, and some also stained for M opsin (Fig. 1A, right). The prevalence of coexpression and the intensity of M-opsin staining declined toward the inferior margin of the retina. At distances >3.0 mm inferior to the optic disk, M-opsin staining was detected in fewer than 1% of the cones.

To estimate the M/S opsin ratio in inferior retina, one would need to assume that the antibodies stain each opsin with equal efficiency. Because this assumption probably does not hold (Hack and Peichl, 1999; Applebury et al., 2000; Nikonov et al., 2005), we view the measurements in inferior retina as indicating only qualitatively that S opsin is expressed much more strongly than M opsin.

Measuring horizontal cell M, S, and rod weights: flash experiments

We estimated cone contributions to horizontal cell response (“cone weights”) from the responses of the cell to monochromatic flashes. As described in Appendix B, the analysis took into account a horizontal cell contrast–response nonlinearity (Fig. 2B,E) (see Fig. 7).Figure 2 shows action spectra obtained for two cells, one from superior retina (C) and one from inferior retina (F). Fits to individual cells as weighted sums of M, S, and rod contrast spectral sensitivities are also shown in Figure 2, C and F. The fitting procedure is described in Appendix B. The fits are generally good with some deviation at the shortest wavelengths, for which the data become somewhat irregular.

There is a striking difference between the photoreceptor contrast weights obtained from the spectral fits in superior and inferior retina. Mean ± SE weights obtained in superior retina (n = 14) were as follows: M, 0.52 ± 0.03; S, 0.02 ± 0.01; rod, 0.46 ± 0.03. Mean ± SE weights obtained in inferior retina (n = 8) were as follows: M, 0.09 ± 0.01; S, 0.50 ± 0.03; rod, 0.41 ± 0.04. Rod weights did not differ significantly between superior and inferior retina (t test, p = 0.31). The distribution of weights obtained in individual horizontal cells at the main background intensity studied (4.76 log₁₀ Rh*/rod/s) is shown in Figure 3A as green dots (superior retina) and green circles (inferior retina). The weights obtained for the two retinal regions are well separated, with M-opsin input dominant in the superior retina and S-opsin input dominant in the inferior retina.

Figure 3.

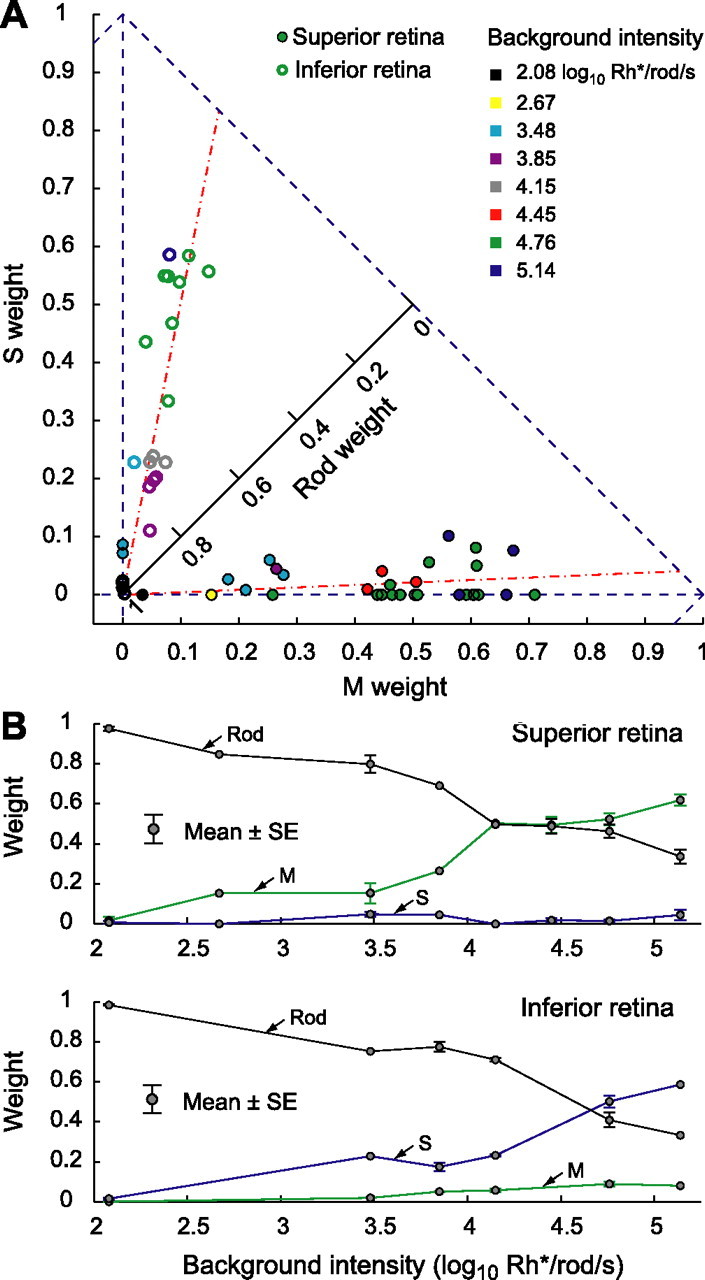
When background intensity increased, relative cone contribution to horizontal cell responses increased but relative rod contribution decreased.A, Photoreceptor weights of cells collected at eight background levels. The backgrounds had similar relative spectra but varied in overall intensity from 2.08 to 5.14 log₁₀ Rh*/rod/s. Each dot or circle represents the relative M, S, and rod weights inferred from the best fit to the measured spectral sensitivity for a single cell and intensity level. Because the relative weights sum to 1, they may be represented in a two-dimensional plot. The x- and y-axes provide the M and S weights, respectively. The rod weight may be visualized by noting the position of a plotted point along a third axis that extends from the origin at a 45° angle. Points closer to the origin had higher rod weight. Points above the 45° axis had higher S weight than M weight and vice versa. Dots represent cells from superior retina, and circles represent cells from inferior retina. We fitted all of the data of each retinal area with a straight line (red lines). Slopes of the fits describe relative M and S contributions as a fraction of total cone input (superior retina, 0.96/0.04; inferior retina, 0.17/0.83).B, Mean photoreceptor weights (error bars show ±1 SE) are plotted against background intensity (M, green line; S, blue line; rod, black line). Top shows data from superior retina, and bottom shows data from inferior retina. Rod contribution decreased with background intensity but did not drop to 0 at the highest intensity backgrounds used.

In addition to cone input, horizontal cells also received significant input from rods at the main background intensity used. This is revealed by the fact that fits to the action spectra without a rod contribution deviate from the data (Fig. 2C,F). We return below to the question of how rod and cone weights vary with background intensity.

Our fits were obtained using M- and S-opsin spectral sensitivities based on the nomogram of Govardovskii et al. (2000), with λ_max values of 430 and 529 nm (Jacobs and Deegan, 1994). Rod spectral sensitivity was derived directly from our measurements at low-light levels (see below). Because there is an ∼30 nm range in values for guinea pig S-cone photopigment λ_max reported in the literature (Jacobs and Deegan, 1994; Parry and Bowmaker, 2002; Parry et al., 2004), we verified our choice of cone pigment λ_max by fitting the data at which M- and S-opsin λ_max values were also allowed to vary as free parameters. The optimal value of M-opsin λ_max obtained was 527.5 nm for the cell shown in Figure 2C and 527.3 nm for all cells from superior retina (n = 14) at the main background. The optimal value of S-opsin λ_max obtained was 433.4 nm for the cell shown in Figure 2F and 430.2 nm for all cells from inferior retina (n = 8) at the main background. These values are in good agreement with the published values of Jacobs and Deegan (1994). We used their published values in our primary analyses. Assuming a value of 410 nm for S-opsin λ_max leads to a poor fit to the action spectrum shown in Figure 2F, with 2.1 times larger root mean squared error but similar weights: M, 0.07; S, 0.52; and rod, 0.41.

We estimated cone and rod weights across a broad range of background light intensities. All of the backgrounds had similar relative spectra (for the isomerization rates produced in each receptor type for each background, see supplemental Table 1, available at www.jneurosci.org as supplemental material). As background intensity increased from 2.08 to 5.14 log₁₀ Rh*/rod/s, rod contribution decreased but still remained significant at the most intense background (Fig. 3). In parallel, cone input gradually increased and was evident at a background of 2.67 log₁₀ Rh*/rod/s (2.09 log₁₀ Rh*/M cone/s and 1.99 log₁₀ Rh*/S cone/s) (Fig. 3A, yellow dot). The ratio of M- and S-opsin weights is relatively stable across background intensities. The red dashed lines in Figure 3A are fit to the data across background intensities and correspond to M/S ratios of 0.96:0.04 (superior retina) and 0.17:0.83 (inferior retina).

Measuring rod spectral sensitivity

Horizontal cells can receive rod input through rod–cone gap junctions (Sharpe and Stockman, 1999; Bloomfield and Dacheux, 2001; Sterling, 2004). We measured action spectra of horizontal cells against a dim background with isomerization rates of 1.50 (M), 1.39 (S), and 2.08 (rod) log₁₀ Rh*/photoreceptor/s (Fig. 4C). At this background, the waveforms of the flash responses (Fig. 4A) resembled those reported for primate retina at low (10 troland) light levels (Smith et al., 2001). The action spectra we measured were well fit using rod spectral sensitivities derived from two types of nomograms (Baylor et al., 1987; Govardovskii et al., 2000), with λ_max close to 500 nm. This value matches that reported previously for guinea pig rods (Jacobs and Deegan, 1994; Parry and Bowmaker, 2002). In addition, the similarity of the spectral sensitivity obtained from superior and inferior retina indicates minimal cone contributions for this background intensity. We fit the mean data with a polynomial and used this fit as our best estimate of rod spectral sensitivity for the other calculations reported in this paper.

Measuring horizontal cell M, S weights: flicker experiments

To estimate M- and S-cone contrast weights for the flicker experiments, we presented each cell with modulations of various combinations of M and S contrasts produced as the mixture of the blue and green primaries of the LCD system (C_M and C_S) (Fig. 5A, top row). Negative M contrast represents modulations in which the M component of the modulation is 180° out-of-phase with the S component. We estimated M and S contrast weights from the data using a linear–nonlinear (LNL) model (Appendix C) (Fig. 5B) (Chichilnisky, 2001; Chatterjee and Callaway, 2002; Chichilnisky and Kalmar, 2002; Zaghloul et al., 2003).

Figure 5.

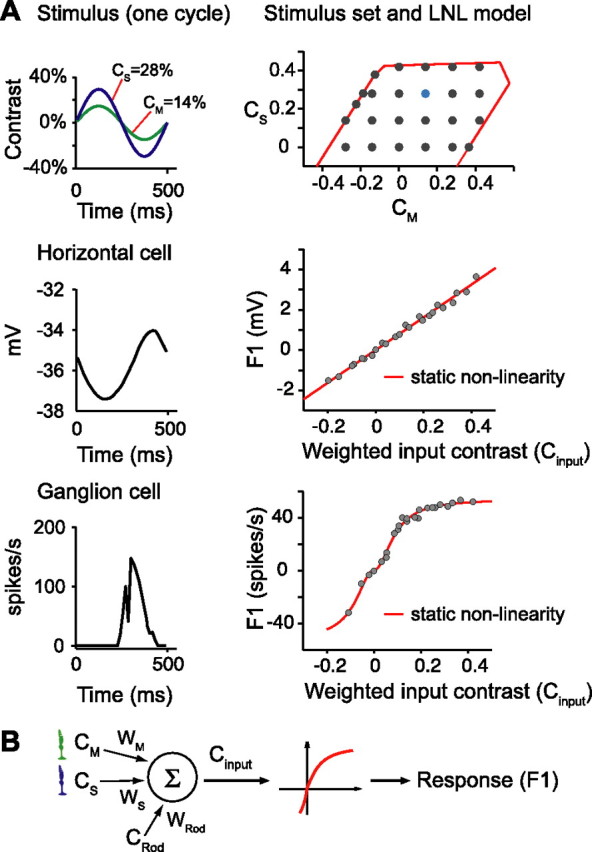
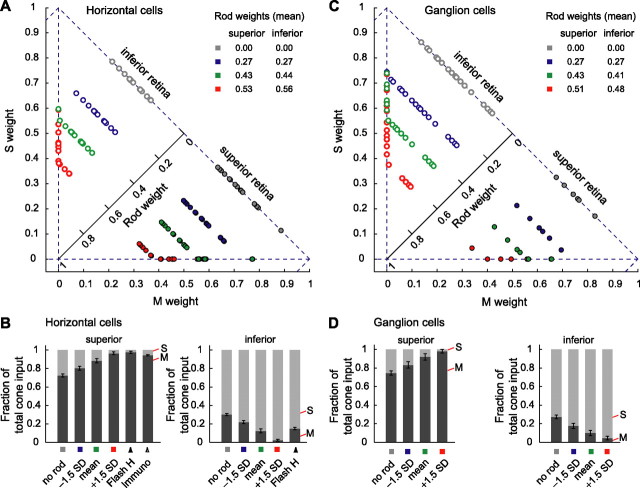
LNL model describes the responses of cells to flicker and was used to estimate M- and S-cone weights.A, Responses to flicker. Left column shows a stimulus (top) that sinusoidally modulates excitation of M and S opsins against a uniform background and the responses of a horizontal cell (smoothed membrane potential, middle) or a ganglion cell (peristimulus time histogram, bottom panel) to this stimulus. Right column shows a set of sinusoidally modulated stimuli (top, M and S contrasts plotted; cyan dot, the stimulus shown on the left; red line is the gamut limitation of our display) and how the F1 responses to these stimuli (gray dots) for horizontal and ganglion cells (middle and bottom) were described by the LNL model (see B and Appendix C). The derived static nonlinearity for the horizontal cell was essentially linear over the range of contrasts used, whereas the ganglion cell showed clear saturation.B, Linear nonlinear model. The linear component of the model used a weighted sum of receptor contrasts as C_input. The nonlinear component predicted the response (F1) of the cell from C_input through a parameterized static nonlinearity. Cone weights and parameters describing the static nonlinearity were found through numerical search by minimizing the difference between model prediction (red line) and responses (gray dots) (right middle and right bottom plots in A). To correct for rod contribution to cell response, the rod contrast weight was set at a fixed value before fitting the cone weights and parameters of the nonlinearity. In Appendix C, we show that the fit quality and derived nonlinearity are independent of the rod contrast weight assumed. We used the data from the flash experiments to set the value for the rod contrast weight.

Because our flicker stimuli consisted of the mixture of two primaries, we could not independently estimate rod input from the flicker data (Appendix C). Therefore, we took the estimates of rod input obtained in the flash experiment at the same background level (w_Rod = 0.44 ± 0.12, mean ± SD, combining measurements from superior and inferior retina) and included this in the LNL model calculations. We then found the M- and S-cone contrast weights and parameters of the static nonlinearity that best accounted for the data from each cell. The green points plotted in Figure 6A (and B) show the horizontal cell cone weights obtained in this manner. As with the flash experiments, the data reveal large differences between superior and inferior retina. As shown in the figure, these differences are robust with respect to variation in the assumption about the magnitude of rod input.

Figure 6.

Distributions of M and S weights differed between different retinal areas but were similar across cell types.A, Cone weights of horizontal cells estimated from flicker data. To estimate cone weights, we included rod input in the analysis, fixing the rod weights at the mean level measured in the flash experiments at the same background intensity and retinal region (green dots and circles in Fig. 3A). The resulting estimates are shown as green dots and circles in the present figure. We also estimated cone weights under different assumptions about rod input. Additional rod weights assumed were no rod input (gray) and ±1.5 SD away from the mean estimate (red and blue). In the fits, we constrained the cone weights to be positive, which, for some cells, altered the rod weight to a smaller value when derived M or S weights equaled 0. The rod weights shown in the insets are the mean values used in calculations, which are smaller than the nominal values because of the alteration procedure described in the previous sentence. Across the range of rod weights assumed, clear separation of the data from superior and inferior retina holds. The background produced 4.16 (M), 4.12 (S), and 4.76 (rod) log₁₀ Rh*/photoreceptor/s. All panels used the same background.B, Comparison of mean cone weights from A with those from the horizontal cell flash data and cone opsin ratio estimates from immunostaining. Both panels plot M and S weights as fractions of total cone input. Error bars (indicating SE) are plotted only for M cones. Bars marked with squares summarize data in A. For horizontal cells in superior retina, assuming higher rod weights leads to a higher fraction of M versus of S input and vice versa in inferior retina. The effect of varying assumed rod weight is small relative to the effect of retinal location. Bars labeled Flash H represent cone weights obtained for horizontal cells in the flash experiments. For superior retina, the bar labeled Immuno represents the fraction of M and S cones of all cones, which we also take as the opsin ratio. Inferior retina lacks this bar because immunostaining could not quantify the ratio of M- to S-opsin expression. Qualitatively, S-opsin expression greatly exceeds M-opsin expression in inferior retina.C, Cone weights of ganglion cells estimated from flicker. The same format as A is shown. Results from horizontal and ganglion cells are similar.D, Summary of cone weights in C. The same format as B is shown. For ganglion cells, in superior retina, assuming higher rod weights leads to a higher fraction of M input versus that of S and vice versa in inferior retina. The effect of varying rod weight is small relative to the effect of retinal location. Together with B, the plot establishes that the cone weights from the flicker are similar for horizontal and ganglion cells and are consistent with cone weights from the flash data for horizontal cells and the opsin ratio obtained from immunostaining.

In six horizontal cells (four at main background and two at dimmer backgrounds), we were able to obtain cone weight estimates from both the flash and flicker protocols. To compare the estimates obtained from the two protocols, we reanalyzed the flicker data from these cells using the estimate of rod input obtained for the same cell from the flash data. The estimates obtained from the two methods were in good agreement. (For both M- and S- cone weights, expressed as fraction of total cone inputs, mean absolute deviation was 0.08 and maximum deviation was 0.16.)

Measuring brisk-transient ganglion cell M, S weights

We measured responses of brisk-transient ganglion cells to the flicker stimuli. Cone contrast weights for these cells were estimated using the same procedure as for the horizontal cell flicker data. As with horizontal cells, cone contrast weights to brisk-transient ganglion cells differ greatly with retinal location (Fig. 6C,D). The difference in cone weights between regions also survived variation in the assumption about the magnitude of rod input. Comparison across the two cell types, but at the same retinal location and with the same assumption about rod input, reveals similar M and S weights (Fig. 6B,D).

Discussion

Opsin expression predicts cone input to horizontal and brisk-transient ganglion cells

Cone inputs to horizontal cells correlate strongly with the dual gradients of M and S opsin demonstrated by immunostaining. In superior retina, the agreement was quantitative, as shown in Figure 6B. In inferior retina, we could not quantify the M/S opsin ratio by immunostaining; nevertheless, the two measures agreed qualitatively. Furthermore, the cone weights were the same for brisk-transient ganglion cells (Fig. 6B,D); thus, as signals flow from outer to inner retina, the weighting is preserved. This conclusion assumes that rod weights are the same for horizontal and ganglion cells. This assumption seems justified because, at the high light levels used here, the rod signal enters the cone pathway by coupling to the cone terminal electrically and provides a common signal to all downstream neurons (Sharpe and Stockman, 1999; Bloomfield and Dacheux, 2001; Sterling, 2004).

Previous studies in primate retina on L- and M-cone inputs to horizontal cells and midget and parasol ganglion cells suggested a principle that relative expression of cone opsins is preserved postreceptorally (Dacey et al., 2000; Deeb et al., 2000; Diller et al., 2004). Our finding is consistent with this principle.

Our findings about the functional consequences of the dual opsin gradient agree with those from previous studies in mouse that used regional electroretinography (Calderone and Jacobs, 1995) and that mapped the distribution of ganglion cells with different cone weights (Ekesten et al., 2000; Ekesten and Gouras, 2005). Our studies extend the previous results by quantifying the effect for two specific classes of retinal neurons.

Brisk-transient ganglion cells correspond to M cells in the primate retina, which are responsible for behavioral contrast detection (Merigan and Maunsell, 1990, 1993; Dhingra et al., 2003; Silveira et al., 2004). That these cells follow the dual opsin gradient supports the hypothesis that the opsin gradients optimize contrast detection across spectral variation along the vertical meridian. Although the ecological basis for this optimization presumably lies in the spectral shift between ground and sky (Szél et al., 2000; Osorio and Vorobyev, 2005), a detailed account awaits a fuller characterization of the guinea pig's photic environment and the signal-to-noise properties of its photoreceptors. Recent work has begun to characterize noise sources in the photoreceptors of various species and how these vary between rods and cones and between cones of different classes (Schneeweis and Schnapf, 1999; Rieke and Baylor, 2000; Burns and Baylor, 2001; Sampath and Baylor, 2002; Ala-Laurila et al., 2004; Dunn and Rieke, 2006; Nikonov et al., 2006).

Contrast versus intensity weights

In our analysis, we followed previous authors (Chatterjee and Callaway, 2002; Diller et al., 2004; Johnson et al., 2004; Horwitz et al., 2005) and derived photoreceptor weights using a contrast measure. These weights describe the relationship between the contrast of the stimuli and the response of the postreceptoral cells. The rationale for this choice is that contrast weights are invariant with respect to changes in the chromaticity and intensity of the background if photoreceptors adapt according to Weber's Law (i.e., gain for each class of receptor inversely proportional to background isomerization rate for that class). Weber's Law provides a reasonable first-order description of photoreceptor adaptation over much but not all of their operating range (Demontis et al., 1993; Schneeweis and Schnapf, 1999). Indeed, if Weber's Law adaptation perfectly described the behavior of the coupling between photoreceptors and postreceptoral neurons, the relative contributions of rods and cones would not change with background intensity when expressed as contrast weights. This prediction is clearly falsified by our data (Fig. 3) for large changes in background intensity.

Because there are deviations from Weber's Law adaptation, it is worth considering whether our conclusions depend strongly on the choice to use contrast weights. Intensity weights describe the relationship between the incremental intensity of the stimuli seen by each photoreceptor class and cell response. We describe this reanalysis and show the results in the supplemental material (particularly supplemental Figs. 1, 2, available at www.jneurosci.org as supplemental material). None of the basic conclusions of the paper are sensitive to the choice of whether to evaluate receptor contribution in terms of contrast or incremental intensity. In particular, the relative M- and S-cone weights are essentially similar in the intensity weight analysis. This invariance is in part a consequence of the fact that we carefully chose the chromaticity of our backgrounds so that they produced similar isomerization rates in the M and S cones.

The biggest change resulting from the reanalysis in terms of intensity weights is a reduction in the estimated magnitude of rod contribution. Note, however, that the spectral fits shown in Figure 2, C and F, do not change when the weights are expressed in terms of intensity instead of contrast, so that the deviations for the no-rod fits are invariant with respect to this choice.

Rods contribute to responses at high light levels

Mammalian rods, including those of guinea pig, show Weber's Law adaptation at background levels up to ∼4 log₁₀ Rh*/rod/s (Tamura et al., 1989; Nakatani et al., 1991; Demontis et al., 1993). These measurements were made using suction microelectrode recording from isolated rod outer segments and relatively short adaptation times. If such adaptation continues to even higher light levels in whole-mount retina under the steady adaptation conditions that we used, it could explain why we observe rod contributions at yet higher light levels (5.14 log₁₀ Rh*/rod/s).

Our spectral measurements show that light reflected from ground in shade produced 4.2–6.4 log₁₀ Rh*/rod/s in guinea pig, whereas light reflected from ground in direct sunlight produced 5.0–6.8 log₁₀ Rh*/rod/s. These comparisons suggest that rods contribute substantially to daylight vision.

Appendix A: photoreceptor parameters

Table 1 provides the parameters we used to determine the photoreceptor sensitivities and peak isomerization probabilities. For cones, the value of λ_max was used in conjunction with the nomogram developed by Govardovskii et al. (2000) to generate the relative cone sensitivity. This was then adjusted for pigment self-screening and scaled according to the peak isomerization probability derived using the other constants given in Table 1. For rods, the spectral sensitivity was determined from a polynomial fit to horizontal cell action spectra measured on the dimmest background. This was then scaled to fit the rod sensitivity derived from the nomogram computed with λ_max = 500 nm, and the peak isomerization sensitivity was taken from this scaled version.

Table 1.

Parameters used to calculate photoreceptor isomerization rates

Photoreceptor type	M cone	S cone	Rod	Units	Source
λmax	529	430	500	nm	(Jacobs and Deegan, 1994)
Outer segment length	8.0	8.0	16.2		Unpublished data from our laboratory
Outer segment diameter	2.0	2.0	2.0	μm	Unpublished data from our laboratory
Inner segment diameter	2.8	2.8	2.4	μm	Unpublished data from our laboratory
Axial specific density	0.0045	0.004	0.011	μm−1	(Parry and Bowmaker, 2002)
Axial optical density	0.036	0.032	0.170		Calculated from other parameters
Peak isomerization probability	0.053	0.047	0.229		Calculated from other parameters

Appendix B: estimating action spectra from flash data for horizontal cells

This appendix describes how we estimate horizontal cell action spectra. There are two key steps to the processing. The first step normalizes the measured response at each wavelength to that of a reference flash presented at 520 nm. This step compensates for a drift in gain that can occur during measurements from a single cell. The second step corrects for a static nonlinearity in the contrast–response function of horizontal cells.

Drift correction

As described in Materials and Methods, we measured the responses of horizontal cells to reference flashes presented at 520 nm. The intensity of the reference flashes was held constant for each cell but was chosen individually for each cell so as to produce an easily measurable response. We used linear interpolation on the responses to the reference flashes to provide an estimate of how the cell would have responded to the reference flash at any time during the experiment. We divided the measured response to each test flash by the estimate of the reference flash response at the corresponding time. This produced a drift-corrected response R_c(λ) = R(λ)/R(520) for each test flash, where R(λ) is the raw measured response to a test flash of wavelength λ, and R(520) denotes the interpolated estimate of the response of the reference flash response at the time of the test flash. We used this procedure for 43 of 48 cells. For the other five cells, interspersed reference flash measurements were not made, and, for these cells, we took R_c(λ) = R(λ).

Correction for static nonlinearity

If horizontal cells responded linearly with flash stimulus contrast at all wavelengths, we could convert drift-corrected responses to action spectra directly by dividing the drift-corrected response at each wavelength by the flash intensity I(λ) at that wavelength. This procedure, however, would produce distorted action spectra estimates if some of the flashes drove the cells outside of their linear operating range. To avoid such distortion, we corrected for response nonlinearity using an LNL model (Chichilnisky, 2001; Chatterjee and Callaway, 2002; Chichilnisky and Kalmar, 2002; Zaghloul et al., 2003).

The LNL model describes the response of the cell as the result of passing an input contrast C_input(λ) through a nonlinear response function. The input contrast is taken as the weighted sum of the contrasts C_M(λ), C_S(λ), and C_Rod(λ) seen by the M cones, S cones, and rods in response to the test flash at wavelength λ:

Here, u_M^c, u_S^c, and u_Rod^c are the M-cone, S-cone, and rod contrast weights. The values of C_M(λ), C_S(λ), and C_Rod(λ) are calculated from the spectral sensitivity of the photoreceptors S_Mⁱ(λ), S_Sⁱ(λ), and S_Rodⁱ(λ), the test flash intensity I(λ), and the isomerization rates seen by each receptor class to the background. We denote these background isomerization rates as Rh_M,bg*, Rh_S,bg*, and Rh_Rod,bg*. The contrasts are then computed as C_M(λ) = I(λ)S_Mⁱ(λ)/Rh_M,bg*, C_S(λ) = I(λ)S_Sⁱ(λ)/Rh_S,bg*, and C_Rod(λ) = I(λ)S_Rodⁱ(λ)/Rh_Rod,bg*.

The nonlinear response function is taken to have the form

The parameters C₀, n, and R_max denote the semi-saturation constant, exponent, and maximum response amplitude. For each background level, we took the parameters C₀ and n as common to all horizontal cells, whereas the value of parameter R_max varied from cell to cell.

We analyzed the data from each background level separately. To fit the LNL model to the horizontal cell data from each background, we used an iterative procedure. First, we initialized the action spectrum of each cell under the assumption that the cell responded linearly. We then obtained initial estimates of u_M^c, u_S^c, and u_Rod^c for each cell by fitting the action spectrum as the weighted sum of the contrast sensitivities of the three photoreceptor types. This initial fit allowed us to proceed by iterating between two steps.

The first step determined the parameters of the static nonlinearity that best accounted for the data from all cells at the same background. The second step redetermined the weights u_M^c, u_S^c, and u_Rod^c for each cell, after correcting for the common nonlinearity determined in the first step. We found that this procedure converged rapidly and accounted for the data well.

Step 1: fitting the nonlinearity

Given values for u_M^c, u_S^c, and u_Rod^c for each cell, we can compute the value of C_input(λ) for every test flash presented to every cell. We assumed that individual cells could have different R_max. As a numerical convenience, rather than fitting R_max to each cell, we scaled the drift-corrected responses from each cell so that the initial slope of the contrast–response function [evaluated for data corresponding to C_input(λ) ≤ 0.45] was the same. We then used numerical search to determine C₀, n, and a single R_max^scaled that best accounted for the set of scaled responses for all cells.

Step 2: correcting for the nonlinearity in the estimation of u_M^c, u_S^c, and u_Rod^c

Given the results of step 1, we used numerical search to find the parameters u_M^c, u_S^c, and u_Rod^c and R_max that best fit the drift-corrected responses R_c(λ) responses for each cell, through Equations B1 and Equations B1. During this fit, we held C₀ and n constant at the values obtained in step 1.

We then iterated the procedure, using contrast weights u_M^c, u_S^c, and u_Rod^c obtained in step 2 to repeat step 1 and so forth. The error measure minimized in both steps 1 and 2 was the root mean squared error between the log₁₀ transformed values of the test flash R_c(λ) and their predictions from the model. When the fit error after the first step was reduced by <1% compared with the previous iteration, we performed one final execution of the second step and then terminated the procedure.Figure 7 shows the nonlinearity obtained for the main background after the final step, along with the entire set of test flash data for that background. The plotted data are scaled as described for step 1.Figure 2, B and E, shows the same nonlinearity with the data (scaled in the same way) from two individual cells.

Figure 7.

Reponses to monochromatic flashes of horizontal cells were well described with a common static nonlinearity. Response for each cell (superior retina, dark gray dots; inferior retina, light gray dots) was scaled to have the same initial slope of the contrast–response function (see Appendix B). Red line is the common nonlinearity described using Equation B2 with the following parameters: C₀ = 0.868, n = 1.247, and R_max^scaled = 3.191. The same nonlinearity was plotted in Figure 2, B and E.

We applied this procedure separately for the horizontal cell flash data from each background, except for the dimmest background. On the dimmest background, the responses to our set of presented flashes were within the linear regimen (Fig. 4B), and, for this background intensity, we simply adopted the linear approximation.

The iterative analysis provides us with direct estimates of the photoreceptor contrast weights for each cell (u_M^c, u_S^c, and u_Rod^c), and, from these, we can construct a predicted action spectrum. To correct the data for comparison with this prediction (Fig. 2C,F), we invert the static nonlinearity using the result of the final iteration of step 2. This allows us to compute an action spectrum A(λ) from the drift-corrected responses R_c(λ) through

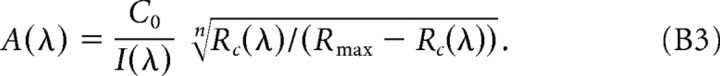Each datum plotted in Figure 2, C and F, was obtained using Equation B3. Only the shape of the action spectra A(λ) are of interest here, so the plotted data and predictions shown for each cell were shifted vertically by a common amount on the log₁₀ sensitivity axis so that the theoretical value A(520) = 1. Similarly, we report relative contrast weights

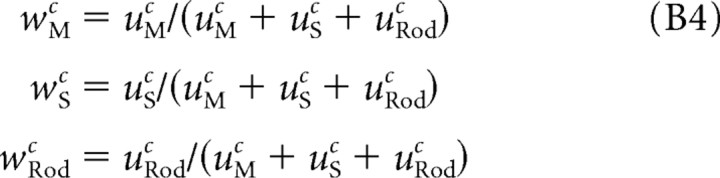in this study, because a scale factor common to u_M^c, u_S^c, and u_Rod^c trades off perfectly with the semi-saturation constant through Equation B2. Indeed, the normalization in Equation B4 was applied during the fitting process to allow the parameter search to converge to a unique value of C₀.

Appendix C: LNL model for horizontal and ganglion cell flicker data

To estimate M- and S-cone contrast weights from the flicker data, we also used the LNL model to describe cell responses (see Appendix B, Eqs. B1 and B2) (Fig. 5B). We fit the parameters of the model to each cell separately and also allowed a parameter that could account for the spontaneous activity of the cells. Because the flicker stimuli were constructed as the superposition of two primaries, the flicker data do not allow unique identification of w_M^c, w_S^c, and w_Rod^c (see below). Thus, in analyzing the flicker data, we fixed w_Rod^c at the value determined from the flash data for horizontal cells. (We also explored the effect of variation of the assumed w_Rod^c on the obtained w_M^c and w_S^c.) In the fits, we constrained w_M^c and w_S^c to be positive by varying the value of w_Rod^c if necessary. Predictions from LNL model generally accounted for the actual response data well (Fig. 5A). In the following, we show that the shape of the nonlinearity derived from the LNL model is independent of the strength of assumed rod input, when the stimuli are produced as a mixture of two primaries.

Static nonlinearity is independent of assumption about magnitude of rod contribution

We show that, for any choice of w_M, w_S, and w′_Rod and w′_Rod, we can find w′_M and w′_S, such that

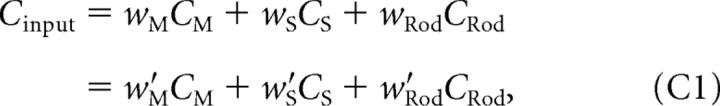with w′_M and w′_S independent of the color direction of the stimulus. This result means that the effect of varying the assumed rod weight may be compensated for perfectly by adjusting the M- and S-cone weights, so that the both the quality of the best fit to the data and the parameters of the static nonlinearity are independent of the assumed rod weight.

We proceed by showing that, when the flicker stimulus is the mixture of two primaries, we can express

where q_M and q_S depend on the spectra of the primaries, the spectral sensitivities of the photoreceptors, and the background but not on the color direction of the flickering stimulus. Using Equation C2, we rewrite

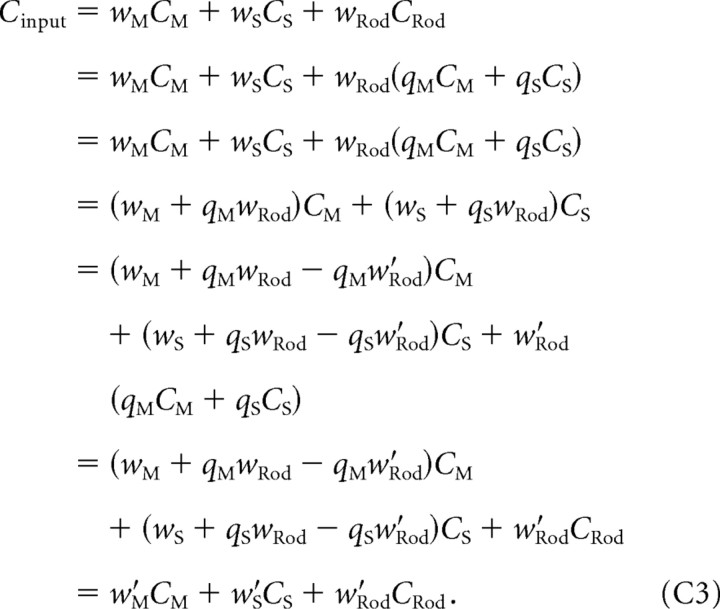This establishes Equation C1 from C2 with w′_M = (w_M + q_Mw_Rod − q_Mw′_Rod) and w′_S = (w_S + q_Mw_Rod − q_Sw′_Rod).

To show the Equations C2 holds, we note that, when flicker is the mixture of two primaries (here green and blue), we can write C_M = v_MGΔP_G + v_MBΔP_B and C_S = v_SGΔP_G + v_SBΔP_B, where ΔP_G is the flicker amplitude of the green primary, ΔP_B is the flicker amplitude of the blue primary, and the constants v are weights that specify how strongly modulating each primary affects the contrast seen by each type of cone. We can invert this two-by-two system of linear equations to obtain expressions for the primary modulations in terms of the cone contrasts: ΔP_G = v_GMC_M + v_GSC_S and ΔP_B = v_BMC_M + v_BSC_S. Finally, the rod contrast is also the weighted sum of the primary modulations, so we have

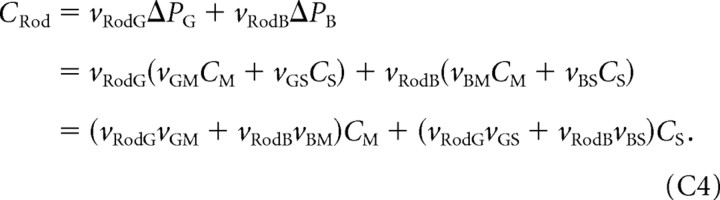This is in the same form as Equation C2, with q_M = (v_RodGv_GM + v_RodBv_BM) and q_S = (v_RodGv_GS + v_RodBv_BS).