An Investigation into the Mechanisms of DNA Strand Breakage by Direct Ionization of Variably Hydrated Plasmid DNA

Abstract

The mechanisms by which ionizing radiation directly causes strand breaks in DNA were investigated by comparing the chemical yield of DNA-trapped free radicals to the chemical yield of DNA single strand break (ssb) and double strand break (dsb), as a function of hydration (Γ). Solid-state films of plasmid pUC18, hydrated to 2.5 < Γ < 22.5 mol, were X-irradiated at 4 K, warmed to room temperature, and dissolved in water. Free radical yields were determined by EPR at 4 K. With use of the same samples, Gel electrophoresis was used to measure the chemical yield of total strand breaks, which includes prompt plus heat labile ssb; G′_total(ssb) decreased from 0.092 ± 0.016 μmol/J at Γ = 2.5 to 0.066 ± 0.008 μmol/J at Γ = 22.5. Most provocative is that at Γ = 2.5 the yield of total ssb exceeds the yield of trapped deoxyribose radicals: G′_total(ssb) – G′_sugar(fr) = 0.06 ± 0.02 μmol/J. Nearly ⅔ of the strand breaks are derived from precursors other than radicals trapped on the deoxyribose moiety. To account for these nonradical precursors, we hypothesize that strand breaks are produced by two one-electron oxidations at a single deoxyribose residue within an ionization cluster.

Introduction

Direct-type effects, that is damage caused by direct ionization of DNA or by transfer of electrons or holes from the hydration shell to the DNA, contribute between 40% and 50% of the damage that causes cell death.^1–5 The remainder is due to indirect effects, which are mediated by water radicals. The latter is more easily studied and, therefore, is better characterized, both quantitatively and mechanistically.^3,6,7 Here we focus on strand break (sb) formation by direct-type effects, using variable levels of hydration to gain insight into the mechanisms responsible for sb produced by direct-type effects. As the hydration level decreases, the contribution of the direct effect increases.

The level of DNA hydration, Γ (mol water/mol nucleotide), has been shown to influence the yields of direct-type damage in DNA exposed to ionizing radiation.^8–17 For water radical cations (holes) formed in the tightly bound solvation shell (Γ < 9–10) of DNA, hole transfer to the deoxyribose backbone and bases occurs rapidly; for the outer lying waters (9–10 < Γ < 23), the rate at which the water radical cation (H₂O^•+) deprotonates (to HO^•) is faster than the transfer rate, with the result that HO^• formation dominates.^12,13,16 Thus, the effective target mass per nucleotide, with respect to hole trapping in DNA as detected by EPR, consists of the nucleotide residue itself, one counterion, and 9 to10 waters per nucleotide. The role of these tightly bound waters is likely to be significant given the high concentration of DNA in vivo.¹⁸ In nucleosomes, it has been estimated at 0.17 g/mL,¹⁹ which corresponds to a Γ of ca. 100 mol water/mol nucleotide.

Via the direct effect, radiation forms radical cations on the deoxyribose–phosphate backbone of DNA. If the backbone radical cation deprotonates, the hole (any site that has lost one electron) is irreversibly trapped as a neutral carbon-centered radical, a known precursor to strand breaks.³ The fact that such deoxyribose damage releases an unaltered free base²⁰ was used by Swarts et al. to measure the chemical yield of free base release as a proxy for the yield of sb formation in lyophilized salmon sperm DNA γ-irradiated at room temperature.⁹ In a more recent work, Yokoya et al. measured total single strand breaks (ssb) for solid-state pUC18 γ-irradiated at 5.6 °C.²¹

Recently we reported that in X-irradiated plasmid DNA hydrated to Γ = 22.5 mol water/mol nucleotide, the yield of total ssb significantly exceeds the yield of trapped deoxyribose radicals.²² In plasmid pUC18 X-irradiated at 4 K, the yield of radicals trapped on the deoxyribose moiety, G_sugar(fr), and the total yield of single strand breaks, G′_total(ssb), were found to be 0.06 and 0.14 μmol/J, respectively. We termed the difference between G′_total(ssb) and G_sugar(fr), 0.14 μmol/J – 0.06 μmol/J = 0.08 μmol/J, the shortfall because this is the fraction of ssb that cannot be accounted for by EPR detected radicals trapped on deoxyribose. One mechanism that could explain the shortfall is hydrogen abstraction by hydroxyl radicals formed in the outer solvation shell (Γ > 9–10). A way to test for the possibility of hydroxyl radical attack, which is an indirect effect, is to vary the level of DNA hydration.

In the present study, the level of hydration was varied from Γ of 2.5 to 22.5 mol water/mol nucleotide. In the course of doing so, we became aware of an error in our earlier work²² related to the choice of target mass used in comparing free radical yields with strand break yields. For radical yields, we employed a target mass consisting of the entire sample (DNA + solvation shell + a small excess of salt) and for sb yields we employed only DNA in the target mass. It is important, however, to utilize the same target mass for both types of yield calculation. In this work, that error is corrected by employing DNA plus its solvation shell as the target mass for all of the yield calculations. This correction has a large impact at Γ = 22.5, where evidence of a shortfall is no longer readily apparent. However, at low levels of hydration, Γ < 10, it is demonstrated that the shortfall is of significant magnitude. The dependency of the shortfall on the degree of hydration argues persuasively against a hydroxyl radical attack mechanism and supports instead a mechanism entailing two one-electron oxidation events at a single deoxyribose.

Materials and Methods

The purification of plasmid pUC18(2686 bp), sample preparation,^22,23 and procedures for sample irradiation¹⁷ have all been described previously. In brief, solid-state film samples of pUC18 plasmid were equilibrated to various levels of hydration (Γ in mol water/mol nucleotide). The films consist of between (92 ± 3)% and (87 ± 4)% DNA, decreasing slightly as Γ increases. The remaining mass is excess salt coming from the 5 mM phosphate buffer employed in the starting solution. Samples were irradiated at 4 K in a Janis Dewar setup²⁴ with X-rays generated by a Varian/Eimac OEG-76H tungsten-target tube operated at 70 kV and 20 mA and filtered by a 25 μm aluminum foil. The dose rate was 24 kGy/h.

Procedures for agarose gel electrophoresis and strand break assay have been described previously.²² Following EPR spectroscopy the films were warmed to room temperature and dissolved in 1X TE buffer (10⁻² mol dm⁻³ Tris, 10⁻³ mol dm⁻³ EDTA, pH 8.0) to 10-fold their weight in volume. Aliquots, added to a loading buffer containing 0.1% bromphenol blue, were assayed by agarose gel electrophoresis at 4 °C in TBE (89 mmol dm⁻³ boric acid, 89 mmol dm⁻³ Tris, 1 mmol dm⁻³ EDTA). The gels were stained with SYBR Green I dye (Molecular Probes, Eugene, OR). The incremental increase in sb yield obtained by post-irradiation heat treatment at 75 °C for 30 min is considered to be the yield of heat labile sites. It is important to note that sb yields are calculated differently than in our previous work. Previously we based the yields of strand breaks on energy absorbed by a target mass consisting of only the mass of DNA. In the current work, the target mass consists of DNA plus the solvent shell.

The concentration of trapped free radicals in plasmids was determined by EPR at 4 K after X-irradiation at 4 K. The EPR spectra show no radicals assignable to excess salt, only DNA trapped radicals. Following EPR, these same samples were used for strand break measurements as described above. The yield of radicals trapped by DNA at 4 K was calculated differently than in our previous work. In past work,^{16,17,22,25–27} the target mass was based on sample mass, consisting of DNA plus solvation shell plus, in the case of films, a small (usually <10%) amount of excess salt. In this work, so as to make a direct comparison with sb yields, the target mass was based on DNA plus solvation; the excess salt is excluded. We take care to use notation that distinguishes this choice of the target mass by placing a prime on all such yields: e.g., G′_sugar(fr) indicates the yield of radicals trapped by deoxyribose that is based on a target mass of DNA plus solvation shell. As shown below, the use of the same target mass for yields of both radicals and ssb corrects our previous comparison²² so as to effectively make the shortfall go to zero at high hydrations.

Results

Free radical and strand break yields were measured in pUC18 plasmid DNA samples as a function of hydration, Γ, in the range 2.5 < Γ < 22.5 mol water/mol nucleotide. At any given Γ, at each dose point within a dose response curve, the same sample of pUC18 DNA was used to determine the concentration of free radicals trapped on the DNA at 4 K, as well as the yields of circular and linear forms of the plasmid DNA following gel electrophoresis.

The yield of ssb was derived from the slope of a straight line fitted to the graph of the logarithm of the fraction of intact supercoiled DNA versus radiation dose. Examples of the dose–response relationships used to measure prompt strand break yields, G′_prompt(ssb), at various levels of hydration are shown in Figure 1. The total yield, G′_total(ssb), includes yields due to both the prompt and the heat-labile strand breaks. The values of G′_prompt(ssb) and G′_total(ssb) determined at different levels of hydration are given in Table 1. We note that at Γ = 2.5 and 22.5, the respective values of G′_total(ssb) of 0.092 ± 0.016 and 0.066 ± 0.008 μmol/J correspond rather well with yields of free base release measured in lyophilized salmon sperm DNA by Swarts et al.,⁹ 0.055 ± 0.006 and 0.073 ± 0.003 μmol/J, respectively. This comparison is of interest because of the expected close correlation between free base release and ssb. But caution needs to be exercised in comparing results entailing different sample preparations. Such differences are known to result in large variations, 100% to 300%, in free-radical-trapping yields.²⁸

Figure 1.

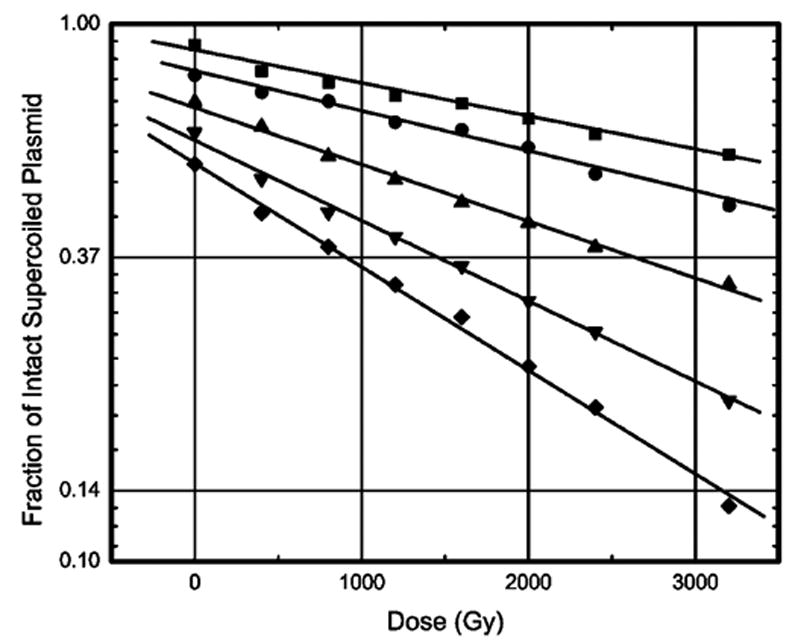
Loss of supercoiled DNA with increasing radiation dose for X-irradiated pUC18 plasmid samples at various Γ. The data include plasmids at (solid square) Γ = 2.5, (solid circle) Γ = 7.5, (solid triangle) Γ = 11.5, (open circle) Γ =15.0, and (solid diamond) Γ = 22.5 mol water/mol nucleotide. An offset has been introduced between each curve. X-irradiation was done at 4 K. The samples were warmed to room temperature and dissolved in 1X TE buffer prior to gel electrophoresis. The data set is fitted with a least-mean-squares straight line of the form y = ce^−mx. From the slope m of this line, the G′(ssb) is calculated at each Γ.

TABLE 1.

Dependence of G′_prompt(ssb), G′_total(ssb), and G′_total(dsb) on Γ for Films of pUC18 X-irradiated at 4 K

	1a	2a	3a	4	5b	6c
G	G′prompt(ssb) (μmol/J)	G′total(ssb)a (μmol/J)	G′total(dsb) (μmol/J)	G′total(ssb)/G′total(dsb)	G′sugar(fr) (μmol/J)	ΔG′ (μmol/J)
2.5 (0.2)	0.069 (0.014)	0.092 (0.016)	0.0052 (0.0008)	18 (6)	0.033 (0.005)	0.06 (0.02)
7.5 (0.6)	0.058 (0.012)	0.081 (0.014)	0.0046 (0.00081)	17 (4)	0.040 (0.006)	0.04 (0.02)
11.5 (0.3)	0.060 (0.008)	0.078 (0.008)	0.0044 (0.0009)	18 (5)	0.056 (0.008)	0.02 (0.02)
15.0 (0.7)	0.063 (0.008)	0.077 (0.009)	0.0047 (0.0008)	17 (4)	0.069 (0.010)	0.01 (0.02)
22.5 (1.1)	0.054 (0.007)	0.066 (0.008)	0.0039 (0.0005)	17 (3)	0.079 (0.012)	−0.01 (0.02)

^aThe standard deviations for G′(ssb) and G′(dsb) were calculated from six different sets of gel electrophoresis data and the standard deviations in determining the mass of DNA + solvation shell.

^bG′_sugar(fr) is determined from a semiempirical model that predicts 89% of the total free radicals are trapped on the bases and 11% on the sugar–phosphate.¹⁷ Unlike the values of G_sugar(fr) in this earlier work, G′_sugar(fr) is based on a target mass consisting of DNA + solvation shell; the excess salt is excluded.

^cΔG′ = G′_total(ssb) – G′_sugar(fr) = the “shortfall”.

Likewise, the yield for double strand breaks, G′_total(dsb), was determined from the slope of a yield dose plot of the fractional abundance of the linear form of the plasmid. The values of G′_prompt(dsb) and G′_total(dsb) are, within the standard deviations, the same. G′_total(dsb) is given in Table 1. A plot of G′_total(dsb) vs Γ, Figure 2, shows a slightly negative slope. The ratio of G′_total(ssb)/G′_total(dsb) remains relatively constant at 17 ± 5 throughout the hydration range (see column 4 of Table 1).

Figure 2.

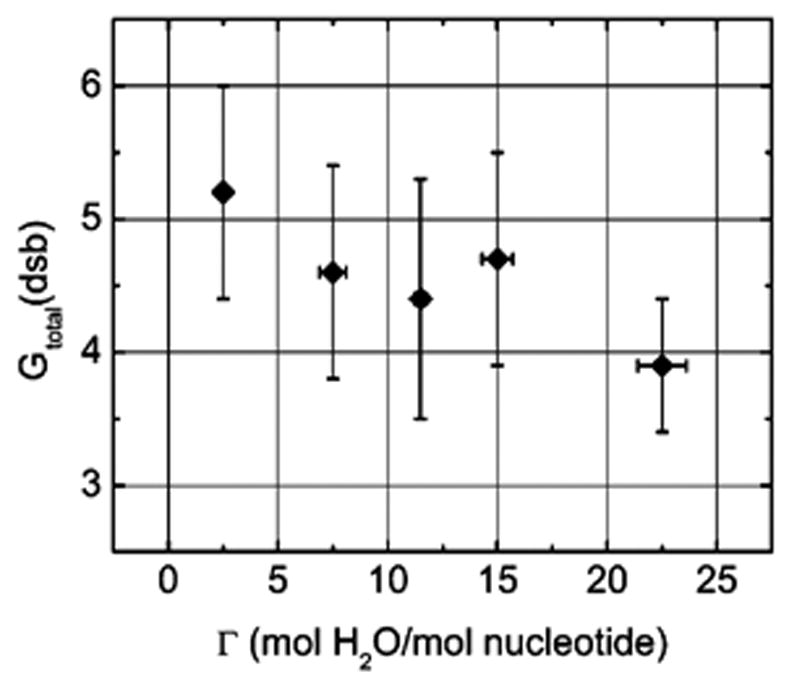
Impact of hydration on the yield of total dsb, G′_total(dsb), for X-irradiated pUC18 plasmid samples measured at 4 K. The data points (filled diamonds) are for prompt plus heat-labile strand breaks.

The free-radical dose–response curves for plasmid pUC18 at various levels of hydration have been published elsewhere.¹⁷ The total free radical yields, G′(ªfr), at each level of hydration were calculated from the slope of the dose–response curves, at doses <6 kGy. The value of G′(ªfr), based on a target mass of DNA plus solvation shell, increased from 0.278 ± 0.007 to 0.625 ± 0.007 μmol/J as Γ is increased from 2.5 to 22.5. The yield of deoxyribose radicals trapped at 4 K, G′_sugar(fr), is the subject of our earlier work.²⁵ For pUC18 hydrated in the range 2.5 < Γ < 22.5, it was found that 89% of the radicals were trapped on the bases and 11% on the sugar–phosphate. It should be noted that to obtain a measure of G′_sugar(fr) the free radical dose response curve was extended to doses far beyond the optimal dose range for measuring strand break yields; therefore, strand break measurements were not made on the high dose samples. Of key interest here is the shortfall, ΔG′, which is defined as the difference between the yield of total ssb, G′_total(ssb), and the yield of deoxyribose trapped radicals, G′_sugar(fr), given in column 5 of Table 1. At Γ = 2.5, the shortfall of 0.06 μmol/J is notably large, yet as Γ increases it shrinks to zero and below. Surprisingly, the dependency of ssb yields on Γ is opposite to that of trapped radical yields.

Discussion

For ionizing radiation, the only precursors to SSB formation are generally assumed to be C centered radicals located on the deoxyribose groups and derived from the loss of H atoms (electron loss followed by deprotonation).³ Until very recently, it has been difficult to determine yields of radical formation and of ssb formation under similar conditions to test this assumption rigorously. The question is whether or not the yield of deoxyribose radicals, trapped at 4 K, is of sufficient magnitude to explain the yield of ssb. We begin by comparing the dependency of G′_total(ssb) and G′_sugar(fr) on Γ, which are plotted in Figure 3. There are three key observations. First, the ssb yield decreases as the hydration shell is filled in. Second, ssb yield decreases in spite of G′_sugar(fr) increasing by more than 2×. And third, the shortfall at Γ = 2.5 is large, i.e., 70% of the ssb cannot be accounted for by trapped deoxyribose radicals yet at Γ = 22.5 the shortfall changes to a small surplus, i.e., every ssb can be attributed to a trapped sugar radical with a little to spare. A relatively simple explanation of the first observation helps to explain the second and the third observations.

Figure 3.

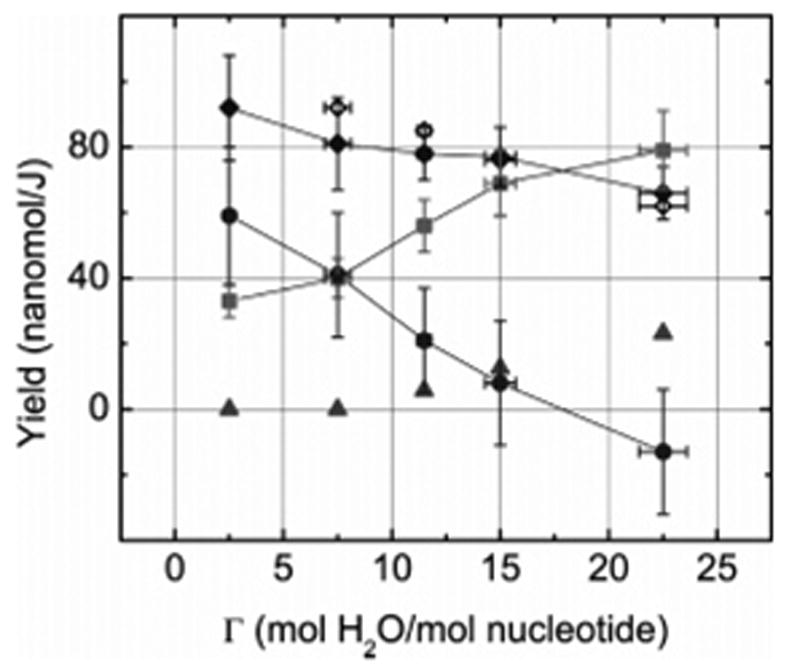
The measured yields in Table 1 are plotted to illustrate the dependence of G′_total(ssb) (solid diamonds) and G′_sugar(fr) (solid squares) on the level of DNA hydration, Γ. Calculated from these yields is the shortfall, ΔG′ = G′_total(ssb) – G′_sugar(fr), designated by solid circles. The open diamonds were calculated based on the predicted dependency of G′_total(ssb) on Γ (see text). The solid triangles indicate the estimated maximum values of G(HO^•). The curves linking adjacent symbols with straight-line segments are meant only to assist in following the data points.

A requisite for ssb formation is oxidation, i.e., loss of one electron or more, of the deoxyribose–phosphate backbone. As reviewed above, holes formed by ionization of the inner solvation shell (Γ < 10) transfer to DNA and produce trapped radicals with approximately the same yields and distribution as obtained by ionizing the DNA directly, while holes formed in the outer shell (Γ > 10) do not transfer, forming HO^• instead.^12,13,16,17 The result is that G′_total(ssb) remains constant in the region Γ < 10 but decreases as Γ exceeds 10, with the decrease being in direct proportion to the fraction of energy absorbed by water in the outer layer. The negative slope is due to water in the outer layer being included in the target mass for yield calculations, but energy absorbed in it not contributing to direct-type ssb formation. By applying these assumptions to the value of G′_total(ssb) at Γ = 2.5, the expected change in G′_totalssb) at higher levels of hydration can be estimated. These points are shown as open diamonds in Figure 3. The predictions of this simple model are consistent with our observations.

Of course outer-shell holes give rise to trapped HO^• at 4 K, which mobilize upon warming to 110–130 K. Once mobilized HO^• reacts to form H₂O₂, or undergo addition reactions with the bases or H-abstraction reactions with the sugar. The yield of HO^•, G(HO^•), in the outer shell of salmon testes DNA at 77 K has been measured by La Vere et al.,¹³ finding G(HO^•) = 0.07 μmol/J based on a target mass consisting of just outer-shell water. Applying 0.07 μmol/J to our samples, the yields of HO^• were estimated. These are shown as solid triangles in Figure 3. If all of the HO^• radicals formed in the outer shell give rise to ssb, then the fraction of G′_total(ssb) assignable to direct-type damage would be the measured values (solid diamonds) less the predicted G(HO^•) (solid triangles). But the effect of HO^• is most likely less than this, because HO^• also reacts with bases to form adducts¹⁴ and dimerizes to form H₂O₂.12

Mechanisms of Strand Break Formation

Four possible mechanisms that might account for the shortfall, ΔG′ (solid circles in Figure 3), have been considered previously:²² (1) dissociative electron attachment (DEA), (2) homolytic bond cleavage by excited states, (3) hydrogen abstraction by hydroxyl radicals formed in the outer solvation shell (Γ > 9–10), and (4) two one-electron oxidations at a single deoxyribose. We argue below that the effect of hydration on the shortfall excludes (3), but while it is inconsistent with (1) it is consistent with (4).

Dissociative Electron Attachment (DEA)

Sanche and collaborators have shown that low-energy electrons (LEE), <20 eV, produce single strand breaks in plasmid DNA by dissociative electron attachment (DEA).^29–32 DEA is a process by which the electrons ejected by ionizing radiation, having reached the low-energy range of 0–30 eV, may fragment DNA components through resonant interactions. The yield of strand breaks by this mechanism and its dependency on hydration level are not yet known.

If the DEA mechanism is used to explain the observed shortfall, it would have to have a maximum impact in dry DNA, Γ = 2.5, and a vanishingly small impact in fully hydrated DNA, i.e., Γ = 22.5. However, in going from dry to fully hydrated DNA, the number of LEE per nucleotide should double due to the added water mass. One would expect, therefore, that the shortfall would double but instead it shrinks to zero. Therefore, either DEA is not a major contributor to the shortfall or even if it does contribute in dry DNA, that contribution is quenched by hydration of DNA.

Hydroxyl Radical Attack

The existence of a shortfall at Γ of 2.5 and 7.5, hydration levels for which HO^• is not formed, proves that HO^• attack is not the source of the shortfall.

Doubly Oxidized Sites

This mechanism, proposed previously,²² is shown in further detail in Scheme 1. The first one-electron oxidation produces a radical cation on the sugar–phosphate backbone, labeled SP^•+. The second oxidation, reaction 3, involves electron transfer from a neutral carbon-centered deoxyribose radical to a base radical cation, where guanine is the most probable base radical cation. Another fate of SP^•+, not shown in Scheme 1, is transfer of the hole into the base stack.¹⁷

Scheme 1.

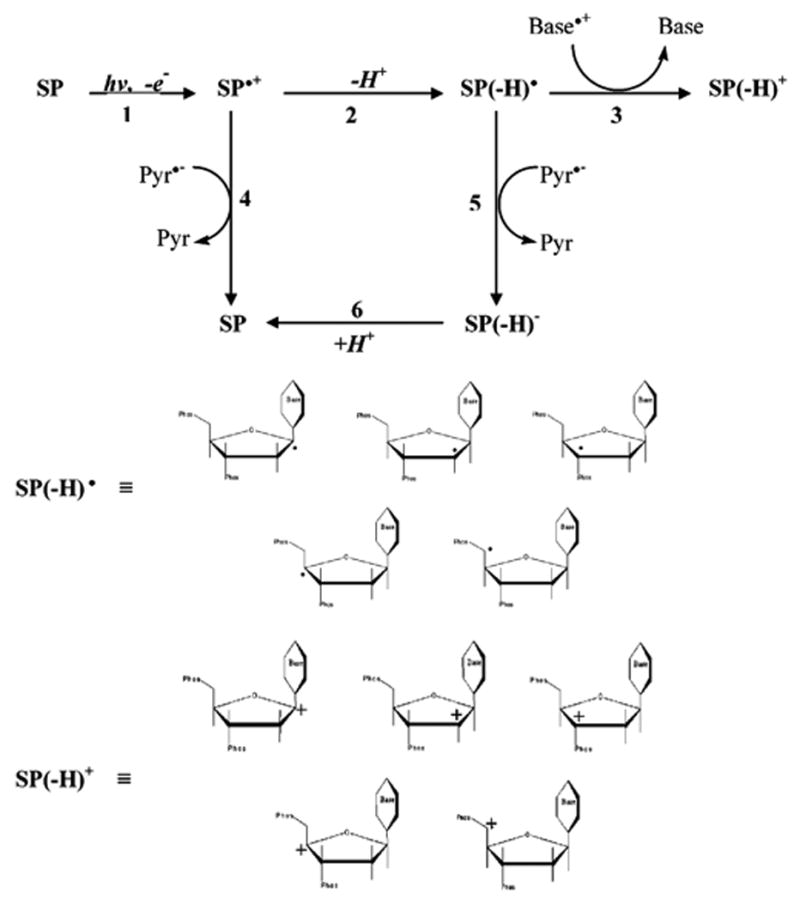
Competing with reaction 3 are the recombination reactions 4 and 5, whereby electron return (via one-electron reduced pyrimidines, Pyr^•−) occurs either before or after the deproto-nation of SP^•+ (reaction 2). Reaction 4 results in a return to the undamaged sugar–phosphate (SP) as does reaction 5 when followed by reaction 6. (For the sake of clarity, other reactions such as between Pyr^•− and SP(−H)⁺, regenerating SP(−H) ^•, or forward reactions such as deprotonation of SP(−H)⁺ are not included in Scheme 1.) The neutral deoxyribose radical, SP(−H) ^•, may be any of the five-carbon-centered radicals shown in Scheme 1 and the forward damage products, SP(−H)⁺, are their corresponding deoxyribose carbocations. As discussed below, the deoxyribose carbocation (or a forward product thereof) concentration is expected to increase linearly with dose. When the DNA films are dissolved in water, these deoxyribose carbocations, or derivative thereof, react with water to give strand breaks. We hypothesize that these deoxyribose carbocations are diamagnetic precursors, i.e., they contain no unpaired electrons (thereby EPR silent), which produce a large portion of the strand break yields not accounted for by trapped deoxyribose radicals under conditions of low DNA hydration.

To understand how the mechanism shown in Scheme 1 could explain the shortfall, it is necessary to distinguish between two different scenarios. In the first, the SP^•+ radical is generated beyond the radius of an ionization cluster (described in radiation chemical jargon as a spur, blob, or short track);³³ in this case, a neutral deoxyribose radical, SP(−H)^•, will be trapped and be observable by EPR at 4 K. When the samples are warmed to room temperature, a large fraction (~90%) of the radicals trapped at 4 K are annealed out^26,34 due to combination reactions such as reactions 3, 4, and 5 but primarily via reactions within the base stack, e.g., Pyr^•− + Base^•+. Warming the sample mobilizes Base^•+ (primarily as Gua^•+), allowing it to hop between guanines.^26,35 If Gua^•+ comes close enough to a deoxyribose radical, reaction 3 may occur. In this circumstance, however, the deoxyribose radicals are detectable at 4 K, a temperature where Gua^•+ is for the most part immobilized by reversible deprotonation at N1. These deoxyribose radicals, whether or not oxidized upon warming, are included in G′_sugar(fr) as strand break precursors and are excluded, therefore, as precursors that could account for the shortfall.

In the second scenario, the SP^•+ radical is formed within a cluster. Reactions 3, 4, and 5 are now favored by high local concentrations. Even at 4 K, where mobility of Gua^•+ is limited (but not zero), high local concentrations would make the rate of reaction 3 competitive. In this case, the concentration of SP-(−H)⁺ increases linearly with dose; a single track generates SP^•+ and Base^•+ in close proximity to one another. Distinguishing reaction 3 from both reactions 4 and 5 is the fact that it is a forward reaction while reactions 4 and 5 return DNA to its undamaged state. An important similarity between reactions 3, 4, and 5 is that these combination reactions compete with radical trapping reactions (formation of SP(−H)^•, Base^•+, and Pyr^•−), thus an increase in trapped radical yields should be reflected in a commensurate decrease in the yield of products due to combination reactions, most importantly SP(−H)⁺. Therefore, the increase in trapped radical yield should be accompanied by a decrease in SP(−H)⁺ yield, as observed (solid circles, Figure 3).

The doubly oxidized site mechanism appears to be quantitatively feasible given the difference between the yield of radicals initially formed and the yield of radicals actually trapped. For example, if we use 1.18 μmol/J as the initial radical yield³⁶ and 0. 302 μmol/J is the yield of trapped radicals in plasmid DNA at Γ = 2.5, the yield of radicals lost to combination reactions is 0.878 μmol/J (radicals not trapped at 4 K = 1.18 – 0.302 μmol/J). Half of these,~0.44 μmol/J, are presumed to be holes. If 1/7 of the transient holes react via reaction 3, the deoxyribose–carbocation yield would be 0.44/7 = 0.06 μmol/J (the amount of the shortfall).

The fact that holes are mobile, even at 4 K, increases the probability of reaction 3. The intraduplex range of a hole is about 10 base pairs.^37,38 At low hydration levels, the interduplex range for hole tunneling is~30 bp and upon increasing the hydration the range decreases, dropping to~10 bp at Γ = 22.³⁹ This drop in tunneling range is consistent with our observed increase in radical yield and decrease in ssb yield that occur over the same hydration levels.

While the kinetics in the reaction scheme remain uncertain, it is possible to address the thermodynamic feasibility of reaction 3. Ab initio molecular orbital calculations of the ionization potentials (IP) and electron affinities (EA) of the deoxyribose radicals indicate that they all have nearly equal electron affinities but their ionization potentials differ substantially.^40–43 Although direct measurement of the redox potentials of the deoxyribose centered radicals is unknown, Wayner et al. have reported the oxidation potential on 19 different carbon-centered radicals.⁴⁴ Using acetonitrile as a solvent, they find a reduction potential of +0.31 V (vs SCE, equivalent to +0.31 + 0.24 = +0.55 V vs NHE) for the couple (O–C⁺–O/O–C^•–O) in 1,3-dioxane. 1,3-Dioxolan-2-yl has a primary structure resembling that of the C1′ deoxyribose radical. On the basis of their reported trends for this series of compounds, and ignoring conformational differences, the C1′ deoxyribose radical and the other four deoxyribose radicals should have similar or even lower oxidation potentials. Assuming that the reduction potentials in acetonitrile do not deviate greatly from those in water, the difference in reduction potential at pH 7 between Gua^•+ (1.29 V) and SP(−H)^• ~0.55 V) is 0.74 V. This difference corresponds to an estimated driving force of ca. −71 kJ/mol, which is large enough to consider the second one-electron oxidation of the deoxyribose radical by Gua^•+ as irreversible. For a radical cation formed on one of the other three bases, the driving force would be larger.⁴⁵ Therefore, we suggest that double one-electron oxidation of the deoxyribose moiety may be a prominent pathway for strand breaks produced by direct ionization.

There are at least two precedents in the literature where double oxidation of the deoxyribose is proposed. Reaction 3 was recently proposed as a key step in the formation of 5-methylene-2-furanone produced by irradiation of DNA when oxygen is absent.⁴⁶ A similar mechanism has been proposed in recent studies^47–49 to explain photochemically generated ssb in 5-bro-mouracil-containing DNA duplexes; in this case, however, the guanine radical cation is produced as a consequence of photo-excitation, which promotes electron transfer from guanine to a neighboring 5-bromouracil. The newly formed 5-bromouracil radical anion eliminates bromide, producing the 5,6-dihydrou-racil-5-yl radical; the latter abstracts hydrogen from a deoxyribose on its 5′ side. The nearby guanine radical cation oxidizes the neutral deoxyribose radical, producing a carbocation (as in reaction 2).

Conclusion

The yield of ssb is increased by hole transfer from the DNA hydration layer to the DNA backbone in a manner parallel to that previously observed for the yield of trapped deoxyribose radicals: i.e., holes generated in the inner solvation shell generate ssb with a probability comparable to holes generated directly in DNA itself and holes generated in the outer solvation shell do not give rise to direct-type ssb.

A comparison of strand break yields with trapped radical yields for the same plasmid samples has made it possible to quantitatively test the premise that DNA-trapped free radicals are the primary precursors to strand breaks. At a hydration level of Γ = 2.5, the yield of radicals trapped on the DNA deoxyribose, G′_sugar(fr), was found to be less than half of the prompt plus heat-labile ssb yield, G′_total(ssb). We conclude, therefore, that in relatively dry DNA a significant fraction of the strand break yield, 0.06 μmol/J, is derived from precursors other than DNA-trapped radicals.

A novel strand break mechanism, whereby strand breaks are produced by two one-electron oxidations at a single deoxyribose, is proposed to be a significant source of strand breaks in DNA. In this mechanism, direct ionization of the sugar–phosphate backbone, followed by deprotonation of the deoxyribose, yields a neutral carbon radical that reacts with a neighboring base radical cation. This electron-transfer reaction, which results in a deoxyribose carbocation plus repaired base, is a reaction that occurs within an ionization cluster; the free radical intermediates are not trapped. The carbocation, upon reaction with water, is expected to result in a strand break.