Evolution of biological complexity

Abstract

To make a case for or against a trend in the evolution of complexity in biological evolution, complexity needs to be both rigorously defined and measurable. A recent information-theoretic (but intuitively evident) definition identifies genomic complexity with the amount of information a sequence stores about its environment. We investigate the evolution of genomic complexity in populations of digital organisms and monitor in detail the evolutionary transitions that increase complexity. We show that, because natural selection forces genomes to behave as a natural “Maxwell Demon,” within a fixed environment, genomic complexity is forced to increase.

Darwinian evolution is a simple yet powerful process that requires only a population of reproducing organisms in which each offspring has the potential for a heritable variation from its parent. This principle governs evolution in the natural world, and has gracefully produced organisms of vast complexity. Still, whether or not complexity increases through evolution has become a contentious issue. Gould (1), for example, argues that any recognizable trend can be explained by the “drunkard's walk” model, where “progress” is due simply to a fixed boundary condition. McShea (2) investigates trends in the evolution of certain types of structural and functional complexity, and finds some evidence of a trend but nothing conclusive. In fact, he concludes that “something may be increasing. But is it complexity?” Bennett (3), on the other hand, resolves the issue by fiat, defining complexity as “that which increases when self-organizing systems organize themselves.” Of course, to address this issue, complexity needs to be both defined and measurable.

In this paper, we skirt the issue of structural and functional complexity by examining genomic complexity. It is tempting to believe that genomic complexity is mirrored in functional complexity and vice versa. Such an hypothesis, however, hinges upon both the aforementioned ambiguous definition of complexity and the obvious difficulty of matching genes with function. Several developments allow us to bring a new perspective to this old problem. On the one hand, genomic complexity can be defined in a consistent information-theoretic manner [the “physical” complexity (4)], which appears to encompass intuitive notions of complexity used in the analysis of genomic structure and organization (5). On the other hand, it has been shown that evolution can be observed in an artificial medium (6, 7), providing a unique glimpse at universal aspects of the evolutionary process in a computational world. In this system, the symbolic sequences subject to evolution are computer programs that have the ability to self-replicate via the execution of their own code. In this respect, they are computational analogs of catalytically active RNA sequences that serve as the templates of their own reproduction. In populations of such sequences that adapt to their world (inside of a computer's memory), noisy self-replication coupled with finite resources and an information-rich environment leads to a growth in sequence length as the digital organisms incorporate more and more information about their environment into their genome. Evolution in an information-poor landscape, on the contrary, leads to selection for replication only, and a shrinking genome size as in the experiments of Spiegelman and colleagues (8). These populations allow us to observe the growth of physical complexity explicitly, and also to distinguish distinct evolutionary pressures acting on the genome and analyze them in a mathematical framework.

If an organism's complexity is a reflection of the physical complexity of its genome (as we assume here), the latter is of prime importance in evolutionary theory. Physical complexity, roughly speaking, reflects the number of base pairs in a sequence that are functional. As is well known, equating genomic complexity with genome length in base pairs gives rise to a conundrum (known as the C-value paradox) because large variations in genomic complexity (in particular in eukaryotes) seem to bear little relation to the differences in organismic complexity (9). The C-value paradox is partly resolved by recognizing that not all of DNA is functional: that there is a neutral fraction that can vary from species to species. If we were able to monitor the non-neutral fraction, it is likely that a significant increase in this fraction could be observed throughout at least the early course of evolution. For the later period, in particular the later Phanerozoic Era, it is unlikely that the growth in complexity of genomes is due solely to innovations in which genes with novel functions arise de novo. Indeed, most of the enzyme activity classes in mammals, for example, are already present in prokaryotes (10). Rather, gene duplication events leading to repetitive DNA and subsequent diversification (11) as well as the evolution of gene regulation patterns appears to be a more likely scenario for this stage. Still, we believe that the Maxwell Demon mechanism described below is at work during all phases of evolution and provides the driving force toward ever increasing complexity in the natural world.

Information Theory and Complexity.

Using information theory to understand evolution and the information content of the sequences it gives rise to is not a new undertaking. Unfortunately, many of the earlier attempts (e.g., refs. 12–14) confuse the picture more than clarifying it, often clouded by misguided notions of the concept of information (15). An (at times amusing) attempt to make sense of these misunderstandings is ref. 16.

Perhaps a key aspect of information theory is that information cannot exist in a vacuum; that is, information is physical (17). This statement implies that information must have an instantiation (be it ink on paper, bits in a computer's memory, or even the neurons in a brain). Furthermore, it also implies that information must be about something. Lines on a piece of paper, for example, are not inherently information until it is discovered that they correspond to something, such as (in the case of a map) to the relative location of local streets and buildings. Consequently, any arrangement of symbols might be viewed as potential information (also known as entropy in information theory), but acquires the status of information only when its correspondence, or correlation, to other physical objects is revealed.

In biological systems the instantiation of information is DNA, but what is this information about? To some extent, it is the blueprint of an organism and thus information about its own structure. More specifically, it is a blueprint of how to build an organism that can best survive in its native environment, and pass on that information to its progeny. This view corresponds essentially to Dawkins' view of selfish genes that “use” their environment (including the organism itself), for their own replication (18). Thus, those parts of the genome that do correspond to something (the non-neutral fraction, that is) correspond in fact to the environment the genome lives in. Deutsch (19) referred to this view by saying that “genes embody knowledge about their niches.” This environment is extremely complex itself, and consists of the ribosomes the messages are translated in, other chemicals and the abundance of nutrients inside and outside the cell, and the environment of the organism proper (e.g., the oxygen abundance in the air as well as ambient temperatures), among many others. An organism's DNA thus is not only a “book” about the organism, but is also a book about the environment it lives in, including the species it co-evolves with. It is well known that not all of the symbols in an organism's DNA correspond to something. These sections, sometimes referred to as “junk-DNA,” usually consist of portions of the code that are unexpressed or untranslated (i.e., excised from the mRNA). More modern views concede that unexpressed and untranslated regions in the genome can have a multitude of uses, such as for example satellite DNA near the centromere, or the polyC polymerase intron excised from Tetrahymena rRNA. In the absence of a complete map of the function of each and every base pair in the genome, how can we then decide which stretch of code is “about something” (and thus contributes to the complexity of the code) or else is entropy (i.e., random code without function)?

A true test for whether a sequence is information uses the success (fitness) of its bearer in its environment, which implies that a sequence's information content is conditional on the environment it is to be interpreted within (4). Accordingly, Mycoplasma mycoides, for example (which causes pneumonia-like respiratory illnesses), has a complexity of somewhat less than one million base pairs in our nasal passages, but close to zero complexity most everywhere else, because it cannot survive in any other environment—meaning its genome does not correspond to anything there. A genetic locus that codes for information essential to an organism's survival will be fixed in an adapting population because all mutations of the locus result in the organism's inability to promulgate the tainted genome, whereas inconsequential (neutral) sites will be randomized by the constant mutational load. Examining an ensemble of sequences large enough to obtain statistically significant substitution probabilities would thus be sufficient to separate information from entropy in genetic codes. The neutral sections that contribute only to the entropy turn out to be exceedingly important for evolution to proceed, as has been pointed out, for example, by Maynard Smith (20).

In Shannon's information theory (22), the quantity entropy (H) represents the expected number of bits required to specify the state of a physical object given a distribution of probabilities; that is, it measures how much information can potentially be stored in it.

In a genome, for a site i that can take on four nucleotides with probabilities

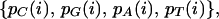1

the entropy of this site is

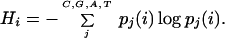2

The maximal entropy per-site (if we agree to take our logarithms to base 4: i.e., the size of the alphabet) is 1, which occurs if all of the probabilities are all equal to 1/4. If the entropy is measured in bits (take logarithms to base 2), the maximal entropy per site is two bits, which naturally is also the maximal amount of information that can be stored in a site, as entropy is just potential information. A site stores maximal information if, in DNA, it is perfectly conserved across an equilibrated ensemble. Then, we assign the probability p = 1 to one of the bases and zero to all others, rendering H_i = 0 for that site according to Eq. 2. The amount of information per site is thus (see, e.g., ref. 23)

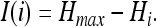3

In the following, we measure the complexity of an organism's sequence by applying Eq. 3 to each site and summing over the sites. Thus, for an organism of ℓ base pairs the complexity is

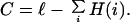4

It should be clear that this value can only be an approximation to the true physical complexity of an organism's genome. In reality, sites are not independent and the probability to find a certain base at one position may be conditional on the probability to find another base at another position. Such correlations between sites are called epistatic, and they can render the entropy per molecule significantly different from the sum of the per-site entropies (4). This entropy per molecule, which takes into account all epistatic correlations between sites, is defined as

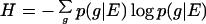5

and involves an average over the logarithm of the conditional probabilities p(g|E) to find genotype g given the current environment E. In every finite population, estimating p(g|E) using the actual frequencies of the genotypes in the population (if those could be obtained) results in corrections to Eq. 5 larger than the quantity itself (24), rendering the estimate useless. Another avenue for estimating the entropy per molecule is the creation of mutational clones at several positions at the same time (7, 25) to measure epistatic effects. The latter approach is feasible within experiments with simple ecosystems of digital organisms that we introduce in the following section, which reveal significant epistatic effects. The technical details of the complexity calculation including these effects are relegated to the Appendix.

Digital Evolution.

Experiments in evolution have traditionally been formidable because of evolution's gradual pace in the natural world. One successful method uses microscopic organisms with generational times on the order of hours, but even this approach has difficulties; it is still impossible to perform measurements with high precision, and the time-scale to see significant adaptation remains weeks, at best. Populations of Escherichia coli introduced into new environments begin adaptation immediately, with significant results apparent in a few weeks (26, 27). Observable evolution in most organisms occurs on time scales of at least years.

To complement such an approach, we have developed a tool to study evolution in a computational medium—the Avida platform (6). The Avida system hosts populations of self-replicating computer programs in a complex and noisy environment, within a computer's memory. The evolution of these “digital organisms” is limited in speed only by the computers used, with generations (for populations of the order 10³-10⁴ programs) in a typical trial taking only a few seconds. Despite the apparent simplicity of the single-niche environment and the limited interactions between digital organisms, very rich dynamics can be observed in experiments with 3,600 organisms on a 60 × 60 grid with toroidal boundary conditions (see Methods). As this population is quite small, we can assume that an equilibrium population will be dominated by organisms of a single species‖, whose members all have similar functionality and equivalent fitness (except for organisms that lost the capability to self-replicate due to mutation). In this world, a new species can obtain a significant abundance only if it has a competitive advantage (increased Malthusian parameter) thanks to a beneficial mutation. While the system returns to equilibrium after the innovation, this new species will gradually exert dominance over the population, bringing the previously dominant species to extinction. This dynamics of innovation and extinction can be monitored in detail and appears to mirror the dynamics of E. coli in single-niche long-term evolution experiments (28).

The complexity of an adapted digital organism according to Eq. 4 can be obtained by measuring substitution frequencies at each instruction across the population. Such a measurement is easiest if genome size is constrained to be constant, as is done in the experiments reported below, although this constraint can be relaxed by implementing a suitable alignment procedure. To correctly assess the information content of the ensemble of sequences, we need to obtain the substitution probabilities p_i at each position, which go into the calculation of the per-site entropy of Eq. 2. Care must be taken to wait sufficiently long after an innovation, to give those sites within a new species that are variable a chance to diverge. Indeed, shortly after an innovation, previously 100% variable sites will appear fixed by “hitchhiking” on the successful genotype, a phenomenon discussed further below.

We simplify the problem of obtaining substitution probabilities for each instruction by assuming that all mutations are either lethal, neutral, or positive, and furthermore assume that all non-lethal substitutions persist with equal probability. We then categorize every possible mutation directly by creating all single-mutation genomes and examining them independently in isolation. In that case, Eq. 2 reduces to

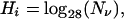6

where N_ν is the number of non-lethal substitutions (we count mutations that significantly reduce the fitness among the lethals). Note that the logarithm is taken with respect to the size of the alphabet.

This per-site entropy is used to illustrate the variability of loci in a genome, just before and after an evolutionary transition, in Fig. 1.

Figure 1.

Typical Avida organisms, extracted at 2,991 (A) and 3,194 (B) generations, respectively, into an evolutionary experiment. Each site is color-coded according to the entropy of that site (see color bar). Red sites are highly variable whereas blue sites are conserved. The organisms have been extracted just before and after a major evolutionary transition.

Progression of Complexity.

Tracking the entropy of each site in the genome allows us to document the growth of complexity in an evolutionary event. For example, it is possible to measure the difference in complexity between the pair of genomes in Fig. 1, separated by only 203 generations and a powerful evolutionary transition. Comparing their entropy maps, we can immediately identify the sections of the genome that code for the new “gene” that emerged in the transition—the entropy at those sites has been drastically reduced, while the complexity increase across the transition (taking into account epistatic effects) turns out to be ΔC ≈ 6, as calculated in the Appendix.

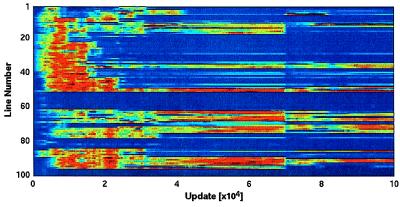
We can extend this analysis by continually surveying the entropies of each site during the course of an experiment. Fig. 2 does this for the experiment just discussed, but this time the substitution probabilities are obtained by sampling the actual population at each site. A number of features are apparent in this figure. First, the trend toward a “cooling” of the genome (i.e., to more conserved sites) is obvious. Second, evolutionary transitions can be identified by vertical darkened “bands,” which arise because the genome instigating the transition replicates faster than its competitors thus driving them into extinction. As a consequence, even random sites that are hitchhiking on the successful gene are momentarily fixed.

Figure 2.

Progression of per-site entropy for all 100 sites throughout an Avida experiment, with time measured in “updates” (see Methods). A generation corresponds to between 5 and 10 updates, depending on the gestation time of the organism.

Hitchhiking is documented clearly by plotting the sum of per-site entropies for the population (as an approximation for the entropy of the genome).

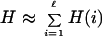7

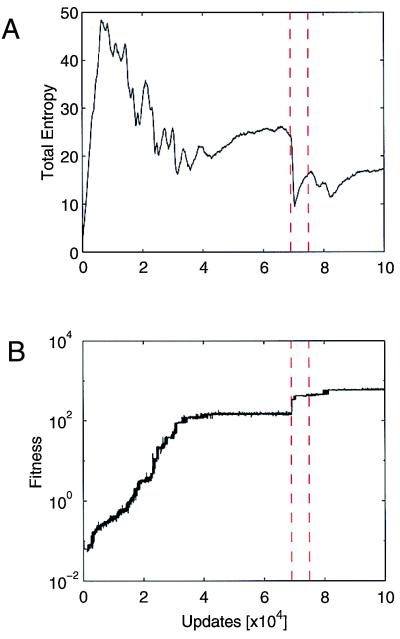
across the transition in Fig. 3A. By comparing this to the fitness shown in Fig. 3B, we can identify a sharp drop in entropy followed by a slower recovery for each adaptive event that the population undergoes. Often, the population does not reach equilibrium (the state of maximum entropy given the current conditions) before the next transition occurs.

Figure 3.

(A) Total entropy per program as a function of evolutionary time. (B) Fitness of the most abundant genotype as a function of time. Evolutionary transitions are identified with short periods in which the entropy drops sharply, and fitness jumps. Vertical dashed lines indicate the moments at which the genomes in Fig. 1 A and B were dominant.

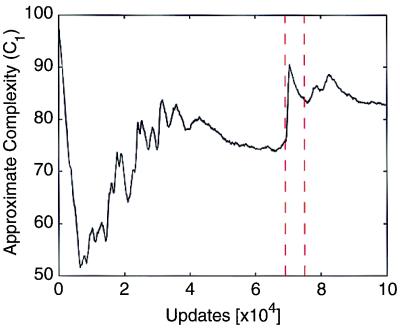
While this entropy is not a perfect approximation of the exact entropy per program in Eq. 5, it reflects the disorder in the population as a function of time. This complexity estimate (4) is shown as a function of evolutionary time for this experiment in Fig. 4. It increases monotonically except for the periods just after transitions, when the complexity estimate (after overshooting the equilibrium value) settles down according to thermodynamics' second law (see below). This overshooting of stable complexity is a result of the overestimate of complexity during the transition due to the hitchhiking effect mentioned earlier. Its effect is also seen at the beginning of evolution, where the population is seeded with a single genome with no variation present.

Figure 4.

Complexity as a function of time, calculated according to Eq. 4. Vertical dashed lines are as in Fig. 3.

Such a typical evolutionary history documents that the physical complexity, measuring the amount of information coded in the sequence about its environment, indeed steadily increases. The circumstances under which this is assured to happen are discussed presently.

Maxwell's Demon and the Law of Increasing Complexity.

Let us consider an evolutionary transition like the one connecting the genomes in Fig. 1 in more detail. In this transition, the entropy (cf. Fig. 3A) does not fully recover after its initial drop. The difference between the equilibrium level before the transition and after is proportional to the information acquired in the transition, roughly the number of sites that were frozen. This difference would be equal to the acquired information if the measured entropy in Eq. 7 were equal to the exact one given by Eq. 5. For this particular situation, in which the sequence length is fixed along with the environment, is it possible that the complexity decreases? The answer is that in a sufficiently large population this cannot happen [in smaller populations, there is a finite probability of all organisms being mutated simultaneously, referred to as Muller's ratchet (29)], as a consequence of a simple application of the second law of thermodynamics. If we assume that a population is at equilibrium in a fixed environment, each locus has achieved its highest entropy given all of the other sites. Then, with genome length fixed, the entropy can only stay constant or decrease, implying that the complexity (being sequence length minus entropy) can only increase. How is a drop in entropy commensurate with the second law? This answer is simple also: The second law holds only for equilibrium systems, while such a transition is decidedly not of the equilibrium type. In fact, each such transition is best described as a measurement, and evolution as a series of random measurements on the environment. Darwinian selection is a filter, allowing only informative measurements (those increasing the ability for an organism to survive) to be preserved. In other words, information cannot be lost in such an event because a mutation corrupting the information is purged due to the corrupted genome's inferior fitness (this holds strictly for asexual populations only). Conversely, a mutation that corrupts the information cannot increase the fitness, because if it did then the population was not at equilibrium in the first place. As a consequence, only mutations that reduce the entropy are kept while mutations that increase it are purged. Because the mutations can be viewed as measurements, this is the classical behavior of the Maxwell Demon.

What about changes in sequence length? In an unchanging environment, an increase or decrease in sequence length is always associated with an increase or decrease in the entropy, and such changes therefore always cancel from the physical complexity, as it is defined as the difference. Note, however, that while size-increasing events do not increase the organism's physical complexity, they are critical to continued evolution as they provide new space (“blank tape”) to record environmental information within the genome, and thus to allow complexity to march ever forward.

Methods.

For all work presented here, we use a single-niche environment in which resources are isotropically distributed and unlimited except for central processing unit (CPU) time, the primary resource for this life-form. This limitation is imposed by constraining the average slice of CPU time executed by any genome per update to be a constant (here 30 instructions). Thus, per update, a population of n genomes executes 30 × n instructions. The unlimited resources are numbers that the programs can retrieve from the environment with the right genetic code. Computations on these numbers allow the organisms to execute significantly larger slices of CPU time, at the expense of inferior ones (see refs. 6 and 8).

A normal Avida organism is a single genome (program) composed of a sequence of instructions that are processed as commands to the CPU of a virtual computer. In standard Avida experiments, an organism's genome has one of 28 possible instructions at each line. The set of instructions (alphabet) from which an organism draws its code is selected to avoid biasing evolution toward any particular type of program or environment. Still, evolutionary experiments will always show a distinct dependence on the ancestor used to initiate experiments, and on the elements of chance and history. To minimize these effects, trials are repeated to gain statistical significance, another crucial advantage of experiments in artificial evolution. In the present experiments, we have chosen to keep sequence length fixed at 100 instructions, by creating a self-replicating ancestor containing mostly non-sense code, from which all populations are spawned. Mutations appear during the copy process, which is flawed with a probability of error per instruction copied of 0.01. For more details on Avida, see ref. 30.

Conclusions.

Trends in the evolution of complexity are difficult to argue for or against if there is no agreement on how to measure complexity. We have proposed here to identify the complexity of genomes by the amount of information they encode about the world in which they have evolved, a quantity known as “physical complexity” that, while it can be measured only approximately, allows quantitative statements to be made about the evolution of genomic complexity. In particular, we show that, in fixed environments, for organisms whose fitness depends only on their own sequence information, physical complexity must always increase. That a genome's physical complexity must be reflected in the structural complexity of the organism that harbors it seems to us inevitable, as the purpose of a physically complex genome is complex information processing, which can only be achieved by the computer which it (the genome) creates.

That the mechanism of the Maxwell Demon lies at the heart of the complexity of living forms today is rendered even more plausible by the many circumstances that may cause it to fail. First, simple environments spawn only simple genomes. Second, changing environments can cause a drop in physical complexity, with a commensurate loss in (computational) function of the organism, as now meaningless genes are shed. Third, sexual reproduction can lead to an accumulation of deleterious mutations (strictly forbidden in asexual populations) that can also render the Demon powerless. All such exceptions are observed in nature.

Notwithstanding these vagaries, we are able to observe the Demon's operation directly in the digital world, giving rise to complex genomes that, although poor compared with their biochemical brethren, still stupefy us with their intricacy and an uncanny amalgam of elegant solutions and clumsy remnants of historical contingency. It is in no small measure an awe before these complex programs, direct descendants of the simplest self-replicators we ourselves wrote, that leads us to assert that even in this view of life, spawned by and in our digital age, there is grandeur.

Epistasis and Complexity

Estimating the complexity according to Eq. 4 is somewhat limited in scope, even though it may be the only practical means for actual biological genomes for which substitution frequencies are known [such as, for example, ensembles of tRNA sequences (4)]. For digital organisms, this estimate can be sharpened by testing all possible single and double mutants of the wild-type for fitness, and sampling the n mutants to obtain the fraction of neutral mutants at mutational distance n, w(n). In this manner, an ensemble of mutants is created for a single wild-type resulting in a much more accurate estimate of its information content. As this procedure involves an evaluation of fitness, it is easiest for organisms whose survival rate is closely related to their organic fitness: i.e., for organisms who are not “epistatically linked” to other organisms in the population. Note that this is precisely the limit in which Fisher's Theorem guarantees an increase in complexity (21).

For an organism of length ℓ with instructions taken from an alphabet of size D, let w(1) be the number of neutral one-point mutants N_ν(1) divided by the total number of possible one-point mutations

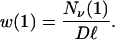8

Note that N_ν(1) includes the wild-type ℓ times, for each site is replaced (in the generation of mutants) by each of the D instructions. Consequently, the worst w(1) is equal to D − 1. In the literature, w(n) usually refers to the average fitness (normalized to the wild-type) of n-mutants (organisms with n mutations). While this can be obtained here in principle, for the purposes of our information-theoretic estimate, we assume that all non-neutral mutants are nonviable**. We have found that for digital organisms the average n-mutant fitness closely mirrors the function w(n) investigated here.

Other values of w(n) are obtained accordingly. We define

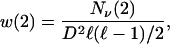9

where N_ν(2) is the number of neutral double mutants, including the wild-type and all neutral single mutations included in N_ν(1), and so forth.

For the genome before the transition (pictured on the left in Fig. 1) we can collect N_ν(n) as well as N₊(n) (the number of mutants that result in increased fitness) to construct w(n). In Table 1, we list the fraction of neutral and positive n-mutants of the wild type, as well as the number of neutral or positive found and the total number of mutants tried.

Table 1.

Fraction of mutations that were neutral (first column), or positive (second column); total number of neutral or positive genomes found (fourth column); and total mutants examined (fifth column) as a function of the number of mutations n, for the dominating genotype before the transition

n	fν(n)	f+(n)	Total	Tried
1	0.1418	0.034	492	2,700
2	0.0203	0.0119	225	10,000
3	0.0028	0.0028	100	32,039
4	4.6 10−4	6.5 10−4	100	181,507
5	5.7 10−5	1.4 10−4	100	1.3 106
6	8.6 10−6	2.9 10−5	100	7.3 106
7	1.3 10−6	5.7 10−6	100	5.1 107
8	1.8 10−7	1.1 10−6	34	1.0 109

Note that we have sampled the mutant distribution up to n = 8 (where we tried 10⁹ genotypes), to gain statistical significance. The function is well fit by a two-parameter ansatz

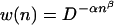10

introduced earlier (8), where 1 − α measures the degree of neutrality in the code (0 < α < 1), and β reflects the degree of epistasis (β > 1 for synergistic deleterious mutations, β < 1 for antagonistic ones). Using this function, the complexity of the wild-type can be estimated as follows.

From the information-theoretic considerations in the main text, the information about the environment stored in a sequence is

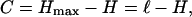11

where H is the entropy of the wild-type given its environment. We have previously approximated it by summing the per-site entropies of the sequence, thus ignoring correlations between the sites. Using w(n), a multisite entropy can be defined as

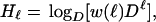12

reflecting the average entropy of a sequence of length ℓ. As D^ℓ is the total number of different sequences of length ℓ, w(ℓ)D^ℓ is the number of neutral sequences: in other words, all of those sequences that carry the same information as the wild type. The “coarse-grained” entropy is just the logarithm of that number. Eq. 12 thus represents the entropy of a population based on one wild type in perfect equilibrium in an infinite population. It should approximate the exact result of Eq. 5 if all neutral mutants have the same fitness and therefore the same abundance in an infinite population.

Naturally, H_ℓ is impossible to obtain for reasonably sized genomes as the number of mutations to test to obtain w(ℓ) is of the order D^ℓ. This is precisely the reason why we chose to approximate the entropy in Eq. 4 in the first place. However, it turns out that in most cases the constants α and β describing w(n) can be estimated from the first few n. The complexity of the wild-type, using the ℓ-mutant entropy (12), can be defined as

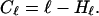13

Using Eq. 10, we find

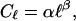14

and, naturally, for the complexity based on single mutations only (completely ignoring epistatic interactions)

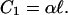15

Thus, obtaining α and β from a fit to w(n) allows an estimate of the complexity of digital genomes including epistatic interactions. As an example, let us investigate the complexity increase across the transition treated earlier. Using both neutral and positive mutants to determine w(n), a fit to the data in Table 1 using the functional form of Eq. 10 yields β = 0.988(8) [α is obtained exactly via w(1)]. This in turn leads to a complexity estimate C_ℓ = 49.4. After the transition, we analyze the new wild type again and find β = 0.986(8), not significantly different from before the transition [while we found β = 0.996(9) during the transition]. The complexity estimate according to this fit is C_ℓ = 55.0, leading to a complexity increase during the transition of ΔC_ℓ = 5.7, or about 6 instructions. Conversely, if epistatic interactions are not taken into account, the same analysis would suggest ΔC₁ = 6.4, somewhat larger. The same analysis can be carried out taking into account neutral mutations only to calculate w(n), leading to ΔC_ℓ = 3.0 and ΔC₁ = 5.4.