An overview of fast convergent ordered-subsets reconstruction methods for emission tomography based on the incremental EM algorithm

Abstract

Statistical reconstruction has become popular in emission computed tomography but suffers slow convergence (to the MAP or ML solution). Methods proposed to address this problem include the fast but non-convergent OSEM and the convergent RAMLA [1] for the ML case, and the convergent BSREM [2], relaxed OS-SPS and modified BSREM [3] for the MAP case. The convergent algorithms required a user-determined relaxation schedule. We proposed fast convergent OS reconstruction algorithms for both ML and MAP cases, called COSEM (Complete-data OSEM), which avoid the use of a relaxation schedule while maintaining convergence. COSEM is a form of incremental EM algorithm. Here, we provide a derivation of our COSEM algorithms and demonstrate COSEM using simulations. At early iterations, COSEM-ML is typically slower than RAMLA, and COSEM-MAP is typically slower than optimized BSREM while remaining much faster than conventional MAP-EM. We discuss how COSEM may be modified to overcome these limitations.

1. Introduction

In emission tomography, the reconstruction of vast quantities of noisy, low-count data in practical times remains a challenge. The convenient FBP (Filtered backprojection) reconstruction algorithm is widely used. However, FBP and its analytical relatives do not always lend themselves to specialized acquisition geometries. In addition, it has been shown that statistical reconstructions have outperformed FBP [4].

Statistical reconstruction is useful in emission computed tomography due to its ability to accurately model noise, imaging physics, and to incorporate prior knowledge about the object. Statistical reconstruction approaches use iterative algorithms that optimize objective functions based on maximum likelihood (ML) or maximum a posteriori (MAP, a.k.a. penalized likelihood) principles. An additional advantage of MAP and ML solutions is that their statistical properties such as covariance, mean and local point spread function can be predicted using theoretical expressions [5]. A drawback of statistical reconstruction algorithms is that they are slow. It is a challenge to devise convergent ML and MAP algorithms that require few iterations to approach the fixed-point solution and to reduce the number of the algorithm-specific parameters that must be hand-tuned. Earlier attempts to address the speed problem included preconditioned conjugate-gradient [7] and coordinate descent methods [8], but each of these had practical drawbacks.

In [9], an ordered subsets expectation maximization (OSEM) algorithm achieved an order of magnitude speedup over conventional (non-OS) EM by using only a subset of the projection data per sub-iteration. The OSEM algorithm is fast, parallelizable and preserves positivity. However, these early OS methods did not converge to the ML fixed-point solution. An algorithm [1], termed row-action maximum likelihood algorithm (RAMLA), used a relaxation schedule, i.e. a relaxation parameter at each iteration of an OSEM-like update, to attain convergence. The relaxation schedule had to satisfy certain properties as a prerequisite for convergence. In practice, this relaxation schedule must be determined by trial and error to ensure good speed. More recently, RAMLA was extended to the MAP case in BSREM (Block Sequential Modified EM) [2], modified BSREM [3], and relaxed OS-SPS (OS Separable Paraboloidal Surrogates) [3]. These MAP approaches also required a user-determined relaxation schedule. A practical solution to the problem of determining a relaxation schedule remains open.

To overcome the need of relaxation schedules in these OS algorithms, we formulated relaxation-free COSEM (Complete-Data OSEM) algorithms [11,12]. COSEM, while derived in terms of an algebraic transformation [13], is a form of incremental EM algorithm [14]. We independently introduced COSEM-ML and COSEM-MAP in terms of algebraic transformations [11,12], but learned shortly after that a COSEM-ML algorithm for emission tomography had been independently derived [15] using incremental-EM approaches [14]. No experimental results were presented in [15]. We later extended COSEM-MAP to a list-mode version [16]. Despite the appeal of COSEM as a relaxation-free convergent algorithm, simulations show that it is not as fast as the aforementioned convergent relaxation-based approaches.

In Sections 2 and 3, we state the problem and derive the COSEM-ML and MAP algorithms. In Section 4, we compare COSEM-MAP speed with that of competitors, and in Section 5, discuss how COSEM can be sped up to close the speed gap with its competitors while maintaining its advantages.

2. Statement of the Problem

Define the object to be an N-dim lexicographically ordered vector f with elements f_j, j = 1, …, N. We model image formation by a simple Poisson model g ~ Poisson(ℋf), where ℋ is the system matrix whose element ℋ_ij indicates the probability of receiving a count in detector bin i from pixel j, and g is the integer-valued random data vector (sinogram) with elements g_i, i = 1, …, M.

The ML problem is written as the minimization of an objective function

$$\widehat{\mathbf{f}}=arg\hspace{0.17em}\underset{\mathbf{f}\ge \hspace{0.17em}0}{min}\hspace{0.17em}{E}_{\text{inc}-\text{ML}}(\mathbf{f})$$ (1)

where the ML objective corresponding to the usual (incomplete data) Poisson likelihood is given by

$$E_{\text{inc}-\text{ML}}(\mathbf{f})=\sum _{ij}{\mathscr{H}}_{ij}{f}_j-\sum _i{g}_{i}log\sum _j{\mathscr{H}}_{ij}{f}_j.$$ (2)

The MAP problem may be similarly stated as the minimization of the ML objective plus a prior objective E_prior. We consider quadratic priors of the form

$$E_{\text{prior}}(\mathbf{f})=\beta {\sum _j\sum _{j^{\prime }\in \mathcal{N}(j)}{w}_{j{j}^{\prime }}(f_j-f_{j^{\prime }})}^2$$ (3)

with smoothing parameter β > 0, and a neighborhood system $\mathcal{N}(j)$ with weights w_jj′. It will be convenient to define E_inc–MAP ≡ E_inc–ML + E_prior.

3. COSEM Objective and Algorithm

The direct minimization of E_inc–ML is difficult. One way of carrying out the minimization is by the well-known ML-EM algorithm. The conventional EM derivation [6] is statistical in nature, but there exists an alternate means for deriving this algorithm via a minimization of a so-called complete data objective function. This objective function is derived from an algebraic transformation of E_inc–ML(f) in Eq.(2), from the use of Jensen’s inequality [17]. We briefly summarize this step. From Jensen’s inequality and the convexity of − log(·), we have that $-log{\sum }_j{\mathscr{H}}_{ij}{f}_j\le -{\sum }_j\frac{C_{ij}}{g_i}log\hspace{0.17em}\frac{g_i{\mathscr{H}}_{ij}{f}_j}{C_{ij}}$

where the new ”complete data” C_ij ≥ 0, ∀ij and ${\sum }_j{C}_{ij}=g_i,\hspace{0.17em}\forall i$ and with equality occurring at $C_{ij}=\frac{g_i{\mathscr{H}}_{ij}{f}_j}{{\sum }_{j^{\prime }}{\mathscr{H}}_{i{j}^{\prime }}{f}_{j^{\prime }}}.$ This allows us to transform the original incomplete-data objective function in Eq.(2) to a new objective, E_comp(f, C) given by:

$$\begin{array}{l}{E}_{\text{comp}}(\mathbf{f},\mathbf{C})=\sum _l\sum _{i\in S_l}\sum _j{C}_{ij}log\frac{C_{ij}}{{\mathscr{H}}_{ij}{f}_j}\\ +\sum _l\sum _{i\in S_l}\sum _j{\mathscr{H}}_{ij}{f}_j+\sum _l\sum _{i\in S_l}{\gamma }_i(\sum _j{C}_{ij}-g_i).\end{array}$$ (4)

Note that the sum over detector bins ∑_i in E_inc–ML in Eq.(2) is replaced in Eq.(4) by a sum over subsets ∑_l∑_i∈Sl where l = 1, …, L indexes subset number and S_l is the set of detector bins belonging to the lth subset. Here, C_ij is the complete data, roughly analogous to the complete data as used in statistical derivations of EM-ML. From its Jensen’s inequality origin, we know that C_ij is real and positive, and that it obeys the constraints ∑_jC_ij = g_i expressed in terms of a Lagrange parameter γ_i. Differentiating Eq.(4) w.r.t. C, setting the result to zero and solving for the Lagrange parameter vector γ by imposing the constraints ∑_jC_ij = g_i we get

$$C_{ij}^{\text{sol}}(\mathbf{f})=g_i\frac{{\mathscr{H}}_{ij}{f}_j}{{\sum }_n{\mathscr{H}}_{in}{f}_n}\hspace{0.17em}\forall i,\hspace{0.17em}\forall j.$$ (5)

Inserting the just established solution (5) into (4), we can write the identity

$$\begin{array}{l}{E}_{\text{comp}}({\mathbf{C}}^{\text{sol}}(\mathbf{f}),\mathbf{f})=\sum _{ij}{\mathscr{H}}_{ij}{f}_j-\sum _i{g}_{i}log\sum _j{\mathscr{H}}_{ij}{f}_j\\ +\text{terms independent of }\mathbf{f}=E_{\text{inc}-\text{ML}}(\mathbf{f})\end{array}$$ (6)

where E_inc–ML(f) is the desired objective function in Eq.(2). We have shown that optimizing only over C (while keeping f fixed) in (4) results in Eq.(2). By optimizing E_comp(f, C) to obtain solutions f̂, Ĉ, we also obtain the solution f̂ of E_inc–ML [17].

One may maximize E_comp(f, C) by a form of grouped coordinate ascent on subsets of C and f, which leads to a convergent and fast OS algorithm. Above, we showed that by first minimizing Eq.(4) w.r.t. C, we obtained Eq.(2). We now show that minimizing Eq.(4) w.r.t. subsets of C results in a convergent ordered subsets EM algorithm (COSEM). First, differentiate Eq.(4) w.r.t. a subset of C and set the result to zero. Solve for the subset S_l of C in terms of f and the Lagrange multiplier γ_i where i ∈ S_l. Then, as before, we can eliminate γ_i but only for i ∈ S_l by enforcing the constraints ∑_jC_ij = g_i, and obtain the update equation for the S_l subset of the complete data C. We then solve for f by setting the derivative of Eq.(4) w.r.t. f to zero. We then repeat the above procedure for the next subset and so on. One can obtain the final update for all subsets of C and f as shown below. The update, in fact, closely resembles that of OSEM itself, but the slight modifications introduced by COSEM-ML ensure convergence to the ML solution. It is worth examining the updates of both algorithms, and these are summarized below:

$$C_{ij}^{(k,l)}=g_i\frac{{\mathscr{H}}_{ij}{f}_j^{(k,l-1)}}{{\sum }_{j^{\prime }}{\mathscr{H}}_{i{j}^{\prime }}{f}_{j^{\prime }}^{(k,l-1)}}\hspace{0.17em}\forall i\hspace{0.17em}\in \hspace{0.17em}{S}_l\hspace{0.17em}\hspace{0.17em}\forall j$$ (7)

$$C_{ij}^{(k,l)}=C_{ij}^{(k,l-1)}\hspace{0.17em}\hspace{0.17em}\forall i\hspace{0.17em}\notin \hspace{0.17em}{S}_l\hspace{0.17em}\hspace{0.17em}\forall j$$ (8)

$${\tilde{f}}_j^{(k,l)}=\frac{{\sum }_i{C}_{ij}^{(k,l)}}{{\sum }_i{\mathscr{H}}_{ij}}\hspace{0.17em}\hspace{0.17em}\forall j$$ (9)

$${\stackrel{⌣}{f}}_j^{(k,l)}=\frac{{\sum }_{i\in S_l}{C}_{ij}^{(k,l)}}{{\sum }_{i\in S_l}{\mathscr{H}}_{ij}}\hspace{0.17em}\forall \hspace{0.17em}j$$ (10)

The updates Eq.(7) and Eq.(10) when combined, form the familiar OSEM update, while the updates Eq.(7), Eq.(8) and Eq.(9) constitute COSEM-ML [11]. The notation $f_j^{(k,l)}$ indicates the update of the jth voxel at the lth subiteration (corresponding to use of the lth subset) of iteration k. When all L subsets have been updated, k is incremented. A first look at details of these updates appears to indicate that COSEM-ML involves many more steps per iteration k than does OSEM, but in [17], we show that the amount of computation is about the same. The updates for COSEM-ML preserve positivity.

We are primarily interested in the MAP case, and note that a COSEM-MAP version is obtainable by adding a prior E_prior(f) to Eq.(4). The updates for C in the COSEM-MAP algorithm remain the same as in Eq.(7) and Eq.(8). When we attempt to derive an update analogous to Eq.(9), the prior introduces a coupling between voxels, and this causes difficulty in deriving a closed-form and parallel update for f. To solve this, we use the method of separable surrogates [21] replacing Eq.(3) by

$$\begin{array}{l}{E}_{\text{priorSS}}(\mathbf{f})=\frac{\beta }{2}\sum _j\sum _{j^{\prime }\in \mathcal{N}(j)}{w}_{j{j}^{\prime }}[(2f_j-f_j^{(k)}\\ -f_{j^{\prime }}^{(k)}{)}^2+{(2f_{j^{\prime }}-f_j^{(k)}-f_{j^{\prime }}^{(k)})}^2]\end{array}$$ (11)

at iteration k. Since the resulting MAP objective function including Eq.(4) and Eq.(11) is a simple, convex 1-D objective w.r.t. f_j, we can trivially find that $f_j^{(k,l)}$ which minimizes it. Setting the derivative of the separable surrogate enhanced complete data MAP objective, Eqs.(4) plus (11), w.r.t. f_j to zero, and defining v_jj′ ≡ w_jj′ + w_j′j, and D_j = ∑_iH_ij, we obtain the final COSEM-MAP update for f [12]:

$$f_j^{(k,l)}=\frac{-b+\sqrt{b^2-4ac}}{2a}$$ (12)

where $a=4\beta {\sum }_{j^{\prime }}{v}_{j{j}^{\prime }},\hspace{0.17em}b=-2\beta {\sum }_{j^{\prime }}{v}_{j{j}^{\prime }}(f_j^{(k,l-1)}+f_{j^{\prime }}^{(k,l-1)})+D_j$ and $c=-{\sum }_i{C}_{ij}^{(k,l)}.$

Note that the $f_j^{(k,l)}$ update preserves positivity and that the COSEM-MAP updates are parallel in the voxel space. The overall computation per (k, l) subiteration is close to that of OSEM.

4. Simulation Results

To assess COSEM-MAP speed we display the normalized objective difference (NOD), versus iteration number k defined as:

$$\text{NOD}(k)=\frac{E_{\text{inc}-\text{MAP}}({\mathbf{f}}^k)-E_{\text{inc}-\text{MAP}}({\mathbf{f}}^{\ast })}{E_{\text{inc}-\text{MAP}}({\mathbf{f}}^0)-E_{\text{inc}-\text{MAP}}({\mathbf{f}}^{\ast })}$$ (13)

where f^k ≡ f^(k,0) and f⁰ is the initial estimate obtained via FBP. We define f* to be the true MAP solution at k = ∞, estimated from 5000 iterations of EM-MAP.

A sinogram (64 angles by 96 bins) with 300K counts was simulated using a 2D 64×64 phantom ( pixel = 5.6 mm), shown in Fig. 1(a). The phantom consists of a background and hot and cold lesions with a contrast ratio of 1:4:8 (cold:background:hot). Uniform attenuation (H₂O at 140 KeV) and depth-dependent blur for a parallel collimator were modeled.

Figure 1.

The 2D 64×64 phantom is shown in (a), while the anecdotal reconstructions are displayed in (b) EM-MAP, (c) COSEM-MAP, and (d) BSREM.

Reconstructions were performed using EM-MAP, BSREM [2] and COSEM-MAP. (Note that EM-MAP is simply COSEM-MAP at L = 1 subset). We chose L = 8 subsets for BSREM and COSEM-MAP, and for all reconstructions set β = 0.06. The relaxation schedule for BSREM was chosen as: ${\alpha }^k=\frac{{\alpha }_0}{{max}_{\{j,l\}}{\sum }_{i\in S_l}{\mathscr{H}}_{ij}+k}$ with α₀ = 3.2. This schedule obeys the constraints in [2]. The schedule was chosen to attain rapid convergence at early iterations. Anecdotal reconstructions for each algorithm are shown in Fig. 1 at iteration 30.

We plot NOD vs. k for each reconstruction in Fig. 2. At early iterations, the speed of COSEM-MAP lies between that of BSREM and EM-MAP, and by iteration 25, the NOD’s of COSEM-MAP and BSREM cross each other. We also plot NOD(k) (not shown here) for COSEM-MAP with varying numbers of subsets (L= 4, 8, 16, 32, 64). After an initial speedup at L = 4, further speedup with increasing L is modest and is not as good as that observed with competing OS-type algorithms.

Figure 2.

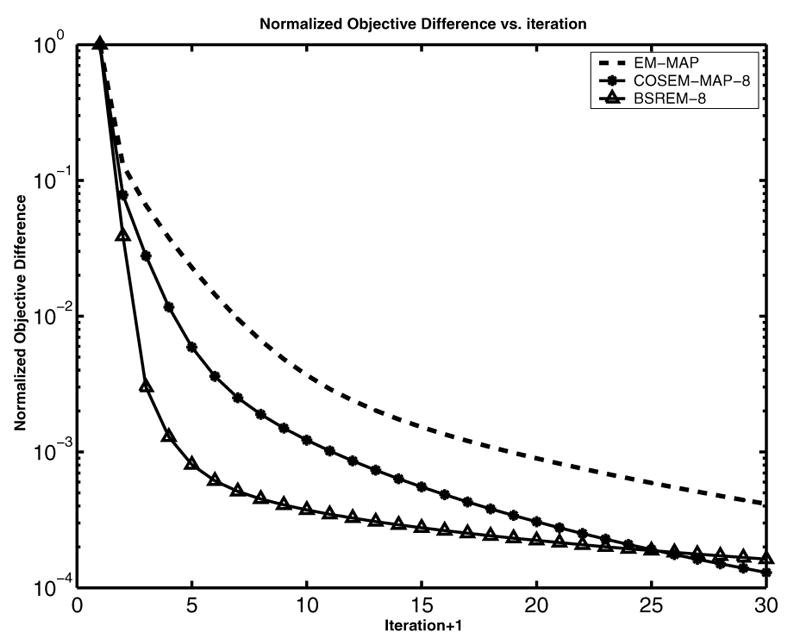
Normalized objective difference for EM-MAP, COSEM-MAP, and BSREM at L=8.

5. Discussion

We have derived new convergent complete data ordered subsets algorithms for ML (COSEM-ML) and MAP (COSEM-MAP) reconstruction. It is straightforward to include randoms or scatter via an affine term s̄, corresponding to $\mathbf{g}\sim Poisson\hspace{0.17em}(\mathscr{H}\mathbf{f}+\overline{\mathbf{s}})$, in the algorithms. Detailed convergence proofs are presented in [17].

It is unknown whether COSEM converges monotonically. (By monotonic, we mean that the objective decreases at each outer loop iteration k.) In our many simulations with clinically realistic imaging parameters, we have not yet observed non-monotonicity.

Though the simulations in Sec. 4 are not extensive, the results are quite typical, and the speed gap relative to relaxation-based methods cannot be closed by simply choosing a better L or initial condition. One might consider speeding up COSEM while maintaining its desirable properties. In separate publications [22,18,23], we have demonstrated that this is possible with an “enhanced” COSEM (ECOSEM) algorithm for MAP and ML versions.

In ECOSEM, the basic strategy is to apply an automatically computed parameter that controls a trade-off between a COSEM update and a faster OSEM update at each sub-iteration, while maintaining convergence. Simulations results for ECOSEM-ML [18] show its speed to approach that of optimized RAMLA.

In sum, we have presented COSEM-ML and COSEM-MAP for emission tomography based on our notion of a complete data energy. The COSEM algorithms needs no user-specified relaxation schedule as do competitors. While the early-iteration speed of COSEM is slower than that of competitors, we are developing faster enhanced ECOSEM versions competitive in speed with RAMLA and BSREM.