Selectivity enhancement of anion-responsive electrodes by pulsed chronopotentiometry

Abstract

A large and robust selectivity improvement of ion-selective electrodes is presented for the measurement of abundant ions. An improvement in selectivity by more than two orders of magnitude has been attained for the hydrophilic chloride ions measured in a dilute background of the lipophilic ions perchlorate and salicylate in a pulsed chronopotentiometric measurement mode. This is attributed to a robust kinetic discrimination of the dilute lipophilic ions in this measuring mode, which is not possible to achieve in classical potentiometry. Maximum tolerable concentrations of the interfering ions are found to be on the order of 30 μM before causing substantial changes in potential. As an example of practical relevance, the robust detection of chloride in 72 μM salicylate (reflecting 1:10 diluted blood) with a detection limit of 0.5 mM chloride is demonstrated. Corresponding potentiometric sensors did not give a useful chloride response under these conditions.

Introduction

Selectivity is one of the most important requirements for ion selective electrodes to be used reliably to measure the analyte of interest in the target sample. This is especially crucial in the analysis of clinical samples where the concentrations of ions vary only by a few percent and only sub-millivolt deviations of potential may be tolerable. While highly selective ionophore-based liquid membrane cation selective electrodes have been used successfully [1, 2], the development of their counterpart, sufficiently selective, carrier-based anion selective electrodes is still challenging [3–8]. Many works attempting to avoid the interference of lipophilic anions, mainly salicylate, on the measurement of the clinically important hydrophilic anions such as chloride and carbonate have been reported [6, 9–14]. The groups of Cha and Hulanicki proposed the use of hydrophilic diffusional membranes coated on the ion-selective electrode membrane to kinetically hinder the mass transport properties of dilute interferences [9, 10, 12]. However, eliminating the interference from lipophilic anions on the potentiometric determination of hydrophilic anions in a robust fashion is still a difficult task. Even many of the commonly used ionophore-based anion selective electrodes could not circumvent such interferences in potentiometric anion analyses. For example, carbonate selective electrodes based on trifluoroacetophenone derivatives and chloride selective electrodes based on metalloporphyrins exhibited strong interference from salicylate on the determinations of carbonate and chloride ions, respectively [1, 5, 11].

The most widely used anion selective electrodes have been ionophore-free polymeric membrane ion selective electrodes containing lipophilic quaternary ammonium or phosphonium salts as anion exchangers [7]. But the selectivity of such electrodes toward anions is dictated by the relative free energy of solvation of the anions in the aqueous and polymeric membrane phase following the Hofmeister selectivity sequence in which more lipophilic anions are preferred. When such electrodes are used for potentiometric analysis of hydrophilic anions in the presence of lipophilic anions the determination of the former is severely affected due to interference from the latter. This interference has its root in the design of the potentiometric sensors. The incorporated lipophilic anion exchangers induce permselectivity of the membrane, which follows the Hofmeister selectivity pattern. The counterions of the ion exchangers are displaced by more lipophilic anions of the sample according to the classical zero current ion exchange principle. It is a well established fact that the initial response of such electrodes is dictated by a steady state kinetic control, i.e., the flux of ions from the bulk of solution to the membrane interface and then into the membrane bulk [15, 16]. But upon long-term contact with a membrane, equilibrium is eventually achieved and the membrane loses sensitivity to the activities of the discriminated hydrophilic anions [17].

Measuring under nonequlibrium electrochemical processes by galvanostatic control may alleviate the problems mentioned above. Here, galvanostatically controlled ion sensors, lacking ion-exchanger sites and hence preventing spontaneous extractions are utilized. A current pulse of known magnitude and duration is applied to the sensor to force the flux of ions from the sample side toward the polymeric membrane. This is followed by a zero-current measurement pulse whereby the previously extracted background ions are exchanged with the analyte ion from the sample according to zero current counterdiffusion principle. In the third step, all the previously extracted ions are again expelled from the membrane by applying a baseline potential pulse. A stripping time of more than 10-fold longer than the uptake time is usually recommended for effective expelling of the ions extracted in the first step [18]. The concentration and charge sign of the extracted ions and the magnitude and the direction of transmembrane ion fluxes are controlled instrumentally by the magnitude and the sign of the applied current, i.e., by galvanostatic control [19, 20]. This measurement protocol offers membrane renewal between measurement pulses to ensure stable and reproducible sensor signals and hence renders the response signal unaffected by long-term contact of the membrane with the sample as the previously extracted anions are again expelled before the next measuring pulse.

The focus of this work is improving the selectivity of ion selective electrodes by measuring under nonequilibrium conditions utilizing galvanostatically controlled ion sensors. This novel measuring mode was exploited recently for the detection of multianalytes with a single sensor [19], reversible electrochemical detection of polyions [19, 21], determining free and total concentration of an analyte with the same sensor [22], enhanced sensitivity of sensors [20, 23] and detection of surface binding effects [24]. In this work the selectivity enhancement of such sensors is elucidated. The results are attributed to an instrumentally induced kinetic mass transport control of the sensor response.

Experimental

Reagents

The membrane components, high molecular weight poly(vinyl chloride) (PVC), bis(2-ethylhexyl) sebacate (DOS), 2-nitrophenyl octyl ether (o-NPOE), tetradodecylammonium tetakis(4-chlorophenyl) borate (ETH 500), tridodecylmethylammonium chloride (TDMACl) and tetrahydrofuran (THF) were purchased from Fluka Chemical Corp, Milwaukee, WI). All the inorganic salts were purchased from Fluka. Nanopure water (resistance 18.2 MΩ cm) was used to prepare aqueous solutions of the appropriate salts.

Membrane preparation

Ion-selective membranes (~200 μm thick) were prepared by solvent casting with THF as a solvent, a membrane cocktail containing 10 weight % of the inert lipophilic salt ETH 500 and PVC and o-NPOE 1:2 by weight for the pulsed chronopotentiometric measurements. The membrane for the zero current potentiometric experiments contained 1.5 weight % TDMACl and 1:2 by weight PVC and DOS and prepared by solvent casting with THF.

Electrodes

The membranes were cut with cork borer (6 mm in diameter) from the parent membrane and incorporated onto a Philips electrode body (IS-561, Glasblaserei Moller, Zurich, Switzerland). The membrane area was 20 mm². The inner solution was in contact with an internal Ag/AgCl electrode. The external reference electrode was a double-junction Ag/AgCl electrode with saturated KCl as inner solution and a 1 M LiOAc as a bridge electrolyte. A high surface area coiled Pt-wire was used as a counter electrode. The working electrodes were conditioned in a solution identical to the inner filling solution for at least 12 hours prior to experiments and kept in the conditioning solution when experiments were not underway.

Experimental setup

A conventional three-electrode setup was used for the pulse galvanostatic measurements where an internal Ag/AgCl electrode acted as the working electrode and the external reference electrode and counter electrode were immersed into the sample solution. The galvanostatic measurements were conducted with an AFCBI bipotentiostat (Pine Instruments, Grove City, PA) controlled by a PCI-MIO-16E4 interface board and LabVIEW 5.0 data acquisition software (National Instruments, Austin, TX) on a Macintosh computer. The solution was stirred for 20 s after each addition of sample and then stopped for 20 s before measurement in a quiescent solution (at short pulse times stirring did not influence the sensor response, see also [21]). The potentials were sampled as the average value during the last 10% of the anodic current pulse time. An uptake time of 1 s and a stripping time of 15 s were used throughout. A baseline potential pulse of 0 V versus Ag/AgCl was applied as a stripping potential. For the details of potentiostatic/galvanostatic control switching system see ref. [19]. Zero current potentials were measured with 16-channel EMF monitor (EMF 16, Lawson Labs, Phoenixville Pike, PA) versus the same reference electrode as in the galvanostatic measurements. All experiments were conducted at room temperature (21 – 22 °C)

Theory

A suitable electrical current imposed across an ion-selective membrane void of lipophilic ion-exchanger will result in a flux of ions from the sample into the membrane phase. Any dilute, thermodynamically preferred interfering ions will be locally depleted relative to the bulk concentration of the interfering ion. The level of practical interference is here approximated by a simple model, developed in analogy to earlier work where pulsed galvanostatically controlled sensors were first introduced [19].

The electrode response is a direct function of the phase boundary potential at the sample–membrane interface:

$$E_{PB}=\frac{RT}{zF}ln\frac{k_I{c}_I}{[I^z]}$$ (1)

where c_I and [I^z] are the phase boundary concentrations (strictly, activities) of I^z (with charge z) at the sample and membrane side, respectively, and k_I includes the free energy of transfer for I^z. A current i is imposed across the membrane and results in ion fluxes for every extractable sample ion of suitable charge. It is here assumed that ions remain uncomplexed in the membrane phase. This results in the following relationship for a sample containing two such ions I^zI and J^zJ :

$$i{\delta }_m=AF{D}_{m}z\left([I^z]+[J^z]\right)$$ (2)

where A is the electrode area for a planar membrane surface, D_m is the diffusion coefficient in the membrane phase, and δ_m is the diffusion layer thickness in the membrane. Note that the membrane bulk concentration of either ion is zero because no ion-exchanger is present in the membrane.

The conditions of flux continuity across the phase boundary may be written for both ions as [25]:

$$q=\frac{c_{I,b}-c_I}{[I^z]}$$ (3)

and

$$q=\frac{c_{J,b}-c_J}{[J^z]}$$ (4)

where the parameter q is given by the ratio of the diffusion coefficients and diffusion layer thicknesses in both phases [25]:

$$q=\frac{D_m{\delta }_{aq}}{D_{aq}{\delta }_m}$$ (5)

For a current pulse of sufficiently short duration, the Nernst diffusion layers in both phases may be approximated as follows to give a simplified relationship for q that depends only on the diffusion coefficients:

$$q\approx \frac{D_m\sqrt{D_{aq}t}}{D_{aq}\sqrt{D_{m}t}}=\sqrt{\frac{D_m}{D_{aq}}}$$ (6)

The local ion-exchange equilibrium involving two ions I^z and J^z may be conveniently described as a function of the unbiased selectivity coefficient [26]:

$$K_{IJ}^{pot}=\frac{c_I[J^z]}{[I^z]c_J}$$ (7)

Equation 4 is solved for c_J and the result inserted into eq 7 to give:

$$K_{IJ}^{pot}=\frac{c_I[J^z]}{[I^z]\left(c_{J,b}-q[J^z]\right)}$$ (8)

Equation 2 is solved for [J^z] and the result inserted into eq 8 to give:

$$c_I=K_{IJ}^{pot}[I^z]\left(c_{J,b}-q\left\{\frac{i{\delta }_m}{zAF{D}_m}-[I^z]\right\}\right){\left\{\frac{i{\delta }_m}{zAF{D}_m}-[I^z]\right\}}^{-1}$$ (9)

For primary ion concentrations c_I that are sufficiently concentrated (c_I >> q [I^z]) to not cause depletion at the membrane surface, equation 9 represents a simple implicit relationship between the sample concentration c_I (which is approximately the sample bulk concentration) and the membrane phase boundary concentration [I^z]. Dilute interferences J will deplete at the membrane surface on the basis of equation 4 and their influence on the potential will be smaller than thermodynamically expected. If no such depletion processes would occur, the sample phase boundary concentrations in equation 7 may be substituted for bulk sample concentrations, and the corresponding relationship to equation 9 would be found as:

$$K_{IJ}^{pot}=\frac{c_I}{[I^z]c_{J,b}}\left\{\frac{i{\delta }_m}{zAF{D}_m}-[I^z]\right\}$$ (10)

The detection limit of this class of sensors may, on the basis of the 1976 IUPAC recommendation [27] be understood as the cross-section between the two extrapolated linear segments of the calibration curve at low concentrations. For high primary ion concentrations where sample depletion is negligible, the detection limit may be calculated as the primary ion concentration in the membrane phase boundary, [I^z], that reaches half its ideal value. This ideal, unperturbed situation may here be calculated with equation 2 in the absence of interferences J:

$${[I^z]}_{ideal}=\frac{i{\delta }_m}{zAF{D}_m}$$ (11)

At the detection limit, equation 9 is therefore expressed as: 1

$$c_I(DL)=K_{IJ}^{pot}{c}_{J,b}-\frac{1}{2}q{K}_{IJ}^{pot}{[I^z]}_{ideal}$$ (12)

which may be compared to the classical case in the absence of sample depletion for the interfering ion (equation 10):

$$c_I(DL)=K_{IJ}^{pot}{c}_{J,b}$$ (13)

Clearly, detection limits are lower according to equation 12 compared to equation 10. The lowering of the detection limit may be influenced by a number of parameters, including membrane selectivity and applied current density. Note that the detection limit according to this definition may only be reached at interfering ion concentrations that are above the critical concentration, c_{J, b} > 0.5q[I^z]_ideal Otherwise eq 12 returns a negative concentration, indicating that the measurement of the primary ion is not affected by the interfering ion to reach the detection limit of the sensor. Equation 12 may be rewritten to express the highest tolerable interfering ion concentration that will give the detection limit of the electrode as:

$$c_{J,b}(DL)=\frac{c_I}{K_{IJ}^{pot}}+\frac{1}{2}q{[I^z]}_{ideal}$$ (14)

The more the interfering ion can be thermodyanically discriminated against, the higher the tolerable interfering ion concentration. For interfering ions that are highly thermodynamically preferred, the first term on the RHS of equation 14 is small, and the limiting concentration can be estimated as 0.5 q[I^z]_ideal. With diffusion coefficients in the membrane phase of about three orders of magnitude smaller than in the aqueous phase (for PVC–NPOE (1:2) [28]), q is about 0.03 for short pulse times (equation 6). If [I^z]_ideal is on the order of 2 mM (depending on the chosen experimental parameters), the limiting interfering ion concentration is estimated as ca. 30 μM. Lower concentrations are not expected to give significant levels of interference, while higher levels will lead to near-complete breakdown of the electrode response to the abundant hydrophilic ion.

Results and Discussion

As an example of high practical importance, ionophore-free anion-responsive membrane were studied here. While the membranes contain no ion-exchanger, the anodic current pulse renders the membranes anion-responsive [19]. Such ionophore-free systems are known to respond to sample anions in the order of increasing lipophilicity according to the established Hofmeister sequence. In classical potentiometry, the ion-selective membrane is doped with an anion-exchanger and conditioned at the front and backside with a salt of the anion to be determined. If such a membrane is exposed to a sample solution that contains another anion of sufficient lipophilicity and concentration, that ion will spontaneously ion-exchange with the primary ion from the membrane. This may lead to measurement errors and memory effects, some of which may be minimized with prolonged reconditioning cycles and short exposure times to such samples. If an anion-exchanger membrane is exposed to salts of anions in the order of decreasing lipophilicity, near-Nernstian response slopes are expected for the most lipophilic anions only, but diminish for the less lipophilic ions. These non-Nernstian electrode slopes are an indication of incomplete ion-exchange with the previously extracted (and more lipophilic) anion from the membrane. This may limit the use of such membrane electrodes in situations where the nature of the detected ion may change, for example as chromatographic detectors, for selectivity determinations, and for drug screening purposes or lipophilicity measurements.

The problem mentioned above is alleviated here by working with membranes that lack ion-exchange properties and where ion extraction is initiated on demand with a discrete galvanostatic pulse. One key advantage for this protocol is the expectation that prolonged exposure to lipophilic electrolytes will not alter the sensor response, as long as spontaneous extraction of that electrolyte is still suppressed. With ionophore-free membranes this is, however, not easily observed. Each galvanostatic pulse is followed by a zero current pulse to measure the potential, and a prolonged potential pulse to backextract the ions into the aqueous phase. Figure 1 presents the observed potentials for the selectivity determination anions in the order of decreasing lipophilicity. Here, near-Nernstian response slopes are observed for all anions, indeed suggesting a lack of undesired memory effect. The calculated selectivity coefficients and observed electrode slopes are summarized as follows: logK_Cl,ClO4^pot = 5.1, −58 mV dec⁻¹; K_Cl,SCN^pot = −4.0, −60 mV dec⁻¹; K_Cl,I^pot = 3.5, −58 mV dec⁻¹; K_Cl,NO3^pot = 2.0, −57 mV dec⁻¹; K_Cl,Br^pot = 1.1, −56 mV dec⁻¹. The electrode slope towards chloride was found as 59 mV dec⁻¹.

Figure 1.

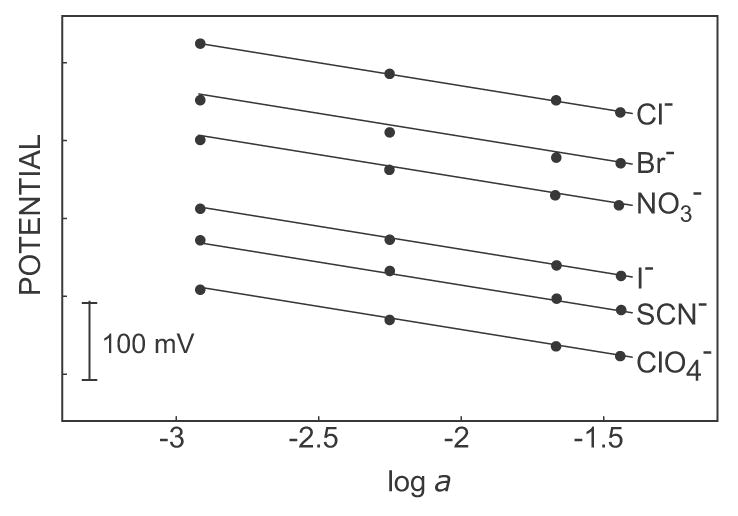
Selectivity of the pulsed chronopotentiometrically controlled ion-selective electrode (pulstrode). Responses to anions for calibrations were made in the order of decreasing lipophilicity, ClO₄⁻ to Cl⁻.

These results encouraged us to explore whether such instrumentally controlled membrane electrodes may be used to discriminate in a robust fashion against dilute, lipophilic interfering ions. Such situations often occur in practice, including in clinical analysis where dilute lipophilic ions such as salicylate may interfere in the clinical assessment of chloride levels, for instance. Figure 2 presents the observed response curve for the anion sensing membrane to incremental NaClO₄ concentrations in the presence of 0.1 M NaCl. A double pulse sequence was employed here, with a 1-s 3 μA (15 μA/cm²) current pulse followed by a 15-s baseline potential pulse at 0 mV. Perchlorate is about 5 orders of magnitude more lipophilic than chloride. Thermodynamically, therefore, this calibration curve is expected to exhibit a detection limit around 1 μM. The cross-section of the two linear extrapolated segments of each calibration curve is indeed around the micromolar level, confirming the thermodynamics of the system. However, significant perchlorate response starts at about 1.5 orders of magnitude higher concentration levels with a significant potential step. This so-called super-Nernstian response slope is well documented in the literature and occurs because of depletion effects at the membrane surface. Specifically, the current pulse results in an anion flux in direction of the membrane, effectively depleting perchlorate anions from the membrane surface. Because of this mass transport limitation, lower perchlorate concentrations in the sample are incapable of effectively competing with the more abundant chloride ions. This results in a kinetic discrimination of perchlorate at low concentrations. Note that such processes also occur in zero current potentiometry because the ion-exchange and extraction process results in a similar ion flux in direction of the membrane. Unlike here, however, such processes are normally transient and result in memory effects and unstable behavior upon prolonged exposure to such samples.

Figure 2.

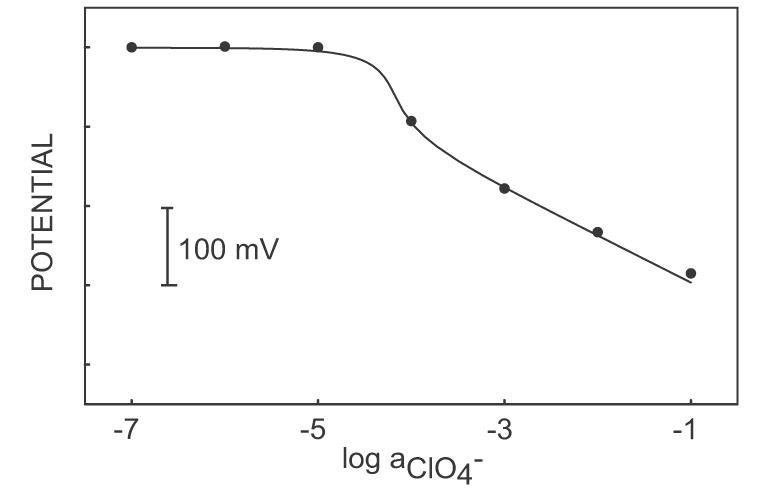
Calibration curve for NaClO₄ in a 0.1 M NaCl background in the pulse chronopotentiometric measuring mode. The dots show experimental electrode response and the solid line shows response as calculated from theory with the following parameters: D_m = 2 x 10⁻⁸ cm² s⁻¹, D_aq = 2 x 10⁻⁵ cm² s⁻¹, i = 3 μA, δ_m = 2 μm, A = 0.2 cm², and K_I,ClO4^pot = 10⁵.

The analytically perhaps more important, alternate experiment of adding NaCl to a background of 10 μM NaClO₄ is shown in Figure 3. The observed detection limit is about 5 x 10⁻⁴ M, significantly lower than the thermodynamically expected value (ca. 1 M). This suggests that abundant ions of limited lipophilicity may be determined in a dilute background of highly lipophilic ions. Figure 4 presents the response to NaCl added to 1 mM Na₂SO₄ in the presence and absence of NaClO₄. Lower concentration of NaClO₄ (10 μM, for example) does not interfere with the determination of NaCl, while 100 μM NaClO₄ exhibits a very large interference (see Figure 2 also). The highest tolerable interfering ion concentration that will give the detection limit of the electrode is calculated to be 4 x 10⁻⁵ from equation 14, using the parameter q = 0.03 (estimated from eq 6, taking into account D_m = 2 x 10⁻⁸ cm² s⁻¹ and D_aq = 2 x 10⁻⁵ cm² s⁻¹) and [I^z]_ideal = 2 mM (calculated from eq 11 with i = 3 μA, δ_m = 2 μm, A = 0.2 cm², D_m = 2 x 10⁻⁸ cm² s⁻¹) and K_IJpot = 10⁵. Note that the highest tolerable interfering ion concentration can be increased by increasing the applied current pulse or pulse time (see equations 11 and 14).

Figure 3.

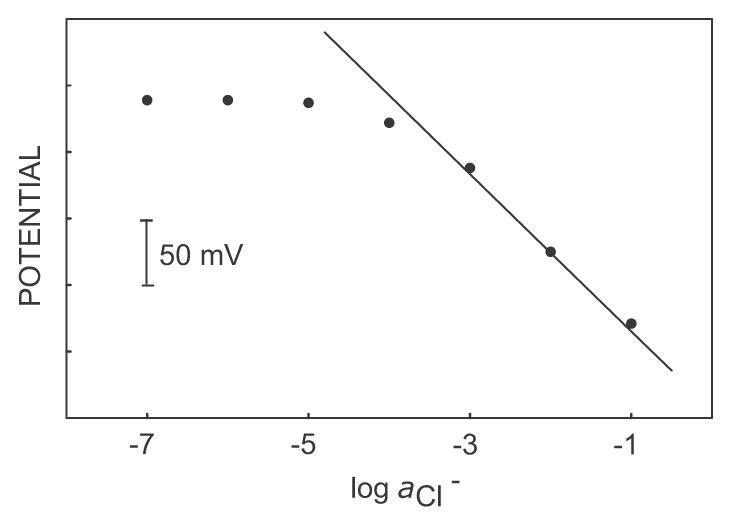
Calibration curve in pulse chronopotentiometric mode of sodium chloride in a background of 1 mM Na₂SO₄ and 10 μM NaClO₄. The solid line shows the theoretical response to chloride ions in perchlorate background below the maximum tolerable interfering concentration.

Figure 4.

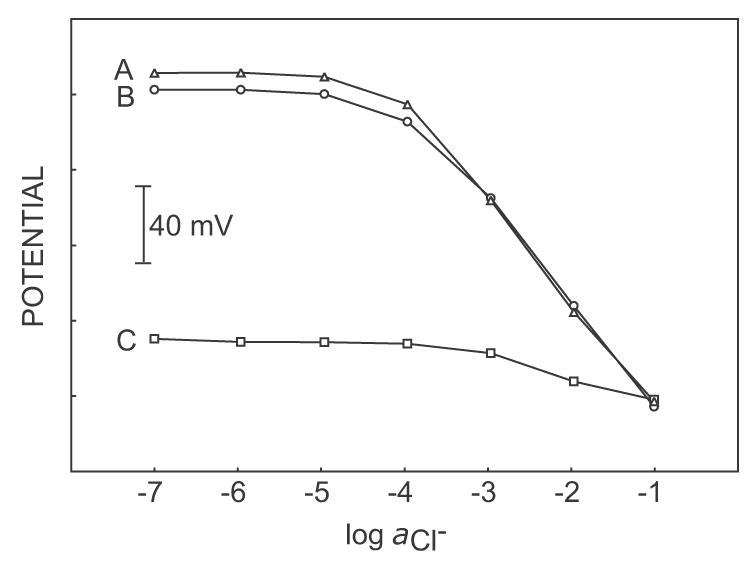
Calibration curves in pulse chronopotentiometric mode of sodium chloride in (A) 1 mM Na₂SO₄, (B) 1 mM Na₂SO₄ containing 10 μM NaClO₄ and (C) 1 mM Na₂SO₄ containing 100 μM NaClO₄. Only the highest concentration of perchlorate leads to complete breakdown of the chloride response, as expected by theory.

The electrode response reproducibilities upon repeated and alternative exposure of the pulstrode and potentiometric sensors to 0.001 M and 0.01 M NaCl, each in 10 μ M NaClO₄ are shown in Figure 5. The electrodes were rinsed with deionized water between the measurements. A good reproducibility with a standard deviation of 0.5 ± 0.1 mV is observed for the sensor under galvanostatic control both for the fresh electrode and the electrode conditioned in the solution of the lipophilic perchlorate ion solution for 24 h. In contrast, the classical potentiometric sensor exhibits a strong potential drift. Here, after conditioning in dilute pechlorate solution the response to chloride is almost completely lost owing to the thermodynamic preference of perchlorate (Figure 5B).

Figure 5.

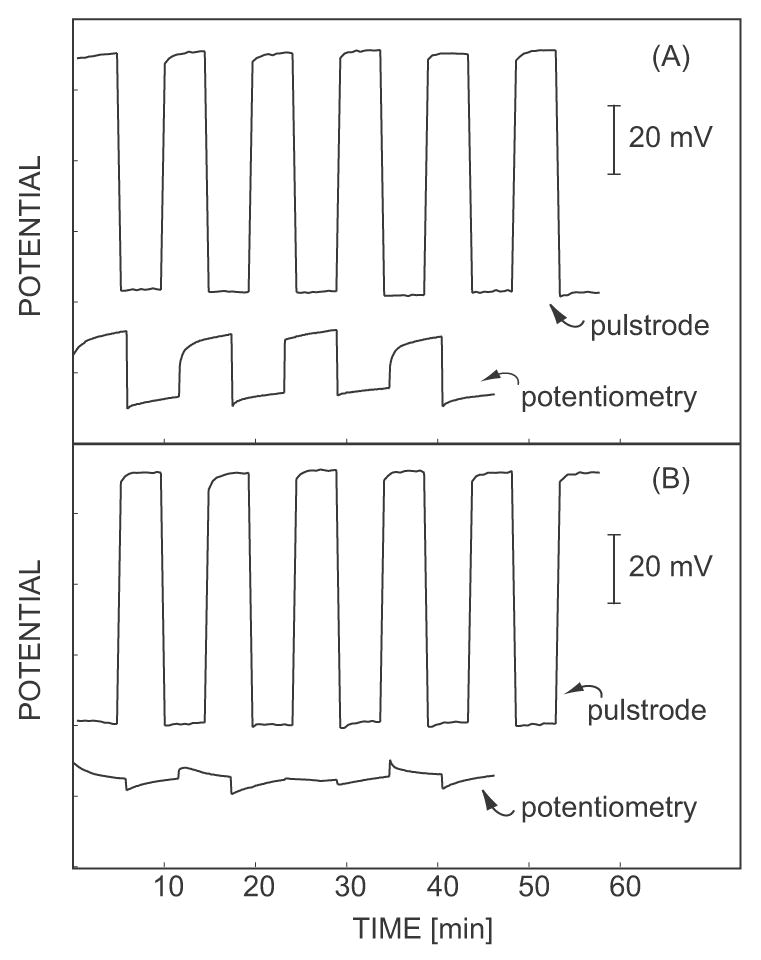
Pulstrode and potentiometric electrode response reproducibility on alternative measurement of 0.001 M NaCl (higher potential) and 0.01 M NaCl (lower potential) each in 10 μM NaClO₄: (A) Fresh electrodes conditioned in 0.01 M NaCl and (B) the same electrodes after conditioning in 0.01 M NaCl containing 10 μM NaClO₄ for 24 hours.

As an example of practical clinical utility, the chloride response in a background of salicylate was explored. Therapeutic salicylate levels are typically 720 μM [12], unfortunately too high to allow the present system to kinetically discriminate against this interference. Therefore, the composition of 10-fold diluted blood, as used in a number of clinical analyzers, was mimicked and a 72 μM salicylate background chosen for this purpose. Figure 6 shows the calibration curves to chloride in this background with the galvanostatically-controlled sensor (A) and with classical potentiometry (B). For the pulsed chronopotentiometric sensor the detection limit was found as about 5 x 10⁻⁴ M, more than 2 orders of magnitude lower than the thermodynamically expected value (ca. 72 mM; salicylate is about 3 orders of magnitude more lipophilic than chloride). Figure 6B shows the calibration curve, under the same conditions as Figure 6A, of NaCl for classical potentiometry. Here, however, a Nernstian response is not obtained even for higher concentrations of NaCl up to 0.1 M, demonstrating the usefulness of the pulsed chronopoteniometric method described here. Clearly, the adaption of this technology to the measurement of undiluted whole blood sample would be an important goal. While sample stirring has been found to exhibit only a marginal influence on the response of this type of pulsed galvanostatic sensors (see also [19]), the increase in sample viscosity of biological samples and adsorption of biomolecules on the membrane surface might translate into somewhat higher tolerable interfering ion levels (larger q value in equation 14). However, the most likely successful strategy will be the implementation of the pulsed chronopotentiometric approach introduced here in conjunction with a membrane coating that will hinder the ion diffusion kinetics as proposed in [9, 10, 12], a topic of current research in our laboratory.

Figure 6.

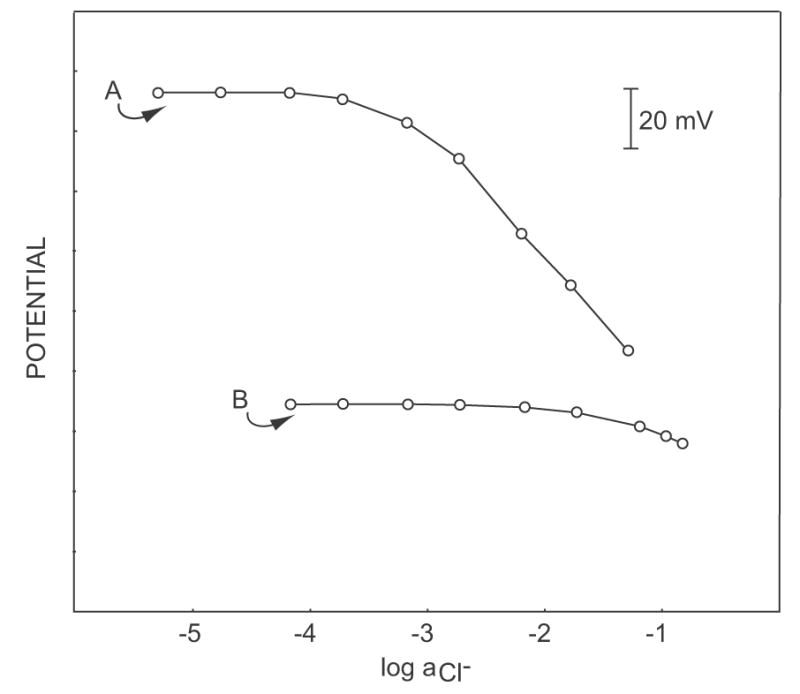
Calibration curves of sodium chloride in a background of phosphate buffer, pH 7.4, containing 72 μM sodium salicylate: (A) pulstrode mode, (B) potentiometry. The conditioning and inner filling solution was 0.01 M NaCl in phosphate buffer, pH 7.4.

Conclusions

The pulsed chronopotentiometric control of ion selective electrodes free of ion-exchanger sites is a promising technique to alleviate some limitations of zero current potentiometry. In this work, a dramatically reduced interference of lipophilic anions on the measurement of hydrophilic anions is elucidated, with the determination of less lipophilic chloride ion in the presence of the more lipophilic anions, perchlorate and salicylate, as example. This can be used as a universal recipe for analogous measuring systems where the interference of dilute lipophilic ions on the measurement of more abundant hydrophilic ions is to be avoided, especially if designing a sufficiently selective membrane is difficult. This is a valuable finding in the development of ISE-based analyses for anions.