Abstract
The elastic shear modulus G and swelling pressure ω are studied for a basic, pH-responsive hydrogel synthesized by crosslinking copolymerization of co-monomers hydroxypropyl methacrylate and N,N-dimethylaminoethyl methacrylate with crosslinker tetraethylene glycol dimethacrylate. Under normal conditions of use as a “smart” material, hydrogel swelling ratio Q and pH vary simultaneously, but here G and ω values are presented as a function of pH with Q held constant and vice-versa. At fixed pH, G decreases with increase in Q in a power law dependence, as predicted by the Flory-Rehner model. However, at fixed Q, G increases with decrease in pH (i.e, increase in degree of ionization). The pH effect is more pronounced than the volume effect, thus the hydrogel stiffens as it swells in response to pH change. At high pH, ω values of the uncharged hydrogel obey the Flory-Rehner model, whereas explicit ionic contributions can be identified at lower pH values.
Keywords: Elastic shear modulus, pH-responsive hydrogel, osmotic pressure
Introduction
A “smart” hydrogel is a crosslinked polymer network that absorbs or desorbs large quantities of water in response to some environmental trigger such as change in temperature, pH, or concentration of some analyte [1,2]. Smart hydrogels have been envisioned for use in miniature sensors [3], actuators [4], and autonomous drug delivery devices [5]. Hydrogels containing basic moieties that are uncharged at high pH and charged at low pH are pH responsive, swelling at sufficiently low pH values due to the accumulation of fixed positive charges along the polymer backbone. The hydrogel studied here is of this type due to the presence of a pendant tertiary amine on the comonomer N,N-dimethylaminoethyl methacrylate (DMA).
The elastic shear modulus G of a smart hydrogel is important for multiple reasons. First of all, one may need to manipulate the value of G in order to tailor mechanical properties of a hydrogel for certain applications [6]. Secondly, the value of G is an important determinant of the swelling response of a smart hydrogel, as may be seen in the following idealized analysis of hydrogel response under typical use conditions. Assume that a basic pH-responsive hydrogel is being used to sense the pH value of an aqueous solution, and further assume that the water in the surrounding solution is at its reference chemical potential value μref. At lower pH values, the polyelectrolyte chains will have a large osmotic pressure Π that favors swelling. However, this swelling tendency will be opposed by an entropic polymer chain-stretching penalty approximately equal to G [7,8]. The difference between these two opposing driving forces is the osmotic swelling pressure of the hydrogel, ω = Π – G[7,8]. Here and throughout this communication, ω is defined as the chemical potential of water within the hydrogel subtracted from the reference value (μref), divided by the molar volume of water. Further assume that the environmental water chemical potential value equals μref (implying ω = 0 at equilibrium) after the environmental pH value is suddenly decreased. The decrease in pH will increase hydrogel degree of ionization i, and the hydrogel will respond by swelling until ω returns to zero at a new equilibrium state. The key point here is that pH, i, swelling ratio Q, and possibly G all differ in value between the initial and final states in this hypothetical experiment. This was also the case in previous studies of the hydrogel modulus at a pH-induced transition [9–12]. However, ambiguity arises in the interpretation of the results, because both Q and i might be expected to affect G. As an alternative, one can imagine lowering pH and simultaneously lowering the chemical potential of water in the environment below μref (i.e. increasing the value of ω) in such a way that Q remains constant. This is the essence of our novel approach, and it was achieved via addition of an osmotic deswelling agent to the surrounding solution with the hydrogel enclosed in a semi-permeable membrane. The advantage of this approach is that it allows one to deconvolute the effects of i and Q on G, and also provides a test of the Flory-Rehner model [7].
Experimental
Materials and hydrogel synthesis
Polyelectrolyte hydrogels of a type widely studied in the literature [3,13–15] were prepared from three monomers: hydroxypropyl methacrylate(HPMA), (N,N-dimethylamino)ethyl methacrylate (DMA), and tetraethylene glycol dimethacrylate (TEGDMA). The monomer DMA contains a pH-sensitive tertiary amine, TEGDMA is a crosslinker, and HPMA was included to obtain a transition pH ≈ 8 [13,15]. Hydrogels containing HPMA/DMA/TEGDMA at a nominal mole ratio of 70/30/02 were prepared by free radical crosslinking copolymerization as in Reference 15.
Osmotic swelling pressure measurements
The reference environmental solution (infinite bath), with water at its reference chemical potential μref, was chosen to be an aqueous solution at 25 0C containing 150 mM NaCl, with pH adjustment using HCl. Hydrogels of known dry mass md were equilibrated with this reference solution, at which point gel swelling pressure ω = 0 by definition. Next known concentrations of an osmotic deswelling agent (poly(vinyl pyrrolidone), PVP, Mn = 29 kDa) were added to the environmental solution, and equilibrated with the gel for 8 – 10 days. In order to prevent penetration of PVP into the gel, the latter was separated from the environmental solution by a semipermeable membrane (dialysis bag) [16]. At equilibrium, the swelling pressure ω of the gel inside the dialysis bag (with respect to μref ) is equal to the known Π value [17] of the PVP solution outside. Periodically the mass of the gel mg was measured, and used to calculate the polymer weight fraction c = md/mg, with Q ≈ 1/c. The pH in the surrounding liquid phase was checked every day and adjusted if necessary to maintain the desired pH. Reversibility was checked by transferring gels into PVP solutions at different Π values.
Elastic (shear) modulus measurements
Shear modulus data were obtained from uniaxial compression measurements using a TA.XT2I HR Texture Analyser (Stable Micro Systems, UK). Equilibrated gel samples were rapidly transferred from the dialysis bag into this apparatus, which measures the deformation (± 0.001 mm) as a function of an applied force (± 0.01 N). Stress-strain isotherms were determined at 25 0C in about 3–5 minutes with no detectable change in gel weight. The absence of sample volume change and barrel distortion was confirmed, and stress-strain isotherms were found to fit the Mooney-Rivlin relation [18,19]. Under these conditions, the shear modulus is linearly related to Young’s modulus and can be calculated from the stress-strain curve.
Results and discussion
Elastic shear modulus
Figure 1 shows the values of the shear modulus G at various degrees of osmotic deswelling; each curve corresponds to a different fixed pH value. The abscissa is the polymer weight fraction in the gel, c ≈ 1/Q. As expected, G values monotonically increase with c at fixed pH. When we fit the results to the power law expression G ∞ cm, we find that m approaches the Flory-Rehner prediction of 1/3 at high c for all pH values. However, the value of m is only about 1/7 for highly charged gels at low c. The value of m that best fits the data over the entire concentration range is given at each pH in Table 1. The deviation of m from 1/3 may be a consequence of the finite network chain extensibility neglected in the Flory-Rehner model [7,18]. If so, then finite extensibility effects occur over a wider range of swelling ratios at low pH (Fig. 1).
1.
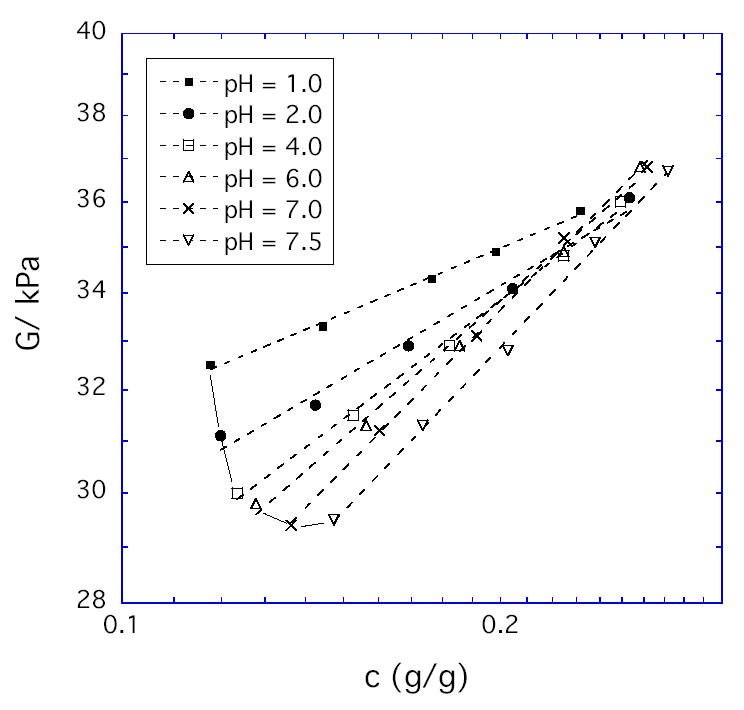
Elastic shear modulus as a function of polymer weight fraction for HPMA/DMA/TEGDMA hydrogels (70/30/02 mole ratio) at the pH values given in the legend and at fixed environmental NaCl concentration (0.15 M).
Table 1.
Swelling pressure parameters and shear modulus at various pH values
| pH | A (kPa) | n | m | Gc,e (kPa) | G at ce (kPa) | ce |
|---|---|---|---|---|---|---|
| 1.0 | 13,120 | 2.32 | 0.14 | 91.3 | 32.5 | 0.117 |
| 2.0 | 11,942 | 2.36 | 0.20 | 78.6 | 31.1 | 0.119 |
| 4.0 | 11,365 | 2.41 | 0.26 | 73.5 | 30.0 | 0.124 |
| 6.0 | 10,278 | 2.44 | 0.30 | 67.9 | 29.8 | 0.128 |
| 7.0 | 7,426 | 2.53 | 0.34 | 48.0 | 29.4 | 0.136 |
| 7.5 | 6,466 | 2.76 | 0.35 | 33.1 | 29.5 | 0.148 |
A surprising result in Fig. 1 is that G monotonically increases with decrease in pH (increase in ionization i) at fixed c, particularly at low c values. If as discussed in the Introduction this hydrogel is used in the fully swollen state(ω = 0, c = ce) to detect a decrease in pH from 7.0 to 1.0, then Figure 1 shows that G will increase from 29 ± 0.5 kPa to 32 ± 0.5 kPa. This is true even though Q will also increase which tends to reduce G. Thus the hydrogel stiffens as it swells in response to pH change. One possible explanation for this trend is chain stiffening due to finite chain extensibility, which is more significant at lower pH as already noted.
Osmotic swelling pressure
The same experiments used to deswell gels prior to G measurements also provided the values for ω plotted vs. c in Figure 2. The continuous curves in Figure 2 were obtained by least squares fit to a scaling relation that accurately describes uncharged hydrogels [8]:
2.
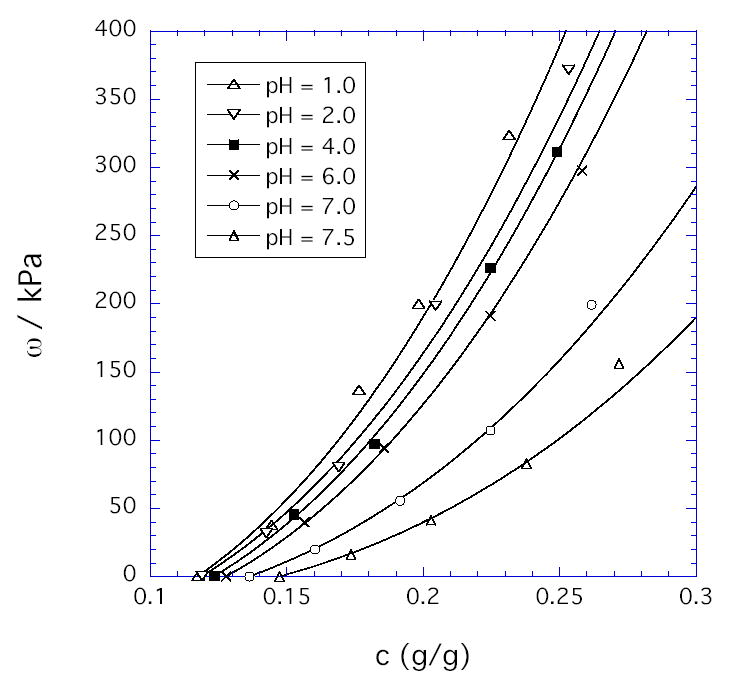
Osmotic swelling pressure as a function of polymer weight fraction in the HPMA/DMA/TEGDMA hydrogels (70/30/02 mole ratio) at the pH values given in the legend and at fixed environmental NaCl concentration (0.15 M). The solid curves were obtained by least squares fit to a scaling equation (Equation 1).
| (1) |
The first term in Eq. (1) corresponds to the osmotic contribution, and the second term corresponds to the entropic chain-stretching penalty denoted Gc. For simplicity, we used the m values determined experimentally from the concentration dependence of the shear modulus (dashed curves in Figure 1). Gc,e is the value of Gc at c = ce. Eq. (1) fits the data well at all pH values with the values of A, n, and Gc,e given in Table 1. As expected theoretically [7,8,20], A decreases with decrease in solvent quality (increase in pH), while n increases from its good solvent value of 2.3 (at low pH) and approaches its theta value of 3.0 (at pH ≈ 7.5). For polyelectrolytes, the osmotic term in Eq. (1) should include both an ionic contribution Πion and a contribution Πmix for mixing of fully neutralized uncharged chains [7]. At the collapse transition, expected to occur at a pH value of 7.7 – 8.0 [13], the osmotic pressure vanishes and deswelling measurements would not be meaningful. Thus we choose 7.5 as a reference pH at which Πion is assumed to be approximately zero, with residual electrostatic interactions screened by the salt (0.15M). The validity of this assumption is verified by the closeness of the observed scaling exponent n to its theta value (3.0) for neutral polymers (Table 1). With this assumption, Πmix can be equated to the value of Acn as determined at the reference pH of 7.5. At pH below the reference value, the Πion values shown in Figure 3 were calculated as Acn –Πmix. As noted previously [11], the pH dependence of Πion is weaker than predicted by Donnan theory. Least-squares-fit to the second term in Eq. (1) provides a value for the hydrogel modulus Gc during osmotic deswelling experiments. For uncharged gels, Gc has been found to equal the shear modulus G obtained in constant-volume experiments, despite the difference in the type of mechanical deformation [8]. The results presented here (Table 1) show that G appears to be approaching Gc at pH = 7.5, but at lower pH values, Πclus ≡ G - Gc is substantially negative (Figure 3). We speculate that the present gels, synthesized with high crosslinker content, contain densely crosslinked regions (microclusters) dispersed in a loosely crosslinked matrix. Since such clusters might be expected to contribute significantly to the resistance of the gel to volume change but not to shear, Πclus < 0. At pH =1, Figure 4 compares the various terms in our proposed decomposition
3.
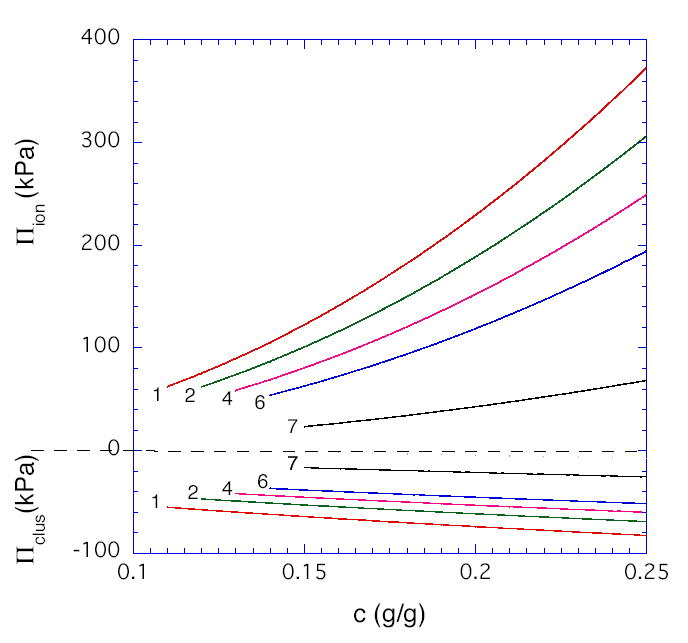
Estimated value of the counterion contribution to the osmotic swelling pressure, and of the contribution of microclusters to the swelling pressure, as a function of polymer concentration in the HPMA/DMA/TEGDMA hydrogels (70/30/02 mole ratio) at various pH values.
4.
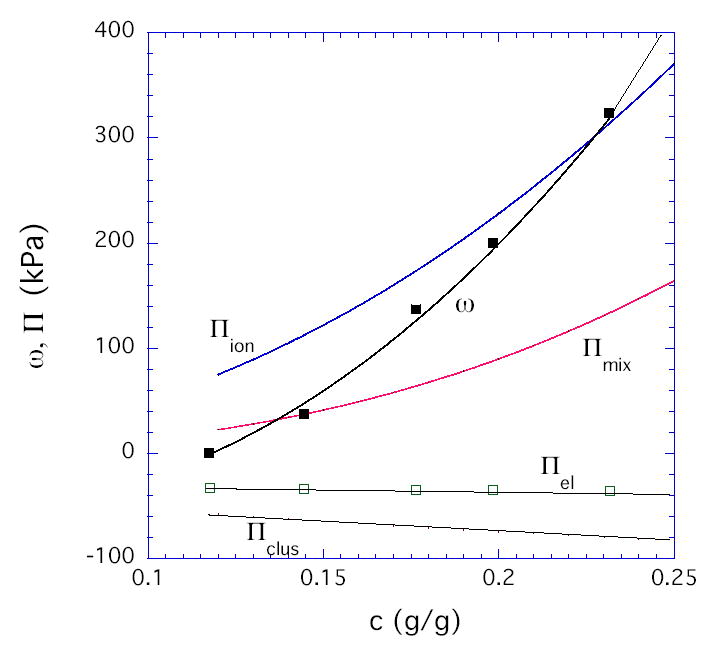
At pH = 1, the concentration dependence of the four contributions to the osmotic swelling pressure for the HPMA/DMA/TEGDMA hydrogels (70/30/02 mole ratio).
| (2) |
where Πmix = Acn at pH 7.5, Πion = Acn –Πmix, Πel = − G, and Πclus = G- Gc. In summary, simple scaling analysis in conjunction with the Flory-Rehner model provides insight into the osmotic swelling behavior of polyelectrolyte gels, and a simple formalism is proposed to separate the ionic, elastic, and mixing terms in gels having different degrees of ionization.
Acknowledgments
F.H. acknowledges the support of the Intramural Research Program of the NICHD, NIH. This work was also partially supported by a grant from the National Institutes of Health (No. EB004947 to J.J.M.)
References
- 1.Gehrke SH. Adv Polym Sci. 1993;110:81. [Google Scholar]
- 2.Galaev IY, Mattiasson B. Trends in Biotechnology. 1999;17:335. doi: 10.1016/s0167-7799(99)01345-1. [DOI] [PubMed] [Google Scholar]
- 3.Han IS, Han MH, Kim J, Lew S, Lee YJ, Horkay F, Magda JJ. Biomacromolecules. 2002;3:1271. doi: 10.1021/bm0255894. [DOI] [PubMed] [Google Scholar]
- 4.Beebe DJ, Moore JS, Bauer JM, Yu Q, Liu RH, Devadoss C, Jo BH. Nature. 2000;404:588. doi: 10.1038/35007047. [DOI] [PubMed] [Google Scholar]
- 5.Gu Y, Baldi A, Ziaie B, Siegel RA. Proceedings 2nd Annual International IEEE-EMBS Conference on Microtechnologies in Medicine & Biology; Madison, WI, USA. 2 – 4 May 2002; pp. 406–409. [Google Scholar]
- 6.Kirker KR, Prestwich GD. J Polym Sci Polym Phys. 2004;42:4344. [Google Scholar]
- 7.Flory PJ. Principles of Polymer Chemistry. Ithaca, NY: Cornell Univ. Press; 1953. [Google Scholar]
- 8.Horkay F, Hecht AM, Geissler E. J Chem Phys. 1989;91:2706. [Google Scholar]
- 9.Hasa J, Ilavsky MJ. Polym Sci Polym Phys. 1975;13:263. [Google Scholar]
- 10.Luo LB, Kato M, Tsurata T, Kataoka K, Nagasaki Y. Macromolecules. 2000;33:4992. [Google Scholar]
- 11.Okay O, Durmaz S. Polymer. 2002;43:1215. [Google Scholar]
- 12.Johnson BD, Beebe DJ, Crone WC. Mater Sci Eng C. 2004;24:575. [Google Scholar]
- 13.Siegel RA, Firestone BA. Macromolecules. 1988;21:3254. [Google Scholar]
- 14.Goldraich M, Kost J. Clinical Materials. 1993;13:135. doi: 10.1016/0267-6605(93)90100-l. [DOI] [PubMed] [Google Scholar]
- 15.Jung DY, Magda JJ, Han IS. Macromolecules. 2000;33:3332. [Google Scholar]
- 16.Horkay F, Zrinyi M. Macromolecules. 1982;15:1306. [Google Scholar]
- 17.Vink H. Europ Polym J. 1971;7:1411. [Google Scholar]
- 18.Treloar LRG. The Physics of Rubber Elasticity. Oxford, UK: Clarendon; 1976. [Google Scholar]
- 19.Dusek K, Prins W. Adv Polym Sci. 1969;6:1. [Google Scholar]
- 20.de Gennes P-G. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell Univ. Press; 1979. [Google Scholar]


