Quantitative and Qualitative β Diversity Measures Lead to Different Insights into Factors That Structure Microbial Communities

Abstract

The assessment of microbial diversity and distribution is a major concern in environmental microbiology. There are two general approaches for measuring community diversity: quantitative measures, which use the abundance of each taxon, and qualitative measures, which use only the presence/absence of data. Quantitative measures are ideally suited to revealing community differences that are due to changes in relative taxon abundance (e.g., when a particular set of taxa flourish because a limiting nutrient source becomes abundant). Qualitative measures are most informative when communities differ primarily by what can live in them (e.g., at high temperatures), in part because abundance information can obscure significant patterns of variation in which taxa are present. We illustrate these principles using two 16S rRNA-based surveys of microbial populations and two phylogenetic measures of community β diversity: unweighted UniFrac, a qualitative measure, and weighted UniFrac, a new quantitative measure, which we have added to the UniFrac website (http://bmf.colorado.edu/unifrac). These studies considered the relative influences of mineral chemistry, temperature, and geography on microbial community composition in acidic thermal springs in Yellowstone National Park and the influences of obesity and kinship on microbial community composition in the mouse gut. We show that applying qualitative and quantitative measures to the same data set can lead to dramatically different conclusions about the main factors that structure microbial diversity and can provide insight into the nature of community differences. We also demonstrate that both weighted and unweighted UniFrac measurements are robust to the methods used to build the underlying phylogeny.

Understanding differences in the composition of microbial communities is of major importance in microbial ecology. Advances in sequencing technology have allowed many microbial communities to be characterized using gene sequences amplified directly from environmental samples. However, methods for analyzing these sequences have lagged far behind the rate of data acquisition. Two important parameters of communities, including microbial communities, are α diversity (the diversity within each sample, e.g., the number of species observed in an environment), and β diversity (the partitioning of biological diversity among environments or along a gradient, e.g., the number of species shared between two environments) (Table 1) (31). Here, we focus on β diversity, which can be measured in many different ways. These measures can be broadly divided into two categories: qualitative measures, which use the presence/absence of data to compare community composition, and quantitative measures, which also take the relative abundance of each type of organism into account (Table 1). Examples of commonly used qualitative measures of β diversity include the Sörensen and Jaccard indices; quantitative measures include the Sörensen quantitative index and the Morisita-Horn measure (see reference 16 for a review).

TABLE 1.

Measurements of diversity

Measure	Measurement of α diversity	Measurement of β diversity
Only presence/absence of taxa considered	Qualitative (species richness)	Qualitative
Additionally accounts for the no. of times that each taxon was observed	Quantitative (species richness and evenness)	Quantitative

Although quantitative and qualitative measures of diversity are tightly correlated in a range of theoretical distributions governing species abundance (4, 8, 19), empirically, these types of measures are often uncorrelated and can provide different but equally illuminating views of diversity (27). Most direct comparisons of quantitative and qualitative measures to date have focused on α diversity, the diversity within each sample. These studies have provided overwhelming evidence that quantitative and qualitative measures of diversity can paint markedly different pictures of diversity over a range of taxa and spatial scales. For example, in treeless Appalachian spider communities, rare, transient species dominated qualitative measures of α diversity, but ecological factors such as the availability of flying insect prey determined which species were abundant in a given community and thus dominated the quantitative measures (28). In human-modified grassland plots, qualitative α diversity was primarily influenced by levels of phosphorus and potassium, but quantitative α diversity was primarily influenced by levels of calcium, the carbon-to-nitrogen ratio, and organic matter (15). Other studies of plant diversity in alpine tundra (1), shrub-steppe (17), and tallgrass prairie (23) and of phytoplankton diversity (32) have also found important and biologically meaningful differences in quantitative and qualitative α diversity. Although these studies all focused on α diversity, we expect that similar differences between quantitative and qualitative diversity will also be found in β diversity and, therefore, that a combination of qualitative and quantitative approaches for measuring β diversity is also desirable.

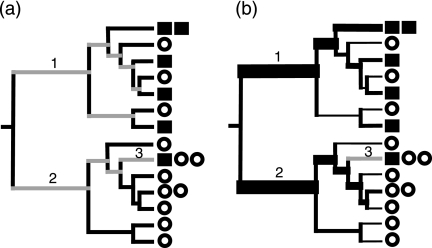
Most β diversity measures, including those listed above, treat each species or operational taxonomic unit (OTU; typically defined by a sequence similarity threshold) in the sample as equally related. Newer β diversity measures that incorporate phylogenetic information are more powerful because they account for the degree of divergence between sequences (13, 18, 29, 30). Phylogenetic β diversity measures can also be either quantitative or qualitative depending on whether abundance is taken into account. The original, unweighted UniFrac measure (13) is a qualitative measure. Unweighted UniFrac measures the distance between two communities by calculating the fraction of the branch length in a phylogenetic tree that leads to descendants in either, but not both, of the two communities (Fig. 1A). The fixation index (F_ST), which measures the distance between two communities by comparing the genetic diversity within each community to the total genetic diversity of the communities combined (18), is a quantitative measure that accounts for different levels of divergence between sequences. The phylogenetic test (P test), which measures the significance of the association between environment and phylogeny (18), is typically used as a qualitative measure because duplicate sequences are usually removed from the tree. However, the P test may be used in a semiquantitative manner if all clones, even those with identical or near-identical sequences, are included in the tree (13).

FIG. 1.

Calculation of the unweighted and the weighted UniFrac measures. Squares and circles represent sequences from two different environments. (a) In unweighted UniFrac, the distance between the circle and square communities is calculated as the fraction of the branch length that has descendants from either the square or the circle environment (black) but not both (gray). (b) In weighted UniFrac, branch lengths are weighted by the relative abundance of sequences in the square and circle communities; square sequences are weighted twice as much as circle sequences because there are twice as many total circle sequences in the data set. The width of branches is proportional to the degree to which each branch is weighted in the calculations, and gray branches have no weight. Branches 1 and 2 have heavy weights since the descendants are biased toward the square and circles, respectively. Branch 3 contributes no value since it has an equal contribution from circle and square sequences after normalization.

Here we describe a quantitative version of UniFrac that we call “weighted UniFrac.” We show that weighted UniFrac behaves similarly to the F_ST test in situations where both are applicable. However, weighted UniFrac has a major advantage over F_ST because it can be used to combine data in which different parts of the 16S rRNA were sequenced (e.g., when nonoverlapping sequences can be combined into a single tree using full-length sequences as guides). We use two different data sets to illustrate how analyses with quantitative and qualitative β diversity measures can lead to dramatically different conclusions about the main factors that structure microbial diversity. Specifically, qualitative measures that disregard relative abundance can better detect effects of different founding populations, such as the source of bacteria that first colonize the gut of newborn mice and the effects of factors that are restrictive for microbial growth such as temperature. In contrast, quantitative measures that account for the relative abundance of microbial lineages can reveal the effects of more transient factors such as nutrient availability.

MATERIALS AND METHODS

Weighted UniFrac.

Weighted UniFrac is a new variant of the original unweighted UniFrac measure that weights the branches of a phylogenetic tree based on the abundance of information (Fig. 1B). Weighted UniFrac is thus a quantitative measure of β diversity that can detect changes in how many sequences from each lineage are present, as well as detect changes in which taxa are present. This ability is important because the relative abundance of different kinds of bacteria can be critical for describing community changes. In contrast, the original, unweighted UniFrac (Fig. 1A) is a qualitative β diversity measure because duplicate sequences contribute no additional branch length to the tree (by definition, the branch length that separates a pair of duplicate sequences is zero, because no substitutions separate them).

The first step in applying weighted UniFrac is to calculate the raw weighted UniFrac value (u), according to the first equation:

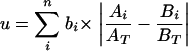Here, n is the total number of branches in the tree, b_i is the length of branch i, A_i and B_i are the numbers of sequences that descend from branch i in communities A and B, respectively, and A_T and B_T are the total numbers of sequences in communities A and B, respectively. In order to control for unequal sampling effort, A_i and B_i are divided by A_T and B_T.

If the phylogenetic tree is not ultrametric (i.e., if different sequences in the sample have evolved at different rates), clustering with weighted UniFrac will place more emphasis on communities that contain quickly evolving taxa. Since these taxa are assigned more branch length, a comparison of the communities that contain them will tend to produce higher values of u. In some situations, it may be desirable to normalize u so that it has a value of 0 for identical communities and 1 for nonoverlapping communities. This is accomplished by dividing u by a scaling factor (D), which is the average distance of each sequence from the root, as shown in the equation as follows:

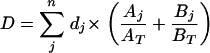Here, d_j is the distance of sequence j from the root, A_j and B_j are the numbers of times the sequences were observed in communities A and B, respectively, and A_T and B_T are the total numbers of sequences from communities A and B, respectively.

Clustering with normalized u values treats each sample equally instead of treating each unit of branch equally: the issues involved are similar to those involved in performing a multivariate analysis using the correlation matrix to treat each variable equally independent of scale or, using the covariance matrix, to take the scale into account. Scaling by D also allows for comparison with unweighted UniFrac values, which also always have a value between 0 and 1.

Multivariate analyses and tests of robustness to sequencing effort.

Weighted UniFrac can be used to compare many communities simultaneously using standard multivariate statistical methods. In this respect, it resembles unweighted UniFrac (13), F_ST (18), and other β diversity measures that can be treated as distance metrics (16). In the case studies below, we use a hierarchical clustering method called unweighted pair group method with arithmetic averages (UPGMA) (25) to cluster the community samples. It should be noted that this method is used only to relate the community samples to one another; it is not used to build the phylogenetic tree that relates the sequences. UPGMA sequentially joins the least different samples to create a tree structure describing the differences between communities. We also use principal coordinates analysis (PCoA) (7), in which a distance matrix is used to plot the n samples in (n − 1)-dimensional space. The vectors in this space, or factors that describe as much variation as possible, can be plotted as axes in two dimensions for visualization or regressed on environmental variables (e.g., chemistry or temperature) using general linear model regressions to determine which environmental factors have the largest impact on community composition. PCoA is analogous to a related, widely used technique called principal components analysis (PCA). The distinction is that PCA begins with a table of the number of times each phylotype was observed in each environment, whereas PCoA begins with a table of distances between each pair of environments. The output of PCoA is a list of factors (labeled factor 1, factor 2, etc. in descending order of importance) and the factor weighting for each sample (allowing each sample to be plotted in the factor space).

Because microbial communities are usually too complex to sample completely, we measured the robustness of the UPGMA and PCoA results to sequencing effort using a sequence jackknifing technique in which the UPGMA and PCoA clusters are regenerated using a subset of the sequences. Specifically, the same number of sequences are randomly selected from each environment for many replicate trials. Nodes in the UPGMA cluster that are recovered in a large percentage of the jackknife trials are considered robust to sampling effort, particularly if only a small proportion of the data was subsampled from each environment during each jackknife replicate. The positions of the points in jackknifed PCoA scatterplots are the average for the jackknife replicates and are displayed with ellipses representing the interquartile range (IQR) in each axis. If the IQRs are small, the same result would likely be achieved with a different sample of sequences from the same distribution, but if the IQRs are large we might expect to see different relationships.

Case studies.

We chose two studies that compared the community composition of related environments using 16S rRNA genes sequenced directly from environmental samples (20, 21). The first study examined the relative influences of mineral chemistry, temperature, and geography on microbial community composition in acidic thermal springs in Yellowstone National Park (18a). The second study examined the influences of obesity and kinship on microbial community composition in the mouse gut (11).

By analyzing the data from each study with both unweighted UniFrac (a qualitative measure) and weighted UniFrac and F_ST (both quantitative measures), we show that quantitative and qualitative β diversity measures can lead to substantially different conclusions about the main factors that structure microbial diversity. In both studies, the results from the weighted and unweighted analyses suggest that different factors affect the presence/absence and relative abundance of microbial lineages.

RESULTS

Study 1: acid thermal springs in Yellowstone National Park.

Mathur et al. (18a) assessed the relative contributions of mineral chemistry, temperature, and geographical location on bacterial community composition in acidic thermal springs in Yellowstone National Park. Sediment was sampled from two sulfur-rich springs in the Amphitheatre Springs (AS) area and an iron-rich spring located ∼2 km away in the Roaring Mountain (RM) area. In each spring, sediment was sampled at temperatures of 60°C, 65°C, and 70°C. In addition, samples were taken from an AS spring that had both iron- and sulfur-rich sediments as well as mixed iron-sulfur sediments at 75°C. The springs all had similarly low pH levels (∼1.5).

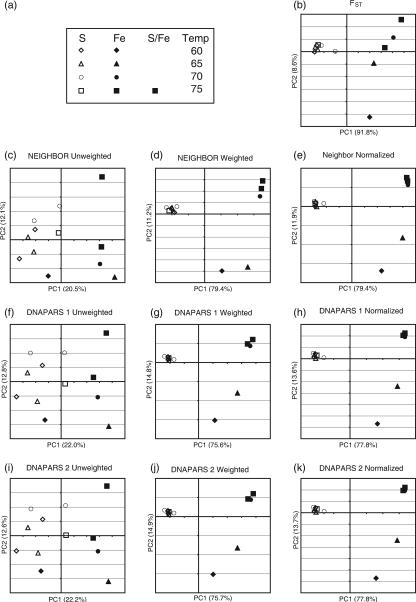
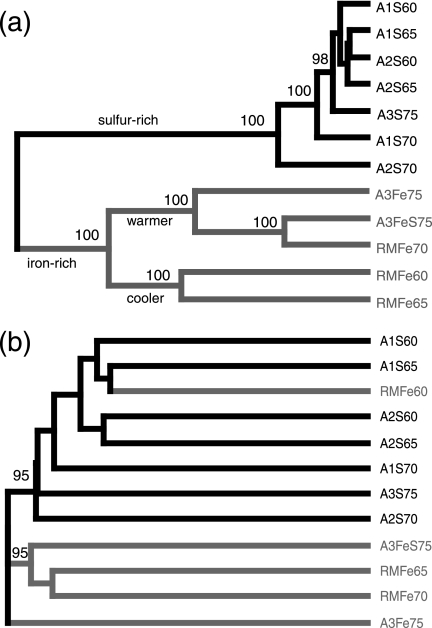
Mathur et al. (18a) generated 16S rRNA gene libraries of between 65 and 96 sequences representing between 8 and 53 unique sequences for the 12 samples. Based on the analysis of this sequence information, Mathur et al. concluded that mineral chemistry was by far the most important factor for controlling community composition and that temperature had a secondary effect. The clearest statistical evidence for this conclusion resulted from PCoA of pairwise F_ST values. Factor 1 from the PCoA accounted for 85.7% of the variation in the data and correlated strongly with chemistry. Specifically, sulfur-rich springs clustered apart from springs rich in iron or iron and sulfur. Factor 2 explained only 7.8% of the variation and was correlated with temperature in the iron-rich samples.

The strong correlation with chemistry detected using the quantitative F_ST values was primarily due to differences in the relative abundances of bacterial lineages rather then the types of microorganisms present. Comparing the F_ST analysis to the results of PCoA and hierarchical clustering with both weighted and unweighted UniFrac demonstrated that the F_ST results were consistent with the results of weighted UniFrac but not unweighted UniFrac (Fig. 2), as expected because both F_ST and weighted UniFrac are quantitative measures.

FIG. 2.

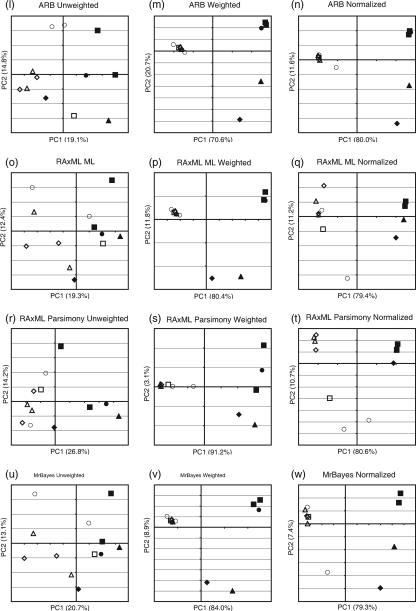
PCoA analysis of hot spring sediment samples with F_ST and unweighted, weighted, and normalized weighted UniFrac using a variety of trees. Shown is a plot of the first two principal coordinate axes (factors) for PCoA using each tree-building method and a UniFrac algorithm. Rows show the effects of different tree-building methods; columns show the effects of applying unweighted UniFrac (first column), weighted UniFrac (second column), and weighted UniFrac with the branch length normalization (third column). (a) The legend describes which symbol applies to which sample. Fe-containing springs have solid symbols; springs that contain only S have hollow symbols. Temperature (°C) is denoted by the shape of the symbol. (b) PCoA clustering using F_ST values as distances. (c through e) Neighbor-joining tree from NEIGHBOR. (f through h) and (i through k) Two representative parsimony trees from DNAPARS. (l through n) ARB parsimony insertion tree. (o through q) RAxML maximum likelihood tree. (r through t) RAxML parsimony guide tree, no branch lengths. (u through w) MrBayes consensus tree.

To test whether the algorithm used to build the phylogenetic tree affects the result, we applied weighted and unweighted UniFrac to seven different phylogenetic trees (Fig. 2), as follows: (i) a neighbor-joining tree, in which we used the DNADIST program of PHYLIP 3.62 (6) with the F84 model of nucleotide substitution to create a distance matrix, which we used as input to PHYLIP's NEIGHBOR program (Fig. 2c to e); (ii) two representative maximum parsimony trees, in which we used two equally parsimonious trees (the first and the last in the file) from the DNAPARS program of PHYLIP 3.62 (Fig. 2f to k); (iii) an ARB parsimony insertion tree where we inserted the sequences into a tree containing >10,000 small-subunit rRNA sequences (an augmented version of the ARB database described in reference 9), using the parsimony insertion tool of ARB (14), and then removed all but the sequences from this study (Fig. 2l to n); (iv) the maximum likelihood tree and the parsimony guide tree of RAxML-HPC 6.0 (26), in which we generated these using the general time-reversible model of nucleotide substitution (Fig. 2o to t); and (v) a tree generated with MrBayes 3.5 (24) where we sampled trees from 100,000 generations after 500,000 generations of burn-in on four Markov chains and built the consensus tree from this sample (Fig. 2u to w). All of the trees were rooted with an archaeal outgroup. For all but the ARB parsimony insertion tree (Fig. 2l to n trees), the ends of the alignments were trimmed prior to the analysis so that the aligned sequences were all the same length. For the UniFrac and F_ST analyses, hypervariable regions of the 16S rRNA molecule were excluded using a lane mask, “lanemaskPH,” provided in a publicly available ARB database (9).

We evaluated the similarities of the seven phylogenetic trees using both the nodal distance algorithm (NDA) (2) and a partition metric (22) (Table 2). The NDA value is the sum of the differences in distance between each pair of sequences in the phylogenetic tree (2). We scaled the branch lengths so that they summed to 1 in each of the seven trees. The partition metric counts the number of tree nodes (partitions) that are not shared between the two trees (22) (Table 2). We divided the result by the total number of partitions so that the values are expressed as fractions.

TABLE 2.

Pairwise comparisons of the phylogenetic trees evaluated in this study^a

Phylogenetic tree type	Phylogenetic tree type
	NJ	MP1	MP2	ARB	RAxML	RAxML pars	MrBayes
NJ		142.1	143.0	310.6	198.0	1024.3	333.9
MP1	0.60		17.5	252.7	155.6	1125.6	248.6
MP2	0.62	0.10		246.0	147.8	1125.5	246.3
ARB	0.71	0.70	0.67		287.8	1266.2	316.0
RAxML	0.67	0.60	0.59	0.75		1167.5	189.9
RAxML pars	0.68	0.57	0.56	0.73	0.59		1320.5
MrBayes	0.71	0.46	0.44	0.73	0.61	0.67

^aShown are pairwise comparisons of the phylogenetic trees evaluated in Fig. 2 using the NDA (boldface type; upper triangle of matrix; results are arbitrary values with greater values indicating greater dissimilarity) and a partition metric (lower triangle of matrix; results are fractions indicating dissimilarity, ranging from 0 to 1). Methods are as follows: NJ, neighbor joining, as implemented in NEIGHBOR; MP1 and MP2, maximum parsimony, as implemented in DNAPARS; ARB, parsimony insertion, as implemented in Arb; RAxML, maximum likelihood, as implemented in RAxML; RAxML pars, RAxML parsimony insertion guide tree; MrBayes, Bayesian tree as implemented in MrBayes. All values along the diagonal are 0 for both methods (because each tree is identical to itself).

We applied unweighted and weighted UniFrac with and without branch length normalization to each tree (Fig. 2). PCoA of the pairwise F_ST and weighted UniFrac measurements produced almost identical results (Fig. 2). As observed by Mathur et al. (18a), environmental chemistry explained the majority of genetic variability among the samples. Factor 1 correlated strongly with the chemistry of the springs and explained 70.6 to 91.8% of the variation for the different tests (Fig. 2). Factor 2 explained between 3.1 and 20.7% of the variation and, as observed by Mathur et al. (18a), correlated with the temperature in the Fe samples. Specifically, 60°C and 65°C samples from the Fe springs clustered together, as did 70°C and 75°C samples. This temperature effect was more pronounced in the weighted UniFrac analysis than for F_ST (Fig. 2). Regression analysis of these two PCoA factors on environmental variables confirmed these patterns (data not shown), as did hierarchical clustering (see Fig. 4).

FIG. 4.

Hierarchical clustering of hot spring sediment samples with weighted and unweighted UniFrac. The percentage support for nodes supported at least 70% of the time with sequence jackknifing is indicated. The name of each sample indicates the spring (e.g., A1, A2, and A3 are different springs from the Amphitheatre Springs area, and RM is from the Roaring Mountain area), whether the sample is sulfur rich (S), iron rich (Fe), or both (FeS), and the temperature. The names and branches are colored black for S samples and gray for Fe and FeS samples. (a) Weighted UniFrac with the neighbor-joining tree and (b) unweighted UniFrac with the neighbor-joining tree.

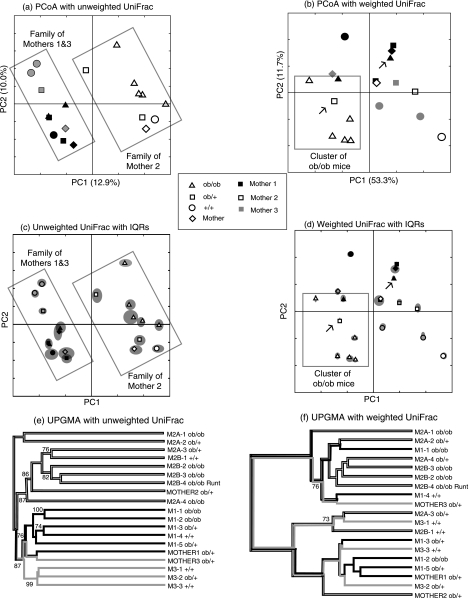
Sequence jackknifing of the PCoA point locations and the hierarchical clusters illustrated that these results were robust to sample size (Fig. 3 and Fig. 4). When only 50 of the 65 to 96 sequences were randomly selected from each sample 100 times, almost all of the nodes in the hierarchical clustering were supported 100% of the time (Fig. 4a). These well-supported nodes included the nodes grouping the sulfur-rich samples, the iron-rich samples, and the warmer and cooler iron-rich samples. In addition, the average PCoA point locations for the jackknife replicates were the same as those for the entire data set, and the IQRs for these point locations were extremely small (Fig. 3b).

FIG. 3.

Jackknifing of PCoA analysis of hot spring sediment samples with unweighted and weighted UniFrac. Shown is a plot of the first two principal coordinate axes (factors) for PCoA with the neighbor-joining tree. Point locations are the average location in the 100 jackknife replicates. Only 50 randomly selected sequences from each sample were used in each replicate (the range of sequences per sample was 65 to 96). Gray ellipses represent the IQR for the 100 jackknife replicates. The 95% confidence intervals for the point locations were also calculated and were considerably smaller than the IQRs (data not shown). The symbols are the same as those shown in Fig. 2.

In contrast, PCoA and hierarchical clustering of unweighted UniFrac values did not show a strong effect of mineral chemistry on differences between microbial communities. Using unweighted UniFrac measurements to cluster greatly diminished our ability to discriminate between samples. Factors 1 and 2 combined accounted for only about 30% of the variance on average (compared to about 90% for the weighted analysis) (Fig. 2), and sequence jackknifing using 50 sequences from each sample resulted in larger IQRs for the PCoA point locations than for weighted UniFrac (Fig. 3a). In addition, only two nodes in the hierarchical clustering were recovered >50% of the time (Fig. 4b). Although sulfur- and iron-rich samples still generally grouped together in the hierarchical clustering, sample RMFe60, the coolest of all of the iron-rich samples, now clustered with other 60°C and 65°C samples rather than the other iron-rich samples, in a jackknife-supported node. This change indicated that temperature had a greater effect on the clustering with unweighted UniFrac. In the weighted analysis, factor 1 correlates significantly with temperature (r², 0.34 to 0.49; mean r², 0.39; P, <0.05 in all cases; corresponding r² values for factor 1 in the weighted UniFrac range from 0.08 to 0.17 [mean 0.11] were not significant) and is less clearly associated with mineral chemistry than factor 1 of weighted UniFrac values. This result indicates that the strong correlations with chemistry detected by PCoA of F_ST and weighted UniFrac measurements depended entirely on changes in the relative abundance of the phylogenetic lineages rather than the types of lineages present. In contrast, when the presence/absence of data alone was considered, temperature played a more important role. Thus, a primary advantage of analyzing the same data set with both a qualitative and a quantitative diversity measure (in this case, unweighted and weighted UniFrac) is the ability to identify the relative importance of phylogenetic lineage and abundance on the variation in diversity between environments.

The UniFrac results were not sensitive to the method used to build the phylogeny. For both weighted and unweighted UniFrac, the results were generally similar for the seven phylogenetic trees, even though the trees had considerable differences in both topology (the partition metric shows that 10 to 75% of the clades were unique to one or the other tree) and branch length (generally high NDA values; see Table 2). Despite these differences, weighted UniFrac always separated the samples by chemistry, and unweighted UniFrac always produced a first factor that correlated significantly with temperature. These results suggest that both weighted and unweighted UniFrac analyses are robust to differences in the trees produced by popular tree-building methods. The one tree-building method that is clearly the most different from the remainder is the RAxML parsimony tree (which lacks branch lengths). This loss of information about the extent of divergence may lead to different results. For these samples, applying the normalization for differential branch lengths generally had little effect (compare the second and third columns of graphs in Fig. 2). The normalization did appear to increase the variability of the spread of the sulfur-rich samples along factor 2 depending on the tree-building method, especially for likelihood and Bayesian trees, perhaps indicating that it is less robust than weighted UniFrac without normalization to differences in branch length estimates.

Study 2: obesity and gut microbiota.

Although in the example above, weighted UniFrac identified clearer patterns of variation between samples than unweighted UniFrac, this is not always the case. In the analysis of the effects of obesity and kinship on the microbial population of mouse gut microbiota, quantitative and qualitative β diversity measures again provide completely different perspectives on the main factors that impact microbial community composition. Here, unweighted UniFrac identifies clearer patterns of variation. In their study, Ley et al. sequenced bacterial 16S rRNA genes from the distal ceca of obese and nonobese mice who were the offspring of three different mothers (11). Each mother was heterozygous for a mutation in the gene for the hormone leptin, which affects appetite and causes obesity in homozygous mutants (10, 33). Each mother was mated to a heterozygous male, and litters were produced that contained siblings with each of the three possible genotypes. The littermates were kept in the same cage as their mother until they were weaned at 3 weeks and then kept in their own cages for an additional 5 weeks before being sacrificed. Bacterial 16S rRNA gene clone libraries with between 111 and 484 sequences were produced from the cecal microbial communities for each of the three mothers and for 16 of the offspring (11).

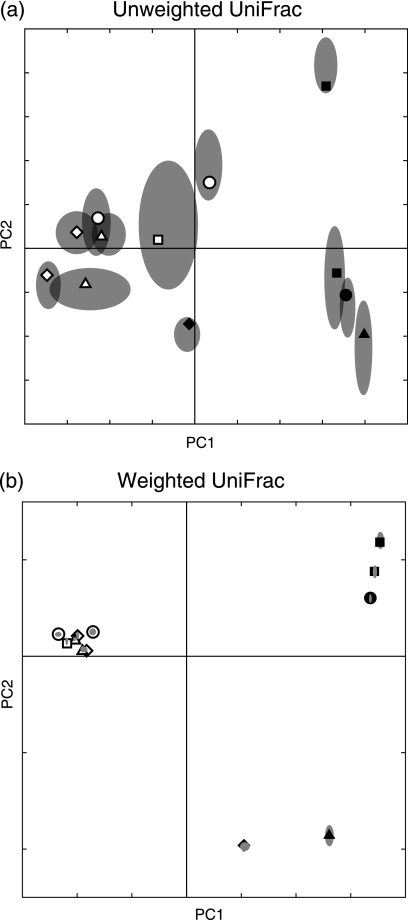
We calculated pairwise values using both weighted and unweighted UniFrac and used both hierarchical clustering and PCoA to cluster the mice based on this sequence information (Fig. 5). Unweighted UniFrac revealed a clear association between microbial diversity and kinship: the mice clustered almost perfectly by mother. The two mothers who were sisters (M1 and M3) clustered together with their offspring. An unrelated mother (M2) and her offspring formed a separate cluster. This result was reliably obtained using both hierarchical clustering and PCoA (Fig. 5) (11). Sequence jackknifing showed that these results were robust to sample size. When 200 sequences were randomly selected from each of the 17 mice with between 200 and 484 sequences, both the node that grouped M1 and M3 with their offspring and the node that grouped M2 with most of her offspring were recovered 87 out of 100 times (Fig. 5e). The two mice represented by less than 200 sequences (M2A-1 and M2A-2) were the only mice that did not group with their mother (Fig. 5e). In addition, none of the IQRs for point locations for M1 and M3 and their offspring overlaps those of M2 and her offspring in the jackknifed PCoA plot (Fig. 5c).

FIG. 5.

Analysis of mouse cecal microbial communities with weighted and unweighted UniFrac. Genotypes are ob/ob for homozygotes for the mutant leptin allele that confers obesity, ob/+ for heterozygotes, and +/+ for wild types. All mothers are ob/+. (a) Plot of the first two principal coordinate axes for PCoA with unweighted UniFrac. Symbols represent individual animals. The rectangles highlight the family of mother 2 and the families of mothers 1 and 3, who are sisters. (b) The same plot for weighted Unifrac. The rectangle highlights the majority of the ob/ob mice. The arrows point to outliers: an ob/ob mouse outside of the ob/ob cluster (black triangle) and an ob/+ mouse inside the ob/ob cluster (white square). (c) Same plot for sequence jackknifing of unweighted UniFrac with a maximum of 200 sequences from each mouse for 100 replicates. The symbols are the average values for the 100 replicates, and the gray ellipses represent the IQR of the point locations. (d) Sequence jackknifing with weighted UniFrac with a maximum of 200 sequences from each mouse for 100 replicates. (e) Hierarchical cluster diagram for unweighted UniFrac. The percentage support for nodes supported at least 70% of the time with sequence jackknifing is indicated. The main clustering is by mother. (f) Hierarchical cluster diagram for weighted UniFrac. The clustering by mother is much less clear, and there is more clustering by ob/ob genotype (and hence by obesity phenotype).

In contrast, when we used weighted UniFrac to account for the abundance information, there was no strong association with kinship. Instead, there was a greater correlation with the obesity genotype (Fig. 5). Individual mice fell into two major clusters, and all but one of the obese mice fell within the first of the two clusters, suggesting that taking the abundance of each type of sequence into account revealed similarities in the bacterial communities in the obese mice that were not detected solely by an examination of phylogenetic lineages. This interpretation is supported by the observation that obese mice contained significantly more organisms from the phylum Firmicutes and significantly fewer bacteria from the Cytophaga-Flexibacter-Bacteroides clade, suggesting that the genotype that leads to obesity has a significant impact on the microbial community (11). Interestingly, one of the ob/ob homozygous mutants was a runt but still clustered with the obese mice, suggesting that the ob/ob genotype, rather than raw nutrient throughput, is the predominant force affecting the cecal microbial community.

DISCUSSION

In both case studies, the use of weighted and unweighted measures of β diversity revealed markedly different factors influencing the microbial communities. The original, unweighted UniFrac measure is well suited to detecting differences in the presence or absence of lineages of bacteria in different communities. In the thermal spring study, unweighted UniFrac clustered the samples mainly by temperature, suggesting that the main effect was whether lineages could survive in each of the different springs. In the obesity study, unweighted UniFrac clustered the different mice almost perfectly by mother. Because the mice were kept in the same cage with their mother until they were weaned and because they all have the same genetic background, the result may have been heavily influenced by founder effects. Although this result was easily explained after the fact (mice in the same cage often eat each others' feces, providing a direct pathway for shared microbial communities), we found it surprising at the time we performed the analysis.

In contrast, our new weighted UniFrac measure is well suited to detecting differences in abundance even when the overall groups of organisms that are present in each sample remain the same. In the thermal spring study, weighted UniFrac clustered the samples primarily by the chemistry of each spring; in the mouse obesity study, weighted UniFrac grouped most of the obese mice together in one cluster. Thus, we expect that weighted UniFrac will be suitable for studying transient changes in microbial communities related to nutrient availability and may also be suited to the analysis of seasonal changes and changes under the influence of different pollutants. We have made an implementation of the weighted measure available through the UniFrac website at http://bmf.colorado.edu/unifrac by selecting the “Use Abundance Weights” option, allowing researchers to run both weighted and unweighted analyses in the context of a convenient Web interface (12).

We demonstrated that neither weighted nor unweighted UniFrac is sensitive to the methodology used to build the underlying phylogenies, which is important because each phylogenetic method has its own strengths and weaknesses (5). Weighted UniFrac performs similarly to F_ST, another quantitative measure of β diversity, but has the advantage over F_ST that it is applied to a phylogenetic tree rather than to a sequence alignment. It can thus be applied to phylogenetic trees that are generated from nonoverlapping sequence, such as trees generated based on top BLAST hits in viral metagenomic analyses (3) or from different regions of the rRNA molecule using ARB's parsimony insertion tool (14). Weighted UniFrac will thus be an important tool for large-scale comparisons across multiple community samples collected by different researchers at different times. Unfortunately, information about the abundance of each sequence in the sample and about whether clones were prescreened for diversity by restriction fragment length polymorphisms or related techniques is typically not available in public databases such as GenBank. Now that methods are available to analyze such data on a global scale, the development of resources that collect this information is more critical than ever.

We conclude that both quantitative and qualitative measures of β diversity have specific niches in the analysis of microbial communities and that using both types of measures will often be critical for understanding the factors that underlie microbial diversity.