Photoreactivation and Dark Repair in UV-Treated Microorganisms: Effect of Temperature

Abstract

Because of the lack of readily available information about the influence of temperature on microorganism reactivation processes subsequent to inactivation with UV radiation, a series of batch reactivation studies were performed at 5, 10, 15, 20, 25, and 30°C. A special effort was made to model the reactivation process to enable the effect of the temperature variable to be quantified. Because an earlier-proposed kinetic model (K. Kashimada, N. Kamiko, K. Yamamoto, and S. Ohgaki, Water Sci. Technol. 33:261-269, 1996), a first-order saturation type, does not adequately fit the data obtained in experiments of reactivation in conditions of light and darkness, a modification of that model is proposed. The new model, which actually coincides with the classical logistic equation, incorporates two kinetic parameters: the maximum survival ratio (S_m) and the second-order reactivation rate constant (k₂). In order to interpret correctly the reactivation occurring in conditions of darkness, a new term for the decay is added to the logistic equation. The new model accurately fits the data obtained in reactivation experiments, permitting the interpretation of the kinetic parameters S_m, k₂, and M (for only repair in darkness), where M is mortality, a zero-order decay rate constant, and their relationship with various environmental conditions, such as microbial type, light, and temperature. The parameters S_m and k₂ (and M for reactivation in conditions of darkness) show exponential dependence on the reactivating temperature, and it is possible to predict their values and hence the reactivation curve from the equations proposed in this work.

UV light is one of the most practical methods used for disinfection in wastewater treatment systems because it can inactivate bacteria, viruses, bacterial spores, and oocysts of protozoa (6, 9). Unlike those for other technologies, such as chlorination and ozonation, one of the technological advantages often put forward for UV disinfection is its lack of sensitivity to temperature variations. This independence from temperature would be expected if UV were a simple photochemical reaction (11). Severin et al. (12) performed a series of batch inactivation studies with bacteria, yeast, and viruses and demonstrated that the effect of temperature on UV inactivation was very small. Abu-ghararah (1) found that the effect of water temperature on the kinetics of the UV disinfection process in the normal operating range of most treatment plants (20 to 40°C) is not statistically significant.

However, the physiological effect of inactivation is not well understood and is complicated by the ability of many organisms to repair UV damage inflicted to their nucleic acids. While the infliction of damage is a purely photochemical reaction that occurs in the few seconds while water is exposed to UV radiation in the disinfection channels, the interplay of reactions which eventually lead to inactivation includes some biochemical reactions which can be affected by temperature. The latter phenomena can take place during the irradiation period, but it is mostly during the postirradiation time that reactivation processes occur if adequate conditions exist.

The principal inactivating effect of UV irradiation is the formation of photoproducts in DNA. Of these photoproducts, the most important is the pyrimidine dimer formed between adjacent pyrimidine molecules on the same strand of DNA, which can interrupt both the transcription and the replication of the DNA. The formation of a dimer can be reversed by two repair mechanisms: photoreactivation and dark repair. Systematic quantitative study of photoreactivation, the more important of the two mechanisms, has suggested a two-step reaction scheme (4).

Step 1 is the formation of a complex between a photoreactivation enzyme (PRE) and the dimer to be repaired. This step does not require light, but it is dependent on temperature, pH, and ionic strength (8).

Step 2 is the release of PRE and repaired DNA. The restoration of the dimer to its original monomerized form is absolutely dependent upon light energy intensity. The reaction occurs in less than a millisecond; consequently, the limiting step of the whole reactivation process is the formation of the PRE-dimer complex. An extended period of exposure to photoreactivating light would enable the release of PRE, which would then be available to form new complexes (step 1).

The effect of temperature on the reactivation phase is still little studied. Chan and Killick (3) investigated the effect of salinity and temperature on the reactivation of Escherichia coli in a marine environment. They found that the effect of salinity is greater than that of temperature, although an Arrhenius tendency was confirmed for the rate constants calculated.

The prediction of temperature effects is complicated by the nature of DNA itself and the complexity of reactions, enzymes, and molecules implicated in the inactivation and repair processes.

Because information about the influence of temperature on the reactivation process subsequent to inactivation with UV radiation is not readily available, batch reactivation studies were performed at 5, 10, 15, 20, 25, and 30°C. A special effort was made to model the reactivation process to enable the effect of the temperature variable to be quantified.

MATERIALS AND METHODS

UV-C irradiation.

UV-C irradiation treatment was performed with a 5.0 m³/h, horizontal-lamp, open-channel UV disinfection system (Trojan Technologies, S.L., Spain) and six low-pressure, high-intensity mercury UV lamps (Philips; 30W UV-C at 254 nm). The UV channel received the water from the unfiltered secondary effluent of the Municipal Wastewater Treatment Plant of Jerez de la Frontera (Spain). The unfiltered secondary effluent characteristics are summarized in Table 1.

TABLE 1.

Wastewater quality characteristics during study period

Parameter	Range	Avg
UV transmittance (%)	36-61	48
Turbidity (NTU)a	2.3-13.3	8.3
Total amt of suspended solid (mg/liter)	4-23	16
Total no. of coliforms (CFU/100 ml)	1.3 × 106 - 1.6 × 107	5.0 × 106
No. of fecal coliforms (CFU/100 ml)	1.7 × 105 - 1.1 × 106	4.9 × 105
No. of fecal streptococci (CFU/100 ml)	8.5 × 104 - 1.0 × 106	3.1 × 105

^aNTU, nephelometric turbidity units.

Bacteria were exposed to a UV-C fluence of 100 mW·s/cm². The UV-C fluence (mW·s/cm²) supplied was calculated as a product of the average UV fluence rate into the reactor (mW/cm²) and the irradiation time (s). The average UV fluence rate was calculated by the point source summation method (2, 5, 10, 13, 14). The exposure time was calculated from the channel volume and the influent flow rate after first ensuring that the plug flow condition existed in the channel through the study of the residence time distribution curves. Irradiation was performed at room temperature, between 15 and 20°C.

Repair conditions.

After UV-C irradiation, the water sample was divided and transferred into two 500-ml glass Erlenmeyer flasks (95% transparent for 360 nm light). One of the two Erlenmeyer flasks was thermostated in a controlled-environment incubator (refrigerated incubator, model no. FOC 225E; VELP Scientifica), which was equipped with one fluorescent lamp (3.7 W; PHILIPS TLD) at six different temperatures: 5, 10, 15, 20, 25, and 30°C (photoreactivation). The range of the lamp wavelengths was 310 to 420 nm, with a broad peak at 360 nm. Irradiation periods were in the range of 30 to 240 min. The UV-A fluence rate of the fluorescent lamp was 0.1 mW/cm² at 360 nm at the sample surface, as estimated by the point source summation method and the distance between the samples and the lamp. The other Erlenmeyer flask was covered immediately with aluminum foil and incubated simultaneously at the same temperature for 240 min (dark repair). The concentration of bacteria was measured every 15 or 30 min by using a pipette to take samples from each Erlenmeyer flask.

Enumeration of microorganisms.

Three bacterial indicators of microbiological contamination have been analyzed: total number of coliforms (TC), number of fecal coliforms (FC), and number of Streptococcus faecalis bacteria (SFB).

All of the microorganisms were analyzed according to the EPA's standard methods for the examination of water and wastewater (14) by using the membrane filter technique. Total coliforms were cultured on MF-Endo agar and incubated at 35°C for 24 h. Fecal coliforms were determined on m-FC agar and with 24 h of incubation at 44.5°C. Finally, S. faecalis isolates were grown on Kenner fecal agar at 37°C for 48 h. After the incubation period, bacterial colonies were counted, and the results were calculated as CFU per 100 ml of sample. For each microorganism and each experimental condition used, tests were repeated at least three times and mean values were obtained from these repeated experiments.

Experiments were repeated three times independently for each microbial indicator and experimental condition used. Standard deviations of triplicates are not presented on the graphs in the interest of clarity. When standard deviation was disproportionate (coefficient of variance, >20%), data were rejected.

The rates of reactivation were assessed by determining microorganism survival from microbial numbers before disinfection and after reactivation phenomenon.

RESULTS

Modeling the reactivation kinetics.

Reactivation is frequently expressed as a function of the survival ratio with respect to the initial microorganism concentration existing before the inactivating treatment. Therefore, survival values were calculated using the following equation:

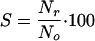(1)

where S is the survival ratio at time t, N_o is the concentration of microorganisms before disinfection (CFU/100 ml), and N_r is the concentration at time t after the beginning of the reactivation phase (CFU/100 ml).

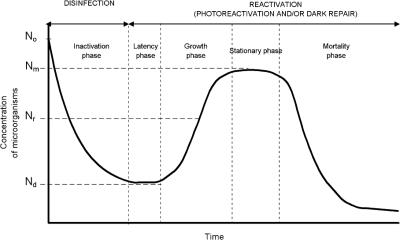
A typical inactivation-reactivation curve as a function of time is shown in Fig. 1. In that figure, it is possible to differentiate the various phases of the process: exponential UV inactivation and the reactivation process, which includes an induction period, the growth phase, the stabilization phase, and the decay period. As stated, reactivation can occur by two mechanisms according to the exposure of the samples to light or darkness.

FIG. 1.

Typical inactivation-reactivation curve as a function of time, where N_o is the concentration of microorganisms before disinfection, N_d is that after disinfection but before reactivation, and N_r is that at time t after the beginning of the reactivation phase. N_m is the maximum concentration of microorganisms reached by reactivation.

Photoreactivation kinetic.

Kashimada et al. (7) proposed an asymptotic model, assuming that the photoreactivation phenomenon follows a saturation-type first-order reaction, as shown by the following equation:

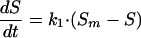(2)

where S_m is the maximum survival ratio (N_m/N_o · 100 [N_m is the maximum concentration of microorganisms {CFU/100 ml}]) and k₁ is the first-order reactivation rate constant.

In the model, the term S_m − S acts as the driving force for the reactivation. As the survival ratio, S, is reaching its maximum value (S_m), the process decelerates, showing an asymptotic tendency.

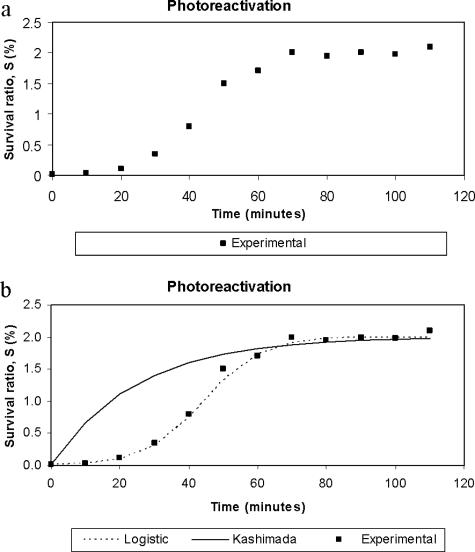
Reactivation curves have been obtained by means of the experiments described below. In Fig. 2a, the typical asymptotic sigmoidal shape of these curves can be observed. In the induction period, the curve suffers imperceptible reactivation, then a rapid exponential growth can be seen, and finally a stabilization period is reached when growth ceases. After applying the model of Kashimada et al. (7), we observed that it did not fit the data correctly, mainly at the beginning of the curve, when an induction period is observed (Fig. 2b). Hence we decided to modify the model, but without increasing the number of parameters. The new model is represented by equation 3:

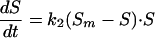(3)

where k₂ is the new growth, second-order reactivation rate constant. This relationship is simply a combination of the second-order equation and the driving force concept employed by Kashimada et al. (7). The equation is really not new because it coincides in its mathematical form with the logistic equation proposed by Verhulst in 1838 (15) to interpret biological population growth. Nevertheless, the originality of our work lies in the innovative application of the equation to microorganism reactivation prediction. The model has the advantage that both kinetic parameters, S_m and k₂, have clear physical significance. On one hand, S_m is the maximum limit of the survival of the microorganisms by reactivation and, on the other hand, k₂ represents the rate at which that value is reached. It can be seen in Fig. 2b that this proposed model correctly fits the experimental data.

FIG. 2.

(a) Typical photoreactivation curve. (b) Curves from the model proposed by Kashimada et al. and the logistic model.

By the integration of equation 3, the following equation is obtained:

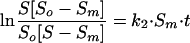(4)

where S_o is the survival immediately after UV disinfection (N_d/N_o · 100 [N_d is the concentration of microorganisms after disinfection {before reactivation} {CFU/100 ml}]).

From equation 4, it is possible to express the variable S as a function of the kinetic parameters k₂, S_m, S_o and time (equation 5) and, as a result, we can easily obtain both parameters S_m and k₂ by nonlinear regression:

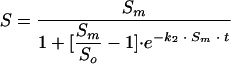(5)

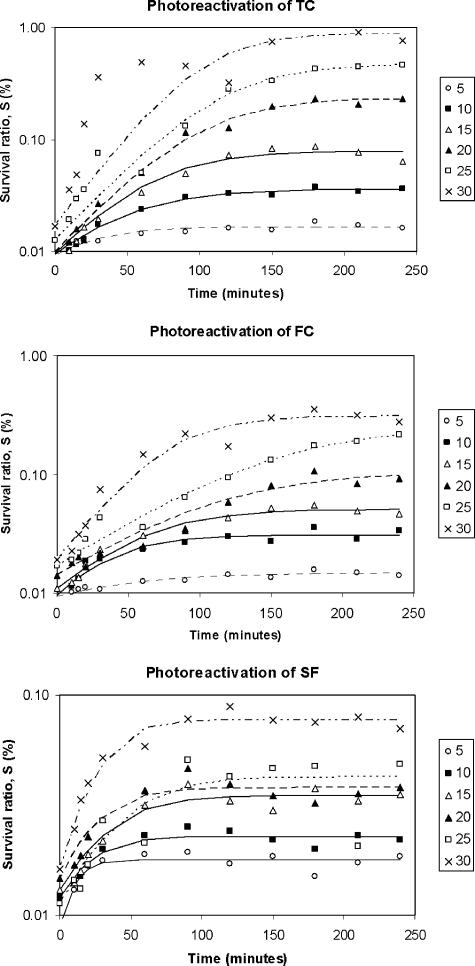
Equation 5 allows the photoreactivation curve over time to be simulated (Fig. 3).

FIG. 3.

Survival ratio (logarithmic scale) versus time of exposure to photoreactivating light for different reactivation temperatures (5 to 30°C). Experimental data and prediction by the logistic model are shown.

Photoreactivation experiments.

As stated, samples were exposed to an inactivating UV-C dose of 100 mW·s/cm² and then to six reactivation temperatures (5, 10, 15, 20, 25, and 30°C). Figure 3 represents the survival ratio (on a logarithmic scale) versus time for TC, FC, and SFB, and the asymptotic shape of the curves can be seen, including an induction period, an exponential growth phase, and finally a stabilization phase. The model described in equation 5 was applied to experimental data by nonlinear regression. Table 2 gives the values of the estimated kinetic parameters S_m and k₂, together with the r² statistics and the optimization function (observed − predicted)². The good fit of the model to the experimental data can be observed.

TABLE 2.

Kinetic parameters of the logistic model applied to photoreactivation experiments^a

Temp (°C)	TC				FC				SFB
	Sm (% survival)	k2 [(%·min)−1]	(Obs − Pred)2 [(% survival)2]	r2	Sm (% survival)	k2 [(%·min)−1]	(Obs − Pred)2 [(% survival)2]	r2	Sm (% survival)	k2 [(%·min)−1]	(Obs − Pred)2 [(% survival)2]	r2
5	0.017	2.264	1.126E-05	0.868	0.015	1.266	4.042E-06	0.917	0.018	6.451	1.410E-05	0.860
10	0.036	0.788	2.299E-05	0.984	0.031	1.185	7.086E-05	0.915	0.023	2.308	2.031E-05	0.902
15	0.079	0.392	5.121E-04	0.952	0.051	0.533	9.834E-05	0.968	0.035	1.144	8.790E-05	0.920
20	0.232	0.135	1.605E-03	0.983	0.106	0.172	9.221E-04	0.930	0.038	1.286	1.600E-04	0.865
25	0.468	0.067	4.119E-03	0.990	0.256	0.070	4.795E-04	0.992	0.042	0.867	8.692E-04	0.682
30	0.881	0.044	3.588E-01	0.800	0.307	0.118	1.392E-02	0.923	0.077	0.801	3.604E-04	0.945

^aObs, observed; Pred, predicted.

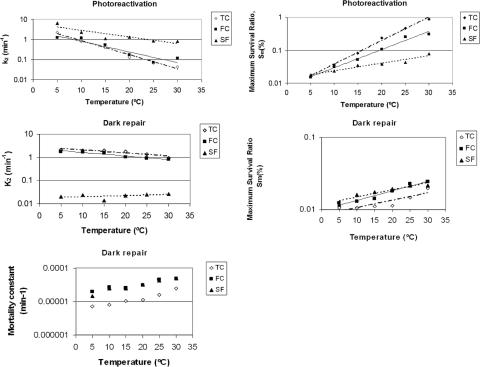
This study indicated similar behavior with respect to the reactivation temperature for the three microbial indicators. Thus, TC, FC, and SFB all showed an expected result: the higher the temperature, the greater the maximum reactivation observed. By comparing upper reactivation limits (S_m), we found the following sequence: TC > FC > SFB. The maximum survival ratio (TC exposed to 30°C) did not exceed 1%. Despite this apparently low percentage, for an N_o of 10⁶ CFU/ml, a reactivation of 10⁴ colonies/ml would be produced; this could cause serious health and environmental problems. On the other hand, if the temperature dependence of k₂ is considered (Table 2 and Fig. 4), the following relationship is observed: the higher the temperature, the smaller the value for the kinetic parameter k₂. Normally, chemical and biochemical rates are increased by temperature, according to the Arrhenius relationship; however, in this case the opposite behavior was observed. In fact, k₂ is not a pure reaction rate constant, but rather is a model parameter that is adjusted to predict the experimental data. Its physical meaning is related to the time required to reach the maximum survival ratio and then the stabilization phase: high k₂ values signify short induction and growth phases. The trend of k₂ versus temperature found in these experiments could be explained as follows: since an elevated temperature provides a higher maximum of reactivation (S_m) then to reach that maximum, more time is required, and thus, the k₂ constant is lower. By comparing the k₂ values for each different microbial indicator (Table 2 and Fig. 4), the following sequence can be seen: TC ≈ FC < SFB. This means that SFB reaches the maximum survival ratio sooner than do TC and FC (Fig. 3), although this maximum is lower than those reached by TC and FC. Therefore k₂ values may depend on particular biochemical repair mechanisms that vary among different microorganisms.

FIG. 4.

Kinetic parameters S_m, k₂, and M of the logistic model for the three microorganism groups assayed: TC, FC, and SFB. A comparison between dark repair and photoreactivation is shown.

In Table 3 and Fig. 4, the consistent behavior of S_m and k₂ with temperature can be seen. On one hand, S_m (the asymptotic limit of the microorganism survival due to photoreactivation) shows a positive exponential trend with the reactivation temperature. This finding indicates that low temperatures represent impediments for the bacteria, making their reactivation less easy, while high temperatures encourage a more extended photoreactivation process. On the other hand, k₂ (the kinetics rate constant) shows an inverse tendency: it decreases with increasing temperature. This finding means that the reactivation phenomenon finishes sooner when the temperature is low because a lower survival level is reached than that with higher temperatures.

TABLE 3.

Exponential dependence of the reactivation parameters S_m, k₂, and M on the temperature of the reactivation phase

Reactivation condition	Microbial indicator	Coefficient for predicting indicated parameter
		k2 = b·e(a · T)			Sm = b·e(a · T)			M = b·e(a · T)
		b	a	r2	b	a	r2	b	a	r2
Photoreactivation	TC	4.277	−0.161	0.985	0.007	0.164	0.995
	FC	2.763	−0.123	0.872	0.008	0.127	0.984
	SFB	5.922	−0.076	0.812	0.014	0.053	0.939
Dark repair	TC	2.790	−0.030	0.825	0.008	0.023	0.771	5.082E-06	0.048	0.930
	FC	2.310	−0.035	0.927	0.010	0.030	0.943	1.684E-05	0.035	0.938
	SFB	0.018	0.011	0.186	0.012	0.023	0.880	1.332E-05	0.044	0.940

^aa and b, exponential regression coefficients; T, temperature.

Dark repair kinetic.

After carrying out the dark repair experiments, it was observed that the curve of the survival of microorganisms versus time showed, after a low and brief reactivation period, a decay phase not detected in photoreactivation experiments. We concluded that in darkness, the reactivation did occur but to a lesser extent than that in illuminated conditions, and then the survival commenced a decreasing tendency (Fig. 5). Therefore the model proposed (equation 5) did not fit these data, and it was necessary to include a term corresponding to the decay process. Observing experimental curves, we decided to probe a zero-order kinetic for this decay process, following equation 6:

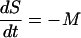(6)

where M, mortality, is a zero-order decay rate constant.

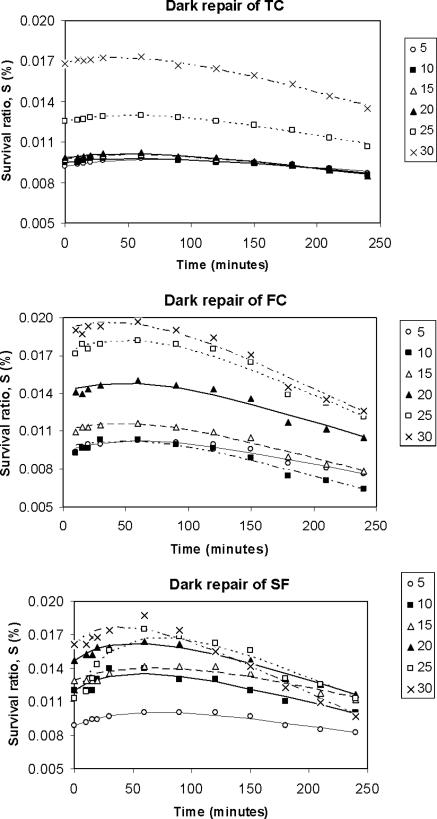
FIG. 5.

Survival ratio (logarithmic scale) versus time of exposure to darkness for different reactivation temperatures (5 to 30°C). Experimental data and prediction by the logistic model are shown.

Equation 7 is obtained by integrating equation 6, and it indicates that the decay term is linear over time

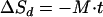(7)

By combining equations 5 and 7, the modified version of the integrated model is obtained, which is also valid for dark repair:

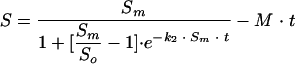(8)

Dark repair experiments.

Figure 5 shows that in conditions of darkness, reactivation occurs to a considerably lower degree than that in the case of photoreactivation. After the maximum survival is reached, a decay process is observed, with survival diminishing according to a linear trend over time. For this reason, a modification has been made to the model (equation 8). In Table 4, the results of applying the model are listed, including the values of the three kinetic parameters estimated: S_m, k₂, and M (mortality rate constant). The last parameter, M, is calculated experimentally from the slope of the linear end of the survival curve (between the 120 min point and the last point at 240 min). The good fit of the model to the experimental data from dark repair experiments can also be seen. The parameters S_m and k₂ have exponential relationships with temperature, similar to those found in the photoreactivation experiments, whereas M seems to be dependent on temperature and the microorganism, having a slight tendency to increase when temperature increases. The value of M ranges between 1 × 10⁻⁵ and 6 × 10⁻⁵ (percent survival per min). Those values are relatively small, since during the 240 min of reactivation, a maximum reduction of survival of only approximately 0.015% will be produced. TC presented lower values of M than did FC and SFB, and the last two reached figures similar to each other (Fig. 4).

TABLE 4.

Kinetic parameters of the logistic model applied to dark repair experiments^a

Temp (°C)	TC					FC					SFB
	Sm (%)	k2 [(%·min)−1]	M (%/min)	(Obs − Pred)2 [(%)2]	r2	Sm (%)	k2 [(%·min)−1]	M (%/min)	(Obs − Pred)2 [(%)2]	r2	Sm (%)	k2 [(%· min)−1]	M (%/min)	(Obs − Pred)2 [(%)2]	r2
5	0.0106	7.21E-06	2.129	6.10E-08	0.938	0.0124	1.98E-05	1.820	3.39E-07	0.960	0.0118	1.47E-05	0.020	2.25E-07	0.950
10	0.0106	7.88E-06	2.000	8.71E-08	0.953	0.0129	2.68E-05	1.652	1.05E-06	0.947	0.0160	2.50E-05	0.024	2.18E-06	0.869
15	0.0111	1.04E-05	2.032	4.12E-08	0.985	0.0141	2.60E-05	1.609	5.14E-07	0.973	0.0174	2.45E-05	0.014	1.32E-06	0.880
20	0.0113	1.11E-05	1.745	6.52E-08	0.978	0.0182	3.16E-05	1.054	1.34E-06	0.948	0.0195	3.24E-05	0.022	6.36E-07	0.977
25	0.0146	1.56E-05	1.391	8.49E-08	0.986	0.0229	4.46E-05	0.909	1.62E-06	0.967	0.0215	4.17E-05	0.025	3.83E-06	0.952
30	0.0198	2.50E-05	0.952	1.92E-07	0.989	0.0242	4.84E-05	0.833	2.11E-06	0.971	0.0215	4.84E-05	0.027	3.59E-06	0.962

^aObs, observed; Pred, predicted.

In Fig. 4, it is possible to compare the photoreactivation and dark repair processes through the kinetic parameters obtained resulting from the application of the model. It can be seen that, at elevated temperatures, S_m is more than 1 order of magnitude higher in the case of photoreactivation, unlike k₂, which is higher in dark experiments where reactivations finish earlier. Table 3 lists the coefficients of the fitted exponential that are useful for predicting the S_m, k₂, and M parameters by type of microorganism, light or dark conditions, and reactivation temperature. Good correlations can be seen, except in the case of k₂ in SFB and darkness, where no variations with temperature are observed and hence a low r² is obtained.

DISCUSSION

The kinetic model proposed by Kashimada et al. (7), a first-order saturation type, does not adequately fit the data obtained in reactivation experiments conducted in conditions of light and darkness, because it does not take into account the existence of an induction period.

A modification of that model is proposed, which consists of changing from a first- to a second-order reaction while keeping the concept of saturation model suggested by Kashimada et al. The new model, which actually coincides with the classical logistic equation, incorporates two kinetic parameters, S_m (maximum survival ratio) and k₂ (reactivation rate constant). In order to interpret correctly the reactivation that occurs in conditions of darkness, a new term for decay, based on the parameter M, the mortality rate constant, is added to the logistic equation. The model accurately fits the data obtained in photoreactivation experiments and permits the interpretation of the estimated kinetic parameters S_m, k₂, and M (only for dark repair) and their relationship with various environmental conditions, such as microbial type, light, and temperature.

With respect to the type of microbial indicator exposed to photoreactivating light, the maximum survival ratio S_m follows the sequence TC > FC > SFB, whereas for the pseudo-second-order kinetics constant k₂, the sequence is SFB > TC = FC. Dark repair was less important than photoreactivation, with the differences between the microbial indicator types therefore being less relevant. The maximum survival ratio (TC exposed to 30°C and to reactivating light) did not exceed 1%; however, despite this apparently low percentage, it could cause serious health and environmental problems.

In the experiments carried out in darkness, S_m was 1 order of magnitude lower than that in the experiments of photoreactivation and, to the contrary, k₂ was greater in darkness experiments.

The new kinetic parameter, M, shows a slight tendency to increase when temperature increases. We suppose that this mortality rate is due to the residual effect of radiation on the bacterial DNA, since the biochemical mechanism of actuation needs some time to be manifested completely. It is possible that mortality does not occur in photoreactivation experiments since, in this situation, the repair of damaged DNA is more effective.

The parameters S_m, k₂, and M, both in photoreactivation and in conditions of darkness, have shown exponential dependence on the reactivating temperature, and it is possible to predict their values and then the reactivation curve from the equations proposed in this work.

S_m increases with the temperature, indicating that the extent of reactivation is favored by elevated temperatures.

However, k₂ diminishes with the temperature of the reactivation. This fact is due to k₂ not being a pure reaction rate constant: it is a model parameter that is adjusted to predict the experimental data. Its physical meaning is related to the time required to reach the maximum survival ratio and then the stabilization phase: high k₂ values signify short induction and growth phases.

M also seems to be dependent on temperature and has a slight tendency to increase when temperature increases. The value of M ranges between 1 × 10⁻⁵ and 6 × 10⁻⁵ (percent survival per min). These are relatively low values since during the 240 min of reactivation there is a maximum reduction of survival of only approximately 0.015%.

Since UV irradiation occurs at room temperature (15 to 20°C), the reactivation experiences at the most extreme temperatures assayed (5 and 30°C) could cause a temperature shock to the bacteria and therefore alter the reactivation process. No control experiments were conducted to quantify this effect separately, but the results of our experiment permit the modeling of the microbial survival after UV-C irradiation at several temperatures. That survival would be a consequence of the combined effect of reactivation and temperature shock.

Nevertheless, TC, FC, and SFB are each heterogeneous groups and the composition of these indicators may change; this new model has the capability of fitting to experiment data from different wastewaters, resulting in new parameters that will permit the prediction of the reactivation process.