EFFECTS OF SOG ON DPP-RECEPTOR BINDING

Abstract

Concentration gradients of morphogens are known to be instrumental in cell signaling and tissue patterning. Of interest here is how the presence of a competitor of BMP ligands affects cell signaling. The effects of Sog on the binding of Dpp with cell receptors are analyzed for dorsal-ventral morphogen gradient formation in vertebrate and Drosophila embryos. This prototype system includes diffusing ligands, degradation of morphogens, and cleavage of Dpp-Sog complexes by Tolloid to free up Dpp. Simple and biologically meaningful necessary and sufficient conditions for the existence of a steady state gradient configuration are established, and existence theorems are proved. For high Sog production rates (relative to the Dpp production rate), it is found that the steady state configuration exhibits a more intense Dpp-receptor concentration near the dorsal midline. Numerical simulations of the evolution of the system show that, beyond some threshold Sog production rate, the transient Dpp-receptor concentration at the dorsal midline would become more intense than that of the steady state, before subsiding and approaching a nonuniform steady state of lower magnitude. The magnitude of the transient concentration has been found to increase by several fold with increasing Sog production rate. The highly intense Dpp activity at and around the dorsal midline is consistent with available experimental observations and other analytical studies.

1. Introduction

The proper functioning of tissues and organs requires that each cell differentiate appropriately for its position. In many cases, the positional information that instructs cells about their prospective fate is conveyed by concentration gradients of morphogens bound to cell receptors. Morphogens are signaling molecules that, when bound to cell receptors, assign different cell fates at different concentrations [1], [2]. Morphogen action is of special importance in understanding development because it is a highly efficient way for a population of uncommitted cells in an embryo to create complex patterns of gene expression in space. This role of morphogens has been the prevailing thought in tissue patterning for over half a century, but only recently have there been sufficient experimental data and adequate analytical studies for us to begin to understand how various useful morphogen concentration gradients are formed [3], [4].

Dorsal-ventral (back-to-belly) patterning in vertebrate and Drosophila (fruit fly) embryos is now known to be regulated by bone morphogenetic proteins (BMP). The BMP activity is controlled mainly by several secreted factors including the antagonists chordin and short gastrulation (Sog). In Drosophila, seven zygotic genes have been proposed to regulate dorsal-ventral patterning. Among them, decapentaplegic (Dpp) encodes BMP homologues that promote dorsal cell fates such as amnioserosa and inhibits development of the ventral central nervous system. The chordin homologue Sog is expressed ventrally and promotes central nervous system development. The phenotype of Sog loss-of-function mutants is intriguing; as expected for a Dpp antagonist, ventral structures are lost but, in addition, the amnioserosa is reduced. This result is paradoxical, as the amnioserosa is the dorsal-most tissue, and thus apparently a BMP antagonist is required for maximal BMP signaling [5], [6], [7], [8].

In principle, morphogen concentration gradients can be generated through the production of morphogens at particular sources, followed by their diffusion and degradation in appropriate regions [4], [9], [10], [11], [12]. In the above Dpp/Sog system, the production of Dpp is pretty much uniform in the dorsal region and absent in the ventral region, while the opposite is true for Sog. However, the Dpp activity has a sharp peak around the midline of the dorsal region in the presence of its “inhibitor” Sog. Mutation of Sog results in a reduction and a broadening of Dpp activity around the midline of the dorsal region. As the system contains many variables, the question of what leads to a sharp concentration peak is difficult to tackle by traditional experimental means.

Recently, Eldar et al. [13] studied a more complex morphogen system that includes the effects of Sog (and other morphogens) on Dpp activities. By performing massive computer calculations to search for molecular networks that support robustness, they found that the presence of the BMP inhibitor Sog stimulates intense Dpp activity at the dorsal midline resulting in highly nonuniform Dpp-receptor concentration in space for the the patterning process. They also showed that the Dpp concentration gradient itself is robust to changes in gene dosage. Two conditions were stipulated in their model to produce agreement with experimentally observed gradient formation. First, the steady state of the system is achieved by shutting off the production of Dpp through setting the production rate to zero 10 minutes after the initiation of the system [14], and there is no degradation of Dpp-receptor complex in the model. Second, the model requires immobility of free Dpp molecules; i.e., Dpp does not diffuse, but diffusion of the Dpp-Sog complexes and other ligands can occur.

For formation of morphogen gradients in a wing imaginal disc (a structure in the larva that will become the wing of the adult fly), Lander, Nie, and Wan [4] and Lou, Nie, and Wan [9] have demonstrated the important biological roles of diffusion for Dpp, and degradation for the Dpp-receptor complex. Without degradation, the steady state of the system is not achievable unless ligand production is shut off after a while, as in [14]. Eldar et al., in a recent paper [15], have also studied how degradation of ligand affects robustness of morphogen gradients. Most recently, the diffusion coefficient of Dpp has been measured in vivo using FCS (fluorescence correlation spectroscopy) techniques [16], and it was found that the magnitude of diffusion coefficient for Dpp is close to the magnitude of the diffusion coefficient for the Dpp-Sog complex used in [14] and hence not negligible.

Given the rather special restrictions on the Dpp/Sog system in [13] and [14], it is desirable to investigate the possibility of an alternative and simpler known biological mechanism for the generation of the intense Dpp activities around the dorsal midline. In this paper, we will extend the dynamic Dpp/Sog system formulated in [17] for morphogen activities in dorsal-ventral patterning by allowing for diffusion of ligands, degradation of the morphogens, and the cleavage of Dpp-Sog complexes by the enzyme Tolloid to free up a fraction τ of Dpp and to degrade part of Sog.

In this study, we will establish a biologically meaningful necessary and sufficient condition for the existence of a steady state. This condition requires a balance of the production of ligands, strength of degradation, and rate of cleavage of Dpp-Sog complex by Tolloid, with no restrictions on the diffusion coefficients of the ligands. To gain insight into the dependence of the morphogen activities on various biological parameters, we will obtain a perturbation solution of the steady state gradients with a biologically relevant assumption that the Sog production rate is high compared to that of Dpp [13], [14]. The solution indicates that the requirement for complete immobility of Dpp is not necessary for a biologically realistic Dpp-receptor gradient that is intense in Dpp activity at the dorsal midline. Finally, we will perform numerical simulations for the dynamics of the system. It is found that the cleavage of Sog-Dpp complex by Tolloid produces a transient peak of the Dpp-receptor concentration around the dorsal midline that is significantly stronger than the corresponding concentration at the steady state. The dependence of the peak on various biological parameters, including Sog production rate and diffusion coefficients, is also investigated. The overall features of the various concentrations of the model are consistent with experimental observations [5], [6], [7], [8]. A more complete model including more biological components and its comparison with new experiments on robustness of morphogen gradients will be presented in a separate paper [18].

2. Mathematical formulation

For an analytical and computational study of the biological phenomenon of interest, a system of partial differential equations and auxiliary conditions is formulated to capture the essential features of the dynamics of the two interacting morphogens. This approach was first applied to study the development of the Drosophila wing imaginal disc [19], [20], [4]. The three basic biological processes involving Dpp in the wing disc are diffusion for free Dpp molecules, their reversible binding with receptors, and degradation of the bound Dpp. The main purpose was to investigate the role of diffusion in the formation of a Dpp-receptor concentration gradient in the wing disc. That system was extended to include the effect of Sog on Dpp activities in a dorsal-ventral configuration [17] in an embryo, with the cleavage of Dpp-Sog complexes by Tolloid implicitly incorporated into the system through the complete recovery of Dpp after cleavage (while the Sog components degrade completely). The cleavage-recovery phenomenon has been suggested by previous experimental studies [21], [22]. Here we consider an even more general system than that in [17] by allowing fractional recovery through the fraction parameter τ, 0 ≤ τ ≤ 1, with τ = 1 corresponding to complete recovery.

The setting for dorsal-ventral patterning in a Drosophila embryo during development is different and more complex than that considered in [4]. As shown in the sketch of the dorsal-ventral cross section of the embryo in Figure 1, Dpp is produced only in the dorsal region (with the rate v_L(x)), while Sog is produced only in the ventral region (with the rate v_S(x)). For a one-dimensional study of the dynamics of Sog and Dpp in the presence of cell receptors, we have idealized the dorsal-ventral annular cross-section of the embryo as a ring and introduced an artificial cut of the ring at the ventral midline to map the cut ring onto the line segment [−X_max, X_max], with X = 0 corresponding to the dorsal midline. Let [L], [S], [LS], [LR] denote the concentrations of Dpp, Sog, Dpp-Sog complexes, and Dpp bound to receptors, respectively. The first three diffuse with coefficients of diffusion D_L, D_S, and D_LS, respectively, while the concentration for the immobile and undegradable receptor is fixed at R₀ and uniformly distributed in [−X_max, X_max]. The system of equations governing the morphogen dynamics of such a system consists of the following four coupled second order differential equations, three of them being nonlinear partial differential equations (PDE) of the reaction-diffusion type:

Fig. 1.

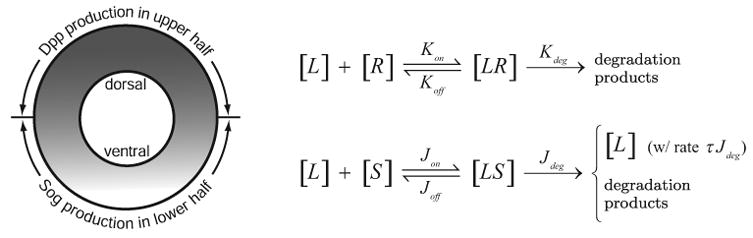
Cross section of a Drosophila embryo, and the reaction schemes with rate constants.

$$\begin{array}{l}\frac{\partial [\text{L}]}{\partial T}=D_{\text{L}}\frac{{\partial }^2[\text{L}]}{\partial X^{\text{2}}}-K_{\text{on}}[\text{L}](R_0-[\text{LR}])-J_{\text{on}}[\text{L}][\text{S}]\\ +K_{\text{off}}[\text{LR}]+(J_{\text{off}}+\tau J_{deg})[\text{LS}]+v_L(X),\end{array}$$ (1)

$$\frac{\partial [\text{LR}]}{\partial T}=K_{\text{on}}[\text{L}](R_0-[\text{LR}])-(K_{\text{off}}+K_{deg})[\text{LR}],$$ (2)

$$\frac{\partial [\text{LS}]}{\partial T}=D_{\text{LS}}\frac{{\partial }^2[\text{LS}]}{\partial X^{\text{2}}}+J_{\text{on}}[\text{L}][\text{S}]-\text{(}{J}_{\text{off}}+J_{deg})[\text{LS}],$$ (3)

$$\frac{\partial [\text{S}]}{\partial T}=D_{\text{S}}\frac{{\partial }^2[\text{S}]}{\partial X^2}-J_{\text{on}}[\text{L}][\text{S}]+J_{\text{off}}[\text{LS}]+v_S(X)$$ (4)

for −X_max < X < X_max and T > 0. The coefficients {K_on, J_on}, {K_off, J_off }, {K_deg, J_deg} are the binding rate constants, the off rate constants, and the degradation rate constants of Dpp and Sog, respectively. With the morphogen activities symmetric about the ventral (as well as dorsal) midline, we must have the following symmetry (no flux) conditions at the two ends of the solution domain:

$$X=\pm X_{max}:\frac{\partial [L]}{\partial X}=\frac{\partial [LS]}{\partial X}=\frac{\partial [S]}{\partial X}=0.$$

The number of independent parameters may be reduced by suitable normalization. Let

$$x=\frac{X}{X_{max}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t=\frac{D_{0}T}{X_{max}^2},$$ (5)

$$\{h_L,h_{LS}\}=\frac{X_{max}^2{R}_0}{D_0}\{K_{on},J_{on}\},$$ (6)

$$\{f_L,f_{LS},g_L,g_{LS}\}=\frac{X_{max}^2}{D_0}\{K_{off},J_{off},K_{deg},J_{deg}\},$$ (7)

$$\{V_L(x),V_S(x)\}=\frac{X_{max}^2}{R_0{D}_0}\{v_L(X),v_S(X)\},$$ (8)

$$\{{\rho }_L,{\rho }_S,{\rho }_{LS}\}=\left\{\frac{D_L}{D_0},\frac{D_{LS}}{D_0},\frac{D_S}{D_0}\right\},$$ (9)

$$\{A,B,C,D\}=\left\{\frac{[\text{L}]}{R_0},\frac{[\text{LR}]}{R_{\text{0}}},\frac{[\text{LS}]}{R_0},\frac{[\text{S}]}{R_{\text{0}}}\right\}.$$ (10)

In these relations, it would seem natural to choose the normalizing diffusion coefficient D₀ to be the maximum of the three diffusion coefficients. However, it turns out to be more appropriate to choose D₀ = D_S to facilitate an appreciation of the implication of the solution. At this time, we will leave D₀ unspecified, but will see in section 4 why it is expeditious to specify it as D_S. In terms of these normalized quantities, (1)–(4) may be written as

$$A_{,t}={\rho }_L{A}_{,xx}-h_{L}A(1-B)-h_{LS}AD+f_{L}B+(f_{LS}+\tau g_{LS})C+V_L(x),$$ (11)

$$B_{,t}=h_{L}A\hspace{0.17em}(1-B)-(f_L+g_L)B,$$ (12)

$$C_{,t}={\rho }_{LS}{C}_{,xx}+h_{LS}AD-(f_{LS}+g_{LS})C,$$ (13)

$$D_{,t}={\rho }_S{D}_{,xx}-h_{LS}AD+f_{LS}C+V_S(x)$$ (14)

for −1 < x < 1 and t > 0, with ( )_,z = ∂( )/∂z for the temporal and spatial derivatives of the dependent variables A, B, C, D.

3. Existence of steady state solutions

In this section, we examine the existence of time-independent (or steady state) solutions of the system (11)–(14) subject to the no flux conditions at the two end points, which can now be written in terms of the normalized unknowns as

$$x=\pm 1:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}_{,x}=C_{,x}=D_{,x}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(t>0).$$ (15)

With the steady state solution independent of time, (12) becomes an algebraic equation and can be solved for B in terms of A:

$$B=\frac{A}{{\alpha }_L+A},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\alpha }_L=\frac{g_L+f_L}{h_L}.$$ (16)

The expression for B is then used to eliminate it from (11), leaving the following three simultaneous equations for the three unknowns A, C, and D:

$${\rho }_L{A}_{,xx}-\frac{g_L{h}_{L}A}{f_L+g_L+h_{L}A}-h_{LS}AD+(f_{LS}+\tau g_{LS})C+V_L=0,$$ (17)

$${\rho }_{LS}{C}_{,xx}+h_{LS}AD-(f_{LS}+g_{LS})C=0,$$ (18)

$${\rho }_S{D}_{,xx}-h_{LS}AD+f_{LS}C+V_S=0$$ (19)

for −1 < x < 1 subject to the boundary conditions (15).

Throughout this section we assume the following:

(A1) f_L, f_LS, g_L, g_LS, h_L, and h_LS are continuous positive functions in [−1, 1];ρ_L, ρ_LS, and ρ_S are positive constants; V_S, V_L are nonnegative integrable functions that satisfy ${\int }_{-1}^1{V}_L>0$ and ${\int }_{-1}^1{V}_S>0$; and τ is a constant satisfying 0 ≤ τ ≤ 1.

If V_L(x) and V_S(x) are continuous, we seek a classical solution of (15)–(19); i.e., A, C, and D are twice continuously differentiable in [−1, 1] that satisfy (15)–(19).

Theorem 3.1

Suppose that (A1) holds and V_L, V_S are continuous in [−1, 1]. Then (15)–(19) has a positive classical solution if and only if both of the following inequalities hold:

$${\int }_{-1}^1{V}_L(x)dx>(1-\tau ){\int }_{-1}^1{V}_S(x)dx,$$ (20)

$${\int }_{-1}^1{V}_L(x)dx\hspace{0.17em}<\hspace{0.17em}(1-\tau ){\int }_{-1}^1{V}_S(x)dx+{\int }_{-1}^1{g}_L(x)dx.$$ (21)

Since ${\int }_{-1}^1{V}_L(x)>0,$ the first condition is trivially satisfied for τ = 1 (full recovery of Dpp), and the second is a distributed version of the necessary and sufficient condition for existence in [9], [10], [11], [12] (that the Dpp production rate must be slower than the degradation rate of the Dpp-receptor complexes). For 0 ≤ τ < 1, these two conditions may be combined to give a similar condition on a nonnegative “effective” Dpp production rate [V_L - (1 - τ )V_S] (see section 5).

Lemma 3.2

If (15)–(19) has a positive classical solution, then (20) and (21) must hold.

Proof

Adding up (17) and (18) and integrating over [−1, 1], we obtain with the help of (15)

$${\int }_{-1}^1{V}_L={\int }_{-1}^1\frac{g_L{h}_{L}A}{f_L+g_L+h_{L}A}+(1-\tau ){\int }_{-1}^1{g}_{LS}C.$$ (22)

Similarly, adding up (18) and (19) and integrating over [−1, 1], we get

$${\int }_{-1}^1{g}_{LS}C={\int }_{-1}^1{V}_S.$$ (23)

It follows from (22) and (23) that

$${\int }_{-1}^1{V}_L={\int }_{-1}^1\frac{g_L{h}_{L}A}{f_L+g_L+h_{L}A}+(1-\tau ){\int }_{-1}^1{V}_S.$$ (24)

For A > 0 in [−1, 1], we have

$$0<{\int }_{-1}^1\frac{g_L{h}_{L}A}{f_L+g_L+h_{L}A}<{\int }_{-1}^1{g}_L,$$ (25)

which along with (24) implies (20)–(21).

In view of Lemma 3.2, we’ll assume that (20)–(21) holds for the rest of this subsection. Our goal is to show that if V_L and V_S are continuous, then the condition (20)–(21) implies that (15)–(19) has at least a positive classical solution. The idea is to introduce some parameter and consider the following system of equations:

$${\rho }_L{\tilde{A}}_{,xx}+\lambda F_1(x,\tilde{A},\tilde{C},\tilde{D})=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1,$$ (26)

$${\rho }_{LS}{\tilde{C}}_{,xx}+\lambda F_2(x,\tilde{A},\tilde{C},\tilde{D})=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1,$$ (27)

$${\rho }_S{\tilde{D}}_{,xx}+\lambda F_3(x,\tilde{A},\tilde{C},\tilde{D})=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1,$$ (28)

$${\tilde{A}}_{,x}={\tilde{C}}_{,x}={\tilde{D}}_{,x}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{at\hspace{0.17em}}x=-1,1,$$ (29)

where λ ∈ (0, 1] and F_i (i = 1, 2, 3) is given by

$$F_1(x,\tilde{A},\tilde{C},\tilde{D})=-\frac{g_L{h}_L\tilde{A}}{f_L+g_L+h_L\tilde{A}}-h_{LS}\tilde{A}\tilde{D}+(f_{LS}+\tau g_{LS})C+V_L,$$ (30)

$$F_2(x,\tilde{A},\tilde{C},\tilde{D})=h_{LS}\tilde{A}\tilde{D}-(f_{LS}+g_{LS})\tilde{C},$$ (31)

$$F_3(x,\tilde{A},\tilde{C},\tilde{D})=-h_{LS}\tilde{A}\tilde{D}+f_{LS}\tilde{C}+V_S.$$ (32)

We establish some a priori estimates for nonnegative classical solutions of (26)–(29).

LEMMA 3.3

Let (Ã, C̃, D̃) be any nonnegative classical solution of (26)–(29). If λ > 0, then à (x) > 0, C̃ (x) > 0, and D̃ (x) > 0 for every x ∈ [−1, 1].

Proof

Similar to (23) we have ${\int }_{-1}^1{g}_{LS}\tilde{C}={\int }_{-1}^1{V}_S.$ Hence C̃ ≥ 0, C̃ ≡⃥ 0. By (27) and (31) we have

$$-{\rho }_{LS}{\tilde{C}}_{,xx}+\lambda (f_{LS}+g_{LS})\tilde{C}=\lambda h_{LS}\tilde{A}\tilde{D}\ge 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1.$$ (33)

This together with C̃,_x(−1) = C̃,_x(1) = 0, via the maximum principle [23], implies that C̃(x) > 0 for every x ∈ [−1, 1]. Since V_L ≡⃥ 0 and V_S ≡⃥ 0, similarly by (26)–(29) and the maximum principle we can show that à > 0 and D̃ > 0 in [−1, 1].

LEMMA 3.4

There exists some constant M >0, independent of λ, such that for any 0 < λ ≤1 and any positive classical solution (Ã, C̃, D̃) of (26)–(29) we have

$$\Vert \tilde{A}{\Vert }_{L^{\hspace{0.17em}\infty }}+\Vert \tilde{C}{\Vert }_{L^{\hspace{0.17em}\infty }}+\Vert \tilde{D}{\Vert }_{L^{\hspace{0.17em}\infty }}\le M.$$ (34)

The proof of Lemma 3.4 is postponed to the appendix. Lemmas 3.3 and 3.4 enable us to define Leray–Schauder degree (see, e.g., [24]) for a certain operator whose Fixed points correspond to positive solutions of (26)–(29).

Set E = {C[−1, 1]}³ and $C_N^2[-1,1]=\{u\in C^2[-1,1]:u_{,x}(-1)=u_{,x}(1)=0\}.$ For any positive constant γ, let $L_{\gamma }^{-1}$ denote the inverse of the operator $L_{\gamma }:=-\gamma \frac{d^2}{d{x}^2}+I:C_N^2[-1,1]\to C[-1,1]$, where I denotes the identity map from C[−1, 1] to itself.

For every λ ∈ [0, 1], define operator T(λ): E → E by

$$T(\lambda )(\tilde{A},\tilde{C},\tilde{D})=\left(\begin{array}{c}{L}_{{\rho }_L}^{-1}[\tilde{A}+\lambda F_1^{+}(x,\tilde{A},\tilde{C},\tilde{D})]\\ L_{{\rho }_{LS}}^{-1}[\tilde{C}+\lambda F_2(x,\tilde{A},\tilde{C},\tilde{D})]\\ L_{{\rho }_S}^{-1}[\tilde{D}+\lambda F_3(x,\tilde{A},\tilde{C},\tilde{D})]\end{array}\right),$$ (35)

where

$$F_1^{+}(x,\tilde{A},\tilde{C},\tilde{D})=\frac{-g_L{h}_{L}A}{f_L+g_L+h_L{A}_{+}}-h_{LS}AD+(f_{LS}+\tau g_{LS})C+V_L,$$ (36)

A₊ = max(A, 0). By standard regularity theory and the embedding theorem, we see that T(λ) is well defined and continuous, and the operator T̃: [−1, 1]× E → E, defined by T̃ (λ, Ã, C̃, D̃) = T(λ)( Ã, C̃, D̃), is continuous and compact. For M given in (34), define

$$\mathrm{\Omega }=\left\{(\tilde{A},\tilde{C},\tilde{D})\in E:0<\tilde{A}(x),\hspace{0.17em}\tilde{C}(x),\hspace{0.17em}\tilde{D}(x)\hspace{0.17em}<\hspace{0.17em}M+1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall x\in [-1,1]\right\}.$$

Ω is an open and bounded subset of E. By Lemmas 3.3 and 3.4, we see that for any λ ∈ (0, 1], [I − T(λ)]⁻¹ {(0, 0, 0)}∉∂Ω. Hence the Leray–Schauder degree, deg (I − T(λ), Ω, (0, 0, 0)), is well defined for 0 < λ ≤ 1. Moreover, by the homotopy invariance of the Leray–Schauder degree [24], deg (I − T(λ),Ω, (0, 0, 0)) is a constant function for 0 < λ ≤ 1. To complete the proof of Theorem 3.1, we need the following result.

PROPOSITION 3.5

There exists δ > 0 such that deg (I − T(λ),Ω, (0, 0, 0)) = 1 for λ ∈ (0, δ).

The detail of the proof of this proposition is not particularly relevant to the proof of Theorem 3.1 and will be given in an appendix of this paper. Assuming Proposition 3.5, we can now complete the proof of Theorem 3.1.

Proof of Theorem 3.1

By Lemma 3.2, it suffices to establish the sufficiency part. By Proposition 3.5, for every 0 < λ ≤ 1, deg (I − T(λ),Ω, (0, 0, 0)) = 1. In particular, deg (I − T(1),Ω, (0, 0, 0)) ≠ 0. This implies that there exists (Ã, C̃, D̃) ∈ Ω such that (I − T(1))(Ã, C̃, D̃) = (0, 0, 0). By standard regularity theory we see that Ã, C̃, D̃ ∈ C²[−1, 1] and is thus a positive classical solution of (15)–(19).

Specific morphogen systems of interest include those with morphogen production rates that are discontinuous in the spatial variable (see section 4). When V_L and V_S are bounded and measurable, we will be seeking C^1,1 solutions of (15)–(19), i.e., functions A,C,D that are differentiable in [−1, 1]; have derivatives A_,x, C_,x, and D_,x Lipschitz continuous in [−1, 1]; and satisfy (15) and for every x ∈ [−1, 1]

$${\rho }_L{A}_{,x}+{\int }_{-1}^x{F}_1={\rho }_{LS}{C}_{,x}+{\int }_{-1}^x{F}_2={\rho }_S{D}_{,x}+{\int }_{-1}^x{F}_3=0.$$ (37)

THEOREM 3.6

Suppose that (A1) holds and that V_L and V_S are bounded measurable. Then (15)–(19) has a positive C^1,1 solution if and only if (20)–(21) holds.

Proof

Suppose that (15)–(19) has a positive C^1,1 solution. Setting x = 1 in (37) and applying the same argument as in the proof of Lemma 3.2, we see that (20)–(21) must hold. On the other hand, if (20)–(21) holds, we can choose a uniformly bounded sequence of continuous positive functions $V_L^n(x)\hspace{0.17em}\text{and\hspace{0.17em}}{V}_S^n(x)$ such that $V_L^n(x)\to V_L$ and $V_S^n(x)\to V_S$ a.e., and $0<{\int }_{-1}^1[V_L^n-(1-\tau )V_S^n]<{\int }_{-1}^1{g}_L.$ By Theorem 3.1 (17)–(19), with V_L and V_S being replaced by $V_L^n\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}{V}_S^n$, respectively, there is a sequence of positive classical solutions, denoted by Aⁿ, Cⁿ, and Dⁿ. As for Lemma 3.4, we can show that there exists some positive constant M, independent of n, such that ‖A_n‖_L∞ + ‖C_n ‖_L∞ + ‖D_n‖_L∞ ≤ M. Furthermore, $\Vert A_{,xx}^n{\Vert }_{L^{\hspace{0.17em}\infty }},\Vert C_{,xx}^n{\Vert }_{L^{\hspace{0.17em}\infty }},\hspace{0.17em}\text{and}\hspace{0.17em}\Vert C_{,xx}^n{\Vert }_{L^{\hspace{0.17em}\infty }}$ are uniformly bounded. By passing to a subsequence if necessary, (Aⁿ, Cⁿ, Dⁿ) converge to some functions (A,C,D) in C¹, and A,C,D satisfy (15) and are nonnegative solutions of (37). From (37) we see that A,_x, C,_x,D,_x are Lipschitz continuous in [−1, 1]. By similar argument as in Lemma 3.3 (but instead using the maximum principle for weak solutions of (15)–(19)), we see that A,C,D are all positive in [−1, 1]. This completes the proof of Theorem 3.6.

Remark 3.7

Note that C ∈ C²[−1, 1]. If V_L and V_S are piecewise continuous, then A and D are also piecewise twice continuously differentiable in [−1, 1].

4. Approximate steady state solutions for VL ≪ VS

In previous studies [13], [14], the constant (in both space and time) Dpp production rate, v̄_L, in the dorsal region was estimated to be significantly smaller than the constant Sog production rate, v̄_S, in the ventral region. In [14], the ratio of the two production rates, defined as ε ≡ v̄_L/v̄_S, is 0.008 for its baseline study. The robustness of the solutions with respect to variations of v̄_S is studied for fixed v̄_L [13].

For v̄_L ≪ v̄_S, so that ε ≪ 1, we obtain below a perturbation solution for the steady state of (15)–(19), with τ = 1 for simplicity. For τ < 1, perturbation solution procedure applies only if (20)–(21) hold. Similar to [14], we assume

$$V_L(x)={\overline{V}}_{L}H\left(\frac{1}{2}-x\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{V}_S(x)={\overline{V}}_{S}H\left(x-\frac{1}{2}\right),$$ (38)

where $({\overline{V}}_L,{\overline{V}}_S)=({\overline{v}}_L,{\overline{v}}_S)X_{max}^2/(R_0{D}_0)$ and H(z) is the unit step function.

With V̄_L ≪ V̄_S, we expect D(x), C(x) = O(V̄_S), O(V̄_S), although the latter may be a smaller fraction of V̄_S. On the other hand, we have A(x) = O(V̄_L) at most, in fact quite a bit smaller since free Dpp should eventually be bound to Sog or receptors, given that Sog is produced at a much higher rate. For these reasons, we set

$$A(x)=\frac{{\overline{V}}_L}{{\mu }_L^2}a(x),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C(x)=\frac{{\overline{V}}_S}{f_{LS}+g_{LS}}c(x),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}D(x)={\overline{V}}_{S}d(x),$$ (39)

where ${\mu }_L^2=g_L/{\alpha }_L$ and a_L = (f_L + g_L)/h_L. Then (17)–(19) become

$$\frac{{\overline{V}}_L}{{\overline{V}}_S}\left[\frac{{\rho }_L}{{\mu }_L^2}{a}^{″}-\frac{a}{1+{\beta }_{L}a}+H\left(\frac{1}{2}-x\right)\right]-{\mu }_D^{2}ad+c=0,$$ (40a)

$${\rho }_{LS}{c}^{″}+(f_{LS}+g_{LS})[{\mu }_D^{2}ad-c]=0,$$ (40b)

$${\rho }_S{d}^{″}-[{\mu }_D^{2}ad-c]-(1-{\sigma }_{LS})c+H\left(x-\frac{1}{2}\right)=0,$$ (40c)

where ()′ = d()/dx, β_L = V̄_L/g_L, σ_LS = f_LS/(f_LS+g_LS) < 1, and ${\mu }_D^2=h_{LS}{\alpha }_L{\overline{V}}_L/g_L$. Using symmetry about x = 0, we need only to consider solutions for 0 < x < 1 with the boundary conditions at x = 0 being again no flux for all three unknowns a, b, and c.

The form of (40a)–(40c) suggests that we seek a perturbation solution of {a, c, d} in ε:

$$\{a(x;\epsilon ),c(x;\epsilon ),d(x;\epsilon )\}=\sum _{n=0}^{\infty }\{a_n(x),c_n(x),d_n(x)\}{\epsilon }^n.$$ (41)

For moderate values of V̄_L so that ${\mu }_D^2$ is not small compared to unity, the three leading term coefficients are determined by

$${\mu }_D^2{a}_0{d}_0-c_0=0,$$ (42a)

$${\rho }_{LS}{c}_0^{″}+(f_{LS}+g_{LS})[{\mu }_D^2{a}_0{d}_0-c_0]=0,$$ (42b)

$${\rho }_S{d}_0^{″}-[{\mu }_D^2{a}_0{d}_0-c_0]-(1-{\sigma }_{LS})c_0+H\left(x-\frac{1}{2}\right)=0.$$ (42c)

The complementary case, ${\mu }_D^2\ll 1,$ can also be analyzed but is not relevant for our biological system.

Upon combining (42a) and (42b) we get

$${\rho }_{LS}{c}_0^{″}=0.$$ (43)

The no flux boundary conditions at x = 0, 1 require c₀(x) ≡ σ₀ for some constant σ₀. To determine σ₀, we note that (23) is still valid and requires

$$\frac{1}{2}{\overline{V}}_S={\int }_0^1{V}_s(x)dx=g_{LS}{\int }_0^{1}C(x)dx={\overline{V}}_S\frac{g_{LS}}{f_{LS}+g_{LS}}{\int }_0^{1}c(x)dx$$ (44)

so that σ₀ = 1/2(1 − σ_LS), i.e.,

$$(1-{\sigma }_{LS})c_0(x)=\frac{1}{2},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le x\le 1.$$ (45)

To determine d₀(x), we use (42a) and (42c) to obtain

$${\rho }_S{d}_0^{″}-(1-{\sigma }_{LS})c_0+H\left(x-\frac{1}{2}\right)=0.$$ (46)

Upon integration and application of boundary conditions at x = 0, 1, as well as the continuity condition at x = 1/2 for d₀, we obtain

$${\rho }_S{d}_0(x)=\{\begin{array}{ll}{\delta }_0+\frac{x^2}{4}\hfill & \left(x\le \frac{1}{2}\right),\hfill \\ {\delta }_0-\frac{1}{8}+\frac{1}{2}\left(x-\frac{x^2}{2}\right)\hfill & \left(x\ge \frac{1}{2}\right),\hfill \end{array}$$ (47)

where δ₀ is an undetermined constant. By (42a) we have also

$$\frac{1-{\sigma }_{LS}}{{\rho }_S}{\mu }_D^2{a}_0(x)=\frac{1-{\sigma }_{LS}}{{\rho }_S}\frac{c_0(x)}{d_0(x)}=\{\begin{array}{ll}\frac{1}{2}\frac{1}{({\delta }_0+\frac{1}{4}{x}^2)}\hfill & \left(x<\frac{1}{2}\right),\hfill \\ \frac{1}{2}\frac{1}{[{\delta }_0-\frac{1}{8}+\frac{1}{2}x-\frac{1}{4}{x}^2]}\hfill & \left(x>\frac{1}{2}\right).\hfill \end{array}$$ (48)

It is rather fortuitous to have a₀′(0) = a₀′(1) = 0 because d₀ and c₀ satisfy no flux conditions at the two end points so that there are no boundary layers adjacent to the two ends.

It remains to determine δ₀. We note that (24) still holds, particularly when τ = 1. In that case, (24) becomes

$$G({\delta }_0)\equiv {\int }_0^1\frac{a_0(x)}{1+{\beta }_L{a}_0(x)}dx=\frac{1}{2}.$$ (49)

It is easy to see that G(δ₀) is strictly monotone decreasing in δ₀ and that G(δ₀) → 0 as δ₀ → ∞. Hence $G({\delta }_0)=\frac{1}{2}$ has at most one positive root, and it has one positive root if and only if $G(0)>\frac{1}{2}$. Note that G(0) can be explicitly computed, and thus $G({\delta }_0)=\frac{1}{2}$ determines δ₀.

Altogether, we have as the corresponding leading terms for the concentrations

$$A(x)\sim \frac{(1-{\sigma }_{LS}){\mu }_D^2{a}_0(x)/{\rho }_S}{R_0{J}_{on,eff}/(D_S/X_{max}^2)},$$ (50)

$$B(x)\sim \frac{{\mathrm{\Gamma }}_{LS}(1-{\sigma }_{LS}){\mu }_D^2{a}_0(x)/{\rho }_S}{1+{\mathrm{\Gamma }}_{LS}(1-{\sigma }_{LS}){\mu }_D^2{a}_0(x)/{\rho }_S},$$ (51)

$$C(x)\sim \frac{1}{2}\frac{{\overline{v}}_S}{J_{deg}{R}_0},$$ (52)

$$D(x)\sim \frac{{\overline{v}}_S/R_0}{D_S/X_{max}^2}[{\rho }_S{d}_0(x)],$$ (53)

where

$$K_{on,eff}\equiv \frac{K_{deg}{K}_{on}}{K_{deg}+K_{off}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{J}_{on,eff}\equiv \frac{J_{deg}{J}_{on}}{J_{deg}+J_{off}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{\Gamma }}_{LS}=\frac{K_{on,eff}}{J_{on,eff}}\frac{D_S}{K_{deg}{X}_{max}^2}.$$ (54)

In Figure 2, the perturbation solutions (50)–(53) are plotted against the numerical solutions obtained through temporal evolution (which will be discussed in the next section). The relative difference between the two solutions is 1.5% for A, 1.4% for B, 4.3% for C, and 2.9% for D for ε = v̄_L/v̄_S = 0.0133 and ${\mu }_D^2=18.4$. This illustrates the approximation and accuracy of the perturbation solution for ε ≪ 1.

Fig. 2.

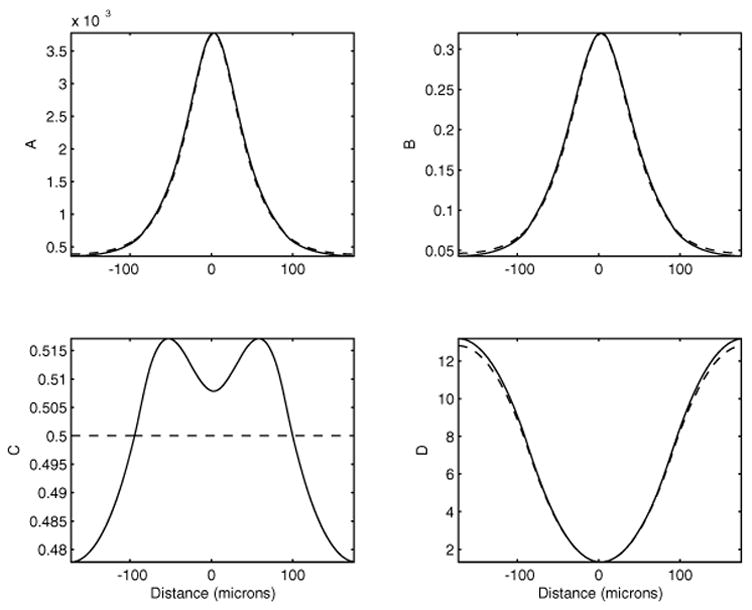
Comparisons between the numerical steady states (solid lines) and the perturbation solutions (dashed lines). The parameters are v̄_L = 8 × 10⁻⁴s⁻¹μM, K_on = 0.4s⁻¹, K_off = 4 × 10⁻⁶s⁻¹, K_deg = 3.2 × 10⁻³ s⁻¹, v̄_S = = 6 × 10⁻² s⁻¹μM, J_on = 6s⁻¹μM, J_off = 10⁻⁵s⁻¹, J_deg = 6 × 10⁻²s⁻¹, τ = 1.

More interesting is the dependence of the leading term solutions (51)–(53) on the biological parameters. The simplest of the four is the uniformly distributed concentration of Dpp-Sog complexes in (53): it depends only on the production rate of Sog per receptor, which is uniform in the ventral region. Free Sog D(x) is proportional to the quadratic function defined in (47) with a magnitude of v̄_S/R₀ modified by the diffusion coefficient of Sog. That D(x) is inversely proportional to D_S is not surprising, since faster diffusion of Sog would move more of it into the dorsal region for binding with the available Dpp there. Note that ρ_Sd₀(x) is independent of the choice of normalizing diffusion coefficient D₀ and the effects of all biological parameters are felt by ρ_Sd₀(x) only implicitly through the parameter δ₀.

Less expected is the dependence of A(x) and B(x) on the biological parameters. From (51), we see that if Γ_LS = O(1), the amplitude of B(x) is determined mainly by Γ_LS. For Γ_LS ≫ 1, we have B(x) ~1, except possibly for a region adjacent to the ventral midline x = 1. In either case, the amplitude of B(x) does not depend explicitly on either of the two production rate parameters v̄_s/R₀ or v̄_L/R₀; the effects of these two parameters on B(x) are felt only through δ₀.

The situation is similar for A(x). It seems unreasonable that A(x) does not tend to zero with v̄_L/R₀ (with the same observation applied to B(x) as well). However, we see from a closer examination of (40a) that ${\mu }_D^2=h_{LS}{\alpha }_L{\overline{V}}_L/g_L$ tends to zero with v̄_L/R₀. For sufficiently small v̄_L/R₀, the first approximation relation (42a) would give c₀(x) = 0. In that case, c(x) should be rescaled (by an additional factor ${\mu }_D^2$) for a proper perturbation solution, while the solution of this section ceases to be applicable. In other words, to apply the perturbation solution {a₀(x), c₀(x), d₀(x)} obtained above, we must have v̄_L/R₀ sufficiently small so that V̄_L V̄_S = v̄_L/v̄_S ≪ 1 but not too small so that ${\mu }_D^2=h_{LS}{\alpha }_L{\overline{V}}_L/g_L$ is not small compared to unity.

5. Numerical solutions for evolutions

The system (1)–(4) can be solved by finite difference schemes [25]. The diffusion terms are approximated by the second order central difference. The temporal evolution is approximated through the fourth order Adams–Moulton predictor-corrector method. The overall accuracy for the method is second order in space and fourth order in time.

For a typical calculation, the time step is chosen to be Δt = 2 × 10⁻⁴ seconds, and the number of points to discretize the entire dorsal and ventral region is N = 64. Smaller time step and larger number of points have been used to check the accuracy and convergence of the calculations.

Similar to [13], the span of both the dorsal region and the ventral region is chosen to be 175μm, i.e., X_max = 175μm. Unlike [13], the diffusion constants for Dpp, Sog, and Dpp-Sog are taken to be the same with D₀ = D_L = D_LS = D_S = 20μm²/second [4], so that ρ_L = ρ_S = ρ_LS = 1 (except for changes indicated in Figures 7 and 8). In this study, the synthesis rates for Dpp and Sog remain the same for all time. In particular, v_L(X) is always chosen to be a nonzero constant, v̄_L, in the dorsal region and zero in the ventral region, while v_S(X) is the opposite, with v_S(X) = v̄_S in the ventral and zero in the dorsal region.

Fig. 7.

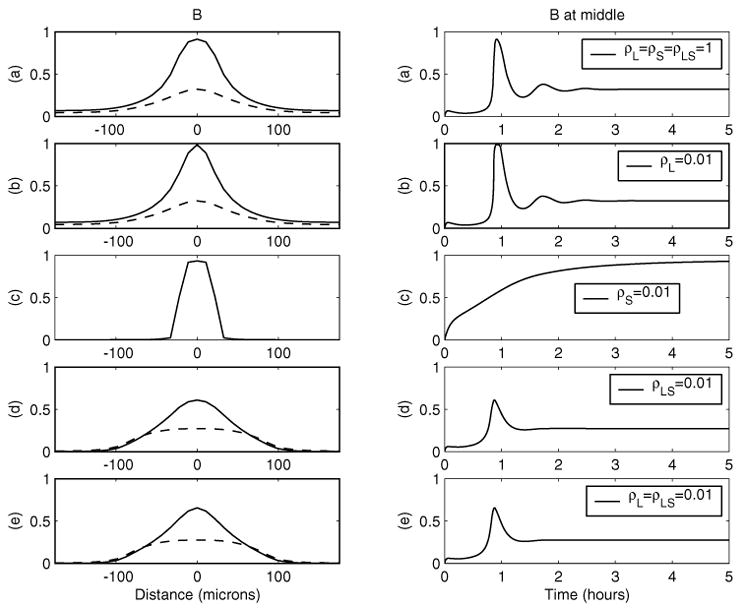
Effect of smaller diffusion constants on the transient peak and steady state. For the left-hand panels, solid line: transient peak; dotted line: steady state. Parameters are as in Figure 3 except for diffusion constants.

Fig. 8.

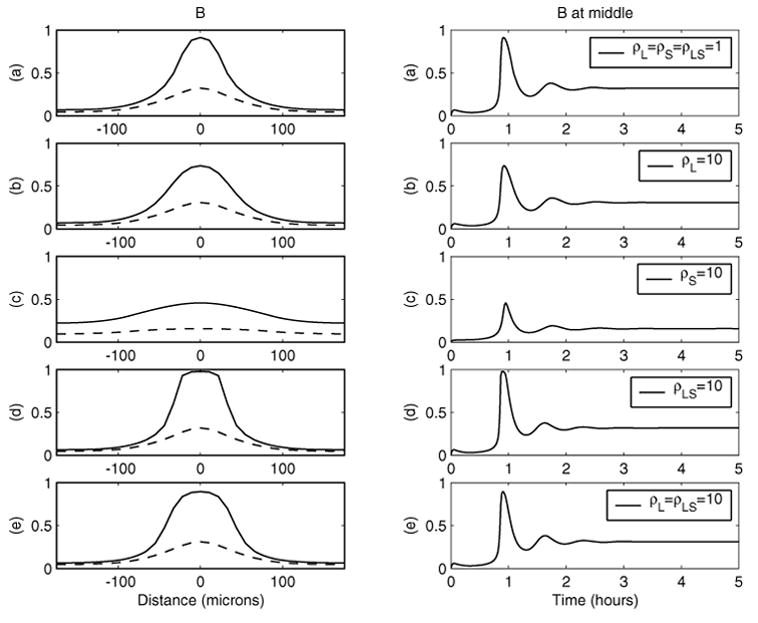
Effect of larger diffusion constants on the transient peak and steady state. For the left-hand panels, solid line: transient peak; dotted line: steady state. Parameters are as in Figure 3 except for diffusion constants.

The dynamics of the system without Sog is very similar to that in [4], even though the ligand is produced from a localized source in [4] while the ligand is produced in the whole dorsal region for the system (1)–(4). For realistic ranges of the biological parameters of the problem, this system typically evolves quickly and monotonically to a steady state within a half hour, with the Dpp-receptor concentration almost uniform around the dorsal region. This behavior is consistent with the experimental observation of [8]. At x = 0 the steady state is approximately equal to v̄_L/(K_degR₀).

Without Sog, the solution at any fixed x is found to be an increasing function of time. This feature is also observed for cases where Sog is synthesized at a slow rate or at a rate comparable to the Dpp production rate. The situation is different if the Sog production rate is significantly larger than the Dpp production rate, which is the most biologically relevant case [13]. In Figure 3, time evolution of a typical system for large v̄_S is plotted. It is observed that the spatial distributions of Dpp and the Dpp-receptor complex continue to have maximum concentrations at the middle of the dorsal region, x = 0, at any instance in time (see the left-hand panels). However, the various morphogen concentrations at x = 0 (the center of the dorsal region) peak at an early time, then oscillate, with the amplitude of oscillations decaying until the concentrations reach their steady state (see the right-hand panels). Therefore we record two interesting curves for Dpp-receptor concentration: the transient solution with the largest value at the dorsal midline and the steady state solution.

Fig. 3.

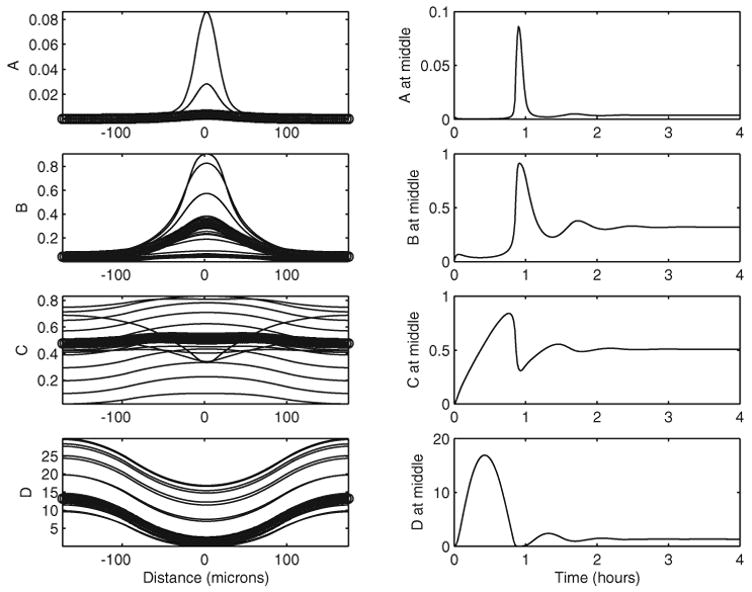
The dynamics of solutions with SOG at every 5 minutes; o in the left-hand panels marks the steady-state solutions. All parameters are the same as for Figure 2.

In Figure 4(a), the steady state for Dpp-receptor concentration of our system (from the same numerical simulations for Figure 3) are plotted. With Sog (v̄_S ≠ 0), the Dpp-receptor in the dorsal region generally has sharper gradient and larger concentration than those without Sog (v̄_S = 0). For the transient solution at its maximal peak magnitude, the concentration with Sog is at least double that without Sog around the middle region. These are consistent with the experimental observation in [8].

Fig. 4.

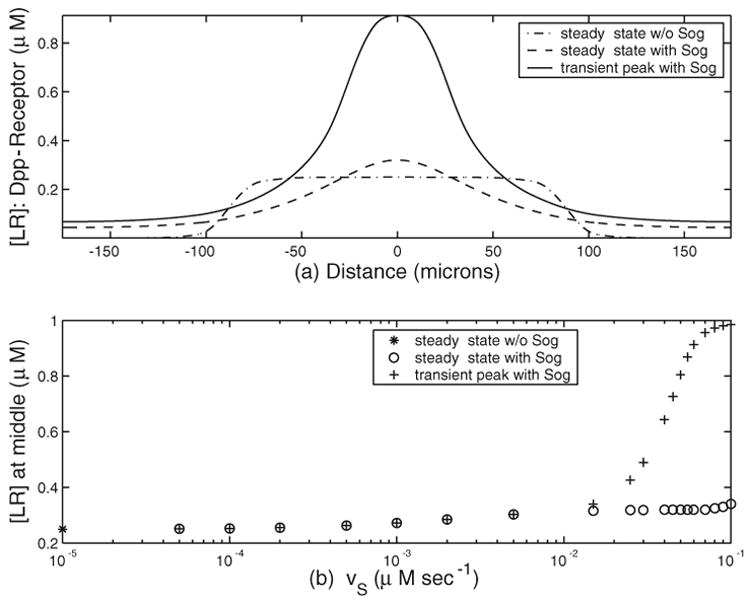
Effect of Sog on the transient and steady state solutions. (a) [LR] as a function of space; (b) [LR] at dorsal midline as a function of v̄_s. Parameters are as in Figure 3.

In steady state, the system with or without Sog has the same total amount of Dpp-receptor complex for τ = 1. This can be shown by simply adding the right-hand sides of (11)–(13) and (13)–(14), respectively, and then integrating them through the whole domain:

$${\int }_{-1}^1{g}_L\mathit{Bdx}={\int }_{-1}^1(V_L(x)-(1-\tau )V_S(x))dx.$$ (55)

This relationship is independent of the presence of Sog when τ = 1. In other words, the effect of inhibitor on Dpp-receptor concentration in the steady state is a spatial redistribution, not an increase or decrease in total concentration aggregated over the entire embryo if all degraded Dpp-Sog complexes, [LS], are cleaved to free up Dpp and degrade only the Sog component.

For the transient solution, the presence of Sog clearly helps build up the Dpp-receptor complexes in terms of both gradient and concentration, as shown in Figure 3. In Figure 4(b), we study how the transient peak of Dpp-receptor and the steady state at the dorsal midline (x = 0) depend on v̄_S. The steady state for B without Sog at x = 0 is 0.25, and its value is plotted at the y-axis in Figure 4(b). For a small amount of Sog, the transient peaks are not high, and the steady state has the largest value at x = 0, as shown for v̄_S/R₀ < 0.01. Also, B(x = 0) at steady state increases as v̄_S increases, and the transient peak begins to deviate from the steady state around v̄_S/R₀ = 0.01. As v̄_S increases by one order of magnitude from 0.015 to 0.1, the transient peak increases from 0.34 to 0.99, while the steady state only from 0.32 to 0.34. Once v̄_S/R₀ becomes large enough, the variation of the transient peak is more sensitively dependent on variation of v̄_S/R₀ than that of the steady state at x = 0. The dependence of the transient peak on other parameters such as J_on and J_deg have been investigated previously in [17] for τ = 1.

When τ < 1, so that only a portion of the degraded Dpp-receptor complex is cleaved to free up Dpp, the dynamics of the system strongly depends on the size of τ when the steady state condition (20)–(21) holds. It is not surprising that for smaller τ, i.e., less free Dpp released from the degraded [LS], the transient and steady peaks of Dpp-receptor complex are lower, as shown in Figure 5(a) for τ = 0.995 and 0.99. However, for τ = 0.99, the concentration of Dpp-receptor complex around the dorsal region is much lower with Sog than without Sog, as shown in Figure 5(a). As demonstrated in (55), a small change of τ will result in a large change of [LR] at steady state for a large v̄_S, which is the case for Figure 5(a). In essence, v_eff ≡ v̄_L − (1−τ) v̄_S can be regarded as an effective production rate for Dpp.

Fig. 5.

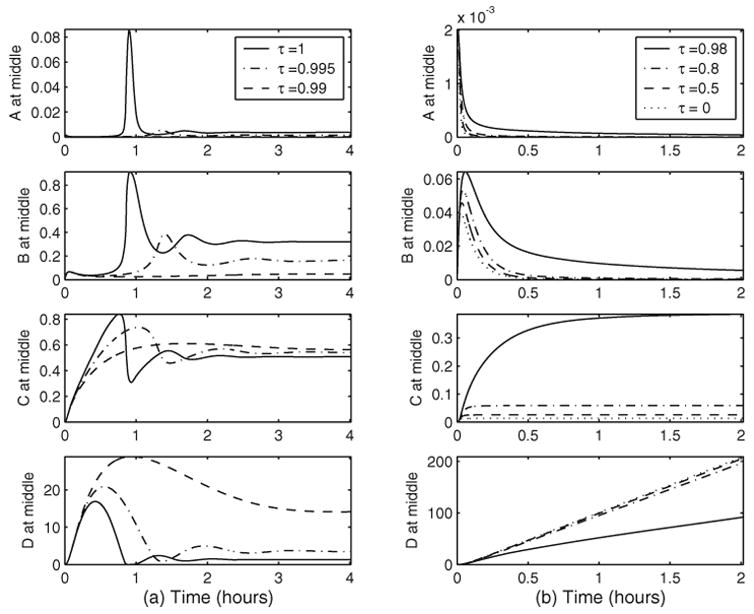
Effect of τ on the steady state solutions. Parameters are as in Figure 3 except for τ. (a) Cases with steady states; (b) cases without steady states.

When the effective production rate v_eff becomes negative, that is, the condition (20)–(21) does not hold, then the system can no longer sustain a steady state. For this situation, the concentrations of both free Dpp and the Dpp-receptor complex are typically very low, and the Dpp-receptor complex reaches the peak before Sog diffuses into the dorsal region from the ventral side and takes over the reaction with Dpp. With the availability of a large amount of Sog and its fast association rate with Dpp, Dpp-Sog reaction dominates. It is interesting to note in Figure 5(b) that as τ varies from 0.98 to 0, the time for Dpp and Dpp-receptor complex to reach their peaks barely changes. This critical time (to reach the peak) is mainly determined by the coefficient of diffusion D_S, which controls the speed of Sog movement into the dorsal zone.

In [14] (hence also in [13]), degradation for [LR] is not allowed in the system (K_deg = 0); therefore the condition (20)–(21) does not hold for any v̄_L > 0. In order to achieve steady state in [13], [14], the models there turned off production of Dpp after 10 minutes (T* = 10 minutes). The effect of the choice of T* and the biological background for the choice T* = 10 minutes were not discussed in [13] and [14]. In Figure 6, we study how our system reacts to the choice of T* if K_deg = 0. It is found that the evolution of [LR] at the dorsal midline becomes monotone, unlike the case in Figure 3, and as expected, the time to reach steady states strongly depends on the choice of T*. In Figure 6, the steady states for [LR] are shown for T* = 5, 8, 10, 12, 15, 20, 30, 45, 60 minutes. The concentration of [LR] varies almost linearly with respect to T* until the receptors are close to being fully occupied when T* is large.

Fig. 6.

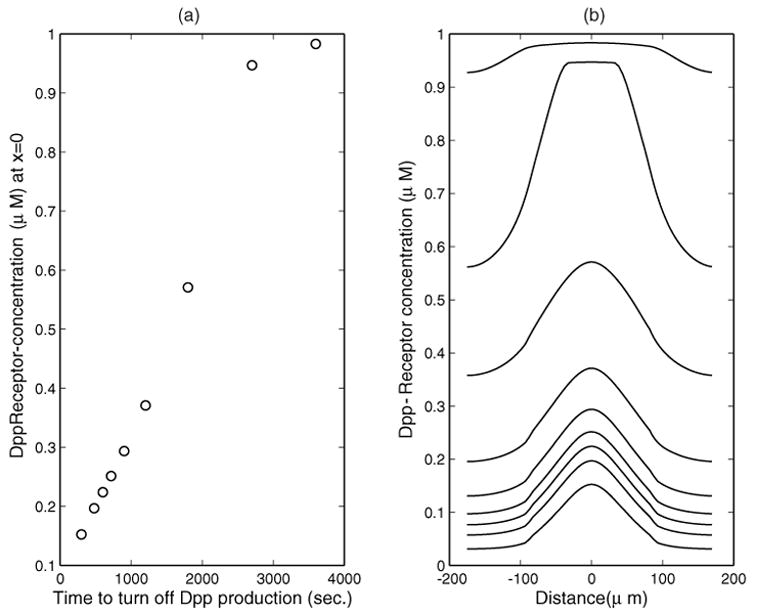
v̄_L is set to zero at different times. (a) [LR] at the dorsal midline at steady state as a function of the time for turning off v̄_L; (b) [LR] at steady states as a function of space for different times of turning off v̄_L, as shown in (a). Other parameters are as in Figure 3 except that K_deg = 0.

Finally, we investigate the effect of diffusion. In Figure 7, Dpp-receptor complexes as functions of time and space are shown for five different choices of diffusion constants. Case (a) has all three diffusion constants the same as in Figure 3, cases (b)–(d) have one of the diffusion constants being 1% of the corresponding value in case (a), and the case (e) has two constants at 1% of the corresponding values in case (a). Similarly in Figure 8, some of the diffusion constants are 10-fold larger than others.

As shown in case (b) of both Figures 7 and 8, the magnitude of the diffusion co-efficient for Dpp has very little effect on the broadness and intensity of Dpp activity at the dorsal midline. This is consistent with the behavior of the leading term perturbation solution. A larger diffusion for Dpp reduces the peak of transient Dpp-activity at the midline slightly and broadens it slightly. On the other hand, a decrease in diffusion constant for Dpp-Sog complexes, as in cases (d) and (e), significantly broadens the Dpp activity around the midline for both peak transient and steady state distributions, with the height of only the transient peak reduced significantly but with almost the same steady state at x = 0. The time to steady state and transient peaks seems to be insensitive to the change of the diffusion constants for Dpp or the Dpp-Sog complex.

As predicted by the perturbation solutions, varying the diffusion coefficient for Sog changes the Dpp activity around the dorsal midline significantly. As shown in Figure 7(c), a smaller diffusion of Sog relative to the diffusion of Dpp leads to more concentrated transient Dpp activity around the dorsal midline, but it takes much longer to reach the steady state, with a monotone increase of Dpp activity around the dorsal midline (i.e., there is no transient peak). On the other hand, larger diffusion of Sog relative to the diffusion of Dpp weakens and broadens the Dpp activity, as in Figure 8(c).

6. Conclusions

The dynamics of Dpp activities in the presence of the inhibitor Sog is analyzed herein to initiate a study of dorsal-ventral morphogen gradient formation in vertebrates and Drosophila embryos. Here we investigate a prototype morphogen system with typical ligand diffusion and degradation, but now with the additional feature of cleavage of Dpp-Sog complexes by Tolloid to free up Dpp. Among the principal results of our investigation is the establishment of a simple and biologically meaningful necessary and sufficient condition for the existence of a steady state gradient in the system. This condition requires a balance of the production rates of ligands, degradation rate of ligand-receptor complex, and rate of cleavage of ligand-inhibitor complex. For high Sog production rates (relative to the Dpp production rate), a perturbation solution has been obtained in terms of elementary functions. This solution exhibits an intense Dpp-receptor concentration near the dorsal midline. Numerical simulations of the evolution of the system confirmed these features of the steady state behavior. In addition, a transient peak of Dpp-receptor concentration at the dorsal midline was found to be even more intense prior to steady state, reaching more than twice the level of the steady state at its peak amount. This transient peak is more sensitively dependent on variation of the production of Sog than the steady state peak. The high Dpp-receptor concentration around the dorsal midline and other features of the system are consistent with experimental observations.

Appendix A

Proof of Lemma 3.4

We show that there exists M₁ > 0 such that ‖C̃‖L^∞ ≤ M₁. As in the proof of Lemma 3.3, ‖C̃‖L¹ ≤ M₂ for some constant M₂ > 0. Integrating (27) in (−1, 1), we get

$${\int }_{-1}^1{h}_{LS}\tilde{A}\tilde{D}={\int }_{-1}^1(f_{LS}+g_{LS})\tilde{C},$$ (56)

which implies that ${\int }_{-1}^1\tilde{A}\tilde{D}\le M_3{\int }_{-1}^1\tilde{C}\le M_2{M}_3$ for some M₃ > 0. Integrating (27) from −1 to x, we get

$${\rho }_{LS}{\tilde{C}}_{,x}+\lambda {\int }_{-1}^x[h_{LS}\tilde{A}\tilde{D}-(f_{LS}+g_{LS})\tilde{C}]=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1.$$ (57)

Hence

$${\rho }_{LS}\Vert {\tilde{C}}_{,x}{\Vert }_{L^{\hspace{0.17em}\infty }}\le \hspace{0.17em}\Vert h_{LS}{\Vert }_{L^{\hspace{0.17em}\infty }}{\int }_{-1}^1\tilde{A}\tilde{D}+\Vert f_{LS}+g_{LS}{\Vert }_{L^{\hspace{0.17em}\infty }}{\int }_{-1}^1\tilde{C}\le M_4$$ (58)

for some constant M₄ > 0. This along with ${\int }_{-1}^1\tilde{C}\le M_2$ implies the L^∞ bound of C̃, which is independent of λ.

Next we show that there exists some constant M₅ > 0 such that ‖Ã‖L^∞ ≤ M₅. To this end, adding up (26) and (27) and integrating from −1 to x, we get

$${\rho }_L{\tilde{A}}_{,x}+{\rho }_{LS}{\tilde{C}}_{,x}=\lambda {\int }_{-1}^x\left[\frac{g_L{h}_L\tilde{A}}{f_L+g_L+h_L\tilde{A}}+(1-\tau )g_{LS}\tilde{C}-V_L\right],$$ (59)

which implies that

$$\Vert {\tilde{A}}_{,x}{\Vert }_{L{\hspace{0.17em}}^{\infty }}\le M_6\left(\Vert {\tilde{C}}_{,x}{\Vert }_{L{\hspace{0.17em}}^{\infty }}+\Vert g_L{\Vert }_{L^{\hspace{0.17em}\infty }}+\Vert {\rho }_{LS}{\Vert }_{L^{\hspace{0.17em}\infty }}{\int }_{-1}^1\tilde{C}+\Vert V_L{\Vert }_{L^{\hspace{0.17em}\infty }}\right):=M_7.$$ (60)

We claim that there exists some constant M₈ > 0 such that ${\int }_{-1}^1\tilde{A}\le M_8.$ To establish this assertion, we argue by contradiction: if not, passing to a subsequence if necessary, we may assume that ${\int }_{-1}^1\tilde{A}\to +\infty$. This together with (60) implies that

$$\mid \frac{\tilde{A}(x)}{{\int }_{-1}^1\tilde{A}}-1\mid \le \frac{\Vert {\tilde{A}}_{,x}{\Vert }_{L^{\hspace{0.17em}\infty }}}{{\int }_{-1}^1\tilde{A}}\le \frac{M_7}{{\int }_{-1}^1\tilde{A}}\to 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall -1\le x\le 1.$$ (61)

Hence à → +∞ uniformly. Similar to (24) we have

$${\int }_{-1}^1{V}_L={\int }_{-1}^1\frac{g_L{h}_L\tilde{A}}{f_L+g_L+h_L\tilde{A}}+(1-\tau ){\int }_{-1}^1{V}_S.$$ (62)

By (61) we have ${\int }_{-1}^1\frac{g_L{h}_L\tilde{A}}{f_L+g_L+h_L\tilde{A}}\to {\int }_{-1}^1{g}_L$, which together with (62) implies that ${\int }_{-1}^1{V}_L={\int }_{-1}^1{g}_L+(1-\tau ){\int }_{-1}^1{V}_S$. However, this contradicts (21). Therefore ${\int }_{-1}^1\tilde{A}$ is uniformly bounded for λ ∈ (0, 1]. This together with (60) yields ‖Ã‖L^∞ ≤ M₅ for some M₅ > 0.

Finally we show that there exists some constant M₉ > 0 such that ‖D̃‖L^∞ ≤ M₉. We argue by contradiction: suppose not; passing to a subsequence if necessary, we may assume that ‖D̃‖L^∞ → ∞ and λ → λ̂ ∈ [0, 1]. Set $\widehat{D}(x)=\frac{\tilde{D}(x)}{\Vert \tilde{D}{\Vert }_{L^{\hspace{0.17em}\infty }}}$. Then D̂ satisfies D̂,_x(−1) = D̂,_x(1) = 0, ‖D̂‖L^∞ = 1, and

$${\rho }_{LS}{\widehat{D}}_{,xx}+\lambda \left[-h_{LS}\tilde{A}\widehat{D}+\frac{f_{LS}\tilde{C}+V_S}{\Vert \widehat{D}{\Vert }_{L^{\hspace{0.17em}\infty }}}\right]=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1.$$ (63)

Since ‖Ã‖L^∞, ‖Ã,_x‖L^∞ are uniformly bounded, we may assume that Ã(x) → A*(x) uniformly in [−1, 1]. From (62) and (20) we see ${\int }_{-1}^1\tilde{A}\ge M_{10}>0$ for some constant M₁₀. Hence A* ≢ 0 since ${\int }_{-1}^{1}A\ast \ge M_{10}>0$. By standard regularity theory we may assume that D̂(x) → D*(x) in C¹[−1, 1], and D* is a weak solution of

$${\rho }_{LS}{D}_{,xx}^{\ast }-\widehat{\lambda }{h}_{LS}{A}^{\ast }{D}^{\ast }=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-1<x<1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{D}_{,x}^{\ast }(-1)=D_{,x}^{\ast }(1)=0.$$ (64)

Moreover, D* ≥ 0 in [−1, 1] and ‖D^*‖L^∞ = 1. If λ̂ > 0, since A* ≢ 0, A* ≥ 0, by the maximum principle we see that D* ≡ 0, which contradicts ‖D^*‖L^∞ = 1; if λ̂ = 0, then it follows from (64) that D* ≡ 1, i.e., D̂(x) → 1 uniformly. Dividing (56) by ‖D̃‖L^∞, we have ${\int }_{-1}^1{h}_{LS}\tilde{A}\widehat{D}={\int }_{-1}^1(f_{LS}+g_{LS})\tilde{C}/\Vert \tilde{D}{\Vert }_{L^{\hspace{0.17em}\infty }}$. Then we obtain ${\int }_{-1}^1{h}_{LS}{A}^{\ast }=0,$ which implies that A* ≡ 0. Contradiction! This completes the proof of (34).

When λ = 0, (Ã, C̃, D̃) is a solution of (26)–(29) if and only if Ã, C̃, and D̃ are all constants. It turns out that a particular triple, denoted by (Â, Ĉ, D̂), is special, where Â, Ĉ, D̂ are defined as follows: by (20)–(21) it is easy to see that there is a unique positive constant, denoted by Â, such that

$${\int }_{-1}^1\frac{g_L{h}_L\widehat{A}}{f_L+g_L+h_L\widehat{A}}={\int }_{-1}^1{V}_L-(1-\tau ){\int }_{-1}^1{V}_S.$$ (65)

Set

$$\widehat{D}=\frac{{\int }_{-1}^1(f_{LS}+g_{LS}){\int }_{-1}^1{V}_S}{\widehat{A}{\int }_{-1}^1{h}_{LS}{\int }_{-1}^1{g}_{LS}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\widehat{C}=\frac{{\int }_{-1}^1{V}_S}{{\int }_{-1}^1{g}_{LS}}.$$ (66)

Lemma A.1

Suppose that (20)–(21) holds. Let (A_λ, B_λ, C_λ) denote positive solutions of (26)–(29). Then as λ → 0+, (A_λ, B_λ, C_λ) → (Â, Ĉ, D̂) uniformly.

Proof

By Lemma 3.4, (A_λ, B_λ, C_λ) are uniformly bounded. By standard regularity theory and the embedding theorem, passing to a subsequence if necessary, we may assume that (A_λ, B_λ, C_λ) → (Â, Ĉ, D̂) uniformly, where Ā, C̄, and D̄ satisfy Ā_xx = C̄_xx = D̄_xx = 0, and Ā_x = C̄_x = D̄_x = 0 at x = −1, 1. Therefore Ā, C̄, D̄ are all nonnegative constants. Passing to the limit in (62) (with à being replaced by A_λ), we have Ā =Â. Similarly we can show that Ĉ = C̄ and D̂ = D̄. Since the limit (Â, Ĉ, D̂) is unique, the convergence (A_λ, B_λ, C_λ) → (Â, Ĉ, D̂) is true for the whole sequence, and the limit is uniform in x.

Lemma A.2

There exists some constant δ₁ > 0 such that if 0 < λ ≤ δ₁, (26)–(29) has a unique positive solution.

Proof

Set X = {u ∈ C[−1, 1] : ${\int }_{-1}^{1}u(x)dx=0$}, Z = {u ∈ X : u,_x(−1) = u,_x(1) = 0}, and define the projection operator P : C[−1, 1] → X by $Pu=u-{\int }_{-1}^{1}u(x)dx$. For (λ, A₀, a₀, C₀, c₀, D₀, d₀) ∈ R¹ × (Z × R¹)³, define F : R¹ × (Z × R¹)³ → (X × R¹)³ by

$$\begin{array}{l}F(\lambda ,A_0,a_0,C_0,c_0,D_0,d_0)=\left(\begin{array}{c}{\rho }_L{A}_{0,xx}+\lambda P{F}_1^{+}(x,A_0+a_0,C_0+c_0,D_0+d_0)\\ {\int }_{-1}^1{F}_1^{+}(x,A_0+a_0,C_0+c_0,D_0+d_0)dx\\ {\rho }_{LS}{C}_{0,xx}+\lambda P{F}_2(x,A_0+a_{0,}{C}_0+c_0,D_0+d_0)\\ {\int }_{-1}^1{F}_2(x,A_0+a_0,C_0+c_0,D_0+d_0)dx\\ {\rho }_S{D}_{0,xx}+\lambda P{F}_3(x,A_0+a_0,C_0+c_0,D_0+d_0)\\ {\int }_{-1}^1{F}_3(x,A_0+a_0,C_0+c_0,D_0+d_0)dx\end{array}\right)\end{array}$$ (67)

By the definition of Â, Ĉ, D̂, F(0, Â, Ĉ, D̂, 0, 0, 0) = (0, 0, 0, 0, 0, 0). The Fréchet derivative of F with respect to (A₀, a₀, C₀, c₀, D₀, d₀) at (λ, A₀, a₀, C₀, c₀, D₀, d₀) = (0, Â, 0, Ĉ, 0, D̂, 0) is given by

$$D_{(A_0,a_0,C_0,c_0,D_0,d_0)}F{\mid }_{(0,\widehat{A},0,\widehat{C},0,\widehat{D},0)}=\left(\begin{array}{cccccc}{\rho }_L\frac{d^2}{d{x}^2}& 0& 0& 0& 0& 0\\ 0& {\rho }_{LS}\frac{d^2}{d{x}^2}& 0& 0& 0& 0\\ 0& 0& {\rho }_S\frac{d^2}{d{x}^2}& 0& 0& 0\\ \ast & \ast & \ast & & & \\ \ast & \ast & \ast & M_{3\times 3}& & \\ \ast & \ast & \ast & & & \end{array}\right),$$ (68)

where M_3×3 is the 3 × 3 matrix

$$\left(\begin{array}{ccc}{\int }_{-1}^1\left[\frac{-g_L{h}_L(f_L+g_L)}{{(f_L+g_L+h_L\widehat{A})}^2}-h_{LS}\widehat{D}\right]& {\int }_{-1}^1(f_{LS}+\tau g_{LS})& -({\int }_{-1}^1{h}_{LS})\widehat{A}\\ ({\int }_{-1}^1{h}_{LS})\widehat{D}& -{\int }_{-1}^1(f_{LS}+g_{LS})& ({\int }_{-1}^1{h}_{LS})\widehat{A}\\ -({\int }_{-1}^1{h}_{LS})\widehat{D}& {\int }_{-1}^1{f}_{LS}& -({\int }_{-1}^1{h}_{LS})\widehat{A}\end{array}\right).$$ (69)

Since the operator $\frac{d^2}{d{x}^2}$, subject to the no flux boundary condition, is an isomorphism from Z to X, we see that the operator D_{(A0,a0,C0,c0,D0,d0)}F|_{(0, Â, 0, Ĉ, 0, D̂, 0)} is invertible from (Z × R¹)³ to (X × R¹)³ if and only if the matrix M_3×3 is invertible. It is straightforward to check that the determinant of M_3×3 is equal to

$$\left({\int }_{-1}^1{h}_{LS}\right)\widehat{D}\cdot {\int }_{-1}^1(f_{LS}+g_{LS})\cdot \left({\int }_{-1}^1{h}_{LS}\right)\widehat{A}(1-{\gamma }_2)(-{\gamma }_1),$$ (70)

where γ₁, γ₂ are defined as

$${\gamma }_1=\frac{{\int }_{-1}^1\frac{g_L{h}_L(f_L+g_L)}{{(f_L+g_L+h_L\widehat{A})}^2}}{\left({\int }_{-1}^1{h}_{LS}\right)\widehat{D}},\hspace{0.17em}\hspace{0.17em}{\gamma }_2=\frac{{\int }_{-1}^1{f}_{LS}}{{\int }_{-1}^1(f_{LS}+g_{LS})}.$$ (71)

Since γ₁ > 0 and 0 < γ₂ < 1, M_3×3 is nondegenerate.

By the implicit function theorem, there exists δ₂ > 0 such that if 0 < λ = δ₂, there is a unique solution to F = 0, denoted by (A_λ(x), a_λ(x), C_λ(x), c_λ(x), D_λ(x), d_λ(x)), in some neighborhood of (Â, 0, Ĉ, 0, D̂, 0). As λ → 0+, (A_λ, a_λ, C_λ, c_λ, D_λ, d_λ) → (Â, 0, Ĉ, 0, D̂, 0) uniformly. In particular, for 0 < ≤ = δ₂, (A_λ+a_λ, C_λ+c_λ, D_λ+d_λ) is the unique positive solution of (26)–(29) in some neighborhood of (Â, Ĉ, D̂). This and Lemma A.1 imply that, for 0 < λ ≪ 1, (26)–(29) has a unique positive solution.

Lemma A.3

Let (A^*, C^*, D^*) denote the unique positive solution of (26)–(29) for 0 < λ ≪ 1. Then for 0 < λ ≪ 1, the Fréchet derivative of T(λ) with respect to (Ã, C̃, D̃) at (A^*, C^*, D^*), denoted by D_{(Ã, C̃, D̃)}T(λ) | _(A*,C*,D*), has no eigenvalue greater than or equal to 1.

Proof

By (35), D_{(Ã, C̃, D̃)}T(λ)| _(A*,C*,D*)(ϕ₁, ϕ₂, ϕ₃) is given by

$$\left(\begin{array}{c}{L}_{{\rho }_L}^{-1}\left\{[1+\lambda \frac{\partial F_1}{\partial \tilde{A}}(x,A^{\ast },C^{\ast },D^{\ast })]{\varphi }_1+\lambda \frac{\partial F_1}{\partial \tilde{C}}{\varphi }_2+\lambda \frac{\partial F_1}{\partial \tilde{D}}{\varphi }_3\right\}\\ L_{{\rho }_{LS}}^{-1}\left\{\lambda \frac{\partial F_2}{\partial \tilde{A}}{\varphi }_1+\left[1+\lambda \frac{\partial F_2}{\partial \tilde{C}}\right]{\varphi }_2+\lambda \frac{\partial F_2}{\partial \tilde{D}}{\varphi }_3\right\}\\ L_{{\rho }_S}^{-1}\left\{\lambda \frac{\partial F_3}{\partial \tilde{A}}{\varphi }_1+\lambda \frac{\partial F_3}{\partial \tilde{C}}{\varphi }_2+\left[\lambda \frac{\partial F_3}{\partial \tilde{D}}+1\right]{\varphi }_3\right\}\end{array}\right),$$

where $\frac{\partial F_i}{\partial \tilde{A}},\frac{\partial F_i}{\partial \tilde{C}},\frac{\partial F_i}{\partial \tilde{D}}$ (i = 1, 2, 3) are evaluated at (x, A*, C*, D*).

We argue by contradiction: suppose that Lemma A.3 fails. Passing to a subsequence if necessary, we may assume that for 0 < λ ≪ 1 the operator D_{(Ã, C̃, D̃)}T(λ)|_(A*,C*,D*) has eigenvalue μ = μ(λ) ≥ 1, with the corresponding eigenfunction (ϕ₁, ϕ₂, ϕ₃) normalized by ‖ϕ₁‖L^∞+‖ϕ₂‖L^∞+‖ϕ₃‖L^∞ = 1. Then (ϕ₁, ϕ₂, ϕ₃) satisfies

$$-\mu {\rho }_L\frac{d^2{\varphi }_1}{d{x}^2}+(\mu -1){\varphi }_1=\lambda \left[\frac{\partial F_1}{\partial \tilde{A}}{\varphi }_1+\frac{\partial F_1}{\partial \tilde{C}}{\varphi }_2+\frac{\partial F_1}{\partial \tilde{D}}{\varphi }_3\right],$$ (72)

$$-\mu {\rho }_{LS}\frac{d^2{\varphi }_2}{d{x}^2}+(\mu -1){\varphi }_2=\lambda \left[\frac{\partial F_2}{\partial \tilde{A}}{\varphi }_1+\frac{\partial F_2}{\partial \tilde{C}}{\varphi }_2+\frac{\partial F_2}{\partial \tilde{D}}{\varphi }_3\right],$$ (73)

$$-\mu {\rho }_S\frac{d^2{\varphi }_3}{d{x}^2}+(\mu -1){\varphi }_3=\lambda \left[\frac{\partial F_3}{\partial \tilde{A}}{\varphi }_1+\frac{\partial F_3}{\partial \tilde{C}}{\varphi }_2+\frac{\partial F_3}{\partial \tilde{D}}{\varphi }_3\right],$$ (74)

$${({\varphi }_1)}_{,x}={({\varphi }_2)}_{,x}={({\varphi }_3)}_{,x}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{at}\hspace{0.17em}x=-1,1,$$ (75)

where $\frac{\partial F_i}{\partial \tilde{A}},\frac{\partial F_i}{\partial \tilde{C}},\frac{\partial F_i}{\partial \tilde{D}}$ (i = 1, 2, 3) in (72)–(74) are evaluated at (Ã, C̃, D̃) = (A*, C*, D*).

It is easy to see that μ(λ) → 1 as λ → 0+, and the corresponding eigenfunctions (ϕ₁, ϕ₂, ϕ₃) → (ϕ̄₁, ϕ̄₂, ϕ̄₃) uniformly, where (ϕ̄₁, ϕ̄₂, ϕ̄₃) are constants satisfying |ϕ̄₁|+ |ϕ̄₂|+|ϕ̄₃| = 1. Set μ(λ) = 1+λμ₁(λ). Since μ(λ) ≥ 1, we have μ₁(λ) ≥ 0. Integrating (72)–(74), we get

$${\int }_{-1}^1\left[\frac{\partial F_1}{\partial \tilde{A}}-{\mu }_1\right]\hspace{0.17em}{\varphi }_1+{\int }_{-1}^1\frac{\partial F_1}{\partial \tilde{C}}\hspace{0.17em}{\varphi }_2+{\int }_{-1}^1\frac{\partial F_1}{\partial \tilde{D}}\hspace{0.17em}{\varphi }_3=0,$$ (76)

$${\int }_{-1}^1\frac{\partial F_2}{\partial \tilde{A}}\hspace{0.17em}{\varphi }_1+{\int }_{-1}^1\left[\frac{\partial F_2}{\partial \tilde{C}}-{\mu }_1\right]\hspace{0.17em}{\varphi }_2+{\int }_{-1}^1\frac{\partial F_2}{\partial \tilde{D}}\hspace{0.17em}{\varphi }_3=0,$$ (77)

$${\int }_{-1}^1\frac{\partial F_3}{\partial \tilde{A}}\hspace{0.17em}{\varphi }_1+{\int }_{-1}^1\frac{\partial F_3}{\partial \tilde{C}}\hspace{0.17em}{\varphi }_2+{\int }_{-1}^1\left[\frac{\partial F_3}{\partial \tilde{D}}-{\mu }_1\right]\hspace{0.17em}{\varphi }_3=0.$$ (78)

We first prove that μ₁ (λ) is uniformly bounded for all 0 < λ ≪ 1. If not, passing to a subsequence if necessary, we may assume that as λ → 0+, μ₁ (λ) → +∞. Divide (76) by μ₁; passing to the limit, we find that ϕ̄₁ = 0. Similarly, ϕ̄₂ = ϕ̄₃ = 0. However, this contradicts |ϕ̄₁| + |ϕ₂| + |ϕ̄₃| = 1. Therefore μ₁(λ) is nonnegative and uniformly bounded. Passing to a subsequence if necessary, we may assume that μ₁(λ) → μ̄₁ ≥ 0 as λ → 0+.

Passing to the limit in (76)–(78), by Lemma A.1, (M_3×3 − μ̄₁ I_3×3) (ϕ̄_1, ϕ̄_2, ϕ̄₃) = (0, 0, 0). Since (ϕ̄₁, ϕ̄₂, ϕ̄₃) ≠ (0, 0, 0), |M_3×3 − μ̄₁ I_3×3| = 0. However, direct calculation yields that |M_3×3− μ̄₁ I_3×3| is equal to

$$\begin{array}{l}-\left({\int }_{-1}^1{h}_{LS}\right)\widehat{D}\cdot {\int }_0^1(f_{LS}+g_{LS})\cdot \left({\int }_{-1}^1{h}_{LS}\right)\hspace{0.17em}\widehat{A}\\ \cdot \{\left({\gamma }_1+\frac{{\overline{\mu }}_1}{({\int }_{-1}^1{h}_{LS})\widehat{D}}\right)\cdot \left(1+\frac{{\overline{\mu }}_1}{{\int }_{-1}^1(f_{LS}+g_{LS})}\right)\cdot \frac{{\overline{\mu }}_1}{({\int }_{-1}^1{h}_{LS})\widehat{A}}\\ +\left[(1-\tau )(1-{\gamma }_2)+\frac{{\overline{\mu }}_1}{{\int }_{-1}^1(f_{LS}+g_{LS})}\right]\cdot \frac{{\overline{\mu }}_1}{{\int }_{-1}^1{h}_{LS}\widehat{A}}\\ +\left({\gamma }_1+\frac{{\overline{\mu }}_1}{({\int }_{-1}^1{h}_{LS})\widehat{D}}\right)\cdot \left(1-{\gamma }_2+\frac{{\overline{\mu }}_1}{{\int }_{-1}^1(f_{LS}+g_{LS})}\right)\},\end{array}$$

which is negative since μ̄₁ ≥ 0, γ₁ > 0, 0 ≤ τ ≤ 1, and γ₂ < 1. Contradiction! This completes the proof of Lemma A.3.

Proof of Proposition 3.5

By Lemma A.2, for 0 < λ ≪ 1, T(λ) has a unique fixed point. By Lemma A.3, 1 is not an eigenvalue of D_{(Ã, C̃, D̃)} T(λ)|_{(A*, C*, D*)}. Hence deg (I − T(λ), Ω, (0, 0, 0) = (−1)^β, where β is the number of eigenvalues (counting algebraic multiplicity) of D_{(Ã, C̃, D̃)} T(λ)|_{(A*, C*, D*)}, which is greater than 1. By Lemma A.3 we see that β = 0. Hence deg (I − T(λ), Ω, (0, 0, 0) = 1 for 0 < λ ≪ 1.