Abstract
Bubble-based acoustic radiation force aims to measure highly localized tissue viscoelastic properties. In the current investigation, acoustic radiation force was applied to laser-induced bubbles to measure age-related changes in the spatial distribution of elastic properties within in vitro porcine lenses. A potential in vivo technique to map lens elasticity is crucial to understanding the onset of presbyopia and develop new treatment options. Bubble-based acoustic radiation force was investigated as a technique to measure the spatial elasticity distribution of the lens in its natural state without disrupting the lens capsule.
Laser-induced optical breakdown (LIOB) generated microbubbles in a straight line across the equatorial plane of explanted porcine lenses with 1 mm lateral spacing. Optical breakdown occurs when sufficiently high threshold fluence is attained at the focus of femtosecond pulsed lasers, inducing plasma formation and bubble generation. A two-element confocal ultrasonic transducer applied 6.5 ms acoustic radiation force-chirp bursts with the 1.5 MHz outer element while monitoring bubble position within the lens using pulse-echoes with the 7.44 MHz inner element. A cross-correlation method was used to measure bubble displacements and determine exponential time constants of the temporal responses. Maximum bubble displacements are inversely proportional to the local Young's modulus, while time constants are indicative of viscoelastic properties.
The apparent spatial elasticity distributions in 41 porcine lenses, ranging from 4 months to 5 years in age, were measured using bubble-based acoustic radiation force. Bubble displacements decrease closer to the porcine lens center, suggesting that the nucleus is stiffer than the cortex. Bubble displacements decrease with increasing lens age, suggesting that porcine lenses become stiffer with age. Bubble-based acoustic radiation force may be well-suited as a potential in vivo technique to spatially map elastic properties of the lens and guide therapeutic procedures aimed at restoring accommodation.
Keywords: Porcine lens, Age dependence, Acoustic radiation force, Mechanical properties, Presbyopia, Ultrasound
1. Introduction
Measuring mechanical property changes of the crystalline lens will help understand the onset of presbyopia and develop new treatment options. Presbyopia results in complete loss of accommodation by around age 50, and age-related increases in lens stiffness are often proposed as the dominant factor (Fisher, 1971, 1973; Glasser and Campbell, 1999; Heys et al., 2004; Weeber et al., 2005). A recent article suggested a possible link between presbyopia and subsequent cataract development from increasing nuclear stiffness (McGinty and Truscott, 2006).
Numerous methods have been used to measure lens mechanical properties, typically applying radial or axial forces. Radial forces attempting to mimic zonular forces generated during disaccommodation have been produced by spinning the lens about its antero-posterior axis (Fisher, 1971, 1973) or mechanically stretching (Fisher, 1977; Hollman et al., 2003; Pierscionek, 1993, 1995). Resulting changes in lens size and shape determine its resistance to deformation. Techniques involving axial compression include loading of whole lenses (van Alphen and Graebel, 1991, Glasser and Campbell, 1999; Kikkawa and Sato, 1963) or isolated lens structures like the nucleus (Czygan and Hartung, 1996). Dynamic mechanical analysis has been recently applied to measure age-related changes in human lenses (Heys et al., 2004; Weeber et al., 2005). Alternate methods have measured penetration resistance using conical probes that pierce through layers of the lens (Czygan and Hartung, 1996; Pau and Kranz, 1991). Finally, an in vivo approach using A-scan ultrasonography to measure axial thickness changes during accommodation has been used in a model for viscoelastic parameters of the lens, zonules, and choroid (Beers and Van der Heijde, 1994a).
Few techniques provide direct measures of the spatial distribution of lens mechanical properties. One exception is the recent in vitro study by Heys et al. (2004), which measured stiffness at 1 mm increments laterally in slices from previously frozen human lenses using dynamic mechanical analysis. Fisher (1971, 1973) modeled the layers of the lens as a series of spinning disk elements parallel to the lens equator, with the nucleus and cortex represented as uniform isotropic elastic materials to infer Young's modulus values for the nucleus and cortex. However, the results from Heys et al. (2004) demonstrate that nuclear and cortical stiffness are not uniform but vary spatially, and a recent study by Burd et al. (2006) questioned the validity of the model assumptions employed by Fisher. An in vivo technique able to measure lens elastic properties with high spatial resolution and minimal disruption of lens structures would represent a significant advance over previous techniques.
Recently, bubble-based acoustic radiation force was introduced to measure tissue elastic properties with high spatial resolution (Erpelding et al., 2004, 2005a, 2005b). In this technique, acoustic radiation force is applied to a microbubble created by laser-induced optical breakdown (LIOB). Breakdown occurs when optical fluence exceeds a threshold at the focus of a femtosecond pulsed laser inducing plasma generation, shock wave emission, and temporary cavitation bubble creation (Fan and Longtin, 2001; Glezer et al., 1997; Vogel and Venugopalan, 2003). Acoustic waves incident upon the highly reflective bubble surface encounter a large momentum change, generating significant radiation force with displacements related to the local stiffness. Acoustic radiation force is a potentially promising in vivo tool since local lens deformation can be generated non-invasively and warrants further investigation.
Previous research demonstrated that bubble displacements from acoustic radiation force are inversely related to the material Young's modulus (Erpelding et al., 2005a). Temporal characteristics of the bubble displacement and subsequent recovery are indicative of local viscoelastic properties. Preliminary in vitro experiments with porcine lenses showed that LIOB bubbles can be created spatially throughout the lens and acoustic radiation force can be applied to estimate local elastic properties (Erpelding et al., 2004, 2005b). Previous acoustic radiation force methods typically use ultrasonic speckle tracking algorithms to image the induced tissue displacement (Nightingale et al., 2002; Sarvazyan et al., 1998; Trahey et al., 2004, Walker, 1999). However, speckle tracking techniques are unable to detect induced displacements within the lens since it is nearly anechoic. For this reason, microbubbles serve not only as efficient force transducers, but also as effective “point” targets enabling highly localized elasticity measurements using acoustic radiation force.
The present study uses bubble-based acoustic radiation force to measure age-related changes in the mechanical properties of porcine lenses with high spatial resolution. Porcine lenses were selected as a readily available tissue model to demonstrate the biological feasibility of the technique. Future research will apply this technique to a similar study with human lenses.
2. Materials and Methods
Porcine Lenses
A total of 41 porcine lenses were acquired from two different suppliers to obtain samples spanning a wide age range. Although the exact age of a particular lens was unknown, general age ranges were given from each supplier. Fresh porcine eyes from 6 month old pigs (range 4 to 8 months) were obtained from a local abattoir prior to thermal treatment. Pig eyes were transported on ice and lens measurements were made within 36 hours post mortem. Fresh porcine eyes from 2-5 year old pigs were obtained from a supplier (VisionTech, Mesquite, TX) and shipped overnight on ice with the eyes placed in saline. Measurements from older lenses were made within 60 hours post mortem.
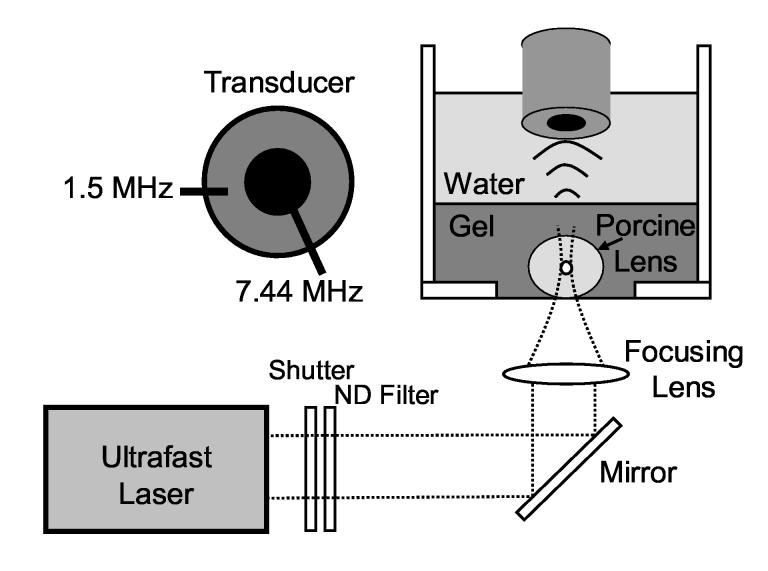
Lenses were removed immediately upon arrival without disruption of the lens capsule. Eye globes were cut near the optic nerve and the vitreous surrounding the posterior lens surface was carefully removed. Zonules were cut to gently dislodge the lens and adherent portions of the ciliary body were removed. Excised lenses were stored in a saline bath (0.9% sodium chloride, Abbott Laboratories, Abbott Park, IL) for several minutes prior to placement into a 5% w/w collagen gelatin (Type-A, Sigma-Aldrich, St. Louis, MO) phantom mixed with deionized water. The phantom fixed the lens at the bottom of a water tank directly above a glass cover slip (160-190 μm thick, Fisher Scientific, Hampton, NH), enabling insonation from above by the ultrasound transducer and illumination from below by the ultrafast laser, as shown in Fig. 1. The phantom with embedded lenses was stored in a refrigerator at 4° C and warmed to room temperature before acoustic radiation force measurements were made.
Fig. 1.
Experimental setup for acoustic radiation force measurements with in vitro porcine lenses. A cross-section of the ultrasound transducer is shown in the upper left corner.
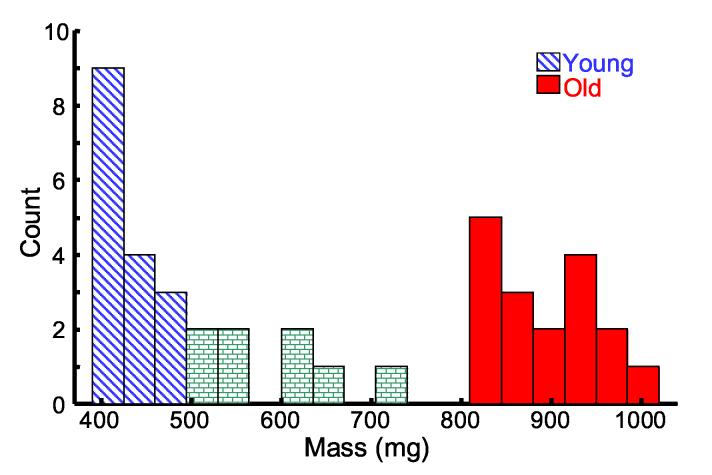
Porcine lens weight increases with age as the lens grows (Vilupuru and Glasser, 2001). Consequently, we recorded lens wet weight to distinguish age between samples. A histogram of lens wet weight from the 41 lenses is presented in Fig. 2. To compare young and old lenses, we averaged over two subsets of the total lens population. The young subset (approximately 6 months old) consisted of lenses with mass less than 500 mg (N = 16, mean = 423 mg, standard deviation = 34 mg) and the old subset (approximately 4-5 years old) consisted of lenses with mass greater than 800 mg (N = 17, mean = 881 mg, standard deviation = 66 mg). Lenses with mass between 500 mg and 800 mg were excluded from both the young and old subsets but were used to examine displacement trends with mass (Fig. 7). The mean equatorial diameter for the young lens population was 10.4 mm (standard deviation = 0.31 mm) compared to 12.3 mm (standard deviation = 0.36 mm) for the old lens population. The young lens population is displayed in diagonal blue bars and the old lens population is displayed in solid red bars in all subsequent figures.
Fig. 2.
* Histogram of the 41 porcine lens masses. Lenses with mass less than 500 mg were included in the young population (N = 16, diagonal blue), while lenses with mass greater than 800 mg comprised the old population (N = 17, solid red). Eight lenses (brick) were excluded from both the young and old subsets.
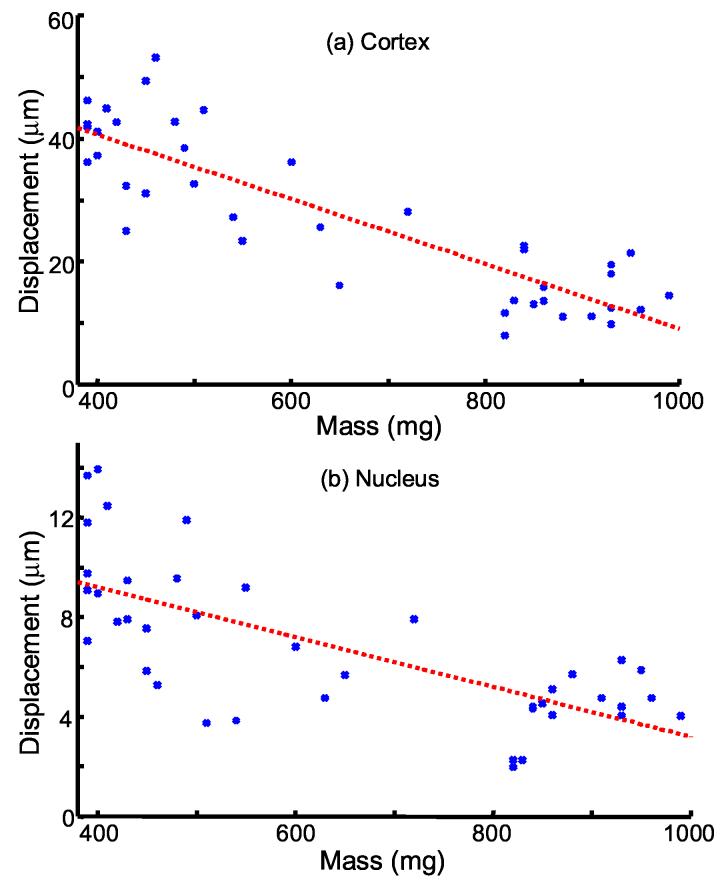
Fig. 7.
* Bubble displacements plotted versus porcine lens mass in the (a) cortex and (b) nucleus. Cortical displacements are averaged over median displacements at 3 and 4 mm from the lens center. Nuclear displacements are averaged over median displacements at 0 and 1 mm from the lens center. Dashed lines are linear fits to data in the cortex (R2=0.76, p < 1e-12) and nucleus (R2=0.51, p < 1e-6).
Laser-Induced Optical Breakdown (LIOB)
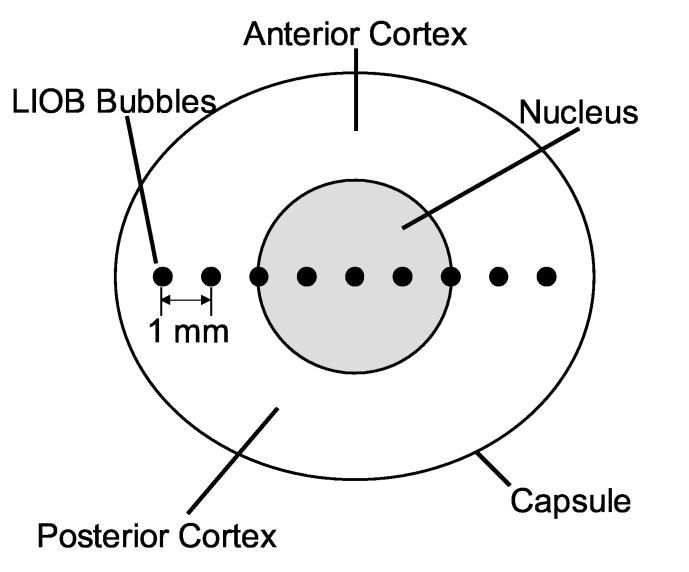
An ultrafast Nd:glass laser (IntraLase Corp., Irvine, CA), described previously (Erpelding et al., 2005a), used 800 fs, 1053 nm pulses to create target microbubbles by LIOB. A mechanical shutter controlled the number of laser pulses delivered (3,000-25,000), while a neutral density filter controlled the laser pulse energy. Laser pulses were directed through an f/2 lens at a 1.5 kHz repetition rate and pulse energy of 13 μJ (11.5 J/cm2). The lens center was located using ultrasound pulse-echoes and the height of the stage supporting the water tank was adjusted so that the foci of the ultrasound transducer and ultrafast laser coincided at the lens equatorial plane. For each lens, a microbubble was created at the lens center and 8 subsequent microbubbles were created at the same depth, spaced laterally by 1 mm intervals. Figure 3 illustrates LIOB bubble locations within an excised porcine lens.
Fig. 3.
Conceptual drawing illustrating LIOB bubbles within an excised porcine lens. LIOB bubbles, not drawn to scale, are spaced by 1 mm increments along the equatorial plane.
Microbubbles created within the porcine lens collapse due to surface tension from the surrounding tissue with a lifetime related to the maximum bubble size. Optical parameters such as laser pulse number and pulse fluence can be used to control bubble size and lifetime (Tse et al., 2005). Previous in vitro measurements using bright-field transmission microscopy show maximum bubble diameters in the range of 30 – 100 μm in porcine lenses using similar optical parameters as the present study (Erpelding et al., 2005b). Nonlinear radial oscillations of the bubble were avoided by using an insonation frequency much greater than the bubble resonance frequency. Bubble size was monitored during radiation force measurements using the magnitude of acoustic backscatter (Erpelding et al., 2005a, 2006), as described below.
Acoustic Radiation Force Measurements
Nine LIOB bubbles were created in each porcine lens at the positions given in Fig. 3. Several seconds after bubble creation, a series of nine 6.5 ms acoustic radiation force chirp bursts were applied consecutively to a single bubble at each position. A two-element confocal ultrasound transducer applied acoustic radiation force with the 1.5 MHz outer element while monitoring bubble displacement within the lens using pulse-echoes with the 7.44 MHz inner element. The foci of the ultrasound transducer and optical focusing lens were aligned axially and laterally. Chirp pulses with linear frequency sweeps from 1.4 MHz to 1.6 MHz were applied to reduce standing wave effects (Erpelding et al., 2006). Chirp pulses were generated by an HP 3314A function generator (Agilent Technologies, Palo Alto, CA) and amplified by 50 dB (ENI model 240L, MKS Instruments, Wilmington, MA).
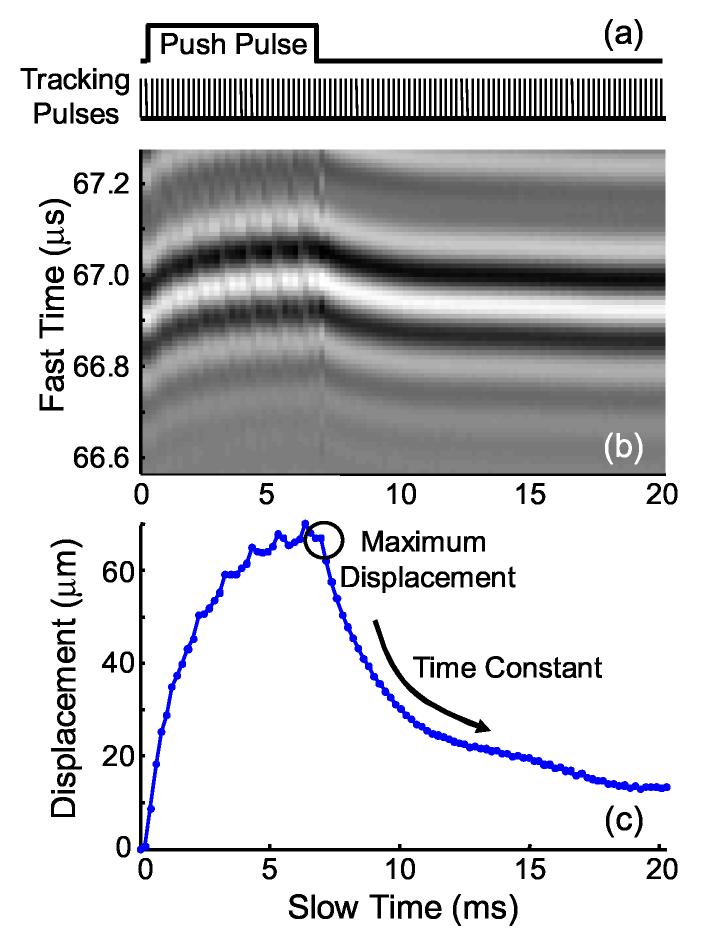
Ultrasound pulse-echoes (A-lines) from multiple firings at a fixed transducer position tracked bubble displacements at a pulse repetition period of 205 μs for 20.5 ms. A timing diagram for ultrasound tracking and acoustic radiation force pulses is given in Fig. 4(a). Individual A-lines can be stacked sequentially to form a wavefield or M-mode image, where slow time is the timing index for ultrasound firings and fast time is the ultrasound propagation time, or depth, along a single A-line. A sample wavefield image from an acoustic radiation force measurement is given in Fig. 4(b). In this example, acoustic radiation force was applied as a 6.7 ms tone burst, which has been suppressed from the image using a subtraction technique. Bubble displacements were calculated using a phase sensitive, cross-correlation method and corresponding displacements are given in Fig. 4(c).
Fig. 4.
* (a) Timing diagram for bubble-based acoustic radiation force experiments. The push pulse represents the radiation force burst duration applied to the outer transducer element. Tracking pulses represent ultrasound firings applied to the center transducer element used to monitor bubble position. (b) Wavefield plot of bubble displacement within a porcine lens in response to a 6.7 ms acoustic radiation force tone burst. Slow time refers to the ultrasound firing index and fast time refers to the ultrasound propagation dimension. (c) Corresponding bubble displacement calculated using a cross-correlation method with the initial bubble position.
Two parameters of interest were determined from acoustic radiation force measurements: the maximum bubble displacement and displacement relaxation time constant. The bubble displacement is proportional to local compliance and the relaxation time constant is indicative of local viscoelastic properties. After acoustic radiation force ends, bubbles return to their initial positions due to restoring forces in the surrounding lens fibers. All quoted displacements refer to the maximum bubble displacement measured using the ultrasound pulse-echo immediately following the acoustic radiation force pulse. Positive displacements correspond to displacements away from the transducer, in the direction of ultrasound propagation. The speed of sound in the lens was assumed to be 1641 m/s (Jansson and Kock, 1962) and all experiments were performed at room temperature. Time constants were determined by fitting the relaxation portion of the bubble displacement curve to an exponential decay function and represent the time needed for the displacement to recover 63% of its maximum displacement.
The acoustic output of the outer element was calibrated using a membrane hydrophone (GEC-Marconi, Chelmsford, UK). For this investigation, the peak rarefactional pressure was 2.1 MPa and spatial-peak, pulse-average intensity was 125 W/cm2.
3. Results
Bubble Displacements
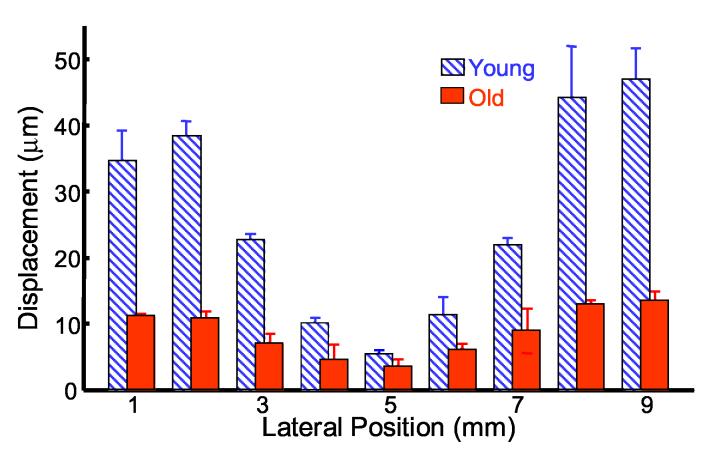
Maximum bubble displacements from nine consecutive acoustic radiation force bursts applied to a single bubble at each position in a porcine lens were measured. The median value of the nine maximum bubble displacements for a single bubble at each position for a typical young and typical old porcine lens are plotted in Fig. 5 to compare spatial and age-related differences. The lateral bubble position is plotted along the x-axis, with 5 mm signifying the lens center. Error bars represent the standard deviation for the nine maximum bubble displacements from consecutive acoustic radiation force bursts applied to a single bubble at each position. The wet weights for the young and old lenses were 400 mg and 960 mg, respectively. Both lenses have the smallest bubble displacements at the lens center and increasing displacements as the distance from the center increases, implying a stiff nucleus surrounded by a more compliant cortex. Both lenses show nearly symmetric displacements about the center, which is expected considering the arrangement of lens fibers. The young lens has larger bubble displacements at each position compared with the old lens, indicating a stiffer old lens as expected.
Fig. 5.
* Bubble displacements in a young (diagonal blue) and old (solid red) porcine lens in response to a 6.5 ms chirp burst. The centers of both lenses are located at 5 mm. Medians and standard deviations (error bars) are determined from maximum bubble displacements in response to consecutive acoustic radiation force burst applied to a single bubble.
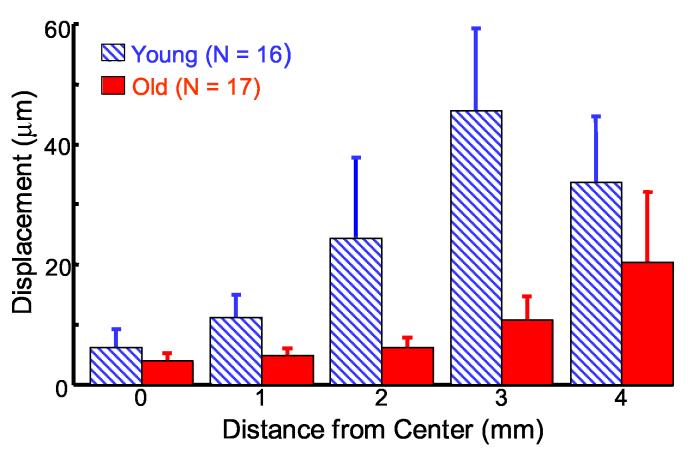
Young and old porcine lens populations were selected based on weight with mean masses of 423 mg and 881 mg for the young (N = 16) and old (N = 17) lenses, respectively. Bubble displacement results for the two porcine lens populations are plotted in Fig. 6 according to their distance from the lens center (0 mm). As a result, two displacements measurements are acquired at each distance from the lens center for a given lens, one from each side. Figure 6 plots the mean maximum bubble displacement at each position from multiple lens samples and error bars represent the standard deviation of displacements from multiple lens samples. A similar trend to the single lens results (Fig. 5) is observed in the overall results from the entire population (Fig. 6). Larger bubble displacements, indicative of more compliant tissue, arise for bubbles placed farther from the lens center.
Fig. 6.
* Mean bubble displacement in populations of young (diagonal blue) and old (solid red) porcine lenses. Error bars represent one standard deviation between multiple lenses.
There is a statistically significant difference (using a paired t-test, two-tail significance) in mean displacements between young and old populations at each position. P-values are as follows: 0 mm (p < 0.01), 1 mm (p < 0.0001), 2 mm (p< 0.0001), 3 mm (p < 0.0001), and 4 mm (p < 0.01). In the young lens population, there are statistically significant differences in the mean displacements from all adjacent positions, with the following p-values: between 0 and 1 mm (p < 0.0005), 1 and 2 mm (p < 0.001), 2 and 3 mm (p < 0.0005), and 3 and 4 mm (p < 0.05). In the old lens populations, statistically significant differences exist between the mean displacements for adjacent positions, except between 0 and 1 mm (p < 0.1). Significant p-values for the old lenses occur between 1 and 2 mm (p < 0.05), 2 and 3 mm (p < 0.0001), and 3 and 4 mm (p < 0.01). These results demonstrate that bubble-based acoustic radiation force can measure age-related differences in the mechanical properties of porcine lenses with good spatial resolution.
The overall bubble displacement trends in the porcine lens cortex and nucleus with increasing lens weight are presented in Fig. 7. The nucleus was represented by averaging the median displacements at 0 mm and 1 mm, while the cortex was represented by averaging the median displacements at 3 mm and 4 mm. In both lens regions, displacements decrease with increasing lens weight. The dashed lines in Fig. 7 are linear fits to measured displacements. Cortical displacements are a stronger fit (R2 = 0.76, p < 1e-12) than nuclear displacements (R2 = 0.51, p < 1e-6). Better agreement may have been achieved if the exact age of each lens was known rather than relying on lens mass.
Bubble Size Normalization
Bubble size needs to be reconciled when assessing mechanical properties using bubble-based acoustic radiation force. As described previously (Erpelding et al., 2005a), the maximum bubble displacement can be approximated by,
| (1) |
where x is the maximum bubble displacement, I is the acoustic intensity, r is the bubble radius, c is the sound speed, and E is the local Young's modulus. Correcting for bubble radius enables a direct relationship between displacement and Young's modulus since the acoustic intensity and sound speed are nearly constant in these experiments.
Relative bubble size can be monitored using the strength of the reflected ultrasound signal from the bubble surface (Erpelding et al., 2005a). Bubble radius is proportional to the square root of the integrated backscatter (SRIB) computed from the signal on the center element of the ultrasound transducer, according to Equation (2),
| (2) |
where b(t) is the backscattered bubble echo and integration is performed over the bubble echo duration. Results for bubble displacements normalized by the SRIB for the young and old lenses are presented in Fig. 8 and will be referred to as normalized displacements. Maximum bubble displacements from consecutive acoustic radiation force bursts applied to a single bubble at each location in a porcine lens are normalized by Eq. 2 (i.e. normalized maximum bubble displacements). Median values for normalized maximum bubble displacements are determined at each position in multiple lens samples. Figure 8 plots the mean and standard deviation of the normalized maximum bubble displacements. Normalized displacements are plotted relative to the mean displacement at the lens center for the old lenses.
Fig. 8.
* Bubble displacements normalized by bubble size for young (diagonal blue) and old (solid red) porcine lenses. Values are plotted relative to the mean normalized displacement at 0 mm for the old lenses. Error bars represent one standard deviation between multiple lenses.
As before, bubble displacements are larger in younger than older lenses at every lateral position. After accounting for differences in bubble size, statistically significant differences in the mean bubble displacements between the young and old lens populations are found at each lateral position except for the lens center (0 mm). P-values are as follows: 1 mm (p < 0.05), 2 mm (p <0.0005), 3 mm (p < 0.0001), 4 mm (p < 0.001). The overall trend remains that smaller displacements are observed in the older lens population, indicating an increase in porcine lens stiffness with age.
Spatial differences in normalized displacement within young and old lenses suggest a decreasing stiffness away from the lens center. Every adjacent position in the young lens population demonstrates a statistically significant difference in mean normalized displacement with the following p-values: between 0 and 1 mm (p < 0.05), 1 and 2 mm (p < 0.0005), 2 and 3 mm (p < 0.0001), and 3 and 4 mm (p < 0.05). The old lens population has significant differences between 1 and 2 mm (p < 0.05) and 2 and 3 mm (p < 0.0005), and no significant difference between 0 and 1 mm and between 3 and 4 mm (p < 0.1). However, mean normalized displacements monotonically increase for both populations, except at 4 mm in the young population. This discrepancy will be addressed in the discussion.
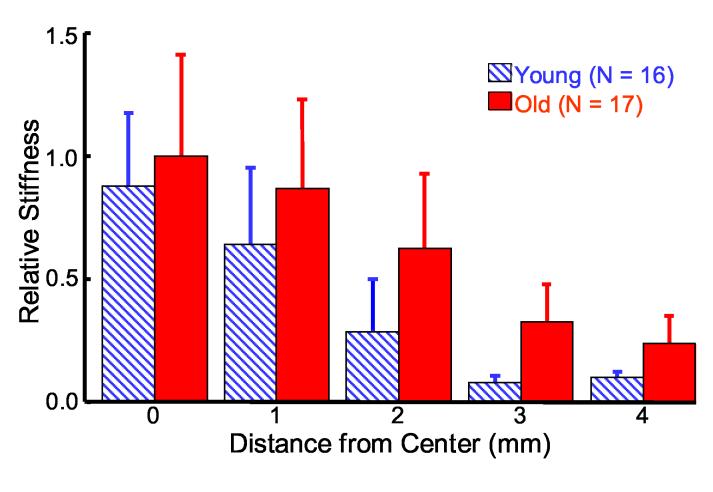
Relative Stiffness
Bubble displacement is inversely proportional to the local Young's modulus according to Equation (1). Thus, relative lens stiffness can be mapped by considering the inverse of displacement. A relative stiffness map for the young and old lenses is presented in Fig. 9 using normalized displacement and plotted relative to the lens center stiffness of the old lenses. Figure 9 confirms the expected trend for increasing stiffness with age and decreasing stiffness away from the lens center. Significant differences between young and old stiffness are observed at 2 mm (p < 0.001), 3 mm (p < 0.0001), and 4 mm (p < 0.0001) and no significant differences at 0 mm or 1 mm (p < 0.1). Adjacent stiffness values for young porcine lenses show significant differences between every position: 0 and 1 mm (p < 0.05), 1 and 2 mm (p < 0.001), 2 and 3 mm (p < 0.001), and 3 and 4 mm (0.05). Adjacent stiffness values for old porcine lenses demonstrate significant differences between 1 and 2 mm (p < 0.05), 2 and 3 mm (p <0.002) and no significant differences between 0 and 1 mm and 3 and 4 mm (p < 0.1).
Fig. 9.
* Relative stiffness map of young (diagonal blue) and old (solid red) porcine lenses according to the inverse of bubble displacements normalized for bubble size. Results are plotted relative to the mean stiffness at 0 mm for the old lenses. Error bars represent one standard deviation between multiple lenses.
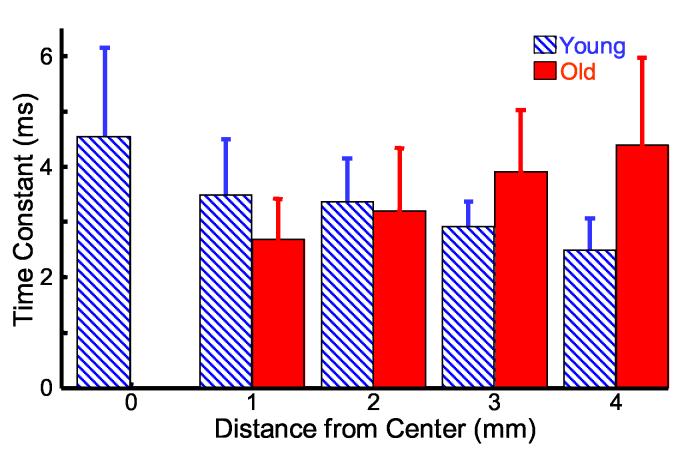
Time Constants
Different models exist for viscoelastic solids including the Voigt model, which consists of a parallel combination of a spring and dashpot (Fung 1981). The Voigt model has been previously applied to describe the response of soft tissue to acoustic radiation force (Erpelding et al., 2005; Walker et al., 2000). Applied forces are opposed by the sum of viscous and elastic forces, producing an exponential displacement time profile with a time constant given by the ratio of the viscous drag coefficient to the spring constant. In other words, the time constant measures the ratio of viscous forces to elastic forces.
If the porcine lens is approximated with the Voigt model, then bubble displacement relaxation after acoustic radiation force can be fit to a single time constant exponential decay. At each lateral position, displacement time profiles are normalized to the maximum displacement and averaged over consecutive acoustic radiation force experiments with the same bubble. A 10 ms window and a least-squared error approach were used to determine the time constants shown in Fig. 10. A cut-off mean squared error of 0.005 was selected to remove temporal responses not fitting a monotonically decreasing exponential function. Bubble responses at the center of old lenses are not adequately represented by this function, most likely due to normalizing the curves by the small maximum displacements observed at that position. For this reason, time constants at the center of the old lenses are withdrawn from Fig. 10. Overall, 64% of the lenses had sub-threshold mean squared error and were included in the time constant results (81% of young lenses, 50% of old lenses).
Fig. 10.
* Time constants for bubble displacement relaxation after acoustic radiation force for young (diagonal blue) and old (solid red) porcine lenses. Time constants are determined by a least-squared error fit of the data to an exponential decay function. Error bars represent one standard deviation between multiple lenses.
* Figs. 2, 4-10 are intended for color reproduction on the Web and in print.
Interestingly, mean time constants increase away from the lens center in the old lens population, while they decrease in the young lens population. Overall, 3-4 ms time constants are observed for bubble relaxation in porcine lenses. Significant differences in mean time constants between young and old lenses are observed at 1 mm (p < 0.05), 3 mm (p < 0.01), and 4 mm (p < 0.001). Significant decreases in adjacent mean time constants for young lenses are observed between 2 and 3 mm (p < 0.05) and 3 and 4 mm (p < 0.05). A longer time constant indicates a slower rate of change in displacement and greater viscous force relative to elastic restoring force.
4. Discussion
Bubble-based acoustic radiation force may be a promising tool to measure age-related changes in lens mechanical properties with high spatial resolution. Spatial resolution is related to bubble size, which can be controlled by laser fluence and pulse number (Tse et. al, 2005). Maximum bubble diameters were on the order of 30-100 μm according to previous measurements using bright field optical transmission microscopy (Erpelding et al., 2005b). The technique requires minimal damage to lens structures and avoids disruption of the lens capsule, which enables more realistic measurement of natural lens mechanical properties. Dynamic mechanical analysis requires lens sectioning to achieve spatial localization but cannot measure mechanical properties of the lens in its natural state (Heys et al., 2004; Weeber et al., 2005). Sectioning techniques work best with previously frozen tissues but the freezing process introduces another possible error source. With minimal disruption to lens fibers and noninvasive lens deformation, bubble-based acoustic radiation force has the potential for clinical in vivo applications. Future studies will need to address the long term bioeffects of bubble-based acoustic radiation force in live animal models.
The precision and minimal collateral damage associated with femtosecond LIOB suggests that bubble-based acoustic radiation force probes the mechanical properties of surrounding intact lens fibers. Krueger et al. (2005) examined cuts made by femtosecond LIOB in rabbit lenses using transmission electron microscopy. A 0.5-1 μm wide electron dense border was observed between the laser cut and surrounding lens fibers, which appeared normal and undisturbed. The results found by Krueger et al. (2005) raise confidence that bubble displacements are likely opposed by intact lens fibers and indicative of local viscoelastic properties.
Mapping porcine lens elastic properties with bubble-based acoustic radiation force demonstrated a stiffer nucleus and softer cortex. This is consistent with the results from Heys et al. (2004) for human lenses older than 40 years old. They also report a stiffer cortex than nucleus in lenses younger than 40 years old. No evidence was found in the present study of a softer lens nucleus than surrounding cortex. However, a shorter porcine lifespan may accelerate age-related changes, which may require testing newborn pigs to determine if a cross-over exists. Also, pigs do not undergo significant accommodation (Vilupuru and Glasser, 2001), so porcine lens stiffness profiles may better match presbyopic human lenses.
In the young lens population, a significant decrease in bubble displacement was observed between 3 and 4 mm from the lens center (Fig. 6 and Fig. 8). The mean displacement in the old lens population increases monotonically at each distance from the lens center. The most likely cause for the displacement decrease at 4 mm in the young lenses is boundary effects due to geometry. The lens grows continuously throughout life, so both weight and size increase with age. In this investigation, the mean equatorial diameter for the young lens population was 10.4 mm compared to 12.3 mm for the old lens population. Consequently, a bubble created 4 mm from the lens center is approximately 1.2 mm from the lens capsule in a young lens compared to 2.1 mm in an old lens. The closer distance to the more elastic capsule may affect the apparent stiffness around the bubble and geometric effects could possibly decrease the acoustic radiation force magnitude at the bubble. An alternative hypothesis is that smaller bubble displacements near the capsule in young lenses are reflective of cellular structure differences near the germinative region, where newly divided cells have yet to lose their membrane-bound organelles. The presence of membrane-bound organelles could serve to increase lens fiber stiffness in this region, reducing bubble displacements. Further experiments on lenses with and without capsules are needed to clarify the exact cause of smaller bubble displacements near the periphery of young porcine lenses.
Previous studies measuring human lens nucleus stiffness have shown a large increase with age (Fisher, 1971, 1973; Heys et al., 2004). A significant decrease in bubble displacement between young and old lenses was observed at the lens center (Fig. 6). However, there was no significant difference between young and old lenses at the lens center after normalizing displacements for bubble size (Fig. 8). Normalized displacements did show a significant difference 1mm away from the lens center, which still likely comprises part of the nucleus. Although there are no published reports of porcine lens stiffness changes with age, subjective assessment of porcine lenses by palpation suggests a stiffer lens nucleus in older samples. The apparent underestimate of the nuclear stiffness in the old lenses may be related to limitations in the current equipment to generate appropriate displacement. Higher intensity acoustic pulses or larger bubbles may be needed to assess nuclear stiffness. Another possibility is that estimating bubble radius using the SRIB may introduce errors that mask the true nuclear stiffness in old porcine lenses. The smallest displacements are observed at the lens center making it most susceptible to error. Estimating bubble radius using optical methods or nonlinear acoustical methods based on bubble resonant effects may be more accurate (Leighton et al., 1996).
Local sources of older porcine lenses were not available, so older eyes had to be shipped overnight from a commercial supplier. The longer transit caused a delayed experiment time for some older lenses relative to young lenses. Older porcine eyes were shipped in saline solution and packed with ice to keep tissue fresh during transit. Of the 17 old porcine lens samples, 6 lenses were experimented on within 36 hours post mortem, matching the experiment time for young lenses, and the remaining 11 lenses were experimented on within 60 hours post mortem. No statistically significant differences between bubble displacements were observed at 4 of the 5 lateral positions in old porcine lenses measured within 36 hours and 60 hours post mortem. The only significant difference in bubble displacements was measured 3 mm (p < 0.005) from the lens center. However, the lack of a global change in bubble displacements throughout the lens suggests the delay before experimentation did not significantly affect lens stiffness.
The results from this study ignore ultrasound attenuation. As ultrasound waves propagate through tissue they are attenuated due to scattering and absorption, reducing the acoustic intensity and radiation force exerted on a bubble. Previously, an in vitro study using human lenses extracted during cataract surgery found a weak correlation (R = 0.67) between hardness and ultrasound attenuation (Tabendeh, et al., 2000). This study was limited to a narrow age range assessed at an ultrasound frequency of 10 MHz. Ultrasound attenuation is frequency dependent and the relatively low push frequency (1.5 MHz) was selected to minimize attenuation in the present investigation.
Spatial differences in ultrasound attenuation along the lens equatorial plane are small considering the ultrasound frequency and small changes in propagation distance. By example, the largest attenuation difference would occur between the lens center and at 4 mm equatorial distance from the center. The difference in acoustic intensities for these positions would be approximately 20% using the attenuation slopes (dB/cm·MHz) reported by de Korte et al. (1994) for 4 month old porcine lenses. In comparison, the young lens used in Fig. 5 has a 750% change in displacements between the lens center (5 mm) and 4 mm away (averaged between 1 and 9 mm). Obviously, attenuation effects are small compared to the difference in bubble displacements. The ultrasound attenuation in porcine lenses from different ages may be related to stiffness changes but the magnitude of age-related attenuation changes are likely small, as well.
Bubble displacements were calculated assuming a constant speed of sound in porcine lenses of 1641 m/s. de Korte et al. (1994) report the speed of sound in 4 month old porcine lenses changes from roughly 1700 m/s at the center to 1600 m/s 4 mm away along the equatorial plane. Possible errors induced from the constant speed of sound assumption are small. Bubble displacements at the lens center may be underestimated by 3.5%, while displacements 4 mm from the lens center may be overestimated by 2.5%, yielding a total possible error between these extreme positions of only 6%. Possible errors induced by speed of sound changes are significantly smaller than displacement differences observed in this study. There are no reports of speed of sound changes in porcine lenses with age. In human lenses, it was reported that the speed of sound remains constant with age (Beers and Van der Heijde, 1994b), suggesting a similar trend for porcine lenses.
Relative stiffness maps (Fig. 9) illustrate differences in the spatial distribution of elastic properties between young and old porcine lenses. Converting bubble displacement to an absolute elastic modulus requires further development. Experiments using a gel phantom with concentric layers of uniform elasticity approximating the lens geometry and stiffness distribution could be used to compare bubble displacements and Young's modulus. A non-homogenous tissue-mimicking phantom would better match the physical environment of the lens. Experimental results could be compared to finite element models for further validation. Comparisons between bubble displacements in porcine lenses and direct mechanical measurements are difficult since comparable spatial resolution is difficult to achieve and slicing fresh lenses is problematic.
Bubble-based acoustic radiation force has been applied in a limited number of human lenses using the current method. A total of seven fresh human lenses from four autopsy donors were acquired from the National Disease Research Interchange (NDRI, Philadelphia, PA). Normalized bubble displacements in the lens nucleus of a 6 year old donor were nearly two orders of magnitude larger than those in the lens nucleus from three older donors (63, 65, and 70 years of age). This suggests that the young human lens was approximately two orders of magnitude more compliant than the older lenses. The lens nucleus in these samples was approximated by averaging displacement measurements made within 1 mm of the lens center. These preliminary results raise confidence that bubble-based acoustic radiation force can map age-related changes in the elastic properties of human lenses.
Bubble-based acoustic radiation force can be used to measure changes in lens mechanical properties during a possible presbyopia treatment. These treatments aim to restore accommodation using optical breakdown to increase lens compliance. Krueger et al. (2001) reported annular cuts in human cadaver lenses with an Nd:YAG laser increased lens compliance as measured by lens spinning measurements. Subsequent studies using a more precise femtosecond Ti:Sapphire laser showed no cataract generation 3 months after optical breakdown in a live rabbit model (Krueger et al., 2005). Previous research by Hollman et al. (2003) ultrasonically observed an increase in human lens deformation by radial stretching after LIOB treatment over a large grid using the same Nd:glass laser as the present study. Finally, Ripken et al. (2005) have created microcuts using a femtosecond Ti:Sapphire laser within porcine lenses and measured an increased deformability during lens spinning measurements.
Bubble-based acoustic radiation force may be well-suited to measure local changes in lens stiffness during laser treatment. It may be possible to use bubbles generated during laser treatment to directly assess lens stiffness changes. Animal models would be needed to correlate changes in local stiffness measured with bubble-based acoustic radiation force to an overall increase in accommodation due to restored deformability. If such a correlation can be demonstrated, then future clinical procedures could rely on bubble-based acoustic radiation force measurements alone for real-time treatment guidance and optimization.
Acknowledgements
We gratefully acknowledge the IntraLase Corporation for use of the ultrafast laser and support from National Institutes of Health grants EY015876 and EB003449 and the Whitaker Foundation. We thank NDRI for acquisition of human lenses.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errorsmaybe discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- van Alphen GWHM, Graebel WP. Elasticity of tissues involved in accommodation. Vision Res. 1991;31:1417–1438. doi: 10.1016/0042-6989(91)90061-9. [DOI] [PubMed] [Google Scholar]
- Beers APA, Van der Heijde GL. In vivo determination of the biomedical properties of the component elements of the accommodation mechanism. Vision Res. 1994a;34(21):2897–2905. doi: 10.1016/0042-6989(94)90058-2. [DOI] [PubMed] [Google Scholar]
- Beers APA, Van der Heijde GL. Presbyopia and velocity of sound in the lens. Optom. Vis. Sci. 1994b;71(4):250–253. doi: 10.1097/00006324-199404000-00004. [DOI] [PubMed] [Google Scholar]
- Burd HJ, Wilde GS, Judge SJ. Can reliable values of Young's modulus be determined from Fisher's (1971) spinning lens measurements. Vision Res. 2006;46(89):1346–1360. doi: 10.1016/j.visres.2005.07.012. [DOI] [PubMed] [Google Scholar]
- Czygan G, Hartung C. Mechanical testing of isolated senile human eye lens nuclei. Med. Eng. Phys. 1996;18(5):345–349. doi: 10.1016/1350-4533(95)00076-3. [DOI] [PubMed] [Google Scholar]
- Erpelding TN, Hollman KW, Juhasz T, O'Donnell M. Bubble-based acoustic radiation force for monitoring intraocular lens elasticity. IEEE Ultrason. Symp. Proc. 2004;1:732–735. [Google Scholar]
- Erpelding TN, Hollman KW, O'Donnell M. Bubble-based acoustic radiation force elasticity imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005a;52(6):971–979. doi: 10.1109/tuffc.2005.1504019. [DOI] [PubMed] [Google Scholar]
- Erpelding TN, Hollman KW, O'Donnell M. Spatially mapping the elastic properties of the lens using bubble-based acoustic radiation force. IEEE Ultrason. Symp. Proc. 2005b;1:613–616. [Google Scholar]
- Erpelding TN, Hollman KW, O'Donnell M. Bubble-based acoustic radiation force using chirp insonation to reduce standing wave effects. Ultrasound Med. Biol. 2006 doi: 10.1016/j.ultrasmedbio.2006.07.039. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan CH, Longtin JP. Modeling optical breakdown in dielectrics during ultrafast laser processing. Applied Optics. 2001;40(18):3124–3131. doi: 10.1364/ao.40.003124. [DOI] [PubMed] [Google Scholar]
- Fisher RF. The elastic constants of the human lens. J. Physiol. 1971;212:147–180. doi: 10.1113/jphysiol.1971.sp009315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RF. Presbyopia and the changes with age in the human crystalline lens. J. Physiol. 1973;228:765–779. doi: 10.1113/jphysiol.1973.sp010111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RF. The force of contraction of the human ciliary muscle during accommodation. J. Physiol. 1977;270:51–74. doi: 10.1113/jphysiol.1977.sp011938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung YC. Springer; New York: 1981. Biomechanics. [Google Scholar]
- Glasser A, Campbell MCW. Biometric, optical, and physical changes in the isolated human cyrstalline lens with age in relation to presbyopia. Vision Res. 1999;39(11):1991–2015. doi: 10.1016/s0042-6989(98)00283-1. [DOI] [PubMed] [Google Scholar]
- Glasser A, Croft MA, Kaufman PL. Aging of the human crystalline lens and presbyopia. Int. Ophthalmol. Clin. 2001;41(2):1–15. doi: 10.1097/00004397-200104000-00003. [DOI] [PubMed] [Google Scholar]
- Glezer EN, Schaffer CB, Nishimura N, Mazur E. Minimally disruptive laser-induced breakdown in water. Optics Letters. 1997;22(23):1817–1819. doi: 10.1364/ol.22.001817. [DOI] [PubMed] [Google Scholar]
- Heys KR, Cram SL, Truscott RJW. Massive increase in the stiffness of the human lens nucleus with age: the basis for presbyopia? Mol. Vision. 2004;10:956–63. [PubMed] [Google Scholar]
- Hollman KW, Lummis W, Herbert D, Liu HH, Juhasz T, O'Donnell M. Ultrasonic determination of laser manipulated changes in the elastic property of the intraocular lens. Proc. IEEE Ultrason. Symp. 2003;1:656–659. [Google Scholar]
- Jansson F, Kock E. Determination of the velocity of ultrasound in the human lens and vitreous. Acta Ophthalmol. 1962;40:420–433. doi: 10.1111/j.1755-3768.1962.tb02390.x. [DOI] [PubMed] [Google Scholar]
- Kikkawa Y, Sato T. Elastic properties of the lens. Exp. Eye Res. 1963;2:210–215. doi: 10.1016/s0014-4835(63)80015-9. [DOI] [PubMed] [Google Scholar]
- de Korte CL, van der Steen AFW, Thijssen JM, Duindam JJ, Otto C, Puppels GJ. Relation between local acoustic parameters and protein distribution in human and porcine eye lenses. Exp. Eye. Res. 1994;59:617–627. doi: 10.1006/exer.1994.1147. [DOI] [PubMed] [Google Scholar]
- Krueger RR, Sun XK, Stroh J, Myers R. Experimental increase in accommodative potential after neodymium:yttrium-aluminum-garnet laser photodisruption of paired cadever lenses. Ophthalmol. 2001;108(11):2122–2129. doi: 10.1016/s0161-6420(01)00834-x. [DOI] [PubMed] [Google Scholar]
- Krueger RR, Kuszak J, Lubatschowski H, Myers RI, Ripken T, Heisterkamp A. First safety study of femtosecond laser photodisruption in animal lenses: Tissue morphology and cataractogenesis. J. Cataract Refract. Surg. 2005;31(12):2386–2394. doi: 10.1016/j.jcrs.2005.05.034. [DOI] [PubMed] [Google Scholar]
- Leighton TG, Phelps AD, Ramble DG, Sharpe DA. Comparison of the abilities of eight acoustic techniques to detect and size a single bubble. Ultrasonics. 1996;34:661–667. [Google Scholar]
- Nightingale K, Scott Soo M, Nightingale R, Trahey G. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound Med. Biol. 2002;28(2):227–235. doi: 10.1016/s0301-5629(01)00499-9. [DOI] [PubMed] [Google Scholar]
- McGinty SJ, Truscott RJW. Presbyopia: the first stage of nuclear cataract? Ophthalmol. Res. 2006;38(3):137–148. doi: 10.1159/000090645. [DOI] [PubMed] [Google Scholar]
- Pau H, Kranz J. The increasing sclerosis of the human lens with age and its relevance to accommodation and presbyopia. Graefe's Arch. Clin. Exp. Opthl. 1991;229:294–296. doi: 10.1007/BF00167888. [DOI] [PubMed] [Google Scholar]
- Pierscionek BK. In vitro alteration of human lens curvature by radial stretching. Exp. Eye Res. 1993;57:629–635. doi: 10.1006/exer.1993.1168. [DOI] [PubMed] [Google Scholar]
- Pierscionek BK. Age-related response of human lenses to stretching forces. Exp. Eye Res. 1995;60:325–332. doi: 10.1016/s0014-4835(05)80114-9. [DOI] [PubMed] [Google Scholar]
- Ripken T, Oberheide U, Ziltz C, Ertmer W, Gerten G, Lubatschowski H. Fs-laser induced elasticity changes to improve presbyopic lens accommodation. Proc. SPIE Int. Soc. Opt. Eng. 2005;5688:278–287. [Google Scholar]
- Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med. Biol. 1998;24(9):1419–1435. doi: 10.1016/s0301-5629(98)00110-0. [DOI] [PubMed] [Google Scholar]
- Tabandeh H, Wilkins M, Thompson G, Nassiri D, Karim A. Hardness and ultrasonic characteristics of the human crystalline lens. J. Cataract Refract. Surg. 2000;26:838–841. doi: 10.1016/s0886-3350(00)00305-9. [DOI] [PubMed] [Google Scholar]
- Trahey GE, Palmeri ML, Bentley RC, Nightingale KR. Acoustic radiation force impulse imaging of the mechanical properties of arteries: in vivo and ex vivo results. Ultrasound Med. Biol. 2004;30(9):1163–1171. doi: 10.1016/j.ultrasmedbio.2004.07.022. [DOI] [PubMed] [Google Scholar]
- Tse C, Zohdy MJ, Ye JY, Norris TB, Balogh LP, Hollman KW, O'Donnell M. Acoustic detection of controlled laser-induced microbubble creation in gelatin. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005;52(11):1962–1969. doi: 10.1109/tuffc.2005.1561665. [DOI] [PubMed] [Google Scholar]
- Vilupuru AS, Glasser A. Optical and biometric relationships of the isolated pig crystalline lens. Ophthal. Physiol. Opt. 2001;21(4):296–311. doi: 10.1046/j.1475-1313.2001.00593.x. [DOI] [PubMed] [Google Scholar]
- Vogel A, Venugopalan V. Mechanisms of pulsed laser ablation of biological tissues. Chem. Rev. 2003;103:577–644. doi: 10.1021/cr010379n. [DOI] [PubMed] [Google Scholar]
- Walker WF. Internal deformation of a uniform elastic solid by acoustic radiation force. J. Acoust. Soc. Am. 1999;105(4):2508–2518. doi: 10.1121/1.426854. [DOI] [PubMed] [Google Scholar]
- Walker WF, Fernandez FJ, Negron LA. A method of imaging viscoelastic parameters with acoustic radiation force. Phys. Med. Biol. 2000;45:1437–1447. doi: 10.1088/0031-9155/45/6/303. [DOI] [PubMed] [Google Scholar]
- Weeber HA, Eckert G, Soergel F, Meyer CH, Pechhold W, van der Heijde RGL. Dynamic mechanical properties of human lenses. Exp. Eye Res. 2005;80(3):425–434. doi: 10.1016/j.exer.2004.10.010. [DOI] [PubMed] [Google Scholar]